Toward the Dynamic Modeling of Transition Problems: The Case of Electric Mobility
Abstract
1. Introduction
2. Theoretical Background
2.1. Technological Innovation Systems
Contextualization of TIS in the E-Mobility Sector
2.2. The Unified Theory of Acceptance and Use of Technology
Contextualization of UTAUT in E-Mobility System
3. Method: System Dynamics Modeling
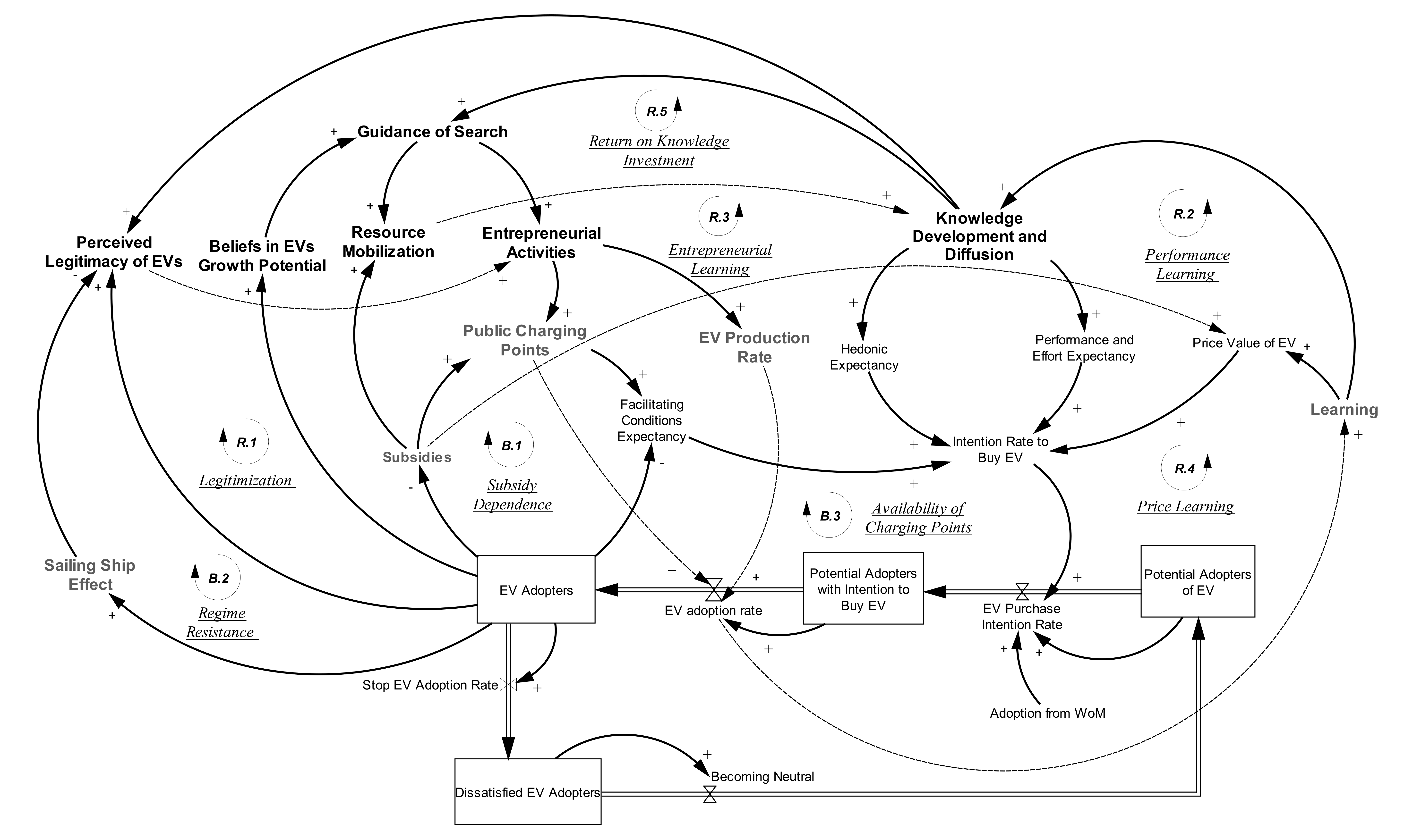
3.1. Model Description
3.2. Dynamics of the Entity Types
3.2.1. Entity Type: E-Mobility Innovation System
3.2.2. Entity Type: Charging Points
3.2.3. Entity Type: EV Pricing
3.2.4. Entity Type: EV Related Subsidies
3.2.5. Entity Type: EV Purchasers
3.3. Experimental Setup
4. Results
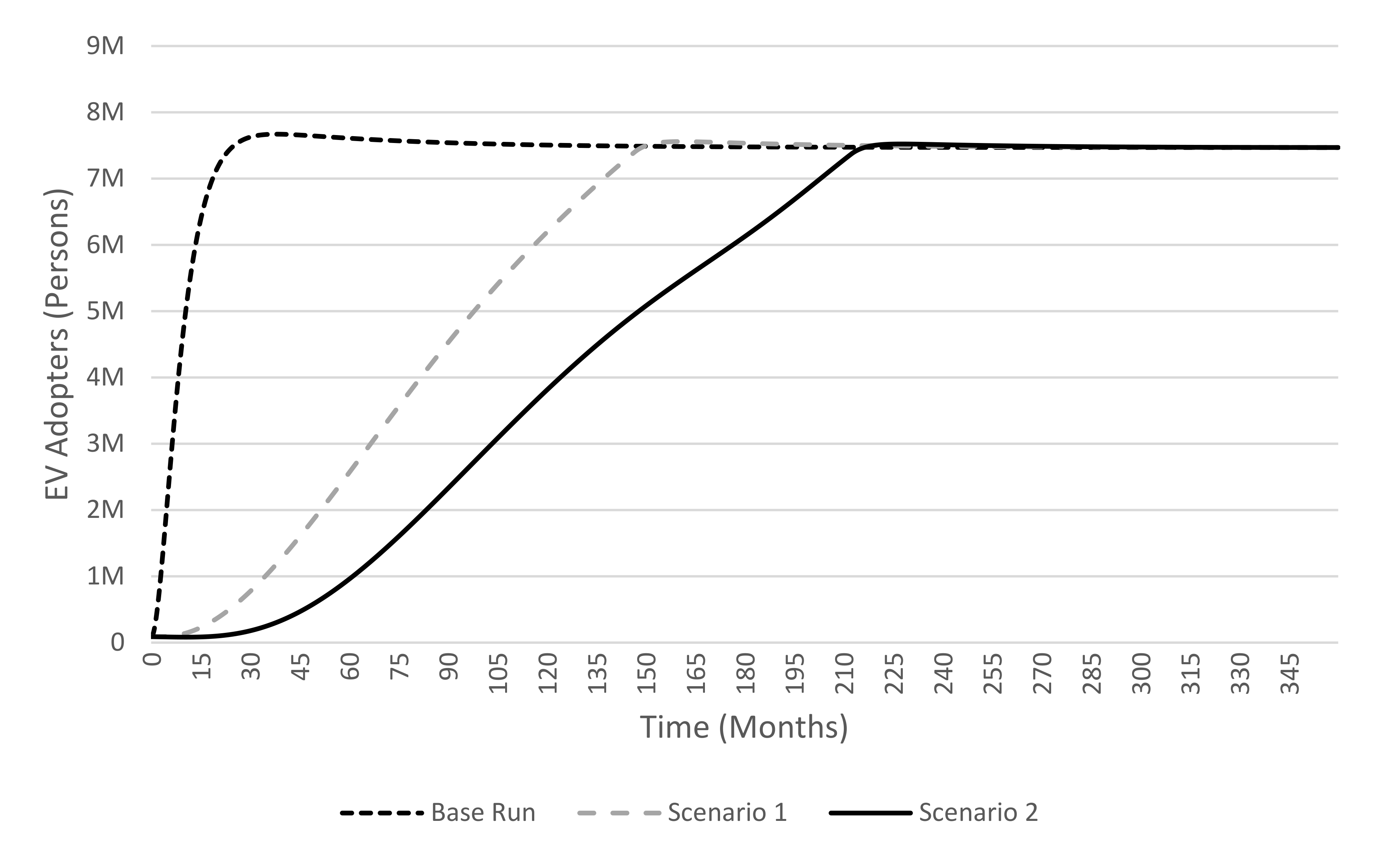
4.1. Base Run
4.2. Analysis of the Scenario Results
4.2.1. Scenario 1
4.2.2. Scenario 2
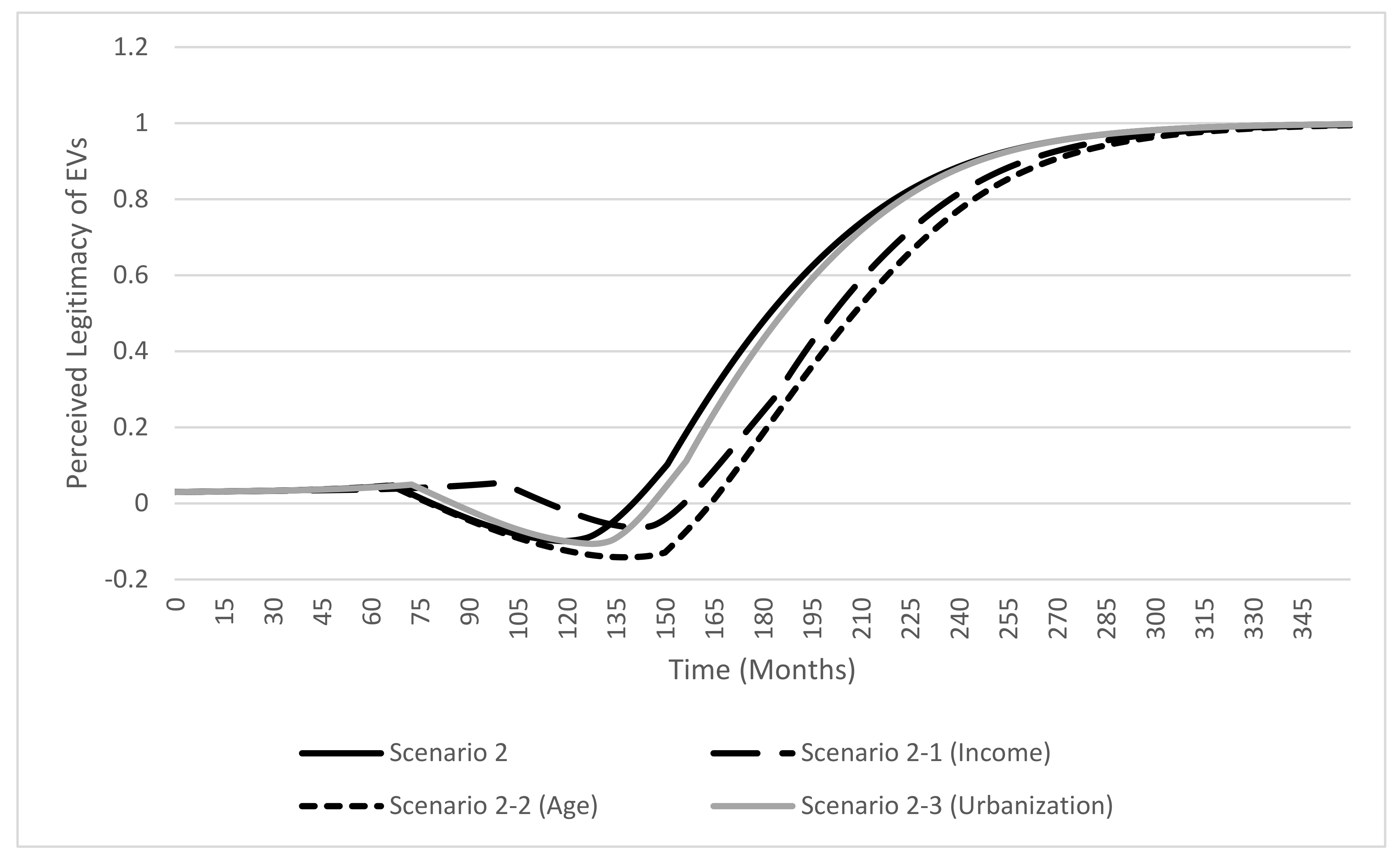
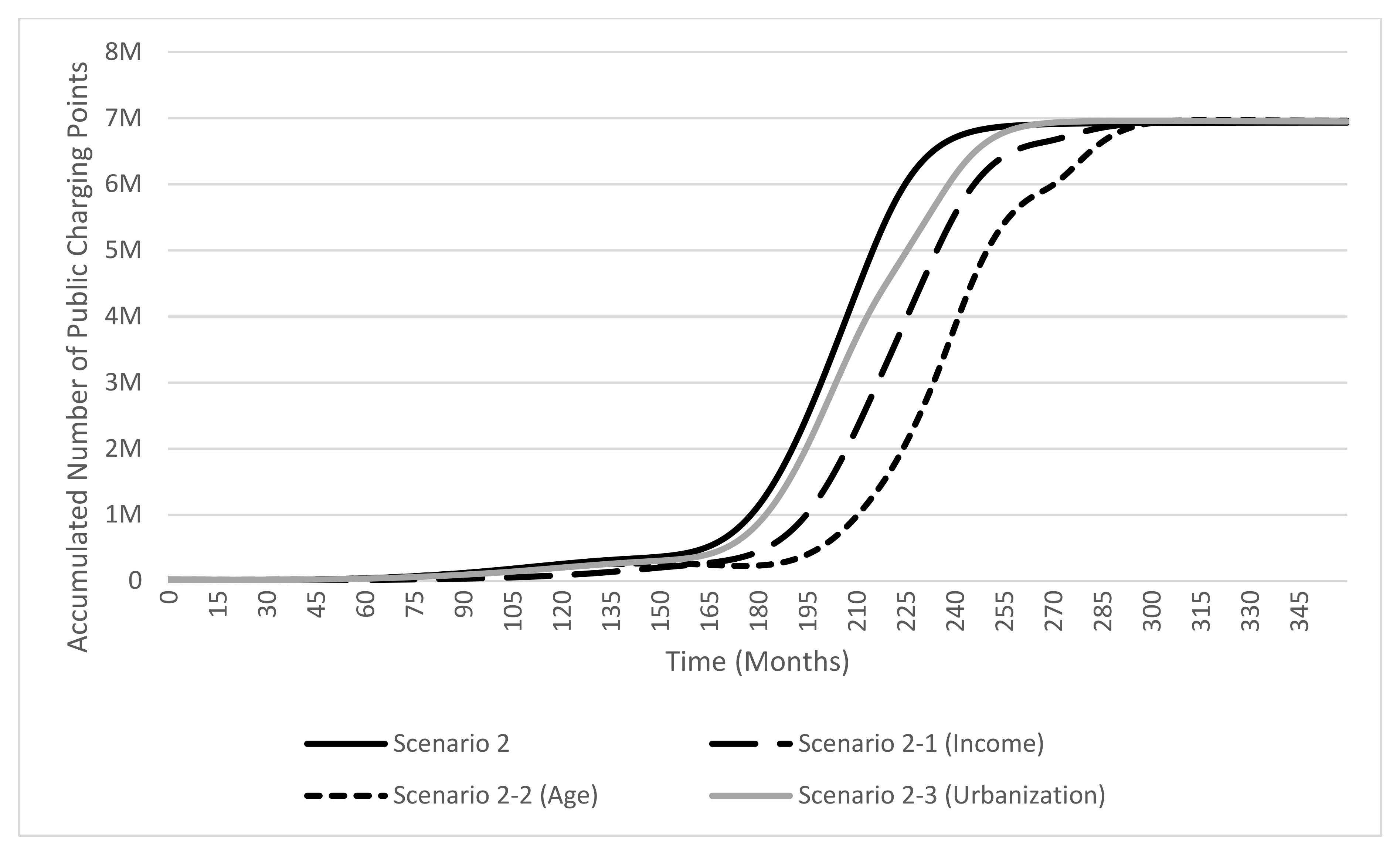
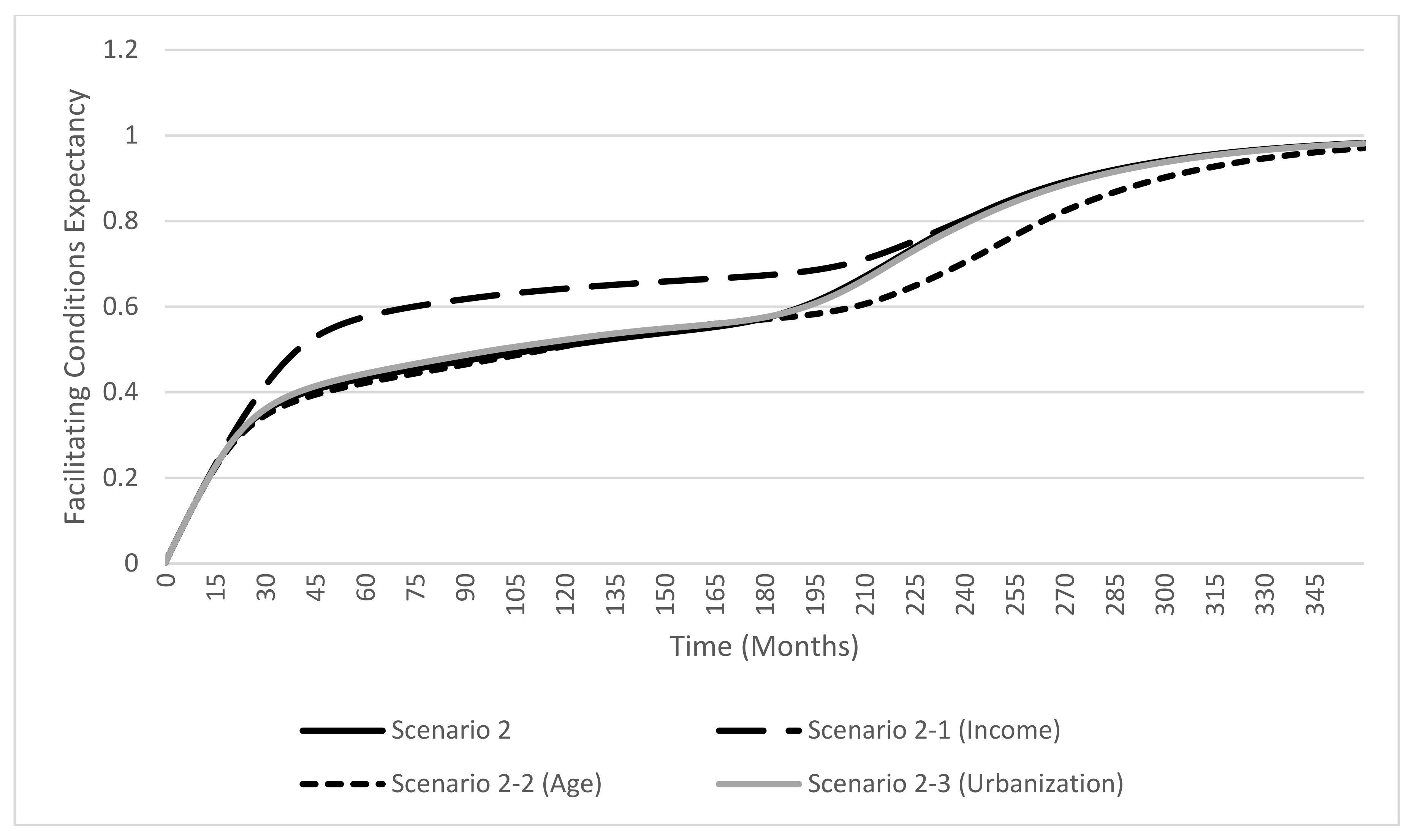
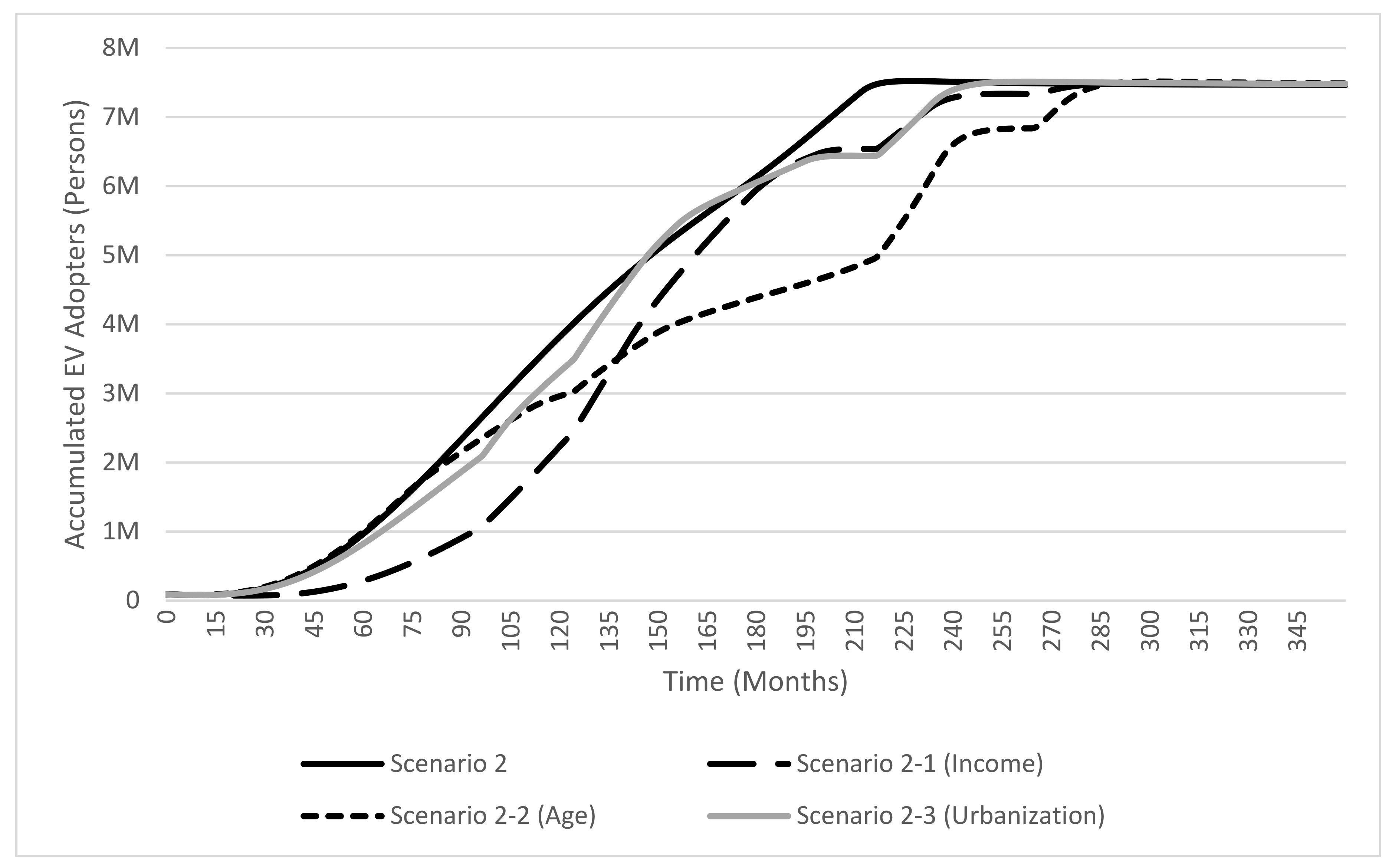
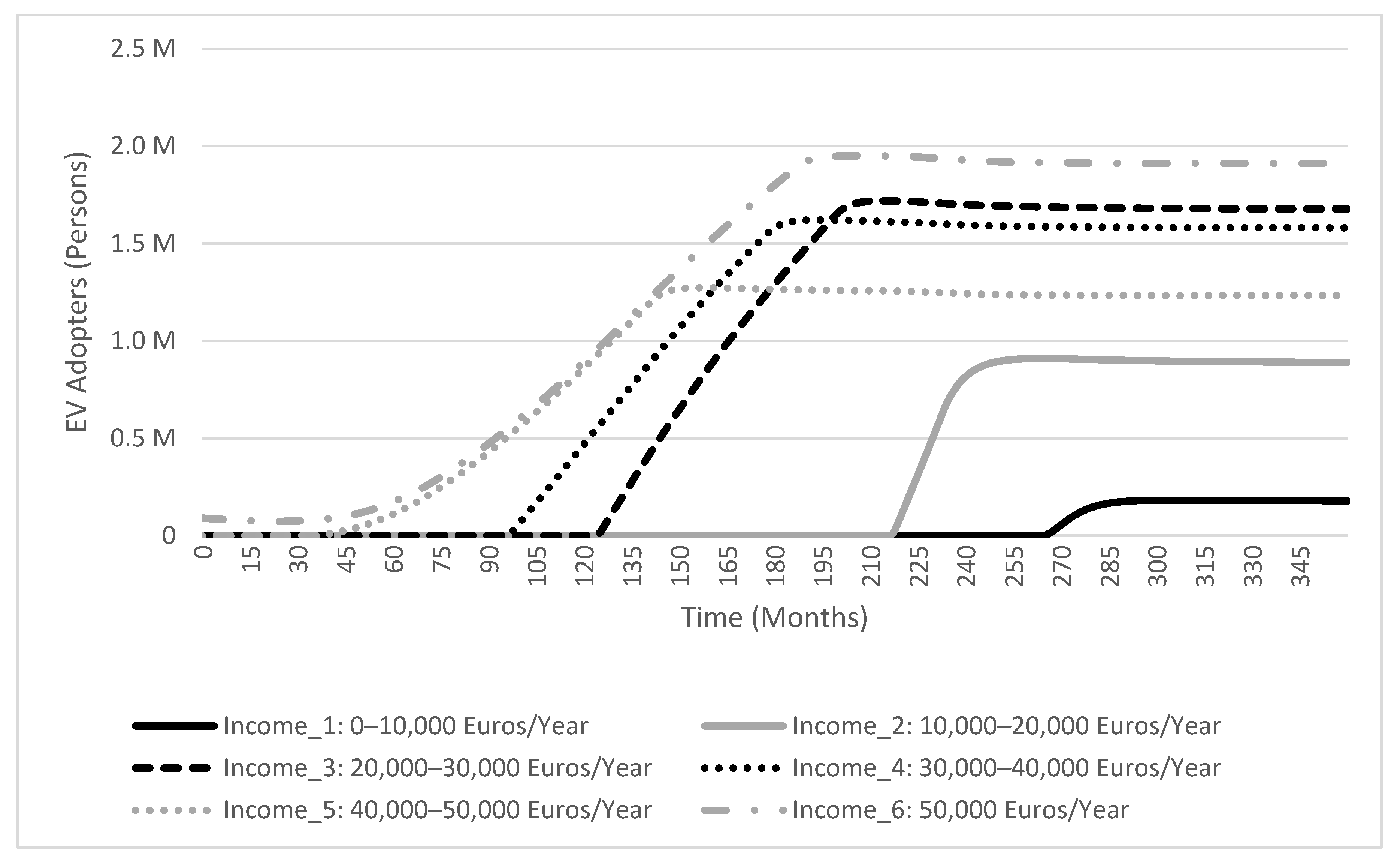
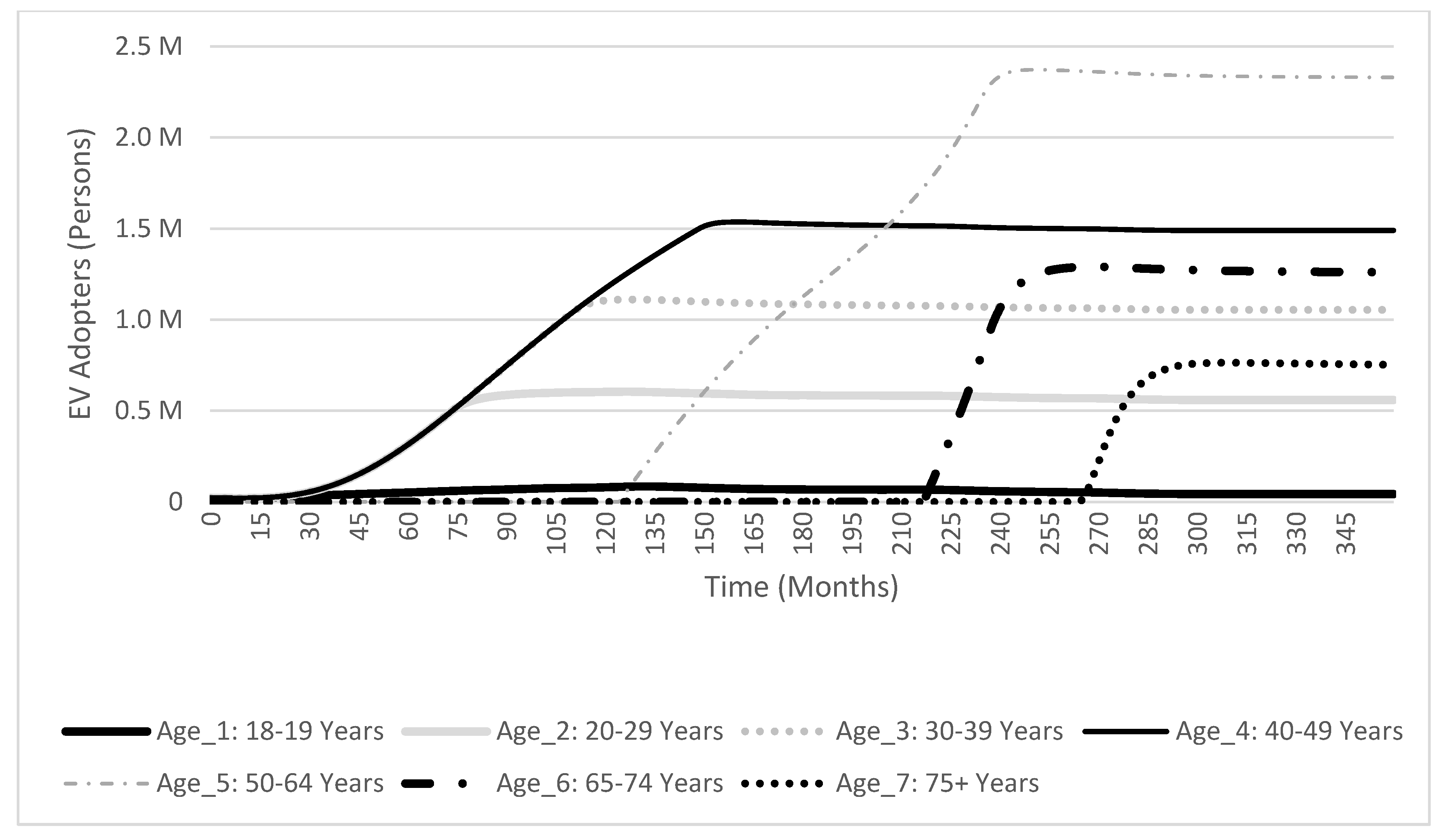
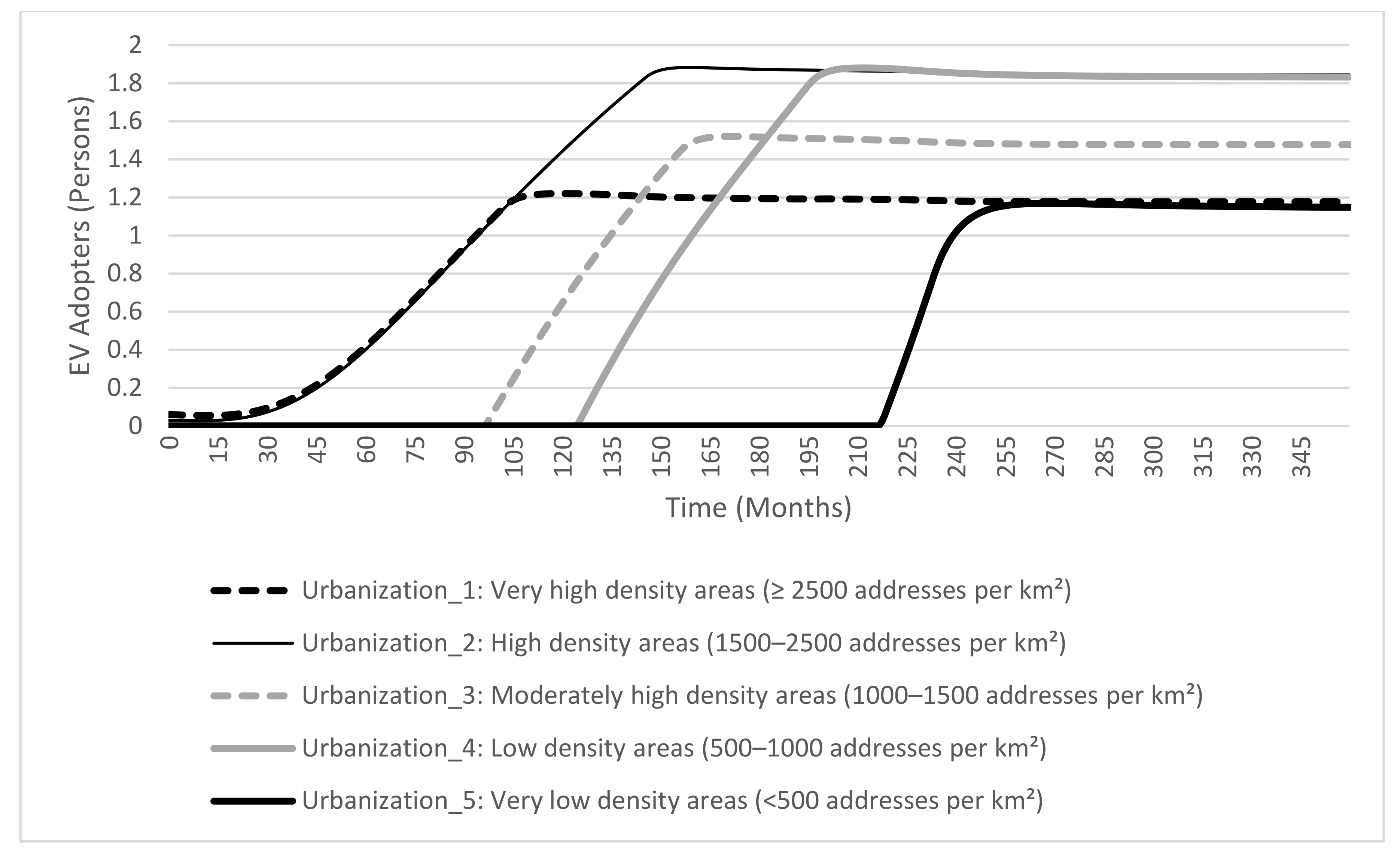
4.2.3. Scenarios 2-1, 2-2, and 2-3
5. Discussion and Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- European Commission. European Transport Policy for 2010: Time to Decide; White Paper; European Commission: Brussels, Belgium, 2001. [Google Scholar]
- Köhler, J.; Whitmarsh, L.; Nykvist, B.; Schilperoord, M.; Bergman, N.; Haxeltine, A. A Transitions model for sustainable mobility. Ecol. Econ. 2009, 68, 2985–2995. [Google Scholar] [CrossRef]
- European Commission. A Sustainable Europe for a Better World: A European Union Strategy for Sustainable Development; COM (2001) 264 final; European Commission: Brussels, Belgium, 2001. [Google Scholar]
- Holden, E.; Linnerud, K.; Banister, D. Sustainable passenger transport: Back to Brundtland. Transp. Res. Part A Policy Pract. 2013, 54, 67–77. [Google Scholar] [CrossRef]
- Banister, D. The sustainable mobility paradigm. Transp. Policy 2008, 15, 73–80. [Google Scholar] [CrossRef]
- Berger, G.; Feindt, P.H.; Holden, E.; Rubik, F. Sustainable Mobility—Challenges for a Complex Transition. J. Environ. Policy Plan. 2014, 16, 303–320. [Google Scholar] [CrossRef]
- Castillo, N.H.; Pitfield, D.E. ELASTIC—A methodological framework for identifying and selecting sustainable transport indicators. Transp. Res. Part D Transp. Environ. 2010, 15, 179–188. [Google Scholar] [CrossRef]
- Litman, T.; Burwell, D. Issues in sustainable transportation. Int. J. Glob. Environ. Issues (IJGENVI) 2006, 6, 331. [Google Scholar] [CrossRef]
- Høyer, K.G. The history of alternative fuels in transportation: The case of electric and hybrid cars. Util. Policy 2008, 16, 63–71. [Google Scholar] [CrossRef]
- Geels, F.W. A socio-technical analysis of low-carbon transitions: Introducing the multi-level perspective into transport studies. J. Transp. Geogr. 2012, 24, 471–482. [Google Scholar] [CrossRef]
- Dijk, M.; Orsato, R.J.; Kemp, R. The emergence of an electric mobility trajectory. Energy Policy 2013, 52, 135–145. [Google Scholar] [CrossRef]
- Yigitcanlar, T.; Fabian, L.; Coiacetto, E. Challenges to Urban Transport Sustainability and Smart Transport in a Tourist City: The Gold Coast, Australia. Open Transp. J. 2008, 2, 29–46. [Google Scholar] [CrossRef]
- Lipman, T.E.; Delucchi, M.A. A retail and lifecycle cost analysis of hybrid electric vehicles. Transp. Res. Part D Transp. Environ. 2006, 11, 115–132. [Google Scholar] [CrossRef]
- Yeh, S. An empirical analysis on the adoption of alternative fuel vehicles: The case of natural gas vehicles. Energy Policy 2007, 35, 5865–5875. [Google Scholar] [CrossRef]
- Kühne, R. Electric buses—An energy efficient urban transportation means. Energy 2010, 35, 4510–4513. [Google Scholar] [CrossRef]
- Tsang, F.; Pedersen, J.S.; Wooding, S.; Potoglou, D. Bringing the Electric Vehicle to the Mass Market: A Review of Barriers, Facilitators and Policy Interventions; Rand Europe: Cambridge, UK, 2012. [Google Scholar]
- Geels, F.W.; Kemp, R.; Dudley, G.; Lyons, G. (Eds.) Automobility in Transition? A Socio-Technical Analysis of Sustainable Transport; Routledge: New York, NY, USA, 2012. [Google Scholar]
- Unruh, G.C. Understanding carbon lock-in. Energy Policy 2000, 28, 817–830. [Google Scholar] [CrossRef]
- Elzen, B.; Wieczorek, A. Transitions towards sustainability through system innovation. Technol. Forecast. Soc. Chang. 2005, 72, 651–661. [Google Scholar] [CrossRef]
- Sierzchula, W.; Bakker, S.; Maat, K.; Van Wee, B. The competitive environment of electric vehicles: An analysis of prototype and production models. Environ. Innov. Soc. Transit. 2012, 2, 49–65. [Google Scholar] [CrossRef]
- Lewe, J.-H.; Hivin, L.; Mavris, D.N. A multi-paradigm approach to system dynamics modeling of intercity transportation. Transp. Res. Part E Logist. Transp. Rev. 2014, 71, 188–202. [Google Scholar] [CrossRef]
- Pasaoglu, G.; Harrison, G.; Jones, L.; Hill, A.; Beaudet, A.; Thiel, C. A system dynamics based market agent model simulating future powertrain technology transition: Scenarios in the EU light duty vehicle road transport sector. Technol. Forecast. Soc. Chang. 2016, 104, 133–146. [Google Scholar] [CrossRef]
- Harrison, G.; Thiel, C. An exploratory policy analysis of electric vehicle sales competition and sensitivity to infrastructure in Europe. Technol. Forecast. Soc. Chang. 2017, 114, 165–178. [Google Scholar] [CrossRef]
- Shepherd, S. A review of system dynamics models applied in transportation. Transp. B Transp. Dyn. 2014, 2, 83–105. [Google Scholar] [CrossRef]
- Bergek, A.; Jacobsson, S.; Carlsson, B.; Lindmark, S.; Rickne, A. Analyzing the functional dynamics of technological innovation systems: A scheme of analysis. Res. Policy 2008, 37, 407–429. [Google Scholar] [CrossRef]
- Venkatesh, V.; Thong, J.Y.L.; Xu, X. Consumer Acceptance and Use of Information Technology: Extending the Unified Theory of Acceptance and Use of Technology. MIS Q. 2012, 36, 157–178. [Google Scholar] [CrossRef]
- Markard, J.; Raven, R.; Truffer, B. Sustainability transitions: An emerging field of research and its prospects. Res. Policy 2012, 41, 955–967. [Google Scholar] [CrossRef]
- Köhler, J.; Raven, R.; Walrave, B. Advancing the analysis of technological innovation systems dynamics: Introduction to the special issue. Technol. Forecast. Soc. Chang. 2020, 158, 120040. [Google Scholar] [CrossRef]
- Markard, J.; Truffer, B. Technological innovation systems and the multi-level perspective: Towards an integrated framework. Res. Policy 2008, 37, 596–615. [Google Scholar] [CrossRef]
- Galli, R.; Teubal, M. Paradigmatic Shifts in National Innovation Systems. In Systems of Innovation. Technologies, Institutions and Organizations; Coombs, R., Ed.; Pinter: London, UK, 1997; pp. 342–370. [Google Scholar]
- Rickne, A. New Technology-Based Firms and Industrial Dynamics: Evidence from the Technological System of Biomaterials in Sweden, Ohio and Massachusetts. Ph.D. Thesis, Department of Industrial Dynamics, Chalmers University of Technology, Gothenburg, Sweden, 2000. [Google Scholar]
- Johnson, A.; Jacobsson, S. Inducement and Blocking Mechanisms in the Development of a New Industry: The Case of Renewable Energy Technology in Sweden. In Technology and the Market: Demand, Users and Innovation; Coombs, R., Green, K., Richards, A., Walsh, V., Eds.; Edward Elgar Pub: Cheltenham, UK, 2001. [Google Scholar]
- Bergek, A. Shaping and Exploiting Technological Opportunities: The Case of Renewable Energy Technology in Sweden. Ph.D. Thesis, Department of Industrial Dynamics, Chalmers University of Technology, Gothenburg, Sweden, 2000. [Google Scholar]
- Bergek, A.; Jacobsson, S. The emergence of a growth industry: A comparative analysis of the German, Dutch and Swedish wind turbine industries. In Change, Transformation and Development; Metcalfe, J.S., Cantner, U., Eds.; Springer Science and Business Media LLC: Heidelberg, Germany, 2003; pp. 197–227. [Google Scholar]
- Liu, X.; White, S. Comparing innovation systems: A framework and application to China’s transitional context. Res. Policy 2001, 30, 1091–1114. [Google Scholar] [CrossRef]
- Hekkert, M.; Suurs, R.; Negro, S.; Kuhlmann, S.; Smits, R. Functions of innovation systems: A new approach for analysing technological change. Technol. Forecast. Soc. Chang. 2007, 74, 413–432. [Google Scholar] [CrossRef]
- Bergek, A.; Hekkert, M.; Jacobssen, S. Functions in innovation systems: A framework for analysing energy system dynamics and identifying goals for system building activities by entrepreneurs and policymakers. In Innovation for a Low Carbon Economy: Economic, Institutional and Management Approaches; Foxon, T.J., Köhler, J., Oughton, C., Eds.; Edward Elgar: Cheltenham, UK, 2008. [Google Scholar]
- Weber, K.M.; Truffer, B. Moving innovation systems research to the next level: Towards an integrative agenda. Oxf. Rev. Econ. Policy 2017, 33, 101–121. [Google Scholar] [CrossRef]
- Bergek, A. Technological innovation systems: A review of recent findings and suggestions for future research. In Handbook of Sustainable Innovation; Boons, F., McMeekin, A., Eds.; Edward Elgar: Cheltenham, UK, 2019; Chapter 11; pp. 200–218. [Google Scholar]
- Suurs, R.A.A. Motors of Sustainable Innovation: Toward a Theory on the Dynamics of Technological Innovation Systems; Utrecht University: Utrecht, The Netherlands, 2009. [Google Scholar]
- Walrave, B.; Raven, R. Modelling the dynamics of technological innovation systems. Res. Policy 2016, 45, 1833–1844. [Google Scholar] [CrossRef]
- Wieczorek, A.J.; Hekkert, M.P. Systemic instruments for systemic innovation problems: A framework for policy makers and innovation scholars. Sci. Public Policy 2012, 39, 74–87. [Google Scholar] [CrossRef]
- Williams, M.D.; Rana, N.P.; Dwivedi, Y.K.; Lal, B. Is UTAUT really used or just cited for the sake of it? A systematic review of citations of UTAUT’s originating article. In Proceedings of the 19th European Conference on Information systems, Helsinki, Finland, 9–11 June 2011; p. 231. [Google Scholar]
- Taiwo, A.A.; Downe, A.G. The theory of user acceptance and use of technology (UTAUT): A meta-analytic review of empirical findings. J. Theor. Appl. Inform. Technol. 2013, 49, 48–58. [Google Scholar]
- Khechine, H.; Lakhal, S.; Ndjambou, P. A meta-analysis of the UTAUT model: Eleven years later. Can. J. Adm. Sci. Rev. Can. Sci. Adm. 2016, 33, 138–152. [Google Scholar] [CrossRef]
- Venkatesh, V.; Morris, M.G.; Davis, G.B.; Davis, F.D. User acceptance of information technology: Toward a unified view. MIS Q. 2003, 27, 425–478. [Google Scholar] [CrossRef]
- Ajzen, I.; Fishbein, M. Understanding Attitudes and Predicting Social Behavior; Prentice-Hall: Englewood Cliffs, NJ, USA, 1980. [Google Scholar]
- Fishbein, M.; Ajzen, I. Belief, Attitude, Intention and Behavior: An Introduction to Theory and Research; Addison-Wesley: Reading, MA, USA, 1975. [Google Scholar]
- Davis, F.D. Perceived usefulness, perceived ease of use, and user acceptance of information technology. MIS Q. 1989, 13, 319–339. [Google Scholar] [CrossRef]
- Davis, F.D.; Bagozzi, R.P.; Warshaw, P.R. User acceptance of computer technology: A comparison of two theoretical models. Manag. Sci. 1989, 35, 982–1003. [Google Scholar] [CrossRef]
- Ajzen, I. The theory of planned behavior. Organ. Behav. Hum. Decis. Process. 1991, 50, 179–211. [Google Scholar] [CrossRef]
- Taylor, S.; Todd, P. Assessing IT Usage: The Role of Prior Experience. MIS Q. 1995, 19, 561–570. [Google Scholar] [CrossRef]
- Taylor, S.; Todd, P.A. Understanding Information Technology Usage: A Test of Competing Models. Inf. Syst. Res. 1995, 6, 144–176. [Google Scholar] [CrossRef]
- Vallerand, R.J. Toward a Hierarchical Model of Intrinsic and Extrinsic Motivation. In Advances in Experimental Social Psychology; Zanna, M.P., Ed.; Elsevier: Amsterdam, The Netherlands, 1997; Volume 29, pp. 271–360. [Google Scholar]
- Venkatesh, V.; Speier, C. Computer Technology Training in the Workplace: A Longitudinal Investigation of the Effect of Mood. Organ. Behav. Hum. Decis. Process. 1999, 79, 1–28. [Google Scholar] [CrossRef]
- Triandis, H.C. Interpersonal Behavior; Brooks/Cole Publishing Company: Monterey, CA, USA, 1977. [Google Scholar]
- Thompson, R.L.; Higgins, C.A.; Howell, J.M. Personal computing: Toward a conceptual model of utilization. MIS Q. 1991, 15, 125–143. [Google Scholar] [CrossRef]
- Rogers, E.M. Diffusion of Innovations, 4th ed.; Free Press: New York, NY, USA, 1995. [Google Scholar]
- Bandura, A. Social Foundations of Thought and Action: A Social Cognitive Theory; Prentice-Hall, Inc.: Upper Saddle River, NJ, USA, 1986. [Google Scholar]
- Compeau, D.R.; Higgins, C.A. Computer Self-Efficacy: Development of a Measure and Initial Test. MIS Q. 1995, 19, 189–211. [Google Scholar] [CrossRef]
- Browne, S.A.; Venkatesh, V. Model of adoption of technology in households: A baseline model test and extension incorporating household life cycle. MIS Quarterly 2005, 29, 399–462. Available online: https://www.jstor.org/stable/25148690 (accessed on 1 May 2018).
- Sovacool, B.K. Experts, theories, and electric mobility transitions: Toward an integrated conceptual framework for the adoption of electric vehicles. Energy Res. Soc. Sci. 2017, 27, 78–95. [Google Scholar] [CrossRef]
- Bass, F.M. A New Product Growth for Model Consumer Durables. Manag. Sci. 1969, 15, 215–227. [Google Scholar] [CrossRef]
- Herr, P.M.; Kardes, F.R.; Kim, J. Effects of Word-of-Mouth and Product-Attribute Information on Persuasion: An Accessibility-Diagnosticity Perspective. J. Consum. Res. 1991, 17, 454–462. [Google Scholar] [CrossRef]
- Gärling, A.; Thøgersen, J. Marketing of electric vehicles. Bus. Strat. Environ. 2001, 10, 53–65. [Google Scholar] [CrossRef]
- Carley, S.; Krause, R.M.; Lane, B.W.; Graham, J.D. Intent to purchase a plug-in electric vehicle: A survey of early impressions in large US cites. Transp. Res. Part D Transp. Environ. 2013, 18, 39–45. [Google Scholar] [CrossRef]
- Holtz, G. Modelling transitions: An appraisal of experiences and suggestions for research. Environ. Innov. Soc. Transit. 2011, 1, 167–186. [Google Scholar] [CrossRef]
- Holtz, G.; Alkemade, F.; De Haan, F.; Köhler, J.; Trutnevyte, E.; Luthe, T.; Halbe, J.; Papachristos, G.; Chappin, E.; Kwakkel, J.; et al. Prospects of modelling societal transitions: Position paper of an emerging community. Environ. Innov. Soc. Transit. 2015, 17, 41–58. [Google Scholar] [CrossRef]
- Halbe, J.; Reusser, D.; Holtz, G.; Haasnoot, M.; Stosius, A.; Avenhaus, W.; Kwakkel, J.H. Lessons for model use in transition research: A survey and comparison with other research areas. Environ. Innov. Soc. Transit. 2015, 15, 194–210. [Google Scholar] [CrossRef]
- McDowall, W.; Geels, F.W. Ten challenges for computer models in Transitions research: Commentary on Holtz et al. Environ. Innov. Soc. Transit. 2017, 22, 41–49. [Google Scholar] [CrossRef]
- Köhler, J.; De Haan, F.; Holtz, G.; Kubeczko, K.; Moallemi, E.A.; Papachristos, G.; Chappin, E. Modelling Sustainability Transitions: An Assessment of Approaches and Challenges. J. Artif. Soc. Soc. Simul. 2018, 21. [Google Scholar] [CrossRef]
- Abbas, K.A.; Bell, M.G.H. System dynamics applicability to transportation modeling. Tranp. Res. Part A Policy Pract. 1994, 28, 373–390. [Google Scholar] [CrossRef]
- Ulli-Beer, S.; Gassmann, F.; Bosshardt, M.; Wokaun, A. Generic structure to simulate acceptance dynamics. Syst. Dyn. Rev. 2010, 26, 89–116. [Google Scholar] [CrossRef]
- Stepp, M.D.; Winebrake, J.J.; Hawker, J.S.; Skerlos, S.J. Greenhouse gas mitigation policies and the transportation sector: The role of feedback effects on policy effectiveness. Energy Policy 2009, 37, 2774–2787. [Google Scholar] [CrossRef]
- Struben, J.; Sterman, J.D. Transition challenges for alternative fuel vehicle and transportation systems. Environ. Plan. B Plan. Des. 2008, 35, 1070–1097. [Google Scholar] [CrossRef]
- Shepherd, S.; Bonsall, P.; Harrison, G. Factors affecting future demand for electric vehicles: A model based study. Transp. Policy 2012, 20, 62–74. [Google Scholar] [CrossRef]
- Kwon, T.-H. Strategic niche management of alternative fuel vehicles: A system dynamics model of the policy effect. Technol. Forecast. Soc. Chang. 2012, 79, 1672–1680. [Google Scholar] [CrossRef]
- Janssen, A.; Lienin, S.F.; Gassmann, F.; Wokaun, A. Model aided policy development for the market penetration of natural gas vehicles in Switzerland. Transp. Res. Part A Policy Pract. 2006, 40, 316–333. [Google Scholar] [CrossRef]
- Walther, G.; Wansart, J.; Kieckhäfer, K.; Schnieder, E.; Spengler, T.S. Impact assessment in the automotive industry: Mandatory market introduction of alternative powertrain technologies. Syst. Dyn. Rev. 2010, 26, 239–261. [Google Scholar] [CrossRef]
- Köhler, J.; Wietschel, M.; Whitmarsh, L.; Keles, D.; Schade, W. Infrastructure investment for a transition to hydrogen automobiles. Technol. Forecast. Soc. Chang. 2010, 77, 1237–1248. [Google Scholar] [CrossRef]
- Leaver, J.D.; Gillingham, K.T.; Leaver, L.H. Assessment of primary impacts of a hydrogen economy in New Zealand using UniSyD. Int. J. Hydrogen Energy 2009, 34, 2855–2865. [Google Scholar] [CrossRef]
- Meyer, P.E.; Winebrake, J.J. Modeling technology diffusion of complementary goods: The case of hydrogen vehicles and refueling infrastructure. Technovation 2009, 29, 77–91. [Google Scholar] [CrossRef]
- Leaver, J.; Gillingham, K.T. Economic impact of the integration of alternative vehicle technologies into the New Zealand vehicle fleet. J. Clean. Prod. 2010, 18, 908–916. [Google Scholar] [CrossRef]
- Park, S.Y.; Kim, J.W.; Lee, D.H. Development of a market penetration forecasting model for hydrogen fuel cell vehicles considering infrastructure and cost reduction effects. Energy Policy 2011, 39, 3307–3315. [Google Scholar] [CrossRef]
- Shafiei, E.; Stefansson, H.; Asgeirsson, E.I.; Davidsdottir, B.; Raberto, M. Integrated Agent-based and System Dynamics Modelling for Simulation of Sustainable Mobility. Transp. Rev. 2012, 33, 44–70. [Google Scholar] [CrossRef]
- Shafiei, E.; Davidsdottir, B.; Leaver, J.; Stefansson, H.; Asgeirsson, E.I. Potential impact of transition to a low-carbon transport system in Iceland. Energy Policy 2014, 69, 127–142. [Google Scholar] [CrossRef]
- Kieckhäfer, K.; Volling, T.; Spengler, T.S. A Hybrid Simulation Approach for Estimating the Market Share Evolution of Electric Vehicles. Transp. Sci. 2014, 48, 651–670. [Google Scholar] [CrossRef]
- Kieckhäfer, K.; Wachter, K.; Spengler, T.S. Analyzing manufacturers’ impact on green products’ market diffusion—The case of electric vehicles. J. Clean. Prod. 2017, 162, S11–S25. [Google Scholar] [CrossRef]
- Yeager, L.; Fiddaman, T.; Peterson, D. Entity-Based System Dynamics; Ventana Systems, Inc., 2014; Available online: http://www.vensim.com/wp-content/uploads/2014/08/Entity-Based-System-Dynamics-v2.pdf (accessed on 23 April 2018).
- Mingers, J.; Brocklesby, J. Multimethodology: Towards a framework for mixing methodologies. Omega 1997, 25, 489–509. [Google Scholar] [CrossRef]
- Rosenberg, N. Perspectives on Technology; Cambridge University Press: Cambridge, UK, 1976. [Google Scholar]
- Utterback, J.M. Mastering the Dynamics of Innovation; Harvard Business School Press: Boston, MA, USA, 1996. [Google Scholar]
- Schot, J.W. The usefulness of evolutionary models for explaining innovation. The case of the Netherlands in the nineteenth century. Hist. Technol. 1998, 14, 173–200. [Google Scholar] [CrossRef]
- Rip, A.; Kemp, R. Technological change. In Human Choice and Climate Change; Rayner, S., Malone, E.L., Eds.; Battelle Press: Columbus, OH, USA, 1998; Volume 2, pp. 327–339. [Google Scholar]
- Geels, F.W. Technological Transitions as evolutionary reconfiguration processes: A multi-level perspective and a case-study. Res. Policy 2002, 31, 1257–1274. [Google Scholar] [CrossRef]
- Rotmans, J.; Kemp, R.; Van Asselt, M. More evolution than revolution: Transition management in public policy. Foresight 2001, 3, 15–31. [Google Scholar] [CrossRef]
- Suurs, R.A.A.; Hekkert, M.P. Motors of sustainable innovation: Understanding Transit. from a technological innovation system’s perspective. In Governing the Energy Transition. Reality, Illusion or Necessity? Verbong, G.P.J., Loorbach, D., Eds.; Routledge: New York, NY, USA, 2012; pp. 152–179. [Google Scholar]
- Schroeder, A.; Traber, T. The economics of fast charging infrastructure for electric vehicles. Energy Policy 2012, 43, 136–144. [Google Scholar] [CrossRef]
- Krupa, J.S.; Rizzo, D.M.; Eppstein, M.J.; Lanute, D.B.; Gaalema, D.E.; Lakkaraju, K.; Warrender, C.E. Analysis of a consumer survey on plug-in hybrid electric vehicles. Transp. Res. Part A Policy Pract. 2014, 64, 14–31. [Google Scholar] [CrossRef]
- Shulock, C.; Pike, E.; Lloyd, A.; Rose, R. Task 4 Report: Complementary Policies. Vehicle Electrification Policy Study. The International Council on Clean Transportation. 2011. Available online: https://www.theicct.org/sites/default/files/publications/ICCT_VEPstudy_Mar2011_no4.pdf (accessed on 1 May 2018).
- Al-Alawi, B.M.; Bradley, T.H. Review of hybrid, plug-in hybrid, and electric vehicle market modeling Studies. Renew. Sustain. Energy Rev. 2013, 21, 190–203. [Google Scholar] [CrossRef]
- Lin, C.; Wu, T.; Ou, X.; Zhang, Q.; Zhang, X.; Zhang, X. Life-cycle private costs of hybrid electric vehicles in the current Chinese market. Energy Policy 2013, 55, 501–510. [Google Scholar] [CrossRef]
- Thiel, C.; Perujo, A.; Mercier, A. Cost and CO2 aspects of future vehicle options in Europe under new energy policy scenarios. Energy Policy 2010, 38, 7142–7151. [Google Scholar] [CrossRef]
- Anable, J.; Schuitema, G.; Stannard, J. Consumer Responses to Electric Vehicles Literature Review. Report for Energy Technology Institute Plug-in Vehicles Infrastructure Project (June 2010). Trans. Res. Lab. Publ. Proj. Rep. 2014. Available online: https://trl.co.uk/uploads/trl/documents/PPR728%20-%20Consumer%20responses%20to%20Electric%20Vehicles%20Literature%20Review.pdf (accessed on 19 December 2020).
- Argote, L. Organizational learning curves: Persistence, transfer and turnover. Int. J. Technol. Manag. 1996, 11, 759–769. [Google Scholar]
- Lant, T.K.; Argote, L. Organizational Learning: Creating, Retaining and Transferring Knowledge, 2nd ed.; Springer: New York, NY, USA, 2013. [Google Scholar]
- Morrison, J.B. Putting the learning curve in context. J. Bus. Res. 2008, 61, 1182–1190. [Google Scholar] [CrossRef]
- Bandhold, H.; Wallner, J.C.; Lindgren, M.; Bergman, S. Plug in Road 2020. Report Based on Consumer Surveys, Interviews and Seminars. Plug in Road 2020. Rapport Baserad på Konsumentundersökning, Intervjuer och Seminarium. Elforsk Rapport 09:40, Stockholm. 2009. Available online: https://energiforsk.se (accessed on 1 May 2018).
- Bjerkan, K.Y.; Nørbech, T.E.; Nordtømme, M.E. Incentives for promoting Battery Electric Vehicle (BEV) adoption in Norway. Transp. Res. Part D Transp. Environ. 2016, 43, 169–180. [Google Scholar] [CrossRef]
- Berger, J.; Milkman, K.L. What makes online content viral? J. Mark. Res. 2012, 49, 192–205. [Google Scholar] [CrossRef]
- East, R.; Hammond, K.; Lomax, W. Measuring the impact of positive and negative word of mouth on brand purchase probability. Int. J. Res. Mark. 2008, 25, 215–224. [Google Scholar] [CrossRef]
- Fiedler, K. (Ed.) Social Communication: Introduction and Overview; Psychology Press: New York, NY, USA, 2007. [Google Scholar]
- Mizerski, R.W. An Attribution Explanation of the Disproportionate Influence of Unfavorable Information. J. Consum. Res. 1982, 9, 301–310. [Google Scholar] [CrossRef]
- Park, C.; Lee, T.M. Antecedents of Online Reviews’ Usage and Purchase Influence: An Empirical Comparison of U.S. and Korean Consumers. J. Interact. Mark. 2009, 23, 332–340. [Google Scholar] [CrossRef]
- Yi, S.; Ahn, J.-H. Managing initial expectations when word-of-mouth matters: Effects of product value and consumer heterogeneity. Eur. J. Mark. 2017, 51, 123–156. [Google Scholar] [CrossRef]
- Linder, S.; Wirges, J. Spatial diffusion of electric vehicles in the German metropolitan region of Stuttgart. In Proceedings of the 51st Congress of the European Regional Science Association: New Challenges for European Regions and Urban Areas in a Globalised World, Barcelona, Spain, 30 August–3 September 2011; pp. 1–27. [Google Scholar]
- Curtin, R.; Shrago, Y.; Mikkelsen, J. Plug-in Hybrid Electric Vehicles. University of Michigan. 2009. Available online: http://ns.umich.edu/Releases/2009/Oct09/PHEV_Curtin.pdf (accessed on 22 April 2018).
- Ozaki, R.; Sevastyanova, K. Going hybrid: An analysis of consumer purchase motivations. Energy Policy 2011, 39, 2217–2227. [Google Scholar] [CrossRef]
- Hidrue, M.K.; Parsons, G.; Kempton, W.; Gardner, M.P. Willingness to pay for electric vehicles and their attributes. Resour. Energy Econ. 2011, 33, 686–705. [Google Scholar] [CrossRef]
- Plötz, P.; Schneider, U.; Globisch, J.; Dütschke, E. Who will buy electric vehicles? Identifying early adopters in Germany. Transp. Res. Part A Policy Pract. 2014, 67, 96–109. [Google Scholar] [CrossRef]
- Lane, B.; Potter, S. The adoption of cleaner vehicles in the UK: Exploring the consumer attitude–action gap. J. Clean. Prod. 2007, 15, 1085–1092. [Google Scholar] [CrossRef]
- Figures Electrical Transport (Cijfers Elektrisch Vervoer). Available online: https://www.rvo.nl/onderwerpen/duurzaam-ondernemen/energie-en-milieu-innovaties/elektrisch-rijden/stand-van-zaken/cijfers (accessed on 28 August 2020).
- Fisher, J.; Pry, R. A simple substitution model of technological change. Technol. Forecast. Soc. Chang. 1971, 3, 75–88. [Google Scholar] [CrossRef]
- Rotmans, J.; Kemp, R. Managing Societal Transitions-Dilemmas and Uncertainties: The Dutch Energy Case-Study. In OECD Workshop on the Benefits of Climate Policy: Improving Information for Policy Makers; 2003; Available online: http://www.oecd.org/environment/cc/2483769.pdf (accessed on 1 May 2018).
- King, J. Part 1: The Potential for CO2 Reduction. The King Review of Low Carbon Cars. 2007. Available online: http://webarchive.nationalarchives.gov.uk/+/http:/www.hm-treasury.gov.uk/d/pbr_csr07_king840.pdf (accessed on 15 May 2018).
- Sperling, D.; Gordon, D. Advanced passenger transport technologies. Annu. Rev. Environ. Resour. 2008, 33, 63–84. [Google Scholar] [CrossRef]
- McKinsey & Company. A Portfolio of Powertrains for EUROPE: A Fact-Based Analysis. 2010. Available online: http://www.fch.europa.eu/sites/default/files/Power_trains_for_Europe_0.pdf (accessed on 15 May 2018).
- Williander, M.; Stålstad, C. Four Business Models for a Fast Commercialization of Plug-in Cars. In Electric Vehicle Business Models; Beeton, D., Meyer, G., Eds.; Springer: Cham, Switzerland, 2015. [Google Scholar]
- Zolfagharian, M.; Walrave, B.; Raven, R.; Romme, A.G.L. Studying transitions: Past, present, and future. Res. Policy 2019, 48, 103788. [Google Scholar] [CrossRef]
- Zolfagharian, M.; Romme, A.G.L.; Walrave, B. Why, when, and how to combine system dynamics with other methods: Towards an evidence-based framework. J. Simul. 2018, 12, 98–114. [Google Scholar] [CrossRef]
- Geels, F.W.; Berkhout, F.; Van Vuuren, D.P. Bridging analytical approaches for low-carbon transitions. Nat. Clim. Chang. 2016, 6, 576–583. [Google Scholar] [CrossRef]
| Inclusion of E-Mobility Innovation System | Inclusion of UTAUT Variables | All EV Purchasers Follow the Same Decision Rule | All EV Purchasers Are Considered as Early Adopters | |
|---|---|---|---|---|
| Base case | No | No | NA | NA |
| Scenario 1 | Yes | No | NA | NA |
| Scenario 2 | Yes | Yes | Yes | Yes |
| Scenario 2-1 | Yes | Yes | No | No |
| Income Scenario | The rules are different for each income class | Various timings for the first adoptions of different income classes | ||
| Scenario 2-2 | Yes | Yes | No | No |
| Age Scenario | The rules are different for each age group | Various timings for the first adoptions of different age groups | ||
| Scenario 2-3 | Yes | Yes | No | No |
| Urbanization Scenario | The rules are different based on the urbanization level in which EV purchasers are living | Various timings for the first adoptions of different groups living in different urbanization levels |
| Scenario | Class of EV Purchasers | Definition | Performance and Effort Weight | Hedonic Weight | Price Weight | Facilitating Conditions Weight |
|---|---|---|---|---|---|---|
| Scenario 2 | Aggregated purchasers | 0.275 | 0.025 | 0.4 | 0.3 | |
| Scenario 2-1 | Income_1 | 0–10,000 € | 0.29 | 0.05 | 0.35 | 0.31 |
| Income_2 | 10,000–20,000 € | 0.3 | 0.075 | 0.3 | 0.325 | |
| Income_3 | 20,000–30,000 € | 0.315 | 0.1 | 0.25 | 0.335 | |
| Income_4 | 30,000–40,000 € | 0.4 | 0.15 | 0.1 | 0.35 | |
| Income_5 | 40,000–50,000 € | 0.6 | 0.2 | 0 | 0.2 | |
| Income_6 | 50,000+ € | 0.275 | 0.025 | 0.4 | 0.3 | |
| Scenario 2-2 | Age_1 | 18–19 | 0.25 | 0.2 | 0.25 | 0.3 |
| Age_2 | 20–29 | 0.3 | 0.175 | 0.25 | 0.275 | |
| Age_3 | 30–39 | 0.35 | 0.15 | 0.25 | 0.25 | |
| Age_4 | 40–49 | 0.4 | 0.125 | 0.25 | 0.225 | |
| Age_5 | 50–64 | 0.45 | 0.1 | 0.25 | 0.2 | |
| Age_6 | 65–74 | 0.5 | 0.075 | 0.25 | 0.175 | |
| Age_7 | 75+ | 0.55 | 0.05 | 0.25 | 0.15 | |
| Scenario 2-3 | Urbanization_1 | Very high density | 0.2 | 0.03 | 0.57 | 0.2 |
| Urbanization_2 | High density | 0.225 | 0.05 | 0.5 | 0.225 | |
| Urbanization_3 | Moderately high density | 0.28 | 0.07 | 0.4 | 0.25 | |
| Urbanization_4 | Low density | 0.3 | 0.1 | 0.3 | 0.3 | |
| Urbanization_5 | Very low density | 0.33 | 0.12 | 0.2 | 0.35 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zolfagharian, M.; Walrave, B.; Romme, A.G.L.; Raven, R. Toward the Dynamic Modeling of Transition Problems: The Case of Electric Mobility. Sustainability 2021, 13, 38. https://doi.org/10.3390/su13010038
Zolfagharian M, Walrave B, Romme AGL, Raven R. Toward the Dynamic Modeling of Transition Problems: The Case of Electric Mobility. Sustainability. 2021; 13(1):38. https://doi.org/10.3390/su13010038
Chicago/Turabian StyleZolfagharian, Mohammadreza, Bob Walrave, A. Georges L. Romme, and Rob Raven. 2021. "Toward the Dynamic Modeling of Transition Problems: The Case of Electric Mobility" Sustainability 13, no. 1: 38. https://doi.org/10.3390/su13010038
APA StyleZolfagharian, M., Walrave, B., Romme, A. G. L., & Raven, R. (2021). Toward the Dynamic Modeling of Transition Problems: The Case of Electric Mobility. Sustainability, 13(1), 38. https://doi.org/10.3390/su13010038






