1. Introduction
In the low-carbon economy, significant attention has focused on wind power as a main source of renewable energy, with the potential to become a hotspot for global energy development in the future [
1,
2]. If offshore wind energy resources are abundant, and wind turbulence intensity and sea surface roughness are less than those on land, then the utilization of offshore wind energy becomes an important way to meet the requirements for energy growth and implement sustainable development [
3,
4]. As technological innovation has matured in this field, a trend for large-capacity development of offshore wind power has emerged and the scale of the wind farm has expanded. In order to meet the reliability and stability requirements of the wind turbine group in the marine environment, a good control strategy is designed to further improve the control effect of a single unit and the whole wind farm.
With the rapid integration of the power system and communication network, the control of the system tends to be networked, intelligent, and comprehensive [
5,
6,
7]. Compared with traditional centralized control, distributed control has more advantages in solving networked system control problems. For example, the risk of failure is dispersed and the reliability of the system is improved [
8,
9,
10]. The offshore wind farm is regarded as a distributed network, each unit in the wind farm is a node in the network, and unit information is exchanged through communication circuits. On the network, the corresponding distributed control strategy can be implemented and the synchronization output of each unit can be adjusted, which can make the wind power system run stably and effectively realize control of the whole wind farm [
11].
Modern power systems are gradually developing with multiple-interconnection and large-scale characteristics. WAMS has been applied to power systems, enabling distributed synchronous measurement and stability control of modern power systems [
12,
13]. WAMS exists in the phasor measurement unit of a wind farm, the communication system and control system of dispatching center. In the WAMS, the time delay of signal transmission is usually large, and presenting a random characteristic. The time delay is inevitable occurring in many power engineering and applications. The time delay in the WAMS may cause the change of the main eigenvalue and the main oscillation frequency in the unstable state. Additionally, time delay leads to the preset controller parameters unavailable, and reduces the stability margin of the system, even worsening the operation condition of the power system. Therefore, the time delay control of the wind turbine cannot be ignored [
14,
15].
In recent decades, the problem of time delay has been widely concerned, and many scholars have put forward many good results. The novel decentralized sliding mode load frequency control (LFC) strategy is proposed for a multiple-area time delay power system with significant wind power penetration in [
16]. In the paper [
17], time delay is considered in command communication from control unit to motor driver in wind turbine, and an inertial supplementary scheme is proposed. The method based on the network predictive control (NPC) is proposed for coordinated design to improve damping, and compensate for the time delay in [
18]. The control methods mentioned above are all based on universal nonlinear model. The specific action position of time delay on the wind turbine model is not considered, also on the coordination between multiple wind turbines. Offshore wind turbine cluster is a complex Multi-input Multi-output (MIMO) nonlinear system. A model having more clear structure and physical meaning is needed to describe wind power system. Generalized Hamiltonian system is an important field in nonlinear system research, and PCH-D model has clear structural characteristics, so it is used in the nonlinear system application and control [
19].
The generalized Hamiltonian system is defined by generalized Poisson bracket, and the Casimir function is one of the special properties of Poisson manifold. Casimir function is used as a conserved quantity to determine the stability of Hamiltonian system at the equilibrium point, and reduce the dimension of finite dimension Hamiltonian system. Therefore, Casimir has been widely used and studied in various fields. Casimir function is used to constrain the state of the finite dimensional port Hamiltonian system; the energy function of the controller is easily shaped to solve the regulation problem [
20]. The Energy-Casimir method is proposed to deal with power preserving system and applied to longitudinal beam vibrations [
21]. Casimir function is an important tool in the design of Hamiltonian system. The design process is simple, and the stability analysis and control of the Hamiltonian system can be advanced by using the Casimir function [
22,
23,
24].
At present, the stability problems of nonlinear time delay system are widely concerned by scholars and engineers in practical engineering and theoretical research. A new adaptive neural network controller is designed based on the traditional Lyapunov-Krasovski function, to obtain the stability criterion of nonlinear time delay system in [
25]. However, in the process of derivation, the matrix inequality is amplified many times, which increases the conservatism of the conclusion. Based on linear matrix inequality (LMI) method, a fuzzy controller of time delay is designed in [
26]. The LMI method needs to find multiple uncertain matrices, and may not be available in the actual nonlinear system, also, the process is more complex. The offshore wind turbine group is affected by time delay in the wide area signal. In this paper, the Casimir function method is proposed to design the time delay controller. In the design process, the amplification of multiple uncertain matrices is avoided, the conservatism brought by amplification of multiple matrix in the other method is overcome, and the control is easier to achieve. Moreover, Casimir function method can combine distributed cooperative control to solve the coordination problem among multiple control objects.
A wind turbine is a typical nonlinear system. In order to realize the control of the doubly fed wind turbine group, the main work in this paper can be summarized as follows:
The Hamiltonian implementation of the doubly fed generator is firstly carried out, and the PCH-D model is obtained; this is well structured with clear physical meaning.
Considering that the single-machine system in the wind farm has input time delay, the closed-loop PCH-D form is embedded into the extended system using the Casimir function. The extended system is confined to the invariant Casimir manifold and controlled by the interconnection of the system under the PCH-D structure, so that closed-loop system maintains the required stability and performance through energy-shaping approaches.
The control problem of the single-machine wind turbine is extended to the control of wind turbine group consisting of multiple units. By combining the Casimir function with distributed control design, a distributed cooperative control strategy is proposed for wind turbines with input time delays. Thus, all wind turbines can achieve global stability synchronization of active power output under input time delay.
3. Controller Design for Doubly Fed Wind Turbine Groups with Input Time Delay
In recent years, the rapid development of the power grid has greatly increased the complexity of its structure and operation. At the same time, smart grid construction requires significant improvement on stability and transmission capability. In wide-area control systems, significant time delays exist in the feedback and transmission process of remote measured signals and local measured signals, and wind power becomes a dynamic system with time delay. Meanwhile, because of this time delay, the control effect of the closed-loop system becomes worse and even causes oscillation, which deteriorates the stability of the system. The offshore wind farm is located at the far end of the power grid. The wind turbines are geographically situated at a certain distance from each other and are affected by different marine environments. Therefore, the time delay of the wide-area signal is usually affected by transmission distance and transmission protocol, which is uncertain and random. That is, the time delays of different units change in a certain range [
36]. In this paper, a coordinated control strategy for offshore wind turbines with input time delay is proposed to solve this problem.
3.1. Controller Design for A Single-Machine System with Input Delay
This section analyzes the control problem of a single-machine system with time delay, and the nonlinear model of a doubly fed wind turbine is transformed into PCH-D form. Then, the Casimir function is introduced and the new energy function is shaped by extending the interconnection. The Hamiltonian function is considered a candidate of a Lyapunov function in the extended system, which makes the extended wind turbine system operate stably at the original equilibrium point.
3.1.1. Problem Description
Considering offshore wind turbine groups, the PCH-D model of a single-machine system is extended to that of a multi-machine system as follows:
The subscript i denotes the parameters of unit i in the network topology.
Assuming that the wind turbine is connected to other machines in the distance, the time delay is inevitable in measurement data. Considering the control inputs are
and
, this feeds back both the local measurement information and the wide area measurement signals, and the wind turbine system is modeled as PCH-D with the input time delay as follows:
where
is the input time delay of the unit
i. The distances between wind turbines are different, and the time delays produced in the wide-area signals of each unit are different. Therefore, the time delays vary within a certain range,
is the minimum delay, and
is the maximum delay in the wind turbine network, and
is an uncertain constant satisfying
.
3.1.2. Design of the Casimir Function
The actual wind turbine system is a nonlinear time delay system. The model described by PCH-D form has clear structural characteristics. Casimir function method is an important analysis tool of Hamiltonian energy theory, and can be used to analyze the stability of the uncertain Hamiltonian system at the equilibrium point. By selecting the Hamiltonian energy function as a candidate function of the Lyapunov function, this method will not change the structural characteristics of the PCH-D model, and does not require the application of an inequality matrix. Therefore, the difficulty of analysis reduced greatly [
23]. In the following, the controller of the time delay control system is designed by Casimir function, and the stability of the system is analyzed.
In order to achieve the required stability performance with input time delay, a new energy function is formed by interconnecting the system in (10) with the following source system in (11):
where,
,
,
, and
is the extended Hamiltonian function for the dynamic controller.
The design of the feedback interconnection controller is as follows:
Through the interconnection, the system is expressed as:
Proposition 1. Function, is the Casimir function of the system in (11), and its necessary and sufficient conditions satisfy:where, Meanwhile, invariant manifolds are defined aswhere,is a constant.
Based on the above definition, to maintain the stable operation of the wind turbine system with input delay, a control strategy is designed based on the Casimir function. The theorem is as follows:
Theorem 1. Considering the doubly fed wind turbine in (4) with input delay on offshore wind farm, a feedback controller is designed as follows:Given the above propositions, the closed-loop single-machine system can maintain stable operation under the condition of input time delay. Proof of Theorem 1. For the PCH-D model in (10), the controller is
By substituting this into the interconnected extended closed-loop system in (13), it is obtained:
where
With the introduction of the Casimir function, the Hamiltonian function can be expressed as follows:
Take the interconnection system to satisfy:
Then,
This satisfies the necessary and sufficient conditions in (14) for the existence of the Casimir function. If the Casimir function
of the extended system can be taken as
, then
This shows that the equilibrium points of the Hamiltonian energy function for the extended single-machine system are , , , which are the same as those without input time delay in the system. The system can be restricted to invariant manifold B, and is regarded as the Lyapunov function of the system. The system in (9) with input time delay can maintain global stability under the action of the source system in (11).
This demonstrates that the PCH-D model of wind turbine can be extended and interconnected through the Casimir function when a time delay exists in the input of a wind turbine. Then, the input time delay controller is designed to maintain the wind turbine stable in the PCH-D form. Simultaneously, the influence of time delay on the system is eliminated and the stability of the system is maintained.
3.2. Controller Design of A Multi-machine System with Input Time Delay
At present, distributed control in the development of smart grid and new energy has attracted great attention of scholars and engineers. A distributed consensus-based power sharing algorithm is introduced to determine the power generations of the subsystems, which enhances load current sharing accuracy among the local distributed generators [
37]. This paper presents a distributed control technique for voltage, frequency and active/reactive power control of the point of common connection (PCC), AC-grid of a wind farm. The distributed control strategy allows maximum power transfer from the wind turbines to the AC-grid, with good dynamic performance during steady-state and transient operation of the AC-grid [
38]. Distributed control is more flexible and extensible, so it is widely used in power generation, transmission and distribution.
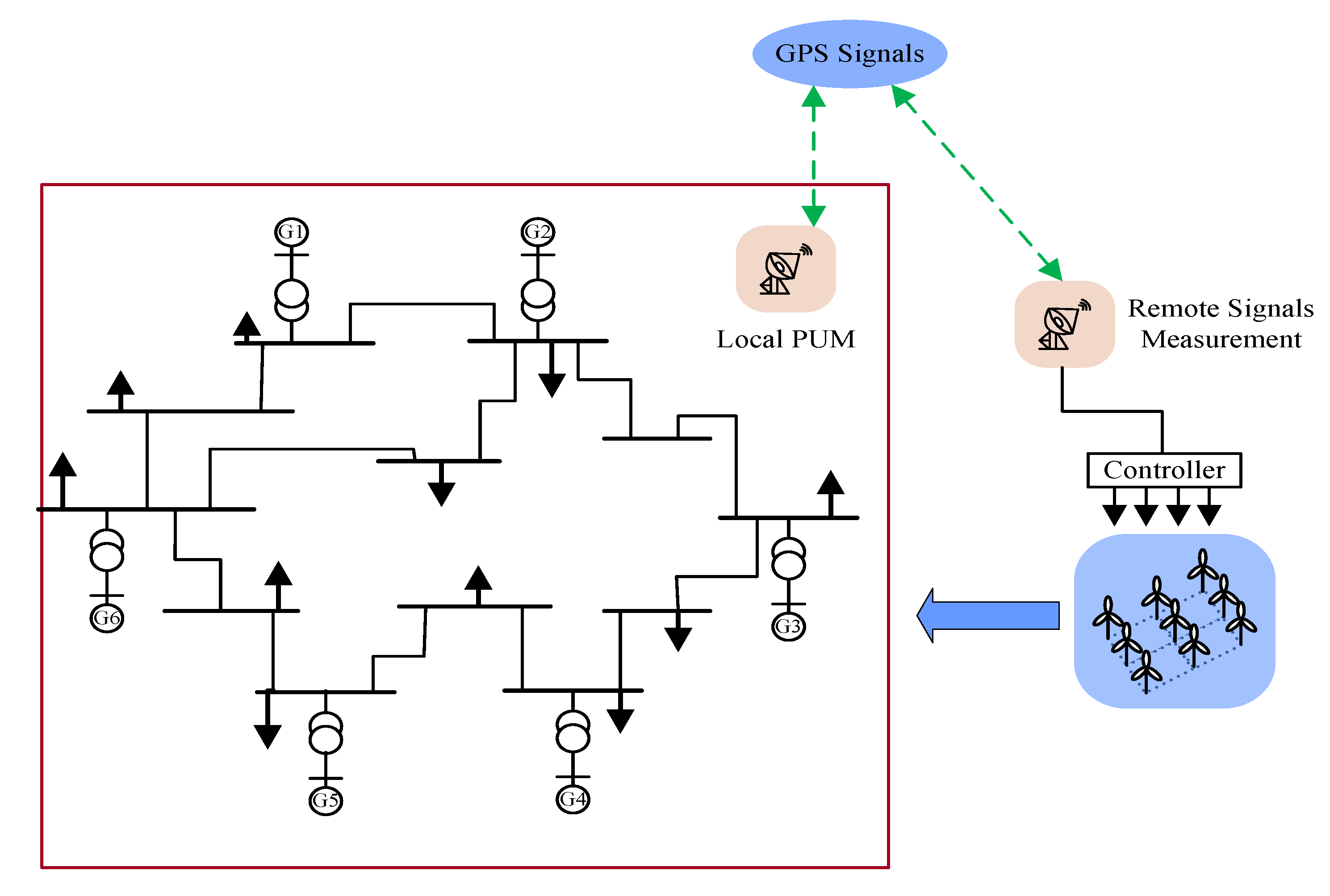
The offshore wind farm contains multiple wind turbines. The communication between the turbines and the main control center is complex. In addition, the offshore environment is complex and changeable, making maintenance of wind turbines difficult. The distributed control structure is adopted for the offshore wind turbine group. Through the communication structure, each unit can obtain the corresponding status information or parameters from the neighboring units and make its decisions with the control strategy. There is no communication between the central controller and each unit. Through communication and independent control strategy, each unit can adjust KE stored in the rotating mass, so that the wind turbines can achieve the desired power output and stable state under the corresponding wind speed. The distributed control greatly reduces the communication burden between the wind turbines and the central controller. The investment of the transmission and distribution equipment is reduced, also the loss of the power grid transmission. The energy utilization rate has been greatly improved. The network diagram of wind turbines with distributed control is shown in
Figure 2:
In the offshore wind farm, wind turbines are interconnected by communication circuits and provide power to the grid. The offshore environment is complex, and the distances between wind turbines are different. The time delay of the wide-area signal of each wind turbine is affected by the distance and the environment, which varies randomly within a certain range. In this section, the controller of single-machine system with input time delay proposed in the previous section is extended to that of multi-machine system with input time delay. For the network of wind turbines, a distributed control strategy is proposed to solve the control problem of the system with different stochastic time delay inputs. The whole wind farm can maintain global stability and improve operational reliability. The design process is as follows:
Assumption 1. Considering the network topology of the offshore wind turbine group, there is, at least, one directed spanning tree existing.
Theorem 2. Consider one offshore wind farm consisting of N wind turbines. The control strategy for wind turbines with stochastic time delays in the input is designed as follows:
where,,,and.
Under the control strategy, the output of each unit in the wind turbine group can converge when there is a time delay in the input, and the active power output can synchronize, so that the whole closed-loop system is globally stable.
Proof of Theorem 2. The control strategy maintains a stable PCH-D structure when a time delay exists in the input of the system. Whereas the control strategy can adjust the whole output of the wind farm, and realize output synchronization of a multi-machine system, to maintain the stable operation of the whole wind farm.
Each unit in the wind farm can be extended to the PCH-D system interconnecting with the source system through the feedback interconnection controller. An extended PCH-D system is obtained as follows:
Then, the control strategy
is substituted into the PCH-D model in (9) in the wind turbine group, and it can be rewritten as follows:
where,
In terms of the Casimir function, it is gotten:
The Lyapunov function of the whole system is set as follows:
Taking the derivative of the Lyapunov function, and substituting the control strategy
into the derivation, we have
Formula
can be rewritten into a vector form as follows:
where, the output is
, and
is
, the Laplacian matrix for the system.
According to LaSalle’s invariant principle [
39], when
, the solutions converge to the set
S, and the output
is satisfied. When the wind turbine operates steadily, it is obtained that
When the system maintains operational stability, the active power output of the wind turbine is equal to its input mechanical power [
40]. Therefore, under the distributed control strategy designed through the Casimir function, the wind turbines with input time delays in a certain range can coordinate with each other to ensure the whole closed-loop system maintains operational stability in terms of the output.
Based on the analysis, when a time delay exists in the input of offshore wind turbines, the Casimir function is used to construct and interconnect the feedback controller, to maintain a stable PCH-D structure in the case of input time delay, which makes the single-machine run stably. When there are time delays in the inputs of all wind turbines in an offshore wind farm, the networked distributed control is applied to each unit so that the machines coordinate with each other. This not only eliminates the influence of time delay, but also maintains the stable operation and greatly improves the reliability of the whole wind farm.
4. Simulation Verification
In this section, MATLAB software is used to simulate and verify the effectiveness of the control strategy. Firstly, the proposed control strategy is used to stabilize the output of the single wind turbine with input time delay. Compared with the control strategy without considering time delay, the control method is proven effective. Then, by using the designed control strategy for the multi-machine system with input delays, the whole wind farm can maintain synchronous output and stable operation. The numerical values of the wind turbine used in the simulation are shown in
Table 1.
4.1. Controller Design for a Single-Machine with Input Delay
In a doubly fed wind turbine cluster, the wind turbines are connected with each other. The local measurement information and wide-area measurement signal is feedback by the control input, therefore, time delay
τ exists in input inevitably.
τ is a constant satisfying
. For the convenience of analysis, only the influence of distance is considered on the value of time delay.
is taken as the shortest delay of wind turbines, and
as the longest delay. In the interconnection system,
is substituted into the designed controller with the Casimir function.
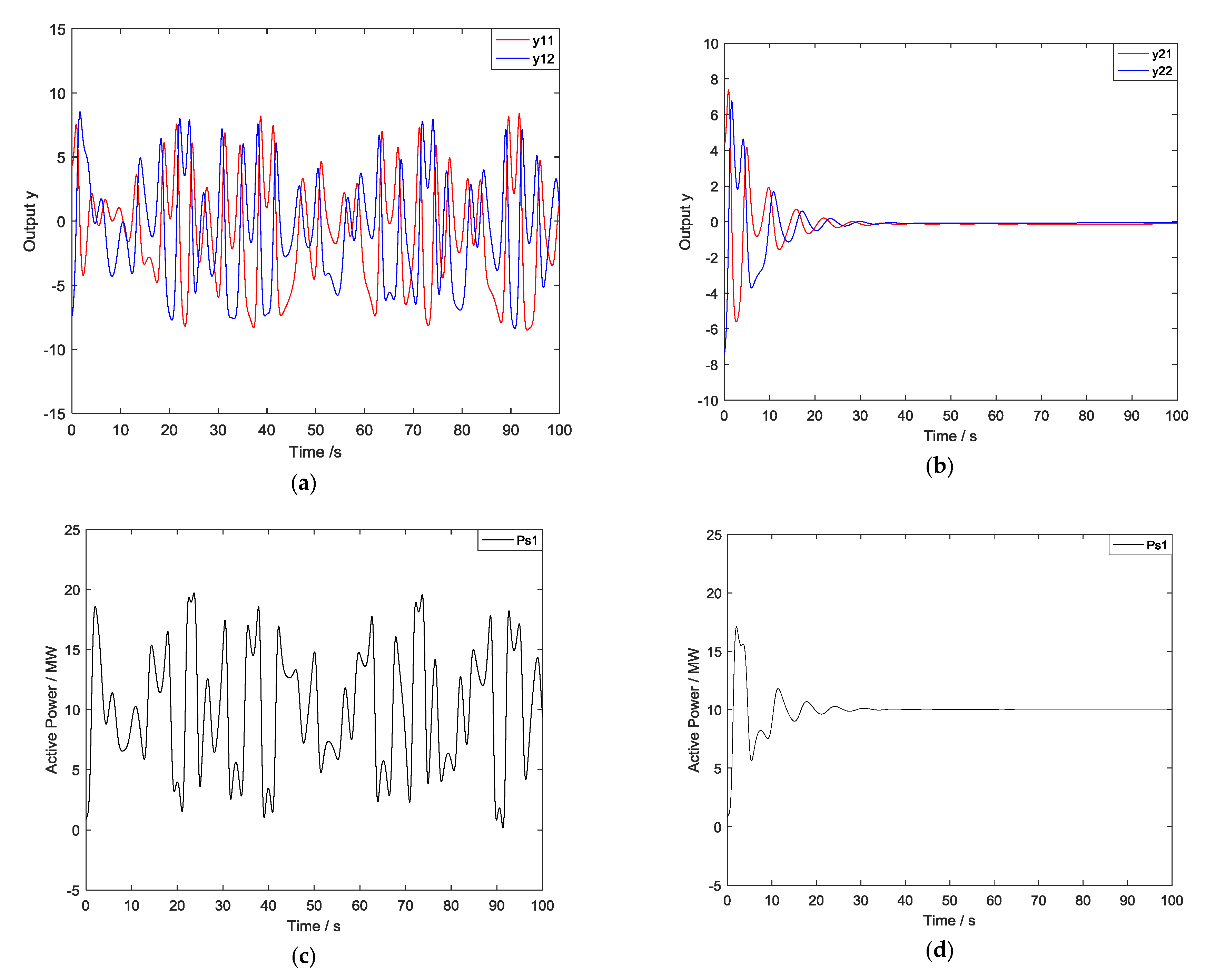
An appropriate initial value is selected to simulate and the simulation results of a single-machine system are shown in
Figure 3. The simulation results of the output response of a single wind turbine with input time delay are shown in
Figure 3a. The simulation results of the output response of a single-machine, controlled by the Casimir function, are shown in
Figure 3b. The simulation results of active power of a single wind turbine with input time delay are shown in
Figure 3c, and the simulation results of the active power controlled by the Casimir function are shown in
Figure 3d.
Figure 3a,c illustrate that the curves of the output response of the unit are unstable and even fluctuate greatly, when there is a time delay
τ in the input of a wind turbine. The maximum active power is
, and the maximum power changed within 1s is
. The stable PCH-D form of the unit is destroyed by the time delay
τ, which causes the system to run unsteadily.
Figure 2d and
Figure 3b show that the output response and active power curve of a single- machine have a certain amplitude of oscillation in a short period of time, and the fluctuation amplitude reduces significantly after 10s. After 25s, the output converges to 0, and the active power output of the unit converges to 10 MW. The system operates stably. The maximum active power is
, and the maximum power changed within 1s is
. The peak time and accommodation time of the active power are
and
respectively, the overshoot is
, and the steady-state error is
.
Through comparison, it can be seen that the single-machine system has oscillation mode due to the input time delay. After the unit is controlled with time delay controller, the system converges rapidly, maintains the global stability, and reduces the steady-state error of the system. It shows that the Casimir function method can effectively solve the oscillation problem caused by input time delay, and also enhance the stability and control accuracy of the system.
4.2. Controller Design for A Multi-Machine with Input Delay
A wind farm contains multiple wind turbines, and multiple wind turbines are affected by time delays, so distributed control is adopted for the wind farm. For the convenience of simulation and analysis, a wind turbine cluster composed of six doubly fed wind turbines is considered in this section. The single line diagram of the wind farm underneath is as follows:
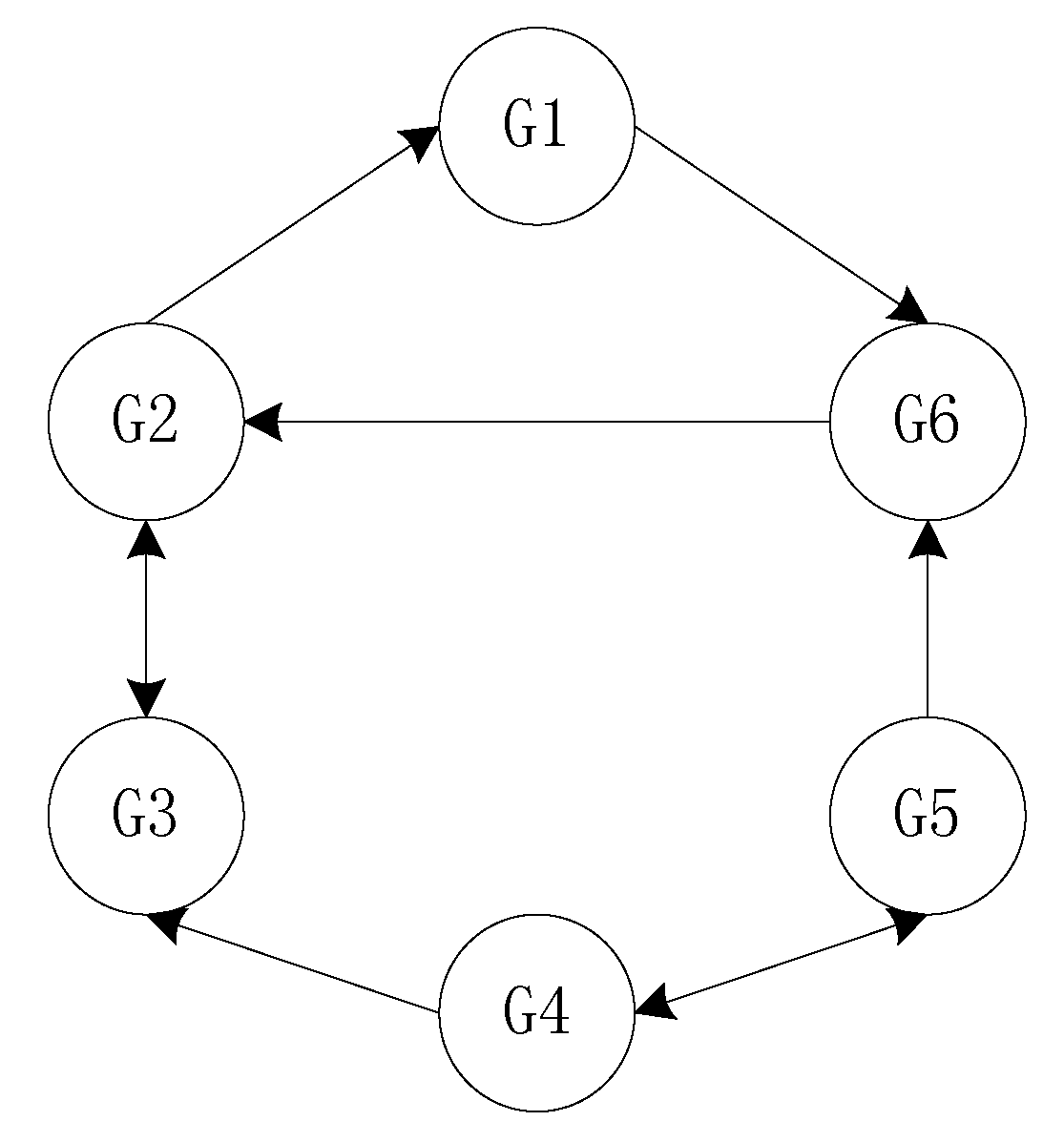
The units G1-G6 in
Figure 4 are regarded as nodes, and the units exchange information with each other through communication lines. The network structure of the G1-G6 is simplified as
Figure 5 as follows:
Figure 5 contains a directed spanning tree. In the distributed time delay control strategy (18), the control strategy
is distributed control strategy, to realize output synchronization of a multi-machine system. There is a directed spanning tree structure in
Figure 5, which satisfies the design conditions of distributed cooperative control strategies for units G1-G6 [
11]. By adopting distributed cooperative control for each unit, the units can be coordinated with each other to achieve a stable output convergence. Therefore, the distributed cooperative control strategy for the wind turbine group without time delay is
Considering the connection direction of unit G1-G6 in
Figure 5, the distributed cooperative control strategies of the units G1-G6 are designed as follows:
There is time delay
in the input of each turbine, and time delay of each unit is different randomly, satisfying
. Based on the above Casimir function, the wind turbines with time delays are controlled through the distributed cooperative control strategies. From Theorem 2 in
Section 3, the control strategy
of wind farm with time delays is Equation (18), the strategy
and strategy
are obtained from Equation (18) and Equation (19) respectively. The distributed control strategies of six units with time delays are designed as follows:
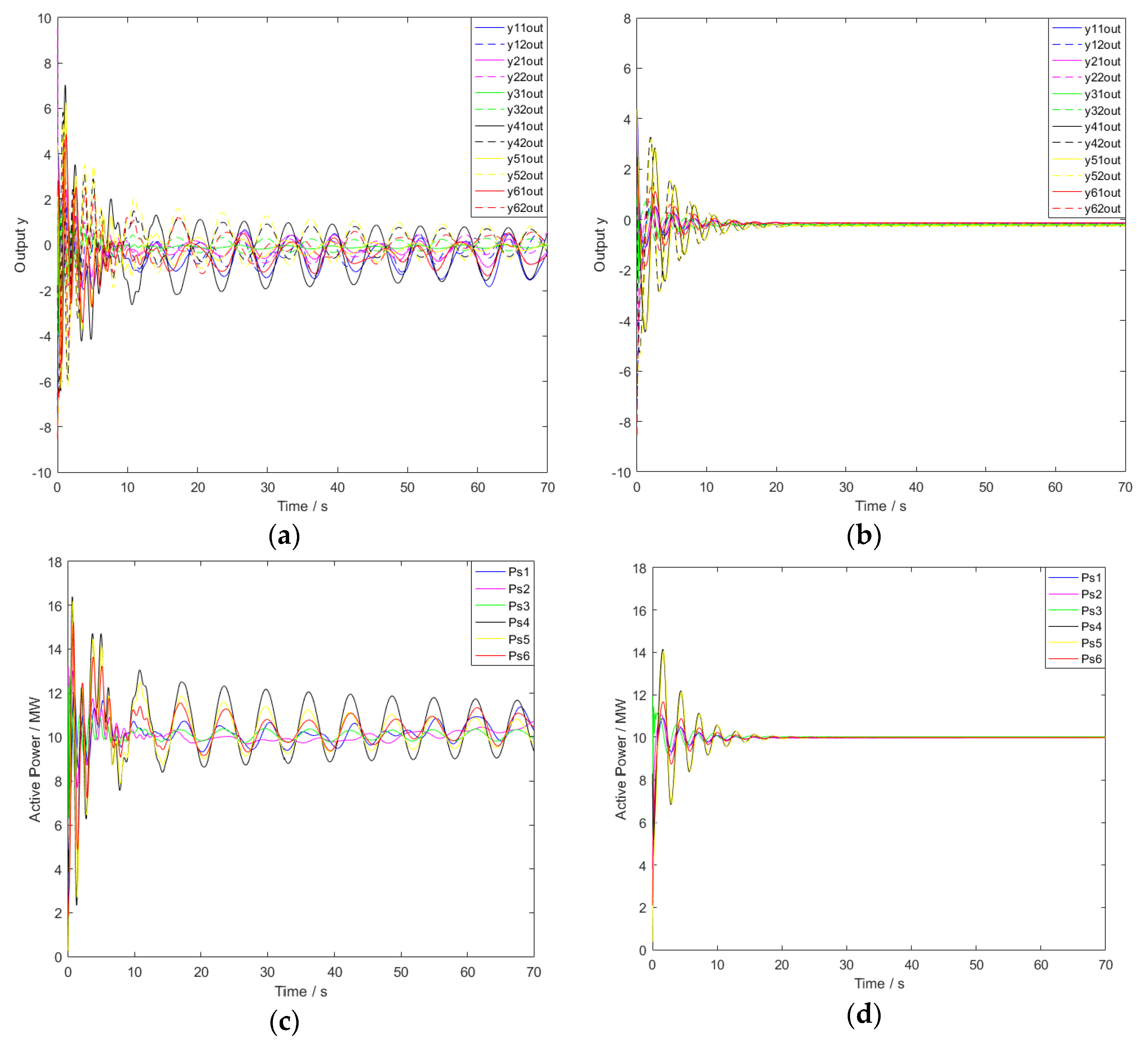
The simulation results of wind turbine groups are shown in
Figure 6. The simulation results of the output response of wind turbines with input time delays are shown in
Figure 6a. The simulation results of the output response of wind turbines controlled by distributed control strategy, are shown in
Figure 6b. The simulation results of active power of wind turbines with input time delays are shown in
Figure 6c, and the simulation results of the active power of wind turbines controlled by time delay control are shown in
Figure 6d.
Figure 3a,b demonstrate that the output of wind turbines fluctuates greatly under the influence of input time delay, and the whole system is in an unstable state. The normal operation of wind turbines is seriously affected by input time delay.
Figure 4a,b demonstrate that the curves of the output response and the active power output fluctuated less at 10 s. After 15 s, the output converges to 0, the active power output of each unit converges to 10 MW, and the output of each unit is synchronous.
Table 2 shows the stability parameters of wind turbines with time delays after distributed time delay control.
In
Table 2, the maximum active power is
, all the accommodation time is within 10s. The fastest accommodation time is unit G1’s. The overshoots of the units are less than 50%, and the steady-state errors of the units are all within 0.04. The distributed control strategy based on Casimir function suppresses the oscillation caused by time delay, and achieves active power stability and output synchronization. After the wind turbine group is controlled by the distributed time delay controller, the convergence speed of the system is faster, also the overshoot and steady-state error is smaller. The distributed time delay control method proposed in this paper can effectively improve the stability and control accuracy of the system.
5. Discussions
In this paper, a distributed time delay controller is proposed, which can effectively solve the time delay problem of offshore doubly fed wind clusters. This method is of great significance to improve the reliability of the power system to meet the demand of the power system.
The third-order DFIG turbine model adopts one-mass drive and ignores the stator transient, so some flux components are not responsible for the turbine’s decaying mode and oscillating mode. The model is more controllable, and more suitable for the actual system. Based on Hamiltonian energy method, the third-order model is transformed into PCH-D model. The PCH-D model can be designed through the input port, and contains the basic structural characteristics of the system. The structure of the model is clear and extensible, also the construction process is simple, which is of great significance in the transient stability analysis of power system.
In large-scale power system, the power will oscillate in a short period of time due to the time delay, which do harm to turbines, power equipment and power grid. The power quality and generation efficiency are reduced, and generation cost is increased. Time delay seriously affects the economic benefits of wind farms. It is necessary to study the time delay control of large-scale power systems. For the PCH-D model, Hamiltonian energy function is used as the Lyapunov function of the system in the Casimir function method. The number of matrix inequalities used in this process is reduced, so the conservatism of the condition is reduced. Casimir method can solve the problem of time delay, and improve the response speed, stability, and control accuracy of wind turbine. This method improves the utilization rate of wind energy, and is a feasible and effective control method in wind power systems.
Instead of the traditional centralized control mode, the distributed control method is adopted to solve the control problem of wind turbine groups in this paper. In the traditional centralized control mode, control decisions are obtained through the calculation of the central control system. The calculation of the central control system is heavily burdened and the turbine system excessively depends on the main control system, resulting in the low reliability and poor flexibility [
41]. In the distributed control mode, the communication all over the network is not needed, so the cost is reduced. Through the design of distributed control strategy, the stability of the system can be improved, and the life of power transmission equipment and power conversion equipment can be prolonged, which is practical and economical.
In summary, the method proposed in this paper is technically and economically advantageous in terms of power generation performance, system simplification, and cost effectiveness. Adopting new control technology and system structure is an important method to analyze power systems and improve energy utilization. The potential research on this method is as follows:
At present, the control technology of single energy has been relatively mature. The comprehensive utilization of various renewable energy is the inevitable choice for energy development [
6]. The distributed control method in this paper, can be applied to the wind power and other energy for comprehensive management or dispatching, to promote the efficient utilization of energy and large-scale consumption of renewable energy.
With the research and development of artificial intelligence in various fields, artificial intelligence plays an important role in the development and utilization of new energy [
42]. An artificial intelligence algorithm is adopted for energy prediction and optimal dispatching to achieve efficient utilization of renewable energy. Based on Casimir method and distributed control theory, the new artificial intelligence theory and algorithm research will be further applied to the dispatching management of offshore doubly fed wind turbine groups, to improve the power quality for users. Intelligent control algorithm is one of the important ways of energy networking in the future.