A Stochastic Interpolation-Based Fractal Model for Vulnerability Diagnosis of Water Supply Networks Against Seismic Hazards
Abstract
1. Introduction
2. Seismic Vulnerability of WSN and Its Modeling Method
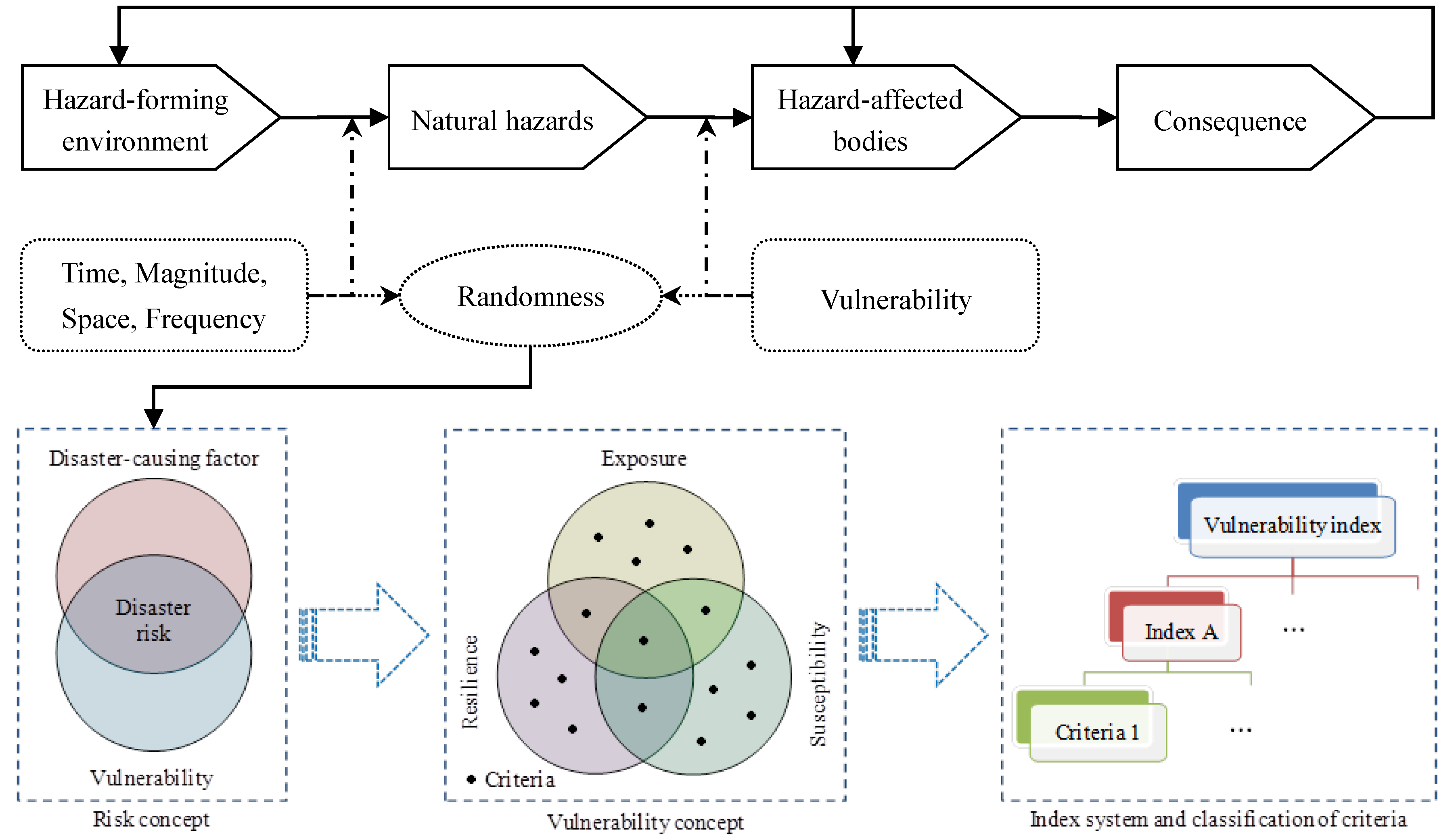
2.1. The Basic Concept of Seismic Vulnerability of the WSN
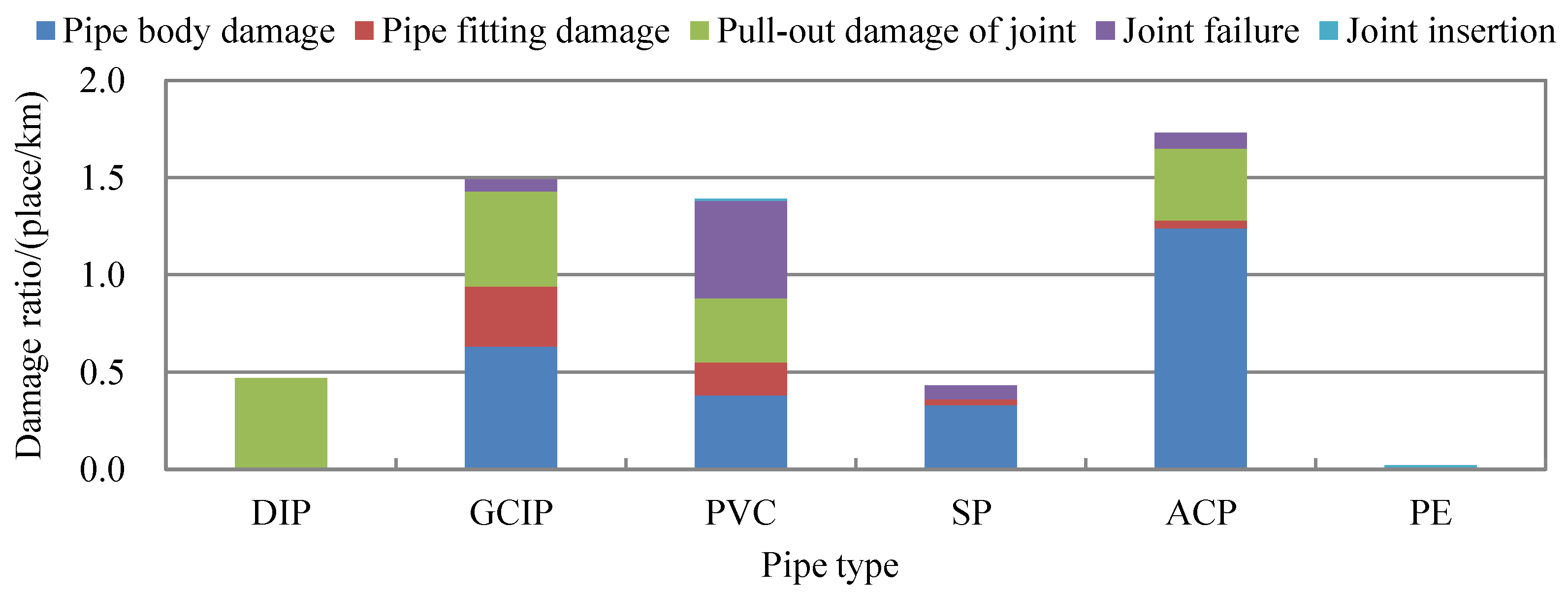
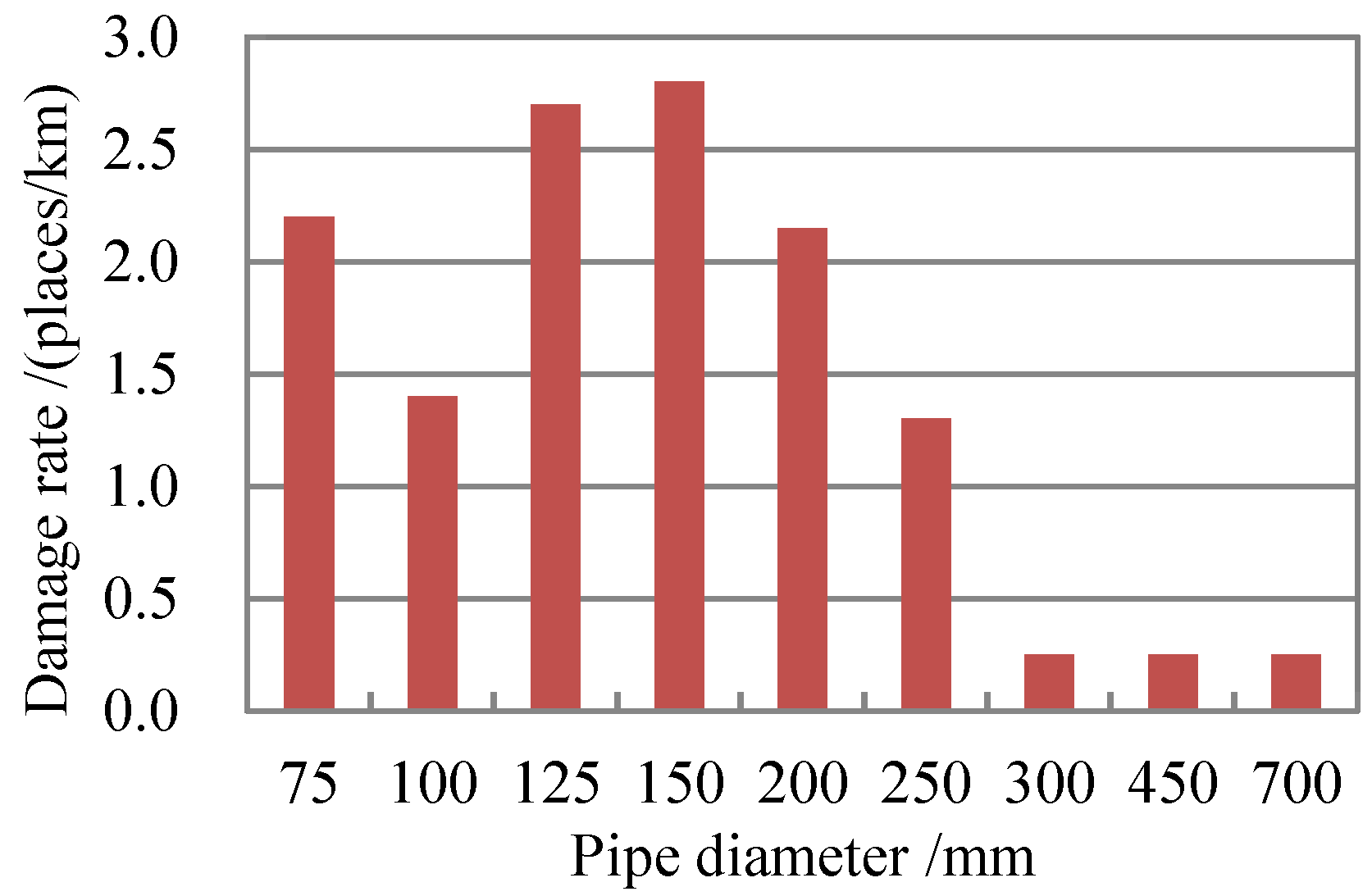
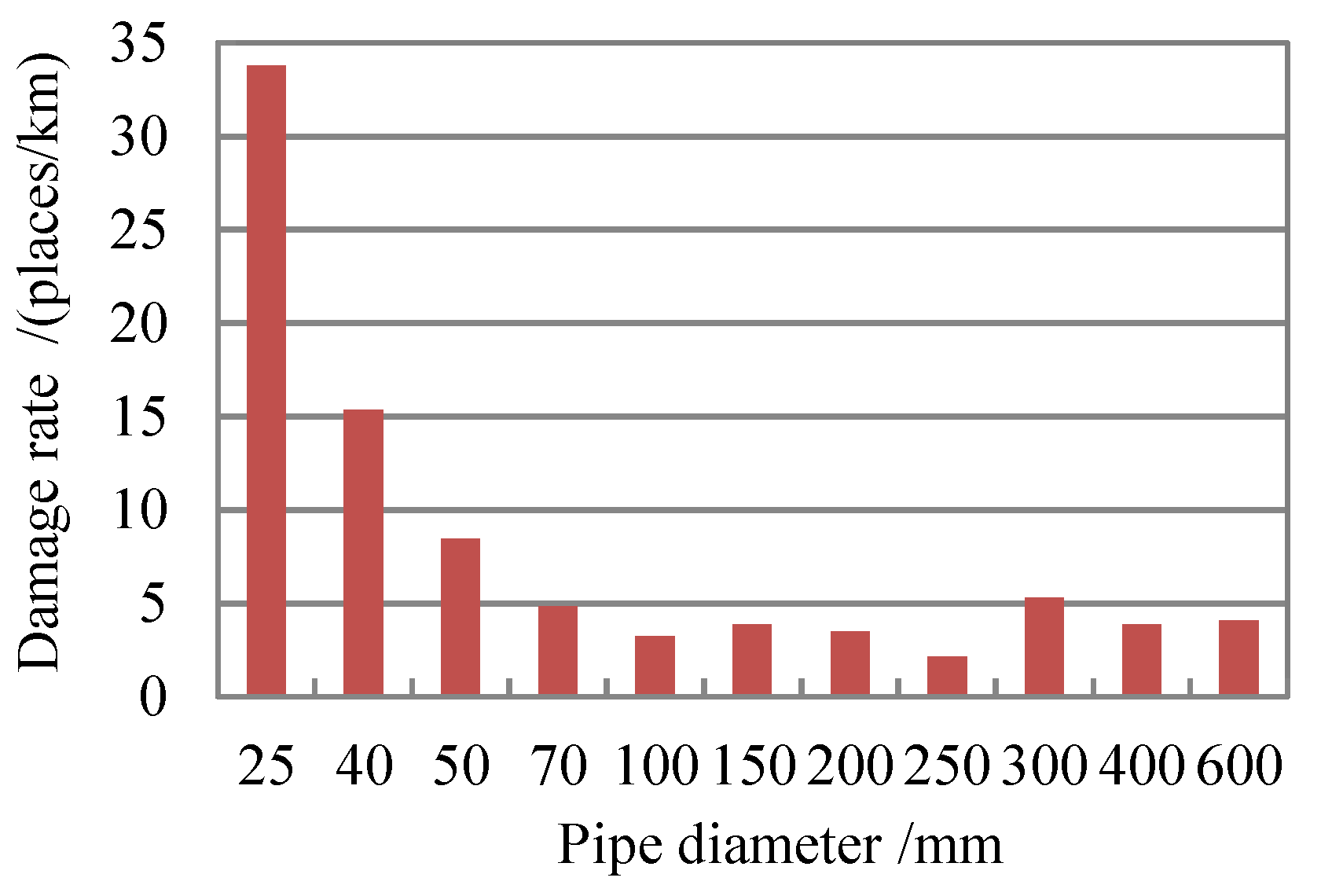
2.2. Analysis of Indices: Searching for the Relationships between Indices and Vulnerability
2.3. Stochastic Interpolation-Based Fractal Model for Seismic Vulnerability Assessment of WSNs
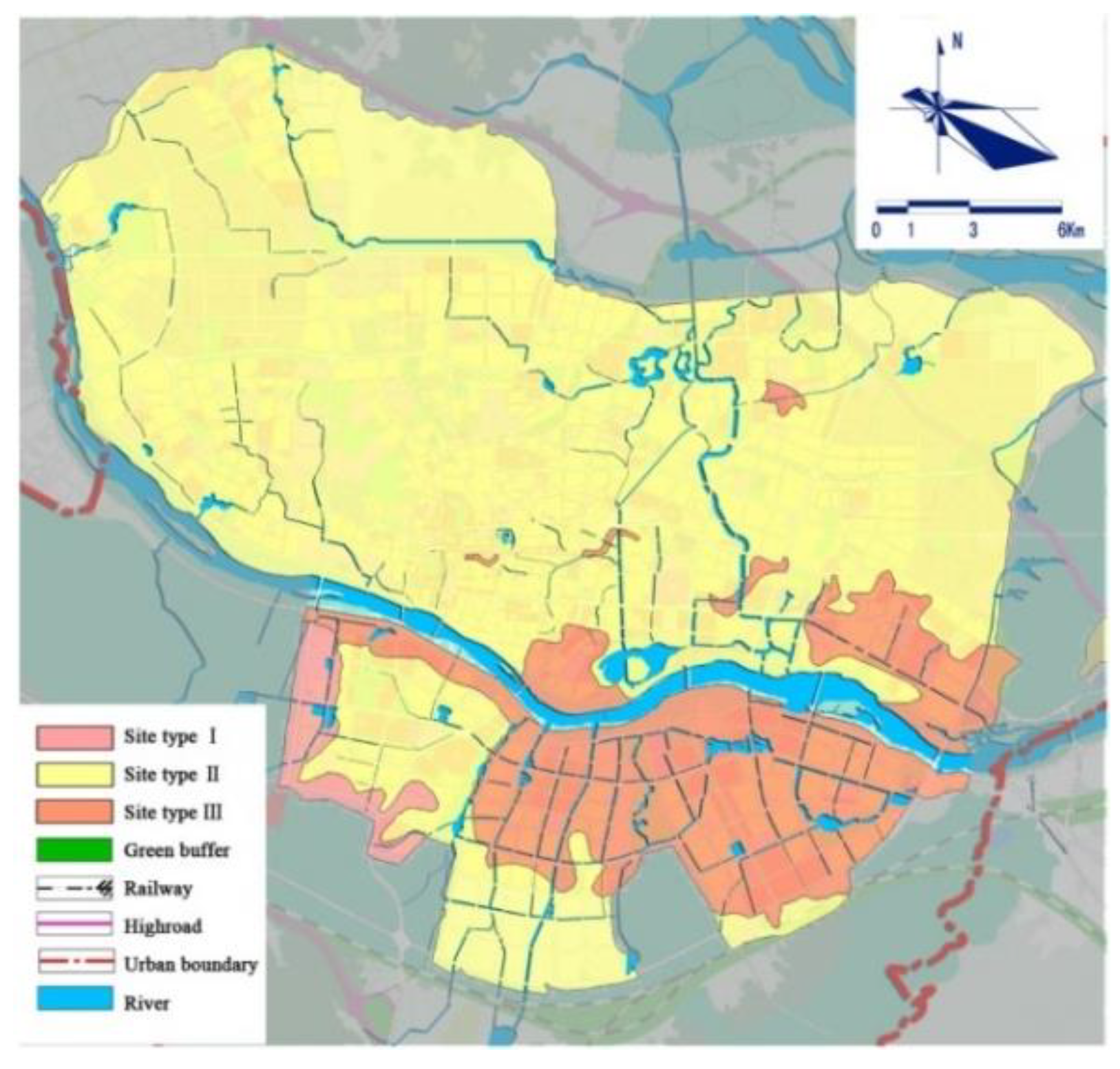
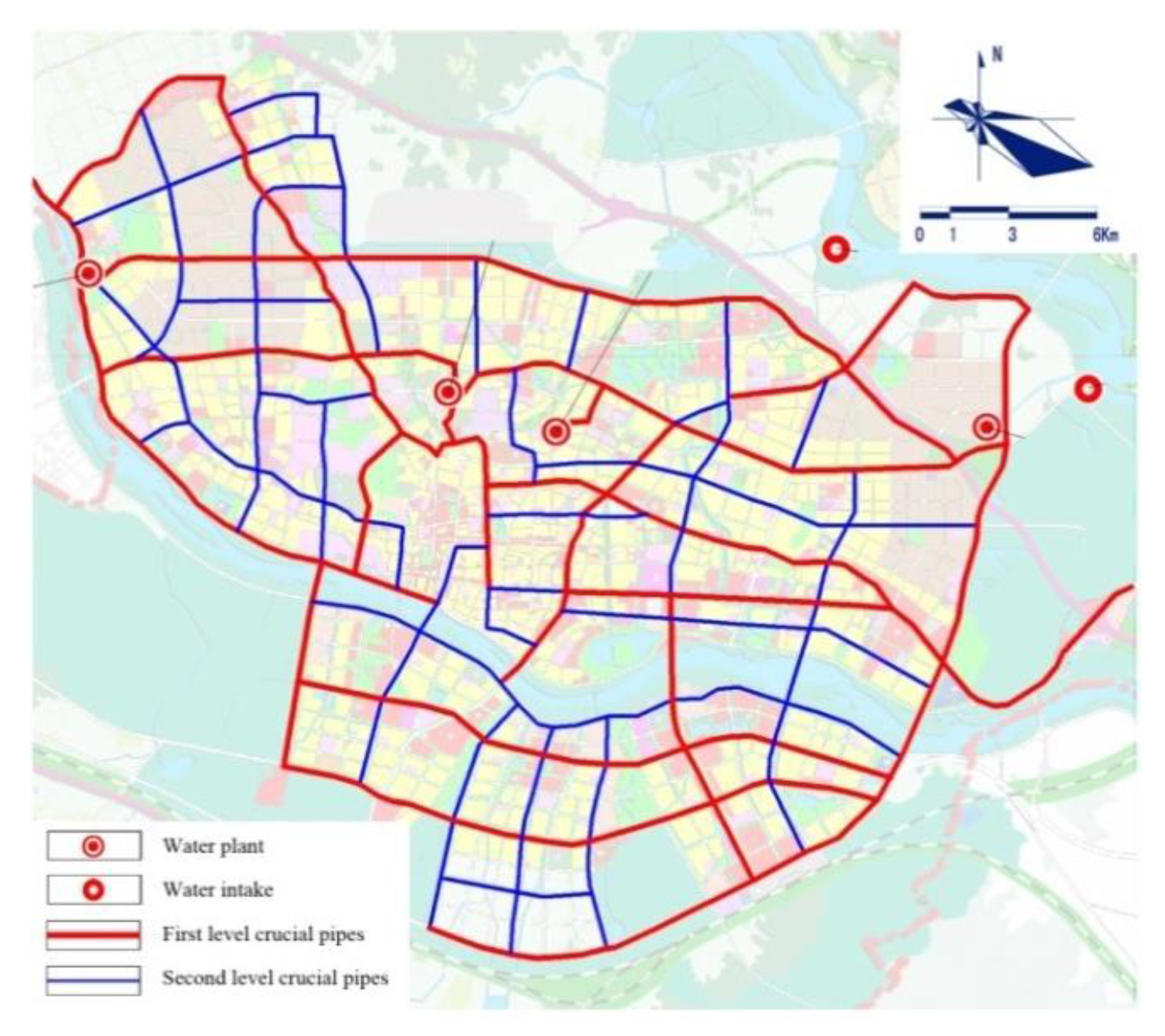
3. Case Study
3.1. Feasibility Analysis of the Model
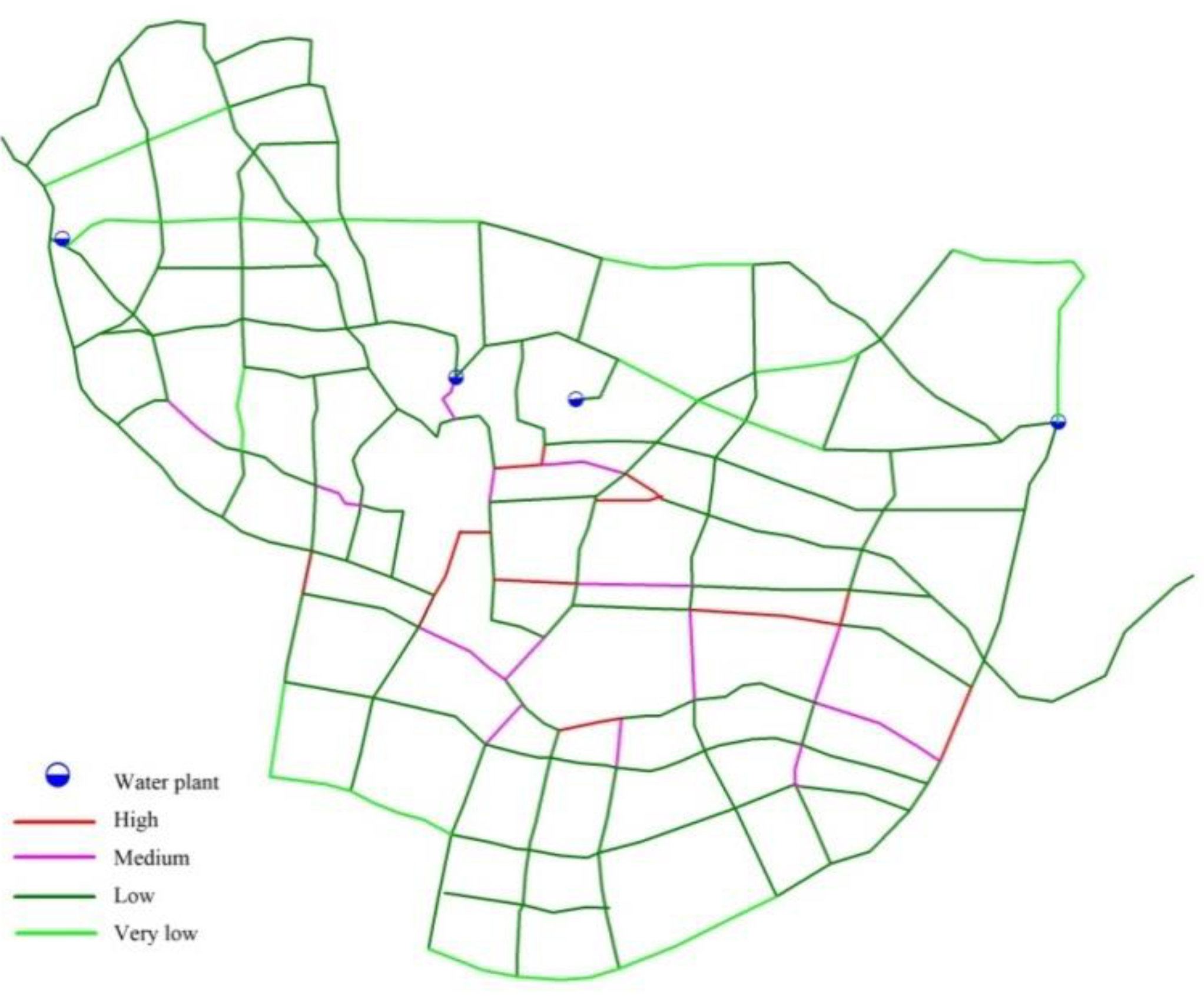
3.2. Application Example
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kanta, L.; Brumbelow, K. Vulnerability, risk, and mitigation assessment of water distribution system for insufficient fire flows. J. Water Resour. Plann Manag. 2013, 139, 593–603. [Google Scholar] [CrossRef]
- Laucelli, D.; Giustolisi, O. Vulnerability assessment of water distribution networks under seismic actions. J. Water Resour. Plann Manage. 2015, 141, 04014082-1–04014082-14. [Google Scholar] [CrossRef]
- Yang, S.L.; Hsu, N.S.; Loule, P.W.F.; Yeh, W.W.G. Water distribution network reliability: Connectivity analysis. J. Infrastruct. Syst. 1996, 2, 54–64. [Google Scholar] [CrossRef]
- Yazdani, A.; Otoo, R.A.; Jeffrey, P. Resilience enhancing expansion strategies for water distribution systems: A network theory approach. Environ. Model Softw. 2011, 26, 1574–1582. [Google Scholar] [CrossRef]
- Wang, S.W.; Wang, Y.; Qian, Z.H.; Liu, S.Q.; Yuan, W.Q.; Zheng, X.M. Investigation and analysis about damage and recovery of water supply system in 5.12 earthquake areas. China Water Wastewater 2009, 25, 2–11. [Google Scholar]
- Miyajima, M. Damage analysis of water supply facilities in the 2011 great east Japan earthquake and tsunami. In Proceedings of the 15th World Conference in Earthquake Engineering, Lisbon, Portugal, 28 September 2012; pp. 24–25. [Google Scholar]
- Giovinazzi, S.; Wilson, T.M.; Davis, C. Lifelines Performance and Management Following the 22 February 2011 Christchurch Earthquake; Highlights of resilience, University of Canterbury: Canterbury, New Zealand, 2011. [Google Scholar]
- Scawthorn, C.; Yamada, Y.; Iemura, H. A model for urban post-earthquake fire hazard. Disasters 1981, 5, 125–132. [Google Scholar] [CrossRef]
- Coppola, D. Introduction to Disaster Management; Elsevier: San Diego, CA, USA, 2007. [Google Scholar]
- Zhou, J.H. Destructive Test Study and Aseismic Analysis of Water Supply Pipeline. Doctoral Dissertation, University of Technology, Dalian, China, 2010. [Google Scholar]
- Toprak, S.; Taskin, F. Estimation of earthquake damage to buried pipelines caused by ground shaking. Nat. Hazards 2007, 40, 1–24. [Google Scholar] [CrossRef]
- Wang, Y.H.; Li, S.C.; Zhong, X.B.; Tian, B.P. Seismic reliability analysis of urban water supply system. World Earthq. Eng. 2014, 30, 224–228. [Google Scholar]
- He, S.H.; Zhao, Y.; Song, C. Seismic connectivity reliability analysis of urban water supply network. J. Disaster Prev. Mitig. Eng. 2011, 31, 585–589. [Google Scholar]
- Liu, W.; Zhao, Y.G.; Li, J. Seismic functional reliability analysis of water distribution networks. Struct. Infrastruct. Eng. 2015, 11, 363–375. [Google Scholar] [CrossRef]
- Hou, B.W.; Du, X.L.; Wang, W. Seismic performance based design of water distribution system considering comprehensive importance of users. China Civil Eng. J. 2015, 48, 11–22. [Google Scholar]
- Liu, W.; Xu, L.; Li, J. Algorithms for seismic topology optimization of water distribution network. Sci. China Technol. Sci. 2012, 55, 3047–3056. [Google Scholar] [CrossRef]
- Cimellaro, G.P.; Solari, D.; Bruneau, M. Physical infrastructure interdependency and regional resilience index after the 2011 Tohoku earthquake in Japan. Earthq. Eng. Struct. Dyn. 2014, 43, 1763–1784. [Google Scholar] [CrossRef]
- Luna, R.; Balakrishnan, N.; Dagli, C.H. Post-earthquake recovery of a water distribution system: Discrete event simulation using colored petri nets. J. Infrastruct. Syst. 2011, 17, 25–34. [Google Scholar] [CrossRef]
- Kozin, F.; Zhou, H. System study of urban response and reconstruction due to earthquake. J. Eng. Mech. 1990, 116, 1959–1972. [Google Scholar] [CrossRef]
- Tabucchi, T.; Davidson, R.; Brink, S. Simulation of post-earthquake water supply system restoration. Civil Eng. Environ. Syst. 2010, 27, 263–279. [Google Scholar] [CrossRef]
- Turner, J.P.; Qiao, J.; Lawley, M.; Richard, J.; Abraham, D.M. Mitigating shortage and distribution costs in damaged water networks. Socio-Econ. Plan. Sci. 2012, 46, 315–326. [Google Scholar] [CrossRef]
- Yoo, D.G.; Jung, D.; Kang, D.; Kim, J.H.; Lansey, K. Seismic hazard assessment model for urban water supply networks. J. Water Resour. Plann. Manag. 2016, 142, 04015055. [Google Scholar] [CrossRef]
- Christodoulou, S.E.; Fragiadakis, M. Vulnerability assessment of water distribution networks considering performance data. J. Infrastruct. Syst. 2015. [Google Scholar] [CrossRef]
- Zhang, Z.P.; Wang, Z.T.; Su, J.Y.; Wang, W. Research on the seismic damage assessment of underground pipelines. China Rural Water Hydropower 2013, 8, 43–47. [Google Scholar]
- Bai, J.L. Study on the seismic risk control of water supply pipelines. Tianjin University: Tianjin, China, 2011. [Google Scholar]
- Wu, J.; Liu, W.L.; Liang, J.; Feng, B.R. Seismic vulnerability evaluation of Beijing’s water supply pipeline. J. Wuhan Univ. Technol. (Inf. Manag. Eng.) 2017, 39, 140–143. [Google Scholar]
- Wang, Z.T.; Wang, W.; Guo, X.D. Seismic vulnerability assessment for water supply network based on nodes importance. Disaster Adv. 2013, 6, 430–436. [Google Scholar]
- Halfaya, F.Z.; Bensaibi, M.; Davenne, L. Seismic vulnerability of buried water pipes. Adv. Environ. Sci. Eng. 2012. [Google Scholar] [CrossRef]
- O’Rourke, M.J.; Ayala, G. Pipeline damage due to wave propagation. J. Geotech. Eng. 1993, 119, 123–134. [Google Scholar] [CrossRef]
- Burton, I.; Katers, R.W.; White, G.F. The Environment as Hazard, 2nd ed.; The Guildford Press: New York, NY, USA, 1993. [Google Scholar]
- Shi, P.J. Theory and practice of disaster study. J. Nat. Disaster 1996, 5, 6–17. [Google Scholar]
- Wisner, B.; Blaikie, P.; Cannon, T.; Davis, I. At Risk: Natural Hazards, People’s Vulnerability and Disasters, 2nd ed.; Routledge: London, UK, 2004. [Google Scholar]
- United Nations Disaster Relief Organization. Mitigating Natural Disasters Phenomenal Effects and Options a Manual for Policy Makers and Planners; United Nations Disaster Relief Organization: New York, NY, USA, 1991. [Google Scholar]
- Gentile, F.; Bisantino, T.; Trisorio, L.G. Debris-flow risk analysis in south Gargano watersheds (Southern Italy). Nat. Hazards 2008, 44, 1–17. [Google Scholar] [CrossRef]
- United States Agency for International Development. Interduction to Disaster Risk Reduction; USAI: Washington, DC, USA, 2011.
- McGuire, B.; Mason, I.; Kiburn, C. Natural Hazards and Environmental Change; Arnold: London, UK, 2002. [Google Scholar]
- Intentional Strategy for Disaster Reduction. Living with Risk, A Global Review of Disaster Reduction Initiatives; United Nations publication: Geneva, Switzerland, 2004. [Google Scholar]
- Alexander, D. Natural Disaster; UCL Press: London, UK, 1993. [Google Scholar]
- Smith, K. Environmental Hazards: Assessing Risk and Reducing Disaster, 3rd ed.; Routledge: New York, NY, USA, 2000. [Google Scholar]
- Gill, J.C.; Malamud, B.D. Reviewing and visualizing the interaction of natural hazards. Rev. Geophys. 2014, 52, 680–722. [Google Scholar] [CrossRef]
- Jin, S.M. Research on Earthquake Disaster Risk and Resilience of Urban Water Supply System. Master Dissertation, Institute of Technology, Harbin, China, 2013. [Google Scholar]
- Balica, S.F.; Douben, N.; Wright, N.G. Flood vulnerability indices at varying spatial scales. Water Sci. Technol. 2009, 60, 2571–2580. [Google Scholar] [CrossRef]
- United Nations International Strategy for Disaster Reduction. UNISDR Terminology for Disaster Risk Reduction; United Nations International Strategy for Disaster Reduction (UNISDR): Geneva, Switzerland, 2009. [Google Scholar]
- Balica, S.F.; Wright, N.G.; Meulen, F. A flood vulnerability index for coastal cities and its use in assessing climate change impacts. Nat. Hazards 2012, 64, 73–105. [Google Scholar] [CrossRef]
- Ndah, A.B.; Odihi, J.O. A systematic study of disaster risk in Brunei Darussalam and options for vulnerability-based disaster risk reduction. Int. J. Disaster Risk Sci. 2017, 8, 208–223. [Google Scholar] [CrossRef][Green Version]
- Ye, Y.X.; Okada, N. Earthquake Disaster Comparatology; China Building Industry Press: Beijing, China, 2008. [Google Scholar]
- Yang, C. Study on Seismic Damage Assessment of Urban Water Supply Pipe Network. Master’s Thesis, Zhejiang University, Hangzhou, China, 2010. [Google Scholar]
- Liu, H.X. Earthquake Damage of Tangshan Earth- Quake; Seismological Press: Beijing, China, 1986. [Google Scholar]
- Jiang, H. Analysis of Buried Pipeline Response to Seismic Wave Propagation. Master’s Thesis, Huazhong University of Science & Technology, Wuhan, China, 2011. [Google Scholar]
- Wu, G.Z.; Xu, Z.X.; Li, C.Y. Water eutrophication assessment and validation based on fractal theory. Water Resour. Prot. 2012, 28, 12–16. [Google Scholar]
- Niu, Y.C.; Zhou, Z.F.; Wang, L.; Dan, Y.S.; Feng, Q. Comprehensive evaluation of soil nutrients in Guizhou agricultural products areas based on the fractal interpolation model. Environ. Chem. 2018, 37, 2207–2218. [Google Scholar]
- Nu, Z.G.; Jiang, W.; Lu, R.Q.; Zhang, H.W. Research on the vulnerability assessment model of water supply systems based on catastrophe theory. J. Harbin Inst. Technol. 2012, 44, 135–138. [Google Scholar]

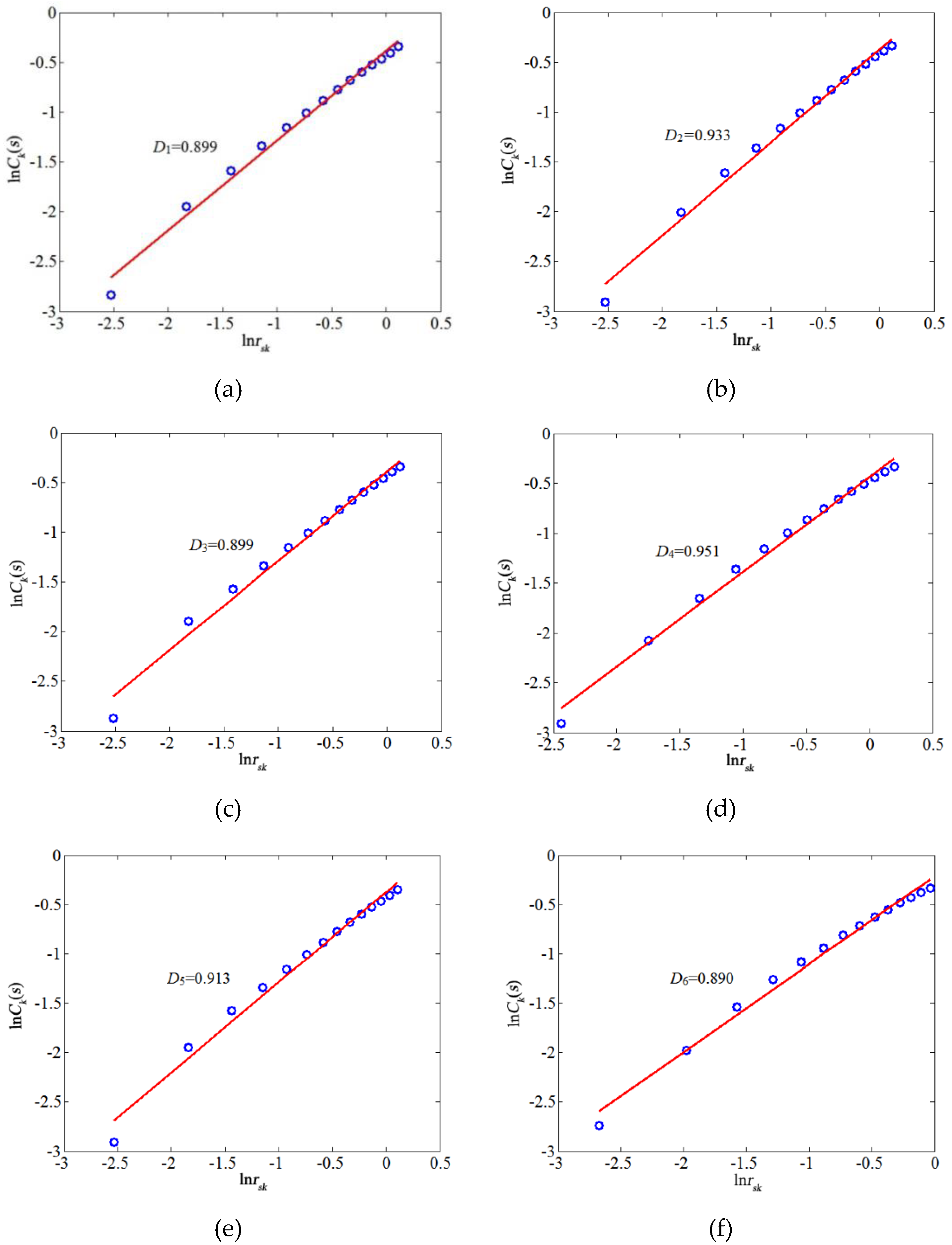
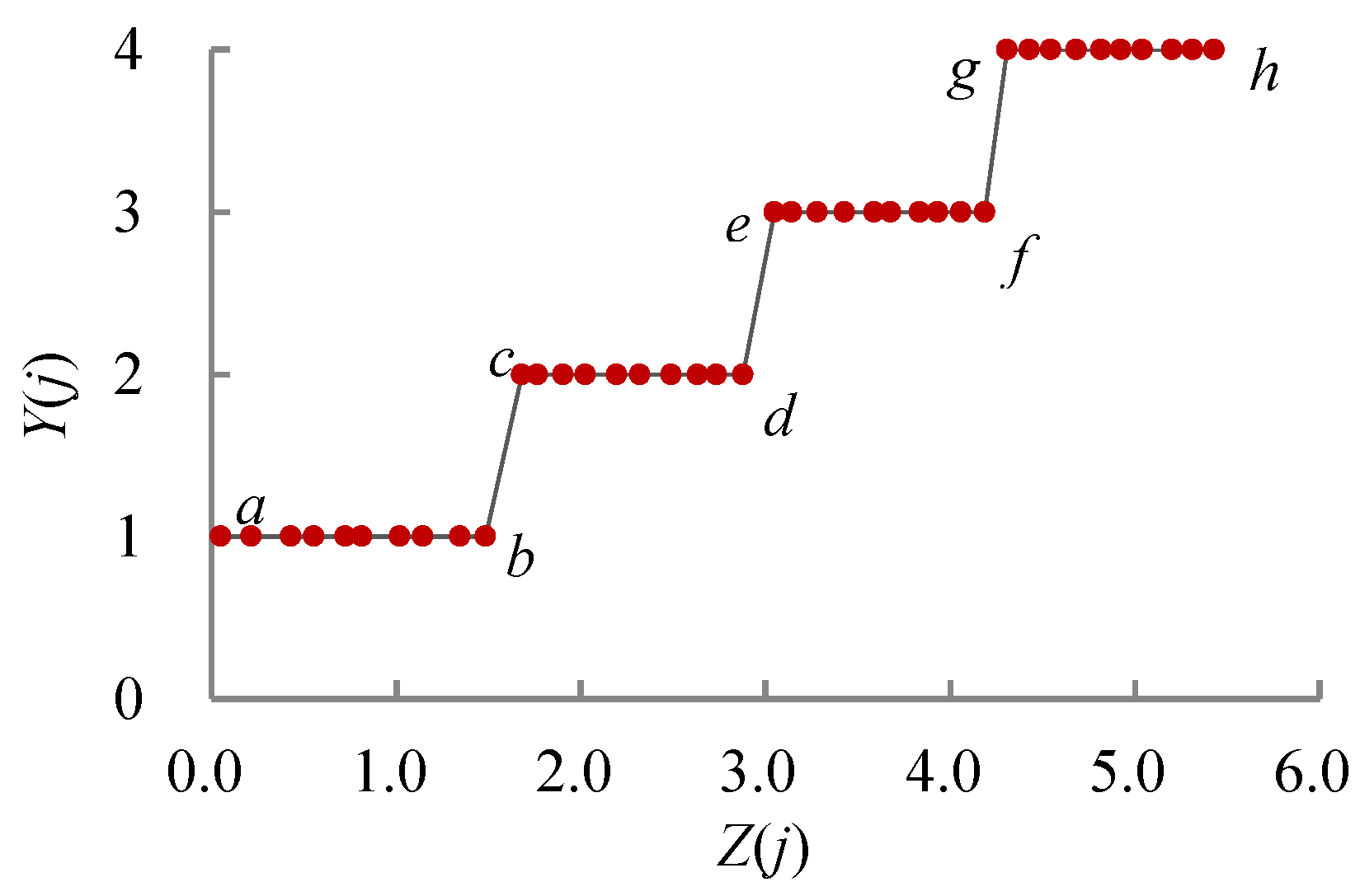
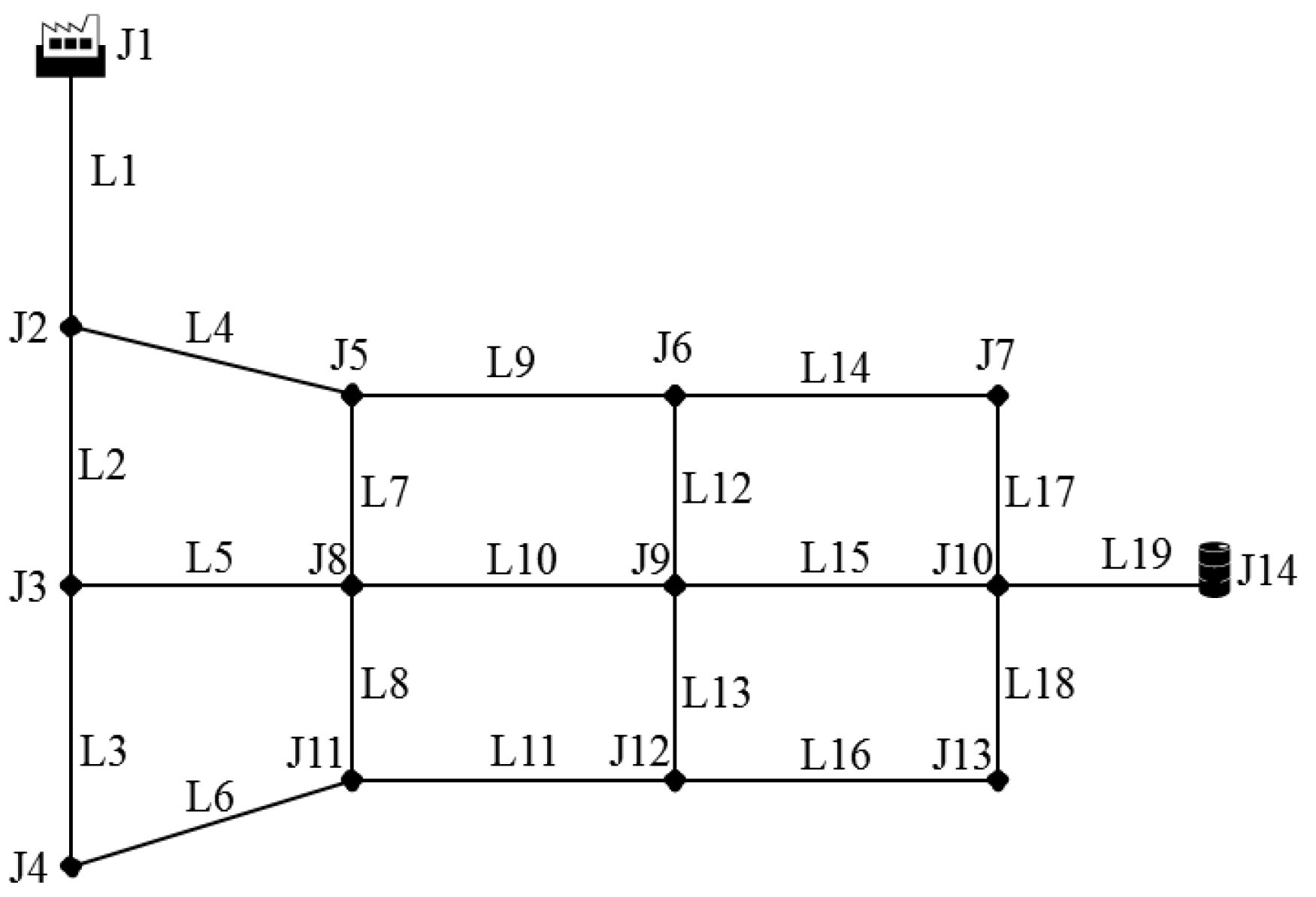
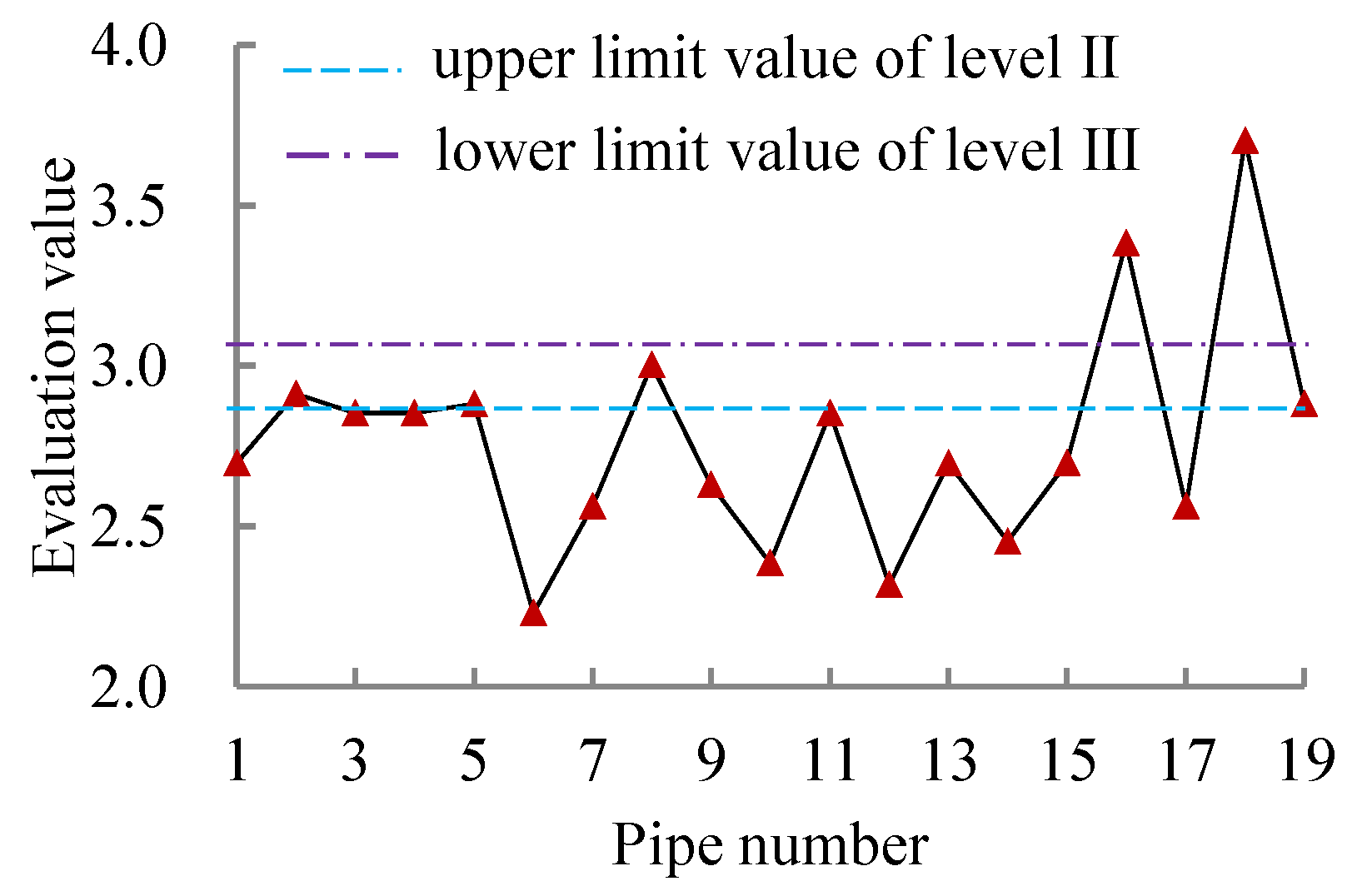
| District | Seismic Intensity (Degree) | Soil Type of the Site | Damage Rate (Places/km) |
|---|---|---|---|
| Tianjin City | 7–8 | Type 3 | 0.18 |
| Tanggu district | 8 | Type 3 | 4.18 |
| Hangu district | 9 | Type 3 | 10.00 |
| Tangshan city | 10–11 | Type 2 | 4.00 |
| San Fernando | 8 | Type 1 | 0.09 |
| Los Angeles | 6 | Type 2 | 0.62 |
| Sendai area | 9 | Type 1 | 0.03 |
| Type 2 | 0.22 | ||
| Type 3 | 0.87 |
| Grade | x1 | x2 (mm) | x3 | x4 (Year) | x5 | x6 (m) |
|---|---|---|---|---|---|---|
| High (IV) | Wrapped FRP pipe Asbestos cement pipe Concrete pipe | x2 ≤ 200 | Adhesion connection Threaded connection Asbestos cement Self-stressing cement | 50 ≤ x4 | Type 4 | x6 ≤ 0.5 |
| Medium (III) | Plain cast-iron pipe Prestressed reinforced concrete pipe | 200 < x2 ≤ 500 | Welding | 30 ≤x4 < 50 | Type 3 | 0.5 < x6 ≤ 1 |
| Low (II) | Polyvinyl chloride pipe Steel pipe Ductile cast-iron pipe | 500 < x2 ≤ 800 | Hot-melt connection Flange connection | 10 ≤ x4 < 30 | Type 2 | 1 < x6 ≤ 2 |
| Very low (I) | Polythene pipe Steel–plastic compound pipe | 800 < x2 | Rubber ring connection | x4 < 10 | Type 1 | 2 < x6 |
| Grade | x1 | x2 (mm) | x3 | x4 (Year) | x5 | x6 (m) |
|---|---|---|---|---|---|---|
| High (IV) | 3.5–4.5 | 0–200 | 3.5–4.5 | 50–70 | 3.5–4.5 | 0.0–0.5 |
| Medium (III) | 2.5–3.5 | 200–500 | 2.5–3.5 | 30–50 | 2.5–3.5 | 0.5–1.0 |
| Low (II) | 1.5–2.5 | 500–800 | 1.5–2.5 | 10–30 | 1.5–2.5 | 1.0–2.0 |
| Very low (I) | 0.5–1.5 | 800–1200 | 0.5–1.5 | 0–10 | 0.5–1.5 | 2.0–4.0 |
| Grade | x1 | x2 | x3 | x4 | x5 | x6 |
|---|---|---|---|---|---|---|
| High (IV) | 0.750–1.000 | 0.833–1.00 | 0.750–1.000 | 0.714–1.000 | 0.750–1.000 | 0.875–1.000 |
| Medium (III) | 0.500–0.750 | 0.583–0.833 | 0.500–0.750 | 0.429–0.714 | 0.500–0.750 | 0.750–0.875 |
| Low (II) | 0.250–0.500 | 0.333–0.583 | 0.250–0.500 | 0.143–0.429 | 0.250–0.500 | 0.500–0.750 |
| Very low (I) | 0.000–0.250 | 0.000–0.333 | 0.000–0.250 | 0.000–0.143 | 0.000–0.250 | 0.000–0.500 |
| No | x1 | x2 | x3 | x4 | x5 | x6 | Y(j) | No | x1 | x2 | x3 | x4 | x5 | x6 | Y(j) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.011 | 0.018 | 0.012 | 0.001 | 0.004 | 0.008 | 1 | 21 | 0.523 | 0.602 | 0.519 | 0.432 | 0.514 | 0.752 | 3 |
| 2 | 0.028 | 0.049 | 0.029 | 0.014 | 0.035 | 0.083 | 1 | 22 | 0.528 | 0.608 | 0.531 | 0.484 | 0.530 | 0.763 | 3 |
| 3 | 0.075 | 0.096 | 0.070 | 0.035 | 0.054 | 0.145 | 1 | 23 | 0.569 | 0.634 | 0.568 | 0.491 | 0.555 | 0.779 | 3 |
| 4 | 0.083 | 0.127 | 0.078 | 0.052 | 0.094 | 0.176 | 1 | 24 | 0.593 | 0.675 | 0.599 | 0.522 | 0.577 | 0.791 | 3 |
| 5 | 0.107 | 0.158 | 0.107 | 0.068 | 0.122 | 0.235 | 1 | 25 | 0.614 | 0.698 | 0.622 | 0.566 | 0.623 | 0.808 | 3 |
| 6 | 0.127 | 0.168 | 0.131 | 0.079 | 0.134 | 0.258 | 1 | 26 | 0.630 | 0.721 | 0.627 | 0.585 | 0.643 | 0.824 | 3 |
| 7 | 0.157 | 0.202 | 0.163 | 0.087 | 0.167 | 0.348 | 1 | 27 | 0.665 | 0.751 | 0.659 | 0.622 | 0.664 | 0.837 | 3 |
| 8 | 0.176 | 0.236 | 0.177 | 0.109 | 0.182 | 0.377 | 1 | 28 | 0.682 | 0.776 | 0.684 | 0.640 | 0.683 | 0.843 | 3 |
| 9 | 0.213 | 0.293 | 0.210 | 0.116 | 0.213 | 0.434 | 1 | 29 | 0.703 | 0.803 | 0.717 | 0.665 | 0.704 | 0.853 | 3 |
| 10 | 0.244 | 0.331 | 0.228 | 0.131 | 0.246 | 0.452 | 1 | 30 | 0.730 | 0.815 | 0.740 | 0.687 | 0.741 | 0.872 | 3 |
| 11 | 0.272 | 0.350 | 0.270 | 0.162 | 0.275 | 0.519 | 2 | 31 | 0.754 | 0.844 | 0.767 | 0.717 | 0.752 | 0.882 | 4 |
| 12 | 0.277 | 0.372 | 0.284 | 0.184 | 0.279 | 0.544 | 2 | 32 | 0.784 | 0.851 | 0.778 | 0.765 | 0.779 | 0.892 | 4 |
| 13 | 0.306 | 0.393 | 0.305 | 0.213 | 0.306 | 0.569 | 2 | 33 | 0.801 | 0.868 | 0.818 | 0.780 | 0.804 | 0.904 | 4 |
| 14 | 0.326 | 0.410 | 0.327 | 0.246 | 0.335 | 0.578 | 2 | 34 | 0.838 | 0.896 | 0.828 | 0.817 | 0.830 | 0.918 | 4 |
| 15 | 0.361 | 0.453 | 0.369 | 0.259 | 0.352 | 0.617 | 2 | 35 | 0.858 | 0.915 | 0.853 | 0.856 | 0.858 | 0.930 | 4 |
| 16 | 0.375 | 0.466 | 0.380 | 0.295 | 0.392 | 0.637 | 2 | 36 | 0.879 | 0.925 | 0.891 | 0.869 | 0.883 | 0.942 | 4 |
| 17 | 0.422 | 0.498 | 0.410 | 0.337 | 0.410 | 0.655 | 2 | 37 | 0.905 | 0.935 | 0.908 | 0.905 | 0.905 | 0.957 | 4 |
| 18 | 0.430 | 0.527 | 0.439 | 0.363 | 0.450 | 0.677 | 2 | 38 | 0.948 | 0.964 | 0.941 | 0.936 | 0.931 | 0.972 | 4 |
| 19 | 0.452 | 0.536 | 0.456 | 0.375 | 0.460 | 0.721 | 2 | 39 | 0.967 | 0.972 | 0.969 | 0.955 | 0.972 | 0.980 | 4 |
| 20 | 0.483 | 0.561 | 0.491 | 0.404 | 0.491 | 0.729 | 2 | 40 | 0.987 | 0.988 | 0.990 | 0.990 | 0.993 | 0.993 | 4 |
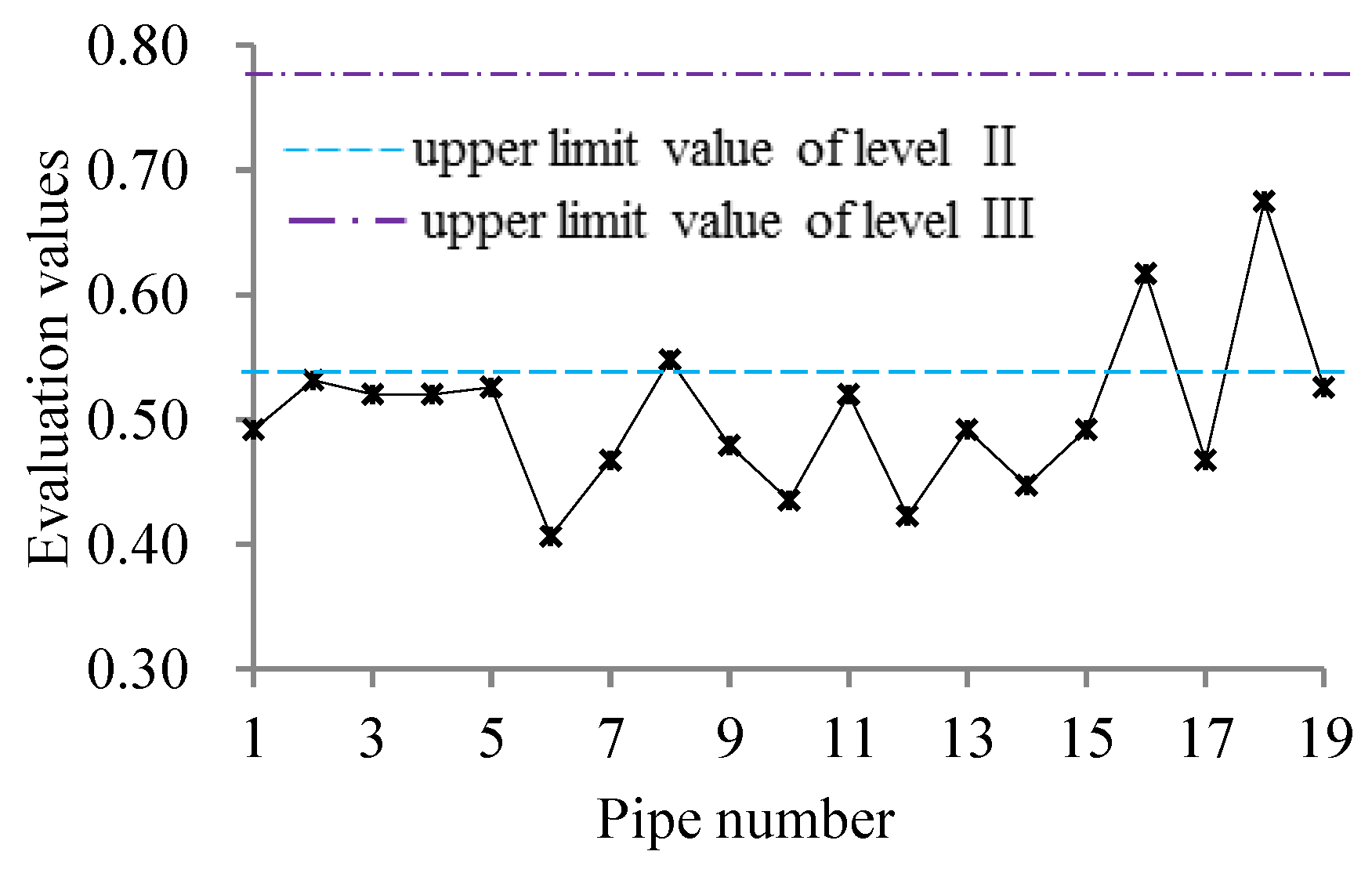
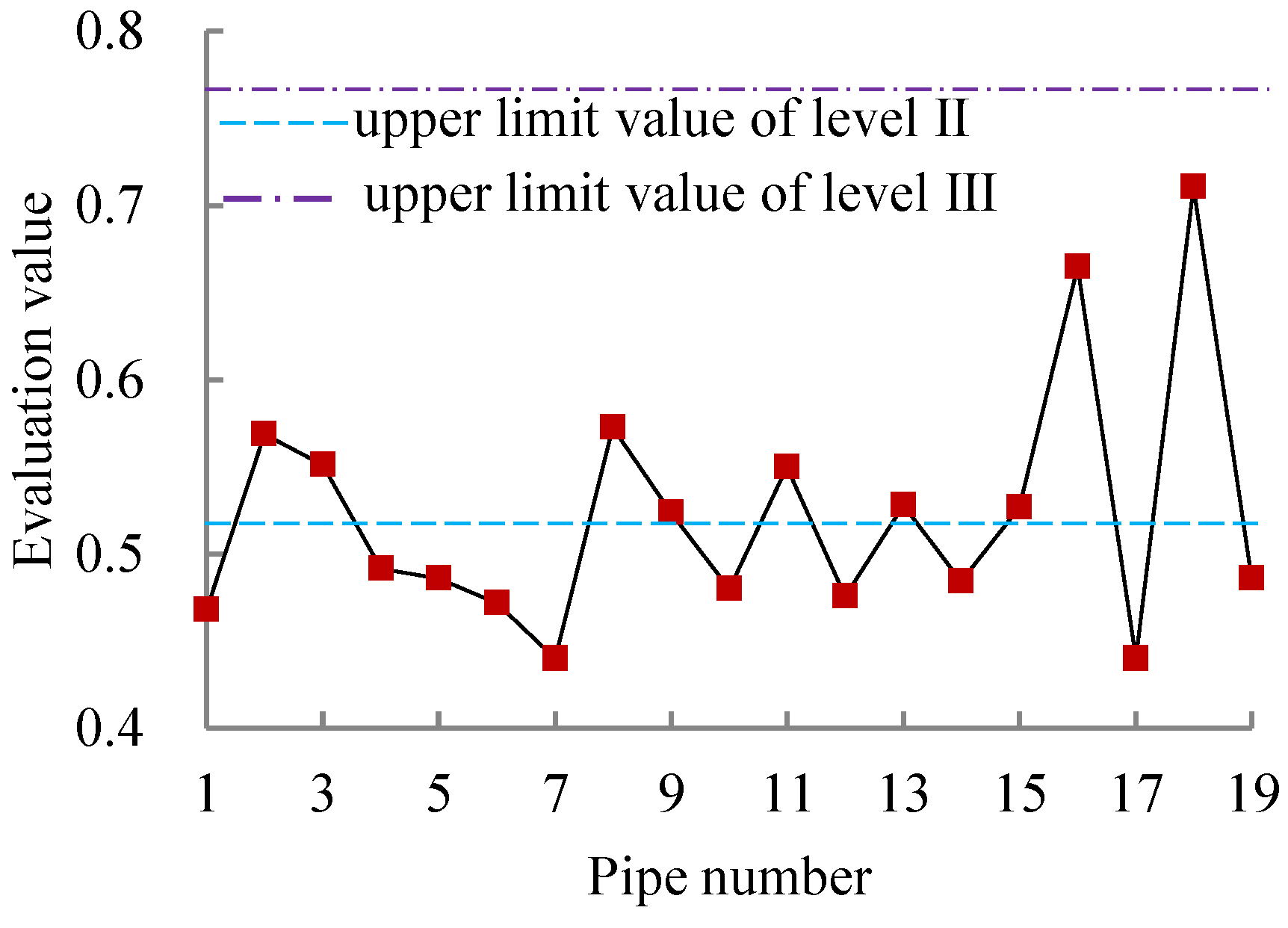
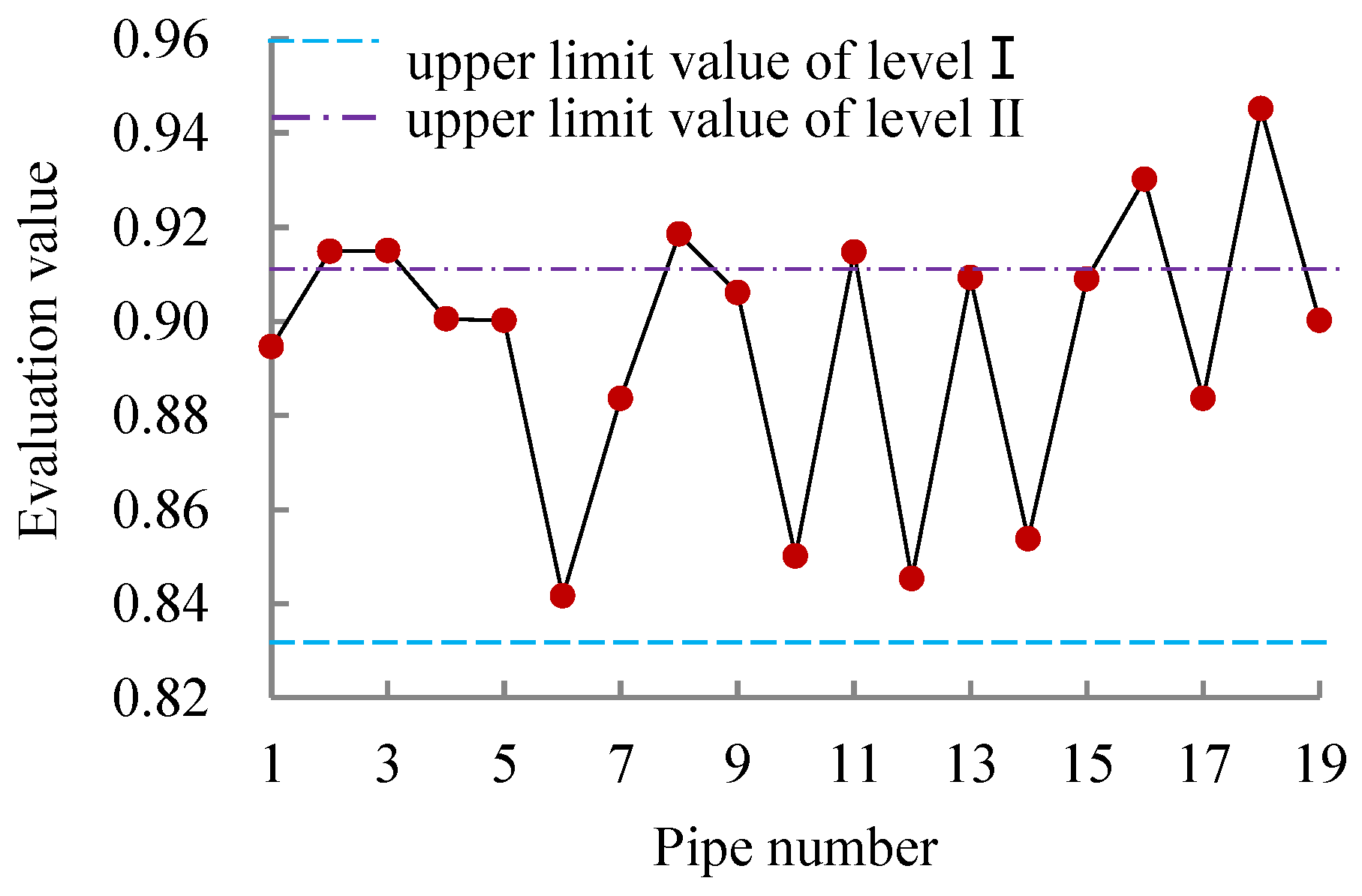
| No. | The Proposed Method in This Paper | AHP-Based Assessment Method [27] | Catastrophe Progression Method [26,52] | ||||
|---|---|---|---|---|---|---|---|
| Evaluation Value | Grade Value | Grade | Evaluation value | Grade | Evaluation value | Grade | |
| 1 | 2.697 | 2 | II | 0.468 | II | 0.895 | II |
| 2 | 2.913 | 2.2 | [II,III] | 0.568 | III | 0.915 | III |
| 3 | 2.853 | 2 | II | 0.551 | III | 0.915 | III |
| 4 | 2.853 | 2 | II | 0.491 | II | 0.900 | II |
| 5 | 2.882 | 2.0 | II | 0.486 | II | 0.900 | II |
| 6 | 2.229 | 2 | II | 0.472 | II | 0.842 | II |
| 7 | 2.562 | 2 | II | 0.440 | II | 0.883 | II |
| 8 | 3.002 | 2.7 | [II,III] | 0.572 | III | 0.919 | III |
| 9 | 2.630 | 2 | II | 0.524 | III | 0.906 | II |
| 10 | 2.386 | 2 | II | 0.480 | II | 0.850 | II |
| 11 | 2.852 | 2 | II | 0.550 | III | 0.915 | III |
| 12 | 2.318 | 2 | II | 0.476 | II | 0.845 | II |
| 13 | 2.698 | 2 | II | 0.528 | III | 0.909 | II |
| 14 | 2.453 | 2 | II | 0.484 | II | 0.854 | II |
| 15 | 2.696 | 2 | II | 0.527 | III | 0.909 | II |
| 16 | 3.381 | 3 | III | 0.665 | III | 0.930 | III |
| 17 | 2.562 | 2 | II | 0.440 | II | 0.883 | II |
| 18 | 3.701 | 3 | III | 0.711 | III | 0.945 | III |
| 19 | 2.882 | 2.0 | II | 0.486 | II | 0.900 | II |
| No | x1 | x2 /mm | x3 | x4 /Years | x5 | x6 /m |
|---|---|---|---|---|---|---|
| 1 | Concrete pipe | 800 | Rubber ring | 20 | 3 | 1.1 |
| 2 | Steel pipe | 400 | Welding | 13 | 3 | 1.1 |
| 3 | Steel pipe | 600 | Welding | 20 | 3 | 1.1 |
| 4 | Concrete pipe | 600 | Rubber ring | 20 | 3 | 1.1 |
| 5 | Grey cast-iron pipe | 300 | Rubber ring | 15 | 3 | 0.7 |
| 6 | Steel pipe | 1200 | Welding | 10 | 3 | 1.2 |
| 7 | Nodular cast iron pipe | 300 | Rubber ring | 8 | 3 | 0.7 |
| 8 | Steel pipe | 400 | Welding | 13 | 3 | 0.7 |
| 9 | Steel pipe | 800 | Welding | 15 | 3 | 1.1 |
| 10 | Steel pipe | 1200 | Welding | 15 | 3 | 0.8 |
| 11 | Steel pipe | 600 | Welding | 15 | 3 | 0.8 |
| 12 | Steel pipe | 1200 | Welding | 10 | 3 | 0.8 |
| 13 | Steel pipe | 800 | Welding | 20 | 3 | 1.1 |
| 14 | Steel pipe | 1200 | Welding | 20 | 3 | 0.8 |
| 15 | Steel pipe | 800 | Welding | 15 | 3 | 0.8 |
| 16 | Nodular cast-iron pipe | 200 | Asbestos cement | 8 | 3 | 0.4 |
| 17 | Nodular cast-iron pipe | 300 | Rubber ring | 8 | 3 | 0.7 |
| 18 | Gray cast-iron pipe | 200 | Asbestos cement | 15 | 3 | 0.4 |
| 19 | Gray cast-iron pipe | 300 | Rubber ring | 15 | 3 | 0.7 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, C.; Li, Y.; Yin, H.; Zhang, J.; Wang, W. A Stochastic Interpolation-Based Fractal Model for Vulnerability Diagnosis of Water Supply Networks Against Seismic Hazards. Sustainability 2020, 12, 2693. https://doi.org/10.3390/su12072693
Liu C, Li Y, Yin H, Zhang J, Wang W. A Stochastic Interpolation-Based Fractal Model for Vulnerability Diagnosis of Water Supply Networks Against Seismic Hazards. Sustainability. 2020; 12(7):2693. https://doi.org/10.3390/su12072693
Chicago/Turabian StyleLiu, Chaofeng, Yawei Li, He Yin, Jiaxin Zhang, and Wei Wang. 2020. "A Stochastic Interpolation-Based Fractal Model for Vulnerability Diagnosis of Water Supply Networks Against Seismic Hazards" Sustainability 12, no. 7: 2693. https://doi.org/10.3390/su12072693
APA StyleLiu, C., Li, Y., Yin, H., Zhang, J., & Wang, W. (2020). A Stochastic Interpolation-Based Fractal Model for Vulnerability Diagnosis of Water Supply Networks Against Seismic Hazards. Sustainability, 12(7), 2693. https://doi.org/10.3390/su12072693





