Energy and Emission Efficiency of the Slovak Regions
Abstract
1. Introduction
1.1. Structural Change and Energy and Emission Efficiency
1.2. Literature Review
1.3. Research Gap
1.4. Research Hypothesis, Data Sources and Research Methods
- Research question 1 concerns the key drivers of energy and emission efficiency: What was the key driver of energy production and emission efficiency—an increase in value added or a decrease in the consumption of energy and the production of emissions?
- Research question 2 is concerned with the regional patterns of energy and emission efficiency: What regions accounted for the highest improvements in energy efficiency, emission efficiency, and energy-eco efficiency in the long term?
- The following hypothesis on the effects of the European Structural and Cohesion Funds on energy and emission efficiency was proposed: Assistance from the European Structural and Cohesion Funds increased the energy and emission efficiency in Slovakia.
1.5. Data Sources
- The Operational Programme Competitiveness and Economic Growth (OPCEG) implemented Policy Measure 1.1 ‘Innovation and Technology Transfers’. The policy measure allocated €369.30m to the purchase of new technologies. The policy measure aimed at a ‘growth in competitiveness and value added, and decrease in energy consumption and undesirable ecological impacts of manufacturing’. The policy measure was implemented in all 79 Slovak districts.
- OPCEG Policy Measure 2.1 ‘Increase in Efficiency in Production and Consumption of Energy’ targeted ‘increasing efficiency of primary energy resources’ and ‘increasing share of renewable resources in the total energy consumption’. The policy measure allocated €94.71 m in 53 out of a total of 79 Slovak districts.
- The Operational Programme Environment (OPE) implemented several green initiatives. OPE Policy Measure 3.1 supported projects aimed at decreasing emissions in industry. The policy measure allocated €142.43 m in 50 out of a total of 79 Slovak districts.
1.6. Research Methods
2. Energy and Emission Efficiency of the Slovak Regions
2.1. Drivers of Energy and Emission Efficiency
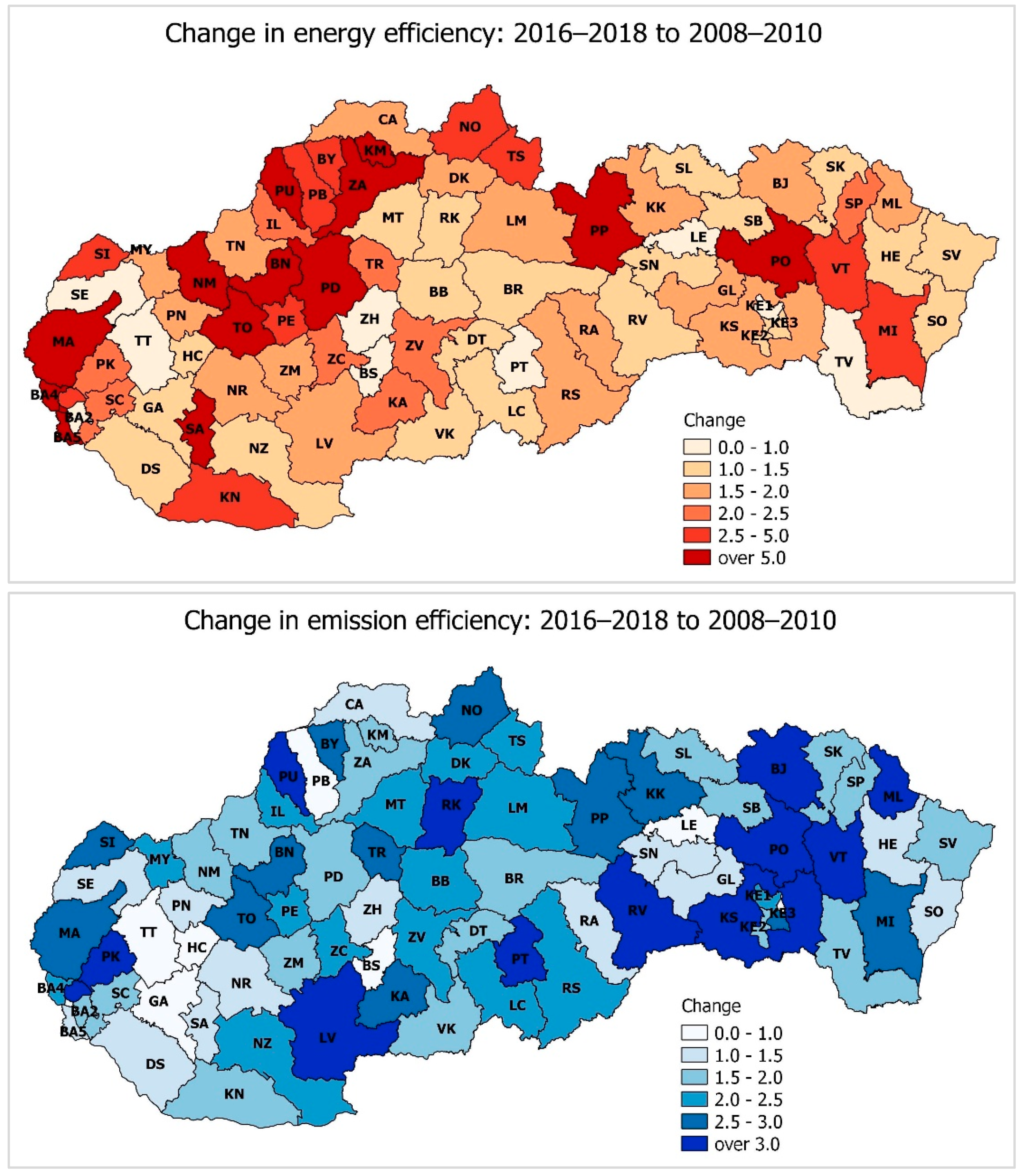
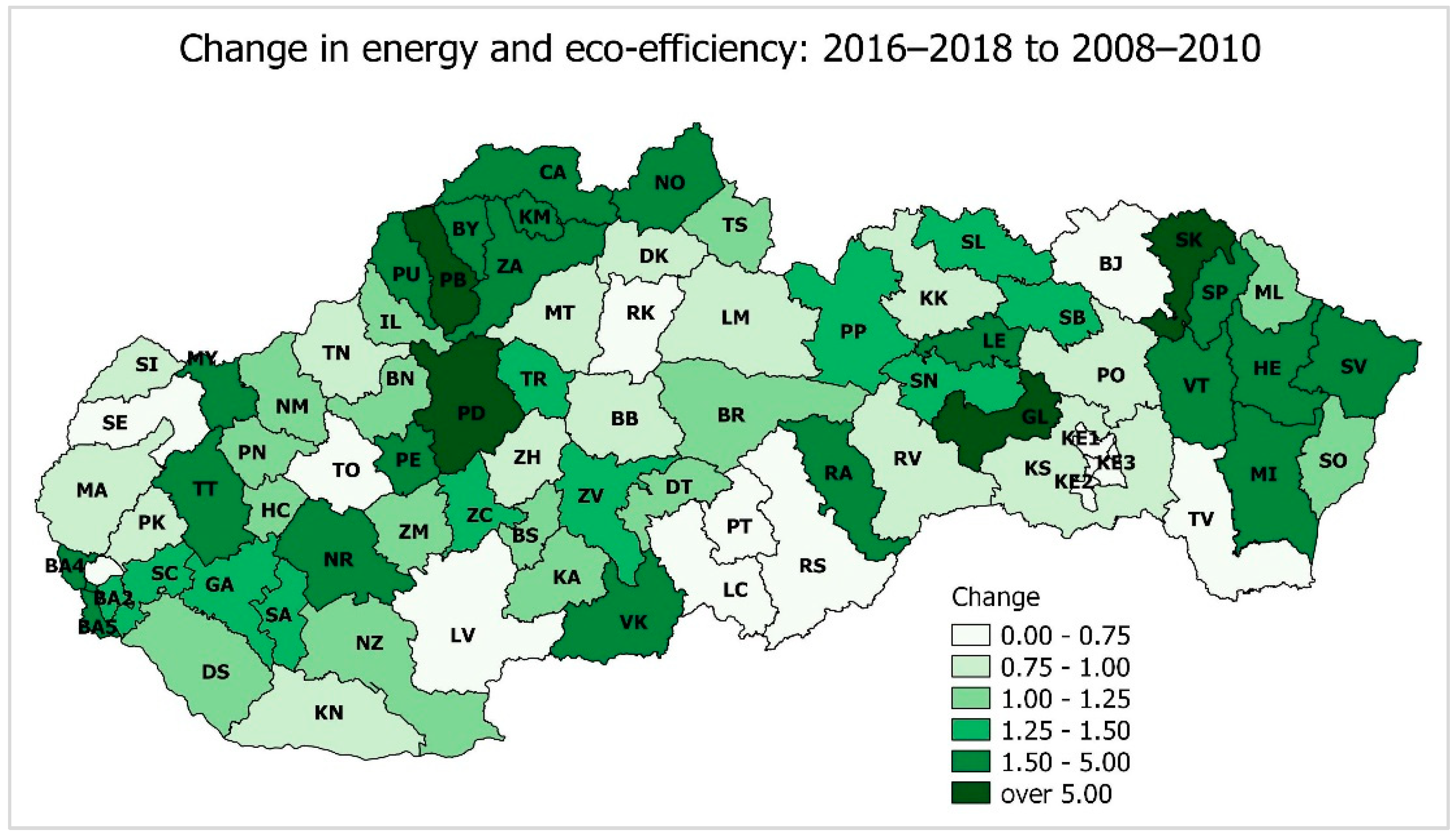
2.2. Regional Patterns of Energy and Emission Efficiency
3. Impact of Policy Interventions on Energy and Emission Efficiency
3.1. Pre-Intervention and Post-Intervention Periods
3.2. Construction of Treatment and Control Groups
3.3. Computation of Propensity Scores: Selection of Covariates
- The
- average GVA per kilowatt/hour increased by 1.251 times in districts with no support, and by 1.641 times in districts supported by OPCEG Policy Measure 2.1.
- The
- average GVA per m3 of natural gas increased by 1.679 times in districts with no support, and by 2.386 times in districts supported by OPCEG Policy Measure 2.1.
- The
- average GVA per kilogramme of diesel increased by 1.380 times in districts with no support, and by 1.481 times in districts supported by OPCEG Policy Measure 2.1.
- The
- average GVA per kilogramme of CO increased by 1.235 times in districts with no support, and by 0.908 times in districts supported by OPE Policy Measure 3.1.
- The
- average GVA per kilogramme of NOx increased by 2.006 times in districts with no support, and by 2.338 times in districts supported by OPE Policy Measure 3.1.
- The
- average GVA per kilogramme of SO2 increased by 3.314 times in districts with no support, and by 2.772 times in districts supported by OPE Policy Measure 3.1.
- The
- average GVA per kilogramme of particulate matter increased by 2.737 times in districts with no support, and by 2.088 times in districts supported by OPE Policy Measure 3.1.
3.4. Correlation Analysis
4. Discussion
5. Conclusions, and Directions for Further Research
Author Contributions
Funding
Conflicts of Interest
Appendix A
| 2008–2010 | 2011–2015 | 2016–2018 | 2008–2010 | 2011–2015 | 2016–2018 | |
|---|---|---|---|---|---|---|
| Indicator | Average | Standard Deviation | ||||
| gross value added (GVA), 2008 constant prices, annual averages | ||||||
| average GVA, €m | 153.49 | 185.58 | 249.03 | 299.50 | 304.81 | 360.71 |
| GVA, EUR per 1 inhabitant | 1969.52 | 2466.26 | 3370.59 | 2798.45 | 3089.19 | 3851.81 |
| energy consumption, annual averages | ||||||
| electricity, MWh | 211,429.88 | 217,710.84 | 216,949.79 | 525,944.35 | 534,995.75 | 488,947.12 |
| natural gas, 000 m3 | 42,507.34 | 38,672.49 | 34,414.78 | 129,838.34 | 103,269.30 | 91,274.05 |
| diesel, tonnes | 6788.73 | 7070.39 | 8638.58 | 9665.55 | 9302.64 | 13,264.47 |
| emissions, annual averages | ||||||
| NOx, tonnes | 556.03 | 494.68 | 403.15 | 724.27 | 649.85 | 484.87 |
| CO, tonnes | 2072.50 | 2289.87 | 3142.15 | 4949.15 | 6161.98 | 6529.42 |
| SO2, tonnes | 852.82 | 739.18 | 340.21 | 3933.45 | 3966.44 | 896.82 |
| particle matters, tonnes | 423.27 | 448.92 | 334.32 | 284.21 | 301.08 | 221.62 |
| B | S.E. | Wald | df | Sig. | Exp(B) | |
|---|---|---|---|---|---|---|
| OPCEG 2.1: Nagelkere R square = 0.300 | ||||||
| Constant | 4.414 | 1.991 | 4.914 | 1 | 0.027 | 82.585 |
| Population density | −0.003 | 0.002 | 4.224 | 1 | 0.040 | 0.997 |
| Real wages | −0.018 | 0.008 | 4.691 | 1 | 0.030 | 0.983 |
| Population with tertiary education | 0.031 | 0.112 | 0.075 | 1 | 0.785 | 1.031 |
| Share of urban population | 0.046 | 0.026 | 3.078 | 1 | 0.079 | 1.047 |
| OPE 3.1: Nagelkerke R square = 0.157 | ||||||
| Constant | 0.195 | 1.561 | 0.016 | 1 | 0.901 | 1.215 |
| Population density | −0.002 | 0.001 | 2.399 | 1 | 0.121 | 0.998 |
| Real wages | 0.002 | 0.006 | 0.063 | 1 | 0.801 | 1.002 |
| Population with tertiary education | −0.147 | 0.102 | 2.090 | 1 | 0.148 | 0.863 |
| Share of urban population | 0.043 | 0.024 | 3.188 | 1 | 0.074 | 1.044 |
| Change in: | CO Efficiency | NOx Efficiency | SO2 Efficiency | Particulates Efficiency | Electricity Efficiency | Natural Gas Efficiency | Diesel Efficiency |
|---|---|---|---|---|---|---|---|
| OPCEG 1.1, €m | −0.187 | −0.019 | −0.130 | −0.030 | 0.217* | 0.248** | 0.052 |
| OPCEG 2.1, €m | −0.138 | −0.101 | −0.096 | −0.133 | −0.164 | 0.214 | −0.050 |
| OPE 3.1, €m | −0.144 | −0.141 | −0.129 | −0.116 | −0.040 | −0.105 | 0.024 |
| x | N | Minimum | Maximum | Mean | Std. Deviation |
|---|---|---|---|---|---|
| OPCEG 1.1 | 79 | 0.108 | 26.264 | 4.675 | 4.949 |
| OPCEG 2.1 | 53 | 0.039 | 7.496 | 1.787 | 1.872 |
| OPE 3.1 | 50 | 0.028 | 25.550 | 2.849 | 4.695 |
References
- The European Green Deal. Communication from the Commission to the European Parliament, the European Council, the Council, the European Economic and Social Committee and the Committee of the Regions; EUROPEAN COMMISSION: Brussels, Belgium, 2019. [Google Scholar]
- Eurostat. Gross Value Added and Income by A*10 Industry Breakdowns; nama_10_a10; Eurostat: Brussels, Belgium, 2020. [Google Scholar]
- Wan, J.; Baylis, K.; Mulder, P. Trade-facilitated technology spillovers in energy productivity convergence processes across EU countries. Energy Econ. 2015, 48, 253–264. [Google Scholar] [CrossRef]
- Honma, S.; Hu, J.-L. Total-factor energy productivity growth of regions in Japan. Energy Policy 2009, 37, 3941–3950. [Google Scholar] [CrossRef]
- Wang, C. Sources of energy productivity growth and its distribution dynamics in China. Resour. Energy Econ. 2011, 33, 279–292. [Google Scholar] [CrossRef]
- Atalla, T.; Bean, P. Determinants of energy productivity in 39 countries: An empirical investigation. Energy Econ. 2017, 62, 217–229. [Google Scholar] [CrossRef]
- Avval, S.H.M.; Rafiee, S.; Jafari, A.; Mohammadi, A. Improving energy productivity of sunflower production using Data Envelopment Analysis (DEA) approach. J. Sci. Food Agric. 2011, 91, 1885–1892. [Google Scholar] [CrossRef]
- Hu, J.-L.; Wang, S.-C. Total-factor energy efficiency of regions in China. Energy Policy 2006, 34, 3206–3217. [Google Scholar] [CrossRef]
- Li, Y.; Chiu, Y.; Lin, T.-Y. Energy and environmental efficiency in different Chinese regions. Sustainability 2019, 11, 1216. [Google Scholar] [CrossRef]
- Ozkara, Y.; Atak, M. Regional total-factor energy efficiency and electricity saving potential of manufacturing industry in Turkey. Energy 2015, 93, 495–510. [Google Scholar] [CrossRef]
- Huang, H.; Wang, T. The Total-factor energy efficiency of regions in China: Based on three-stage SBM model. Sustainability 2017, 9, 1664. [Google Scholar] [CrossRef]
- Sun, Z.; An, C.; Sun, H. Regional differences in energy and environmental performance: An empirical study of 283 cities in China. Sustainability 2018, 10, 2303. [Google Scholar] [CrossRef]
- Hu, J.-L.; Lio, M.-C.; Kao, C.-H.; Lin, Y.-L. Total-factor energy efficiency for regions in Taiwan. Energy Sour. Part B 2012, 7, 292–300. [Google Scholar] [CrossRef]
- Shi, G.-M.; Bi, J.; Wang, J.-N. Chinese regional industrial energy efficiency evaluation based on a DEA model of fixing non-energy inputs. Energy Policy 2010, 38, 6172–6179. [Google Scholar] [CrossRef]
- SOSR. Statistical Office of the Slovak Republic—Datacube Database; Statistical Office of the Slovak Republic: Bratislava, Slovakia, 2020.
- Ozarisoy, B.; Altan, H. Adoption of energy design strategies for retrofitting mass housing estates in Northern Cyprus. Sustainability 2017, 9, 1477. [Google Scholar] [CrossRef]
- Davis, L.W.; Fuchs, A.; Gertler, P. Cash for coolers: Evaluating a large-scale appliance replacement program in Mexico. Am. Econ. J. Econ. Policy 2014, 6, 207–238. [Google Scholar] [CrossRef]
- Fowlie, M.; Greenstone, M.; Wolfram, C. Do energy efficiency investments deliver? Evidence from the weatherization assistance program. Q. J. Econ. 2018, 133, 1597–1644. [Google Scholar] [CrossRef]
- Charnes, A.; Cooper, W.; Rhodes, E. Measuring the efficiency of decision-making units. Eur. J. Oper. Res. 1979, 3, 339. [Google Scholar] [CrossRef]
- Tone, K. A slacks-based measure of efficiency in data envelopment analysis. Eur. J. Oper. Res. 2001, 130, 498–509. [Google Scholar] [CrossRef]
- Tone, K.; Tsutsui, M. An epsilon-based measure of efficiency in DEA—A third pole of technical efficiency. Eur. J. Oper. Res. 2010, 207, 1554–1563. [Google Scholar] [CrossRef]
- Fare, R.; Grosskopf, S.; Norris, M.; Zhang, Z. Productivity growth, technical progress, and efficiency change in industrialized countries. Am. Econ. Rev. 1994, 84, 66–83. [Google Scholar]
- Cooper, W.W.; Seiford, L.M.; Tone, K. Data Envelopment Analysis: A Comprehensive Text with Models, Applications, References and DEA-Solver Software, 2nd ed.; Springer: New York, NY, USA, 2007; ISBN 978-0-387-45281-4. [Google Scholar]
- Gillingham, K.; Keyes, A.; Palmer, K. Advances in evaluating energy efficiency policies and programs. In Annual Review of Resource Economics; Rausser, G.C., Zilberman, D., Eds.; Annual Reviews: Palo Alto, CA, USA, 2018; Volume 10, pp. 511–532. ISBN 978-0-8243-4710-9. [Google Scholar]
- Imbens, G.W.; Wooldridge, J.M. Recent developments in the econometrics of program evaluation. J. Econ. Lit. 2009, 47, 5–86. [Google Scholar] [CrossRef]
- Pearl, J. Causality. Available online: /core/books/causality/B0046844FAE10CBF274D4ACBDAEB5F5B (accessed on 1 March 2020).
- Miteva, D.A.; Pattanayak, S.K.; Ferraro, P.J. Evaluation of biodiversity policy instruments: What works and what doesn’t? Oxf. Rev. Econ. Policy 2012, 28, 69–92. [Google Scholar] [CrossRef]
- Austin, P.C. An introduction to propensity score methods for reducing the effects of confounding in observational studies. Multivar. Behav. Res. 2011, 46, 399–424. [Google Scholar] [CrossRef] [PubMed]
- DeLia, D.; Hoover, D.; Cantor, J.C. Statistical uncertainty in the medicare shared savings program. Medicare Medicaid Res. Rev. 2012, 2. [Google Scholar] [CrossRef] [PubMed]
- Pirracchio, R.; Resche-Rigon, M.; Chevret, S. Evaluation of the propensity score methods for estimating marginal odds ratios in case of small sample size. BMC Med. Res. Methodol. 2012, 12, 70. [Google Scholar] [CrossRef]
- Midi, H.; Sarkar, S.K.; Rana, S. Collinearity diagnostics of binary logistic regression model. J. Interdiscip. Math. 2010, 13, 253–267. [Google Scholar] [CrossRef]
- Field, A. Discovering Statistics Using IBM SPSS Statistics. Available online: https://uk.sagepub.com/en-gb/eur/discovering-statistics-using-ibm-spss-statistics/book257672 (accessed on 29 February 2020).
- Winter, D.C.F.J. Using the student’s “t”-test with extremely small sample sizes. Pract. Assess. Res. Eval. 2013, 18, 1–12. [Google Scholar]
- SOSR. Innovation Activities of the Slovak Enterprises in 2006–2008, 2008–2010, 2010–2012, 2012–2014 and 2014–2016; Statistical Office of the Slovak Republic: Bratislava, Slovakia, 2020.
| Authors | Objective | Energy Types | Method(s) | Period | Sample Size |
|---|---|---|---|---|---|
| [8] | Total-factor energy efficiency of regions in China | conventional energy (coal, petroleum, natural gas) and biomass energy (proxied by total sown area of farm crops). | total-factor energy efficiency / CCR DEA | 1995–2002 | 29 administrative regions |
| [4] | Total-factor energy productivity growth of regions in Japan | electricity (industrial, private), gasoline, kerosene, oil (gas, heavy) gas (city, butane, propane), coal, coke. | total-factor energy productivity / CCR DEA | 1993–2003 | 47 prefectures |
| [14] | Regional industrial energy efficiency in China | coal, coke, gasoline, kerosene, oil (diesel, fuel), gas (natural, liquefied petroleum, refinery gas, gas), other petroleum products, heat, electricity. | CCR and BCC DEA models | 2000–2006 | 28 administrative regions |
| [5] | Sources of energy productivity growth in China’s provinces | total energy consumption. | Shephard output distance functions / CCR DEA | 1990–2005 | 29 provinces |
| [4] | Energy productivity of sunflower production | chemical fertilisers, biocides, diesel fuel, electricity, farmyard manure, irrigation water, human labour and machine power. | BCC DEA model | 2009–2010 | 95 randomly selected farms |
| [13] | Total-factor Energy Efficiency for Regions in Taiwan | electricity (domestic, commercial, industrial), gasoline, diesel. | CCR DEA model | 1999–2005 | 16 counties and 7 cities |
| [10] | Regional total-factor energy efficiency and electricity saving potential of manufacturing industry in Turkey | electricity. | radial and non-radial DEA models with undesirable outputs | 2003–2012 | 26 regions of Turkey |
| [11] | Total-Factor Energy Efficiency of Regions in China | electricity. | SBM DEA | 2000–2012 | 276 cities in China |
| [12] | Regional differences in energy and environmental performance in China | electricity in the industrial sectors. | geographically weighted regression / DEA–Luenberger productivity index | 2010–2014 | 283 cities in China |
| [9] | Energy and environmental efficiency in Chinese cities | total energy consumption. | meta-undesirable EBM DEA model | 2013–2016 | 31 cities in China |
| CCR | SBM | EBM |
|---|---|---|
| Model | Type | Variables | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Outputs | Inputs | ||||||||
| energy efficiency | SBM | ELECT | GAS | DIES | 1 | ||||
| emission efficiency | SBM | CO | SO2 | NO | PM | 1 | |||
| energy-eco efficiency | SBM | ELECT | GAS | DIES | CO | SO2 | NO | PM | |
| scores | ranks | |||||
|---|---|---|---|---|---|---|
| ccr | sbm | ebm | rccr | rsbm | rebm | |
| ccr | 1 | |||||
| sbm | 0.756 | 1 | ||||
| ebm | 0.756 | 0.856 | 1 | |||
| rccr | −0.968 | –0.688 | –0.744 | 1 | ||
| rsbm | –0.692 | –0.883 | –0.889 | 0.686 | 1 | |
| rebm | –0.703 | –0.768 | –0.936 | 0.739 | 0.937 | 1 |
| District | Code | Change in GVA | Energy Efficiency | Emission Efficiency | Energy Eco-Efficiency |
|---|---|---|---|---|---|
| Bánovce nad Bebravou | BN | 2.201 | 9.523 | 2.640 | 1.004 |
| Banská Bystrica | BB | 1.690 | 1.306 | 2.216 | 0.809 |
| Banská Štiavnica | BS | 0.324 | 0.254 | 0.226 | 1.167 |
| Bardejov | BJ | 2.457 | 1.951 | 3.403 | 0.326 |
| Bratislava I | BA1 | 1.911 | 6.361 | 0.577 | 1.761 |
| Bratislava II | BA2 | 0.957 | 0.874 | 1.568 | 1.355 |
| Bratislava III | BA3 | 1.328 | 3.828 | 4.366 | 0.649 |
| Bratislava IV | BA4 | 2.798 | 10.141 | 2.241 | 3.922 |
| Bratislava V | BA5 | 1.693 | 5.059 | 1.197 | 4.444 |
| Brezno | BR | 1.558 | 1.365 | 1.981 | 1.174 |
| Bytča | BY | 4.268 | 4.098 | 2.638 | 2.208 |
| Čadca | CA | 2.222 | 1.788 | 1.162 | 1.704 |
| Detva | DT | 1.751 | 1.460 | 1.782 | 1.205 |
| Dolný Kubín | DK | 2.179 | 1.729 | 2.030 | 0.838 |
| Dunajská Streda | DS | 1.600 | 1.408 | 1.037 | 1.124 |
| Galanta | GA | 1.339 | 1.050 | 0.942 | 1.404 |
| Gelnica | GL | 2.076 | 1.929 | 1.209 | 18.868 |
| Hlohovec | HC | 0.909 | 1.026 | 0.652 | 1.242 |
| Humenné | HE | 1.436 | 1.471 | 1.446 | 1.859 |
| Ilava | IL | 1.881 | 2.347 | 2.181 | 1.083 |
| Kežmarok | KK | 2.008 | 1.703 | 2.999 | 0.756 |
| Komárno | KN | 1.938 | 2.896 | 1.521 | 0.808 |
| Košice-okolie | KS | 2.161 | 1.991 | 3.508 | 0.816 |
| Košice I | KE1 | 1.233 | 0.974 | 2.305 | 0.066 |
| Košice II | KE2 | 1.583 | 1.251 | 1.708 | 0.086 |
| Košice III | KE3 | 1.676 | 1.325 | 0.855 | 0.476 |
| Košice IV | KE4 | 1.566 | 1.238 | 2.504 | 0.650 |
| Krupina | KA | 2.628 | 2.039 | 2.796 | 1.095 |
| Kysucké Nové Mesto | KM | 2.266 | 8.982 | 1.771 | 1.653 |
| Levice | LV | 2.018 | 1.776 | 3.528 | 0.637 |
| Levoča | LE | 0.190 | 0.151 | 0.141 | 1.587 |
| Liptovský Mikuláš | LM | 1.927 | 1.832 | 2.422 | 0.913 |
| Lučenec | LC | 1.550 | 1.252 | 2.265 | 0.747 |
| Malacky | MA | 2.328 | 13.270 | 2.749 | 0.984 |
| Martin | MT | 1.651 | 1.405 | 2.078 | 0.979 |
| Medzilaborce | ML | 2.251 | 1.663 | 6.136 | 1.022 |
| Michalovce | MI | 1.766 | 2.714 | 2.580 | 2.404 |
| Myjava | MY | 2.125 | 1.851 | 2.033 | 1.650 |
| Námestovo | NO | 4.361 | 3.430 | 2.863 | 2.463 |
| Nitra | NR | 1.629 | 1.848 | 1.235 | 2.105 |
| Nové Mesto nad Váhom | NM | 1.670 | 5.207 | 1.990 | 1.111 |
| Nové Zámky | NZ | 1.547 | 1.382 | 2.324 | 1.005 |
| Partizánske | PE | 2.561 | 3.685 | 2.322 | 1.656 |
| Pezinok | PK | 2.396 | 2.352 | 3.547 | 0.820 |
| Piešťany | PN | 1.429 | 1.920 | 1.425 | 1.068 |
| Poltár | PT | 0.733 | 0.632 | 6.082 | 0.169 |
| Poprad | PP | 2.710 | 11.342 | 2.658 | 1.353 |
| Považská Bystrica | PB | 2.137 | 2.643 | 0.485 | 6.757 |
| Prešov | PO | 2.569 | 7.022 | 3.611 | 0.833 |
| Prievidza | PD | 1.460 | 7.181 | 1.832 | 43.478 |
| Púchov | PU | 3.534 | 9.534 | 3.948 | 1.558 |
| Revúca | RA | 1.466 | 1.508 | 1.427 | 1.524 |
| Rimavská Sobota | RS | 1.375 | 1.555 | 2.441 | 0.540 |
| Rožňava | RV | 1.378 | 1.286 | 3.030 | 0.919 |
| Ružomberok | RK | 1.327 | 1.064 | 4.254 | 0.382 |
| Sabinov | SB | 1.590 | 1.263 | 1.531 | 1.284 |
| Senec | SC | 1.806 | 2.170 | 1.524 | 1.357 |
| Senica | SE | 1.172 | 0.926 | 1.077 | 0.523 |
| Skalica | SI | 1.527 | 3.702 | 2.536 | 0.832 |
| Snina | SV | 1.821 | 1.471 | 1.626 | 1.595 |
| Sobrance | SO | 1.563 | 1.160 | 1.434 | 1.056 |
| Spišská Nová Ves | SN | 1.083 | 1.435 | 1.102 | 1.318 |
| Stará Ľubovňa | SL | 1.798 | 1.412 | 1.696 | 1.304 |
| Stropkov | SP | 2.556 | 2.233 | 1.794 | 1.653 |
| Svidník | SK | 1.349 | 1.059 | 1.670 | 20.408 |
| Šaľa | SA | 1.811 | 6.229 | 1.292 | 1.326 |
| Topoľčany | TO | 2.266 | 6.701 | 2.950 | 0.560 |
| Trebišov | TV | 1.010 | 0.812 | 1.552 | 0.532 |
| Trenčín | TN | 1.588 | 1.535 | 1.935 | 0.942 |
| Trnava | TT | 1.084 | 0.999 | 0.779 | 1.572 |
| Turčianske Teplice | TR | 2.820 | 2.134 | 2.597 | 1.427 |
| Tvrdošín | TS | 2.029 | 3.247 | 2.186 | 1.099 |
| Veľký Krtíš | VK | 1.725 | 1.436 | 1.991 | 1.531 |
| Vranov nad Topľou | VT | 3.193 | 3.415 | 3.041 | 2.070 |
| Zlaté Moravce | ZM | 1.700 | 1.948 | 1.588 | 1.212 |
| Zvolen | ZV | 2.364 | 2.208 | 2.155 | 1.488 |
| Žarnovica | ZC | 2.635 | 2.120 | 2.063 | 1.464 |
| Žiar nad Hronom | ZH | 1.133 | 0.895 | 1.038 | 0.884 |
| Žilina | ZA | 2.132 | 8.265 | 1.973 | 1.898 |
| Average | SK | 1.619 | 2.907 | 2.127 | 1.305 |
| Energy Source | Period | Support | Descriptives | t-Test | ||||
|---|---|---|---|---|---|---|---|---|
| N | Mean | Std. Dev. | t | df | Sig. (2-Tailed) | |||
| Energies | ||||||||
| electricity: GVA per kilowatt/hours | 2008–2010 | no | 20 | 1.70 | 1.66 | 1.011 | 71 | 0.323 |
| yes | 53 | 1.31 | 0.73 | |||||
| 2016–2018 | no | 20 | 2.13 | 1.35 | −0.073 | 71 | 0.938 | |
| yes | 53 | 2.15 | 1.17 | |||||
| natural gas: GVA per m3 | 2008–2010 | no | 20 | 14.06 | 17.67 | 1.491 | 71 | 0.151 |
| yes | 53 | 8.00 | 6.90 | |||||
| 2016–2018 | no | 20 | 23.61 | 28.86 | 0.836 | 71 | 0.406 | |
| yes | 53 | 19.07 | 16.68 | |||||
| diesel: GVA per kg | 2008–2010 | no | 20 | 32.41 | 38.78 | 0.933 | 71 | 0.124 |
| yes | 53 | 23.94 | 19.43 | |||||
| 2016–2018 | no | 20 | 44.71 | 56.23 | 0.701 | 71 | 0.490 | |
| yes | 53 | 35.47 | 28.83 | |||||
| Emissions | ||||||||
| pollution source | period | support | descriptives | t-test | ||||
| N | Mean | Std. Dev. | t | df | Sig. (2-tailed) | |||
| CO emissions: GVA per kg | 2008−2010 | no | 12 | 472.80 | 1024.18 | 1.087 | 60 | 0.300 |
| yes | 50 | 149.55 | 223.15 | |||||
| 2016−2018 | no | 12 | 583.67 | 1486.85 | 1.042 | 60 | 0.320 | |
| yes | 50 | 135.76 | 176.88 | |||||
| NOx emissions: GVA per kg | 2008−2010 | no | 12 | 455.43 | 547.46 | 0.540 | 60 | 0.598 |
| yes | 50 | 364.47 | 413.75 | |||||
| 2016–2018 | no | 12 | 913.68 | 1181.36 | 0.168 | 60 | 0.869 | |
| yes | 50 | 852.26 | 912.83 | |||||
| SO2 emissions: GVA per kg | 2008−2010 | no | 12 | 1734.44 | 2234.01 | 0.608 | 60 | 0.552 |
| yes | 50 | 1310.55 | 1863.68 | |||||
| 2016−2018 | no | 12 | 5748.38 | 6799.77 | 1.016 | 60 | 0.327 | |
| yes | 50 | 3633.04 | 4917.91 | |||||
| particulate matters: GVA per kg | 2008−2010 | no | 12 | 1069.42 | 2559.62 | 1.044 | 60 | 0.337 |
| yes | 50 | 324.90 | 444.05 | |||||
| 2016−2018 | no | 12 | 2927.01 | 7317.85 | 1.063 | 60 | 0.310 | |
| yes | 50 | 678.44 | 692.65 | |||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baláž, V.; Nežinský, E.; Jeck, T.; Filčák, R. Energy and Emission Efficiency of the Slovak Regions. Sustainability 2020, 12, 2611. https://doi.org/10.3390/su12072611
Baláž V, Nežinský E, Jeck T, Filčák R. Energy and Emission Efficiency of the Slovak Regions. Sustainability. 2020; 12(7):2611. https://doi.org/10.3390/su12072611
Chicago/Turabian StyleBaláž, Vladimír, Eduard Nežinský, Tomáš Jeck, and Richard Filčák. 2020. "Energy and Emission Efficiency of the Slovak Regions" Sustainability 12, no. 7: 2611. https://doi.org/10.3390/su12072611
APA StyleBaláž, V., Nežinský, E., Jeck, T., & Filčák, R. (2020). Energy and Emission Efficiency of the Slovak Regions. Sustainability, 12(7), 2611. https://doi.org/10.3390/su12072611






