Substantiating the Logistics Chain Structure While Servicing the Flow of Requests for Road Transport Deliveries
Abstract
1. Introduction
2. Methodology
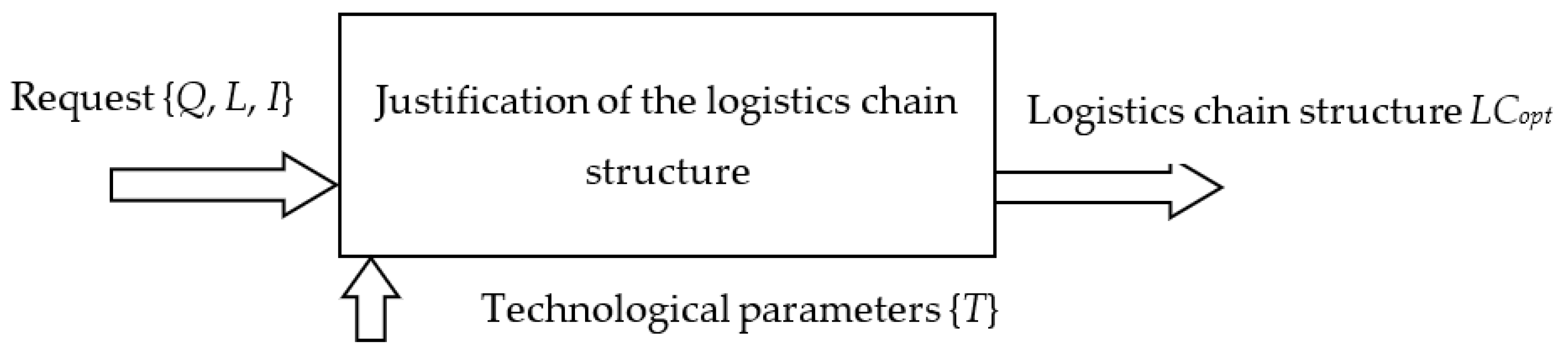
2.1. Problem Statement
- The formation of alternative LC variants, determining the structure of the technological scheme. Alternatives are determined on the basis of the availability of cargo terminals, customs points, as well as partner forwarders operating in the appropriate geographic area.
- The efficiency evaluation for a set of alternative structures. The assessment is carried out on the basis of average market value indicators, while taking the random nature of technological parameters into account. The result of the evaluation for each LC variant is a random value of the efficiency criterion.
- The selection of the optimal LC structure and subsequent measures related to the determination of the LC participants and the development of specific technological processes. The choice of the optimal LC structure is carried out on the basis of a comparative assessment of characteristics of random variables that describe the effectiveness criterion for each alternative structure. For the presented formulation of the problem (1), the choice is made according to the minimum expected value of the total costs.
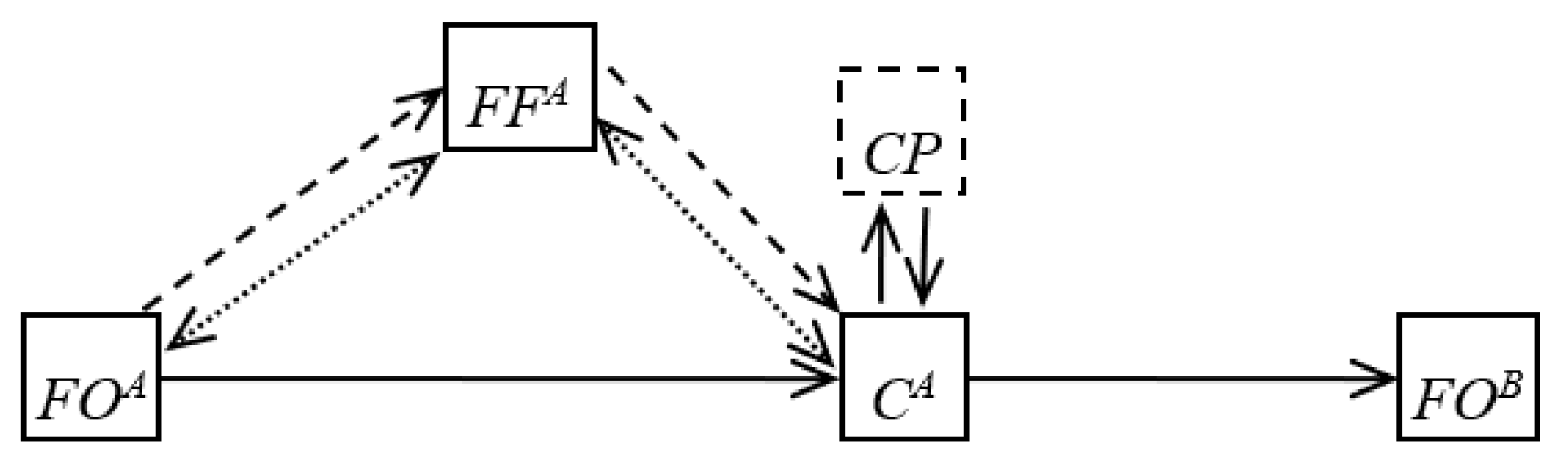
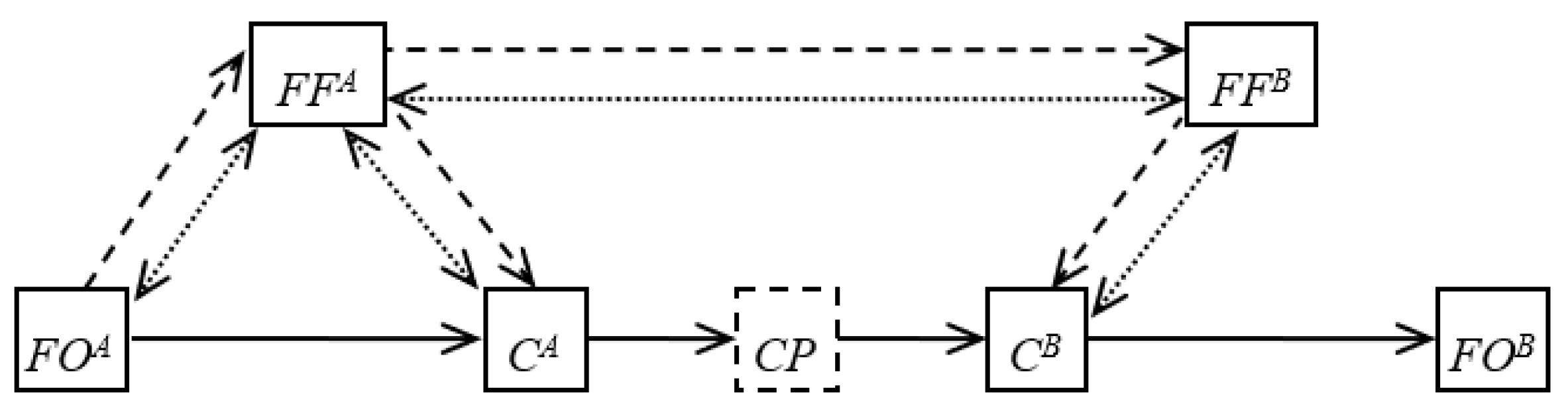
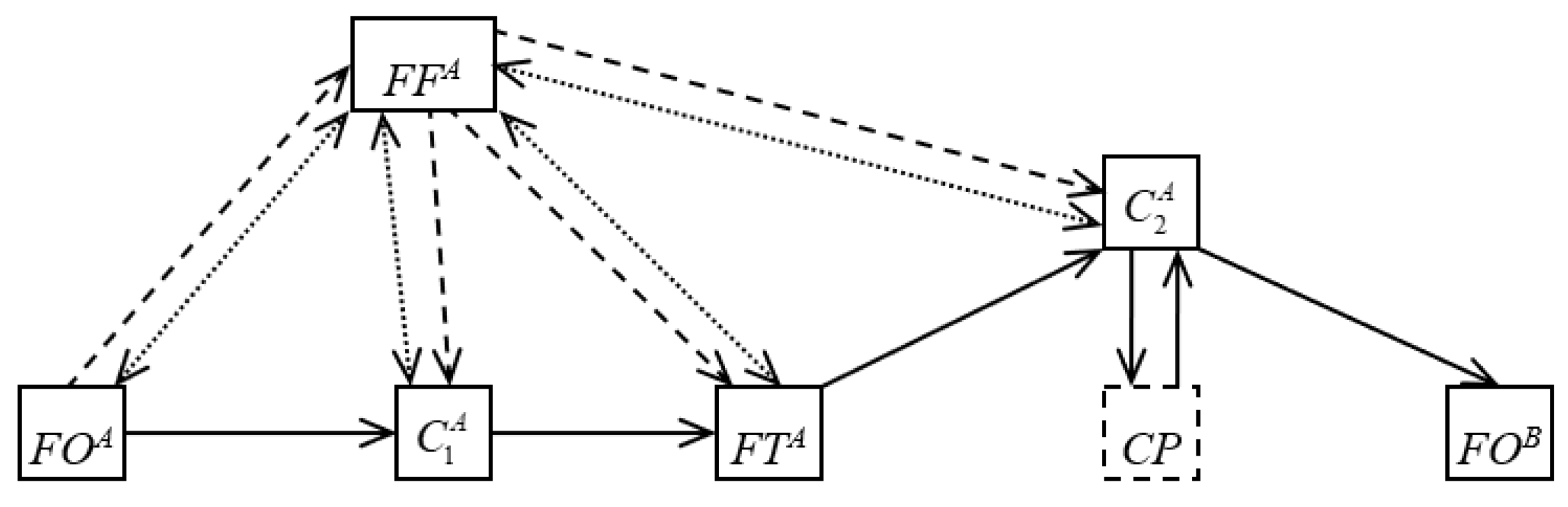
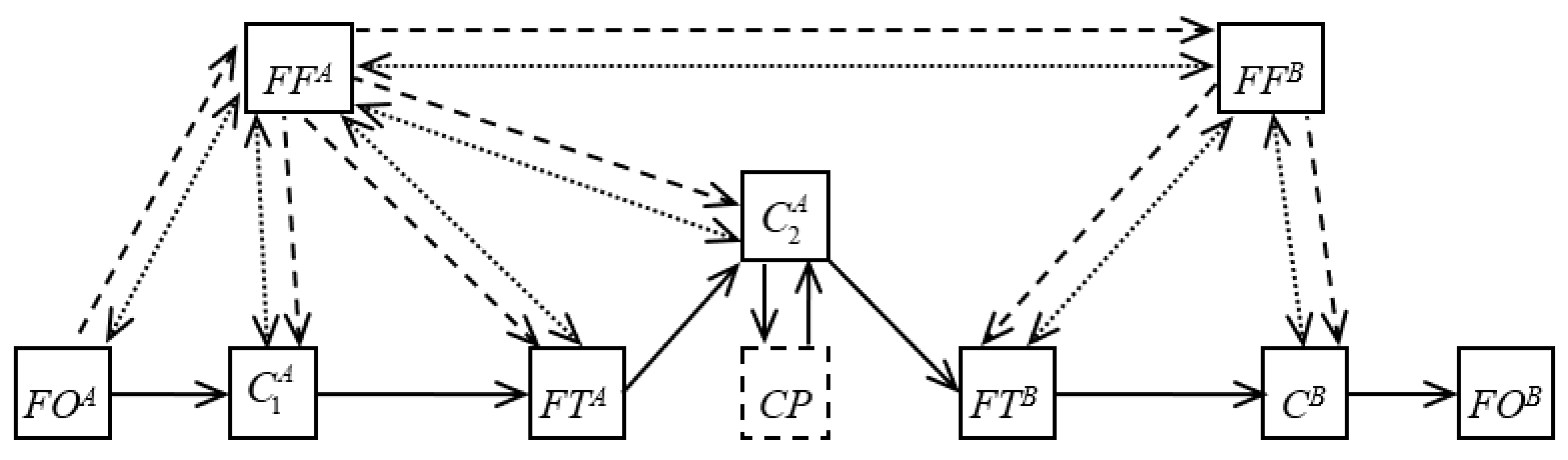
2.2. Basic Alternative Variants of the Logistics Chains’ Structure
2.3. Evaluating the Effectiveness of the Logistic Chain Structures
- costs of finding a client;
- costs associated with the preparation of documentation for the delivery of a shipment from a consignor to a consignee;
- costs of finding a carrier, partner forwarder (if appropriate), 3PL-provider (if appropriate);
- costs of the organization and implementation of loading and unloading processes;
- costs of the carrier (carriers) services;
- expenses for payment of the 3PL-provider (providers) services;
- customs payments; and,
- tax deductions.
- costs of forming a transport package;
- losses due to freezing of funds that constitutes the shipment value; and,
- payment for the services of forwarders.
- direct costs of delivery operations;
- costs of idle time under loading and unloading;
- costs of idle time in the customs point; and,
- tax deductions.
- costs of transshipment (unloading and loading);
- costs of the formation and disbandment of transport packages;
- costs of interim storage operations;
- tax deductions.
3. Results
4. Discussion
- set the incoming requests’ interval as a constant parameter (for the flow of requests, the expected value of the requests interval is taken);
- define ranges on the set of possible values of the delivery distance;
- for the accepted value of the requests’ arrival interval and the upper bound of the delivery distance range, determine the roots of equation (23) for all pairs of the LC structures; and,
- the obtained solutions determine the bounds of the areas of the most efficient use of the alternative LC structures, the corresponding dependencies of the total costs form the lower polygonal chain on the graph.
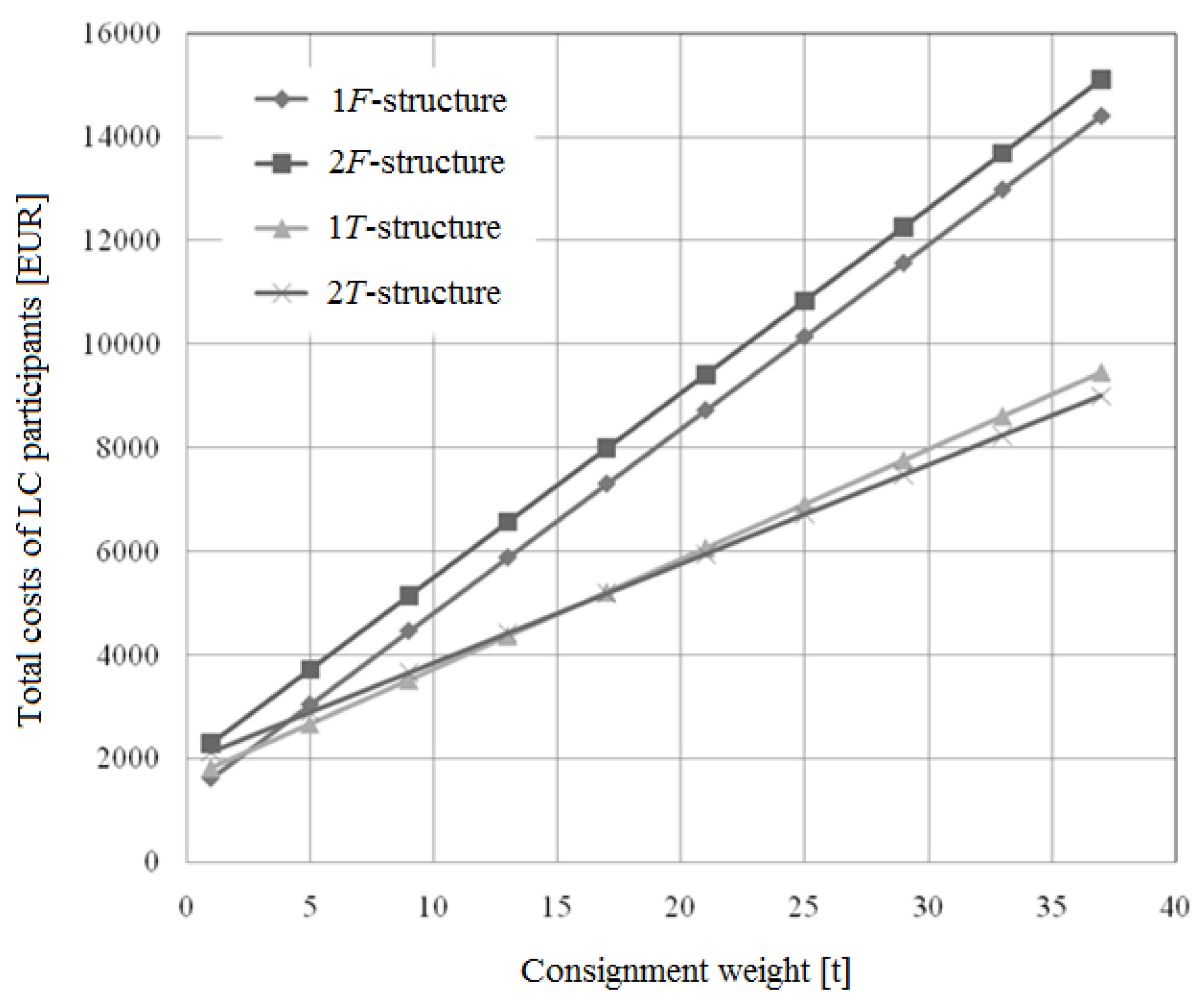
- the use of the simplest version of the LC is optimal for the delivery by road transport of small consignments (up to three tons);
- the use in road transport of the LC variant with the participation of two freight forwarders is not characterized by the lowest possible total costs regardless of the values of the consignment weight and the delivery distance; therefore, the 2F-variant of the LC should only be used in cases when it is not possible to arrange delivery without the participation of the contractor forwarder; and,
- the bounds of the areas of the most effective LC structures (for the consignment volume as a parameter) inversely depend on the delivery distance.
- having the areas substantiated for the given demand parameters, decision-makers (freight forwarders or other logistics operators) can choose the proper LC structure without calculating the costs for all possible alternative structures;
- the proposed methodology contributes to decreasing of the clients servicing time and reduces possible mistakes made by operators while making a decision concerning the LC structure, and in total – supports the sustainable operation of transport on a regional scale; and,
- the areas of the most efficient use of the LC structures can be implemented in specialized tools of information systems supporting decisions of logistics operators.
5. Conclusions
Funding
Conflicts of Interest
Appendix A
- is time spent by a dispatcher while searching for a customer (h);
- is the number of employed dispatchers.
- justification of the LC structure for servicing the received request for the consignment delivery;
- search for a carrier (carriers) and conclusion of relevant agreements;
- search for contractors for loading operations (if this type of work is not performed by other participants) and conclusion of contracts with them;
- registration of transport and customs documentation;
- search for a cargo terminal and conclusion of relevant contracts; and,
- search for a foreign partner forwarder and conclusion of relevant agreements.
Appendix B
- ;
- ;
- .
- ;
- ;
- .
References
- Carvalho, H.; Fonseca, H. A multivariate data analysis of logistics structure as a factor of competitiveness. Braz. J. Oper. Prod. Manag. 2017, 14, 90–100. [Google Scholar] [CrossRef]
- Melnyk, S.A.; Narasimhan, R.; DeCampos, H.A. Supply chain design: Issues, challenges, frameworks and solutions. Int. J. Prod. Res. 2014, 52, 1887–1896. [Google Scholar] [CrossRef]
- Blos, M.F.; da Silva, R.M.; Wee, H.-M. A framework for designing supply chain disruptions management considering productive systems and carrier viewpoints. Int. J. Prod. Res. 2018, 56, 5045–5061. [Google Scholar] [CrossRef]
- Yao, X.; Askin, R. Review of supply chain configuration and design decision-making for new product. Int. J. Prod. Res. 2019, 57, 2226–2246. [Google Scholar] [CrossRef]
- Bányai, T.; Tamás, P.; Illés, B.; Stankevičiūtė, Ž.; Bányai, Á. Optimization of municipal waste collection routing: Impact of industry 4.0 technologies on environmental awareness and sustainability. Int. J. Environ. Res. Public Health 2019, 16, 634. [Google Scholar] [CrossRef] [PubMed]
- Bányai, T. Real-time decision making in first mile and last mile logistics: How smart scheduling affects energy efficiency of hyperconnected supply chain solutions. Energies 2018, 11, 1833. [Google Scholar] [CrossRef]
- Calleja, G.; Corominas, A.; Martínez-Costa, C.; de la Torre, R. Methodological approaches to supply chain design. Int. J. Prod. Res. 2018, 56, 4467–4489. [Google Scholar] [CrossRef]
- Nobil, A.H.; Jalali, S.; Niaki, S.T.A. Financially embedded facility location decisions on designing a supply chain structure: A case study. Syst. Eng. 2018, 21, 520–533. [Google Scholar] [CrossRef]
- Jahani, H.; Abbasi, B.; Alavifard, F.; Talluri, S. Supply chain network redesign with demand and price uncertainty. Int. J. Prod. Econ. 2018, 205, 287–312. [Google Scholar] [CrossRef]
- Jabbarzadeh, A.; Fahimnia, B.; Sheu, J.-B.; Moghadam, H.S. Designing a supply chain resilient to major disruptions and supply/demand interruptions. Transp. Res. Part B Methodol. 2016, 94, 121–149. [Google Scholar] [CrossRef]
- Claypool, E.G.; Norman, B.A.; Needy, K.L. Design for supply chain: An analysis of key risk factors. Ind. Eng. Manag. 2015, 4, 156. [Google Scholar] [CrossRef]
- Samson, D.; Gloet, M. Integrating performance and risk aspects of supply chain design processes. Prod. Plan. Control 2018, 29, 1238–1257. [Google Scholar] [CrossRef]
- Hoseinpour, P.; Ahmadi-Javid, A. Designing service system networks with interruption risks. Int. Trans. Oper. Res. 2019, 26, 2561–2578. [Google Scholar] [CrossRef]
- Moreno-Camacho, C.A.; Montoya-Torres, J.R.; Jaegler, A.; Gondran, N. Sustainability metrics for real case applications of the supply chain network design problem: A systematic literature review. J. Clean. Prod. 2019, 231, 600–618. [Google Scholar] [CrossRef]
- Yun, Y.S.; Chuluunsukh, A.; Gen, M. Design and implementation of sustainable supply chain model with various distribution channels. Adv. Intell. Syst. Comput. 2020, 1002, 469–482. [Google Scholar] [CrossRef]
- Sherafati, M.; Bashiri, M.; Tavakkoli-Moghaddam, R.; Pishvaee, M.S. Supply chain network design considering sustainable development paradigm: A case study in cable industry. J. Clean. Prod. 2019, 234, 366–380. [Google Scholar] [CrossRef]
- Allaoui, H.; Guo, Y.; Sarkis, J. Decision support for collaboration planning in sustainable supply chains. J. Clean. Prod. 2019, 229, 761–774. [Google Scholar] [CrossRef]
- Razm, S.; Nickel, S.; Sahebi, H. A multi-objective mathematical model to redesign of global sustainable bioenergy supply network. Comput. Chem. Eng. 2019, 128, 1–20. [Google Scholar] [CrossRef]
- Resat, H.G.; Unsal, B. A novel multi-objective optimization approach for sustainable supply chain: A case study in packaging industry. Sustain. Prod. Consum. 2019, 20, 29–39. [Google Scholar] [CrossRef]
- Wang, F.; Lai, X.; Shi, N. A multi-objective optimization for green supply chain network design. Decis. Support Syst. 2011, 51, 262–269. [Google Scholar] [CrossRef]
- Jabbarzadeh, A.; Haughton, M.; Pourmehdi, F. A robust optimization model for efficient and green supply chain planning with postponement strategy. Int. J. Prod. Econ. 2019, 214, 266–283. [Google Scholar] [CrossRef]
- Almetova, Z.; Shepelev, V.; Shepelev, S. Optimization of Delivery Lot Volumes in Terminal Complexes. Transp. Res. Procedia 2017, 27, 396–403. [Google Scholar] [CrossRef]
- Naumov, V. Modeling demand for freight forwarding services on the grounds of logistics portals data. Transp. Res. Procedia 2018, 30, 324–331. [Google Scholar] [CrossRef]
- Rohaninejad, M.; Sahraeian, R.; Tavakkoli-Moghaddam, R. Multi-echelon supply chain design considering unreliable facilities with facility hardening possibility. Appl. Math. Model. 2018, 62, 321–337. [Google Scholar] [CrossRef]
- Cui, J.; Zhao, M.; Li, X.; Parsafard, M.; An, S. Reliable design of an integrated supply chain with expedited shipments under disruption risks. Transp. Res. Part E Logist. Transp. Rev. 2016, 95, 143–163. [Google Scholar] [CrossRef]
- Sajedinejad, A.; Chaharsooghi, S.K. Multi-criteria supplier selection decisions in supply chain networks: A multi-objective optimization approach. Ind. Eng. Manag. Syst. 2018, 17, 392–406. [Google Scholar] [CrossRef]
- Sabri, Y.; Micheli, G.J.L.; Nuur, C. How do different supply chain configuration settings impact on performance trade-offs? Int. J. Logist. Syst. Manag. 2017, 26, 34–56. [Google Scholar] [CrossRef]
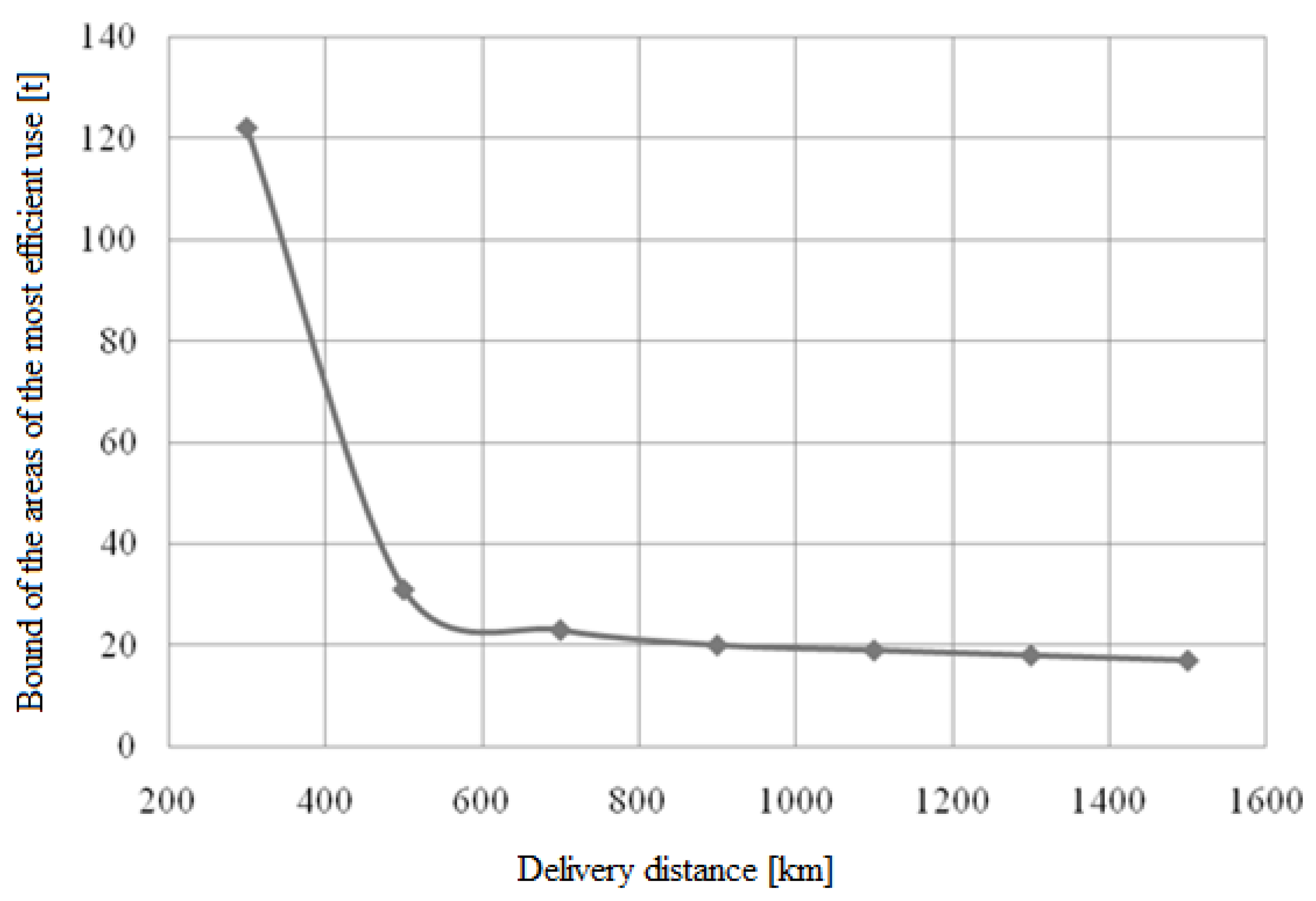
| Delivery Distance | 1F-Structure | 2F-Structure | 1T-Structure | 2T-Structure |
|---|---|---|---|---|
| up to 300 km | up to 3 tons | - | 3…122 tons | more than 122 tons |
| 301…500 km | up to 3 tons | - | 3…31 tons | more than 31 tons |
| 501…700 km | up to 3 tons | - | 3…23 tons | more than 23 tons |
| 701…900 km | up to 2 tons | - | 2…20 tons | more than 20 tons |
| 901…1100 km | up to 2 tons | - | 2…19 tons | more than 19 tons |
| 1101…1300 km | up to 2 tons | - | 2…18 tons | more than 18 tons |
| more than 1300 km | up to 2 tons | - | 2…17 tons | more than 17 tons |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Naumov, V. Substantiating the Logistics Chain Structure While Servicing the Flow of Requests for Road Transport Deliveries. Sustainability 2020, 12, 1635. https://doi.org/10.3390/su12041635
Naumov V. Substantiating the Logistics Chain Structure While Servicing the Flow of Requests for Road Transport Deliveries. Sustainability. 2020; 12(4):1635. https://doi.org/10.3390/su12041635
Chicago/Turabian StyleNaumov, Vitalii. 2020. "Substantiating the Logistics Chain Structure While Servicing the Flow of Requests for Road Transport Deliveries" Sustainability 12, no. 4: 1635. https://doi.org/10.3390/su12041635
APA StyleNaumov, V. (2020). Substantiating the Logistics Chain Structure While Servicing the Flow of Requests for Road Transport Deliveries. Sustainability, 12(4), 1635. https://doi.org/10.3390/su12041635





