A Mixed Integer Linear Programming Method for Simultaneous Multi-Periodic Train Timetabling and Routing on a High-Speed Rail Network
Abstract
1. Introduction
- (1)
- It needs to search a specific travel path for each train at its each visited station and to make trains of the same period-type enter and leave off the same station with the same headway to let them operate periodically.
- (2)
- Trains of the same period-type travel with an identical headway, which is more than any minimum safety headways. Moreover, the sequence of these trains occupying tracks in either sections or at stations is constant. Therefore, the requirements of all types of safety time-intervals among them are automatically satisfied, so we only need to consider some safety intervals among trains of different period-types.
- (1)
- A mixed integer linear programming model is formulated for the simultaneous multi-periodic train timetabling and routing, and the commercial solver WebSphere ILOG CPLEX (International Business Machines Corporation, New York, NY, USA) is applied to solve it. This model optimizes the entering time and leaving time of all trains and also searches for their routes of arrival–departure tracks at their visited stations.
- (2)
- A strategy is designed to partly predetermine the sequence of trains occupying the same arrival–departure track, and it is greatly useful to improve the solve efficiency of our model.
2. Literature Reviews
2.1. Reviews on Aperiodic Train Timetabling and Routing
2.2. Reviews on Periodic Train Timetabling and Routing
3. Problem Description
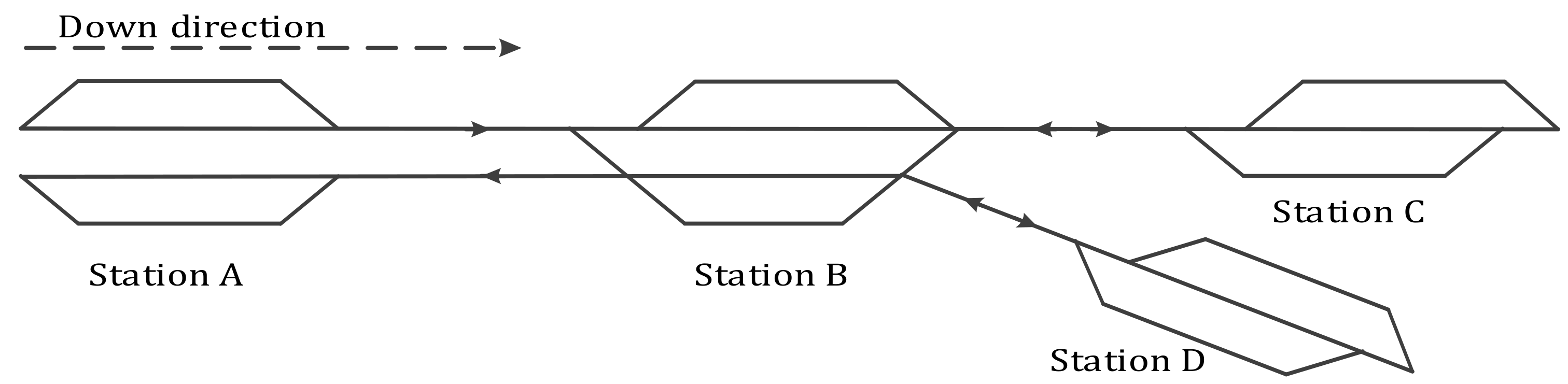
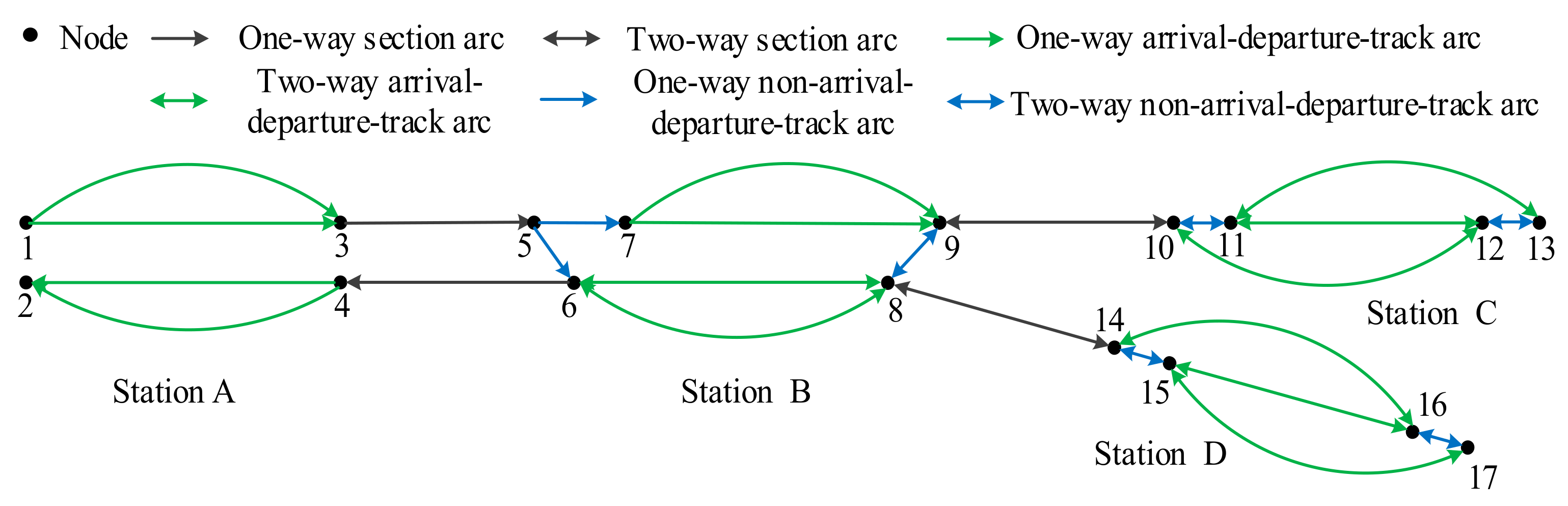
3.1. Representation of Rail Networks
3.1.1. Representation of a Physical Railway Network
3.1.2. Representation of a Constructed Railway Network
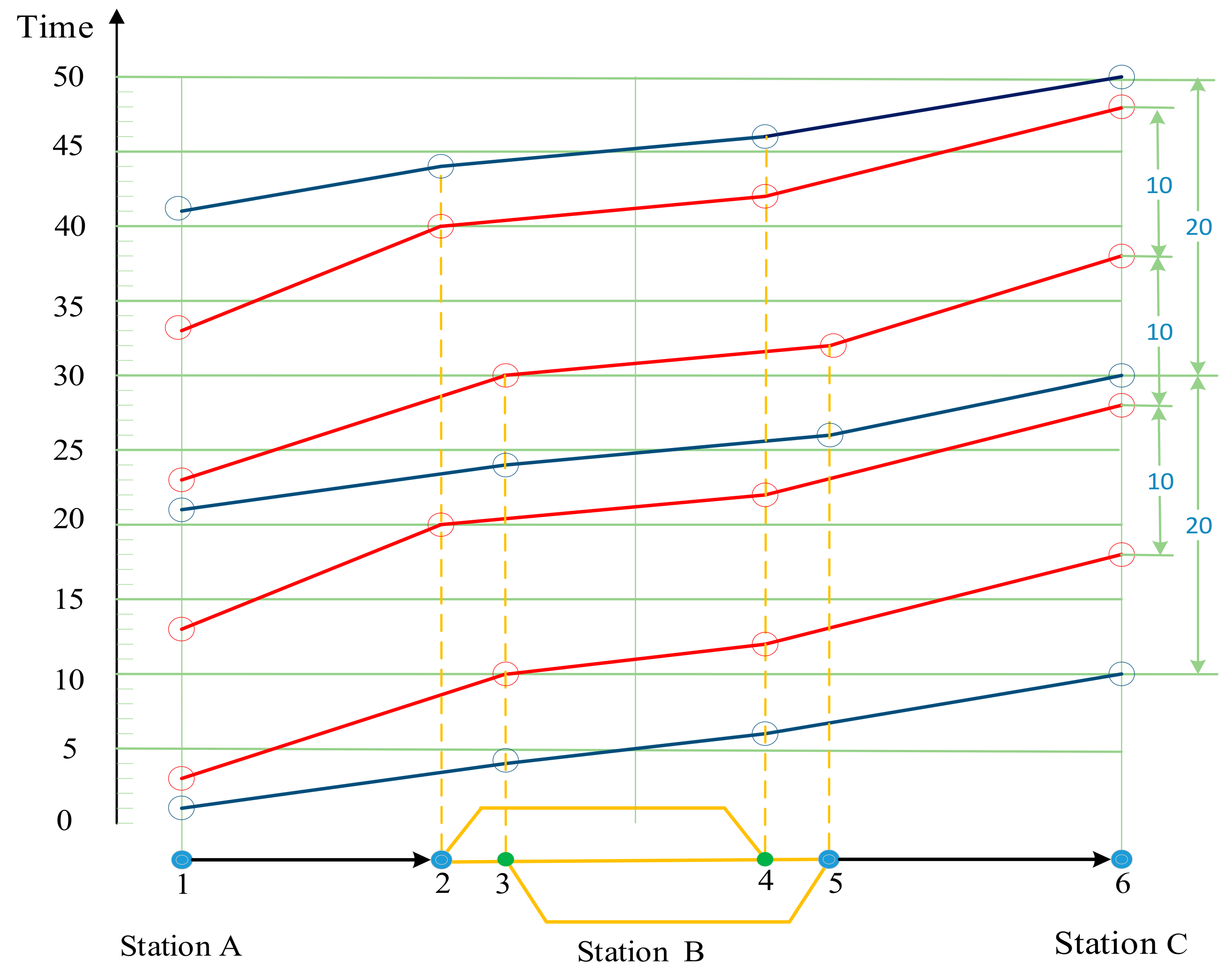
3.2. Description of Multiple Period-Types of Trains
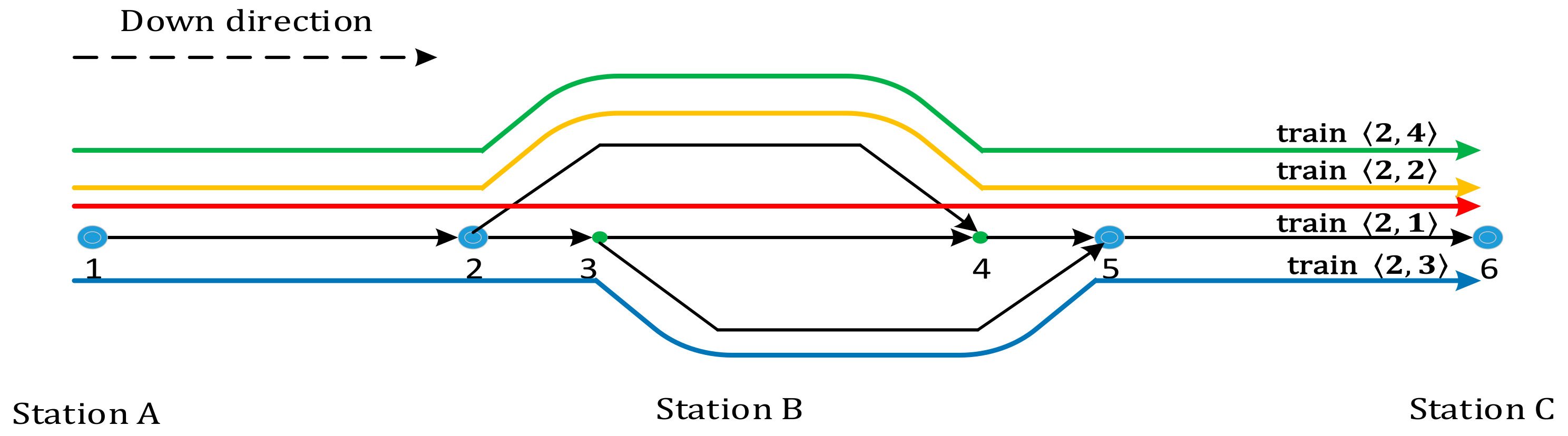
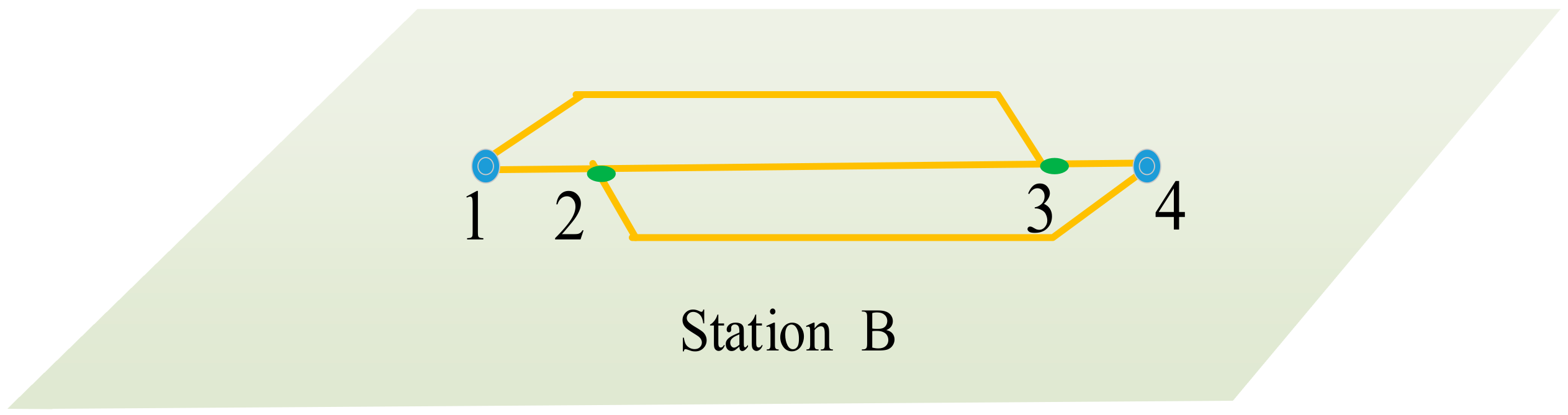
3.3. Paths Choosing of Trains of a Period-Type at Stations
3.4. Definition for Integrated Routing and Scheduling of Multi-Periodic Trains
- (1)
- A rail network, which is denoted by the directed graph, consists of nodes and multiple types of arcs.
- (2)
- Trains of multiple period-types, whose visited stations, stops and operation period-lengths are pre-determined.
- (3)
- All required operation time parameters, such as the minimum safety arrival time interval and minimum safety departure time interval, minimum and maximum running time in each section, and minimum and maximum dwelling time at each station.
4. A Mixed Integer Linear Programming Model
4.1. Modeling Assumptions
4.2. Decision Variables
4.3. Objective of Minimizing the Total Travel Time of Trains
4.4. Constraints
5. A Strategy for Simplifying Model
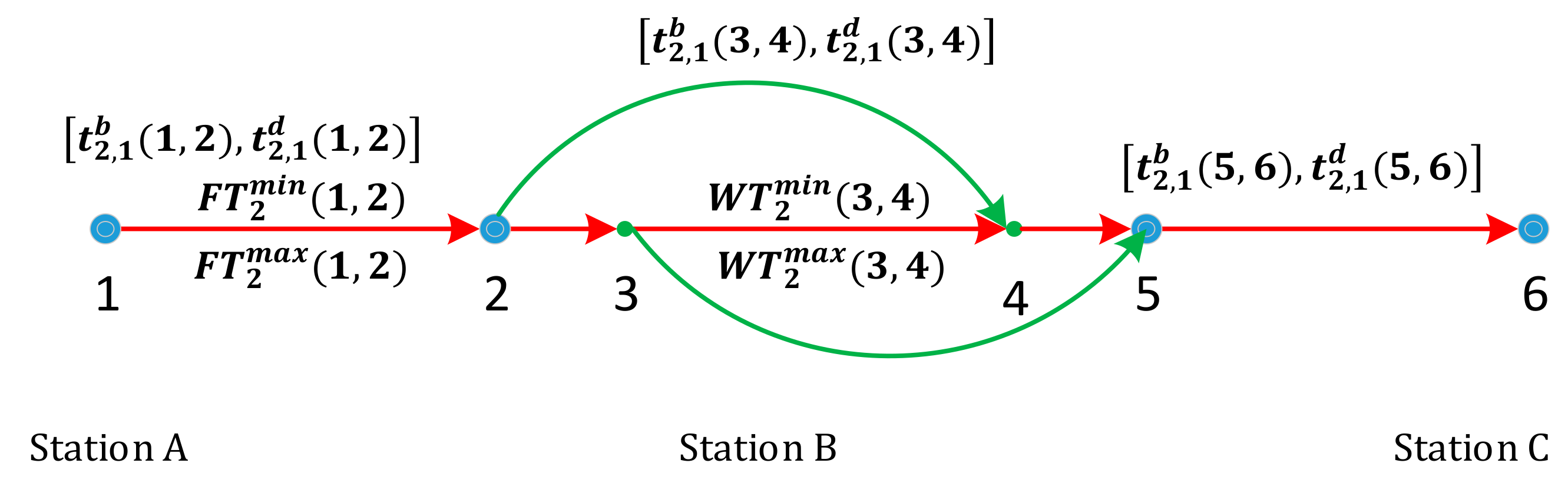
5.1. Description of Added Notations
5.2. The Simplified Strategy
6. Numerical Analysis
6.1. Performance, Efficiency, and Stability Analysis on a Small Constructed Rail Network
6.1.1. Inputs and Parameters
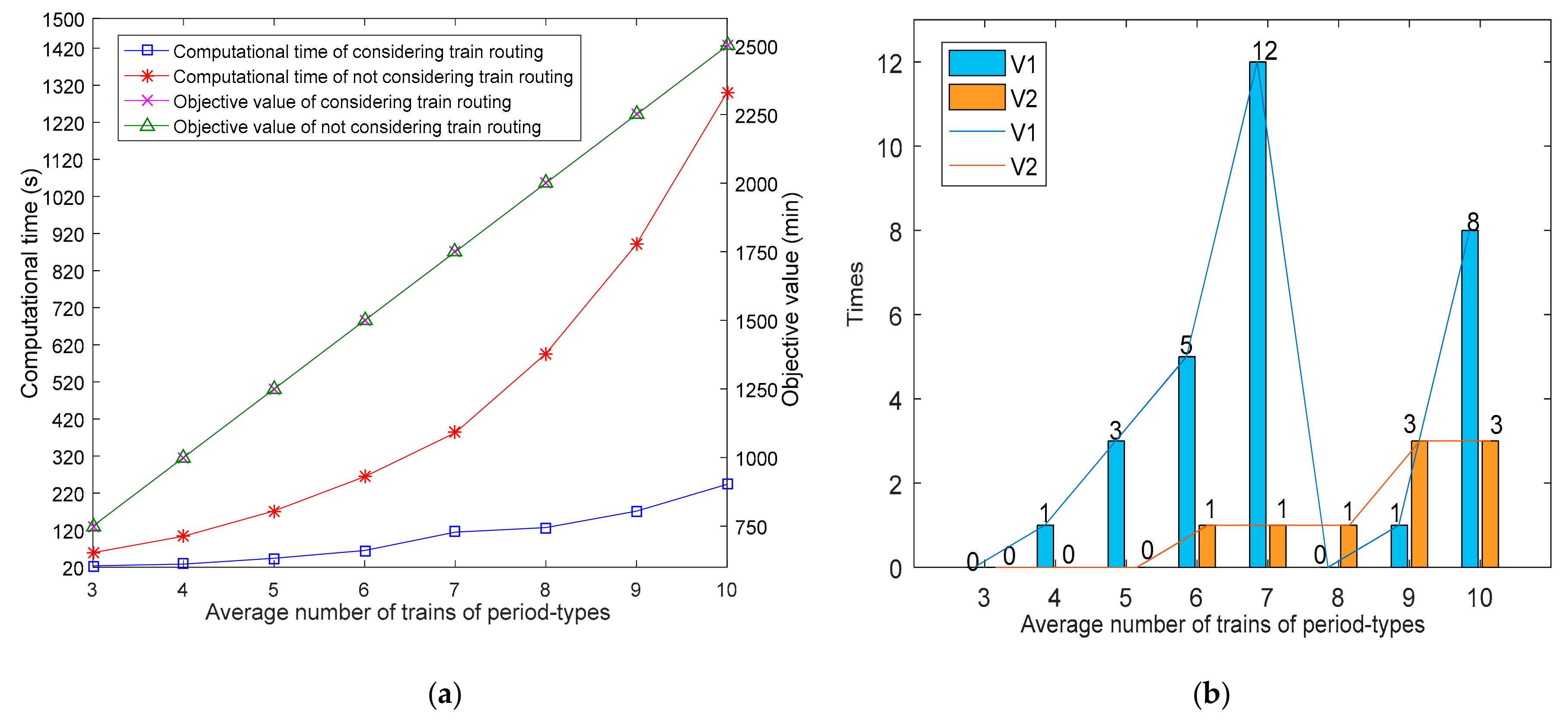
6.1.2. The Benefits of Integrating Train Scheduling and Train Routing at Stations
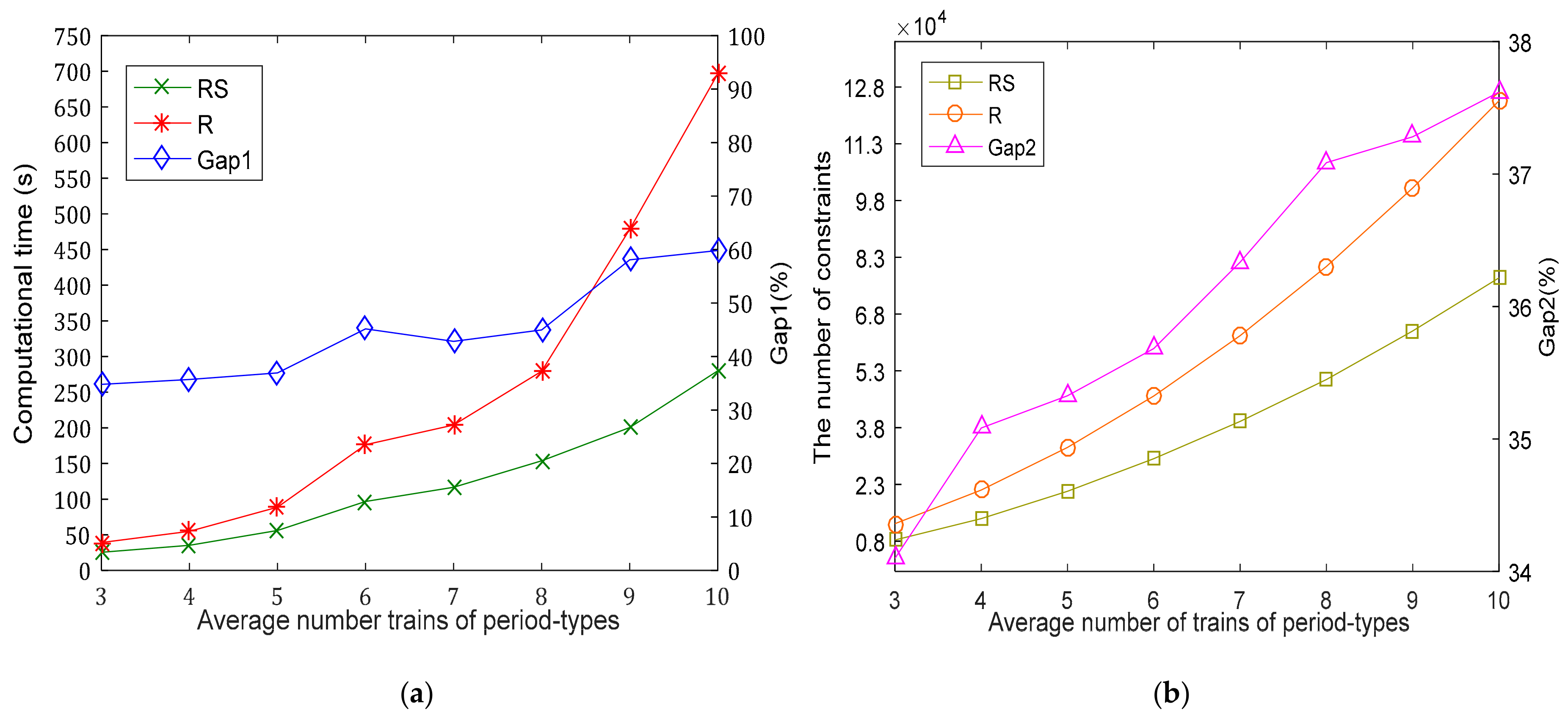
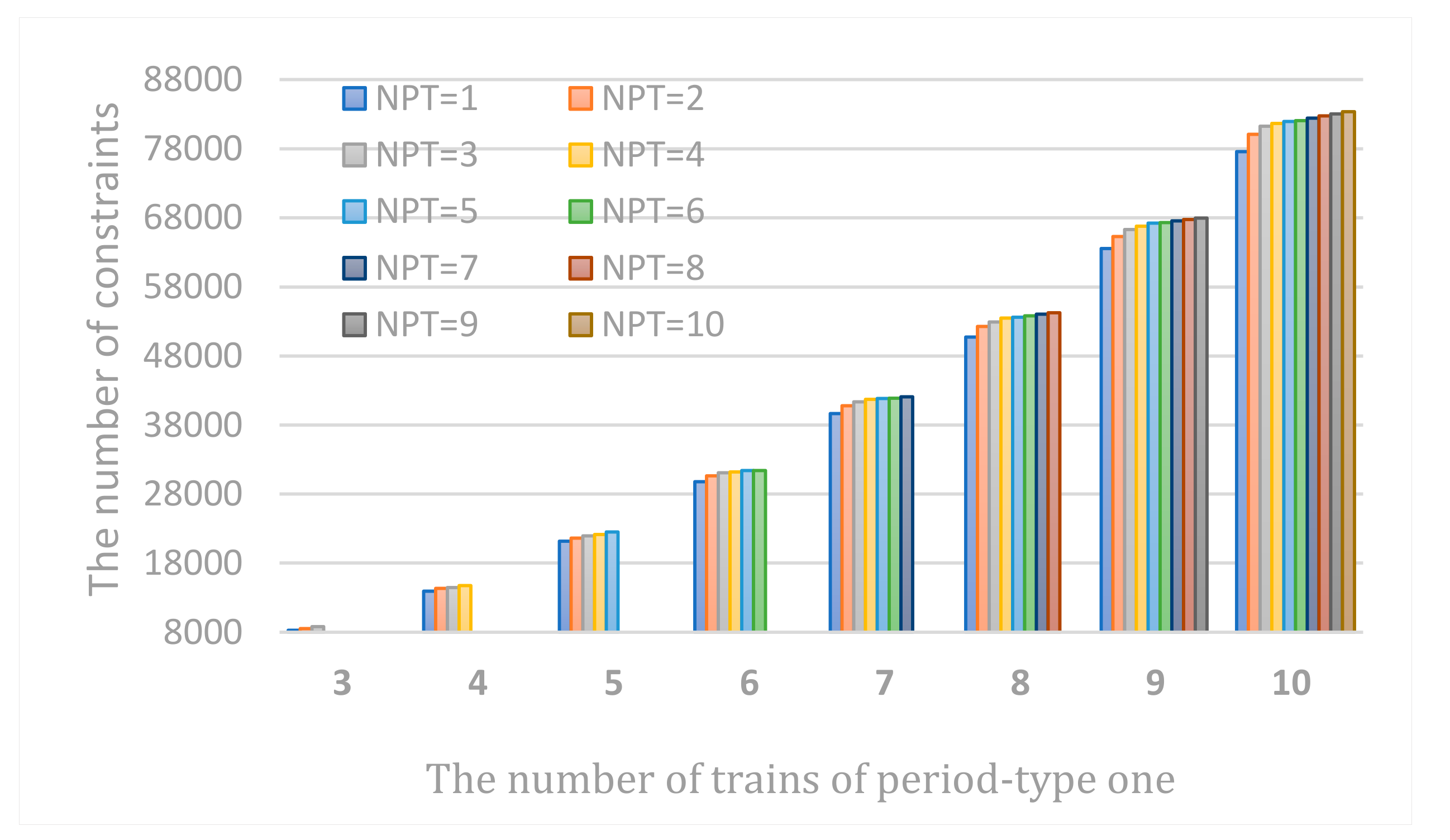
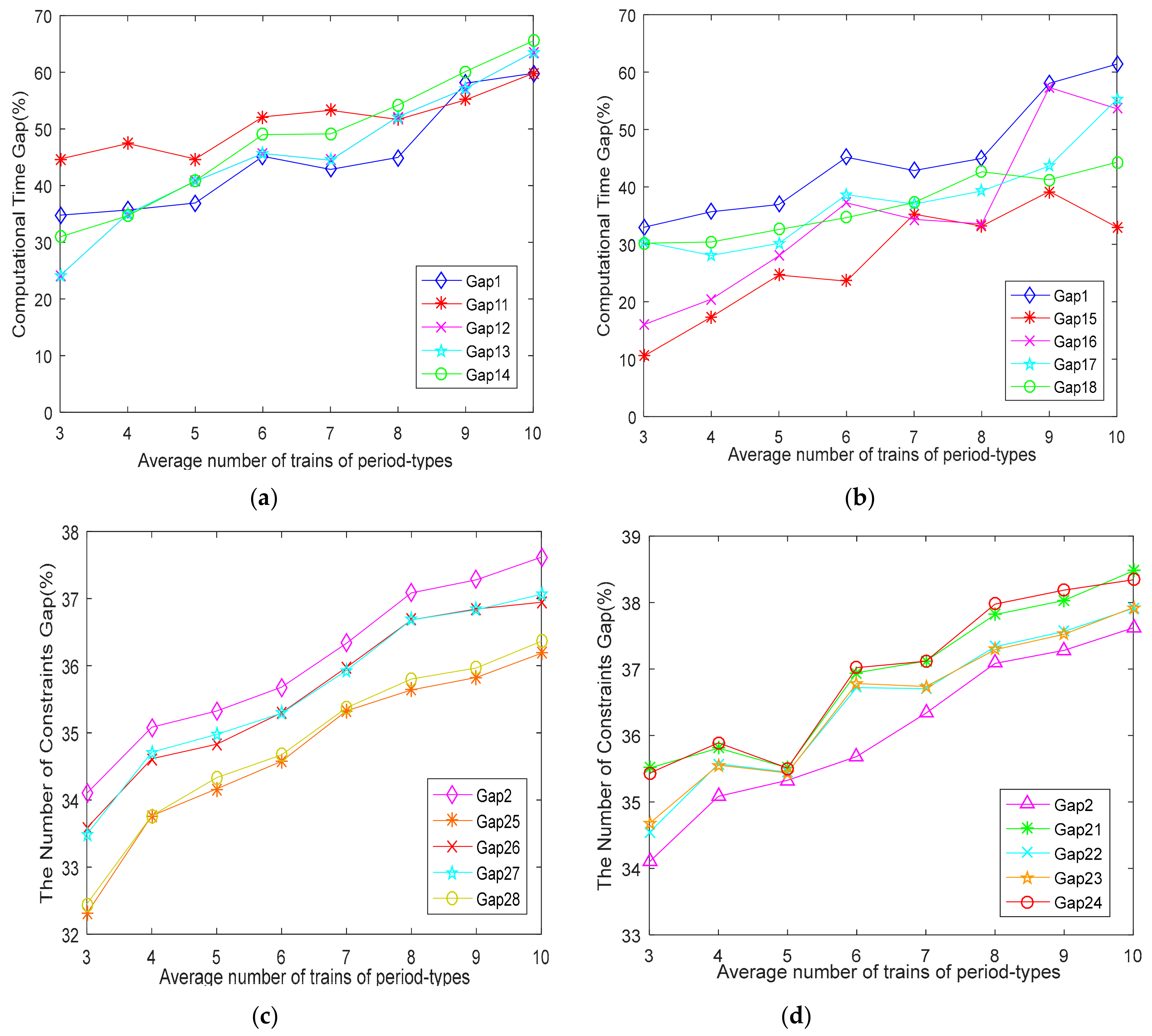
6.1.3. The Contribution of the Solving-Simplify Strategy to Solve Efficiency of Our Model
- CTR, CTRS are respectively computational time of R and RS.
- CONR, CONRS are respectively the number of constraints of R and RS.
6.1.4. Performance and Stability Analysis of the Model
- (1)
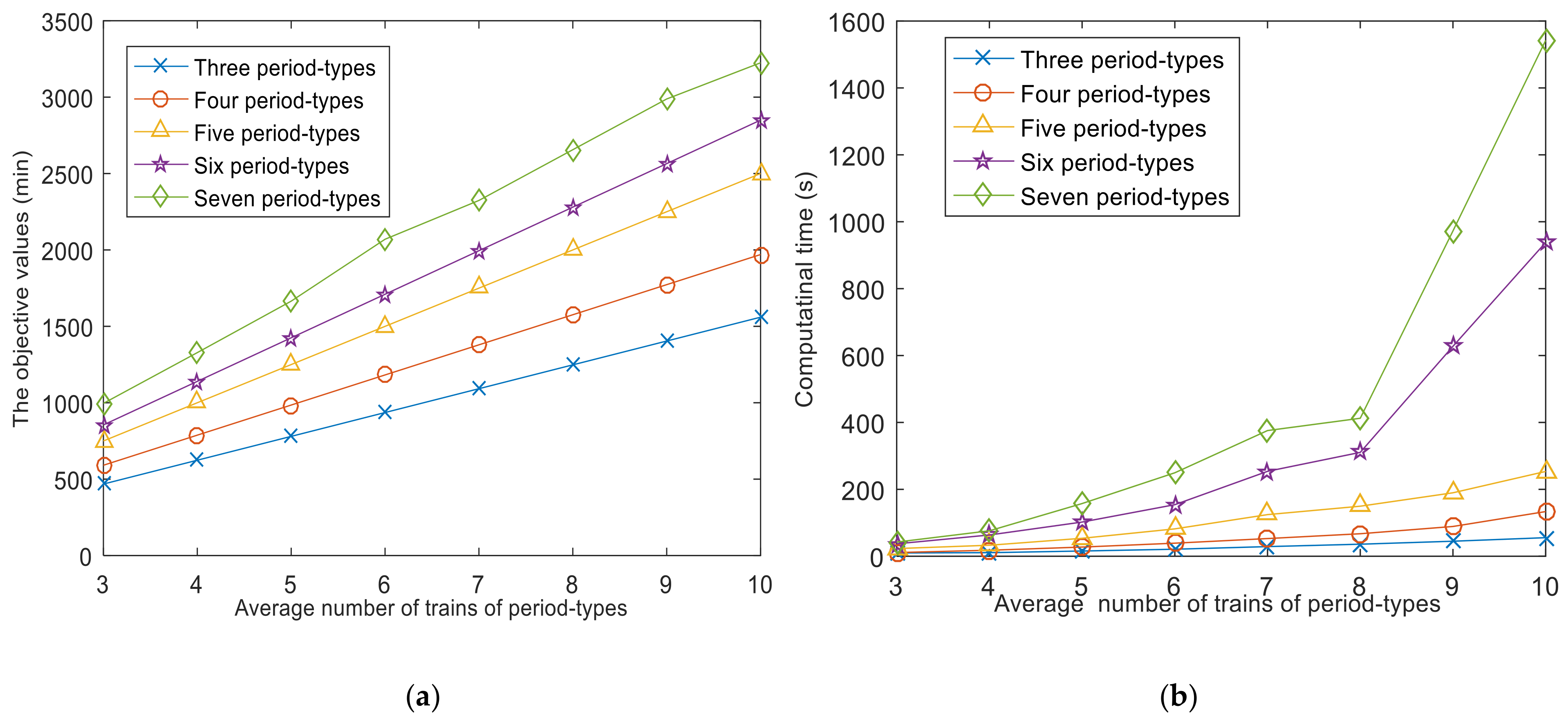
- Performance analysis with increasing the ANTP
- (2)
- Performance analysis with increasing the number of period-types
- (3)
- Stability analysis of the simplified strategy with changing running time or dwelling time
- ■
- Category 1: Contracting the running time range in sections and dwelling time range at stations by decreasing their maximum or increasing their minimum.
- ■
- Category 2: Expanding the running time range in sections and dwelling time range at stations by increasing their maximum or decreasing their minimum.
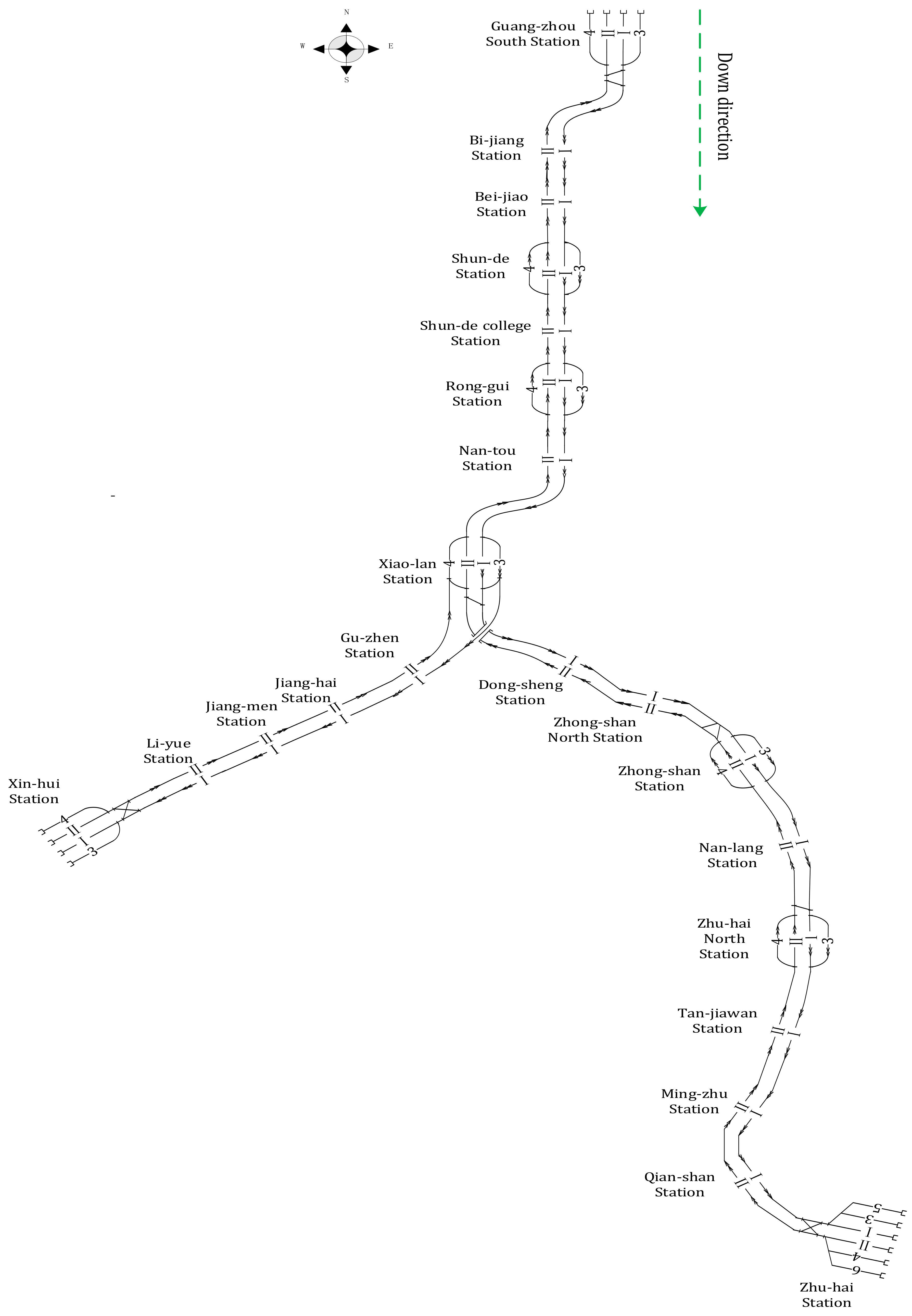
6.2. Application Analysis Based on the Guang-Zhu Inter-City Rail
- (1)
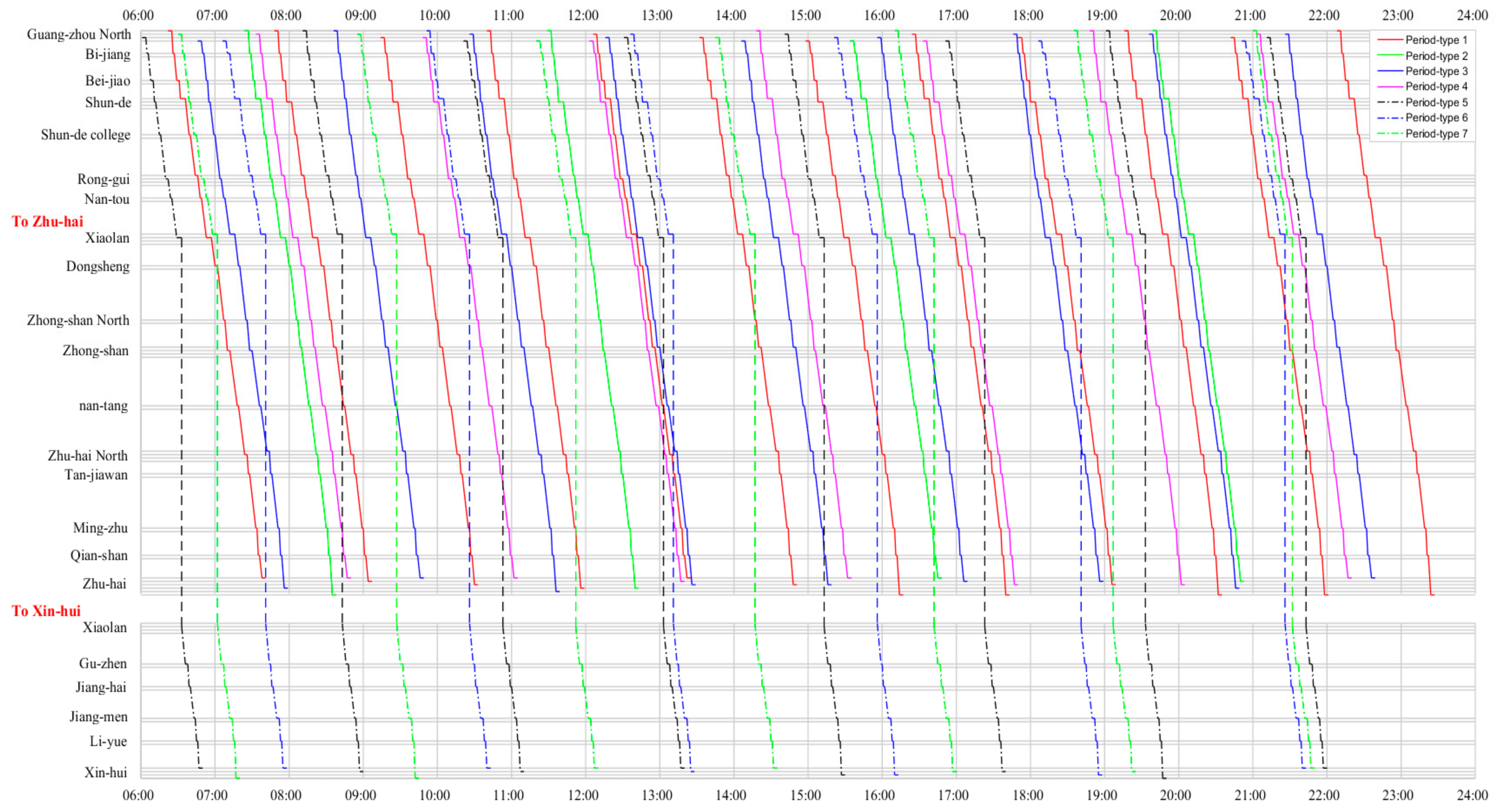
- Trains of the same period-type have the same stop plan, enter and leave off each visited station with the same period-length to make the train timetable more regular. Thus, it can provide convenience for passengers, attract more passengers, and achieve good social and economic benefits for the high-speed railway. Moreover, this kind of regularity can also improve the efficiency of transportation organization on a high-speed railway network. Moreover, the trains’ chosen arrival–departure tracks at each visited station can be different so as to realize the efficient allocation of traffic resources on a high-speed railway.
- (2)
- The running time of trains of each period-type almost cross the whole operation time to meet passenger demand over the day, and the strict period-length ensures the regularities of multi-periodic trains to provide convenience for passengers. Furthermore, the number of trains of each period-type may be different according to changes in passenger demand. For example, it needs to operate 12 trains in the period-type 1, the first train’s departure time is 06:25, and the last train’s arrival time is 23:24, while it only needs to operate four trains in the period-type 2, the first train’s departure time is 07:27, and the last train’s arrival time is 20:50.
7. Conclusions and Further Studies
- (1)
- Based on a large number of numerical examples, it is obvious that our proposed mixed integer linear programming model has good performance, stability, and practicability in solving the problem of simultaneous multi-periodic train timetabling and routing.
- (2)
- The simplified strategy in our model can greatly reduce the computational time by 30–50%, so as to improve the solve efficiency by reducing the number of constraints, and it is also proved that it has a good stability by changing its main impact factors. Moreover, the more trains that operate, the more obvious the effect is.
- (3)
- Train timetables that consider trains’ routes at stations can eliminate conflicts among trains at stations to improve the efficiency of trains’ operating. It is especially obvious with increasing the number of trains. For example, in Figure 8, when the ATNP is 6, it first occurs when more than two trains conflicts at the same station. When the ATNP is 7, the times of conflicts reached more than 13.
- (4)
- Compared with an aperiodic train timetable, a multi-periodic train timetable has higher computation efficiency that can be improved from 30% to 67.2% with increasing the number of period-types. In addition, trains’ operating density on a multi-periodic train timetable can better satisfy the time-varying of passenger demand to provide better service for passengers on a high-speed rail network.
- (1)
- Take more practical factors in the process of train operating into account, such as acceleration, deceleration, and dwelling of trains in the sections, so that the obtained train timetable is more feasible when applied to the real-world situations. Moreover, the robustness of a train timetable should also be considered to cope with possible delays or disturbances.
- (2)
- To consider the distribution of passenger demand in the process of the multi-periodic train timetabling and routing so as to design a train timetable that can match with the change of passenger demand. Some indicators related with passenger service level can also be added. Moreover, based on the change of passenger demand, we can adjust the stop plan of trains to reduce the unnecessary stops of trains and unnecessary usage of arrival–departure tracks at stations.
- (3)
- The optimization of periodic and non-periodic train timetabling or routing on a high-speed rail network. While most trains are arranged to run with a fixed regular interval, some non-periodic trains are allowed to operate at some time-periods with higher passenger demand.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mu, S.; Dessouky, M. Efficient dispatching rules on double tracks with heterogeneous train traffic. Transp. Res. Part B Methodol. 2013, 51, 45–64. [Google Scholar] [CrossRef]
- Cai, X.; Goh, C. A fast heuristic for the train scheduling problem. Comput. Oper. Res. 1994, 21, 499–510. [Google Scholar] [CrossRef]
- Caprara, A.; Fischetti, M.; Toth, P. Modeling and Solving the Train Timetabling Problem. Oper. Res. 2002, 50, 851–861. [Google Scholar] [CrossRef]
- Caimi, G.; Chudak, F.; Fuchsberger, M.; Laumanns, M.; Zenklusen, R. A New Resource-Constrained Multicommodity Flow Model for Conflict-Free Train Routing and Scheduling. Transp. Sci. 2011, 45, 212–227. [Google Scholar] [CrossRef]
- Pellegrini, P.; Marlière, G.; Rodriguez, J. Optimal train routing and scheduling for managing traffic perturbations in complex junctions. Transp. Res. Part B Methodol. 2014, 59, 58–80. [Google Scholar] [CrossRef]
- Xu, X.; Li, K.; Yang, L. Scheduling heterogeneous train traffic on double tracks with efficient dispatching rules. Transp. Res. Part B Methodol. 2015, 78, 364–384. [Google Scholar] [CrossRef]
- Sparing, D.; Goverde, R.M.P. A cycle time optimization model for generating stable periodic railway timetables. Transp. Res. Part B Methodol. 2017, 98, 198–223. [Google Scholar] [CrossRef]
- Odijk, M.A. A constraint generation algorithm for the construction of periodic railway timetables. Transp. Res. Part B Methodol. 1996, 30, 455–464. [Google Scholar] [CrossRef]
- Zhou, W.; Yang, X. Timetable Optimization for High-Speed Rail with Multiple Operating Periods: Solving Method Based on a Framework of Lagrangian Relaxation Decomposition. Transp. Res. Rec. J. Transp. Res. Board 2016, 2546, 43–52. [Google Scholar] [CrossRef]
- Zhou, W.; Tian, J.; Xue, L.; Jiang, M.; Deng, L.; Qin, J. Multi-periodic train timetabling using a period-type-based Lagrangian relaxation decomposition. Transp. Res. Part B Methodol. 2017, 105, 144–173. [Google Scholar] [CrossRef]
- Samà, M.; D’Ariano, A.; Pacciarelli, D.; Corman, F. Lower and upper bound algorithms for the real-time train scheduling and routing problem in a railway network. IFAC-PapersOnLine 2016, 49, 215–220. [Google Scholar] [CrossRef]
- Mees, A. Railway scheduling by network optimization. Math. Comput. Model. 1991, 15, 33–42. [Google Scholar] [CrossRef]
- Törnquist, J.; Persson, J.A. N-tracked railway traffic re-scheduling during disturbances. Transp. Res. Part B Methodol. 2007, 41, 342–362. [Google Scholar] [CrossRef]
- Szpigel, B. Optimal train scheduling on a single track railway. Oper. Res. 1972, 72, 343–352. [Google Scholar]
- D’Ariano, A.; Pacciarelli, D.; Pranzo, M. A branch and bound algorithm for scheduling trains in a railway network. Eur. J. Oper. Res. 2007, 183, 643–657. [Google Scholar] [CrossRef]
- Dessouky, M.M.; Lu, Q.; Zhao, J.; Leachman, R.C. An exact solution procedure to determine the optimal dispatching times for complex rail networks. IIE Trans. 2006, 38, 141–152. [Google Scholar] [CrossRef]
- Cardillo, D.D.L.; Mione, N. k L-list λ colouring of graphs. Eur. J. Oper. Res. 1998, 106, 160–164. [Google Scholar] [CrossRef]
- Zwaneveld, P.J.; Kroon, L.G.; Van Hoesel, S.P. Routing trains through a railway station based on a node packing model. Eur. J. Oper. Res. 2001, 128, 14–33. [Google Scholar] [CrossRef]
- Caimi, G.; Burkolter, D.; Herrmann, T. Finding Delay-Tolerant Train Routings through Stations. Oper. Res. Proc. 2005, 2004, 136–143. [Google Scholar]
- Lusby, R.M.; Larsen, J.; Ehrgott, M.; David, R. Railway track allocation: Models and methods. OR Spectr. 2011, 33, 843–883. [Google Scholar] [CrossRef]
- Billionnet, A. Using Integer Programming to Solve the Train-Platforming Problem. Transp. Sci. 2003, 37, 213–222. [Google Scholar] [CrossRef]
- Goverde, R.M.; Hansen, I.A. Performance indicators for railway timetables. In Proceedings of the IEEE International Conference on Intelligent Rail Transportation (ICIRT), Beijing, China, 30 August–1 September 2013; pp. 301–306. [Google Scholar]
- Burggraeve, S.; Vansteenwegen, P. Robust routing and timetabling in complex railway stations. Transp. Res. Part B Methodol. 2017, 101, 228–244. [Google Scholar] [CrossRef]
- Mazzarello, M.; Ottaviani, E. A traffic management system for real-time traffic optimisation in railways. Transp. Res. Part B Methodol. 2007, 41, 246–274. [Google Scholar] [CrossRef]
- Dewilde, T.; Sels, P.; Cattrysse, D.; Vansteenwegen, P. Robust railway stationplanning: An interaction between routing, timetabling and platforming. J. Rail Transp. Plan. Manag. 2013, 3, 68–77. [Google Scholar]
- Lee, Y.; Chen, C.Y. A heuristic for the train pathing and timetabling problem. Transp. Res. Part B Methodol. 2009, 43, 837–851. [Google Scholar] [CrossRef]
- Castillo, E.; Gallego, I.; Ureña, J.M.; Coronado, J.M. Timetabling optimization of a mixed double- and single-tracked railway network. Appl. Math. Model. 2011, 35, 859–878. [Google Scholar] [CrossRef]
- Morlok, E.K.; Peterson, R.B. Final report on a development of a geographic transportation network generation and evaluation model. Transp. Res. Forum. 1996, 90, 26–44. [Google Scholar]
- Li, F.; Gao, Z.; Li, K.; David, Z.; Wang, W. Train Routing Model and Algorithm Combined with Train Scheduling. J. Transp. Eng. 2013, 139, 81–91. [Google Scholar] [CrossRef]
- Zhou, W.; Teng, H. Simultaneous passenger train routing and timetabling using an efficient train-based Lagrangian relaxation decomposition. Transp. Res. Part B Methodol. 2016, 94, 409–439. [Google Scholar] [CrossRef]
- Wardman, M.; Shires, J.; Lythgoe, W.; Tyler, J. Consumer benefits and demand impacts of regular train timetables. Int. J. Transp. Manag. 2004, 2, 39–49. [Google Scholar] [CrossRef]
- Johnson, D.; Shires, J.; Nash, C.; Tyler, J. Forecasting and appraising the impact of a regular interval timetable. Transp. Policy 2006, 13, 349–366. [Google Scholar] [CrossRef]
- Serafini, P.; Ukovich, W. A Mathematical Model for Periodic Scheduling Problems. SIAM J. Discret. Math. 1989, 2, 550–581. [Google Scholar] [CrossRef]
- Goverde, R.M.P. Improving Punctuality and Transfer Reliability by Railway Timetable Optimization; Delft University Press: Delft, The Netherlands, 1999. [Google Scholar]
- Kroon, L.G.; Peeters, L.W.P. A Variable Trip Time Model for Cyclic Railway Timetabling. Transp. Sci. 2003, 37, 198–212. [Google Scholar] [CrossRef]
- Lindner, T. Train Schedule Optimization in Public Rail Transport. Ph.D. Thesis, Technische Universität Braunschweig, Braunschweig, Germany, 2000. [Google Scholar]
- Heydar, M.; Petering, M.E.; Bergmann, D.R. Mixed integer programming for minimizing the period of a cyclic railway timetable for a single track with two train types. Comput. Ind. Eng. 2013, 66, 171–185. [Google Scholar] [CrossRef]
- Nachtigall, K.; Voget, S. A genetic algorithm approach to periodic railway synchronization. Comput. Oper. Res. 1996, 23, 453–463. [Google Scholar] [CrossRef]
- Sels, P.; Cattrysse, D.; Vansteenwegen, P. Automated platforming & routing of trains in all Belgian railway stations. Expert Syst. Appl. 2016, 62, 302–316. [Google Scholar]
- Nachtigall, K. Periodic network optimization with different arc frequencies. Discret. Appl. Math. 1996, 69, 1–17. [Google Scholar] [CrossRef]



| Research | Aperiodic or Periodic | Objects | Methods |
|---|---|---|---|
| Mees [12], Caprara et al. [3], Törnquist and Persson [13] | aperiodic | timetabling | neglected the layouts of stations |
| Szpigel [14], D’Ariano et al. [15], Dessouky et al. [16] | aperiodic | timetabling | pre-determined routes at stations of trains |
| De Luca et al. [17], Zwaneveld et al. [18], Caimi, Burkolter and Herrmann [19], Lusby et al. [20], Billionnet [21] | aperiodic | routing | with a given train timetable |
| Mazzarello and Ottaviani [24], Dewilde et al. [25], Yusin and Chen [26], Castillo et al. [27] | aperiodic | timetabling and routing | optimizing them interactively and iteratively |
| Morlok and Peterson [28], Li et al. [29], Pellegrini et al. [5], Xu et al. [6], Zhou and Teng [30] | aperiodic | timetabling and routing | simultaneous timetabling and routing |
| Serafini and Ukovich [33], Odijk [8], Goverde [34], Kroon and Peeters [35], Lindner [36], Heydar, Petering and Bergmann [37] | periodic | timetabling | based on PESP |
| Nachtigall and Voget [38], Caprara et al. [3], els, Cattrysse and Vansteenwegen [39] | periodic | timetabling | genetic algorithms, directed graphs, and spanning trees |
| Caimi et al. [4], Sparing and Goverde [7], Burggraeve and Vansteenwegen [23] | periodic | timetabling and routing | optimizing them respectively or interactively |
| Zhou and Yang [9], Zhou and Tian [10], Zhou and Teng [30] | multi-periodic | timetabling | neglected the layouts of stations |
| This paper | multi-periodic | timetabling and routing | simultaneous timetabling and routing |
| Objects | Symbols | Defined Range | Descriptions |
|---|---|---|---|
| Rail network | Set of stations on the rail network | ||
| Set of arcs on the rail network | |||
| Set of section arcs on the rail network | |||
| TA | Set of station arcs on the rail network | ||
| Set of arrival–departure track arcs on the rail network | |||
| Set of one-way arcs on the rail network | |||
| Set of two-way arcs on the rail network | |||
| Set of arcs at station | |||
| The index of nodes | |||
| Set of arcs entering node | |||
| Set of arcs departing from node | |||
| The index of arcs | |||
| Trains | Number of period-types | ||
| The index of period-type | |||
| Number of trains of period-type | |||
| The index of train | |||
| ; | The th train of period-type | ||
| Set of stations visited by trains of period-type | |||
| Set of alternative nodes of trains of period-type | |||
| Set of alternative origin nodes of trains of period-type | |||
| Set of alternative terminal nodes of trains of period-type | |||
| Set of alternative entering nodes of stations of trains of period-type | |||
| Set of alternative leaving nodes of stations of trains of period-type | |||
| Set of alternative arcs of trains of period-type | |||
| Minimum operation time on section arc for trains of period-type | |||
| Maximum operation time on section arc for trains of period-type | |||
| Minimum dwelling time on arrival–departure track arc (i,j) for trains of period-type w | |||
| Maximum dwelling time on arrival–departure track arc for trains of period-type | |||
| Minimum safety time interval of trains entering section by node from the same direction | |||
| Minimum safety time interval of trains leaving off section arc by node from the same direction | |||
| Minimum safety time interval of trains occupying the arc | |||
| The earliest departure time of the first train of period-type at its origin | |||
| The latest departure time of the first train of period-type at its origin | |||
| ; | The th set for train on arc | ||
| The period-length of period-type | |||
| Others | Planning time horizon | ||
| A very big positive number |
| Variables | Defined Range | Descriptions |
|---|---|---|
| ; | 0–1 binary decision variable, if the th train of period-type visits a non-section arc , then ; otherwise, . | |
| ; | The time of the th train of period-type entering arc If it doesn’t visit arc , then | |
| ; | The time of the th train of period-type leaving off arc . If it doesn’t visit arc , then . | |
| ; | 0–1 binary variable, if the th train of period-type visits arc after the train of period-type from either the same direction or two opposite directions, then ; otherwise, . |
| Objects | Symbols | Defined Range | Descriptions |
|---|---|---|---|
| trains | The earliest time of train entering arc | ||
| The latest time of train entering arc | |||
| The earliest time of train leaving off arc | |||
| The latest time of train leaving off arc |
| sets | Cancelled Constraints | Adjusted Constraints |
|---|---|---|
| constraint (16) | ||
| constraint (16) | ||
| constraint (16) (23) | ||
| constraint (16) | ||
| constraint (17) | ||
| constraint (17) | ||
| constraint (17) (24) | ||
| constraint (17) | ||
| constraints (18) and (19) | ||
| constraints (18) and (19) | ||
| constraint (18) and (19) (25) | ||
| constraint (19) | ||
| constraint (20), (21) and (22) | ||
| constraint (20), (21) and (22) |
| Direction | Period-type | Traverse Stations | Stop Stations | Range of Departure Time of the First Train at Origin |
|---|---|---|---|---|
| A–F | 1 | A, B, C, D, E, F A, B, C, D, E, F | B, C, D, E | (06:00, 06:30) |
| 2 | B, C | (06:45, 07:00) | ||
| 3 | A, B, C, D, E, F | C, E | (09:30, 09:45) | |
| A–H | 4 | A, B, C, G, H | B, C, G | (06:15, 06:45) |
| 5 | A, B, C, G, H | C, G | (09:55, 10:05) |
| Sections | A–B | B–C | C–D | D–E | E–F | C–G | G–H |
|---|---|---|---|---|---|---|---|
| Maximum | 8 | 7 | 7 | 12 | 12 | 10 | 10 |
| Minimum | 6 | 6 | 5 | 10 | 10 | 7 | 7 |
| Stations | A | B | C | D | E | F | G | H |
|---|---|---|---|---|---|---|---|---|
| Maximum | 4 | 9 | 9 | 4 | 4 | 4 | 4 | 4 |
| Minimum | 2 | 3 | 5 | 1 | 1 | 2 | 1 | 2 |
| NPT | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| NTPO | ||||||||||
| 3 | 1 | 2 | 3 | -- | -- | -- | -- | -- | -- | -- |
| 4 | 1 | 2 | 3 | 4 | -- | -- | -- | -- | -- | -- |
| 5 | 1 | 2 | 3 | 4 | 5 | -- | -- | -- | -- | -- |
| 6 | 1 | 2 | 3 | 4 | 5 | 6 | -- | -- | -- | -- |
| 7 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | -- | -- | -- |
| 8 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | -- | -- |
| 9 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | -- |
| 10 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Test Instances | Category 1 | Category 2 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
| Running time in sections | maximum | −2 | −1 | — | — | +2 | +1 | — | — |
| minimum | — | — | +1 | +2 | — | — | −1 | −2 | |
| Dwelling time at stations | maximum | −2 | −1 | — | — | +2 | +1 | -- | — |
| minimum | — | — | +1 | +2 | — | — | −1 | −2 | |
| Operation Direction | Period-Type | Sequence of Stop Stations | Number of Operation Trains |
|---|---|---|---|
| Guangzhou South to Zhu-hai | 1 | Guangzhou South, Bei-jiao, Shun-de, Rong-gui, Xiao-lan, Dong-sheng, Zhong-shan, Zhu-hai North, Zhu-hai | 12 |
| 2 | Guangzhou South, Shun-de, Xiao-lan, Zhu-hai | 4 | |
| 3 | Guangzhou South, Xiao-lan, Zhong-shan, Zhu-hai North, Zhu-hai | 9 | |
| 4 | Guangzhou South, Shun-de, Rong-gui, Xiao-lan, Dong-sheng, Zhu-hai | 7 | |
| Guangzhou South to Xin-hui | 5 | Guangzhou South, Bei-jiao, Rong-gui, Xiao-lan, Gu-zhen, Xin-hui | 8 |
| 6 | Guangzhou South, Shun-de, Rong-gui, Xiao-lan, Jiang-men, Xin-hui | 6 | |
| 7 | Guangzhou South, Shun-de college, Rong-gui, Xiao-lan, Gu-zhen, Jiang-men, Xin-hui | 7 |
| Sections | Max | Min | Sections | Max | Min |
|---|---|---|---|---|---|
| Guangzhou South to Bi-jiang | 3 | 1 | Nan-lang to Zhu-hai North | 5 | 4 |
| Bi-jiang to Bei-jiao | 3 | 2 | Zhu-hai North to Tang-jiawan | 3 | 1 |
| Bei-jiao to Shun-de | 3 | 1 | Tang-jiawan to Ming-zhu | 6 | 5 |
| Shun –de to Shun-de college | 4 | 3 | Ming-zhu to Qian-shan | 3 | 1 |
| Shun-de college to Rong-gui | 5 | 3 | Qian-shan to Zhu-hai | 4 | 2 |
| Rong-gui to Nan-tou | 4 | 2 | Xiao-lan to Gu-zhen | 5 | 3 |
| Nan-tou to Xiao-lan | 5 | 4 | Gu-zhen to Jiang-hai | 3 | 1 |
| Xiao-lan to Dong-sheng | 5 | 3 | Jiang-hai to Jiang-men | 5 | 3 |
| Dong-sheng to Zhong-shan North | 6 | 5 | Jiang-men to Xin-yue | 2 | 1 |
| Zhong-shan North to Zhong-shan | 4 | 2 | Xin-yue to Xin-hui | 3 | 1 |
| Zhong-shan to Nan-lang | 6 | 5 |
| Stations | Max | Min | Sections | Max | Min |
|---|---|---|---|---|---|
| Guangzhou South | 5 | 3 | Zhong-shan | 5 | 2 |
| Bi-jiang | 2 | 1 | Nan-lang | 2 | 1 |
| Bei-jiao | 5 | 2 | Zhu-hai North | 5 | 2 |
| Shun –de | 8 | 4 | Tang-jiawan | 2 | 1 |
| Shun-de college | 2 | 1 | Ming-zhu | 2 | 1 |
| Rong-gui | 3 | 2 | Qian-shan | 2 | 1 |
| Nan-tou | 2 | 1 | Gu-zhen | 2 | 1 |
| Xiao-lan | 8 | 4 | Jiang-hai | 2 | 1 |
| Dong-sheng | 5 | 2 | Jiang-men | 2 | 1 |
| Zhong-shan North | 2 | 1 | Xin-yue | 5 | 3 |
| RS and R | Objective Value (OBJ)/minutes | Computational Time (CT)/seconds | Number of Constraints | ||
|---|---|---|---|---|---|
| RS | 3494 | 1018.78 | 44.23% | 195349 | 35.17% |
| R | 3494 | 1826.73 | 301312 |
| Period-Type | Period-Length | Number of Trains | Departure Time of the First Train | Departure Time of the Last Train | Travel Time of Single Train |
|---|---|---|---|---|---|
| 1 | 86 | 12 | 06:25 | 22:11 | 69 |
| 2 | 245 | 4 | 07:27 | 19:42 | 64 |
| 3 | 110 | 9 | 06:49 | 21:29 | 63 |
| 4 | 135 | 7 | 07:36 | 21:06 | 67 |
| 5 | 130 | 8 | 06:04 | 21:14 | 49 |
| 6 | 165 | 6 | 07:09 | 20:54 | 52 |
| 7 | 145 | 7 | 06:33 | 21:03 | 50 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, W.; You, X.; Fan, W. A Mixed Integer Linear Programming Method for Simultaneous Multi-Periodic Train Timetabling and Routing on a High-Speed Rail Network. Sustainability 2020, 12, 1131. https://doi.org/10.3390/su12031131
Zhou W, You X, Fan W. A Mixed Integer Linear Programming Method for Simultaneous Multi-Periodic Train Timetabling and Routing on a High-Speed Rail Network. Sustainability. 2020; 12(3):1131. https://doi.org/10.3390/su12031131
Chicago/Turabian StyleZhou, Wenliang, Xiaorong You, and Wenzhuang Fan. 2020. "A Mixed Integer Linear Programming Method for Simultaneous Multi-Periodic Train Timetabling and Routing on a High-Speed Rail Network" Sustainability 12, no. 3: 1131. https://doi.org/10.3390/su12031131
APA StyleZhou, W., You, X., & Fan, W. (2020). A Mixed Integer Linear Programming Method for Simultaneous Multi-Periodic Train Timetabling and Routing on a High-Speed Rail Network. Sustainability, 12(3), 1131. https://doi.org/10.3390/su12031131





