The Use of a Simulation Model for High-Runner Strategy Implementation in Warehouse Logistics

Abstract

This paper examines the use of computer simulation methods to streamline the process of picking materials within warehouse logistics. The article describes the use of a genetic algorithm to optimize the storage of materials in shelving positions, in accordance with the method of High-Runner Strategy. The goal is to minimize the time needed for picking. The presented procedure enables the creation of a software tool in the form of an optimization model that can be used for the needs of the optimization of warehouse logistics processes within various types of production processes. There is a defined optimization problem in the form of a resistance function, which is of general validity. The optimization is represented using the example of 400 types of material items in 34 categories, stored in six rack rows. Using a simulation model, a comparison of a normal and an optimized state is realized, while a time saving of 48 min 36 s is achieved. The mentioned saving was achieved within one working day. However, the application of an approach based on the use of optimization using a genetic algorithm is not limited by the number of material items or the number of categories and shelves. The acquired knowledge demonstrates the application possibilities of the genetic algorithm method, even for the lowest levels of enterprise logistics, where the application of this approach is not yet a matter of course but, rather, a rarity.

1. Introduction

Warehouse logistics is now facing many challenges in reducing the volume of required inventory, accelerating logistics processes, more efficient use of the available infrastructure, the introduction of new technologies, and the use of information and analytical tools. To manage these trends, it is possible to apply the so-called progressive approaches that are based, e.g., on the use of various analytical and predictive software tools. This trend is described in more detail by Zunic et al. [1], who dealt with the issue of optimization algorithms to create a method of effective strategic and quantitative object placement while picking within a medium-sized warehouse.

Warehouse processes can be implemented in several ways and according to different strategies. The choice of a specific warehousing strategy usually depends on basic warehousing tasks, the structure and size of customer orders, the equipment of the logistics units, material handling costs in individual sub-processes (financial and time costs), storage availability, and work resources [2]. Brynzer and Johansson describe the issue of warehousing processes and their impact on warehousing logistics in more detail [3]. The warehouse management system and warehouse processes are currently considered to be key factors in corporate logistics [4].

All these facts need to be considered not only when designing new warehouses [5], but also when improving logistics processes in existing and operational warehouses [6].

In addition to the warehousing processes in individual warehouses, it is necessary to pay attention to the area of warehouse allocation within logistics networks. Jacyna-Golda and Izdebski have examined this issue in more detail [7]. They state that the location of storage facilities is a complex problem aimed at several objectives. Various mathematical models can be used to determine this location, describing the location according to accepted constraints and criteria. In their research, the authors further state that the problem of locating a warehouse in the logistics network is the problem of optimizing several criteria, which depends on quantitative and qualitative criteria. Optimization criteria generally take the form of the minimum storage costs, the costs of transporting goods through storage facilities, and the costs of transporting material to the storage facility.

Within warehouse logistics, it is possible to use a wide range of optimization approaches to improve its processes. Povoda et al. [8] describe, in more detail, the optimization algorithm for the problem of scheduling activities in logistics warehouses. The algorithm they present is based on genetic programming and the use of parallel processing. For better performance, the authors proposed a new optimization method called “priority rules”. The paper describes the finding that the three proposed priority rules help the algorithm to prevent deadlocks in local optimums and to obtain better results from optimization using genetic programming. Ribino et al. [9] implemented an agent-based simulation to analyze the behavior of automatic logistics warehouses under the influence of specific factors. As a result, they gained indicators to support decision-making in improving warehouse performance.

As part of the optimization of the activities of warehousing processes, attention is also paid to issues focused on the area of transport and handling equipment. Al-Shaebi et al. [10] examined the behavior of forklift drivers, examining the average number of pallet movements per operating hour in a warehouse using various statistical and regression analyses. Overall, it can be stated that the area of transport is very important in warehousing logistics [11]. Transport, in the field of warehousing logistics, affects its processes regardless of the type of warehousing system [12]. At the same time, transport also influences the processes of supplying warehouses and the subsequent sale of products. The work of Clarke and Wright is one of the most well-known works in this field [13].

Another area of warehouse logistics that significantly affects the efficiency of processes within the warehouse is picking [14]. Picking not only affects warehousing but also affects other logistics processes within production and production. The picking process is the subject of research in many scientific works, a detailed overview of which is given in De Koster et al. [15]. The same author describes the issue of picking in even more detail in another of his publications [16].

Overall, it can be stated that the issue of warehouse logistics is challenging, and for its effective solution, it is convenient to use the tools of computer simulation, optimization, and mathematical modeling. Georgijevic et al. [17] used mathematical modeling to investigate the issue of the optimal number, size, and location of public logistics warehouses.

However, within warehouse logistics, it is often necessary to solve specific areas of problems that are unique to individual separate warehouses. Even in this case, computer simulation plays an important role. This may be the case, for example, with material handling, the aim of which is to reduce the time needed to pick up a consignment. This problem is described in more detail in [18].

The authors state that up to 60% of all activities in a warehouse are related to material picking, which can represent up to 65% of the total costs. The authors tried to design such an optimization algorithm that would significantly optimize and streamline the entire picking process. The result of their research was an approximation algorithm, which they subsequently successfully verified.

One of the possibilities for improving logistics processes in warehouses is to use an approach that is based on algorithms which will significantly shorten the implementation times of the individual activities needed for picking shipments. This is an issue to which long-term attention has been paid in the field of research. This can be seen in more detail in older works by Elsayed [19,20,21]. Another example of a possible solution to the problem of shortening the picking of consignments is presented by Dekker et al. [22] or Hall [23].

The issue of using genetic algorithms in the field of storage is presented in the work of Hiassat et al. [24]. The authors present the use of the genetic algorithm method on the example of finding a suitable allocation of perishable food warehouses. The model specifically determines the number of warehouses and the size of the inventory of individual retailers. The authors describe the solution of the problem at the macro level, but they do not go into detail on the micro-level. In the presented paper, a similar problem is solved in principle, but unlike the authors, Hiassat et al. [24], the article is solved at the micro-level within one warehouse. The solved task does not have a limited scope; at the same time, it does not take into account the expiration time of individual storage items. The placement of items is made here not based on the place of consumption but based on the required quantity, which results from the requirements of production.

At present, thanks to the development of simulation software, it is possible to increasingly use such approaches that combine the use of optimization approaches and support the introduction of effective methods, such as High-Runner Strategy. The combination then makes it possible to achieve high efficiency of warehouse logistics processes. This approach will be described in the paper in terms of optimizing the placement of individual material items on the relevant shelf positions, while their classification will be accepted based on selected parameters. The sorting process will be implemented based on the results of the optimization calculation using a simulation model. For the needs of optimization, the method of genetic algorithm will be used, while the generally proposed resistance function will be used.

2. Materials and Methods

Optimization of processes within warehouse logistics is a complex problem within various production processes. First of all, we must take into account the fact of whether these are continuous or discrete production processes. This is because the industry of continuous production processes mainly uses production operations that transform variable raw materials into final products with consistent quality. The specificity of the storage process, where bulk substrates predominate, also follows from this. As part of the optimization of storage processes, the available capacities of transport and handling equipment are taken into account. As storage takes place in bulk, optimization in terms of storage capacity plays an important role here.

In contrast, discrete production has a storage system that is based on the diversity of individual storage items. This is because producers in discrete production processes emphasize the assembly of components and subcomponents to create the final products or focus on the manipulation of discrete entities. Optimization in this area is, therefore, more focused on the selection of storage positions of individual material items, the use of the capacity of handling equipment, and shortening the time spent picking. This creates sufficient support for the production process, which thus becomes more efficient and consequently reduces production and operating costs.

However, there are common areas for both systems in connection with optimization, such as the identification and elimination of bottlenecks that prevent the efficiency of production processes from increasing. The common attribute is the continuous search for the optimal performance of the storage process as a whole and not its partial components.

The need for optimization of logistics processes is realized to reduce costs, increase efficiency, and implement various cost-saving measures. Warehousing is a complex process that significantly affects other elements in the logistics chain. In the context of current production, traditional methods of warehouse management without the use of the latest methods and approaches cause many complications and problems and are reflected in the inefficient course of production processes.

Warehouse logistics currently requires the organization of processes that are optimized in terms of time, capacity, and the use of transport and handling equipment.

For the efficient functioning of warehouse logistics processes, it is currently possible to use various methods in combination with computer simulation tools, among which the High-Runner Strategy can be mentioned. The combination of this method and computer simulation tools represents a robust decision-making tool that can significantly streamline the processes within warehouse logistics.

2.1. High-Runner Strategy

“High-Runner Strategy” is the method used by many companies to sell products and provide services. Its principle is based on the classification of products sold and services provided according to customers’ interests. These are the products that have the most impressions, clicks, and purchases and are eagerly sought after by the public (they attract the most interest). As a rule, they are highly variable and extremely sensitive to changes in market prices [25].

However, the principle of this method (Figure 1) can also be used in the field of material storage and subsequent picking. Specifically, this is the matter of placing the material within the warehouse on the basis of the quantity and intensity of demand in production, so that the time required for its picking is as short as possible.

However, for the correct method application, it is necessary to determine a distribution of material that is based on the production plan and accepts available storage options. In the event of a change in demand, it must be variable to change. For this reason, it is necessary to solve the method in the form of an optimization problem.

2.2. High-Runner Strategy Organization of the Warehouse

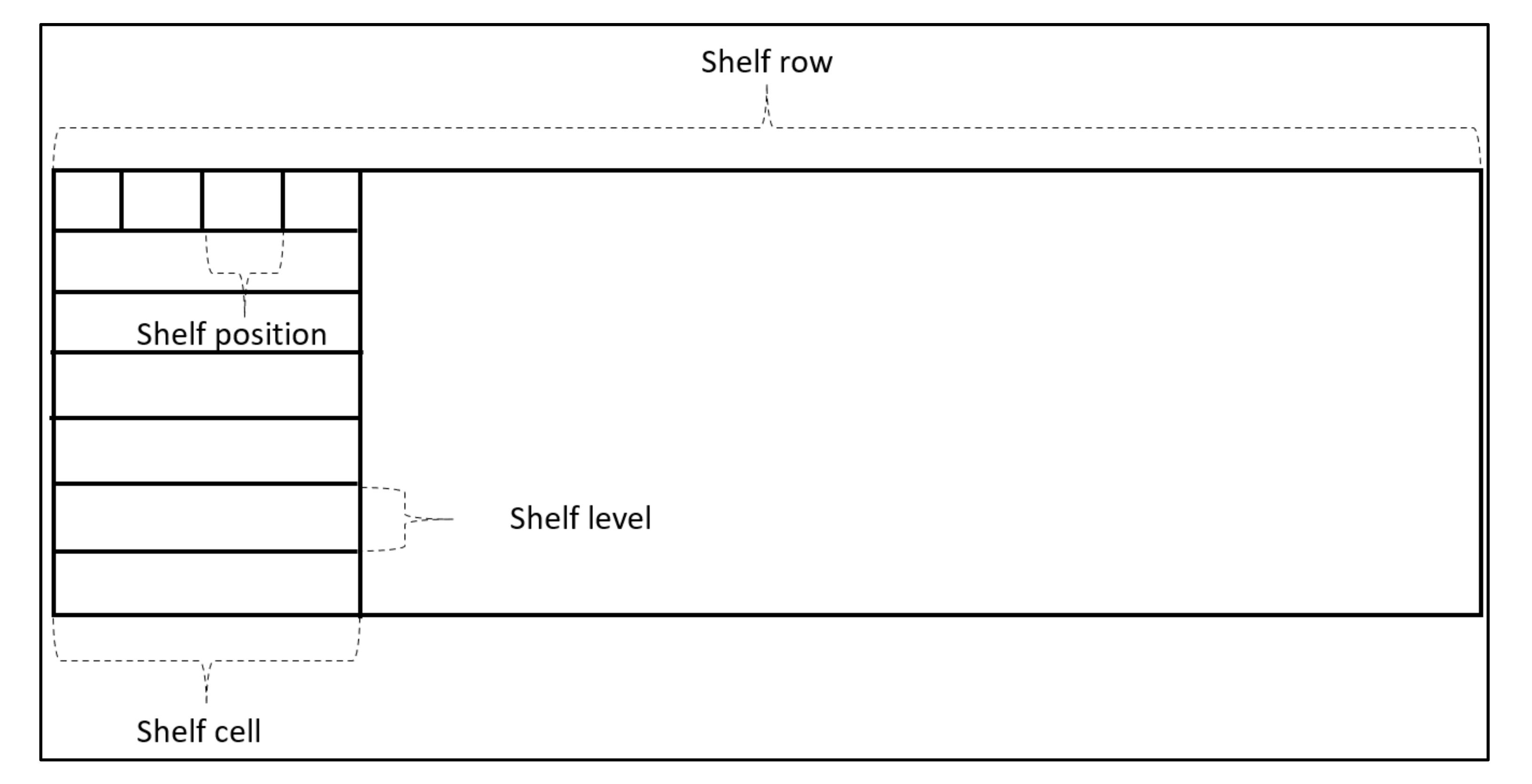
The warehouse for the “High-Runner Strategy” application can consist, for example, of rack rows that must be divided into smaller units, referred to as rack cells. Each shelving cell can have shelving levels further divided into individual shelving positions, in which the transport units are placed (Figure 2). The transport unit can have any shape (pallet, crate, container, etc.).

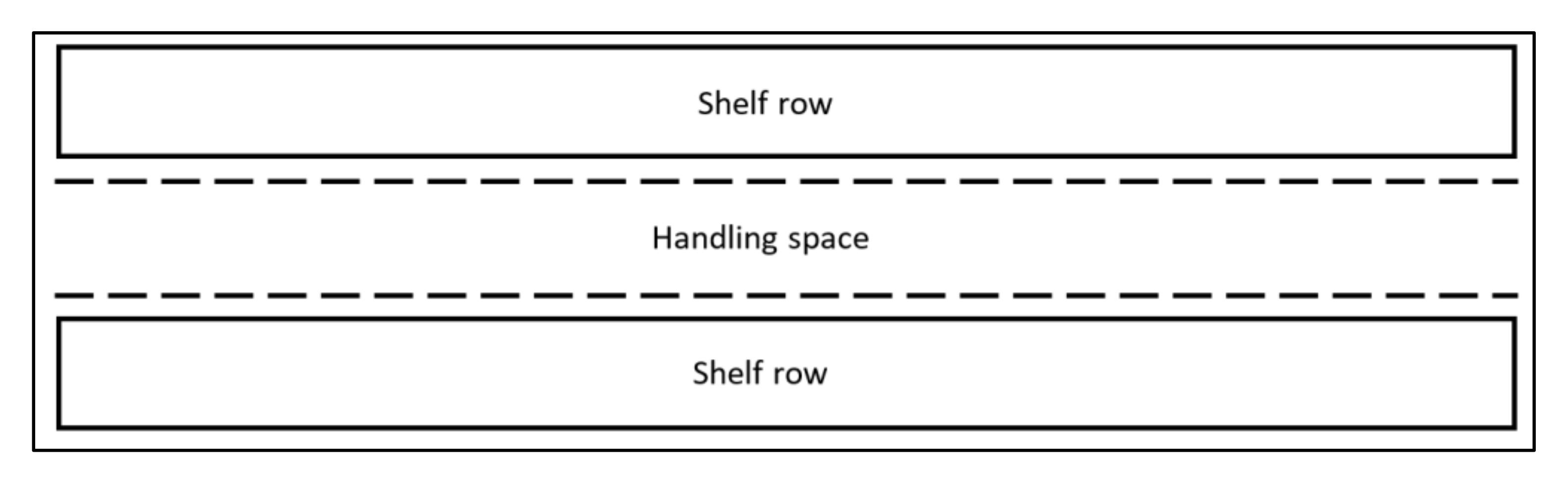
The racks should be placed in the warehouse so that there is a handling aisle between them, along which the technical equipment intended for handling transport units moves (Figure 3). Alternatively, it may be arranged differently, but it must allow access to individual shelving positions. The handling aisle can allow one-way or two-way traffic. If necessary, several handling devices can move along the aisle at the same time. In such a case, however, the collision factor needs to be taken into an account.

Handling devices ensure picking of material for its subsequent distribution by intralogistics systems for production.

3. Theory/Calculation

The optimization problem within the paper is realized for the needs of effective security of supply of a certain number of production lines. Each of these lines has a specific number of workplaces (constant or variable), for which it is necessary to realize by an intralogistics system the distribution of material items. Based on this fact, the order for material delivery to the warehouse is generated.

The optimization problem consists of assigning material items to individual shelving positions. We seek to identify the optimal placement of material items so that their total transport time from the shelf positions to the picking point is as short as possible. The aim is to establish an arrangement so that the items that will be transported most often are at the beginning of the warehouse and their transport route to the place of consumption is as short as possible in terms of time. Other material items that are used in a smaller volume (less frequently) will be placed further from the beginning of the warehouse.

Picking up material from the warehouse is done with the help of operators who use a certain number of forklifts. To ensure production, it is necessary to pick up and then dismantle a certain number of transport units at workplaces.

Let R = {1, …, R} be the set of shelving positions and M = {1, …, M} the set of material items that need to be placed on the shelves.

We assume that we have entered the total number p_m, m = 1, …, M for all material items that need to be placed. Let x_m,_r be the number of material items m placed on the rack r. Mark the distribution matrix of all material items on the shelf positions $x={\left(x_{m,r}\right)}_{m=1,\dots ,M}^{r=1,\dots ,R}$.

Maximum number of items m that can be placed on a rack r—rack capacity for a given item—is ${\widehat{c}}_{m,r}$ (this capacity could be considered the same for all rack positions). Let the handling equipment be able to transport a maximum of ${\tilde{c}}_m$ items m.

Let $t_r^{V-R}$ be the travel time of the device from the picking point to the rack position r, $t_{i,m, r}^{R-V}$, i = 1, …, ${\tilde{c}}_m$ be the time of transporting i pieces of material items m from the rack position r to the picking point and let $t_{m,r}^{MAN}$ be the time of moving one material item m from the rack position r onto the handling equipment (this time could be considered independent of position r). The total time required to transport all material items will be as follows:

$$T\left(x\right)={\displaystyle \sum }_{m=1}^M{\displaystyle \sum }_{r=1}^R\left[x_{m,r}.t_{m,r}^{MAN}+\left[\frac{x_{m,r}}{{\tilde{c}}_m}\right].t_r^{V-R}+\left(\left[\frac{x_{m,r}}{{\tilde{c}}_m}\right]-1\right)t_{{\tilde{c}}_m,m,r}^{R-V}+t_{x_{m,r-\left(\left[x_{m,r}/{\tilde{c}}_m\right]-1\right){\tilde{c}}_m,m,r}}^{R-V}\right]$$

(1)

where $\lceil .\rceil$ indicates the rounding function upwards. Then, the optimization problem is solved:

$$T\left(x\right)\to \begin{array}{c}min\\ x\end{array}$$

(2)

with limits

$${{\displaystyle \sum }}_{r=1}^R{x}_{m,r}=p_m, m=1,\dots ,M,$$

(3)

$$x_{m,r}\le {\widehat{c}}_{m,r}, \mathrm{for} \mathrm{all} m=1, \dots , M; r=1, \dots , R$$

(4)

where (3) requires the placement of all items and (4) provides the capacity requirements of the shelves. The capacity requirements of the handling equipment are incorporated into the total time (1).

To solve the optimization problem associated with the “High-Runner Strategy”, it is currently possible to use several optimization methods such as “Linear Programming”, “Quadratic Programming” or “Stochastic Optimization Algorithms”.

The last method is mainly suitable for the area of “High-Runner Strategy”, as the optimization process of finding a suitable solution can handle difficult computational problems with complicated boundaries and purpose function relatively quickly. The result of the optimization process is usually finding a solution that is acceptable and sufficiently optimal for the case, while finding the real optimum can be achieved only by accepting large time requirements for the calculation, or it cannot even be found. Among the “Stochastic Optimization Algorithms”, the effective use of the genetic algorithm method is suitable for the problematic area associated with storage.

Genetic algorithms belong to a set of evolutionary algorithms (EA) that are part of a large group of metaheuristic optimization algorithms. Unlike previous metaheuristics (Simulated Annealing, Taboo Search), EA uses a population-based search, in which the algorithm works with multiple solutions at once in each generation. The algorithm cyclically creates new generations during the search which aim to iteratively find even better solutions to the problem. Genetic algorithms belong to the group of modern forms of metaheuristics.

Modern forms of metaheuristics can be called intelligent search. Metaheuristics is an iterative process that controls and changes the activity of subordinate heuristics to find high-quality solutions. It can modify a complete solution or a set of solutions in one iteration. Subordinate heuristics can take the form of a high-level procedure, a local search, or just a method to build a solution.

Due to their complexity, metaheuristics are used to solve many optimization problems, especially large-scale problems, usually occurring in practice. This is because conventional exact algorithms often require a large amount of time to find even a suboptimal solution, even for relatively small tasks.

Based on the above facts, the method of genetic algorithm is particularly suitable for solving the mentioned problem of “High-Runner Strategy”.

4. Results

To create a simulation model, it is possible to use a wide portfolio of existing simulation tools, e.g., Tecnomatix Plant Simulation.

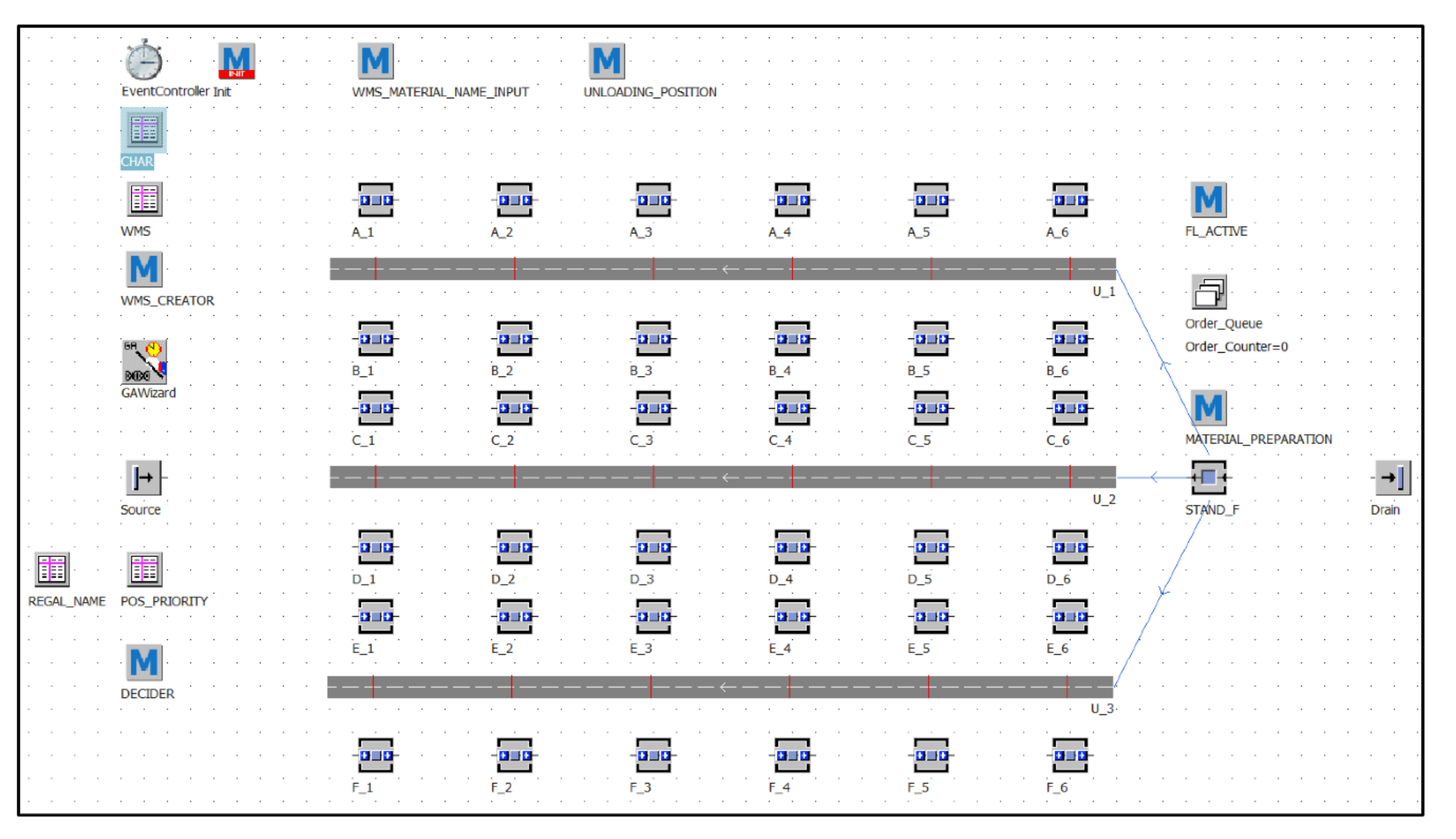
The simulation model is created using standard blocks of the program Technomatix Plant Simulation. It is divided into two parts, which are created from groups of blocks. The first simulated production process generates requirements for the delivery of goods from the warehouse. The second part of the model is a warehouse.

The production part consists of working positions, which are represented as discrete devices with a precise production cycle. The warehouse part of the optimization model contains shelving positions. The SimTalk programming language was used to define individual model functionalities, which is a feature of the blocks within Technomatix Plant Simulation and serves to expand the possibilities of individual blocks.

The basis of the created simulation model is rack storage which is further divided into individual rack cells (Figure 4).

Each shelf cell must be marked as its physical image. The individual blocks of the simulation model, which represent the rack cells, are set up in such a way as to allow the storage of as many material units as in real storage. It is necessary to model a handling aisle between the rack rows to allow the movement of handling equipment. Within the handling aisle, the so-called sensors are defined. By this, the points (places) indicate that transported material is moved from handling equipment to the appropriate racking position and vice versa (Figure 5).

The material to be placed on the shelves in the warehouse is divided according to “High-Runner Strategy” into three basic categories: high-runner, core and trail material. Said categorization is realized based on quantity and time of consumption of individual materials within the production process. The number of units in each category is not limited, but the material with the highest and lowest consumption needs to be identified.

To implement the optimization process, it is appropriate to use the method of genetic algorithm, which belongs to the group of evolutionary algorithms. The fitness function of individual variants is evaluated based on the minimum principle. In this approach, the aim is to find the shortest possible time needed to process the request for picking the material, which will then be distributed to production.

The list of picking materials that enter the optimization calculation is entered into the input table in random order.

At the beginning of the optimization, the list of material items is loaded first and the optimization calculation begins. The result is the determination of the order in which the individual material items will be placed in the shelf positions.

Optimization is performed in the simulation model using the GAWizard block. This is an optimization block that uses the method of a genetic algorithm and is part of a simulation program. To find the optimal solution, it is necessary to define the value of the number of generations and the size of the generation. By default, this block is set to number of generations = 20 and size of generations = 100.

In the simulation model, chromosomes are represented by the time required to pick individual material items from rack positions. Evolution begins with a population of randomly generated individuals and takes place in generations. In each generation, the fitness function is calculated for every individual in the population. Based on this, the suitability of the solution is evaluated during optimization. The optimization calculation ends when the defined number of generations has been reached or a sufficiently satisfactory solution has been found.

Placement in racking positions is carried out within the optimization calculation in such a way that the most required material is placed in a position that is as close as possible to the picking point. In principle, the material with the shortest delivery period should be as close as possible to the picking point and, conversely, the material that is most rarely used will be in a more distant position. Evidence of exactly where the material is in the warehouse (its location) is realized using a WMS (Warehouse Management System) table. To create this, it is possible to use the proposed algorithm in the SimTalk programming language (Figure 6).

The distribution of material from the rack to the picking point by means of the handling tools is realized within the simulation model by means of another algorithm created in the SimTalk program. Its task is to select the material to be delivered to production from the individual shelf positions, place it on the handling tool, and unload it at the picking point. The selection of material is carried out in places on individual handling routes that are defined by sensors.

Verification of the mentioned solution can be demonstrated via the example of a discrete production process consisting of a total of five production lines. Each of them has a constant number of seven workplaces, for which it is necessary to implement the distribution of material items through the intralogistics system.

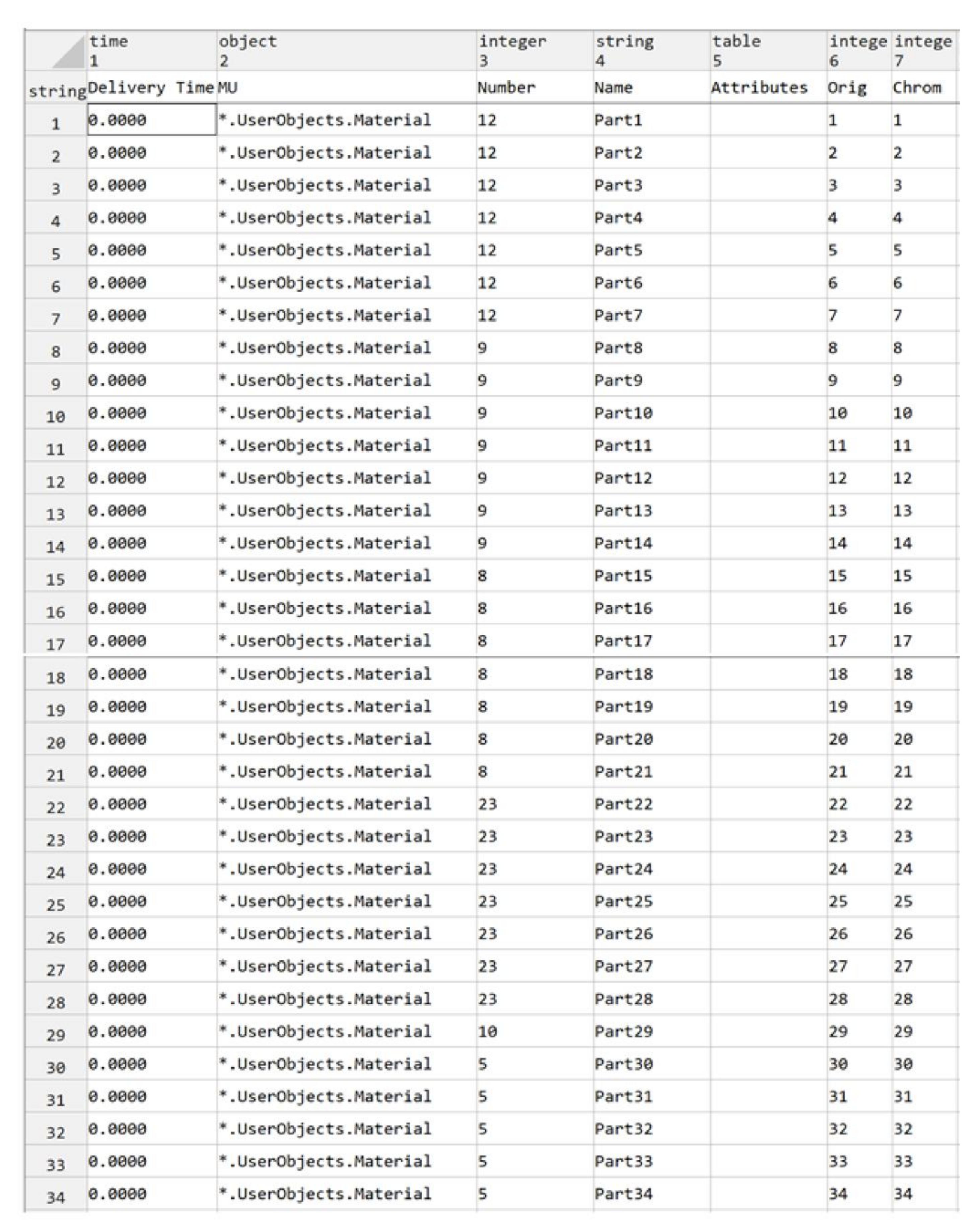
One warehouse operator handles the warehouse, which ensures the picking of material. For production, it is necessary to ensure the delivery of 400 pieces of material items, which are divided into 34 types (categories) (Figure 7).

The calculation of the parameters of optimization was carried out so that the default values were left, i.e., number of generations = 20 and size of generations = 100. The course of the optimization calculation is shown in Figure 8. In the optimization calculation, the chromosome is encoded by a value. Said coding ensures that each chromosome is thus formed by a chain of values.

In Figure 8, it is possible to see the course of optimization calculation and the gradual reduction of total picking time of material items stated as “Best Fitness Value”. “Best Fitness Value” within the optimization calculation determines the suitability of the solution in solving the given problem. Specifically, it evaluates the fitness of concrete individuals in terms of the solution that we expect. The optimization calculation takes place until the fitness function ceases to change or changes over several generations or until a specified number of iterations is reached, which determines how many times a new population will be created. The number of generations in the optimization calculation is given at the very beginning, while the number of chromosomes stays constant and the low-rated chromosomes are replaced by higher-rated ones during calculation. This is a classical approach within the method of a genetic algorithm.

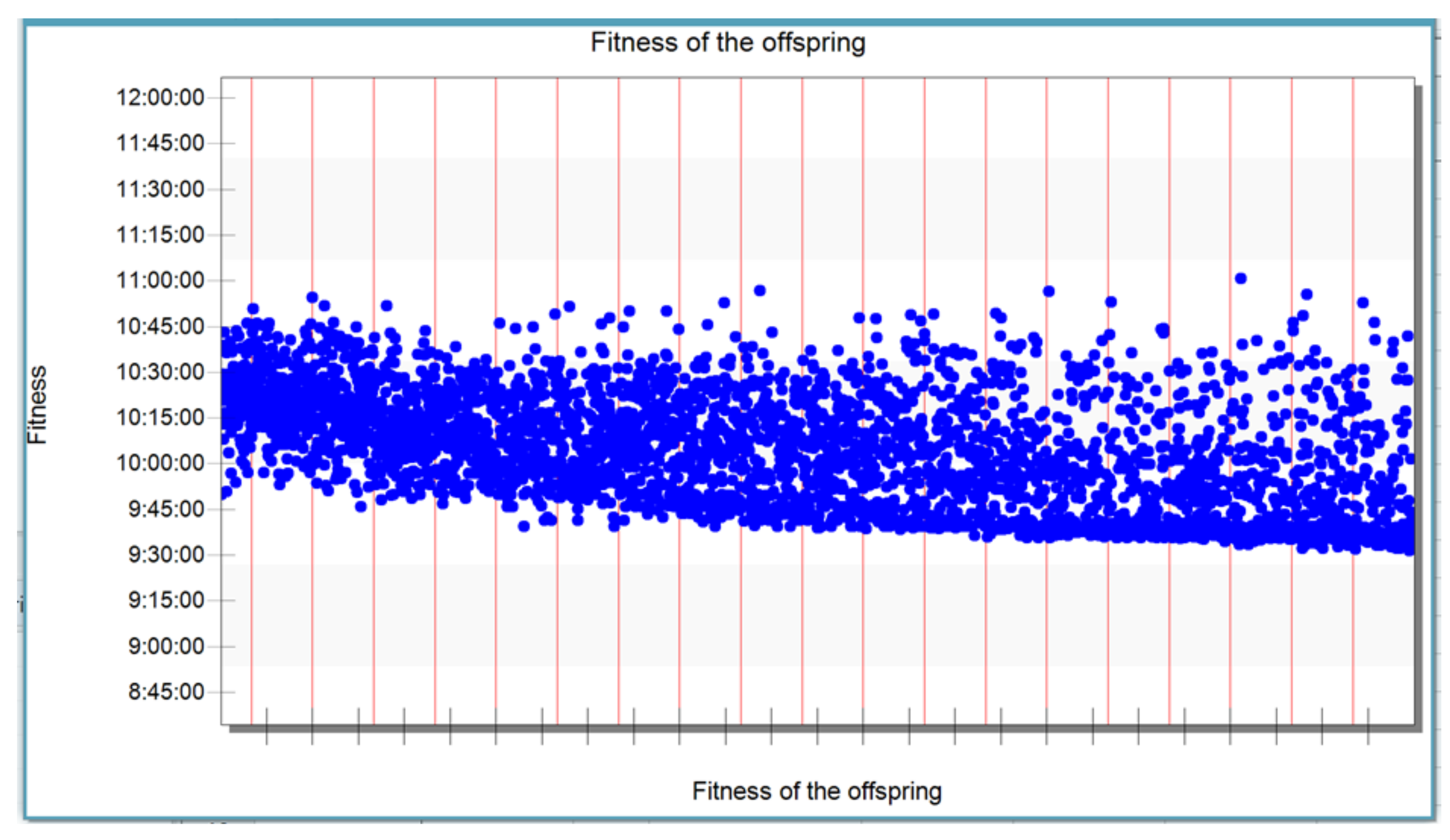
In Figure 9a,b, one can see how the suitability of individual generations of offspring was evaluated during the optimization calculation. Figure 9a,b show the individual generations of offspring with offspring index and the total picking time. In Figure 9a, the early stage of the optimization is shown. As can be seen, the offspring of the initial generation 1 have the total picking time between 39,000 and 35,000 s with an average around 37,000 s. As the optimization progressed in generations 2–4, the most offspring obtained value of the total picking below 37,000 s. Figure 9b shows the final stage of the optimization process. In contrast to the early stages of the optimization, most of the offsprings now have the total picking time below 35,000 s.

Offspring evaluation and the evolution curve are shown in Figure 10 and Figure 11. The total picking time of the offsprings during the whole optimization process is shown in Figure 10. It can be seen that the best total picking time found gradually decreased until the final optimal solution was reached. Figure 11 shows the best, average and the worst value of the total picking time during the optimization. The values quickly drop in the early stage of the optimization and gradually get closer and flatten out, indicating that the optimization process cannot improve the values anymore.

After optimization, the total time to complete the material picking process is 9:31, which represents a significant saving compared to the original time of 10:20. The optimal storage of material items in shelving positions according to categories is 17, 19, 18, 14, 6, 27, 3, 32, 8, 1, 28, 22, 7, 33, 29, 5, 21, 26, 15, 13, 16, 11, 25, 23, 34, 10, 9, 20, 2, 24, 12, 31, 30, 4. In this order, the individual categories of material items should be placed in the racking positions.

5. Conclusions

The simulation model yielded a reduction in the picking time and subsequent supply of individual production positions in the production hall. The model makes it possible to increase the use of picking forklifts when completing a production order. At the same time, the model makes it possible to minimize the mutual blocking of the trucks within one handling aisle among the shelves. The model is variable, i.e., the numbers of shelf positions, locations, and numbers of production positions can be changed.

After optimization, the total time to complete the material picking process is 9:31, which represents a significant saving compared to the original time of 10:20.

The obtained time savings bring the possibility of increasing the production capacity, the use of handling equipment, and an efficient system for placing items within the shelves. All these indicators can subsequently be reflected in the cost area, where they contribute to their reduction and efficient use.

“High-Runner Strategy” is an approach that is already applied in warehouse logistics. However, its implementation is most often realized intuitively, not using its full potential. The method for organizing warehouse positions can be applied within warehouse logistics for both fixed and variable structure of storage positions.

However, in order to increase the efficiency, it is necessary to use suitable simulation software tools that significantly streamline the use of the “High-Runner Strategy” method.

The results obtained in the presented research differ from similarly focused works. As an example, it is possible to mention the research of the authors Ardjmand et al. [26], who used a genetic algorithm in the field of order picking. But these authors did not solve this problem about the influence of the position of storing a goods item in a warehouse on speeding up the picking process. Another similar work [27] deals with the coordination of supply routes which was solved in terms of reducing time for picking of goods. This approach is not possible to apply for the described paper because the paper considers the supply of AGF sets which have nicely defined transport routes and they cannot be changed. As part of the paper, it was selected the way of accelerating the process of supplying and picking of consignments on the base of targeted placement of material items. This approach thus differs from the procedure that used authors Ashgzari and Gue [28]. They searched for the automatized transport system, but this was not based on the use of AGV systems, but conveyor systems. The last work, with which the presented paper can be compared is the paper of the authors Ding et al. [29]. Authors deal with the issue of bottlenecks in the activities of an automated warehouse. Authors deal with the schedule of routes of the supply system in contrast with the optimization of the picking process. This system is less suitable in comparison with the presented work because it does not take into account the requirements of production and does not provide the possibility of adapting to different conditions.

This paper presents a means of optimization of the allocation of cost items within the shelf warehouse. With the help of the optimization simulation model, a significant time saving of 48 min and 36 s during one working change was achieved. The presented procedure has a general application. The presented solution differs from other similar publications focused on the optimization of logistics processes in that it is implemented at the micro-level. Specifically, it is a fact that here, within the optimization and generation of solutions, we work with individual material items, their quantity, and the position at which they are located in the warehouse. The paper also contains a formulation of the resistance function, which can be used to evaluate the fitness value of individual new populations of generations of solutions. The number of chromosomes within generations is unlimited and depends on the number of optimized material items, the number of shelf positions, and the size of production orders for material delivery.

Based on a simplified simulation model, it was proven that the combination of the method and the optimization result can ultimately save time in the process of material picking. The simulation model itself can thus become a control tool that will determine the storage of individual stock items while being sensitive to possible changes. At the same time, it was verified that evolutionary algorithms have their application in the field of warehouse logistics and their use thanks to the development of the possibilities of simulation software should become a common work routine of persons working in the field of warehouse logistics.