Full Real-Time Positioning and Attitude System Based on GNSS-RTK Technology
Abstract
1. Introduction
- Electromechanical gyroscopes and accelerometers: This technology has fallen into disuse and can only be found in old systems. Its accuracy may be very high, but due to the large number of high-precision mechanical elements, its cost and maintenance is also very high. There are many different types, but all rely on the same principle: rotation masses that create torques due to accelerations and rotations, and devices that measure these torques and relate them with angular velocities and accelerations.
- Microelectromechanical systems (MEMSs): This is the most commonly used technology for computing the attitude due to its low cost, low energy consumption, and good performance. The main working principles of this technology are introduced in a very brief way. The main principle for accelerometers relies on a suspended mass with a spring that will be displaced in the direction of the spring due to an acceleration, creating or changing an electrical capacitance. The gyroscopes work in a similar way, with a mass placed over a piezoelectric actuator, which creates a Coriolis force when an angular velocity actuates over the device [9]. Finally, microelectromechanical (MEM) magnetometers use an inductance with a current, and if there exists a magnetic field in the perpendicular direction of the inductance, a Lorentz force is generated [10].
- Optical gyroscopes: These systems are based on the Sagnac effect [11], and are classified into ring gyroscopes (RLGs), which use mirrors for the light circuit, and fiber optic gyroscopes (FOGs), where the light travels through a fiber optic circuit. Their main advantage is the absence of mobile parts, with a lower maintenance. RLGs have more resolution than FOGs and can detect smaller velocities.
2. GNSS-RTK Technology
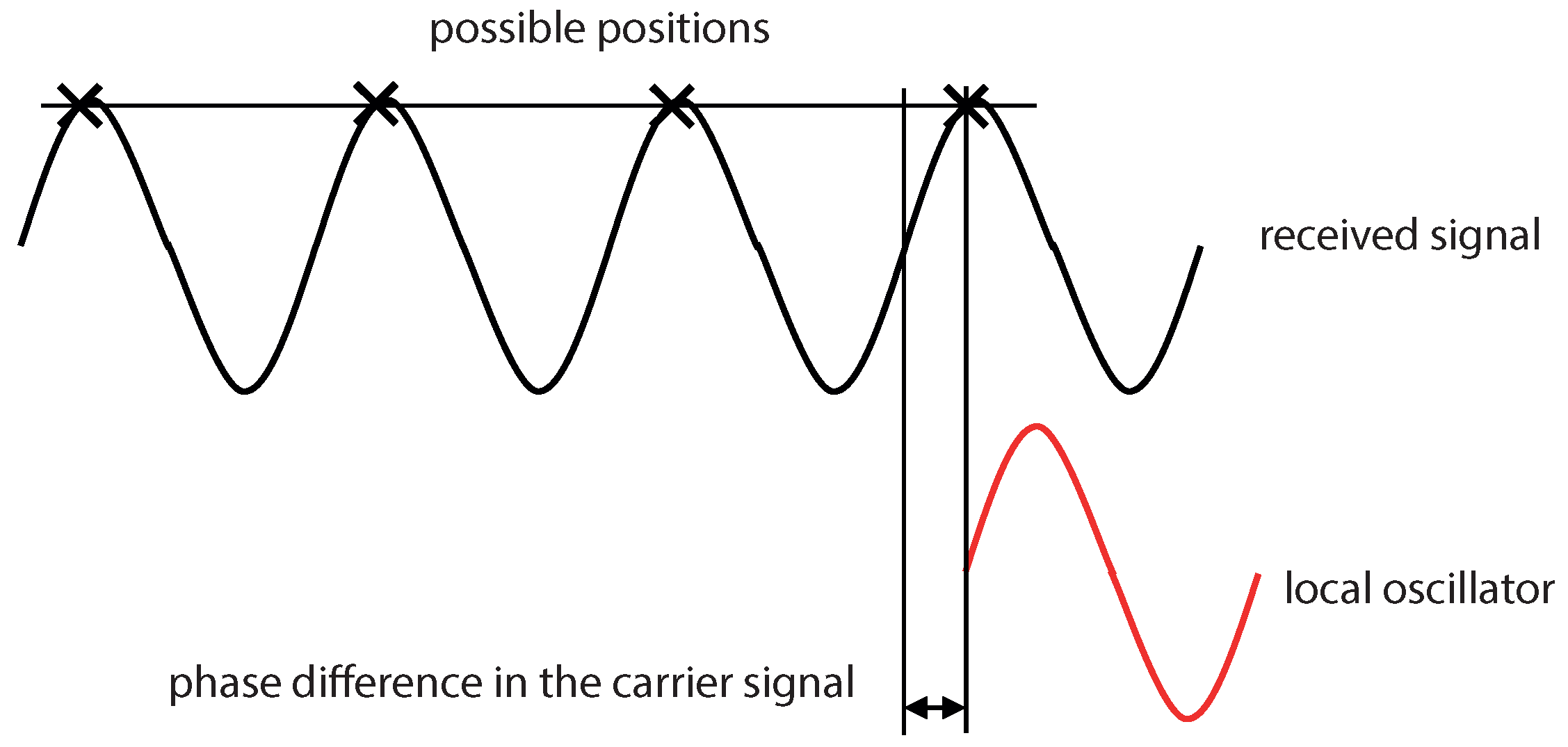
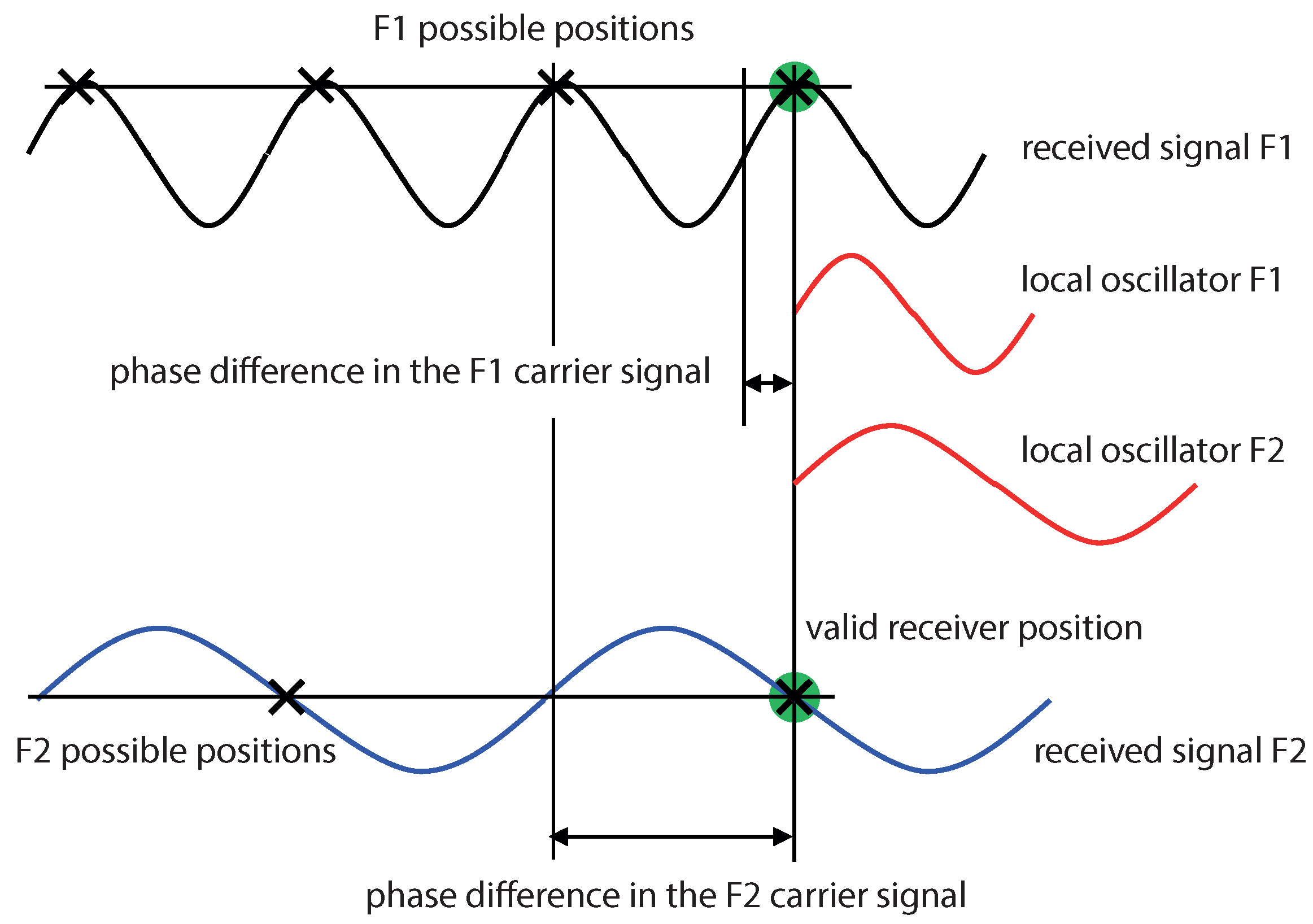
2.1. Position Computation
2.2. GNSS Error Correction
- Satellites’ clocks (±2 m): Satellites’ clocks are high-precision atomic clocks, but they have to be periodically readjusted from terrestrial control stations using more precise clocks. At the orbit height of the satellites, an error of 10 nanoseconds causes a positioning error of approximately 3 m.
- Orbital errors (±2.5 m): The satellites’ orbits are known and periodically retransmitted by other satellites (ephemerides). However, the real orbits are not completely predictable, and their monitoring must be readjusted from terrestrial control stations.
- Ionospheric delay (>5 m): The radio signal propagation of the satellites through the ionosphere has important delays due to solar activity, position, time, etc., which are constant within relatively large geographical areas (50 km of radius).
- Tropospheric delay (±0.5 m): The radio signal propagation of the satellites through the troposphere has delays with similar causes to those of the ionospheric delays, and they are constant within local geographical areas.
- Receiver noise (±0.3 m): Any delay in the signal processing or any error in the oscillator frequency causes position estimation errors.
- Multipath propagation (±1 m): When the signal transmitted by a satellite rebounds in an object, the GNSS receiver measures a larger transmission time than the real one [18]. This delay adds an additional position estimation error.
- Advanced multi-frequency and multi-constellation receivers improve the global accuracy and robustness, and are able to reach an accuracy of one meter in ideal conditions.
- Satellite-based augmentation systems (SBAS) are geostationary satellites that emit corrections that are valid for specific geographical areas.
- The RTK technique described in Section 2.1 provides the best results concerning the global precision. A base, i.e., a receiver whose position is known, may be used to mitigate parts of the errors described above. To know the position of a base with high accuracy, it may be installed over geodesic points of known position, or it can be installed over a point whose position is not initially known, but its average position is computed over a large enough time window. The corrections provided by the base are less effective as the receiver (rover) goes further from the base, since many of these corrections depend on the geographic localization. The accuracy deteriorates at a rate of 2 ppm (parts per million), which corresponds to 2 mm for each kilometer between the base and the rover (baseline). It is important to remark that the absolute position of the rover depends on the absolute position of the base. However, the relative precision of the rover with respect to the base is independent. The installation of a new base requires additional time and equipment, so it is impractical. If infrastructure and Internet connection exist, an alternative solution is to use the GNSS reference station networks. These networks provide corrections by Internet using the NTRIP protocol and allow the rover to move along all the area covered by the networks. In applications where only the relative position between base and rover is important, the absolute position computation of the base may be discarded. In addition, some GNSS receivers can work as a mobile base, which allows the rover to receive corrections from a mobile base with a relative precision of a few centimeters.
- If the position information is not needed in real time, the post-processed kinematic (PPK) technique may be employed. It uses the same method as the RTK technique, but in this case, the receiver records the data and signals received from the satellite. The data of the base or reference stations are subsequently requested in receiver-independent exchange (RINEX) format and post-processed by software, obtaining the same accuracy as the RTK technique. The main drawback of this method is the lack of information in real time, while its main advantage is that real-time corrections are not needed.
- The precise point positioning (PPP) technique uses a different concept. This method generates parameters for the models of the error sources so that the receiver can compensate them. Terrestrial reference stations are needed to compare their known positions with the measurements and then generate these parameters. The main advantage of modeling the error sources is that the scope of application can be global and the bandwidth needed to transmit the model parameters is much smaller than the bandwidth needed to transmit the RTCM (Radio Technical Commission for Maritime) corrections used by the RTK technique. The main drawbacks are that the receivers need more computing capacity to process the error models and the precision is lower than the one obtained with RTK. PPP services require payment, and due to the low data consumption, the information is transmitted by Internet and by satellite.
3. Material and Methods
3.1. Communication Protocols
3.1.1. NMEA 0183
3.1.2. UBX
3.1.3. RTCM Version 3
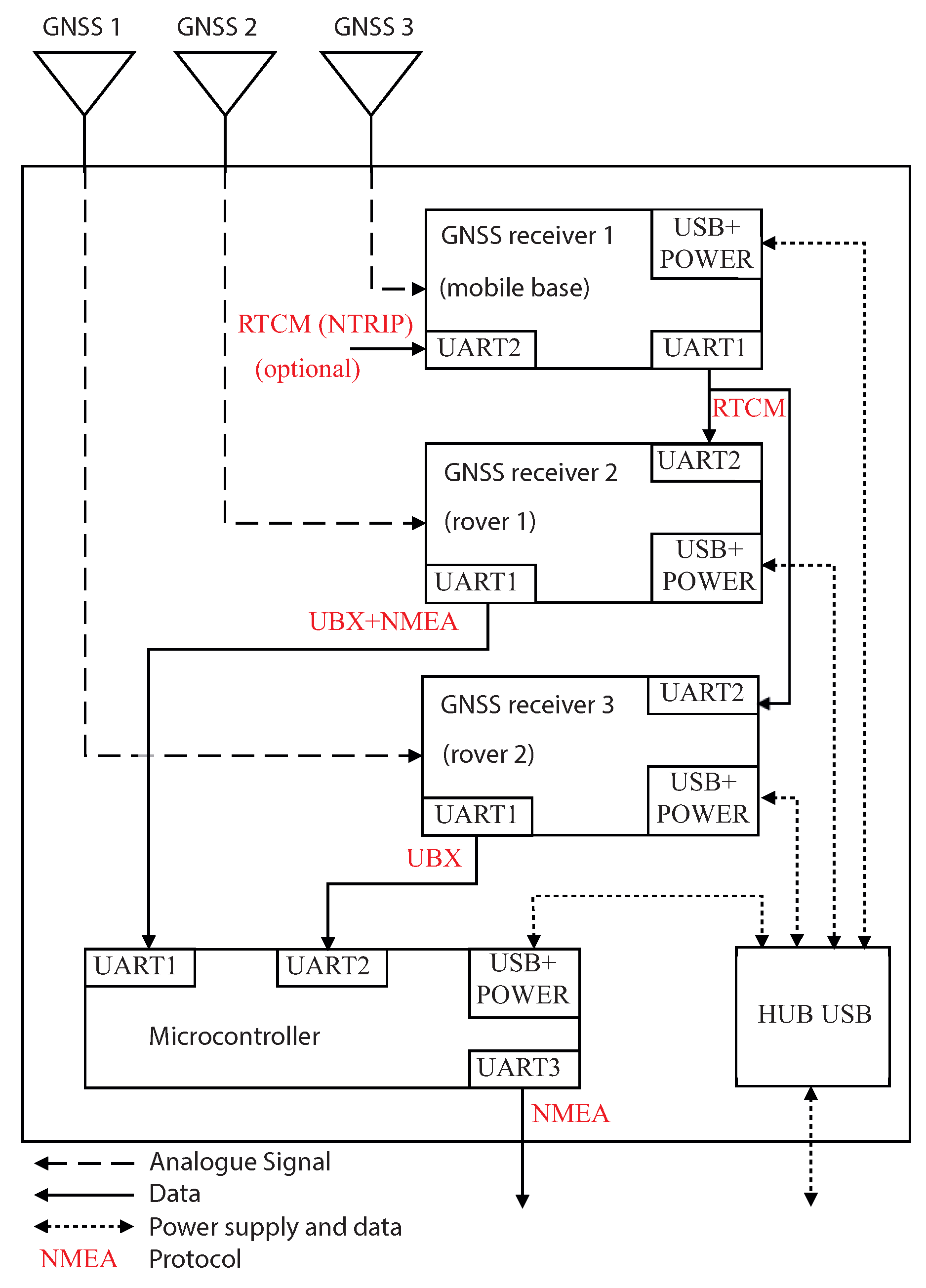
3.2. Prototype Design
- The attitude information is computed as Euler angles (yaw, pitch, and roll) and as cuaternions in the NED (North, East, Down) reference system.
- The position information is given as latitude, longitude, and ellipsoidal height in the WGS84 system.
- The attitude is given with respect to the plane formed by the three antennas of the receivers. The antenna 3 cannot be aligned with antennas 1 and 2, and these two latter define the heading of the solid.
3.2.1. Hardware
3.2.2. Software
- Initialization of the microcontroller peripherals: It is called just once at the beginning, and all parameters are initialized.
- Continuous loop: The microcontroller continuously tests two things: (i) If valid information has been received from the GNSS receivers; in this case, it calls the attitude computation function. (ii) If any of the data buffers of UARTs 1 and 2 have information; in this case, the information is processed.
- Interruptions in the data reception of UARTs (DMA).
4. Results
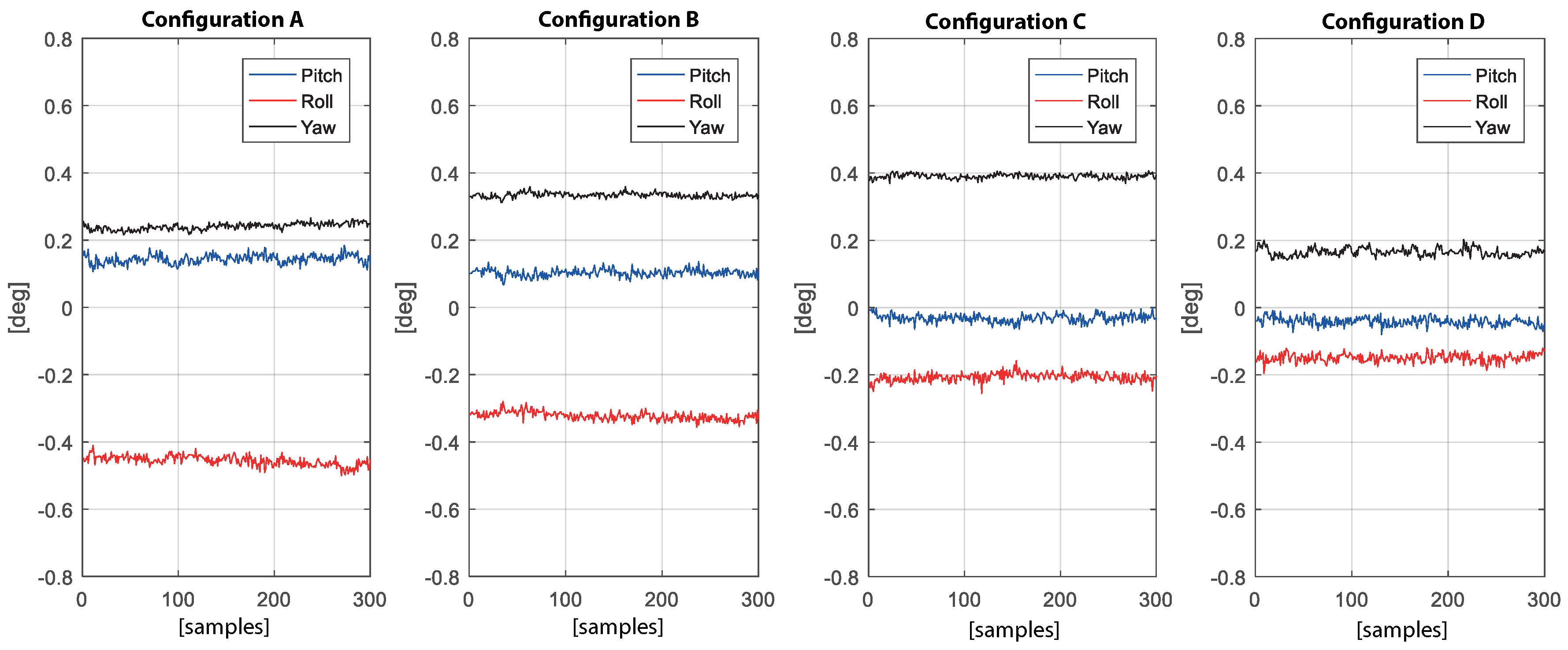
4.1. Precision and Accuracy of Measurements in a Static Configuration
- The antennas of receivers 2 and 3 were placed manually for each configuration.
- The roof does not form a perfect plane due to errors in the construction and bending of structural elements, as can be seen in Figure 10.
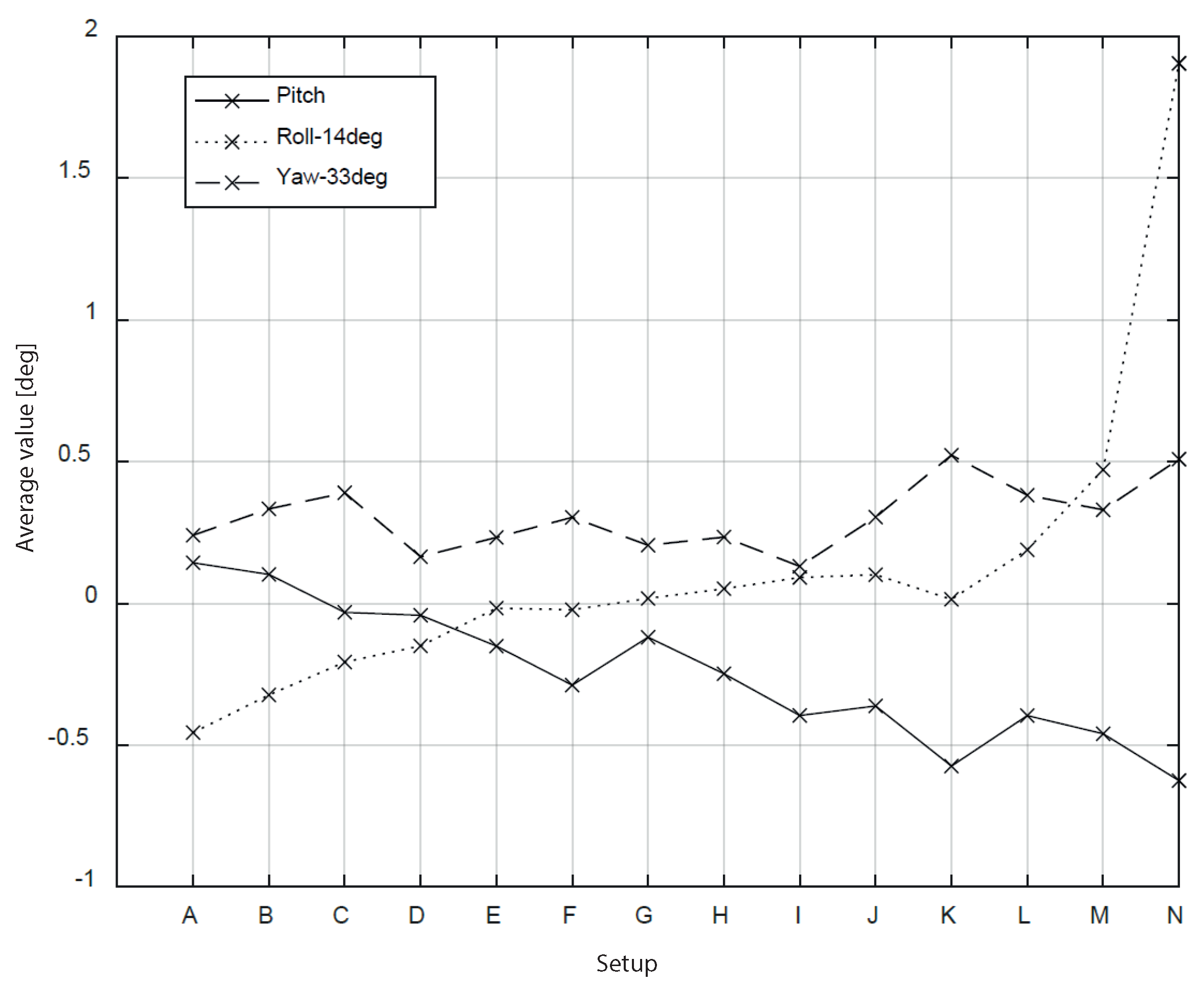
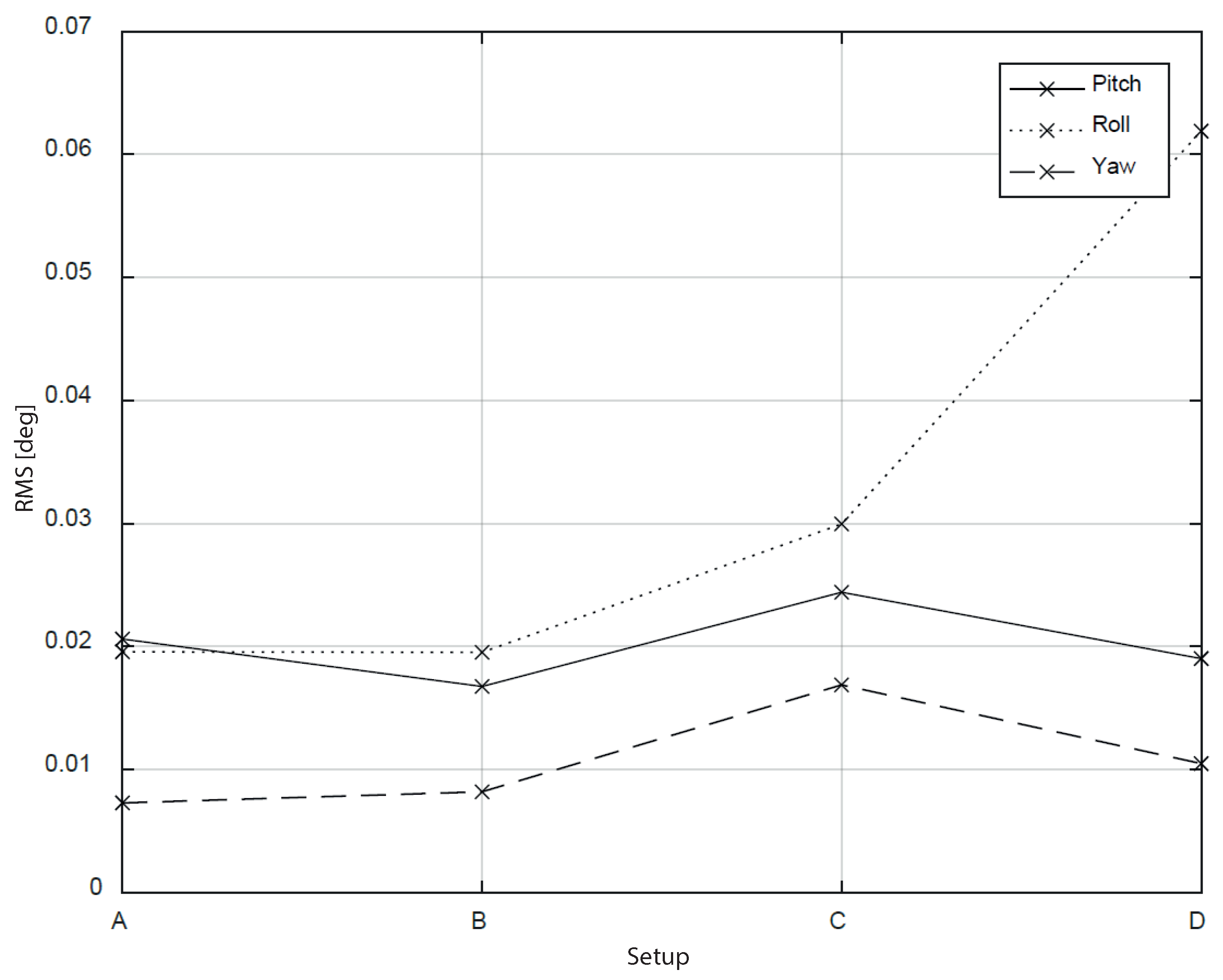
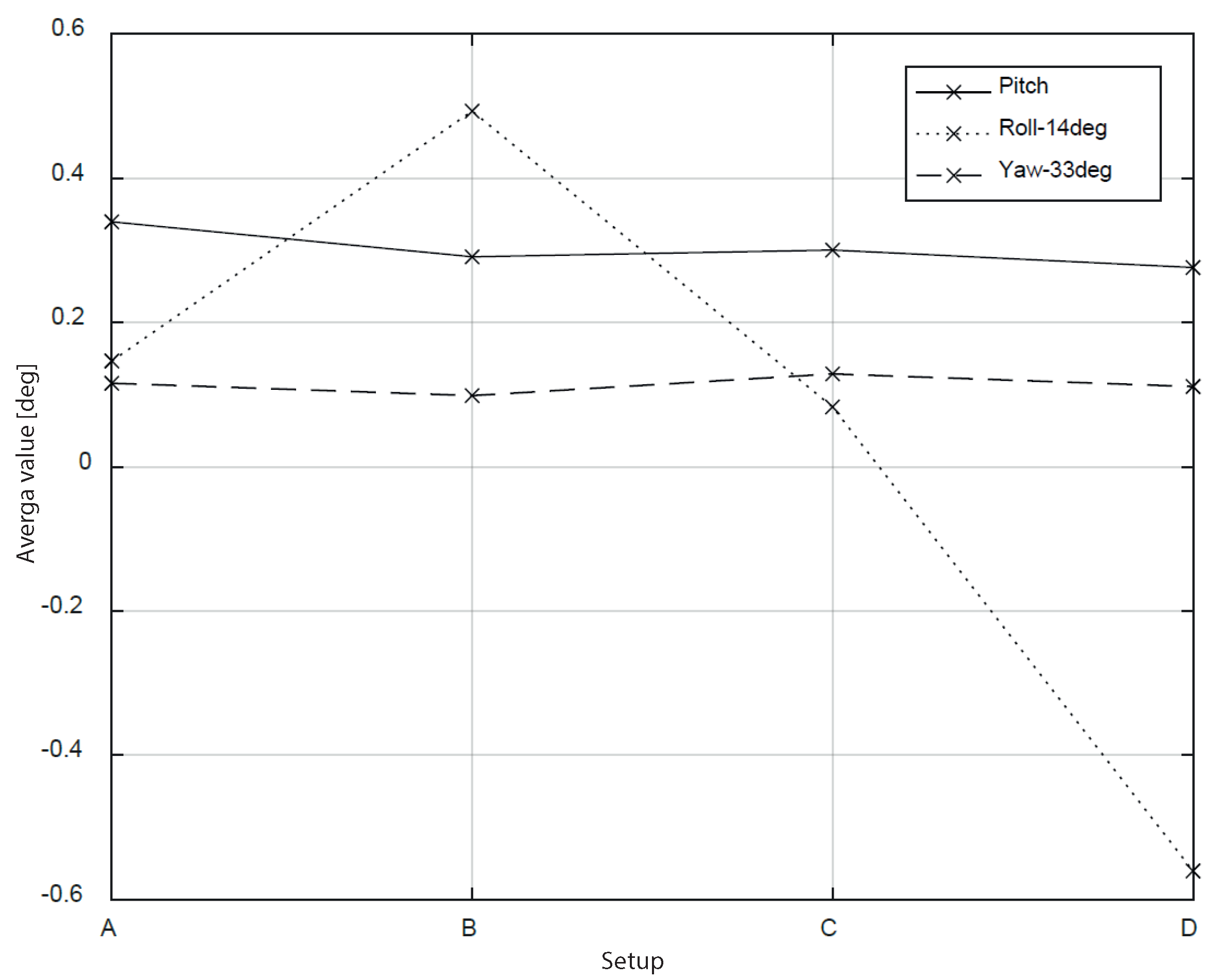
4.2. Robustness of the Algorithm in Non-Orthogonal Configurations
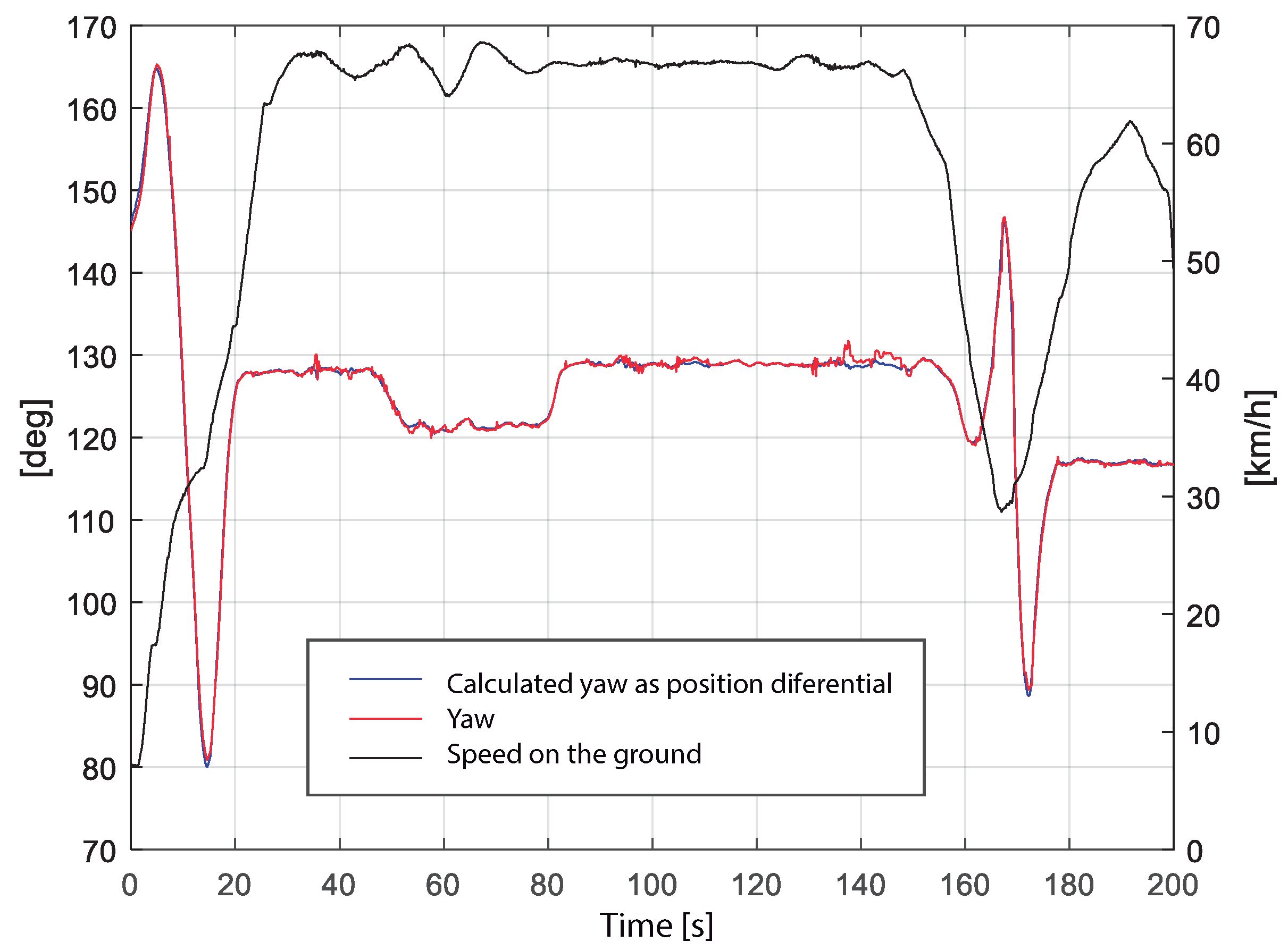
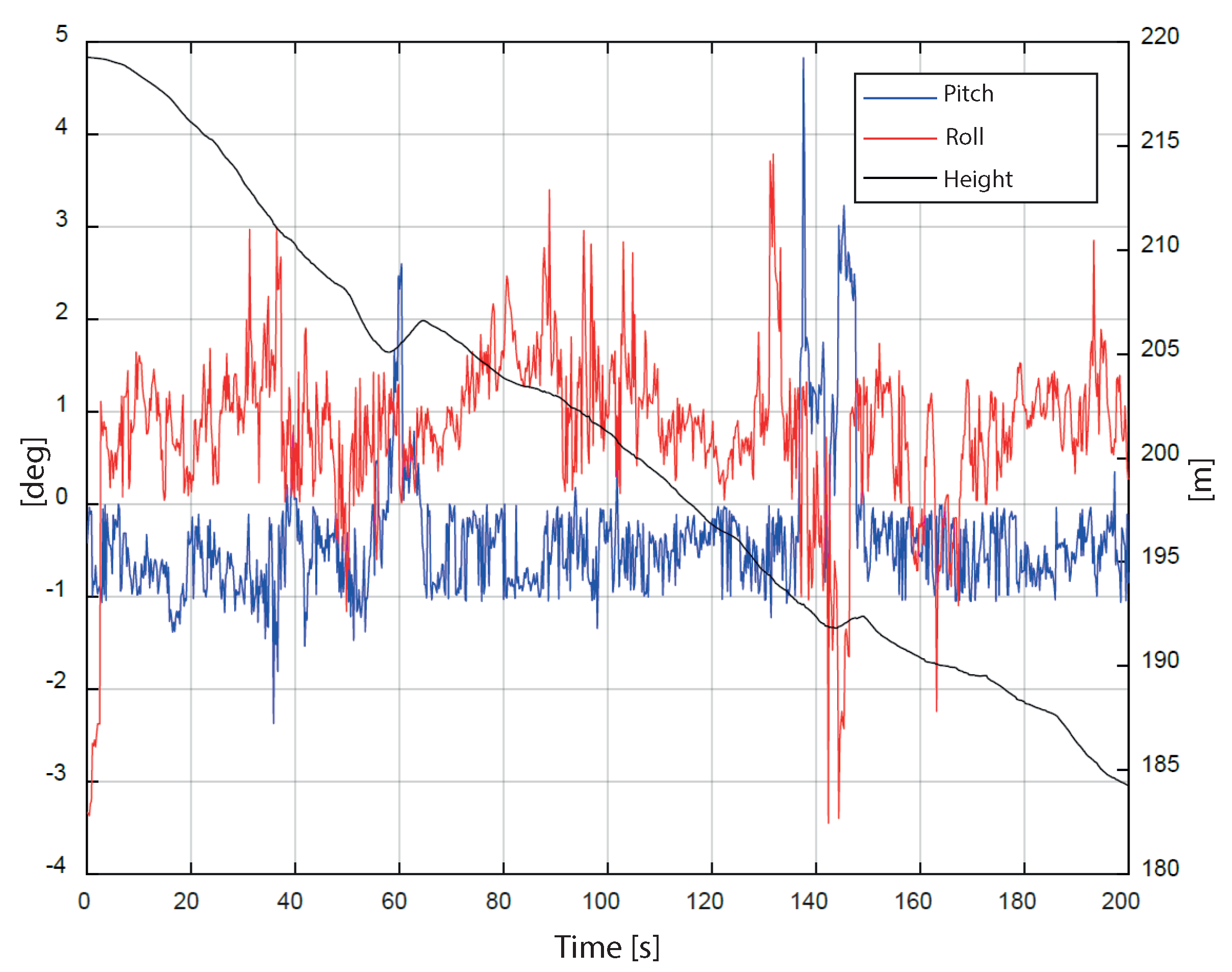
4.3. Accuracy of Measurements in a Dynamic Configuration
5. Conclusions
- No calibrations are required.
- It is an autonomous system, which does not need external corrections.
- Very low cost for the accuracy reported compared to other technologies. The price of the equipment used (excluding the hours of development) is around 700 EUR, and this technology is expected to reduce its costs as it becomes more popular.
- Technology without export restrictions.
- The accuracy of the system can be improved by increasing the distance between antennas. However, for more than 10 m of cable between antenna and receiver, it is necessary to install signal amplifiers or special cables.
- HDOP-type variables, the number of satellites used in position calculation, or the “Fix” type can be used to validate or discard system measurements.
- The vehicle dynamics (<4G) do not affect measurements.
- Low data frequency compared to other technologies. There are GNSS-RTK receivers that operate up to 100 Hz, but their price is higher.
- The system does need to operate outdoors with good visibility of the sky.
- It is not valid for lightweight and small-size systems because the antennas need a minimum distance.
- Analysis and compensation of the multipath error in environments with limited sky visibility, such as urban scenarios.
- System validation in a dynamic configuration with high-precision IMUs.
- Validation of the system and its degradation under high dynamic conditions (>4G).
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Configuration of the Prototype
Appendix A.1. Microcontroller Configuration
| Peripheral | Parameter | Value |
|---|---|---|
| Main clock | Speed | 216 MHz |
| Baudrate | 230,400 bps | |
| UART1 | Mode | asynchronous |
| NVIC Interrupts | RX > DMA1 | |
| Baudrate | 230,400 bps | |
| UART2 | Mode | asynchronous |
| NVIC Interrupts | RX > DMA2 | |
| UART3 | Baudrate | 115,200 bps |
| Mode | asynchronous (8-N-1) | |
| DMA1 | Mode | circular |
| Size | 1 byte | |
| DMA1 | Mode | circular |
| Size | 1 byte |
Appendix A.2. GNSS Receiver Configuration
- Enabled constellations: GPS, GLONASS, Galileo, BeiDou, QZSS
- UART1: 230,400 bps, Protocol out: UBX, 8-N-1
- UART2: 230,400 bps, Protocol out: UBX, 8-N-1 (optional, not used by default)
- Output frequency: 10 Hz
- Enabled messages: RTCM-1077, RTCM-1087, RTCM-1097, RTCM-1127, RTCM-1230, RTCM-4072.0, RTCM-4072.1
- Enabled constellations: GPS, GLONASS, Galileo, BeiDou, QZSS
- UART1: 230,400 bps, Protocol out: UBX, 8-N-1
- UART2: 230,400 bps, Protocol out: UBX, 8-N-1
- Output frequency: 10 Hz
- Enabled messages: UBX-NAV-PVT, UBX-NAV-RELPOSNED, UBX-NAV-EOE, NMEA-GGA (only for GNSS receiver 2)
- MSM: They are a standard of the RTCM protocol, and, particularly, MSM7 offers the maximum information with respect to observation and numeric resolution [35]. Messages MSM7 1077, 1087, 1097, and 1127 correspond to observations of the satellite constellations GPS, GLONASS, Galileo and BeiDou, respectively.
- Message 1230 provides the code/phase deviations of the GLONASS constellation. In this constellation, each satellite emits a different frequency, and this makes the solving of ambiguity even more complex.
- Messages 4072.0 and 4072.1, which are property of U-Blox, are used exclusively for the mobile base functionality, reporting detailed information about its position.
References
- King, A.D. Inertial Navigation—Forty Years of Evolution. GEC Rev. 1998, 13, 140–149. [Google Scholar]
- Im, S.; Hurlebaus, S.; Kang, Y. Summary Review of GPS Technology for Structural Health Monitoring. J. Struct. Eng. 2013, 139, 1653–1664. [Google Scholar] [CrossRef]
- Crasta, N.; Moreno-Salinas, D.; Pascoal, A.; Aranda, J. Multiple autonomous surface vehicle motion planning for cooperative520 range-based underwater target localization. Annu. Rev. Control 2018, 46, 326–342. [Google Scholar] [CrossRef]
- Moreno-Salinas, D.; Pascoal, A.M.; Aranda, J. Optimal sensor placement for multiple target positioning with range-only measurements in two-dimensional scenarios. Sensors 2013, 13, 10674–10710. [Google Scholar] [CrossRef] [PubMed]
- Moreno-Salinas, D.; Pascoal, A.M.; Aranda, J. Optimal sensor placement for acoustic underwater target positioning with range-only measurements. IEEE J. Ocean. Eng. 2016, 41, 620–643. [Google Scholar] [CrossRef]
- Ahmad, N.; Ariffin, R.; Khairi, N.M.; Kasi, V. Reviews on Various Inertial Measurement Unit. Int. J. Signal Process. Syst. 2013, 1, 256–262. [Google Scholar] [CrossRef]
- Tomaszewski, D.; Rapinski, J.; Pelc-Mieczkowska, R. Concept of AHRS Algorithm Designed for Platform Independent Imu Attitude Alignment. Rep. Geod. Geoinform. 2017, 104, 33–47. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, Z.; Sun, P. Quaternion-Based Kalman Filter for AHRS Using an Adaptive-Step Gradient Descent Algorithm. Int. J. Adv. Robot. Syst. 2015, 12. [Google Scholar] [CrossRef]
- Brunetti, F.; Moreno, J.C.; Ruiz, A.F.; Rocon, E.; Pons, J.L. A new platform based on IEEE802.15.4 wireless inertial sensors for motion caption and assessment. In Proceedings of the 28th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, New York, NY, USA, 30 August–3 September 2006; pp. 6497–6500. [Google Scholar] [CrossRef]
- Ren, D.; Wu, L.; Yan, M.; Cui, M.; You, Z.; Hu, M. Design and Analyses of a MEMS Based Resonant Magnetometer. Sensors 2009, 9, 6951–6966. [Google Scholar] [CrossRef]
- Qazizada, M.; Pivarciova, E. Mobile Robot Controlling Possibilities of Inertial Navigation System. Procedia Eng. 2016, 149, 404–413. [Google Scholar] [CrossRef]
- Novatel Inc. An Introduction to GNSS GPS, GLONASS, BeiDou, Galileo and Other Global Navigation Satellite Systems, 2nd ed.; Novatel Inc.: Calgary, AB, Canada, 2015. [Google Scholar]
- Trimble. GPS Tutorial. 2020. Available online: https://www.trimble.com/gps_tutorial/ (accessed on 29 October 2020).
- Teunissen, P. Theory of Carrier Phase Ambiguity Resolution. Wuhan Univ. J. Nat. Sci. 2003, 8, 471–484. [Google Scholar] [CrossRef]
- Blewitt, G. Carrier Phase Ambiguity Resolution for the Global Positioning System Applied to Geodetic Baselines up to 2000 km. J. Geophys. Res. 1989, 94, 10187–10203. [Google Scholar] [CrossRef]
- Delporte, J.; Mercier, F.; Laurichesse, D.; Galy, O. GPS Carrier-Phase Time Transfer Using Single-Difference Integer Ambiguity Resolution. Int. J. Navig. Obs. 2008, 2008, 273785. [Google Scholar] [CrossRef]
- Tang, X.; Feng, X.; Ferreira, V.; Jing Zhou, A. A Procedure for Ambiguity Fixing with Dual-Frequency Phase and Code Observations. Arab. J. Sci. Eng. 2014, 39, 287–294. [Google Scholar] [CrossRef]
- Kumar, G.; Rao, G.; Kumar, M. GPS Signal Short-Term Propagation Characteristics Modeling in Urban Areas for Precise Navigation Applications. Positioning 2013, 4, 192–199. [Google Scholar] [CrossRef][Green Version]
- Hein, G.W. Status, perspectives and trends of satellite navigation. Satell. Navig. 2020, 1, 22. [Google Scholar] [CrossRef]
- Zrinjski, M.; Barković, D.; Matika, K. Development and Modernization of GNSS. Geodetski List 2019, 73, 45–65. Available online: https://hrcak.srce.hr/218855 (accessed on 29 October 2020).
- Barnes, D. GPS Status and Modernization. Presentation at Munich Satellite Navigation Summit 2019. Available online: https://apps.dtic.mil/dtic/tr/fulltext/u2/a550403.pdf (accessed on 29 October 2020).
- Benedicto, J. Directions 2020: Galileo Moves Ahead. GPS World. 2019. Available online: https://www.gpsworld.com/directions-2020-galileo-moves-ahead/ (accessed on 29 October 2020).
- China Satellite Navigation Office. Development of the BeiDou Navigation Satellite System (Version 4.0). December 2019. Available online: http://m.beidou.gov.cn/xt/gfxz/201912/P020191227430565455478.pdf (accessed on 29 October 2020).
- Langley, R.B. Innovation: GLONASS—Past, Present and Future. GPS World. 2017. Available online: https://www.gpsworld.com/innovation-glonass-past-present-and-future/ (accessed on 29 October 2020).
- Krasuski, K.; Ciećko, A.; Bakuła, M.; Wierzbicki, D. New Strategy for Improving the Accuracy of Aircraft Positioning Based on GPS SPP Solution. Sensors 2020, 20, 4921. [Google Scholar] [CrossRef]
- Paziewski, J.; Wielgosz, P. Investigation of some selected strategies for multi-GNSS instantaneous RTK positioning. Adv. Space Res. 2017, 59, 12–23. [Google Scholar] [CrossRef]
- Ciećko, A.; Bakuła, M.; Grunwald, G.; Ćwiklak, J. Examination of Multi-Receiver GPS/EGNOS Positioning with Kalman Filtering and Validation Based on CORS Stations. Sensors 2020, 20, 2732. [Google Scholar] [CrossRef]
- Maxino, T.C.; Koopman, P.J. The Effectiveness of Checksums for Embedded Networks. IEEE Trans. Dependable Secur. Comput. 2006, 6, 59–72. [Google Scholar] [CrossRef]
- Middlestead, R.W. Digital Communications with Emphasis on Data Modems: Theory, Analysis, Design, Simulation, Testing, and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Rubinov, E.; Collier, F.; Fuller, S.; Seager, J. Review of GNSS Formats for Real-Time Positioning. 2020. Available online: https://www.ee.co.za/article/review-of-gnss-formats-for-real-time-positioning.html (accessed on 29 October 2020).
- Henderson, D.M. Euler Angles, Quaternions, and Transformation Matrices; NASA, Lyndon B. Jhonson Space Center: Houston, TX, USA, 1977.
- Barrientos, A.; Peñín, L.F.; Balaguer, C.; Aracil, R. Fundamentos de Robótica; McGraw-Hill/Interamericana de España: Madrid, Spain, 2007. [Google Scholar]
- Hughes, N. Quaternion to/from Euler Angle of Arbitrary Rotation Sequence & Direction Cosine Matrix Conversion Using Geometric Methods. 2017. Available online: https://www.euclideanspace.com/maths/geometry/rotations/conversions/quaternionToEuler/quat_2_euler_paper_ver2-1.pdf (accessed on 29 October 2020).
- Snyder, J.P. Map Projections–A Working Manual; USGS Professional Paper 1395; U.S. Government Printing Office: Washington, DC, USA, 1987. [CrossRef]
- Boriskin, A.; Kozlov, D.; Zyryanov, G. The RTCM multiple signal messages: A new step in GNSS data standardization. In Proceedings of the 25th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2012), Nashville, TN, USA, 17–21 September 2012; pp. 2947–2955. [Google Scholar]






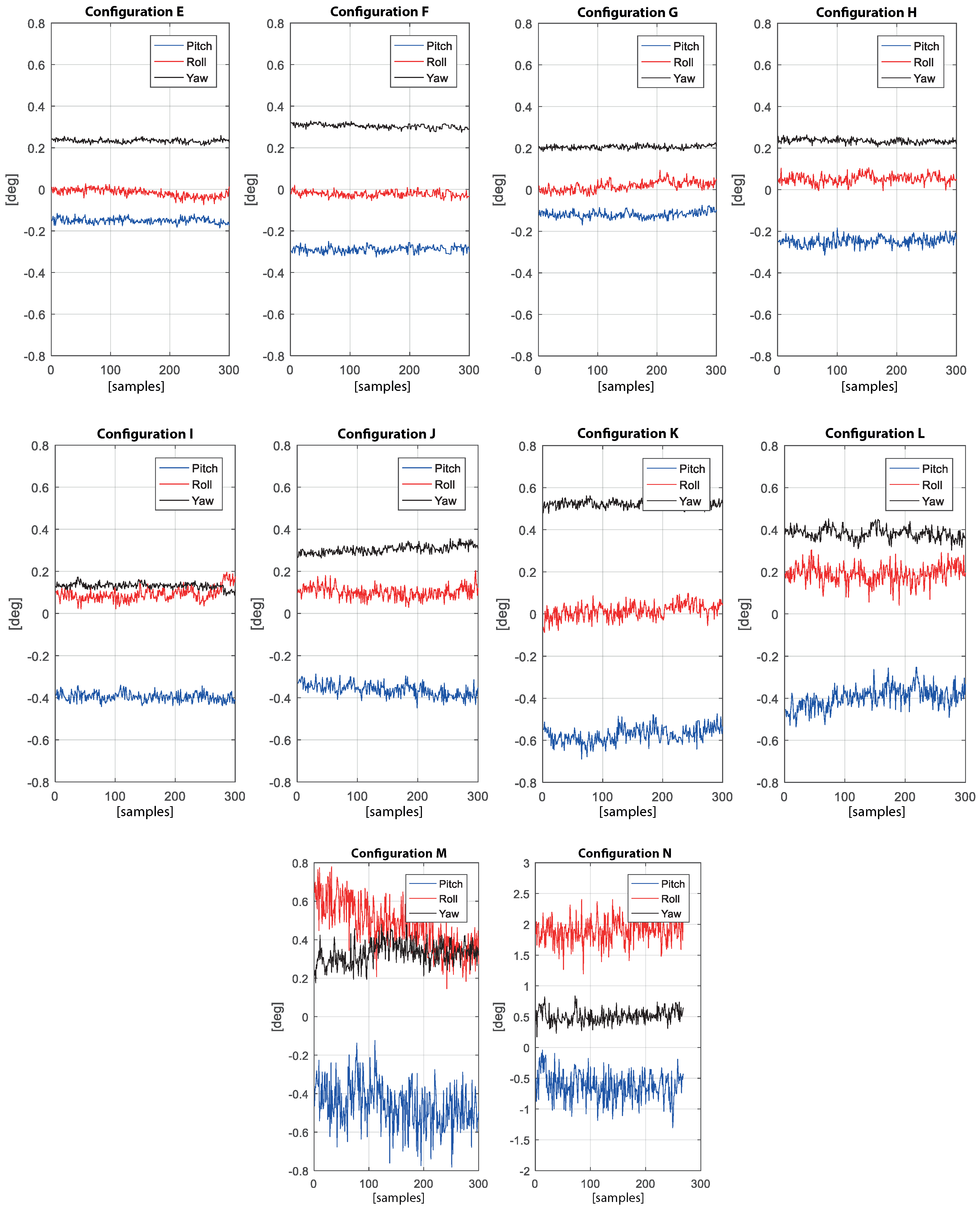


| Configuration | Receiver Antenna Distance 1–2 [m] | Receiver Antenna Distance 1–3 [m] | Angle 2-1 and 3-1 [deg] |
|---|---|---|---|
| A | 6.2 | 6.2 | 90 |
| B | 5.8 | 5.8 | 90 |
| C | 5.4 | 5.4 | 90 |
| D | 5.0 | 5.0 | 90 |
| E | 4.6 | 4.6 | 90 |
| F | 4.2 | 4.2 | 90 |
| G | 3.8 | 3.8 | 90 |
| H | 3.4 | 3.4 | 90 |
| I | 3.0 | 3.0 | 90 |
| J | 2.6 | 2.6 | 90 |
| K | 2.2 | 2.2 | 90 |
| L | 1.8 | 1.8 | 90 |
| M | 1.0 | 1.0 | 90 |
| N | 0.4 | 0.4 | 90 |
| Configuration | Receiver Antenna Distance 1–2 [m] | Receiver Antenna Distance 1–3 [m] | Angle 2-1 and 3-1 [deg] |
|---|---|---|---|
| A | 4.6 | 4.6 | 90 |
| B | 4.6 | 4.6 | 60 |
| C | 4.6 | 4.6 | 40 |
| D | 4.6 | 4.6 | 19 |
| Pitch | Roll | Yaw | |
|---|---|---|---|
| RMS [deg] | 0.295 | 0.459 | 0.338 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Olivart i Llop, J.M.; Moreno-Salinas, D.; Sánchez, J. Full Real-Time Positioning and Attitude System Based on GNSS-RTK Technology. Sustainability 2020, 12, 9796. https://doi.org/10.3390/su12239796
Olivart i Llop JM, Moreno-Salinas D, Sánchez J. Full Real-Time Positioning and Attitude System Based on GNSS-RTK Technology. Sustainability. 2020; 12(23):9796. https://doi.org/10.3390/su12239796
Chicago/Turabian StyleOlivart i Llop, J. M., D. Moreno-Salinas, and J. Sánchez. 2020. "Full Real-Time Positioning and Attitude System Based on GNSS-RTK Technology" Sustainability 12, no. 23: 9796. https://doi.org/10.3390/su12239796
APA StyleOlivart i Llop, J. M., Moreno-Salinas, D., & Sánchez, J. (2020). Full Real-Time Positioning and Attitude System Based on GNSS-RTK Technology. Sustainability, 12(23), 9796. https://doi.org/10.3390/su12239796







