Abstract
Urban freight deliveries are often subject to many access restrictions which creates the need to establish a system of loading bays and to split the last mile delivery into driving and walking parts. A new model based on hard and soft clustering approach is developed to solve the loading bay assignment problem for efficient vehicle routing and walking in last mile delivery. The flexibility of the model is provided by the soft clustering approach based on different membership degrees of customers to loading bays. Especially for instances with large numbers of loading bays, soft clustering seems to give better results, it leads to higher flexibility of city logistics systems, minimal driving distances, and adequately short walking paths, which contribute to the goal of reaching sustainable urban freight deliveries.
1. Introduction
In Europe, 72% of people live in cities, and this percentage is expected to rise to 80% by 2050 [1]. The importance of cities is also growing from a commercial point of view. Cities today already account for 85% of the EU’s total gross domestic product (GDP) [2]. As a result, cities are experiencing a growing demand for transport with increasing congestion, noise, emissions, and other negative effects of transport on the environment and city dwellers [3,4]. These problems are most prevalent in historical cities and city centers, which are generally not designed to cope with such high traffic volumes. These urban areas have major accessibility problems (narrow roads) and a lack of logistics infrastructure [5]. Cities are further hampered by the modern trends of just-in-time delivery and e-commerce, which increase the number of deliveries and consequently lead to fragmentation of urban freight transport [6,7]. This leads to an increase in the number of journeys and low utilization of delivery vehicles [8]. Studies show that lorries account for 15% of urban traffic and more than 20% of CO2 emissions and congestion [9].
Limited space in urban centers does not allow for further expansion of transport and logistics infrastructure. Cities are therefore often restricting access of delivery vehicles to urban centers and see this approach as the only option to ensure sustainable living conditions [10]. The restrictions usually relate to the time of the day and the emission class or size of the delivery vehicles. Strict city centers are often defined as pedestrian zones where access conditions are further restricted. Despite the best intentions of city authorities, such measures worsen the accessibility of locations in city centers, negatively influencing attractiveness for commercial services [11].
With the aim to find intermediate solutions for the preservation and revitalization of urban centers, measures based on consolidation of cargo shipments come to the fore [12]. Many cities are opting to introduce city consolidation centers, where shipments for a large number of customers are collected and combined and then transported to destinations in the city center with smaller but well utilized delivery vehicles (usually electric). Although this approach is from the theoretical point of view very appealing, it often does not reach the necessary critical mass to cover the investment. Despite all efforts, retailers, logistics operators, and other users are still in favor to deliver shipment directly to the address of the customers. An intermediate solution of a special transshipment facility (loading bay) within the city center is therefore needed, to stop or park the delivery vehicle in the proximity of customers and make the last part of the delivery on foot. This solution is perceived as the best compromise between the need for preserving the city center and accessibility.
For efficient delivery to city centers, it is therefore very important to determine the optimal number, capacity, and location of loading bays and to establish an effective management system. In practice, we often encounter the problem of the limited number and capacity of loading bays in urban centers, which as a rule do not have an established system of management and reservation [13]. As there is often no overview of their occupancy, lorries (especially during peak hours) often have difficulty finding a free loading bay near the delivery address. In this case they need to stop on the road or circle inside the city before they finally find a free and available loading bay [14,15,16]. Loading bays are also often occupied illegally by personal vehicles, making this problem even bigger [17,18]. As a result, lorries frequently choose suboptimal transport routes, which leads to longer stays in the city center and consequently has a significant impact on congestion. In such cases, we face the need to dynamically optimize delivery vehicle routing which would allow for the smallest possible mileage and the shortest possible stay in the city center [19].
Cities and their planning departments have been urged to address the problem of last mile delivery and are trying to solve these complex problems from a practical point of view. For example, the Centre for the Study of Urban Planning, Transportation, and Public Facilities in France has developed guidelines for the design of loading bays, which define micro-location, signaling, and access standards for delivery vehicles [20]. The city of Lyon has participated in an experiment entitled “Loading bay of the future”, which allows operators to book the loading bay 24 h in advance. This has led to optimized delivery trips in the city center, a 40% reduction in the number of double parking spaces for deliveries, less congestion and pollution, and an improved image of the city [20]. Vienna has experimented with the “i-Ladezone” project, which deals with the intelligent monitoring of loading bays in an urban environment. The project has developed different management methods to efficiently monitor the occupancy of loading bays by delivery vehicles and cars, trying to keep the loading bays as available as possible [21]. In the city of Lisbon, they tested two technology-based devices: The introduction of parking meters for loading bays and loop vehicle detection sensors installed on the floor of the loading docks. These devices are expected to reduce the number of parking violations and the average duration of freight operations and to increase the satisfaction of transport companies and shop owners [15]. The above-mentioned experience points to the need for further research and testing of dynamic loading bay assignment for urban last mile delivery [22,23,24,25].
The problem of optimal routing and dynamic assignment of delivery vehicles to the loading bays is actually very difficult; not only does the vehicle routing have to be optimized, but also the walking part of the delivery (see also [26]). In the literature, this approach is treated as a two-echelon vehicle routing problem (2E-VRP) [27]. As its name suggests, it originally deals with vehicle routing in both echelons and does not actually address the walking part, which is highly relevant in city logistics. The other specific issue related to loading bays is the dynamics of their occupancy. In this case, the classical 2E-VRP is not sufficient because you have to dynamically adopt vehicle routing to the changing availability of loading bays. This problem is known as two echelon location routing problem (2E-LRP) [27]. In general, very few examples of LRP for urban last mile deliveries can be found in the literature [18,28,29] and to the best of our knowledge, there are no examples of 2E-LRP dealing with loading bays and walking parts of urban last mile delivery.
Scholars working on urban freight transport issues try to solve these complex problems mainly by using specially developed and tailored simulation-based models [30,31]. In the literature we have found only four models that specifically address the cases of loading bays. The first model was developed by Comi et al. [32] who used the discrete event simulation approach to investigate the possibilities of loading bay reservation for last mile delivery in the limited traffic zone of Rome. The second is provided by Zhang and Thompson [33], who developed an agent-based model to study the importance of providing loading bays occupancy information on driving and walking costs. The third model was developed by Mc Load et al. [34], who used a metaheuristic approach to quantify the environmental and financial benefits of using porter and cycle couriers for specific last mile parcel delivery in London. The last one we found was by Nguyen et al. [35], who developed a mathematical model to optimize total delivery time based on dual-mode route planning. The second mode relates to walking time of deliverers and considers them as an important element of the vehicle routing procedure. The main feature of the previously mentioned models is that they all, except Zhang and Thompson [33], deal with a specific real-life problem that results in a very specific solution. This approach is of course very efficient for this specific example, but it does not allow to understand basic (general) principles that could be used for planning loading bay facilities under different circumstances. The other important issue relates to the flexibility of such a system and the dynamic assignment of loading bays if the best loading bay is occupied.
This article attempts to fill this gap by developing a model based on flexible assignment of loading bays for the vehicle routing in urban last mile delivery. The general research aim of the article is not to find the optimal solution for both echelons (routing and walking), but to investigate the efficiency of a flexible assignment of loading bays for vehicle routing and consequently for the walking part of last mile delivery. The solution to this problem is very important, as solutions would enable city authorities to better manage urban freight deliveries and the results could be applicable, to a certain extent, to similar problems in other research areas. For example, the problem of assigning incoming vehicles to loading bays is mathematically similar to the berth allocation problem of ships in seaports [36,37,38], the problem of locating urban public e-charging stations [39], the location of various public services [40], and different types of collection points [41].
2. Materials and Methods
In Letnik et al. [42] a multi-parametric model of the idealized urban area was introduced and applied to different instances of rectangular urban grid structured zones to determine statistically the most relevant number and location of loading bays. The main criterion for the evaluation of the results was the predefined maximum allowed walking distance from the loading bay to the customer. In this paper the existing model is upgraded with vehicle routing algorithm to address also this part of the delivery. The main idea is to investigate the flexible loading bay assignment procedure when the delivery is made to a specific customer or a group of customers in the city center. Many fundamentally different cases can occur where several loading bays are available for delivery to a particular customer and where more customers need to be served from the same loading bay.
To solve this issue, we developed a methodology and examined two different assignment methods to understand which approach is better from the driving and walking distance point of view. In the first approach, only the closest loading bay for each customer in the city center is selected, whereas in the second one, up to three potential loading bays (using the soft clustering approach) can be selected and used. In the continuation of this paper, the first approach is referred to as “hard” and the second as “soft,” which implies to the hard and soft clustering procedure. The model is based on the concept of the idealized urban area, which allows us to simulate and understand basic principles regardless of the characteristics of a particular real-life case.
The above-described problem was broken down into two separate sub-problems, although we are aware that both sub-problems (vehicle routing and on foot delivery) are interconnected. Consequently, the separate solutions of the two sub-problems would therefore at best be an approximation of the optimal solution of the overall problem. Due to approximation, on the other hand, such a simplified approach enables a much more efficient solution to the described problem and of similar real-life problems. Moreover, all assumptions considered in the presented model are based on the data from the cited literature and/or on our own experience, and they follow scientific principles that allow us to easily understand, explain, and generalize the problems under consideration.
2.1. Model Characteristics and Functions
The main elements of the model are the road transport network, access gates, customers’ locations, and location of loading bays (see Figure 1). Idealized urban area is presented graphically as an orthogonal network of roads on which customers, loading bays, and access gates are located. Customers are placed on the road network randomly, following the uniform density. For this purpose, Latin hypercube sampling (LHS) algorithm is used [43]. The positions of loading bays are determined by the fuzzy C-means (FCM) procedure [42], access gates are located randomly on each side of the urban area perimeter also using LHS algorithm.
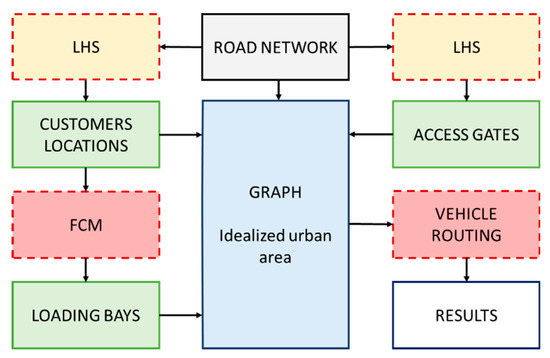
Figure 1.
Scheme of the model.
Note that the model allows to create different instances of orthogonal urban area with different density of network, customers, and loading bays. Example of an idealized city plan with random location of customers (green circles), optimal position of loading bays (red dots), and random location of access gates (black squares) are presented in the Figure 2 below. As can be seen, we assume one can enter and exit the urban area only at specific locations (access gates). This is a reasonable assumption because this is often the case in urban areas with implemented regulated urban access restriction.
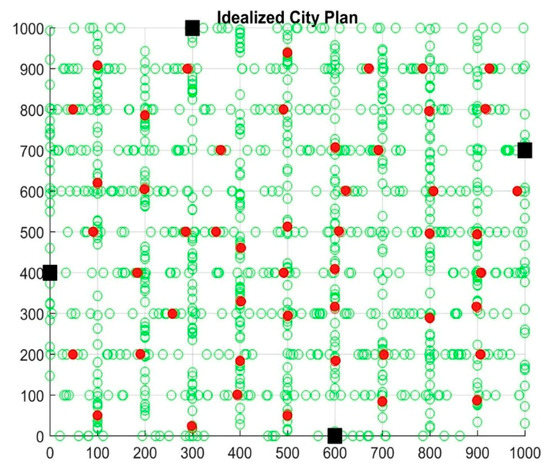
Figure 2.
Example of idealized urban area or city plan.
The model contains two key optimization modules: FCM module, which generates a set of customers locations and provides the input for multiple facility location problem (MFLP), in our case multiple locations of loading bays. Vehicle routing module, which takes as a basis the results of FCM, selects optimal loading bays for specific customers while providing the solution for optimal vehicle routing. FCM is based on the principles of fuzzy logic, while the mathematical origin of vehicle routing is based on integer linear programming. Both procedures were implemented in MATLAB and are briefly presented below.
2.2. Clustering Procedure for Solving Facility Location Problem
Multiple facility location problem can be treated as a classical clustering problem, where customers and facility locations correspond to data points and centers. The clustering criterion is to minimize the sum of distances from each data point to the corresponding cluster center. Potential location of loading bays in the model is therefore determined by using fuzzy C-means (FCM) clustering procedure. FCM was chosen to get some flexibility to the model with the possibility to simulate different membership degrees of customers to cluster centers, in our case loading bays [42].
FCM aims at minimizing the following function [44]:
where:
- -
- = number of customers
- -
- = number of clusters
- -
- = -th data point (each data point corresponds with location of a particular customer)
- -
- = center of cluster
- -
- = degree of membership of customer to cluster
- -
- = parameter of fuzziness
FCM algorithm in implemented in MATLAB and performs the following steps:
- Randomly initialize the cluster membership values, .
- Calculate the cluster centers:
- Update according to the following:
- Calculate the objective function, .
- Repeat steps 2–4 until improves by less than a specified minimum threshold or until after a specified maximum number of iterations.
2.3. Vehicle Routing and Loading Bay Assignment Procedure
Urban last mile delivery mostly involves three shipments while the number of packages per delivery varies significantly depending on the type of cargo and the type of customers [45,46]. Based on this assumption we developed a model which simulates three shipments per delivery which is called a triple delivery. The essence of the simulations is to find the optimal vehicle routing for triple delivery according to the randomly selected three customers , , , the corresponding loading bays , , or , and access gates , , or . Schematic representation of a graph is presented in the Figure 3.
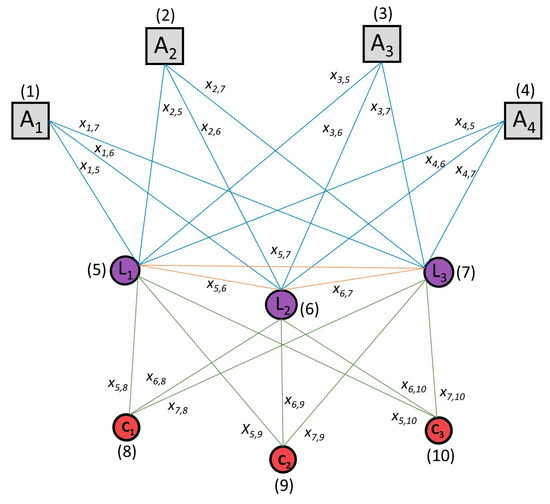
Figure 3.
Schematic representation of a graph containing four access gates (A), three loading bays (L), and three customers (C). The routing is limited to blue and orange connections.
Blue edges in the graph (Figure 3) represent connections between access gates and loading bays (), orange edges represent connections among loading bays (), and green edges represent connections between loading bays and customers (). The customers are not connected because we assume all deliveries are made individually even if one loading bay is selected for several customers.
In order to solve the problem we first consider the hard optimization approach at three loading bays , , , and then also the soft optimization approach on alternative loading bays , , , , , , , , Loading bays are assigned to customers based on FCM clustering procedure considering different membership degrees. Depending on the position of the selected customers and the associated loading bays, the solution of vehicle routing can be, in case of using soft optimization approach, drastically improved, especially if for any .
It is very important to clarify that the aim of supplying the city customers through the limited number of access gates is to avoid “unnecessary” traffic within the urban area. From that point of view, we assumed that the distances between individual access gates are irrelevant. In practice, this means that the costs, and therefore the corresponding negative effects of moving the vehicle from one access gate to another, can be neglected. This is the main assumption and limitation of the described model (of course, the model also allows modelling on the assumption that the distances between the gates are equal to the distances around the perimeter of the square or rectangle on which we are modelling).
The aim of the model is therefore to solve the problem of vehicle routing together with choosing a combination of loading bays and access gates (related to blue and orange lines in Figure 3) and to minimize the sum of all driven kilometers within the city center. The minimum of the objective function (i.e., kilometers) is sought by means of combinatoric optimization via breaking down the problem into all possible outcomes and apply integer linear programming to each outcome in order to find the overall minimum of driven kilometers.
In order to handle the routing integrated with location-allocation problem, there are 54 types of different vehicle routing outcomes. For each outcome, a unique linear program provides the partial optimal solution. The overall optimal solution is the minimum of all partial optimal solutions. Below, we present the necessary inputs to formulate these integer linear programs and explicitly define one of the outcomes and the corresponding integer linear program.
First we need to calculate distances between access gates and loading bays (c) and between loading bays (c; ij). Distances are calculated using Manhattan metrics in the following way:
and
In the above equations stands for the absolute value and is used for the physical point where the indices refer to the particular physical point (e.g., is the coordinate of the point ).
All possible combinations (calculated distances) are written as a cost vector:
Furthermore, the point vector is denoted by:
Next, define rows in the matrix:
which presents the constraints of the integer linear program. For example, to allow that the gate is connected to one of the loading bays , or we define the following line vector:
In a similar way we define , and for allowing that the other three gates are connected to one of the loading bays.
To connect with some gate and with some another loading bay; or we define the following line vector:
and similarly we define and
Finally, the right-hand-side vector, , of the matrix-form constraint equation must be defined. For example, if access gates and are used and the delivery is performed through all three loading bays, we have
Using these notations, the integer linear program for solving optimization of the presented problem, writes as follows:
Minimize , subject to , with for all
For example, for the case of using assess gates and and supplying customers each from its own loading bay; , and , the optimal solution can be found with the help of linear program aiming to minimize the following cost function:
subject to
where for all
For clarification, the constraint means that the solution is starting from or ending in the gate . The constraint means that the gate is not used in the solution. The constraint means that the solution enters and leaves loading bay .
In a similar way we can treat all other feasible solutions for triple delivery using three, two, or one loading bay.
2.4. Potential Solutions/Outcomes
To list all possible outcomes, we use abbreviations which uniquely determine any combination of access gates and loading bays. The first part of the notation defines the number of gates (), the second part the number of loading bays ), and the final part the type of the solution, where: P stands for a path and C for a cycle. The notation stands for a path from Ai to , stands for a cycle on points, , containing gate . And finally, denotes the gate is empty, which becomes relevant only if the customers are each supplied through its own entrance gate.
We are first listing four significantly different outcomes for the case of supplying customers through three loading bays. The first example is to check the solution, where we enter the city through three different access gates A1, A2, and A3 and supply customers each from different loading bays , , and . In this case the entire route can be formally written as: G3-L3-EA4. Another example is to check the outcome, where we enter the city through the access gate and exit through gate and we supply customers each from different loading bays; , and . The entire route can be then formally written as: G2-L3-PA1A2. Next outcome is describes the situation when we enter the city through the access gate and exit through gate to serve two customers each from different loading bay and then to supply the third customer entering and exiting the city through gate . The entire route can be in this case formally written as: G3-L3-PA1A2C2A3. The final example describes the outcome, where we enter the city through only one access gate, , and we supply customers each from its own loading bay; , and . In this final case the entire route can be formally written as: G1-L3-C4A1. To make clearer, the above outcomes are graphically presented in Figure 4.
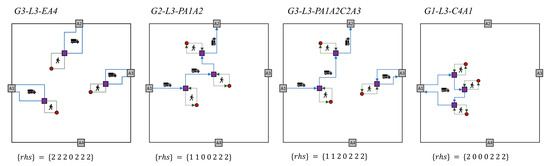
Figure 4.
Graphical presentation of some examples of linear programs when using three loading bays.
In the case of using three loading bays we must in total execute 38 different integer linear programs with different right-hand-side vectors .
Next option is to supply customers through only two loading bays. This means that two out of three customers are served from the same loading bay. We present three examples of significantly different outcomes for this option. The first example is to check the solution, where we enter the city through two different access gates, and . From the gate we visit the first loading bay to supply the first customer and from gate we visit second loading bay to supply the other two customers. In both cases we exit the city through the same gate as we entered. This can be formally written as: G2-L2-C2A1C2A2. Next example is to check the solution of entering the city through access gate and exiting through gate . On the path we visit the first loading bay to supply two customers and then continue to second loading bay to supply the remaining customer. This can be formally written as: G2-L2-PA1A2. Last example is to check the solution, where we enter the city through only one access gate and we supply customers from two loading bays and . From the first loading bay we supply two customers and from the second the remaining one. The entire route can be in this case formally written as: G1-L2-C3A1. For easier understanding, the before-mentioned examples are also graphically and schematically presented in Figure 5.
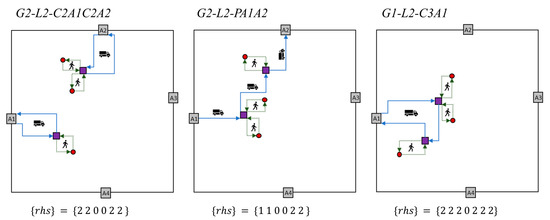
Figure 5.
Graphical presentation of some examples of linear programs when using two loading bays.
In case when using two loading bays we must execute 16 different integer linear programs with different right-hand-side vector .
The last option is to supply three customers simultaneously through only one loading bay. This means that customers are located at a relatively short distance from each other, so the best solution is to stop the truck at one loading bay and supply all customers from there. In this case, only the minimum distance from the selected loading bay to the nearest access gate needs to be found. Therefore, we do not need to run a linear program, we just need to search for the shortest path.
3. Simulation Results
The aim of the simulations is to perform vehicle routing optimization for specific instances of idealized urban areas in order to compare the results of driving and walking distances for different numbers of loading bays using soft and hard optimization approach and to get, if they exist, general relations/rules for vehicle routing phenomenon. Simulations are carried out on a square grid with density of = 11 × 11 roads, customer density of = 1000 customers/km2, and for the following number of loading bays, = 4, 9, 16, 25, 49, and 81. These parameters are carefully selected to represent a typical urban area of European cities as well as possible. For more details see Letnik et al. [47].
The following Figure 6 show some basic examples of idealized urban areas with randomly generated customer locations, corresponding locations of loading bays (generated by FCM procedure), and randomly located access gates. These “instances” are examples of different situations that can occur in real-life. Analyzing large numbers of such instances is the cornerstone of our statistical approach, which first serves to locate the loading bays and then to understand the influence of a flexible assignment of loading bays for vehicle routing and consequently walking distances. Note that these instances form the basis for the simulations shown below.
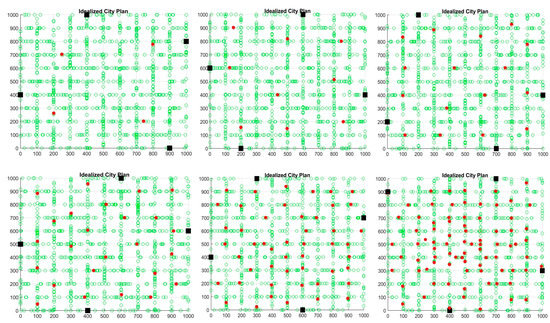
Figure 6.
Examples of randomly generated simulation instances of customers, access gates, and loading bays for 4, 9, 16 on the first row and 25, 49, 81 on the second row.
Vehicle routings and the corresponding walking parts are calculated separately for each instance presented in Figure 6. The algorithm randomly selects three customers for a given instance and then executes all together 54 different types of integer linear programs to find an optimal solution for the driving part to serve these three customers. When the solution of the integer linear program is obtained, the algorithm selects the next triple. The simulations are performed for the density of = 1000 customers/km2, where 333 simulations of a triple delivery are performed for each instance. Note that in the case of hard (soft) optimization approach, the algorithm considers up to three (nine) different potential loading bays for each simulation of triple delivery. This yields that in the statistical analysis we considered simulations for each instance. It is important to mention that optimum is sought from the driving distance point of view, whereby walking part is kept reasonably low by assigning only those loading bays with reasonably high membership values.
Example of expected result of vehicle routing in case of hard and soft clustering approach is presented in Figure 7.
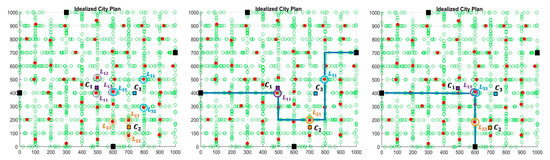
Figure 7.
Example of randomly selected customers () and all potential loading bays (, , , , , , , , ), solution of hard clustering (on the middle), and solution of soft clustering (on the right side).
As can be seen in Figure 7, the hard clustering approach takes into consideration only loading bays with the highest membership degree (, , ), while the soft clustering approach considers also loading bays with the second and third highest membership degrees (, , , , , ). Consequently, shortest driving distances are expected in case of soft clustering approach, as can be seen from the example presented above. Note that on the other hand this results in slightly longer walking distances.
The comparison between the driving and walking distances in the case of a hard and a soft optimization approach is in the following analyzed and presented by cumulative distribution function (CDF) curves. We chose this method because it allows to read simultaneously the minimum, mean, and maximum distances on the same graph, and therefore we can easily compare the differences between hard and soft optimization approach.
3.1. Results—Driving Distances
The understanding of driving distances is important to assess the impact of delivery processes on the environmental parameters of the city. The aim of optimizing delivery is namely to reduce, as much as possible, the kilometers driven within the urban area. In the analysis we are trying to understand the influence of the number of loading bays on the driving distances and their distribution in the overall structure of the delivery. In the following Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14 and Figure 15 and Table 1, Table 2, Table 3, Table 4 “HD” stands for hard driving and “SD” stands for soft driving solution.
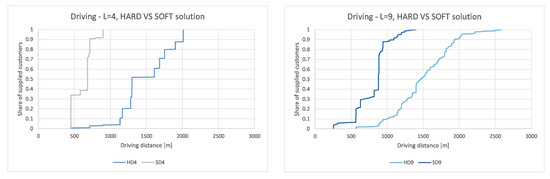
Figure 8.
Cumulative distribution function (CDF) for driving distances, hard and soft approach, = 4 and = 9.
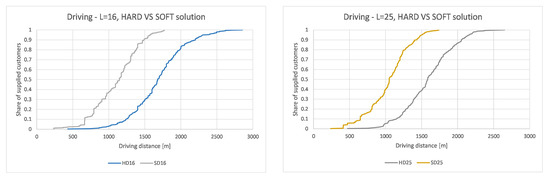
Figure 9.
CDF for driving distances, hard and soft approach, = 16 and = 25.
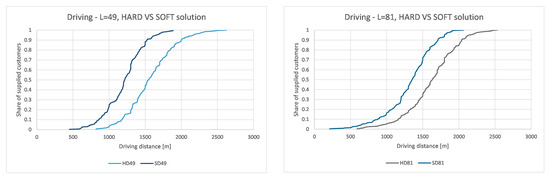
Figure 10.
CDF for driving distances, hard and soft approach, = 49 and = 81.
As can be seen, driving distances are in all cases shorter when using soft optimization approach. It can also be observed that the difference in driving distances between hard and soft optimization approach decreases with the increase in the number of loading bays.
The differences are shown in more detail in the following Table 1.

Table 1.
Maximum, minimum, and average driving distances (hard and soft approach).
Table 1.
Maximum, minimum, and average driving distances (hard and soft approach).
| Max | Min | Avg | Max | Min | Avg | ||
|---|---|---|---|---|---|---|---|
| HD4 [m] | 2.011 | 451 | 1.494 | HD25 [m] | 2.652 | 472 | 1.592 |
| SD4 [m] | 897 | 451 | 624 | SD25 [m] | 1.743 | 237 | 1.044 |
| Difference [m] | −1.114 | 0 | −870 | Difference [m] | −909 | −235 | −548 |
| Difference [%] | −55.4% | 0,0% | −58.2% | Difference [%] | −34.3% | −49.8% | −34.4% |
| HD9 [m] | 2.584 | 566 | 1.499 | HD49 [m] | 2.627 | 818 | 1.577 |
| SD9 [m] | 1.400 | 256 | 809 | SD49 [m] | 1.889 | 451 | 1.213 |
| Difference [m] | −1.184 | −310 | −690 | Difference [m] | −738 | −367 | −363 |
| Difference [%] | −45.8% | −54.7% | −46.1% | Difference [%] | −28.1% | −44.9% | −23.1% |
| HD16 [m] | 2.854 | 429 | 1.695 | HD81 [m] | 2.530 | 590 | 1.617 |
| SD16 [m] | 1.772 | 237 | 1.106 | SD81 [m] | 2.062 | 211 | 1.320 |
| Difference [m] | −1.081 | −193 | −589 | Difference [m] | −468 | −379 | −297 |
| Difference [%] | −37.9% | −44.9% | −34.8% | Difference [%] | −18.5% | −64.3% | −18.4% |
As can be seen from the Table 1, soft optimization approach results with decrease of driving distances in comparison to hard optimization approach for 58.2% if = 4, for 46.1% if = 9, for 34.8% if = 16, for 34, 4% if = 25, for 23.1% if = 49, and for 18.4% if = 81.
3.2. Results—Walking Distances
Walking distances represent the second part of urban last mile delivery. In comparison to driving distances, walking does not cause any negative effects on the environment but still needs to be as short as possible to avoid longer stay of delivery vehicles in the urban area. Also in this case we need to understand the differences of hard and soft optimization approach. In the following figures and tables “HW” stands for hard walking and “SW” stands for soft walking solution.
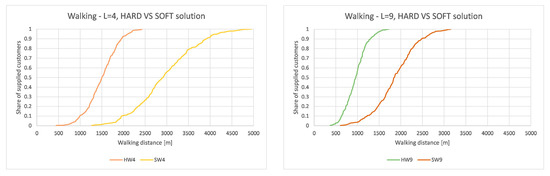
Figure 11.
CDF for walking distances, hard and soft approach, = 4 and = 9.
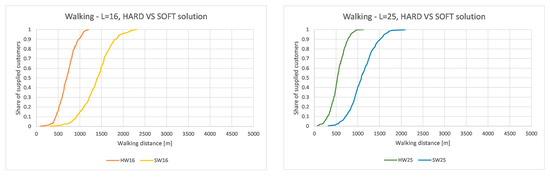
Figure 12.
CDF for walking distances, hard and soft approach, = 16 and = 25.
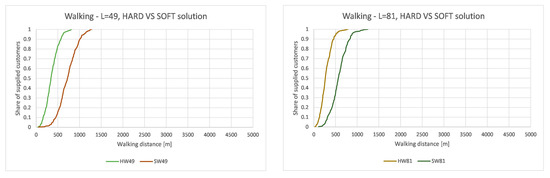
Figure 13.
CDF for walking distances, hard and soft approach, = 49 and = 81.
As can be seen, walking distances are longer when using soft optimization approach which is exactly the opposite as for the case of driving distances presented before. It can also be observed that the difference between hard and soft approach decreases with the increase in the number of loading bays which is similar as by the case of driving distances.
The differences are shown in more detail in the following Table 2.

Table 2.
Maximum, minimum, and average walking distance (hard and soft approach).
Table 2.
Maximum, minimum, and average walking distance (hard and soft approach).
| Max | Min | Avg | Max | Min | Avg | ||
|---|---|---|---|---|---|---|---|
| HW4 [m] | 2.430 | 445 | 1.501 | HW25 [m] | 1.129 | 73 | 539 |
| SW4 [m] | 4.945 | 1.266 | 2.955 | SW25 [m] | 2.099 | 320 | 1.103 |
| Difference [m] | 2.514 | 822 | 1.454 | Difference [m] | 970 | 247 | 563 |
| Difference [%] | 103.5% | 184.8% | 96.8% | Difference [%] | 85.9% | 337.3% | 104.4% |
| HW9 [m] | 1.726 | 369 | 963 | HW49 [m] | 816 | 40 | 358 |
| SW9 [m] | 3.154 | 605 | 1.870 | SW49 [m] | 1.282 | 56 | 724 |
| Difference [m] | 1.428 | 236 | 907 | Difference [m] | 466 | 16 | 366 |
| Difference [%] | 82.8% | 63.8% | 94.1% | Difference [%] | 57.0% | 41.2% | 102.4% |
| HW16 [m] | 1.207 | 94 | 703 | HW81 [m] | 783 | 27 | 284 |
| SW16 [m] | 2.318 | 320 | 1.392 | SW81 [m] | 1.246 | 109 | 577 |
| Difference [m] | 1.111 | 227 | 689 | Difference [m] | 463 | 82 | 293 |
| Difference [%] | 92.1% | 241.9% | 98.0% | Difference [%] | 59.2% | 310.9% | 103.5% |
As can be seen from Table 2, walking distances are, in the case of using soft optimization approach, almost exactly double of those reached by hard optimization approach. In addition, this holds true for different number of loading bays.
3.3. Comparison Between Driving and Walking Distances
Our final aim is to understand the relationship and compare the differences between the driving and walking distances by different number of loading bays. First, we show a comparison for the hard optimization approach.
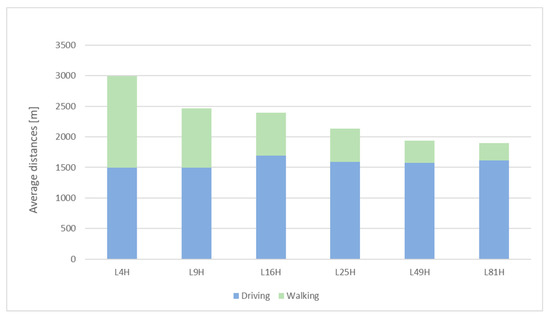
Figure 14.
Average driving and walking distanced, hard approach, = 4–81.
From the chart above we can see:
- The total length of average driving and walking distances decreases with the increase in the number of loading bays.
- The driving distance covered in the hard optimization approach does not show significant deviations with regard to the increase in the number of loading bays.
- Increasing the number of loading bays on the other hand shortens the length of walking distances.
Distances and differences are shown in more detail in the following Table 3.

Table 3.
Comparison between driving and walking distances (hard approach).
Table 3.
Comparison between driving and walking distances (hard approach).
| Sum | Avg | Ratio | Sum | Avg | Ratio | ||
|---|---|---|---|---|---|---|---|
| HD4 [m] | 497.666 | 1.494 | 49.9% | HD25 [m] | 530.015 | 1.592 | 74.7% |
| HW4 [m] | 499.841 | 1.501 | 50.1% | HW25 [m] | 179.647 | 539 | 25.3% |
| Total | 997.507 | 2.996 | Total | 709.662 | 2.131 | ||
| HD9 [m] | 499.203 | 1.499 | 60.9% | HD49 [m] | 525.021 | 1.577 | 81.5% |
| HW9 [m] | 320.762 | 963 | 39.1% | HW49 [m] | 119.205 | 358 | 18.5% |
| Total | 819.966 | 2.462 | Total | 644.225 | 1.935 | ||
| HD16 [m] | 564.286 | 1.695 | 70.7% | HD81 [m] | 538.377 | 1.617 | 85.1% |
| HW16 [m] | 234.146 | 703 | 29.3% | HW81 [m] | 94.408 | 284 | 14.9% |
| Total | 798.432 | 2.398 | Total | 632.785 | 1.900 |
The table reveals:
- Ratio between driving and walking distances is changing with increasing the number of loading bays starting from approximately 50:50 when = 4, 60:40 when = 9, 70:30 when = 16, 57:25 when = 25, 82:18 when = 49, and 85:15 when = 81.
- Considering average walking distances (one way direction and divide with three customers), loading bays should cover 250 m in case of = 4, 160 m in case = 9, 116 m in case = 16, 90 mm in case = 25, 60 m in case = 49, 48 m in case = 81.
We can also show a comparison for the soft optimization approach.
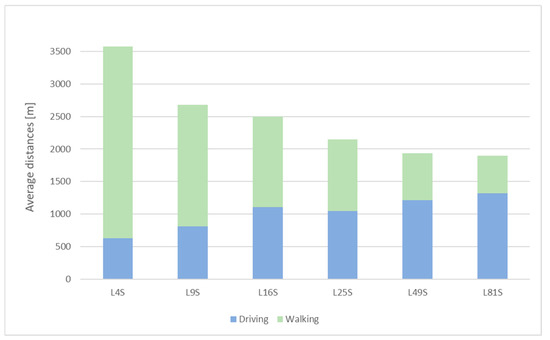
Figure 15.
Average driving and walking distances, soft approach, = 4–81.
From the chart above we can see:
- The total distance (traveling and walking) decreases with the increase in the number of loading bays (similar to what we noticed with the hard optimization approach).
- The ratio between the length of the driving and walking distances is significantly different in this case; with the increase in the number of loading bays, there is a pronounced trend of increasing the length of driving distances and decreasing the length of walking (except for = 16, the length of driving distance is slightly longer than for = 49).
Distances and differences are shown in more detail in the following Table 4.

Table 4.
Comparison between driving and walking distances (soft approach).
Table 4.
Comparison between driving and walking distances (soft approach).
| Sum | Avg | Ratio | Sum | Avg | Ratio | ||
|---|---|---|---|---|---|---|---|
| SD4 | 207.827 | 624 | 29.4% | SD25 | 347.544 | 1.044 | 48.6% |
| SW4 | 499.841 | 1.501 | 70.6% | SW25 | 367.153 | 1.103 | 51.4% |
| Total | 707.667 | 2.125 | Total | 714.697 | 2.146 | ||
| SD9 | 269.288 | 809 | 30.2% | SD49 | 525.021 | 1.213 | 62.6% |
| SW9 | 622.666 | 1.870 | 69.8% | SW49 | 241.228 | 724 | 37.4% |
| Total | 891.953 | 2.679 | Total | 766.249 | 1.938 | ||
| SD16 | 368.194 | 1.106 | 44.3% | SD81 | 538.377 | 1.320 | 69.6% |
| SW16 | 463.655 | 1.392 | 55.7% | SW81 | 192.130 | 577 | 30.4% |
| Total | 831.849 | 2.498 | Total | 730.507 | 1.897 |
The table above shows:
- The share of walking part of triple delivery is large (approximately 70%) by small number of loading bays ( = 4 and = 9).
- Ratio between driving and walking distances is improving with increasing the number of loading bays; approximately 44:56 when = 16, 49:51 when = 25, 63:37 when = 49, and 70:30 when = 81.
- Considering average walking distances (one way direction and divide with three customers), loading bays should cover 250 m in case of = 4, 312 m in case = 9, 232 m in case = 16, 184 m in case = 25, 120 m in case = 49, 96 m in case = 81.
4. Discussion
Urban freight deliveries are often subject to many access restrictions which creates the need to establish a system of loading bays and to split the last mile delivery into driving and walking parts. An open question arises—where and how many loading bays should we provide to perform this transshipment and execute last mile delivery in the most efficient way.
The problem is even more complex because loading bays are sometimes occupied and, in these cases, we need to reroute delivery vehicles and search for the next alternative loading bay. To test different optimization approaches we introduced fuzzy clustering to make the system flexible enough for accommodating also this kind of problem. To stress once again, the approach is based on the following important assumptions:
- The modelled city corresponds to idealized orthogonal urban area with different densities of loading bays;
- Locations of customers and access gates are generated randomly, following the uniform density (simulated by LHS procedure);
- Vehicles can enter and exit the urban area only at specific locations (access gates) and the distances between them (outside the studied area) are considered irrelevant;
- Simulations are restricted on up to three shipments per delivery (triple delivery);
- All deliveries from loading bays to customers are made individually even if one loading bay is selected for several customers.
The aim of the simulations was to understand the influence of different numbers of loading bays on driving and walking distances when using hard and soft (fuzzy) optimization approach. An important finding of the simulation analysis is related to the case of hard optimization approach. We show there is no statistically significant influence of the number of loading bays on the driving distances. In practical terms this means that city authorities are not able to decrease total driving distances with increasing the number of loading bays. The crucial decision parameter for determining the number of loading bays is therefore only the acceptable walking distance, which decreases with increasing numbers of loading bays. This is a very important finding of the model, which we would not encounter if we would run the simulation for specific characteristics of a particular urban area. This result can be seen as a fundamental law that is relevant for all rectangular urban areas.
On the other hand, soft optimization approach shows its efficiency for decreasing driving distances, in particular when the number of loading bays is small. Whereby, in this case, the walking part of the delivery is much higher than in the case of hard clustering optimization approach. The situation on the other hand changes with increasing numbers of loading bays where the walking distances for soft optimization approach becomes much lower and acceptable also from the practical point of view. Lower walking distances are also influencing the time of loading bay occupancy and are therefore additionally important, especially in cases where loading bays have some capacity restrictions. This result shows the importance of understanding the basic relation between walking and driving distances when using different optimization approaches.
We can conclude that a soft optimization approach proves to be an acceptable alternative for decreasing driving distances especially for a larger number of loading bays. We would therefore advise city authorities to plan reasonably large numbers of loading bays in urban areas and to use soft optimization approach when assigning loading bays to the routing of the urban last mile deliveries. This would enable them to reduce the number of driven kilometers and create greater flexibility of the city logistics system. Such a system would also have beneficial results for logistics operators, users, and city dwellers, which are constantly looking for a better, more efficient and sustainable city logistics system.
Before finally confirming this results on some real life cases, further research could also investigate the impact of different densities of the road network (including variants with an uneven distribution of roads that are closer to some specific real-life situations), different densities of customers, and different numbers and location of access gates. Nevertheless, on the results presented in this article and the research experience gained in determining the optimal number and locations of loading bays [42], we assume that the results will not be significantly different from those shown. Another proposal is to run the optimization also for the walking part of delivery, which would additionally save some walking distances.
Author Contributions
Conceptualization, T.L., M.M., and I.P.; methodology, T.L., M.M., and I.P.; software, I.P.; validation, M.M.; formal analysis, T.L.; investigation, T.L., M.M., and I.P.; resources, T.L.; data curation, T.L.; writing—original draft preparation, T.L.; writing—review and editing, T.L., M.M., and I.P.; visualization, T.L. and I.P.; supervision, I.P.; project administration, T.L.; funding acquisition, M.M. and I.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially funded by ARRS (Slovenia), Research program V2-1740, No N1-0063 and No P1-0288.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Fiore, G.M. Space for Cities: Satellite Applications Enhancing Quality of Life in Urban Areas. In Studies in Space Policy; Springer: Cham, Switzerland, 2020; Volume 22, pp. 251–263. [Google Scholar]
- Harris, S.; Weinzettel, J.; Bigano, A.; Källmén, A. Low carbon cities in 2050? GHG emissions of European cities using production-based and consumption-based emission accounting methods. J. Clean. Prod. 2020, 248, 119206. [Google Scholar] [CrossRef]
- Olsson, J.; Hellström, D.; Pålsson, H. Framework of last mile logistics research: A systematic review of the literature. Sustainability 2019, 11, 7131. [Google Scholar] [CrossRef]
- Lindholm, M.; Behrends, S. Challenges in urban freight transport planning—A review in the Baltic Sea Region. J. Transp. Geogr. 2012, 22. [Google Scholar] [CrossRef]
- Rose, W.J.; Mollenkopf, D.A.; Autry, C.W.; Bell, J.E. Exploring urban institutional pressures on logistics service providers. Int. J. Phys. Distrib. Logist. Manag. 2016, 46, 153–176. [Google Scholar] [CrossRef]
- Lim, S.F.W.T.; Jin, X.; Srai, J.S. Consumer-driven e-commerce: A literature review, design framework, and research agenda on last-mile logistics models. Int. J. Phys. Distrib. Logist. Manag. 2018, 48, 308–332. [Google Scholar] [CrossRef]
- Kin, B.; Ambra, T.; Verlinde, S.; Macharis, C. Tackling Fragmented Last Mile Deliveries to Nanostores by Utilizing Spare Transportation Capacity—A Simulation Study. Sustainability 2018, 10, 653. [Google Scholar] [CrossRef]
- Iwan, S. Adaptative Approach to Implementing Good Practices to Support Environmentally Friendly Urban Freight Transport Management. Procedia Soc. Behav. Sci. 2014, 151, 70–86. [Google Scholar] [CrossRef]
- Lindholm, M. Urban freight transport from a local authority perspective—a literature review. Eur. Transp. Trasp. Eur. 2013, 54, 1–3. [Google Scholar]
- Letnik, T.; Marksel, M.; Luppino, G.; Bardi, A.; Božičnik, S. Review of policies and measures for sustainable and energy efficient urban transport. Energy 2018, 163, 245–257. [Google Scholar] [CrossRef]
- Comi, A. A modelling framework to forecast urban goods flows. Res. Transp. Econ. 2020, 80, 100827. [Google Scholar] [CrossRef]
- Simoni, M.D.; Bujanovic, P.; Boyles, S.D.; Kutanoglu, E. Urban consolidation solutions for parcel delivery considering location, fleet and route choice. Case Stud. Transp. Policy 2017, 6, 112–124. [Google Scholar] [CrossRef]
- Letnik, T.; Mencinger, M.; Bozicnik, S. Dynamic Management of Urban Last-Mile Deliveries. City Logist. 2 2018, 23–37. [Google Scholar] [CrossRef]
- Aljohani, K.; Thompson, R.G. An examination of last mile delivery practices of freight carriers servicing business receivers in inner-city areas. Sustainability 2020, 12, 2837. [Google Scholar] [CrossRef]
- Cherrett, T.; Allen, J.; McLeod, F.; Maynard, S.; Hickford, A.; Browne, M. Understanding urban freight activity–key issues for freight planning. J. Transp. Geogr. 2012, 24, 22–32. [Google Scholar] [CrossRef]
- Dezi, G.; Dondi, G.; Sangiorgi, C. Urban freight transport in Bologna: Planning commercial vehicle loading/unloading zones. Procedia Soc. Behav. Sci. 2010, 2, 5990–6001. [Google Scholar] [CrossRef]
- Ezquerro, S.; Moura, J.L.; Alonso, B. Illegal Use of Loading Bays and Its Impact on the Use of Public Space. Sustainability 2020, 12, 5915. [Google Scholar] [CrossRef]
- Aiura, N.; Taniguchi, E. Planning On-Street Loading-Unloading Spaces Considering the Behaviour of Pickup-Delivery Vehicles and Parking Enforcement. J. East. Asia Soc. Transp. Stud. 2005, 6, 2963–2974. [Google Scholar]
- Bányai, T. Real-time decision making in first mile and last mile logistics: How smart scheduling affects energy efficiency of hyperconnected supply chain solutions. Energies 2018, 11, 1833. [Google Scholar] [CrossRef]
- Browne, M.; Allen, J.; Nemoto, T.; Patier, D.; Visser, J. Reducing Social and Environmental Impacts of Urban Freight Transport: A Review of Some Major Cities. Procedia Soc. Behav. Sci. 2012, 39, 19–33. [Google Scholar] [CrossRef]
- Chloupek, A. i-Ladezone: Intelligent monitoring of loading bays in Vienna. Available online: http://www.bestfact.net/wp-content/uploads/2016/01/CL1_031_QuickInfo_iLadezonen-16Dec2015.pdf (accessed on 8 September 2020).
- Patier, D.; David, B.; Chalon, R.; Deslandres, V. A New Concept for Urban Logistics Delivery Area Booking. Procedia Soc. Behav. Sci. 2014, 125, 99–110. [Google Scholar] [CrossRef]
- McLeod, F.; Cherrett, T. Loading bay booking and control for urban freight. Int. J. Logist. Res. Appl. 2011, 14, 385–397. [Google Scholar] [CrossRef]
- Boussier, J.; Cucu, T.; Ion, L.; Breuil, D. Simulation of goods delivery process. Int. J. Phys. Distrib. Logist. Manag. 2011, 41, 913–930. [Google Scholar] [CrossRef]
- DynaLOAD: A simulation framework for planning, managing and controlling urban delivery bays. Transp. Res. Procedia 2017, 22, 335–344. [CrossRef]
- Oliveira, B.; Ramos, A.G.; De Sousa, J.P. A classification of two-tier distribution systems based on mobile depots. Transp. Res. Procedia 2020, 47, 115–122. [Google Scholar] [CrossRef]
- Prodhon, C.; Prins, C. A survey of recent research on location-routing problems. Eur. J. Oper. Res. 2014, 238, 1–17. [Google Scholar] [CrossRef]
- Crainic, T.G.; Ricciardi, N.; Storchi, G. Models for Evaluating and Planning City Logistics Systems. Transp. Sci. 2009, 43, 432–454. [Google Scholar] [CrossRef]
- Hemmelmayr, V.C.; Cordeau, J.-F.; Crainic, T.G. An adaptive large neighborhood search heuristic for Two-Echelon Vehicle Routing Problems arising in city logistics. Comput. Oper. Res. 2012, 39, 3215–3228. [Google Scholar] [CrossRef] [PubMed]
- Russo, F.; Comi, A. A Model For Simulating Urban Goods Transport and Logistics: The integrated Choice of ho.re.ca. Activity Decision-Making and Final Business Consumers. Procedia Soc. Behav. Sci. 2013, 80, 717–728. [Google Scholar] [CrossRef]
- Oskarbski, J.; Kaszubowski, D. Applying a Mesoscopic Transport Model to Analyse the Effects of Urban Freight Regulatory Measures on Transport Emissions—An Assessment. Sustainability 2018, 10, 2515. [Google Scholar] [CrossRef]
- Comi, A.; Schiraldi, M.M.; Buttarazzi, B. Smart urban freight transport: Tools for planning and optimising delivery operations. Simul. Model. Pract. Theory 2018, 88, 48–61. [Google Scholar] [CrossRef]
- Zhang, L.; Thompson, R.G. Understanding the benefits and limitations of occupancy information systems for couriers. Transp. Res. Part C Emerg. Technol. 2019, 105, 520–535. [Google Scholar] [CrossRef]
- McLeod, F.N.; Cherrett, T.J.; Bektas, T.; Allen, J.; Martinez-Sykora, A.; Lamas-Fernandez, C.; Bates, O.; Cheliotis, K.; Friday, A.; Piecyk, M.; et al. Quantifying environmental and financial benefits of using porters and cycle couriers for last-mile parcel delivery. Transp. Res. Part D Transp. Environ. 2020, 82, 102311. [Google Scholar] [CrossRef]
- Nguyê˜n, T.B.T.; Bektaş, T.; Cherrett, T.J.; McLeod, F.N.; Allen, J.; Bates, O.; Piotrowska, M.; Piecyk, M.; Friday, A.; Wise, S. Optimising parcel deliveries in London using dual-mode routing. J. Oper. Res. Soc. 2019, 70, 998–1010. [Google Scholar] [CrossRef]
- Iris, Ç.; Pacino, D.; Ropke, S. Improved formulations and an Adaptive Large Neighborhood Search heuristic for the integrated berth allocation and quay crane assignment problem. Transp. Res. Part E Logist. Transp. Rev. 2017, 105, 123–147. [Google Scholar] [CrossRef]
- Iris, Ç.; Lam, J.S.L. Recoverable robustness in weekly berth and quay crane planning. Transp. Res. Part B Methodol. 2019, 122, 365–389. [Google Scholar] [CrossRef]
- Iris, Ç.; Pacino, D.; Ropke, S.; Larsen, A. Integrated Berth Allocation and Quay Crane Assignment Problem: Set partitioning models and computational results. Transp. Res. Part E Logist. Transp. Rev. 2015, 81, 75–97. [Google Scholar] [CrossRef]
- Csiszár, C.; Csonka, B.; Földes, D.; Wirth, E.; Lovas, T. Urban public charging station locating method for electric vehicles based on land use approach. J. Transp. Geogr. 2019, 74, 173–180. [Google Scholar] [CrossRef]
- Rathore, P.; Sarmah, S.P.; Singh, A. Location–allocation of bins in urban solid waste management: A case study of Bilaspur city, India. Environ. Dev. Sustain. 2020, 22, 3309–3331. [Google Scholar] [CrossRef]
- Schwerdfeger, S.; Boysen, N. Optimizing the changing locations of mobile parcel lockers in last-mile distribution. Eur. J. Oper. Res. 2020, 285, 1077–1094. [Google Scholar] [CrossRef]
- Letnik, T.; Peruš, I.; Božičnik, S.; Mencinger, M. On fundamental principles of the optimal number and location of loading bays in urban areas. Transport 2019, 34, 722–740. [Google Scholar] [CrossRef]
- Husslage, B.G.M.; Rennen, G.; van Dam, E.R.; den Hertog, D. Space-filling Latin hypercube designs for computer experiments. Optim. Eng. 2011, 12, 611–630. [Google Scholar] [CrossRef]
- Bezdek, J.C. Pattern Recognition with Fuzzy Objective Function Algorithms; Springer: Boston, MA, USA, 1981. [Google Scholar]
- Muñuzuri, J.; Cortés, P.; Onieva, L.; Guadix, J. Estimation of Daily Vehicle Flows for Urban Freight Deliveries. J. Urban Plan. Dev. 2012, 138, 43–52. [Google Scholar] [CrossRef]
- Holguín-veras, J.; Sánchez-díaz, I. Freight Demand Management and the Potential of Receiver-Led Consolidation programs. Transp. Res. Part A Policy Pr. 2016, 84, 109–130. [Google Scholar] [CrossRef]
- Letnik, T.; Farina, A.; Mencinger, M.; Lupi, M.; Bozicnik, S. Dynamic Management of Loading Bays for Energy Efficient Urban Freight Deliveries. Energy 2018, 159, 916–928. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).