Traffic State Estimation and Classification on Citywide Scale Using Speed Transition Matrices
Abstract
1. Introduction
- -
- Novel traffic data representation is proposed in form of the STM which application is shown for the traffic state estimation, routing applications, and anomaly detection.
- -
- The methodology for the traffic state estimation on a city-wide scale is proposed based on the STMs and computed COMs.
- -
- The proposed methodology is applied and validated on the real dataset for the City of Zagreb, Croatia.
2. Literature Review
2.1. GNSS Data for Traffic Representation
2.2. Data Modeling Techniques
2.3. Traffic State Estimation Approaches
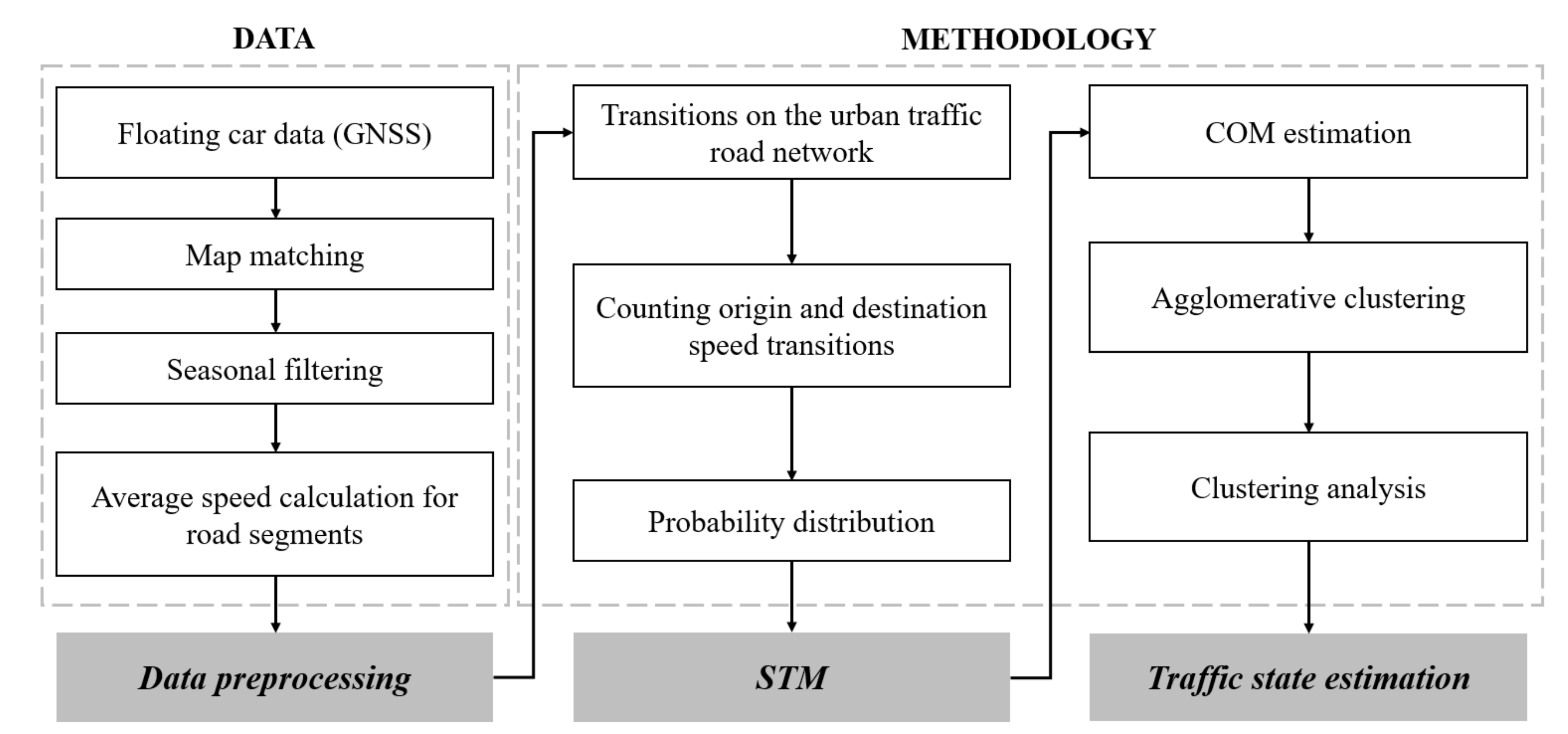
3. Methodology
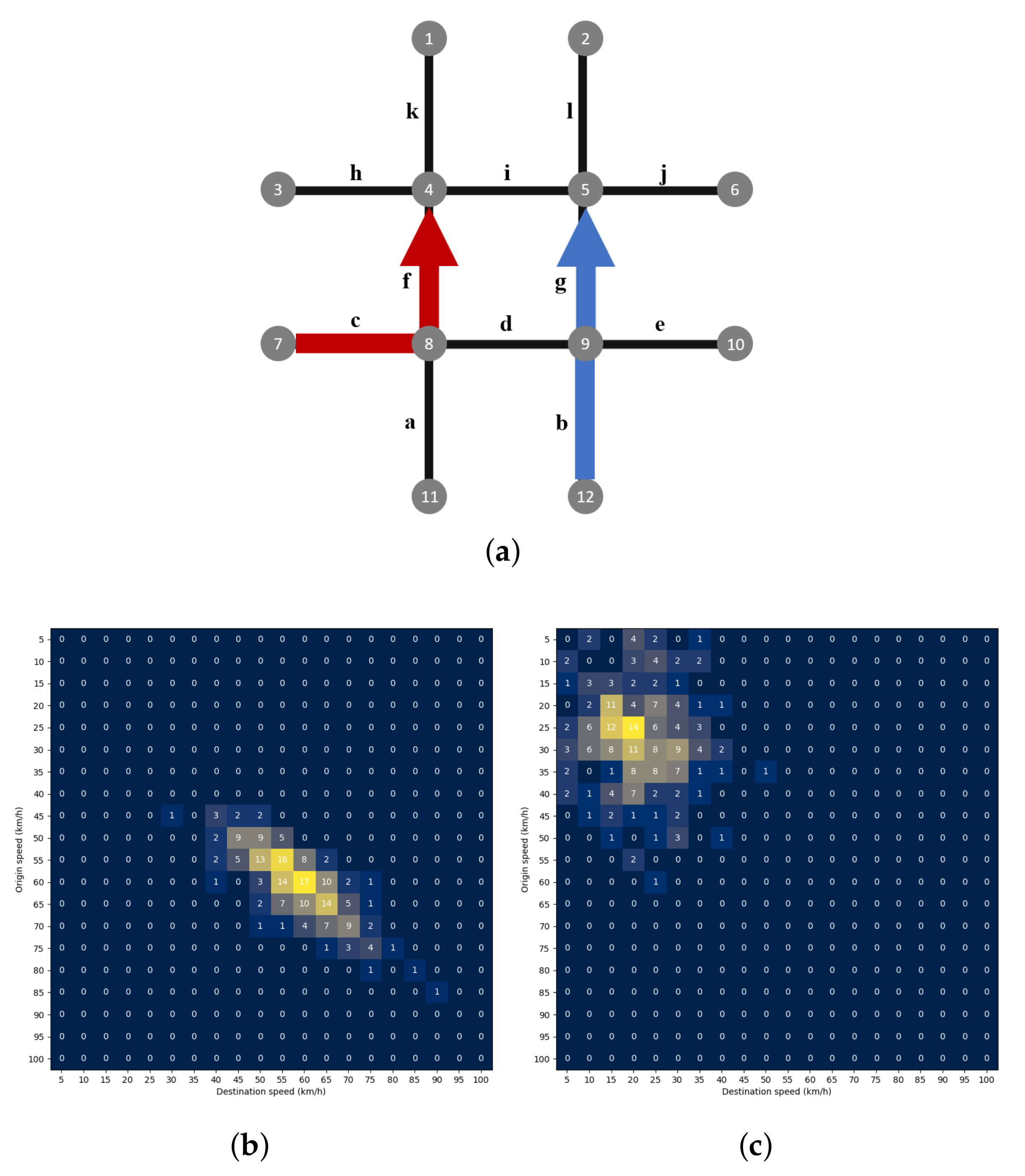
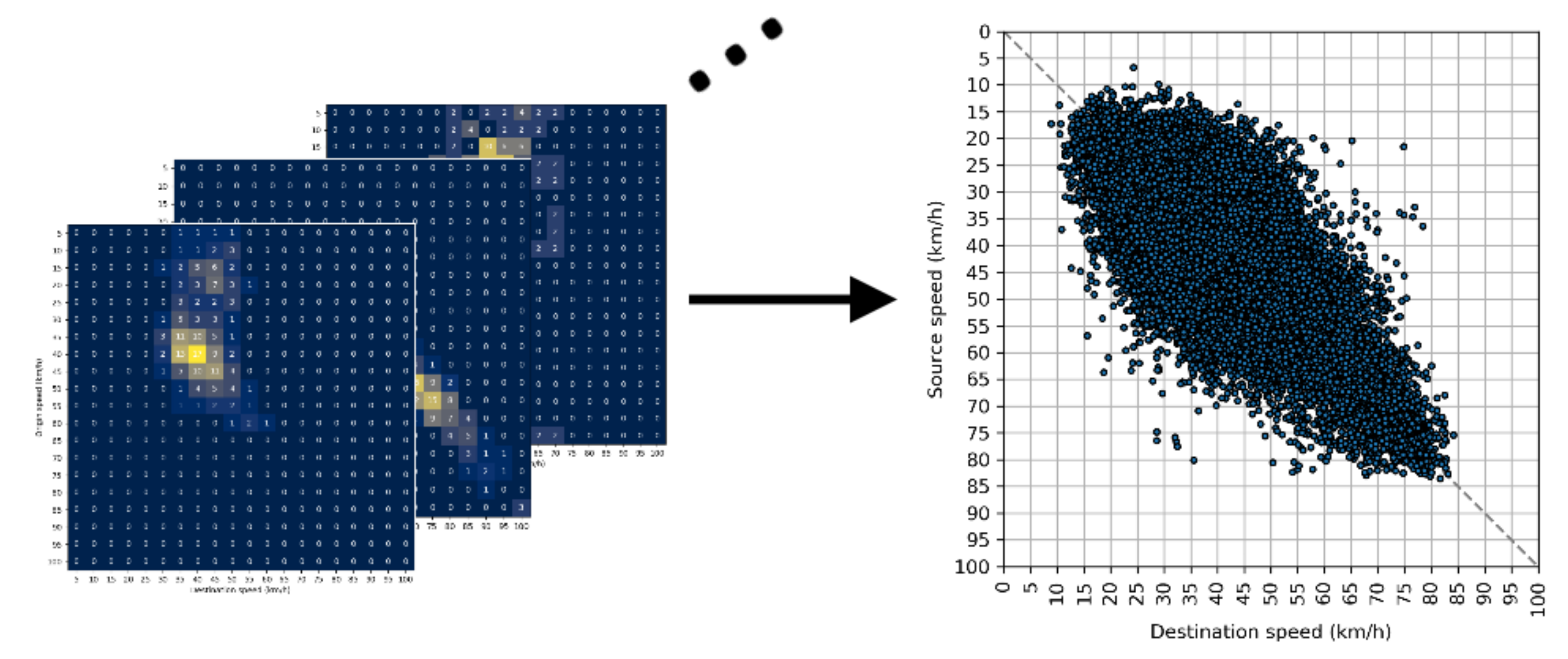
3.1. Speed Transition Matrix
3.2. Center of Mass Estimation
3.3. Clustering
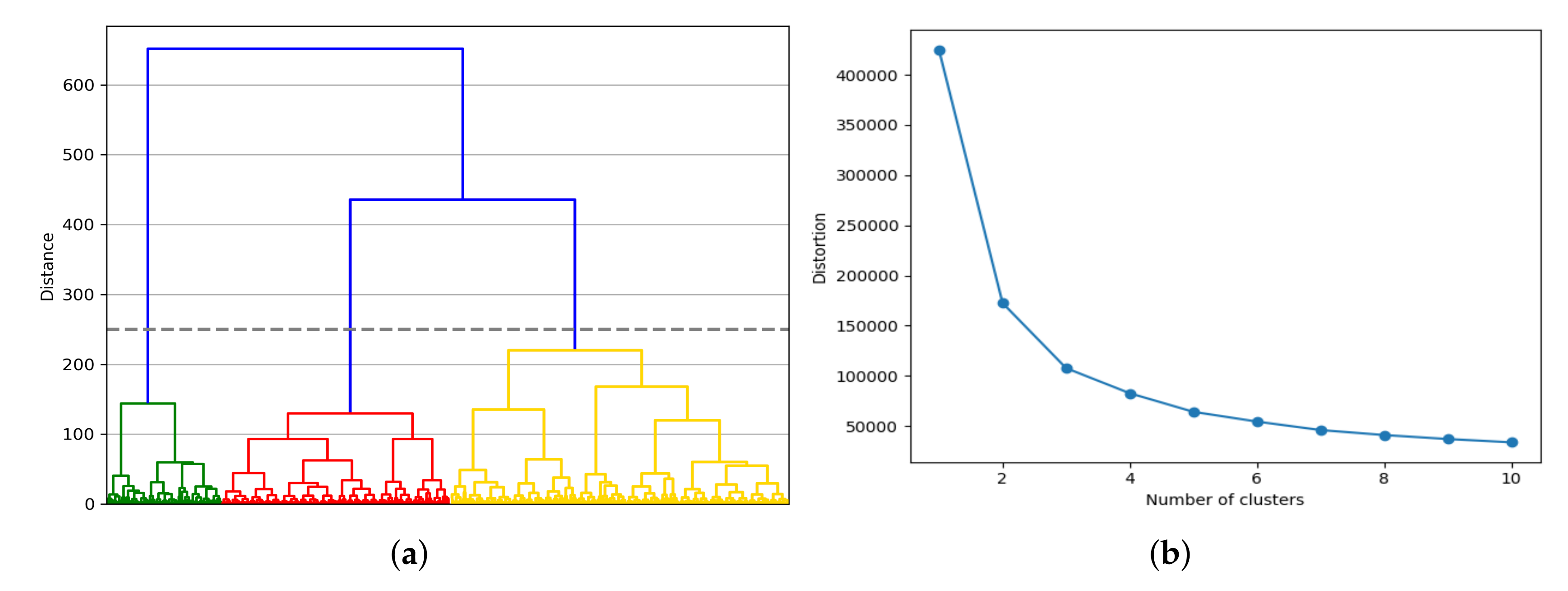
3.3.1. Agglomerative Clustering
3.3.2. Clustering Validation
4. Results
4.1. Data
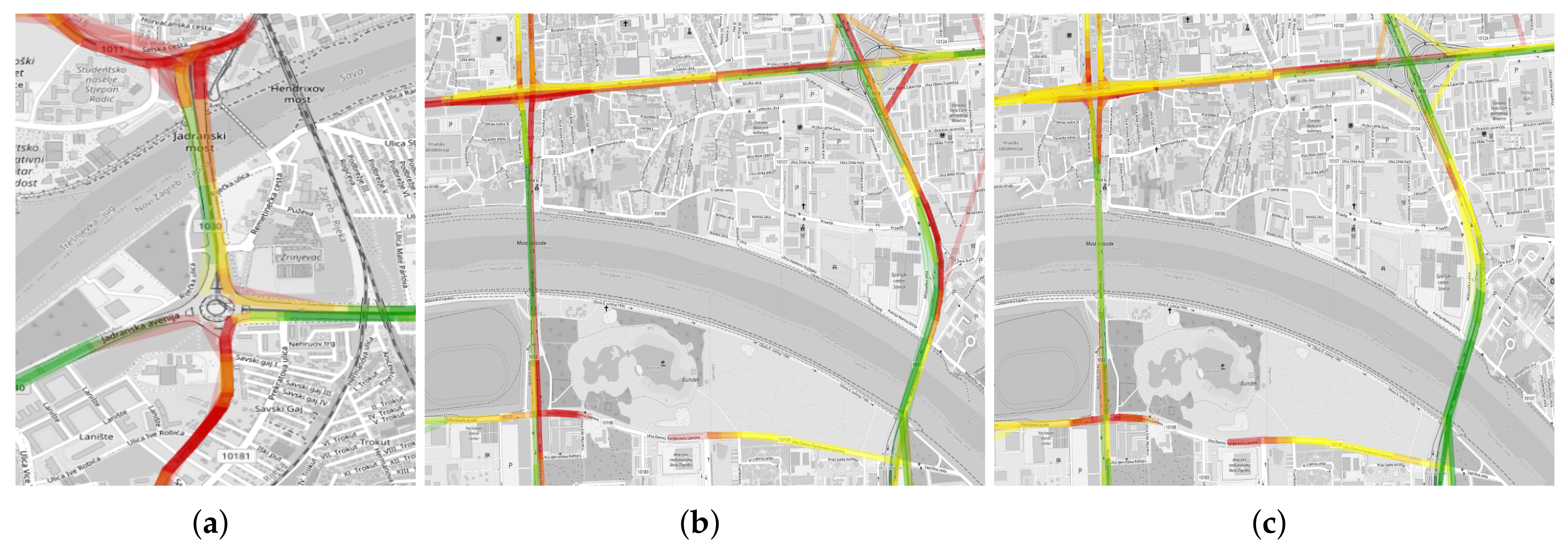
4.2. Traffic State Estimation
4.3. Validation Results
5. Discussion
5.1. Traffic State Estimation
5.2. Routing Applications
5.3. Anomaly Detection
6. Conclusions and Further Research
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gregurić, M.; Mandžuka, S.; Vidović, K. Advanced Applications for Urban Motorway Traffic Control. In Lecture Notes in Networks and Systems; Springer: Berlin/Heidelberg, Germany, 2020; Volume 76, pp. 395–400. [Google Scholar] [CrossRef]
- European Commission. Sustainable Urban Mobility: European Policy, Practice and Solutions. Available online: https://ec.europa.eu/transport/sites/transport/files/2017-sustainable-urban-mobility-european-policy-practice-and-solutions.pdf (accessed on 14 July 2020).
- Chow, A.H.; Santacreu, A.; Tsapakis, I.; Tanasaranond, G.; Cheng, T. Empirical assessment of urban traffic congestion. J. Adv. Transp. 2014, 48, 1000–1016. [Google Scholar] [CrossRef]
- Cambridge Systematics. Traffic Congestion and Reliability: Trends and Advanced Strategies for Congestion Mitigationt (Tech Report). Available online: https://rosap.ntl.bts.gov/view/dot/20656 (accessed on 15 July 2020).
- Servos, N.; Liu, X.; Teucke, M.; Freitag, M. Travel Time Prediction in a Multimodal Freight Transport Relation Using Machine Learning Algorithms. Logistics 2019, 4, 1. [Google Scholar] [CrossRef]
- Pun-Cheng, L.S.C. An Interactive Web-Based Public Transport Enquiry System With Real-Time Optimal Route Computation. IEEE Trans. Intell. Transp. Syst. 2012, 13, 983–988. [Google Scholar] [CrossRef]
- Ouyang, Q.; Lv, Y.; Ma, J.; Li, J. An LSTM-Based Method Considering History and Real-Time Data for Passenger Flow Prediction. Appl. Sci. 2020, 10, 3788. [Google Scholar] [CrossRef]
- Mandžuka, S.; Ivanjko, E.; Vujić, M.; Škorput, P.; Gregurić, M. The Use of Cooperative ITS in Urban Traffic Management. In Intelligent Transport Systems: Technologies and Applications; Wiley: Chichester, UK, 2016; pp. 361–381. [Google Scholar]
- Škrinjar, J.; Abramović, B.; Bukvić, L.; Marušić, Z. Managing Fuel Consumption and Emissions in the Renewed Fleet of a Transport Company. Sustainability 2020, 12, 5047. [Google Scholar] [CrossRef]
- Herrera, J.C.; Work, D.B.; Herring, R.; Ban, X.J.; Jacobson, Q.; Bayen, A.M. Evaluation of traffic data obtained via GPS-enabled mobile phones: The Mobile Century field experiment. Transp. Res. Part Emerg. Technol. 2010, 18, 568–583. [Google Scholar] [CrossRef]
- Herrera, J.C.; Bayen, A.M. Incorporation of Lagrangian measurements in freeway traffic state estimation. Transp. Res. Part B Methodol. 2010, 44, 460–481. [Google Scholar] [CrossRef]
- Kong, Q.; Zhao, Q.; Wei, C.; Liu, Y. Efficient Traffic State Estimation for Large-Scale Urban Road Networks. IEEE Trans. Intell. Transp. Syst. 2013, 14, 398–407. [Google Scholar] [CrossRef]
- Erdelić, M.; Carić, T.; Ivanjko, E.; Jelušić, N. Classification of travel modes using streaming GNSS data. In Transportation Research Procedia; Elsevier B.V.: Amsterdam, The Netherlands, 2019; Volume 40, pp. 209–216. [Google Scholar] [CrossRef]
- Rakha, H.; Tawfik, A. Traffic Networks: Dynamic Traffic Routing, Assignment, and Assessment. In Encyclopedia of Complexity and Systems Science; Meyers, R.A., Ed.; Springer: New York, NY, USA, 2009; pp. 9429–9470. [Google Scholar] [CrossRef]
- Wahle, J.; Annen, O.; Schuster, C.; Neubert, L.; Schreckenberg, M. A dynamic route guidance system based on real traffic data. Eur. J. Oper. Res. 2001, 131, 302–308. [Google Scholar] [CrossRef]
- Juhász, J. Influence of Different Route-choice Decision Modes. Transp. Res. Procedia 2017, 27, 246–252. [Google Scholar] [CrossRef]
- Erdelić, T.; Ravlić, M.; Carić, T. Travel time prediction using speed profiles for road network of Croatia. In Proceedings of the 2016 International Symposium ELMAR, Zadar, Croatia, 12–14 September 2016; pp. 97–100. [Google Scholar] [CrossRef]
- Ma, X.; Dai, Z.; He, Z.; Ma, J.; Wang, Y.; Wang, Y. Learning traffic as images: A deep convolutional neural network for large-scale transportation network speed prediction. Sensors 2017, 17, 818. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, H.; Liu, W.; Chen, F. Discovering Congestion Propagation Patterns in Spatio-Temporal Traffic Data. IEEE Trans. Big Data 2017, 3, 169–180. [Google Scholar] [CrossRef]
- Afrin, T.; Yodo, N. A Survey of Road Traffic Congestion Measures towards a Sustainable and Resilient Transportation System. Sustainability 2020, 12, 4660. [Google Scholar] [CrossRef]
- Rao, M.; Rao, K.R. Measuring Urban Traffic Congestion—A Review. Int. J. Traffic Transp. Eng. 2012, 2, 286–305. [Google Scholar] [CrossRef]
- Liu, X.; Liu, X.; Wang, Y.; Pu, J.; Zhang, X. Detecting Anomaly in Traffic Flow from Road Similarity Analysis. In Web-Age Information Management; Cui, B., Zhang, N., Xu, J., Lian, X., Liu, D., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 92–104. [Google Scholar] [CrossRef]
- Kerner, B. Empirical macroscopic features of spatial-temporal traffic patterns at highway bottlenecks. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2002, 65, 046138. [Google Scholar] [CrossRef]
- Kerner, B.S.; Rehborn, H.; Aleksic, M.; Haug, A. Recognition and tracking of spatial–temporal congested traffic patterns on freeways. Transp. Res. Part C Emerg. Technol. 2004, 12, 369–400. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Krishnakumari, P.; Calvert, S.C.; Vu, H.L.; van Lint, H. Feature extraction and clustering analysis of highway congestion. Transp. Res. Part C Emerg. Technol. 2019, 100, 238–258. [Google Scholar] [CrossRef]
- Kim, J.; Mahmassani, H.S. Spatial and temporal characterization of travel patterns in a traffic network using vehicle trajectories. Transp. Res. Part C Emerg. Technol. 2015, 59, 375–390. [Google Scholar] [CrossRef]
- Thianniwet, T.; Phosaard, S.; Pattara-Atikom, W. Classification of Road Traffic Congestion Levels from GPS Data using a Decision Tree Algorithm and Sliding Windows. In Proceedings of the World Congress on Engineering (WCE), London, UK, 1–3 July 2009; pp. 1–5. [Google Scholar]
- Jin, X.; Srinivasan, D.; Cheu, R.L. Classification of freeway traffic patterns for incident detection using constructive probabilistic neural networks. IEEE Trans. Neural Netw. 2001, 12, 1173–1187. [Google Scholar] [CrossRef]
- Kan, Z.; Tang, L.; Kwan, M.P.; Ren, C.; Liu, D.; Li, Q. Traffic congestion analysis at the turn level using Taxis’ GPS trajectory data. Comput. Environ. Urban Syst. 2019, 74, 229–243. [Google Scholar] [CrossRef]
- Keler, A.; Ding, L.; Krisp, J. Visualization of traffic congestion based on Floating Taxi Data. Kartographische Nachrichten 2016, 66, 7–13. [Google Scholar] [CrossRef]
- Jordaan, I.J. Decisions under Uncertainty: Probabilistic Analysis for Engineering Decisions; Cambridge University Press: Cambridge, UK, 2005; pp. 127–144. [Google Scholar] [CrossRef]
- Nguyen, H.N.; Krishnakumari, P.; Vu, H.L.; van Lint, H. Traffic Congestion pattern classification using multi-class SVM. In Proceedings of the 2016 IEEE 19th International Conference on Intelligent Transportation Systems (ITSC), Rio de Janeiro, Brazil, 1–4 November 2016; pp. 1059–1064. [Google Scholar] [CrossRef]
- HCM2010. Highway Capacity Manual; Transportation Research Board, National Research Council: Washington, DC, USA, 2010. [Google Scholar]
- Carić, T.; Erdelić, T.; Fosin, J.; Matulin, M.; Erdelić, M.; Rožić, L.; Milošević, A. Technical Report of Project SORDITO; Technical Report; Faculty of Transport and Traffic Sciences: Zagreb, Croatia, 2016. [Google Scholar]
- Żochowska, R.; Karoń, G. ITS Services Packages as a Tool for Managing Traffic Congestion in Cities. In Intelligent Transportation Systems—Problems and Perspectives; Sładkowski, A., Pamuła, W., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 81–103. [Google Scholar] [CrossRef]
- Carić, T.; Fosin, J. Using Congestion Zones for Solving the Time Dependent Vehicle Routing Problem. Promet-Traffic Transp. 2020, 32, 25–38. [Google Scholar] [CrossRef]
| Free Flow | Stable Flow | Congestion | |
|---|---|---|---|
| 22:00–05:30 | 28.31% | 54.15% | 17.54% |
| 05:30–06:45 | 27.38% | 53.55% | 19.08% |
| 06:45–07:25 | 19.08% | 42.83% | 38.10% |
| 07:25–08:20 | 13.97% | 32.53% | 53.50% |
| 08:20–15:30 | 12.09% | 33.86% | 54.05% |
| 15:30–17:05 | 13.05% | 35.46% | 51.04% |
| 17:05–19:00 | 15.53% | 40.59% | 43.88% |
| 19:00–22:00 | 19.77% | 46.33% | 33.90% |
| Precision | Recall | F1 Score | |
|---|---|---|---|
| Free flow | 1.00 | 0.84 | 0.91 |
| Stable flow | 0.93 | 1.00 | 0.97 |
| Congestion | 1.00 | 1.00 | 1.00 |
| Accuracy | 0.97 |
| Predicted | Free Flow | Stable Flow | Congestion | |
|---|---|---|---|---|
| Known | ||||
| Free flow | 0.841 | 0.159 | 0 | |
| Stable flow | 0 | 1.000 | 0 | |
| Congestion | 0 | 0.003 | 0.997 | |
| Precision | Recall | F1 Score | |
|---|---|---|---|
| Free flow | 0.99 | 0.95 | 0.97 |
| Stable flow | 0.83 | 1.00 | 0.90 |
| Congestion | 1.00 | 0.81 | 0.89 |
| Accuracy | 0.91 |
| Predicted | Free Flow | Stable Flow | Congestion | |
|---|---|---|---|---|
| Known | ||||
| Free flow | 0.954 | 0.046 | 0 | |
| Stable flow | 0.004 | 0.996 | 0 | |
| Congestion | 0 | 0.191 | 0.809 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tišljarić, L.; Carić, T.; Abramović, B.; Fratrović, T. Traffic State Estimation and Classification on Citywide Scale Using Speed Transition Matrices. Sustainability 2020, 12, 7278. https://doi.org/10.3390/su12187278
Tišljarić L, Carić T, Abramović B, Fratrović T. Traffic State Estimation and Classification on Citywide Scale Using Speed Transition Matrices. Sustainability. 2020; 12(18):7278. https://doi.org/10.3390/su12187278
Chicago/Turabian StyleTišljarić, Leo, Tonči Carić, Borna Abramović, and Tomislav Fratrović. 2020. "Traffic State Estimation and Classification on Citywide Scale Using Speed Transition Matrices" Sustainability 12, no. 18: 7278. https://doi.org/10.3390/su12187278
APA StyleTišljarić, L., Carić, T., Abramović, B., & Fratrović, T. (2020). Traffic State Estimation and Classification on Citywide Scale Using Speed Transition Matrices. Sustainability, 12(18), 7278. https://doi.org/10.3390/su12187278







