Development of Driving Cycle Construction for Hybrid Electric Bus: A Case Study in Zhengzhou, China
Abstract
1. Introduction
2. The HEB Original Driving Data Acquisition
2.1. The Selection of Test Route and Test HEB
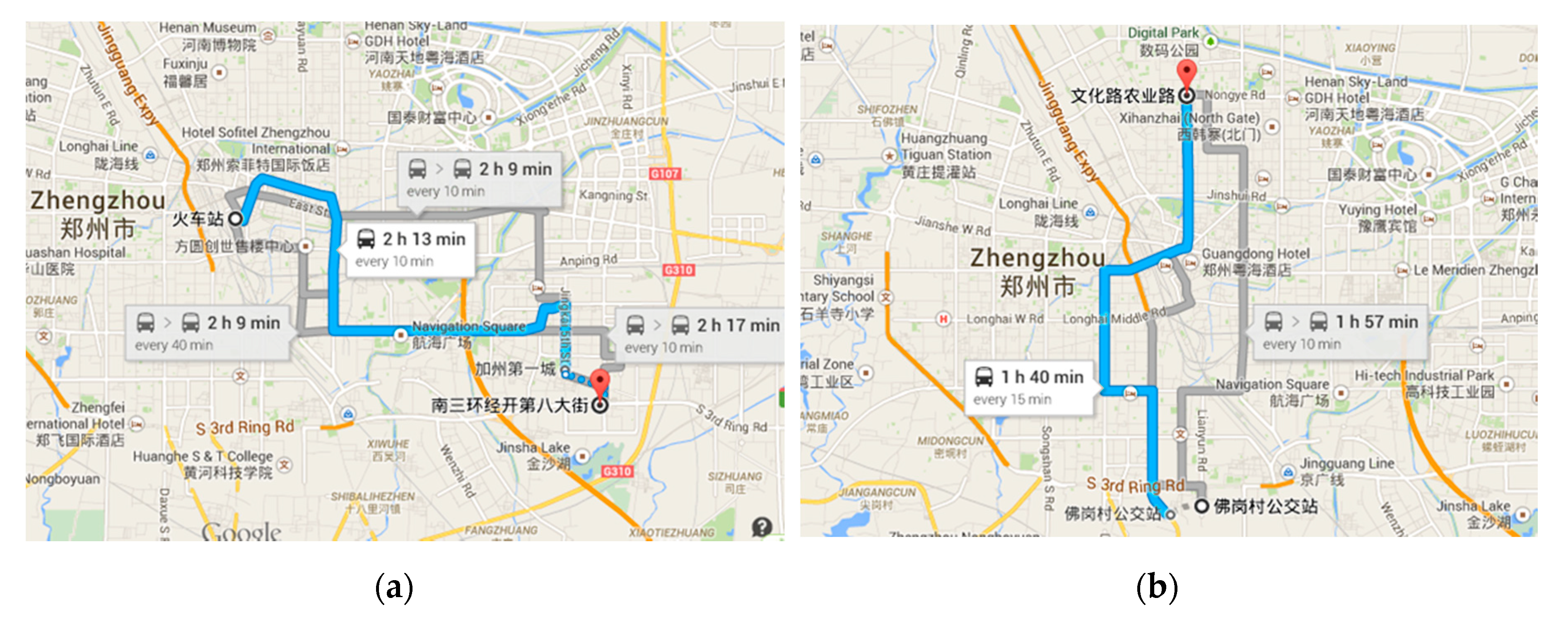
2.1.1. Test Route Selection
- Hybrid electric bus is the only choice to drive on the test route.
- The test route should include both traditional and rapid bus routes.Bus rapid transit (BRT) is a new type of public transport system running between the railway and traditional bus transportation. BRT uses the special bus route to achieve rail transit mode operation, and it has been applied widely in China. The driving states of buses in the BRT routes are totally different from those in the traditional bus routes. Therefore, the construction of an urban driving cycle which fuses traditional bus route and rapid bus route is consistent with the actual operation situation of Chinese urban buses.
- The selected bus route should cover congested and fluent urban regions.
2.1.2. Test Bus Selection
2.2. The Driving Data Acquisition System
2.2.1. Velocity and Acceleration Measurement
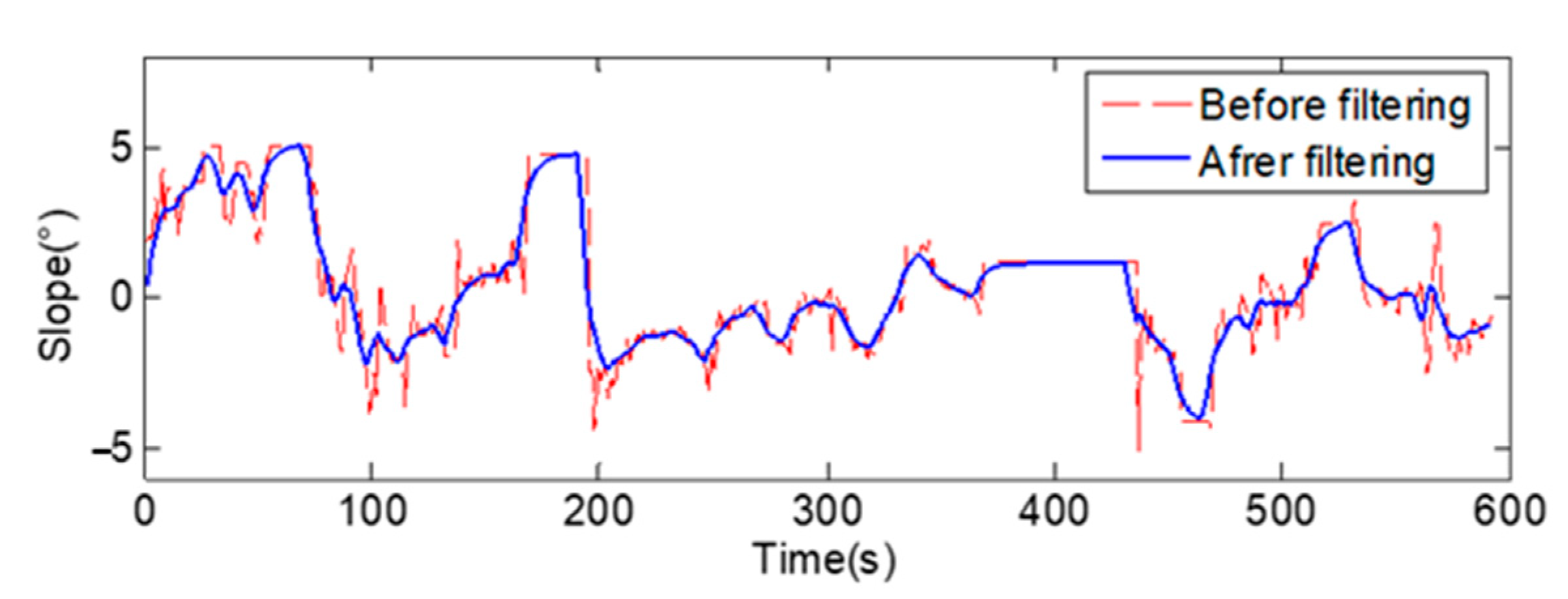
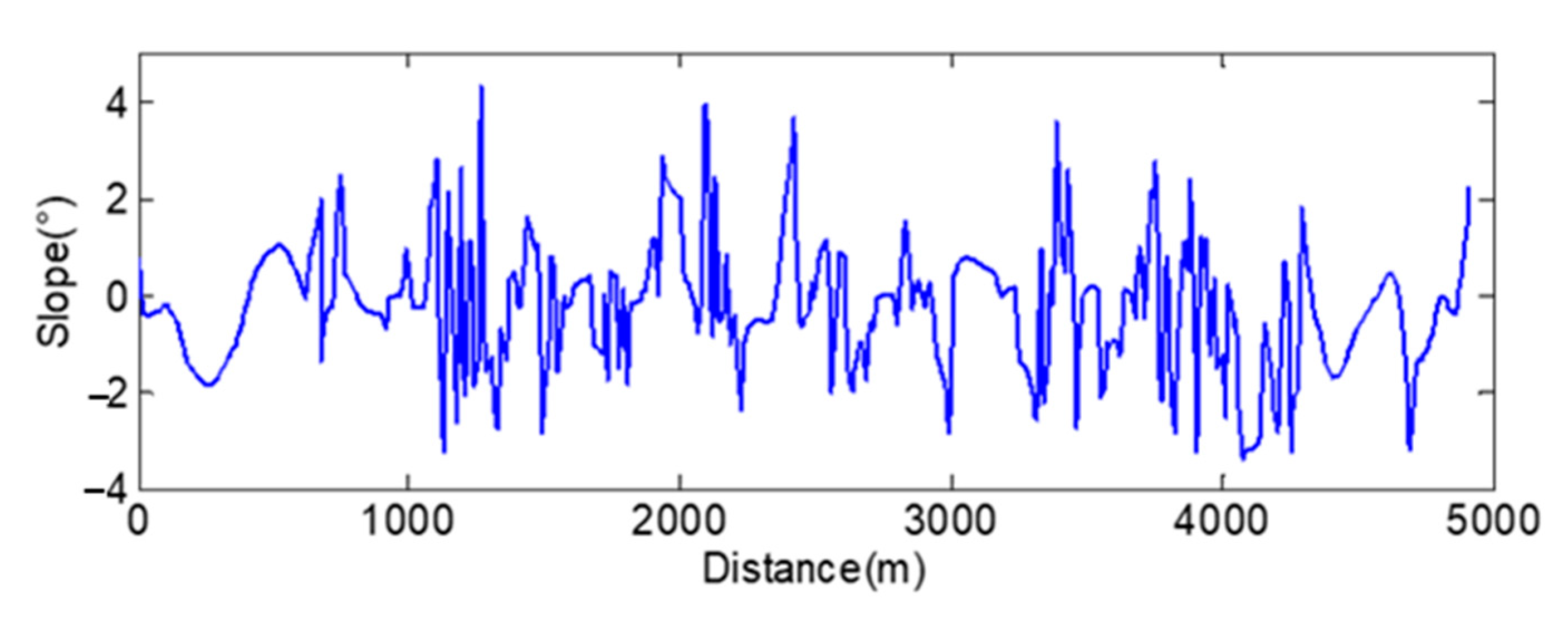
2.2.2. Road Slope Estimation
- Primarily, eliminate slope calculated values with low velocity to avoid the denominator of Equation (1) being close to 0.
- Carry out filtering. If the calculated slope values are higher than 9% [25], then replace them with those of the previous sampling time.
- Perform average filtering against the processed slope values to smooth out the sawtooth signals.
3. Original Data Preprocessing
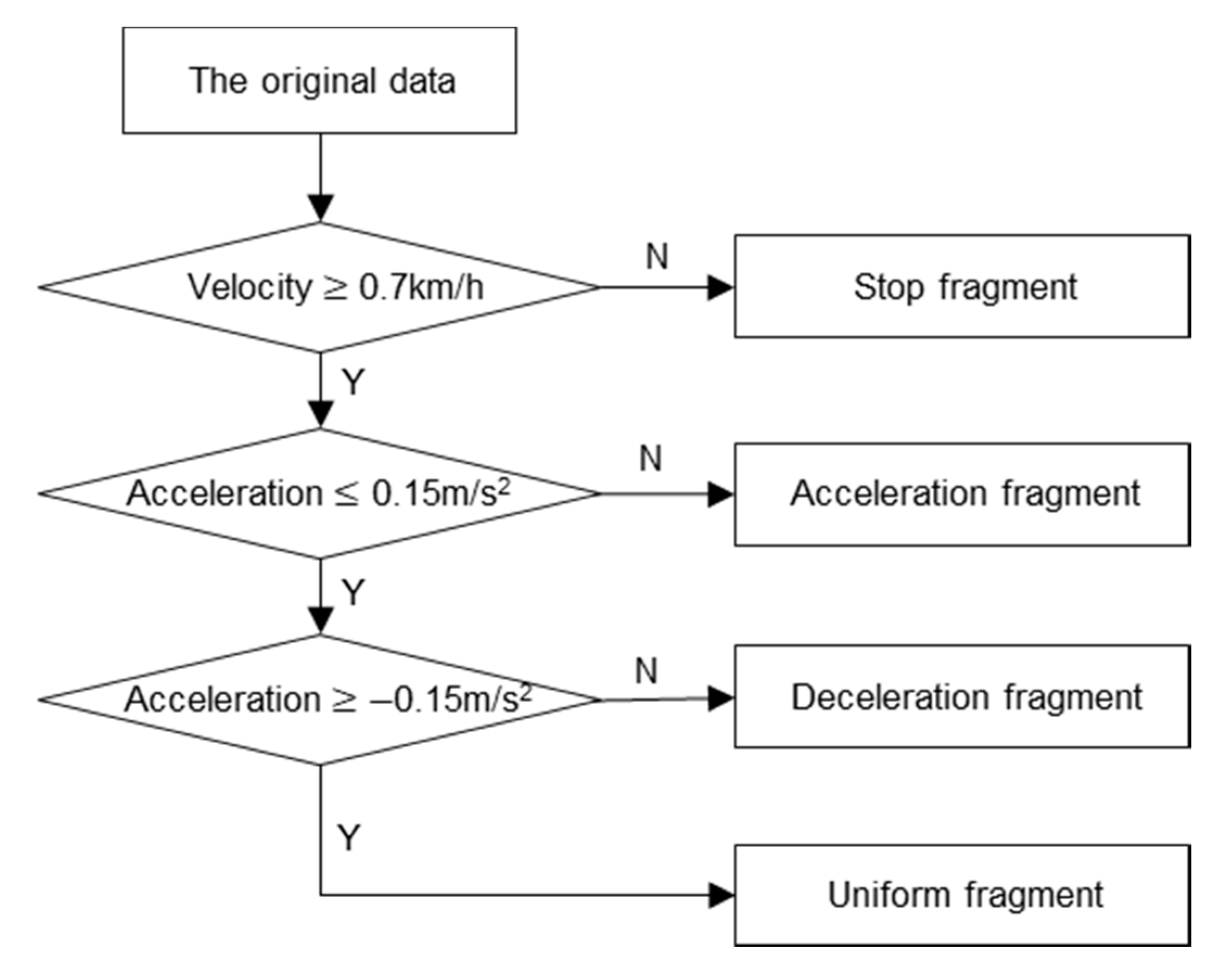
3.1. Velocity Fragment Division
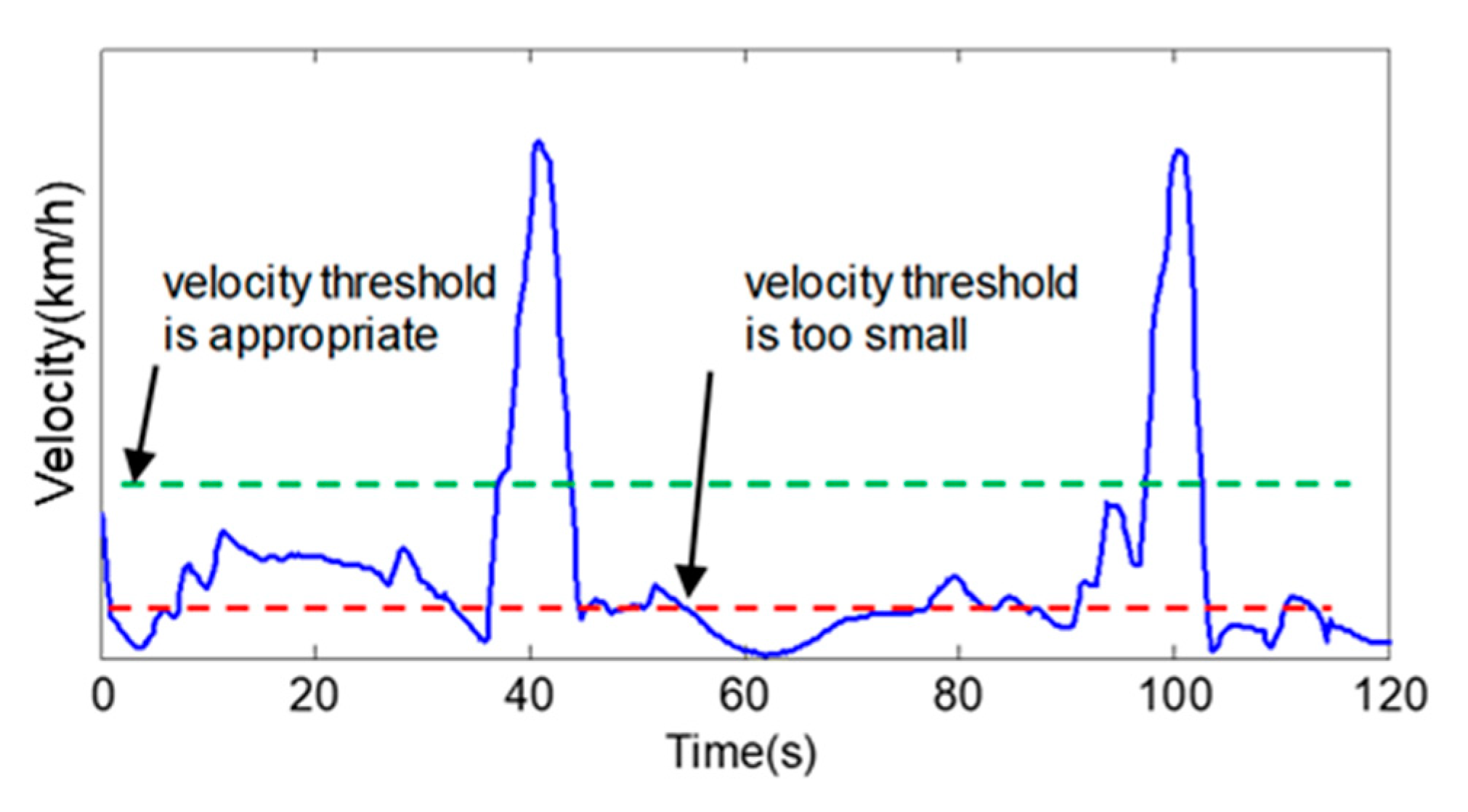
3.1.1. Velocity Threshold Determination
3.1.2. Acceleration Threshold Determination
3.1.3. Basis of Velocity Fragment Division
3.2. Fragement State Cluster Distribution
3.2.1. Calculation of Required Power and Nominal Velocity
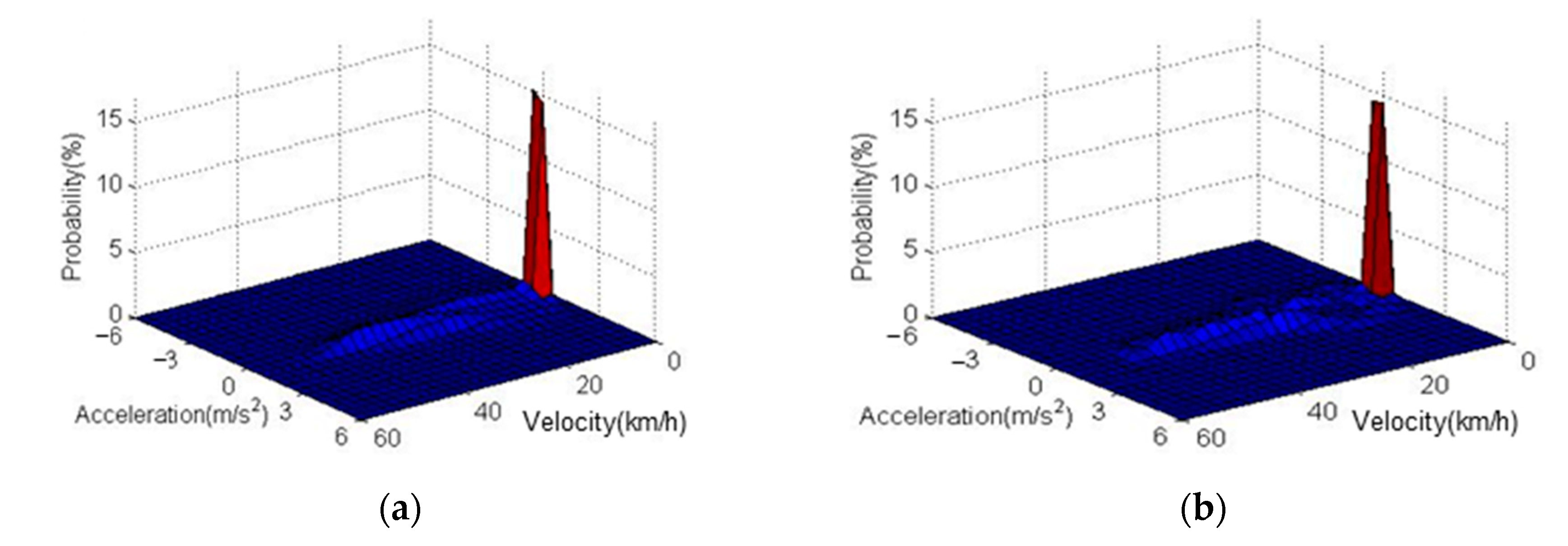
3.2.2. State Cluster Distribution
3.3. Calculation of the Markov Transfer Matrix
3.4. The Statistical Anlysis of Original Data
3.4.1. Characteristic Parameter Matrix of Original Data
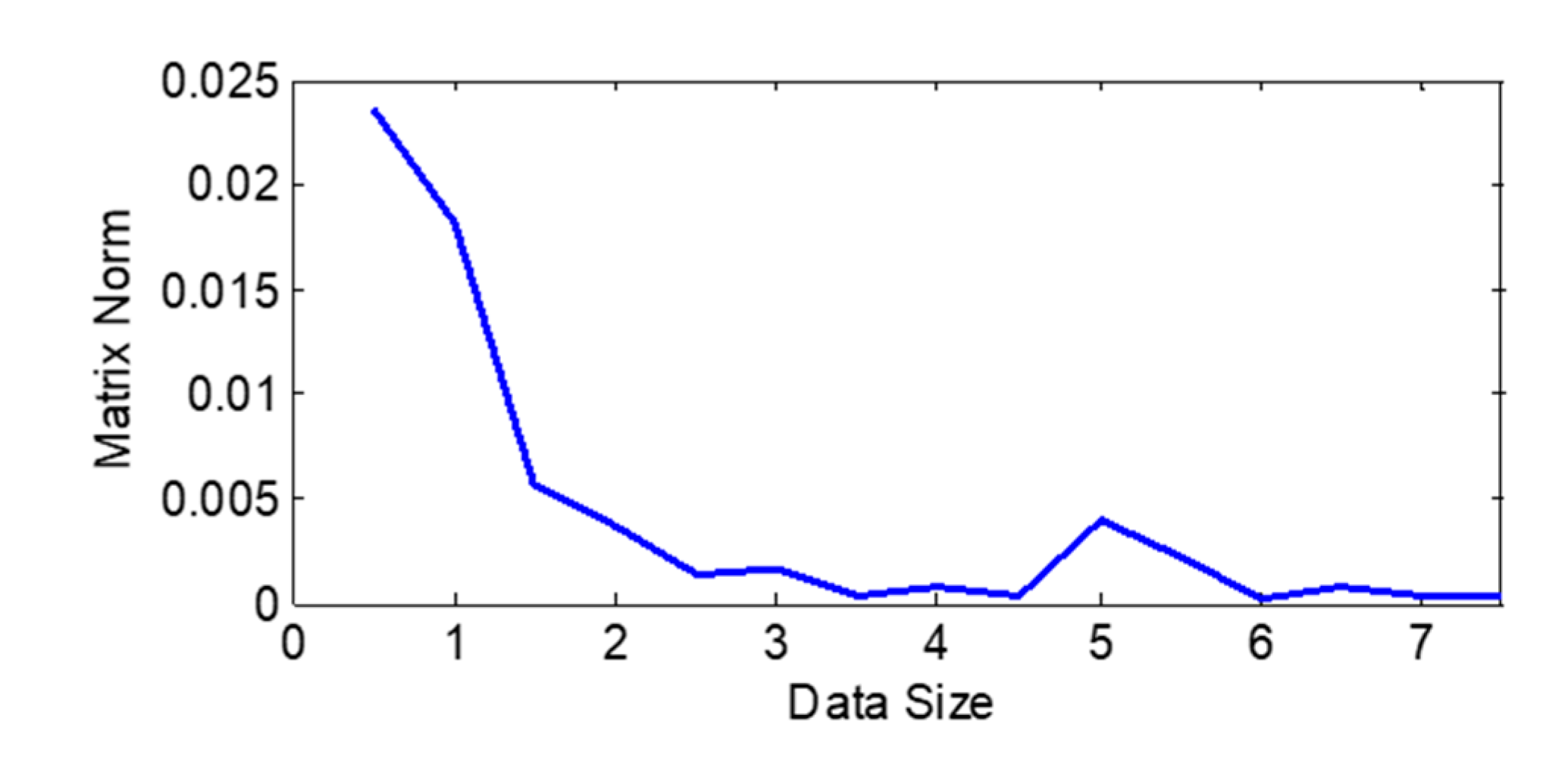
3.4.2. Calculation of PM Value
- Count the characteristic parameters of driving cycle candidates n and construct the n × 16 matrix M.
- Obtain the absolute differentiating value matrix pm through each row of matrix M minus the original characteristic M0:
- Normalize pm. Normalization is necessary for totally different parameter ranges, which can be deduced aswhere pmimax is the maximum value of the matrix pm’s ith column, while pmimin is the minimum one.
- Sum the elements in the kth row in the matrix PM(k,i) to obtain the PM value of the driving cycle.
3.4.3. Sufficient Proof of the Original Data
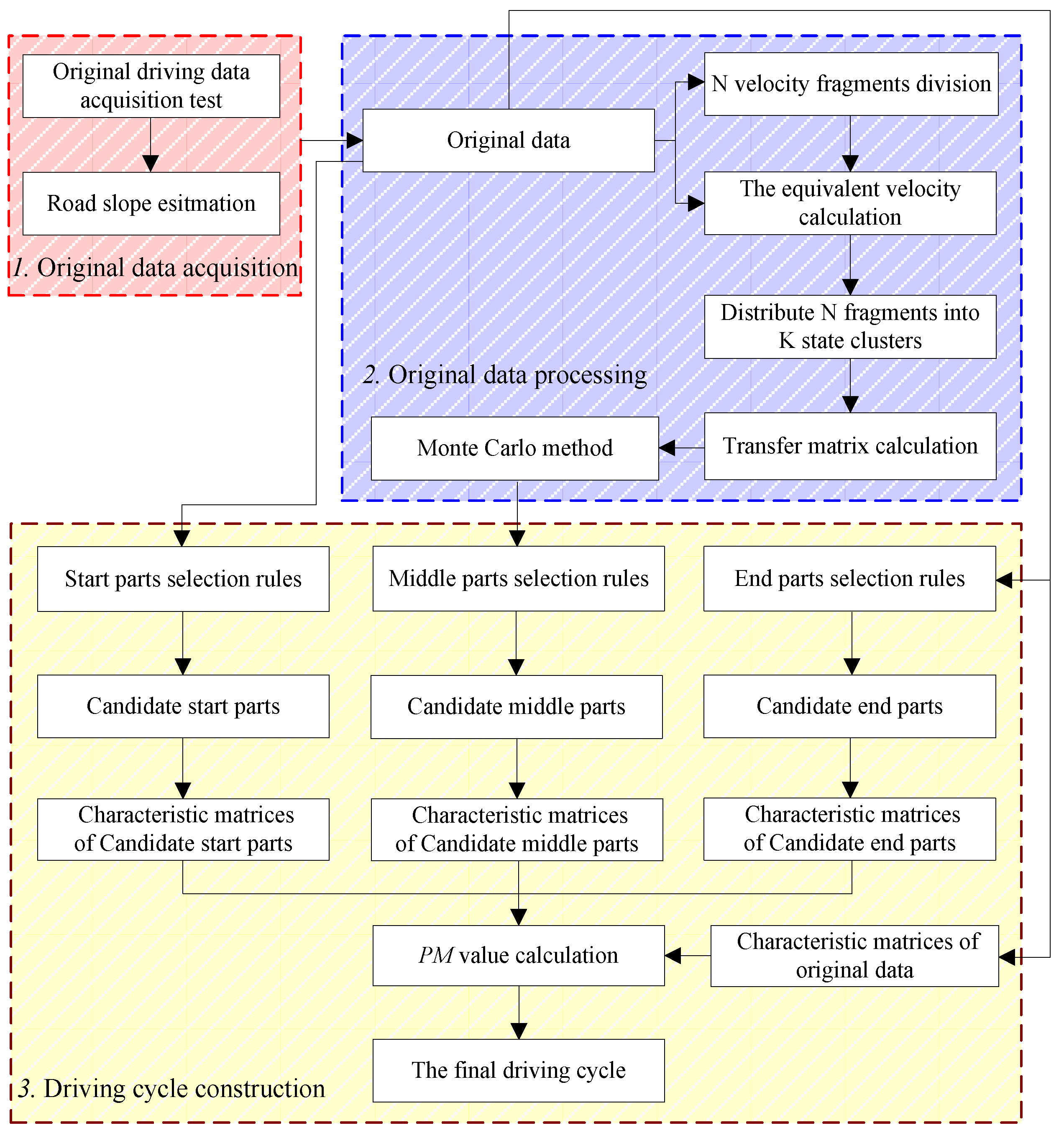
4. Driving Cycle Construction
4.1. Construction of Start Part
4.2. Construction of Middle Part
- Confirm the current state cluster and the transfer probability, which are determined according to the Markov transfer matrix T.
- Generate a random number r in the interval of (0, 1), if r meets the in-equation as follows:Then, the next state cluster of velocity fragment is q.
- Determine the velocity fragments whose velocity differences in current and next state clusters are below 0.5 km/h. The one which has the minimum velocity difference will be the next determined velocity fragment.
- The sampling points which are used in the start part construction will not be used in the middle part construction, and 10 middle part candidates are constructed for optimal selection.
4.3. Construction of End Part
- The velocity of the sampling points that are 10 s prior to the checkpoint is above velocity threshold 0.7 km/h.
- The velocity sampling points which are 5 s later than the checkpoint are below the velocity threshold 0.7 km/h.
- If both the above conditions are met, set the checkpoint at the time t, then the sampling points in the time interval of (t − 114, t + 5) will be chosen as the end part candidates.
- Check all sampling points in the first 60 s of every end part candidate, determine 10 whose velocities in sampling points are closest to the terminal velocity of the constructed middle part, and then set these points as the start times of the 10 end part candidates.
4.4. Construction of Driving Cycle
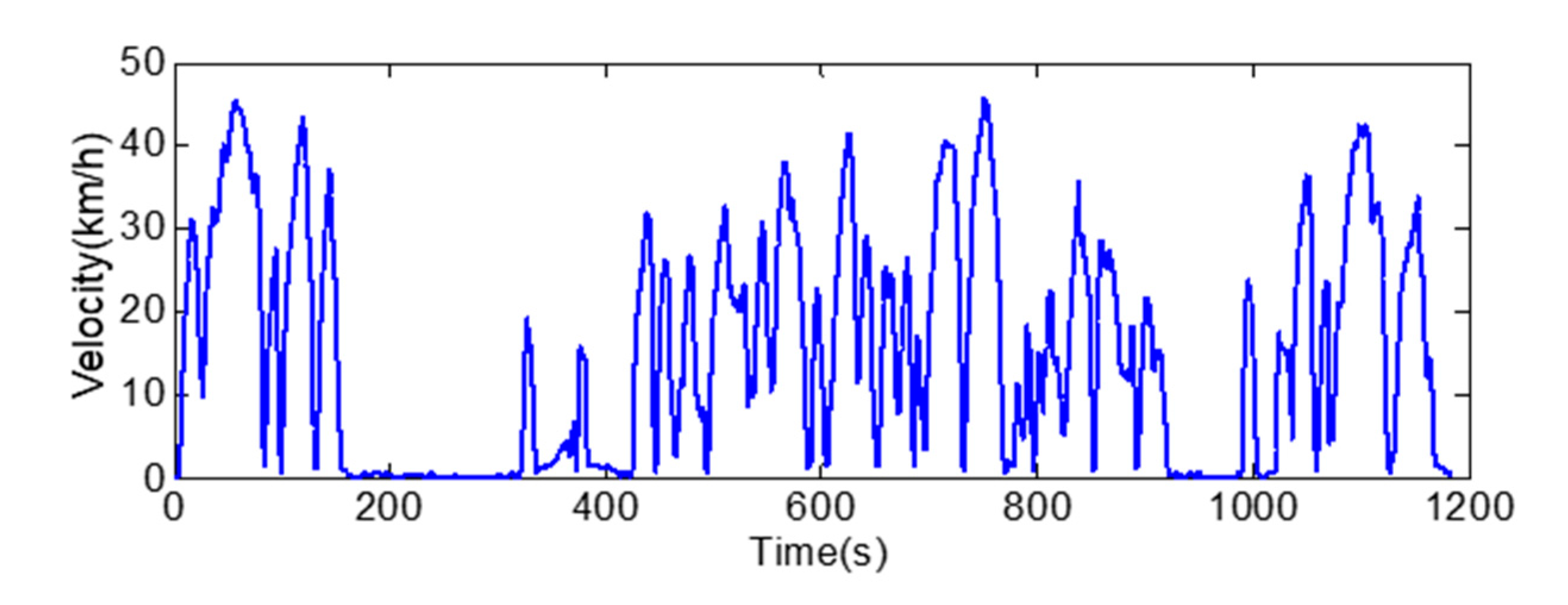
5. Validation of ZZUDC as a Driving Cycle
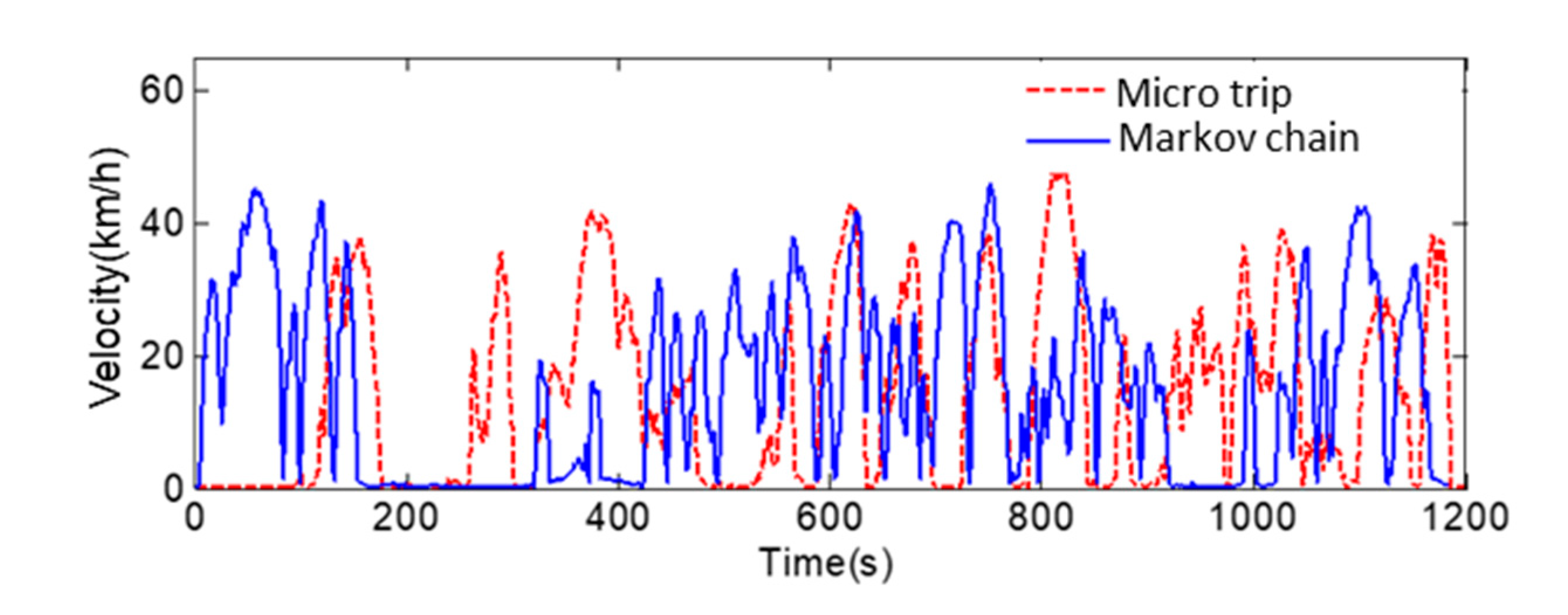
5.1. Comparison between the Driving Cycles Based on Markov and Traditional Micro-Trip
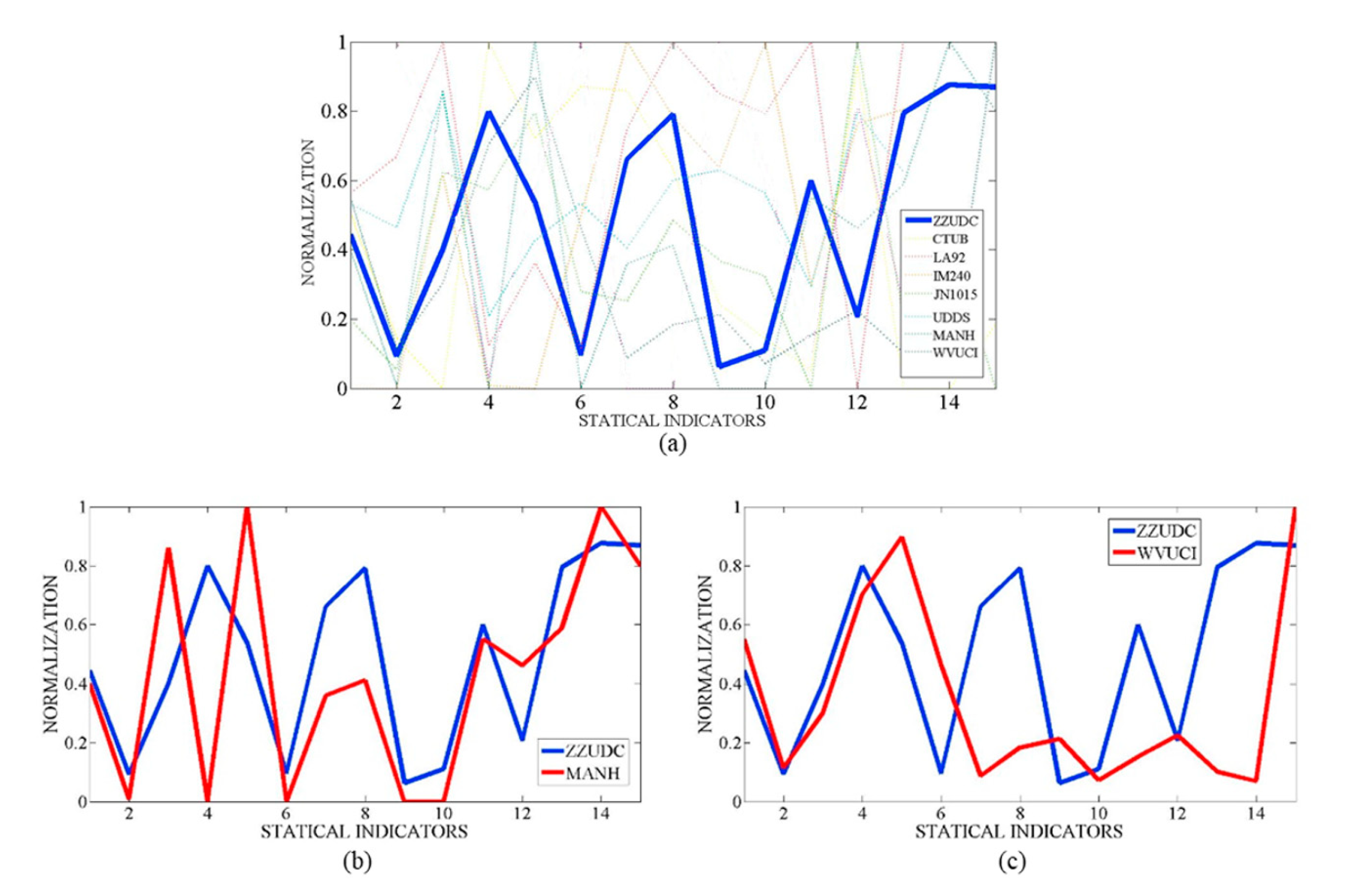
5.2. Comparison between ZZUDC and Other International Cycles
5.2.1. Dynamic Programming
5.2.2. Comparison between the Statistical Characters of Various Driving Cycles
5.3. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Li, L.; Yang, C.; Zhang, Y.; Zhang, L.; Song, J. Correctional DP-based energy management strategy of plug-in hybrid electric bus for city-bus route. IEEE Trans. Veh. Technol. 2014, 64, 2792–2803. [Google Scholar] [CrossRef]
- Nesamani, K.S.; Subramanian, K.P. Development of a driving cycle for intra-city buses in Chennai, India. Atmos. Environ. 2011, 45, 5469–5476. [Google Scholar] [CrossRef]
- Ho, S.H.; Wong, Y.D.; Chang, V.W.C. Developing Singapore Driving Cycle for passenger cars to estimate fuel consumption and vehicular emissions. Atmos. Environ. 2014, 97, 353–362. [Google Scholar] [CrossRef]
- Lien, N.T.Y.; Dung, N.T. The determination of driving characteristics of Hanoi bus system and their impacts on the emission. Vietnam. J. Sci. Technol. 2017, 55, 74. [Google Scholar] [CrossRef]
- Yu, L.; Wang, Z.; Qiao, F.; Qi, Y. Approach to development and evaluation of driving cycles for classified roads based on vehicle emission characteristics. Transp. Res. Rec. 2008, 2058, 58–67. [Google Scholar] [CrossRef]
- André, M. The ARTEMIS European driving cycles for measuring car pollutant emissions. Sci. Total Environ. 2004, 334–335, 73–84. [Google Scholar] [CrossRef]
- Lee, C.P. Development of Driving Cycles for Characterizing Vehicular Emission Factors; Hong Kong Polytechnic University: Hong Kong, China, 2006. [Google Scholar]
- Jiang, P.; Shi, Q.; Chen, W.; Huang, Z.A. A research on the construction of city road driving cycle based on wavelet analysis. Automot. Eng. 2011, 69–70. [Google Scholar]
- Berzi, L.; Delogu, M.; Pierini, M. Development of driving cycles for electric vehicles in the context of the city of Florence. Transp. Res. Part. D Transp. Environ. 2016, 47, 299–322. [Google Scholar] [CrossRef]
- Li, Y.; He, H.; Peng, J. An adaptive online prediction method with variable prediction horizon for future driving cycle of the vehicle. IEEE Access 2018, 6, 33062–33075. [Google Scholar] [CrossRef]
- Shi, S.; Lin, N.; Zhang, Y.; Cheng, J.; Huang, C.; Liu, L.; Lu, B. Research on Markov property analysis of driving cycles and its application. Transp. Res. Part. D Transp. Environ. 2016, 47, 171–181. [Google Scholar] [CrossRef]
- Lin, J. A Markov Process Approach to Driving Cycle Development; University of California, Davis: Davis, CA, USA, 2020. [Google Scholar]
- Lee, T.K.; Adornato, B.; Filipi, Z.S. Synthesis of real-world driving cycles and their use for estimating PHEV energy consumption and charging opportunities: Case study for midwest/U.S. IEEE Trans. Veh. Technol. 2011, 60, 4153–4163. [Google Scholar] [CrossRef]
- Lee, T.C.; Judge, G.G.; Zellner, A. Estimating the Parameters of the Markov Probability Model from Aggregate Time Series Data; North-Holland: Amsterdam, The Netherlands, 1970. [Google Scholar]
- Liu, L.; Huang, C.; Lu, B.; Shi, S.; Zhang, Y.; Cheng, J. Study on the design method of time-variant driving cycles for EV based on Markov Process. In Proceedings of the 2012 IEEE Vehicle Power and Propulsion Conference, Seoul, Korea, 9–12 October 2012; pp. 1277–1281. [Google Scholar]
- Zhang, M.; Shi, S.; Lin, N.; Yue, B. High-efficiency driving cycle generation using a Markov chain evolution algorithm. IEEE Trans. Veh. Technol. 2018, 68, 1288–1301. [Google Scholar] [CrossRef]
- Fontaras, G.; Franco, V.; Dilara, P.; Martini, G.; Manfredi, U. Development and review of Euro 5 passenger car emission factors based on experimental results over various driving cycles. Sci. Total. Environ. 2014, 468–469, 1034–1042. [Google Scholar] [CrossRef] [PubMed]
- Lin, J.; Niemeier, D.A. Estimating regional air quality vehicle emission inventories: Constructing robust driving cycles. Transp. Sci. 2003, 37, 330–346. [Google Scholar] [CrossRef][Green Version]
- Pang, W.K.; Yang, Z.H.; Hou, S.H.; Leung, P.K. Non-uniform random variate generation by the vertical strip method. Eur. J. Oper. Res. 2002, 142, 595–609. [Google Scholar] [CrossRef]
- Eisinger, D.S.; Niemeier, D.A.; Stoeckenius, T.; Kear, T.P.; Brady, M.J.; Pollack, A.K.; Long, J. Collecting Driving Data to Support Mobile Source Emissions Estimation. J. Transp. Eng. 2006, 132, 845–854. [Google Scholar] [CrossRef]
- Esteves-Booth, A.; Muneer, T.; Kirby, H.; Kubie, J.; Hunter, J. The measurement of vehicular driving cycle within the city of Edinburgh. Transp. Res. Part. D Transp. Environ. 2001, 6, 209–220. [Google Scholar] [CrossRef]
- Wirasingha, S.G.; Emadi, A. Classification and review of control strategies for plug-in hybrid electric vehicles. IEEE Trans. Veh. Technol. 2010, 60, 111–122. [Google Scholar] [CrossRef]
- Shen, P.; Zhao, Z.; Li, J.; Zhan, X. Development of a typical driving cycle for an intra-city hybrid electric bus with a fixed route. Transp. Res. Part. D Transp. Env. 2018, 59, 346–360. [Google Scholar] [CrossRef]
- He, K.; Zhu, Z.F. Code for Design of Urban Road Engineering. China Architecture & Building Press: Beijing, China, 2012. [Google Scholar]
- Abou-Nasr, M.; Michelini, J.; Filev, D. Real World Data Mining Applications; Springer International Publishing: Cham, Switzerland, 2015; pp. 343–358. [Google Scholar]
- Hung, W.T.; Tong, H.Y.; Lee, C.P.; Ha, K.; Pao, L.Y. Development of a practical driving cycle construction methodology: A case study in Hong Kong. Transp. Res. Part. D Transp. Environ. 2007, 12, 115–128. [Google Scholar] [CrossRef]
- Fotouhi, A.; Montazeri-Gh, M. Tehran driving cycle development using the k-means clustering method. Sci. Iran. 2013, 20, 286–293. [Google Scholar]
- Peng, J.; Fan, H.; He, H.; Pan, D. A Rule-Based Energy Management Strategy for a Plug-in Hybrid School Bus Based on a Controller Area Network Bus. Energies 2015, 8, 5122–5142. [Google Scholar] [CrossRef]
- Peng, J.; He, H.; Xiong, R. Rule based energy management strategy for a series—Parallel plug-in hybrid electric bus optimized by dynamic programming. Appl. Energy 2017, 185, 1633–1643. [Google Scholar] [CrossRef]
| State 1 | State 2 | State 3 | State 4 | State 5 | State 6 | State 7 | Total | |
|---|---|---|---|---|---|---|---|---|
| State 1 | 7430 | 1878 | 508 | 167 | 14 | 0 | 0 | 9997 |
| Probability | 0.7432 | 0.1879 | 0.0508 | 0.0167 | 0.0014 | 0 | 0 | 1 |
| … | ||||||||
| Probability |
| Route | B17 | 906 |
|---|---|---|
| Single transit operation distance | 15 km | 21 km |
| Bus stops | 27 | 36 |
| Single transit operation time | 2.5–3 h | 3.5–4 h |
| Test acquisition time | 7:00–9:00; 10:00–12:00; 16:00–18:00 | 7:00–11:00; 14:00–18:00 |
| Parameters | Values | Parameters | Values |
|---|---|---|---|
| Length | 12.0 m | Engine displacement | 6494 mL |
| Width | 2.55 m | Engine rated power | 155/2500 kW/rpm |
| Height | 3.05 m | Traction motor rated power | 95/1800 kW/rpm |
| Wheel base | 6.10 m | Maximum velocity | 85 km/h |
| Outfit quality | 12,400 kg | Capacity of power battery packs | 72 Ah |
| Velocity (km/h) | 0–0.4 | 0.4–0.7 | 0.7–1 | 1–1.5 | 1.5–2 | 2–2.5 | 2.5–3 | 3–3.5 | 3.5–4 |
| Probability Distribution (%) | 50.01 | 17.32 | 9.36 | 7.85 | 4.70 | 3.36 | 2.80 | 2.42 | 2.20 |
| Acceleration Absolute Value | 0–0.05 | 0.05–0.1 | 0.1–0.15 | 0.15–0.2 | 0.2–0.25 | 0.25–0.3 | 0.3–0.35 | >0.35 |
| Probability Distribution (%) | 82.09 | 9.92 | 2.59 | 1.23 | 0.75 | 0.60 | 0.49 | 2.33 |
| State 1 | State 2 | State 3 | State 4 | State 5 | State 6 | State 7 | Total | |
|---|---|---|---|---|---|---|---|---|
| State 1 | 7430 | 1878 | 508 | 167 | 14 | 0 | 0 | 9997 |
| Probability | 0.7432 | 0.1879 | 0.0508 | 0.0167 | 0.0014 | 0 | 0 | 1 |
| … | ||||||||
| Probability |
| No. | Characteristic Parameters | Statistic | No. | Characteristic Parameters | Statistic |
|---|---|---|---|---|---|
| 1 | Proportion of stop time | 24.09% | 9 | Maximum acceleration | 4.507 |
| 2 | Proportion of uniform time | 19.91% | 10 | Acceleration standard deviation | 0.5944 |
| 3 | Proportion of acceleration time | 30.31% | 11 | Minimum slope | −4.59° |
| 4 | Proportion of deceleration time | 25.69% | 12 | Maximum slope | 5.61° |
| 5 | Velocity standard deviation | 13.67 | 13 | Average slope | 0.54° |
| 6 | Maximum velocity | 53.762 | 14 | Minimum road power | −32.6027 |
| 7 | Average velocity | 14.8962 | 15 | Maximum road power | 627.1849 |
| 8 | Minimum acceleration | −5.399 | 16 | Average road power | 24.7528 |
| PM Values Sorted by Size | PM Values of Candidate Start Parts | PM Values of Candidate Middle Parts | PM Values of Candidate End Parts |
|---|---|---|---|
| 1 | 2.510540671 | 4.739681266 | 2.501163991 |
| 2 | 2.569868781 | 7.319837123 | 2.737829385 |
| 3 | 2.628233751 | 8.021323306 | 3.613194073 |
| 4 | 2.653348204 | 8.472976857 | 4.692183328 |
| 5 | 2.668761563 | 9.019943662 | 4.924311752 |
| 6 | 2.945562042 | 9.504009244 | 5.055707237 |
| 7 | 3.040904642 | 9.904238173 | 5.510211213 |
| 8 | 3.257100981 | 10.28213778 | 6.020786659 |
| 9 | 3.285076105 | 10.68241299 | 7.054115036 |
| 10 | 3.327682241 | 11.13303276 | 7.404858184 |
| …… | |||
| 912 | 7.463476789 | ||
| 923 | 7.508530394 |
| Characteristic Parameters | Original Data | Markov | Micro-Trip |
|---|---|---|---|
| Proportion of stop time | 24.09% | 22.93% | 32.51% |
| Proportion of uniform time | 19.91% | 14.97% | 16.80% |
| Proportion of acceleration time | 30.31% | 33.32% | 27.30% |
| Proportion of deceleration time | 25.69% | 28.78% | 23.39% |
| Velocity standard deviation | 13.67 | 13.556 | 13.742 |
| Maximum velocity | 53.762 | 49.634 | 48.489 |
| Average velocity | 14.896 | 14.961 | 13.688 |
| Minimum acceleration | −5.399 | −5.399 | −2.777 |
| Maximum acceleration | 4.507 | 4.031 | 2.459 |
| Acceleration standard deviation | 0.594 | 0.700 | 0.542 |
| Minimum slope | −5.154 | −3.398 | −4.888 |
| Maximum slope | 5.152 | 4.789 | 4.762 |
| Average slope | 0.021 | −0.233 | −0.486 |
| Minimum road power | −32.602 | −32.603 | −31.314 |
| Maximum road power | 308.165 | 217.185 | 137.080 |
| Average road power | 24.753 | 26.871 | 21.619 |
| Statistical items | ZZUDC | CTUB | LA92 | IM240 | JN1015 | UDDS | MANHATTAN | WVUCITY |
|---|---|---|---|---|---|---|---|---|
| Time (s) | 1184 | 1314 | 1436 | 241 | 661 | 1370 | 1090 | 1408 |
| Mileage (km) | 4.919 | 5.898 | 15.797 | 3.152 | 4.164 | 11.921 | 3.324 | 5.319 |
| Average acc. (m/s2) | 0.459 | 0.299 | 0.699 | 0.5452 | 0.548 | 0.6375 | 0.6432 | 0.4201 |
| Average dec. (m/s2) | −0.512 | −0.431 | −0.787 | −0.833 | −0.604 | −0.752 | −0.836 | −0.551 |
| Idling proportion (%) | 22.93 | 29.00 | 17.061 | 4.979 | 31.467 | 19.197 | 38.349 | 34.943 |
| Uniform proportion (%) | 14.97 | 36.606 | 15.460 | 26.141 | 20.121 | 27.226 | 12.294 | 25.213 |
| Acc. proportion (%) | 33.32 | 37.367 | 35.097 | 40.249 | 24.962 | 28.102 | 27.156 | 21.591 |
| Dec. proportion (%) | 28.78 | 26.027 | 32.382 | 28.631 | 23.449 | 25.474 | 22.202 | 18.253 |
| Maximum velocity (km/h) | 45.634 | 60 | 108.15 | 91.25 | 69.97 | 90.72 | 40.71 | 57.65 |
| Average velocity (km/h) | 14.961 | 16.16 | 39.60 | 47.08 | 22.68 | 31.32 | 10.98 | 13.60 |
| Maximum acc. (m/s2) | 2.167 | 0.914 | 3.085 | 1.4752 | 0.7933 | 1.4667 | 2.0559 | 1.1433 |
| Minimum dec. (m/s2) | −3.292 | −1.042 | −3.934 | −1.565 | −0.833 | −1.467 | −2.503 | −3.237 |
| RMS1 of acc. (m/s2) | 0.700 | 0.333 | 0.795 | 0.705 | 0.424 | 0.621 | 0.605 | 0.380 |
| Fuel consumption (L/100 km) | 20.509 | 14.985 | — | — | 17.710 | — | 21.288 | 15.419 |
| Electricity consumption (kwh/100 km) | 12.772 | 9.8581 | — | — | 9.081 | — | 12.474 | 13.326 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, J.; Jiang, J.; Ding, F.; Tan, H. Development of Driving Cycle Construction for Hybrid Electric Bus: A Case Study in Zhengzhou, China. Sustainability 2020, 12, 7188. https://doi.org/10.3390/su12177188
Peng J, Jiang J, Ding F, Tan H. Development of Driving Cycle Construction for Hybrid Electric Bus: A Case Study in Zhengzhou, China. Sustainability. 2020; 12(17):7188. https://doi.org/10.3390/su12177188
Chicago/Turabian StylePeng, Jiankun, Jiwan Jiang, Fan Ding, and Huachun Tan. 2020. "Development of Driving Cycle Construction for Hybrid Electric Bus: A Case Study in Zhengzhou, China" Sustainability 12, no. 17: 7188. https://doi.org/10.3390/su12177188
APA StylePeng, J., Jiang, J., Ding, F., & Tan, H. (2020). Development of Driving Cycle Construction for Hybrid Electric Bus: A Case Study in Zhengzhou, China. Sustainability, 12(17), 7188. https://doi.org/10.3390/su12177188








