5.2. Two-Stage Fuzzy Interaction Analysis
For solving the above problem, we plug the parameters into the fuzzy bi-objective programming model (
1), carry out the crisp equivalence transformation, and obtain the CB-MILP model (
26) for the experiments. Afterwards, by setting different feasibility levels
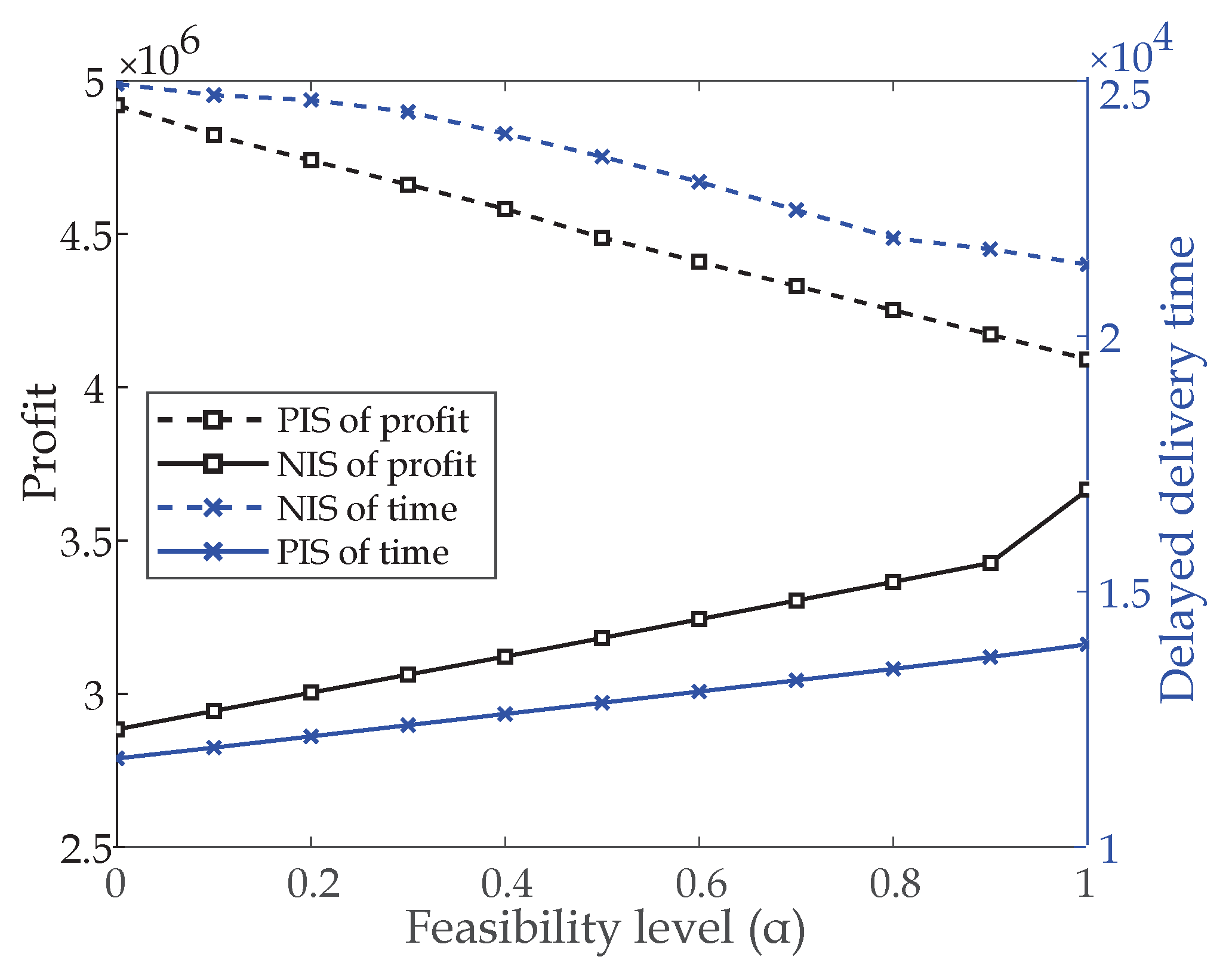
, the PIS of the profit and the NIS of the delayed delivery time representing the optimal solution results when only one of the two objectives is considered are figured out, as shown in
Figure 5. It can be observed that, with the increase of
, the optimal value of the profit marked by the dotted black line decreases, and the optimal value of the delayed delivery time represented by the solid blue line increases. Since the objective functions as well as the constraints of model (
1) are all linear combinations of the triangular fuzzy parameters, the two lines are changing in a linear fashion.
Then, substitute the optimal decision scheme of one goal into the other according to Equation (
28), we obtain the worst values of the two goals, i.e., the NIS of the profit and the PIS of the delayed delivery time, as presented in
Figure 5. Obviously, with the increase of
, the worst cases show a strict monotone tendency and the differences between the PIS and NIS of the objective functions both shrink. As mentioned in
Section 4.1, the PIS and NIS prescribe a limit to the range of one objective while another objective is optimized, thus
Figure 5 indicates that the range of the two objectives narrows with the increase of
. This trend is consistent with common sense, since the feasibility level,
, is a parameter representing the degree of constraint relaxation, i.e., a higher feasibility level is equivalent to a greater degree of constraints satisfaction and a smaller feasible region of the solution. The experimental results can provide decision-makers with the range of the two objective functions at different feasibility levels and help to avoid the risks caused by uncertain factors.
Based on the above PIS and NIS of the two objectives at different feasibility levels with the weight coefficients of
, namely, maximizing the profit is as important as minimizing the delayed delivery time, and the compensation factor of
, the realization levels of the two objectives,
and
, by using the TH fuzzy interaction method are obtained as shown in
Table 3. In general, with the increase of
, the realization levels of the two objectives are relatively high and experience strictly monotone increasing trends. Typically, when
, the most relaxed constraints result in the largest feasible region, and the solution which can immunize against the largest parameter perturbation is achieved, with the minimum realization levels of the two objectives, 80.29%. By contrast, when it comes to
, the tightest constraints lead to the most reliable results with the realization levels of 95.32% and 98.33%. Furthermore, the average realization levels are, respectively, 87.47% and 87.74%, indicating that the TH method is competent to obtain stable and precise solutions.
On the other hand, we can see from
Table 3 that there is little difference between the realization levels, the reason is that the compensation factor is set to be 0.5, and accordingly the objective function of model (
30),
= 0.75 min
+ 0.25 max
, endows a greater weight to the goal with lower realization level, which means the model pays more attention to the short board and is aimed to obtain a compromise and equilibrium solution between the two objectives. For more information, we set the compensation factor as
, i.e.,
, and record the realization levels as well as the gap between them,
, at different feasibility levels in
Table 4. The results explicitly show that the gap tends to decrease with the increase of
and the realization levels of maximizing enterprise profit is constantly higher than that of minimizing customers’ delayed delivery time except for the case of
, demonstrating that the most balanced solution can be obtained when
is between 0.9 and 1.
Therefore, to further explore the sensitivity of the TH method to
, we fix the feasibility level at 0.9 after comparing the solutions of different
and figure out the realization levels of the two objectives as well as the gap between them,
, as illustrated in
Table 5. It shows that the TH method tends to seek equilibrium solutions, for the gap narrows down with the increase of
. Especially, when
,
is equal to
and is constantly unchanged. That is, as
gradually approaches 1, the results pays more attention to optimize the objective with lower realization level, so that a more equilibrium state can be reached. Additionally, we find that
and
evince similar trend of monotonic increase, which is consistent with the conclusion of [
28], verifying the remarkable monotonicity of multiple realization levels with the increase of
while introducing the TH method. Besides, it should be pointed out that, at a fixed feasibility level, when the compensation factor
is small, the TH method can obtain non-equilibrium solutions between multiple objectives, as the realization levels are relatively high.
Ultimately, in order to investigate the joint effect of the weight coefficients and the compensation factor (
,
and
) on the realization levels of the two objectives, we fix
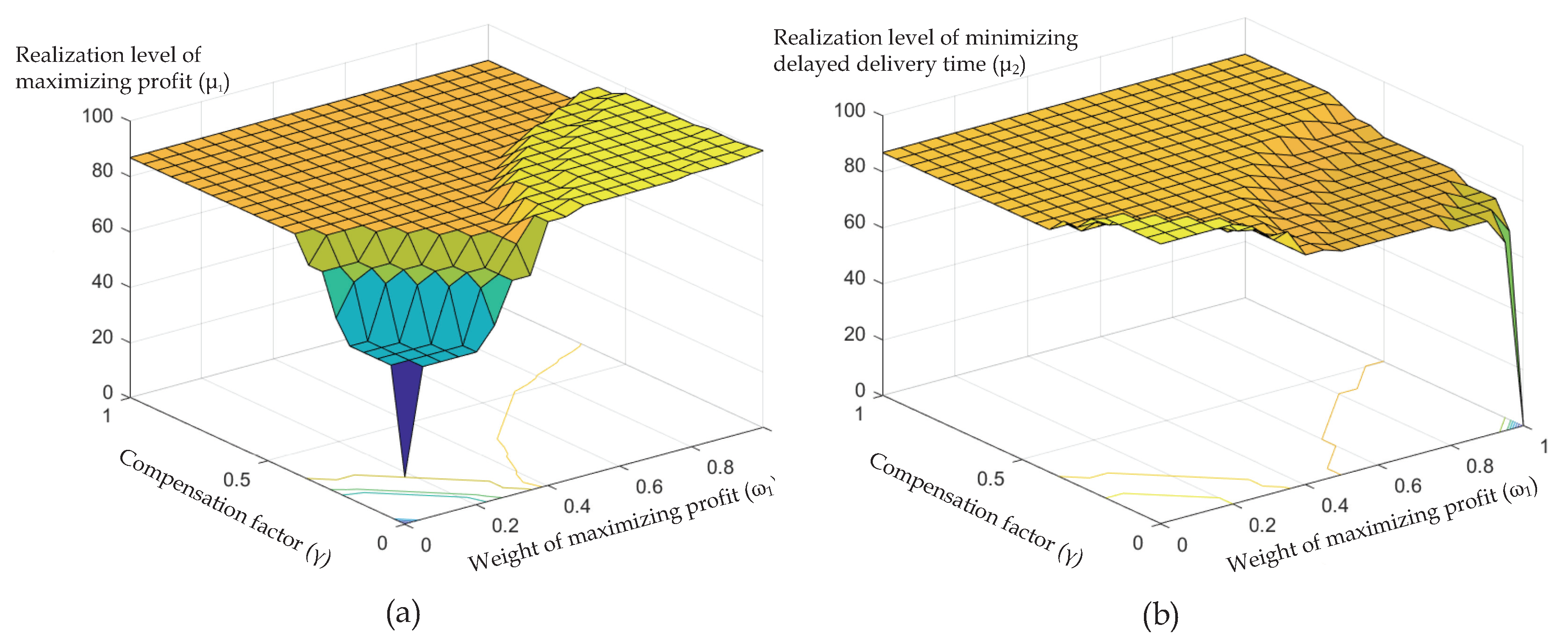
at 0.5 and accordingly depict the results in
Figure 6. It can be seen from
Figure 6a that the weight coefficients of the two objectives have no effect on the realization level of maximizing the enterprise’s profit when
(with
remaining steady at 90%), yet have significant influence when it comes to
. Specifically, when
(
),
maintains a high level of more than 90%; and when
(
) and
, it decreases rapidly and reaches the bottom of 0 with
and
. In
Figure 6b, the similar conclusion can be drawn as
Figure 6a since the tendency of
in
Figure 6b is close to that of
in
Figure 6a if the x-axis,
, is replaced by
. Hence, to get more equilibrium solutions, it is supposed to set a relatively concentrated value of
and
and a relatively high value of
.
To sum up, the above analyses show that while designing the CLSC network in fuzzy environments, the decision-makers can obtain satisfactory solutions by modifying the parameters, i.e., the feasibility level, the compensation factor, and the weight coefficients, according to their preferences, and the fuzzy settings provide more flexible and diversified options for decision-making. In the next section, we will elaborate this advantage in detail by some comparisons with the deterministic problem presented by [
3].
5.3. Comparisons with the Deterministic Problem
By fixing the parameters at
and solving the proposed fuzzy model and the deterministic one in [
3], the comparative results on the optimal solutions at different feasibility levels are depicted in
Table 6 and
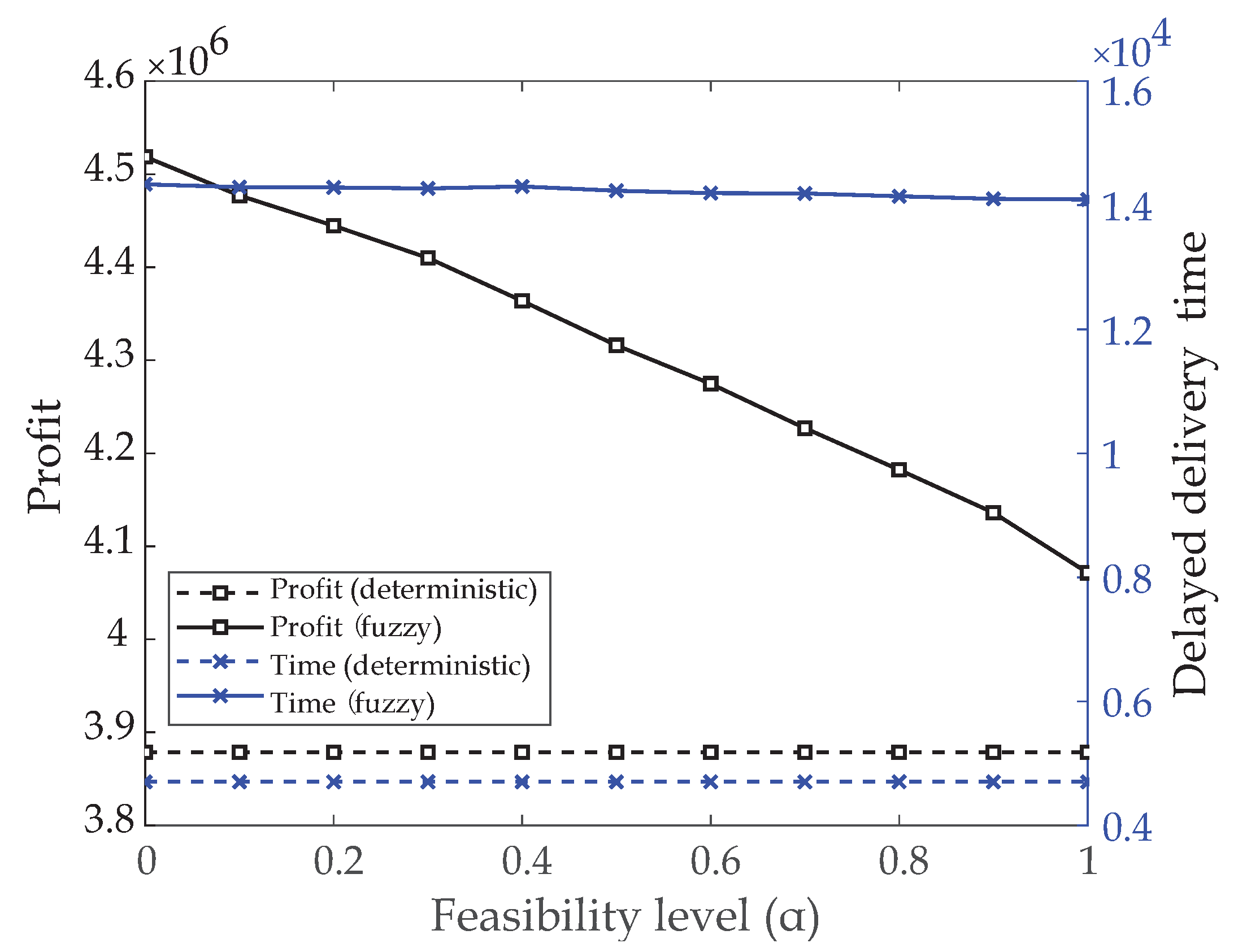
Figure 7.
As we can see from the four curves representing the optimal solutions of the objective functions obtained by using the TH method under deterministic and fuzzy environments, both the profit and the delayed delivery time in the deterministic problem are less than that in the fuzzy one. Furthermore, it also can be observed that the values of the two objectives under fuzzy environments decrease with the feasibility level increases, whereas the results under deterministic environment are constantly unchanged.
Explicitly, the delayed delivery time in fuzzy cases is much longer. At the root, under deterministic environments, Jiang et al. [
3] calculated the delayed delivery time by adding up the non-negative differences between the actual and the expected delivery time, which is equivalent to the treatment of Equation (
5) corresponding to the fuzzy cases. However, in our fuzzy settings, the difference between the fuzzy expected delivery time and the fuzzy actual delayed delivery time are calculated by Equation (
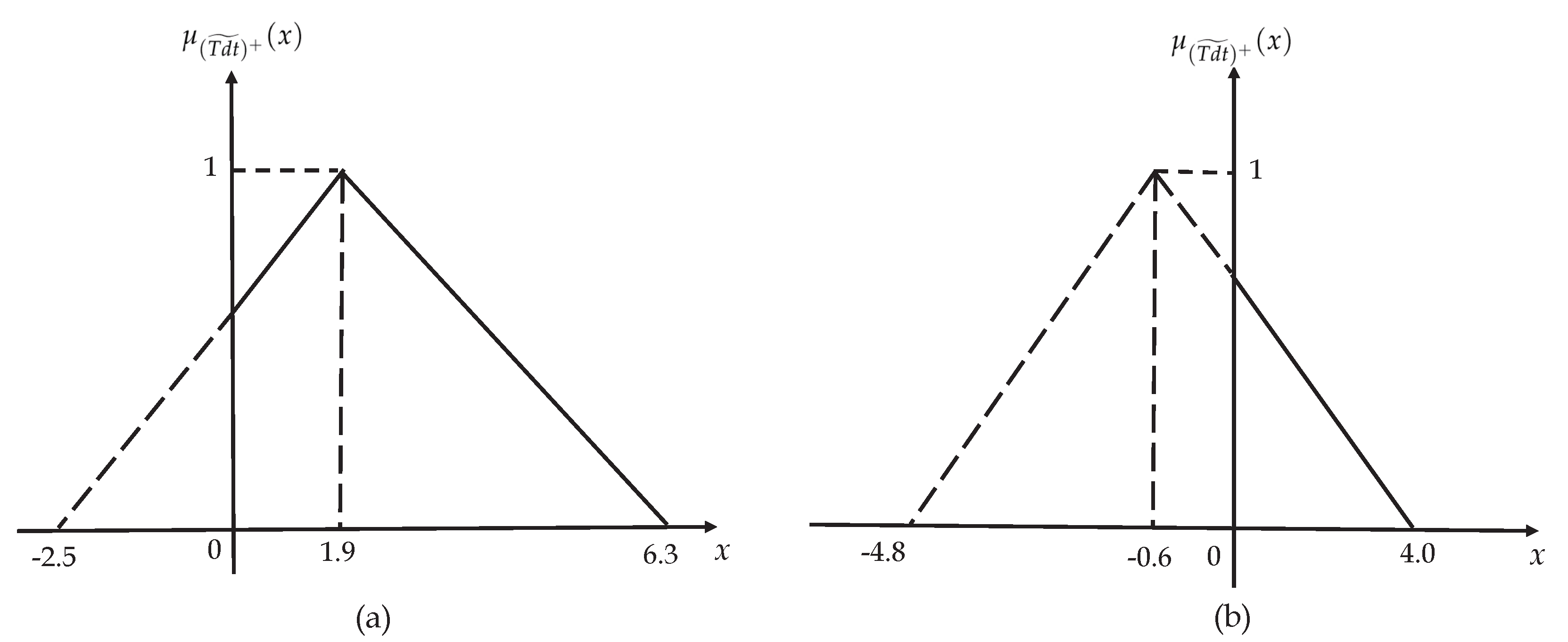
6), since we have proved in
Section 3 with concrete data that the difference between fuzzy numbers cannot be directly calculated by their
s and Equation (
5) may result in a huge deviation. Thus, a big gap between the delayed delivery time under different environments arises, as shown in
Figure 7.
On the other hand, minimizing the delayed delivery time and total profit are two conflicting objectives, that is, a shorter delayed delivery time brings a higher service level and higher cost/lower profit simultaneously. Therefore, in
Figure 7, the profit under fuzzy environments is also larger than the deterministic case. Specifically, the maximum disparity of the two lines, representing the profits under different environments (4,518,735 and 3,878,633, respectively) at
, occupies about 17% (640,102/3,878,633) of the profit in the deterministic case. Then, with the increase of
, the disparity decreases. When coming to
, it narrows down to the minimum (of 192,911).
Furthermore, it is universally acknowledged that the optimal solution of the deterministic case is a degenerate version of the fuzzy case. Henceforth, with the increase of , both the profit and delayed delivery time are supposed to decrease to the deterministic values. However, due to the treatment of calculating the of the delayed delivery time aforementioned, the downtrend of the disparity between the profits under fuzzy and deterministic environments is remarkably more dramatic than that of the delayed delivery time. The results indicate that under fuzzy environments, while the realization levels of the objectives are relatively high, as the constraints become more stringent, improving customer service level is costly for the enterprise, which is quite different from the deterministic cases. Besides, under fuzzy environments, it is more flexible for managers to make decisions by adjusting the feasibility level.
From the above analyses, it is not difficult to conclude that putting the problem of the CLSC network design under fuzzy environments is more reasonable from the perspective of improving enterprise’s profit and flexible management. Since fuzzy numbers are sets on the real line (see Definition 1), it is natural for some researchers to argue that we may set the values of the variables as crisp intervals so that the problem of the CLSC network design can be studied under deterministic environments. Considering that, the following experiment is designed to manifest the essential distinction between the deterministic and fuzzy models.
First, by keeping the other parameters in [
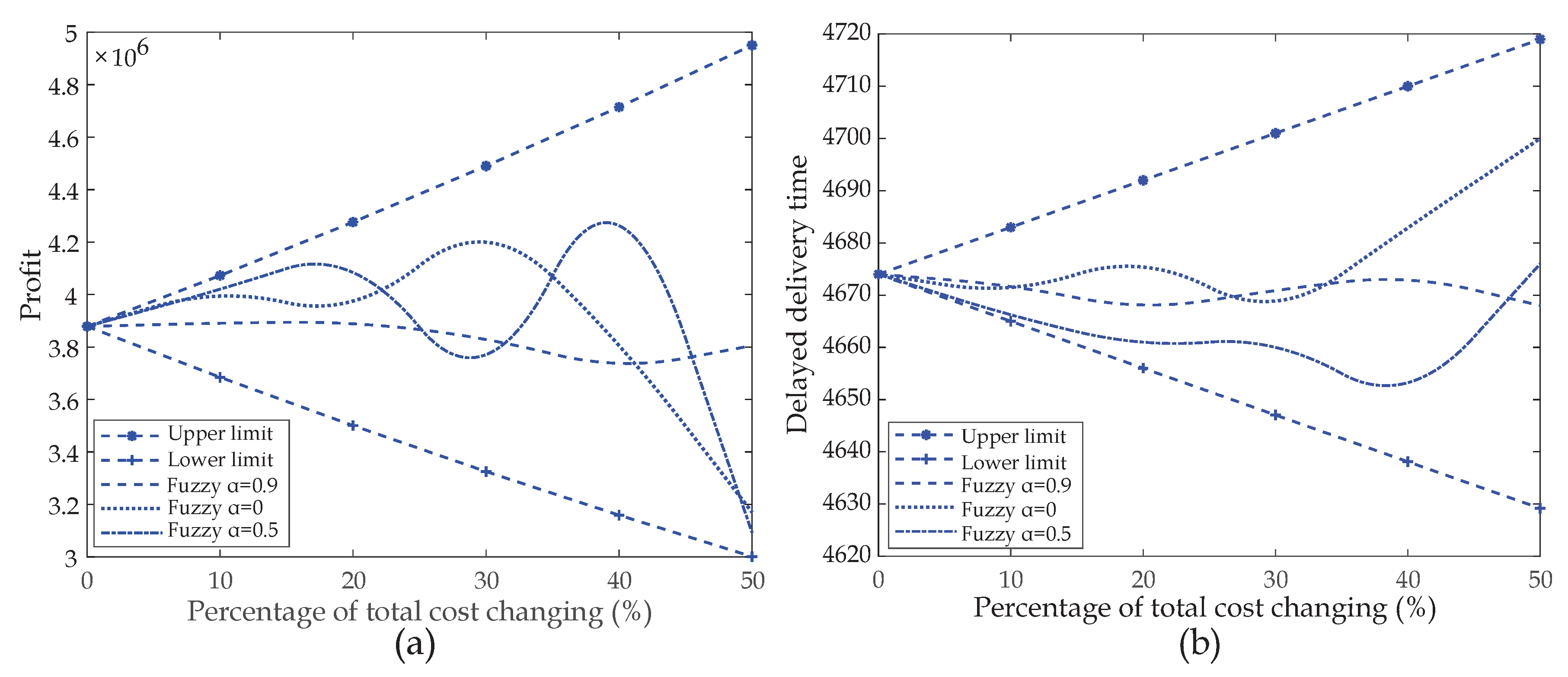
3] unchanged and increasing or decreasing 0 to 50% of the total cost, the two lines representing the range of the profits are obtained, as plotted in
Figure 8a. Since the deterministic total cost can be regarded as a fuzzy number with the spread of 0, we can realize the equivalent increase and decrease of the total cost by adjusting the spread of the fuzzy number under fuzzy environments, that is, expanding the right spread is equivalent to increasing the total cost under deterministic environments, and expanding the left spread is equivalent to decreasing the deterministic total cost. Henceforth, fix
at 0.9, adjust the spreads of the cost coefficients to realize the equivalent variations of the total cost, and set
as 0, 0.5, and 0.9, respectively, the three curves standing for the optimal profits under fuzzy environments can be figured out and depicted in
Figure 8a. It should be noted that in our solution framework, the fuzzy parameters in the original model (
2) are all deffuzified by their
s. Thus, the profit obtained are a crisp value rather than a fuzzy number and its variation is relatively lower with regard to the variation of the total cost. However, by setting the value of the total cost as a crisp interval and substituting the extreme values into Jiang et al. [
3]’s model, we can merely obtain the upper and lower limit of the profit whose range is proportionally changing with respect to the variation of the total cost. As a result, the three curves are in the middle of the two lines, demonstrating that the solutions of the fuzzy settings are less fluctuant than that of the deterministic settings. Additionally, we can see that the three curves representing the solutions at different feasibility levels are quite different from each other. As mentioned in Definition 3, the feasibility level
is the essential parameter of transforming the fuzzy constraints into their crisp counterparts, and a higher level is equivalent to more strict constraints. Therefore, the solutions with higher feasibility levels are less fluctuant, which is consistent with
Figure 8a that the dashed curve with
is more stable than the dotted one with
and the dotted-dashed one with
, and the profit of
is much higher even though the variation of the total cost is large.
Analogously, while keeping the other parameters unchanged, a comparative experiment on the influence of total cost over another objective of minimizing the delayed delivery time under deterministic and fuzzy environments is also conducted, and the results are depicted in
Figure 8b. We can also conclude that the fuzzy model is superior to the deterministic one, and the curve with
is most stable among the three curves. Especially, the delayed delivery time at
is mostly lowest, showing that
is more appropriate for the decision-maker from the perspective of improving customer service levels if the variation of the total cost is small.
Above all, the comparative results of the optimal solutions illustrated in
Table 6 and
Figure 7 confirm the superiority of the fuzzy model proposed in this paper over the deterministic one presented by Jiang et al. [
3] in maximizing enterprise’s profit and flexible management. In addition, the curves (representing the fluctuation of the profit/delayed delivery time in the proposed fuzzy settings which assumes the uncertain total cost as fuzzy numbers) and lines (standing for the upper and lower limits of the objectives under deterministic environments) in
Figure 8 demonstrate the reasonableness and necessity of taking fuzziness into account while designing the CLSC network, since the solutions under fuzzy environments are less fluctuant and can offer more accurate information about the objectives. If the fuzzy approach was not applied and the market’s uncertainty was handled by restricting the parameter’s range, then we can merely obtain an interval of the profit/delayed delivery time. Such a result could be of high uncertainty and less useful for decision-making. Besides, the comparisons between the curves with different
show that the decision-maker can obtain stable and ideal solutions by adjusting the feasibility level, i.e., the key parameter for transforming the fuzzy constraints into crisp ones.
5.4. Discussions
In this section, several experiments are carried out to validate the feasibility and necessity of investigating the CLSC design problem under fuzzy environments and the performance of the proposed solution framework in solving the fuzzy CLSC model. In order to exemplify the superiority of the fuzzy model over the deterministic one, the data set is selected from the work of [
3] and modified by replacing the crisp parameters into symmetric triangular fuzzy ones. The results with different feasibility levels
, compensation factor
, and weights of objectives
w indicate that these parameters play crucial rules on the performance of the proposed method. Specifically, a higher feasibility level meaning stricter constraints is conducive to a higher-quality and more stable solution, a lager compensation factor and more evenly weights tend to make the solution more balanced.
Furthermore, the comparative experimental study between the fuzzy model and the model in [
3] show that putting the problem of the CLSC network design under fuzzy environments is more reasonable from the perspective of improving enterprise’s profit and flexible management since the profit of the fuzzy model is higher than that of the deterministic one, and the differences of the profits and delayed delivery times both decrease with the increase of the feasibility level. In the last two experiments, we also illustrate the difference between handling the market’s uncertainty by restricting the parameters’ range and assuming the uncertain parameters as fuzzy numbers, that is, the deterministic settings can merely provide a range of the objectives, whereas the fuzzy settings can offer more accurate and stable information.
It should be pointed out that although the proposed solution framework is tested only on a bi-objective case with symmetric fuzzy parameters, it can be extended to solve many other CLSC variants with slight modifications, such as the problems with multiple objectives, more diversified recovery options or complicated risk preferences. Therefore, it is highly flexible and applicable for the decision makers who are in need of solving various types of practical CLSC problems. Moreover, it is easy to understand and implement, and is very successful in returning high-quality solutions since the realization levels of both objectives are demonstrated to be high as long as the above-mentioned parameters are reasonably selected.