1. Introduction
Terminals are locations where freight either originate, terminate, or are handled in the transportation process [
1]. Multimodal transport terminals are facilities that participate in the delivery of goods as essential elements of supply chains, providing the distribution and warehousing services for different modes of transport. This definition reflects the most significant functions of multimodal transport terminals as elements of logistics chains—loading and unloading of transportation units and the intermediate storage of goods.
As basic subsystems of a multimodal terminal, the following elements should be distinguished: a warehouse and its loading and unloading bays. As a bay here we understand a space in a warehouse where goods are put in or taken out. In the case of the direct handling of shipments, loading and unloading bays can be considered as a single subsystem—a loading–unloading bay. The storage areas of a terminal and the servicing machines at the terminal bays constitute its basic production resources.
The process of logistics management at transport terminals is a complex multi-level process. The crucial managerial problem for such compound systems as multimodal transport terminals is the proper data management aiming at obtaining, processing, and analyzing information about the system parameters (including characteristics of demand, technological processes, and the resulting efficiency indicators). To ensure the quality and adequacy of the data on transport terminals’ functioning, the advanced data management systems are being developed [
2], data envelopment analysis is being implemented [
3], and complex network data models are being constructed [
4]. For the purposes of comparative analysis and evaluation of the multimodal terminals’ sustainability level, surveys are held [
5,
6,
7] and the Analytical Hierarchy Process method is used [
8].
However, decision-making on the choice of service technologies and the amount of production resources requires preliminary justification using the advanced models of a transport hub functioning. Existing approaches to the modelling of technological processes of transport terminals are mainly based on analytical models [
9,
10,
11,
12,
13,
14] that do not allow researchers to estimate the complex influence of a set of random external factors on the efficiency of the hub’s operation. Thus, the research direction of creating new models of operation of transport terminals using modern mathematical methods and information technologies is relevant, and the use of the resulting methodologies can increase the efficiency of the processes of logistics management and ensure the sustainable development of the transport system.
In recent studies of multimodal transport systems, two main directions should be mentioned – solving problems at the level of the macro-logistic system and dealing with operational tasks at the micro-level.
The problems that are usually solved at the macro-level are the localization of transport hubs in the nodes of a transport network [
15,
16,
17,
18], the modernization of the fleet [
9], and the resource planning at the scale of the supply network [
19].
At the micro-level, the main tasks are the justification of managerial decisions on servicing of material flows in transport hubs [
12,
20], the estimation of the intermodal terminal capacity [
21], the optimization of the servicing machines’ load [
22], the optimization of technological operations [
23,
24,
25], the synchronization of the modes of transport interacting in the freight terminal [
26], and the inventory optimization problems [
27]. It should be mentioned that problems of rationalizing the terminal resources’ parameters (the terminal’s capacity, the machine’s load, the warehouse parameters) are being solved separately despite the production facilities constitute the unified servicing sub-system of a terminal.
The problem of the emissions’ reduction is usually being solved at the macro-level—by studying the emissions’ parameters at the scale of a region or a supply chain [
5,
6,
7,
16,
17], but can also be considered as the sub-problem at the micro-level: the emissions-decrease measures may be developed for the given hub.
Models of a transport terminal representing in detail the internal technological processes are usually used as the basic tool to solve problems at the micro-level [
24,
28,
29,
30]. It is widely accepted that these models are developed based on a systematic approach, which supposes the identification of links between components of the research object and the impact of each element on the system’s efficiency. As the most relevant recent studies, where the models of the transport terminal operation were proposed, the papers [
16,
19,
29,
31] should be noted. The authors use contemporary mathematical and modelling tools, such as queuing theory methods [
28,
32], variations of linear and non-linear programming [
10,
19,
20,
33,
34], evolutionary algorithms [
17,
26,
29], specific numerical simulations’ techniques [
23,
31], and advanced heuristics [
21,
35].
As the indicators of the efficiency of multimodal terminals, the costs characteristics are usually used [
10,
11,
14]. However, the technological parameters representing the duration of operations are also used as the objective functions for solving the optimization problems in multimodal terminals [
4,
26,
35]. Recently, the environmental-related costs are considered in a number of publications [
6,
7,
17,
36] as the criterion of the transport terminals’ functioning.
To increase the efficiency and ensure the sustainable development of a multimodal transport terminal, the structure and capacity of its facilities (e.g., warehouse capacity, the number of handling machines) should be optimized in a way that takes into account the stochastic nature of incoming and outgoing material flows. For solving the managerial problems related to the sustainable development of multimodal transport terminals, the implementation of a simulation model is usually the most appropriate approach [
28,
29,
37], because numerical computer simulations allow considering stochastic parameters of demand and technological operations during the decision-making process.
The goal of this paper is to present an approach toward optimizing the production resources of a multimodal transport terminal by using numerical computer simulations of the servicing technological process. Our research contributes to the direction of improving the structure of the terminal’s production facilities at the micro-level of the decision-making process. We aim to fill the research gap of the complex evaluation of resources needed to serve the stochastic demand for the services of multimodal freight terminals. In this paper, we propose to consider stochastic parameters of demand as parameters of incoming and outgoing flows of requests for the services of terminals. We also investigate the influence of demand parameters on the efficiency of the terminal functioning for the set of possible servicing technologies used in multimodal transport terminals while processing the requests for loading operations.
The paper has the following structure: the second part contains the list of problems related to transport hub logistics management and presents the efficiency criterion for solving the listed problems; the third part depicts the design and results of the simulation experiment performed in order to define the functional dependence of the efficiency criterion on the numerical characteristics of the terminal’s production resources and parameters of the demand for the transport hub services; in the fourth part, the case study of the proposed approach for the Amur-Harbor cargo area of the Dnipro River Port is presented; the last part contains short conclusions and directions for further research.
2. Problem Statement and the Methodology
The function of transport hubs as components of macro-logistics systems within transport markets is characterized by the presence of a number of problems of a technological and organizational character. Analysis of the practical aspects of transport hub functioning, where different means of transport interact in the process of material flow service, allows us to distinguish the following problem situations:
upon a consignment arriving at the transport node that requires intermediate storage in a warehouse or additional processing, there is a situation where there is no available free warehouse space or unused handling machines and workers to implement the consignment processing;
when vehicles arrive at the transport hub for loading, there is the situation when the expected load is not available at the warehouse due to the fact that previous processing operations were not performed;
when vehicles arrive at the transport node for loading or unloading, there is the situation when other vehicles are using the loading/unloading bay, which leads to non-productive downtime of vehicles in anticipation of handling operations;
when servicing vehicles in a transport hub, the duration of direct servicing operations is greater than is declared;
for a consignment that can be handled by the direct variant, processing is carried out according to the scheme “transport–warehouse–transport” due to the lack of direct transshipment bays.
For the above problem situations, the following reasons for their occurrence can be distinguished:
the structure of the servicing system’s production resources does not correspond to the structure of demand for services provided in the transport node to other entities of the transport services market (there are no properly equipped direct-loading bays for different pairs of vehicles in the transport node, there are no areas for additional operations of the material flow processing, etc.);
the capacity of the transport node’s production resources does not correspond to the demand parameters (the processing capacity of the loading bays does not provide servicing of the material flow or is larger than necessary, the capacity of the warehouse for the subunits of the transport node does not correspond to the demand for intermediate storage, etc.);
the material flow processing operations are not organized properly.
The presented reasons for the emergence of problem situations in the process of functioning of transport terminals are the result of a partial or complete absence of a systematic approach to managing transport hubs as logistics systems.
When solving problems of optimizing the structure and capacity of production resources of transport terminals as elements of macro-logistic systems, we propose the use of a specific indicator of efficiency
defined as the ratio of profit from customers’ service in the transport terminal to the cost of production resources involved in the servicing process:
where
is the total amount of cargo that was loaded and unloaded in the transport terminal during a given time period (tons);
is an averaged tariff for processing of 1 ton of cargo in a transport terminal (EUR/ton);
is the total costs of the servicing operations in a transport terminal during the given time period (EUR);
is the total cost of production resources used in the material flow processing (EUR).
The proposed criterion contains the commonly used logistics management indicator (the total cost of service) but also allows internal system characteristics (costs of production resources) to be considered.
Management decisions concerning optimization of transport hub technological processes are accepted based on the analysis of simulation results. The results of modelling are the functional dependencies of the efficiency criterion on a set of factors characterizing the input impacts:
where
are numeric parameters of production resources;
If the functional dependence (2) has a minimum relative to a given characteristic of the production resources
, then the managerial decision on choosing the optimal variant of the transport terminal’s operation is taken on the basis of the solution obtained for the following equation:
Let us define
as the set of the basic characteristics of the transport terminal’s resources—the number of handling machines and the capacity of warehouses:
where
represents the total capacity of the transport hub’s warehouses, (tons);
and are the number of handling machines (cranes, forklifts, etc.) in the loading and unloading bays, respectively.
In this case, the total cost of production resources could be estimated in the following way:
where
is the average carrying value of one handling machine at the loading bay (EUR);
Characteristics of incoming and outgoing material flows could represent the demand for transport hub services:
where
and
are the expected values of a consignment weight in the incoming and the outgoing material flows (tons);
For the formulation of the mathematical model of the terminal operation as a functional dependence of the efficiency criterion on the numerical characteristics of the production resources and demand parameters, we define the total volume of cargo that is loaded or unloaded in the transport terminal during a given period in the following way:
where
is the level of the material flow service;
To define the influence of parameters and on the efficiency criterion (1), the functional dependencies and should be determined. That cannot be done analytically but can be achieved by running numerical simulations of a transport terminal’s operation: the parameters of the production resources and the demand characteristics are considered as the input parameters to the simulation model of the terminal’s operation process, total costs, and the servicing level are obtained as the result of multiple runs of the simulation model, and the dependencies and are evaluated based on the simulations’ results by the means of the regression analysis.
Implementation of simulation models for transport terminal operation is proposed using object-oriented programming principles following the described approach to formalization of a multimodal transport terminal. The authors have developed the class library, which could be used as the basic modelling tool for simulations of technological processes in multimodal transport hubs. The proposed class library is in C# programming language and may be downloaded at [
38]. The full description of the developed software and examples of its use are presented in [
24] and [
32].
3. Experimental Studies
Depending on the given variant for handling the incoming and outgoing material flows, three variants of technological requests servicing process in a transport terminal could be considered:
the service with transshipments through the warehouse (W-variant): loaded vehicles, arriving at the transport node, are unloaded to the warehouse at the loading bay of TW-type (“transport–warehouse” type); empty vehicles, arriving at the transport node, are loaded from the warehouse at the loading bay of WT-type (“warehouse–transport” type);
the service with direct transshipments (D-variant): loaded vehicles are unloaded at the loading bay of TT-type (“transport–transport” type), while at the same time loading is implemented for empty vehicles that came to the transport node for that purpose;
the mixed variant of the service (M-variant): some of the loaded vehicles are serviced at the direct transshipment loading bay, while some of the vehicles, which came for loading, are serviced at the same time; other vehicles are serviced through the warehouse at the TW- and WT-type loading bays.
The random variable of the unit costs of the idle vehicle arriving at the transport hub is determined in the model as the parameter of a machine that serves a request. The experiment examines the interaction in the transport terminal of three modes of transport—road, rail, and river. The specific idle costs are taken for a type of transport as the average, for the different models of vehicles of one type of transport, the specific costs of idle time are not differentiated.
In order to provide a statistically valid estimation of the influence of input parameters on the efficiency criterion, it was decided to carry out a full-featured experiment. The numerical characteristics of the production resources of a transport hub and the parameters of the incoming and outgoing material flows, presented in
Table 1, were used as input factors in the full-featured simulation experiment. The numerical characteristics of the Amur Harbor cargo area of the Dnipro River Port were used as the basis for the simulation experiment.
For the direct variant of the material flow servicing, the bounds of the variation in the number of servicing machines on the front of the direct handling are taken in the range from 1 to 7 units. In order to take into account the possible nonlinear influence of the input factors on the efficiency indicators of the hub operation, the experiment considered four levels of variation of the input parameters (to determine the linear dependence of the efficiency criterion on the input factors, it was enough to consider two levels of variation—the upper and lower bounds). Thus, for the four levels of variation of the input parameters, the number of series in the simulation experiment for the variant of servicing through the warehouse is 16384; for the mixed variant of service—4096; and for the direct variant of servicing—1024.
Using the developed software, based on the described simulation experiment plan, the expected values for each series for the following indicators of the transport hub operation are determined:
the total time of vehicle servicing;
the total downtime of handling machines;
the total volume of goods processed in the transport hub;
the total amount of ton-hours of cargo storage in the transport hub’s warehouse;
the total expenses for material flow processing at the transport hub;
the level of the material flow service;
the efficiency criterion of the transport hub operation.
Since the efficiency criterion is determined on the basis of the total costs of the material flow processing and the level of the material flow service (the volume of serviced cargo is defined as the product of the level of service and the total volume of cargo processed in the transport hub), the analysis of the influence of parameters of production resources and demand is carried out for these two indicators. At the same time, the reproducibility of the experiment has been verified based on the integral indicator—the proposed criterion for the transport hub efficiency.
A preliminary analysis of alternative hypotheses using a regression statistical models allowed the rejection of all functional dependencies with a non-zero free coefficient: hypotheses about linear, logarithmic, and power dependencies were considered for and for the described variants of the technological process of the multimodal terminal.
The results of regression analysis suggest that in the most adequate way the functional dependencies of the service level on the numerical parameters of the productive resources of the multimodal transport hub and the parameters of the demand for the services of the hub are described by the following expressions:
where
,
, and
are the values of the service level for the corresponding variants of the technological process (
W-,
D-, and
M-variants).
The functional dependencies of the total costs of the material flow servicing from the parameters of the production resources and the numerical characteristics of demand, in accordance with the results of regression analysis, are most accurately described based on power models:
where
,
, and
are the total servicing costs for the respective variants of the material flow service (UAH). The calculations of total costs were performed in Ukrainian hryvnias (UAH)—the national currency of Ukraine because this currency was the base for estimations of the cost-related initial data used to run numeric simulations. However, the used currency does not affect the values of the proposed criterion (1) as this indicator is dimensionless.
The determination coefficient for the evaluated dependencies (8) and (9) has values in the range from 0.89 to 0.94, this indicates the high adequacy of the obtained regression models.
It should be noted that the models (9) return the proper values of expenses for the conditions of the Ukrainian market of transport services. For other transport markets, the simulations should be run with the corresponding values of costs in order to obtain proper functional dependencies.
The substantiation of numerical characteristics of production resources, as well as organizational influences, is proposed to be carried out using the efficiency criterion (1) as the definition of such values of the parameters and that result in the increase of the efficiency criterion value. The parameters include the number of handling machines on the loading bays and the capacity of the warehouse, and the variant of the technological process of the material flow servicing in the multimodal transport hub is considered as the parameter.
4. Case Study: Optimizing Resources of the Amur Harbor Cargo Area at the Dnipro River Port
The optimal amount of production resources should ensure the maximum possible value of the efficiency criterion for the given characteristics of demand. According to (3), the optimal value of a numerical parameter is defined as the extremum of the criterion function with respect to the corresponding parameter.
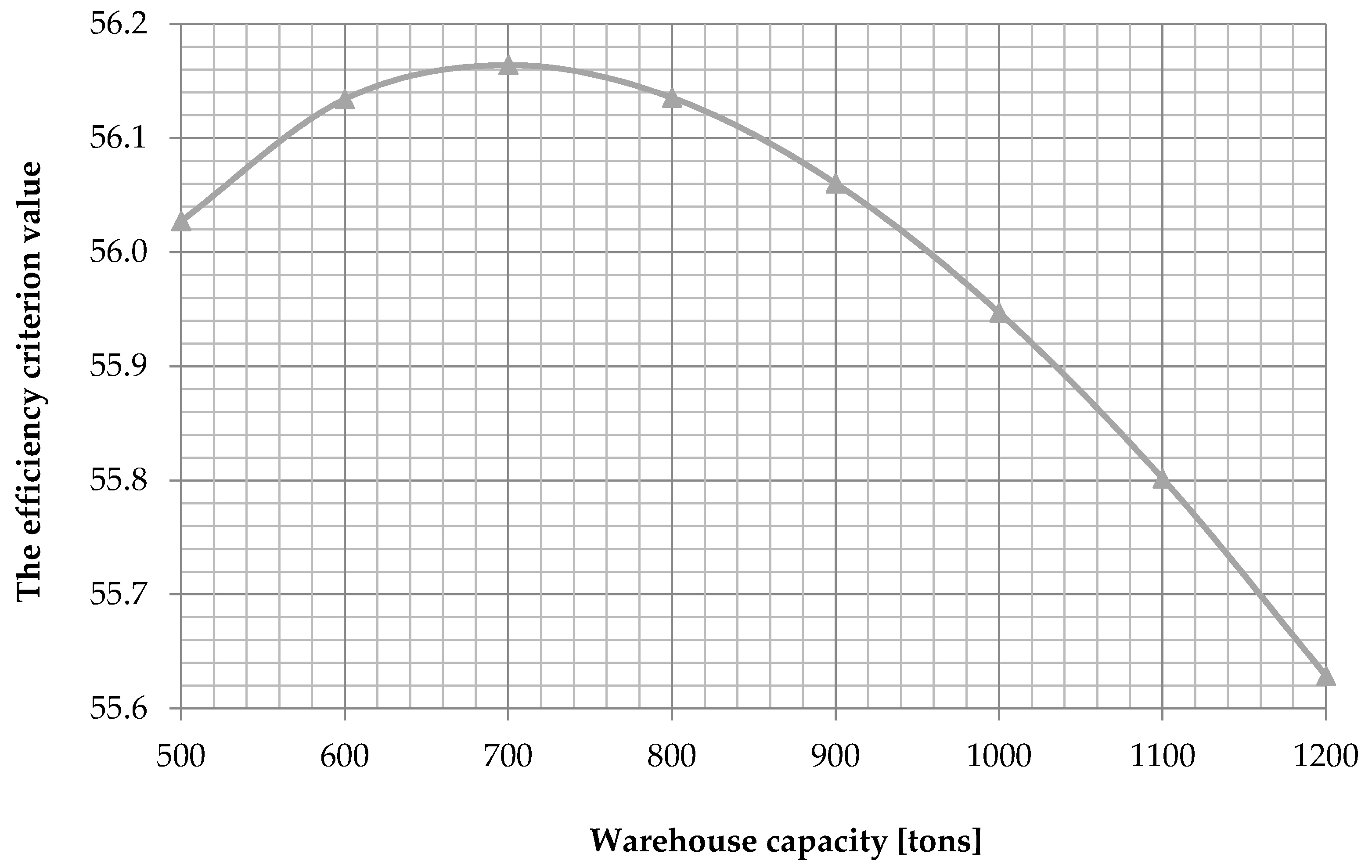
The analysis of the obtained functional dependences
allows us to assert that there is an extremum with respect to the value of the capacity of the transport hub’s warehouse, with this extremum characterizing the maximum possible value of the efficiency criterion of the transport hub operation (see
Figure 1).
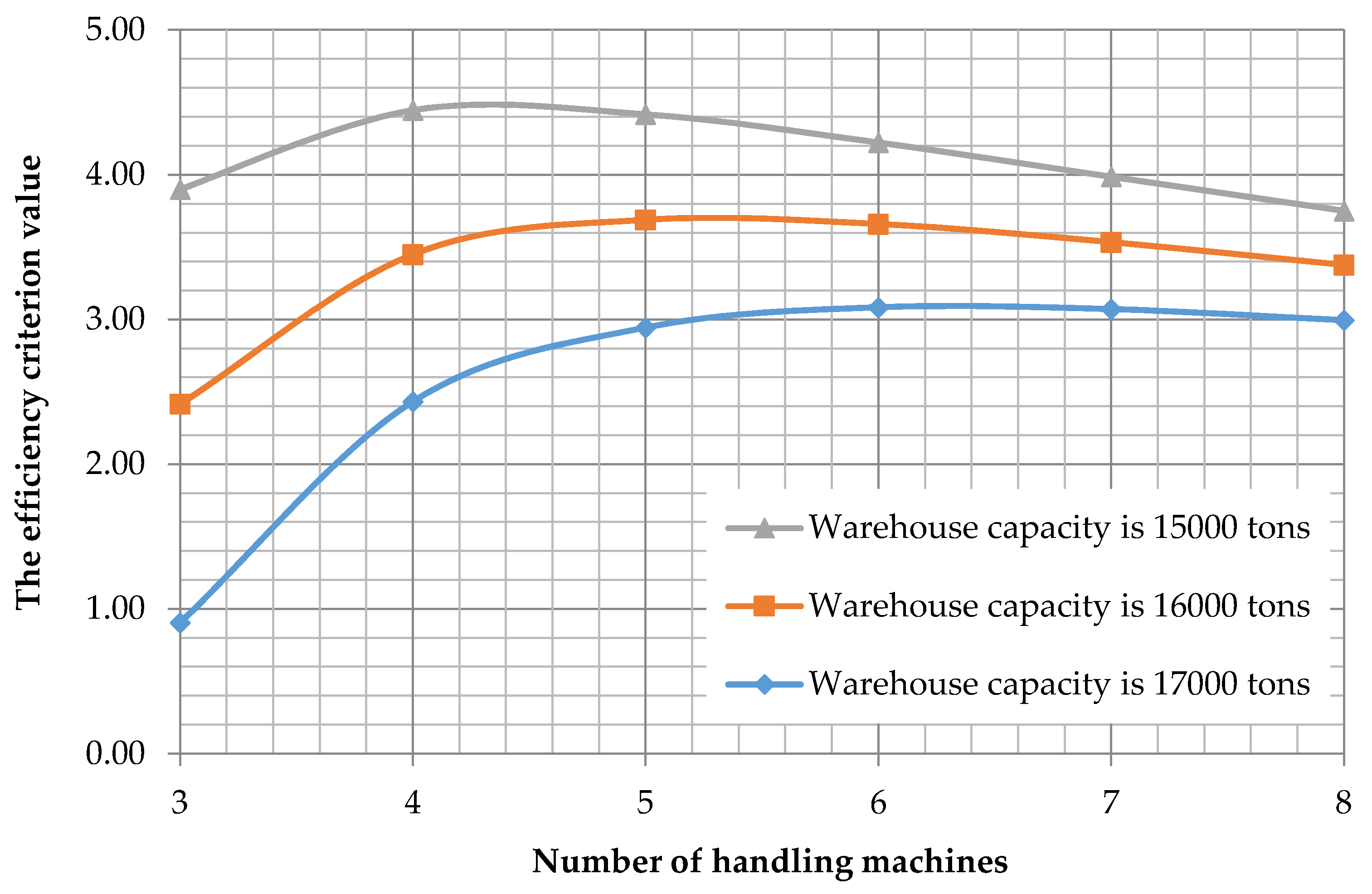
The same assertions should be done about the efficiency criterion extremum with respect to the number of handling machines at the loading bay (see
Figure 2).
Let us determine the type of functional dependence of the efficiency criterion from the numerical characteristics of the production resources for the variant of the material flow service with transshipments through the warehouse for the Amur Harbor cargo area of the Dnipro River Port.
For a stated warehouse capacity of
, the dependence (1) takes the following form:
where
;
;
;
;
.
Differentiating (10) with respect to
, after transformations, we obtain the following equation for estimations of the optimal capacity of a warehouse:
where
;
For the number of handling machines at the loading bay of the incoming material flow, the efficiency criterion dependence for the W-variant of the servicing technology could be presented in the following form:
where
;
;
;
;
.
The equation for the estimation of the extremum of the function (12) with respect to the number of machines at the unloading bay, after the differentiation and corresponding transformations, takes the form:
where
;
;
;
;
.
The dependence of the efficiency criterion of a multimodal transport hub on the number of loading machines at the loading bay for the technology of material flow service with transshipments through the warehouse is similar to (12):
where
;
Then, the optimal number of loading machines at the output material flow service bay is defined as the root of the following nonlinear equation:
where
;
;
;
.
For the variant of the material flow service with transshipments through the warehouse, the number of handling machines at the unloading bay
, and the number of machines at the loading bay
as well. Thus, the equation to determine the optimal capacity of the warehouse takes the following form:
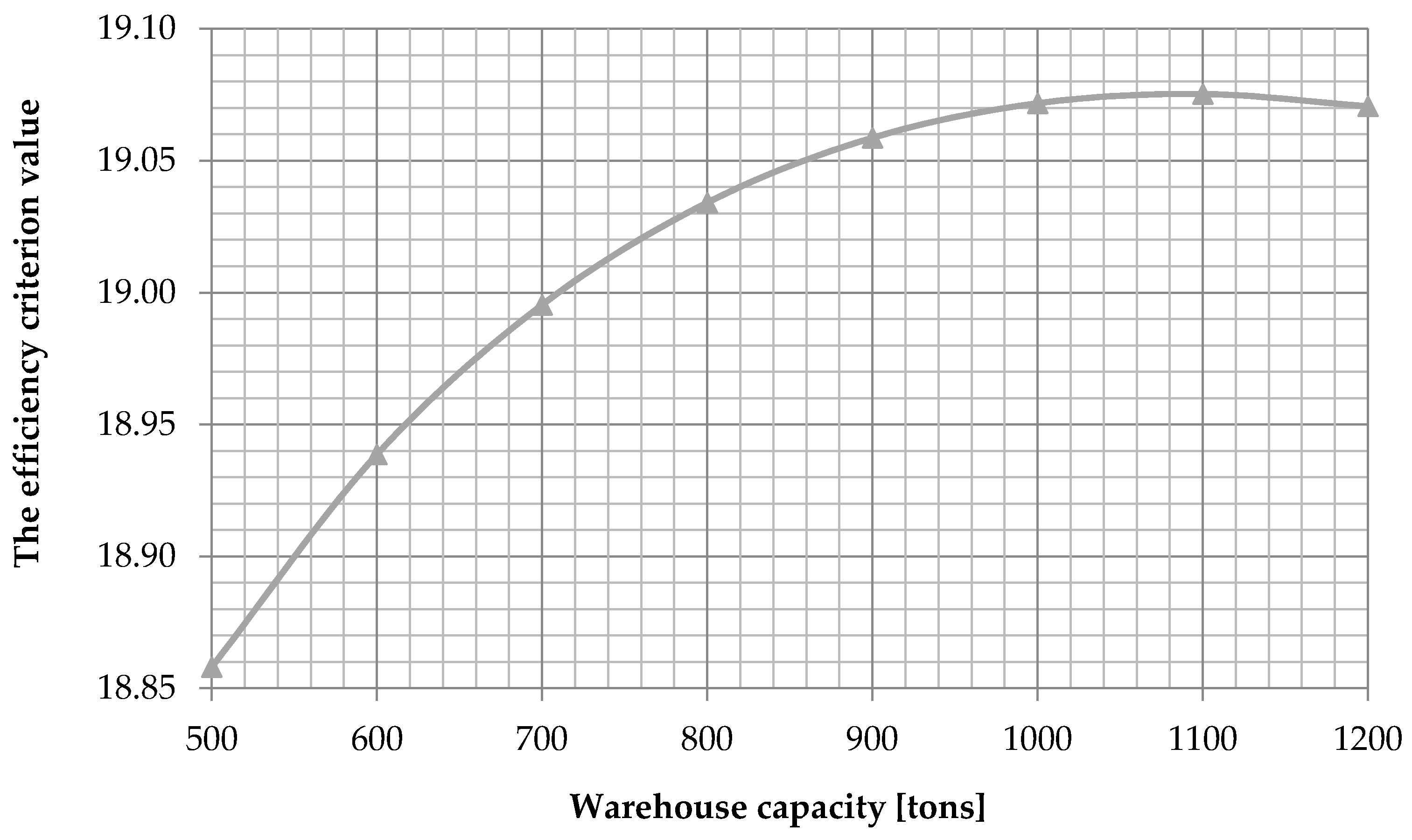
The use of the bisection root search procedure with an accuracy of 10
0 allowed us to determine that the optimal warehouse capacity equals to
tons. The values of the efficiency criterion representing the described set of parameters are shown in
Figure 3.
Let us show that the obtained values of productive resources are optimal for the client servicing for the variant with transshipments through the warehouse at the Amur Harbor cargo area of the Dnipro River Port. For this purpose, we define
for
and
tons, as well as the value
for
and
tons. On the basis of (13) and (15), we obtain the following equations:
It’s easy to make sure that the integer root of the Equation (17) is , and the integer root of the Equation (18) is . It confirms that the optimal number of handling machines equals 3 for loading and unloading bays. The number of machines is the same, because the coefficients in Equations (17) and (18) are very similar, which can be explained by similar characteristics of input and output flows of requests for services in the Amur Harbor hub.
Since the values of each of the parameters are optimal with the corresponding optimal values of the other two numeric characteristics of the production facilities, it can be argued that the obtained set contains the optimal numerical characteristics of the production resources of the Amur Harbor cargo area for the variant of the material flow service with transshipments through the warehouse.
The conducted research yields the following managerial insights:
the operational expenses are not sufficient indicator to evaluate the efficiency of the multimodal terminal functioning: the costs of production facilities and the income as the resulting indicators must be considered as well; the proposed criterion allows combining of the mentioned indicators in one integral criterion to be used as the objective function while the decision-making process;
the level of the demand service in multimodal transport terminals depends on the demand parameters and characteristics of the production facilities; the balance of these numeric characteristics should be considered while the justification of the amount of the resources needed to satisfy the demand;
while making the decision on the number of production recourses needed at the multimodal transport terminal, the demand parameters should be evaluated (and forecasted) for the long-term perspective, as far as the changes in the number of handling machines and the warehouse capacity are the strategic decisions;
the optimal number of handling machines at the loading bays and the warehouse capacity of the multimodal transport terminal should be estimated in complex, as the productive resources are the elements of the unified servicing sub-system.
5. Conclusions
The proposed simulation model of multimodal transport terminal operation, developed with the use of object-oriented programming principles, should be considered as an effective tool for conducting experimental studies. The presented simulation model allows researchers to study the influence of the transport hub’s criterion of efficiency on the numerical parameters of production resources and organizational influences and to take into account the stochastic nature of the demand for the transport terminal services.
The proposed full-featured simulation experiment allows the impact of the numerical parameters of the production resources to be determined, as well as the demand for the services of the transport hub on the criterion of efficiency of its operation for the alternative variants of the servicing process.
The regression models obtained using the analysis of the experimental results allowed us to formalize the dependence of the criterion of efficiency on the input control parameters for different variants of material flow service. The analysis of the regression models has allowed us to obtain the equations to substantiate the numerical characteristics of production resources in the multimodal transport terminal.
As a direction for future research, the studies of demand parameters should be mentioned: in this paper, the normal distribution of the consignment weight and the exponential distribution of the time interval between the requests in the flow were used (such distributions are typical for the Amur-Harbor cargo area), but these regularities should be also confirmed for other transport hubs. Another direction for future studies is confirmation of the dependencies of the proposed efficiency criterion on numerical characteristics of the transport terminal resources and parameters of demand for services of the transport hub.