A Fuzzy Demand-Profit Model for the Sustainable Development of Electric Vehicles in China from the Perspective of Three-Level Service Chain

Abstract

Electric vehicles have great potential in dramatically reducing environmental pollution, which has become an important strategic direction for future sustainable development. With the influence of policy support and market, the construction of new energy supply infrastructure in China has achieved remarkable outcomes. However, according to the actual use of the new energy supply facilities, there is still a severe imbalance between long queues and unattended charging stations in some areas. Therefore, this paper aims to establish a fuzzy demand-profit model to accurately optimize new energy supply from the perspective of the three-level service chain. Then, based on authoritative historical sales data of electric vehicles in China in 2011–2018, the model is used to analyze the fuzzy demand for electric vehicle charging capacity. The research results indicate that the fuzzy demand-profit model is an effective tool to promote the coordination of new energy supply, which will provide support for the sustainable development of electric vehicles in China.

1. Introduction

With the increasing pressure of environmental protection and emission control regulations, the development of traditional automotive industry is becoming more and more difficult [1]. For instance, Wang et al. [1] pointed out that passenger car emissions (e.g., CO, NOx, PM10, and CO₂) are eight times that of 2005. As part of the new energy drives, pure electric vehicles have great potential in reducing environmental pollution, which has become an important strategic direction of sustainable development in the future [2]. Meanwhile, in recognition of these problems brought by traditional automotive, the relevant government departments in China have issued a series of policies and implementation measures to support the rapid development of the new energy industries [3]. Among them, the “Energy Conservation and New Energy Vehicle Industry Development Plan (2012–2020)” issued by the State Council clarifies the strategic positioning of China’s new energy vehicle industry, mainly driven by pure electric drives [4]. The continuous and stable supply of new energy is a necessary condition for the development of the new energy industry. It is also the key to the recognition of new energy vehicles in the end consumption segment [5]. With the influence of policy support and market, the construction of new energy supply infrastructure has also achieved remarkable outcomes. According to the authoritative statistics, the total number of charging piles in China reached 450,000 in 2018, ranking first in the world [6]. However, it is commonly appreciated that the new energy automobile industry is still in the growth stage. At present, there are still many problems to be solved, such as the low coverage of charging infrastructure, uneven layout, inconvenience, and charging queuing time, which hinder the actual effective demand [7]. Furthermore, there is a severe imbalance between long queues and unattended charging stations in some areas in terms of the actual use of the new energy supply facilities. To solve the problem of imbalance, it is necessary to ensure information symmetry among new energy users, charging pile operators, and power suppliers, to carry out charging pile construction and energy supply according to the demand, and to improve the efficiency of resource allocation. Meanwhile, the demand of new energy users is the basis for the construction of charging pile operators, as well as the basis for power suppliers to provide energy supply to charging pile operators. Therefore, the study of their disharmony should be analyzed as a three-level service chain composed of these three participants.

To address the incoordination problems, many research studies have been conducted in optimizing the supply chain. For instance, Reybiers et al. [8,9] investigated how to design contracts and perform quality control in a bi-level supply chain. Cachon et al. [10,11,12] attempted to design contracts to solve the incoordination problem between suppliers and manufactures under asymmetry information. Indeed, contract theory provides the fundamental support for solving the supply chain coordination problems [13,14], but due to the uncertain demand considered in the supply chain, it faces new challenges. How to develop the contracts under a particular environment becomes a negligible problem in modeling supply chain coordination [15,16].

Achievements could be drawn from the existing supply chain models of manufacturing, fresh, and logistics. Many scholars have only briefly processed the uncertain demand in the supply chain and researched this basis. Some researchers focused on manufacturing supply chain [17,18,19,20,21,22,23]. For example, the research by Rong et al. [17] studied the inventory model with fuzzy stochastic demand, while Sadeghi et al. [21] established a supplier inventory management model under uncertain demand constraints, under the area of fuzzy demand, and designed the cost allocation and quality control contract. Some other researchers concentrated on the perishable supply chain [24,25,26,27,28]. For example, Xu et al. [25] used the triangular fuzzy number to construct the retailer decision model. Findings in the emergency supply chain are also of value [29,30,31,32,33,34]. Alsalloum et al. [29] developed a dynamic inventory strategy for emergency materials under triangular fuzzy information. Zheng et al. [32] studied the distribution of material demand and network distribution under uncertain demand in emergency rescue. More researchers have focused on logistics and distribution [35,36,37,38,39]. For example, Fazayeli et al. [39] planned vehicle paths based on the fuzzy demand of customers. In addition, scholars have also probed into the decision-making model [40,41,42,43,44,45,46,47]. Sang et al. [43] compared the supply chain returns of decentralized decision-making and centralized decision-making under fuzzy demand. At the same time, other researchers explored the expected profit of the supply chain in two decision-making modes under the uncertain demand for returnable goods [44,45,46,47]. Generally, most of the mentioned studies aimed at profit maximization or cost minimization in the supply chain, discussing the quantitative matching relationship among various links in the supply chain or upstream and downstream related links under fuzzy demand, realizing the balanced development in supply chain management, which will provide references in the imbalances of the energy supply service.

There are two main types of new energy supply services, namely charging and battery replacement. Considering that the proportion of the battery replacement service in the existing supply service is not representative, this paper mainly studies the charging services. In terms of charging services, new energy supply services mainly involve three main bodies: the power supplier, the charging pile operator, and the end user, in which the demand of new energy end users is the ultimate source of profit. In previous research on new energy supply, the view of single subject is usually adopted [48,49,50,51,52,53]. For example, Moon et al. [48] studied the impact of large-scale new energy implementation on the power system from the power supplier perspective, while Yıldız et al. [50] researched on the charging station operator as the profit subject for charging station location optimization, and Camus et al. [53] studied the utilization pattern of end users based on the analysis of energy supply demand. From the perspective of the three-level operation structure of power suppliers, charging pile operators, and end users in the new energy supply service chain, similarities could be drawn from the three-level operational structure of manufacturers, wholesalers, and retailers in the general commodity supply chain. The homogeneity with the new energy supply service chain allows for research from the perspective of the service chain as a whole. It can effectively reduce the inconsistency in the new energy supply services. Although the new energy supply service chain is composed of a three-level operational structure, the unique characteristics of new energy supply service operation process do not require pre-ordering, inventory, transportation, and return, so it is different from the general commodity supply chain. These differences are mainly manifested in the fact that excess energy supply provided by the power supplier cannot be easily stored. The goods provided by the power supplier and the charging pile operator do not need to be transported after the completion of the network improvement. As the energy supply is a one-way output, the end users cannot revoke the energy supply service after receiving it, and the demand of the end user determines the profit level of the whole new energy supply service chain.

The potential benefits of integrating new energy supply of electric vehicles into existing power grids have been widely recognized, but large-scale investment is also needed, such as line network transformation and power supply boosting, to ensure the continued stability of new energy supply. In order to achieve a sufficient balance between supply and demand, reduce unnecessary energy waste, and ensure the stability of the power grid, the power supplier needs to make additional power demand plans according to the charging demand forecast of the electric vehicle. At the same time, the supplier should request for quantitative demand data when accepting the charging pile operators’ contracts. On one hand, cost compensation can be obtained as soon as possible. On the other hand, it can prevent charging pile operators from constructing non-operating stations to obtain government subsidies. In order to obtain a quick return on investment, the charging pile operators must further promote the effective demand of new energy sources to complete the contract quantity. Other scholars have quantified the energy saving and emission reduction benefits of electric vehicles [54,55,56], such as Boqiang et al. [54] who formulated a strategy to meet energy demand under the carbon emission constraints. Grubb et al. [56] suggested that the low carbon efficiency of electric vehicle charging piles should be taken as an investment strategy. Based on the survey of all levels of the new energy supply service chain, starting from the overall perspective of the service chain, taking the end user’s demand as the premise, obscuring the undetermined demand, and considering the change in demand over time, the quantity and profit of the supply chain was studied, allowing for the coordination of limited resources and operation efficiency improvement.

The above discussions demonstrate that few studies have paid close attention to the imbalance problem of new energy supply infrastructure from the perspective of the three-level service chain. The aim of this paper is, therefore, to build the three-level new energy supply service chain of charging service and to establish a fuzzy demand model and profit model. The remainder of this paper is organized as follows. Section 2 introduces the basic structure of the target supply chain. The fuzzy demand-profit model is presented in Section 3. Empirical results are given in Section 4. Results analysis is discussed in Section 5, and the conclusion of this paper is presented in Section 6.

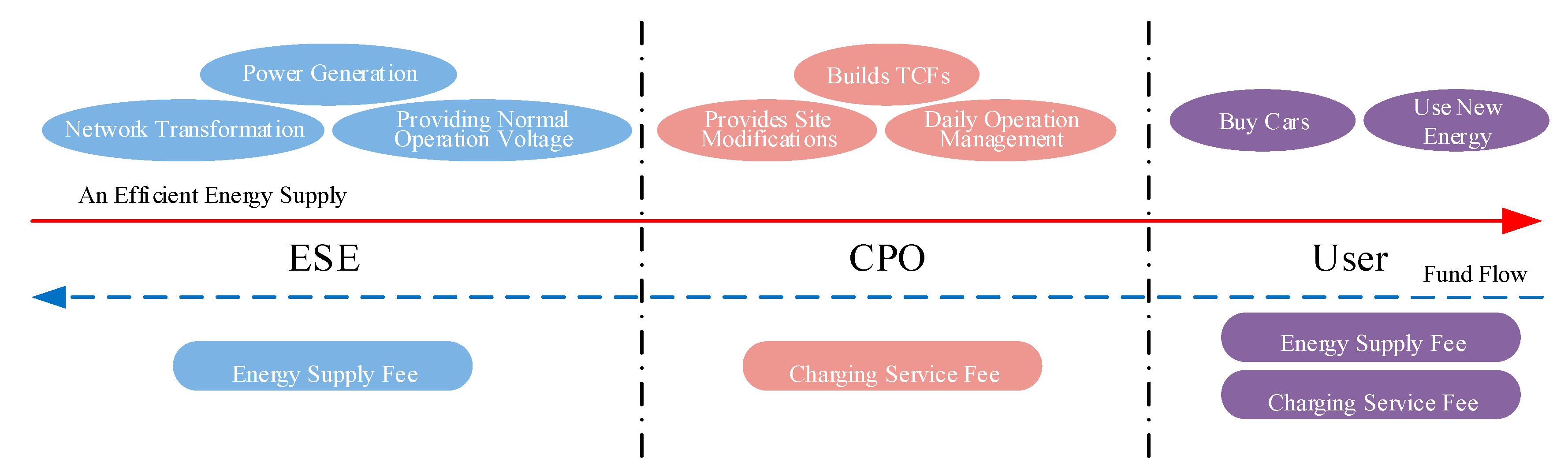
2. New Energy Supply Service Chain

The concept of the service chain is proposed based on the understanding of service management. Ken Ruggles [57] (2005) considered it a relationship chain connected with different service providers, providing consumers with comprehensive and high-quality services and improving the service quality of business to consumers.

In practices of new energy supply, electricity supply enterprises (ESEs) cooperate with various charging pile operators (CPOs) to provide end users with an efficient energy supply through the charging facilities(TCFs). During this process, CPOs need to obtain (purchase) energy supply from ESEs and transmit (sell) it to electric vehicle users through the charging facilities. In this service chain, electricity suppliers and charging pile operators need to work together to meet the energy service needs of end users. In this regard, charging pile operators pay electricity suppliers to obtain energy supply and collect charges by selling electricity to end users, as shown in Figure 1.

Figure 1 illustrates that in the single-format service chain for new energy supply:

The electricity supplier is responsible for power generation, electricity transmission, and providing normal operation voltage to the charging pile operator.

The charging pile operators do not need to order electricity from the power supplier in advance or maintain energy storage facilities. Instead, the primary investment of the charging pile operator is to build new charging infrastructure, and provide updates and maintenance to old devices in daily operations for end users using the charging service.

The costs from end users consist of two parts, namely, the fee for purchasing electricity and the fee for paying charging service.

Furthermore, in Figure 1, the red solid arrow line indicates the direction of energy supply: power suppliers supply energy to charging pile operators, who supply energy to new energy users through charging infrastructure. The blue arrow line indicates the fund flow: New Energy Vehicle users need to pay to charge pile operators to receive energy supply services, and charging pile operators also need to pay electricity suppliers.

3. Model Development

To describe the demand of new energy supply and the profit status of each subject in the service chain of new energy supply, the uncertain demand model and the profit model for the new energy supply single-format service chain are established, respectively.

3.1. The Fuzzy Demand Model for the New Energy Supply Single-Format Service Chain

The role of electric vehicles in mitigating carbon emission has been fully recognized. As the electric vehicle industry is still in the growth stage, due to factors such as the construction of charging facilities and the convenience of charging, the actual number of electric vehicle charging may be different from the charge demand predicted by the number of electric vehicles. There is still a gap between demand and actual effective demand. Moreover, the large deviations in the actual effective demand bring great difficulty to the allocation of resources in the new energy supply chain. Considering the actual deviation, the demand is usually set as the minimum possible effective fuzzy demand, the most likely effective fuzzy demand, and the maximum effective fuzzy demand. The resource allocation under this fuzzy set can reduce the incoordination of the service chain. The triangular fuzzy number is a crucial method to transform the uncertain variable into effective fuzzy sets. The actual effective demand in the new energy supply can be set as the triangular fuzzy number to study service chain contract. Therefore, it can be assumed that the effective demand of new energy supply could be formulated through the triangular fuzzy variable $\tilde{S}=\left(s_1,s_2,s_3\right)$, where $s_2$ within the $s_1<s_2<s_3$ set is the center point of the triangular fuzzy variable, meaning that the demand from new energy users will be approximately $s_2$. $s_1$ is the minimum demand, and $s_3$ is the maximum demand. The actual rate of $s_1$, $s_2$, $s_3$ is determined through the collection of data and subsequent analysis. The function of $\tilde{S}$ is:

$${\mu }_{\tilde{S}\left(x\right)}=\{\begin{array}{l}\frac{x-s_1}{s_2-s_1},x\in \left[s_1,s_2\right]\\ \frac{s_3-x}{s_3-s_2},x\in \left(s_2,s_3\right]\\ 0,x\notin \left[s_1,s_3\right]\end{array}$$

(1)

The fuzzy demand of new energy $\tilde{S}$ is taken using $\lambda$, and can be indicated using ${\tilde{S}}_{\lambda }=\left[{\tilde{S}}_{\lambda }^L,{\tilde{S}}_{\lambda }^R\right]$, where ${\tilde{S}}_{\lambda }^L$ is the left hand side and ${\tilde{S}}_{\lambda }^R$ is the right hand side of ${\tilde{S}}_{\lambda }$:

$${\tilde{S}}_{\lambda }^L=\inf \left\{x\in R:{\mu }_{\tilde{S}\left(x\right)}\ge \lambda \right\}=L^{-1}\left(\lambda \right)=s_1+\left(s_2-s_1\right)\lambda$$

(2)

$${\tilde{S}}_{\lambda }^R=\sup \left\{x\in R:{\mu }_{\tilde{S}\left(x\right)}\ge \lambda \right\}=R^{-1}\left(\lambda \right)=s_3-\left(s_3-s_2\right)\lambda$$

(3)

Hence, the expected fuzzy demand for new energy users could be calculated through:

$$\mathrm{E}\left(\tilde{S}\right)=\frac{1}{2}{\displaystyle {\int }_0^1\left[L^{-1}\left(\lambda \right)+R^{-1}\left(\lambda \right)\right]}d\lambda$$

(4)

3.2. The Profit Model for the New Energy Supply Single-Format Service Chain

In the new energy supply industry, charging services is the most commonly used. The sector of battery replacement is relatively small and has little impact on the profit of the overall service chain. Therefore, this paper only studies the charging service mode. The variables considered in this paper are as follows:

(a)

The power supplier provides energy supply guarantee for the charging pile operator. In order to ensure the safe and orderly supply of energy, the power supplier needs to transform and increase the voltage of the network. This investment cannot be completed suddenly, and the charging pile operators need to provide a contract price and quantity to ensure the use of new investment can obtain a quick return on investment. Assume that before the investment of the new infrastructure, the charging pile operator and power suppliers arrive at the contract price of $p$ and quantity of $q$ and the energy supplier charges the charging pile operator at the energy supply price of $p_1$;

(b)

It is assumed that the power supplier adopts the same charging standard to the charging pile operator and provides a homogeneous energy supply service. The power supplier needs to invest a fixed cost of $c_{ef}$ to boost voltage for ensuring the quality and stability of the contract quantity and variable costs of $c_{ev}$ such as maintenance;

(c)

The charging price charged by the charging pile operator to provide energy supply to the end user is $p_2$. This price includes charging a service fee and the energy supply fee collected by the generation power supplier;

(d)

The charging pile operator provides end users with continuous and stable energy supply services. The fixed costs such as the construction of the charging infrastructure is $c_{cf}$, and the variable costs such as operation management is $c_{cv}$;

(e)

The price of end user using traditional fossil fuel energy is $p_0$, thus fulfilling the relationship of $p_0>p_2>p_1$;

(f)

The cost for the end user to choose alternative charging methods (e.g., home charging stations) is $c_{uv}$;

(g)

End users are advocates of low carbon emissions and will consider their contribution to the reducing carbon emissions. At the same time, they are rational economic people who pay attention to the cost of new energy use, hope to trade the reduced carbon emissions and convert them into their own economic benefits, and set the carbon emission reduction between new energy and traditional energy contribution value as $\xi$;

(h)

Fisker has announced that it will use the patented technology to run an electric vehicle for 800 km with a charging time of only 1 min. Volkswagen and many other car companies have released the latest technological breakthroughs, which can achieve a charging range of 450–6000 km within 15–30 min. From progress of these charging technologies, the charging time of new energy vehicles will not affect consumer demand. Therefore, this paper does not consider the impact of charging time on the charging demand.

Based on the above variable settings, the profit of the electricity supplier, the charging pile operator, the end user, and the entire new energy supply single-format service chain are:

$${\tilde{\prod }}_{ESE}=p_1\ast \min \left\{q,\tilde{S}\right\}-c_{ev}\ast \min \left\{q,\tilde{S}\right\}-c_{ef}\ast q$$

(5)

$${\tilde{\prod }}_{CPO}=p_2\ast \min \left\{q,\tilde{S}\right\}-\left(c_{cv}+p_1\right)\ast \min \left\{q,\tilde{S}\right\}-c_{cf}\ast q$$

(6)

$${\tilde{\prod }}_{Users}=\left(p_0-p_2\right)\ast \min \left\{q,\tilde{S}\right\}-c_{uv}\ast \tilde{S}+\xi \ast q$$

(7)

$$\tilde{\prod }={\tilde{\prod }}_{ESE}+{\tilde{\prod }}_{CPO}+{\tilde{\prod }}_{Users}$$

(8)

According to the relationship between the fuzzy demand of new energy $\tilde{S}$ and the quantity of contract supply $q$, it can be divided into the following two scenarios:

Scenario 1 when $q\in \left[s_1,s_2\right]$, the $\lambda$ of $\min \left\{q,\tilde{S}\right\}$ is:

$${\left(\min \left\{q,\tilde{S}\right\}\right)}_{\lambda }=\{\begin{array}{l}\left[L^{-1}\left(\lambda \right),q\right],\lambda \in \left[0,L\left(q\right)\right]\\ \left[q,q\right],\lambda \in \left(L\left(q\right),1\right]\end{array}$$

(9)

At this point, the fuzzy expected profit of the power supplier is:

$$\begin{gathered} E\left({\tilde{\prod }}_{ESE}\right)=p_1\ast E\left[\min \left\{q,\tilde{S}\right\}\right]-c_{ev}\ast E\left[\min \left\{q,\tilde{S}\right\}\right]-c_{ef}\ast q \\ =\left(p_1-c_{ev}\right)\ast \left[\frac{1}{2}{\displaystyle {\int }_0^{L\left(q\right)}\left[L^{-1}\left(\lambda \right)+q\right]}d\lambda +\frac{1}{2}{\displaystyle {\int }_{L\left(q\right)}^1\left[q+q\right]}d\lambda \right]-c_{ef}\ast q \end{gathered}$$

(10)

The fuzzy expected profit of the power supplier against $q$ is the second derivative $\frac{d^{2}E\left({{\displaystyle \tilde{\prod }}}_{ESE}\right)}{d{q}^2}=-\frac{1}{2}{p}_1{L}^{\prime }\left(q\right)<0$, thus, when $q\in \left[s_1,s_2\right]$, $E\left({{\displaystyle \tilde{\prod }}}_{ESE}\right)$ is related to the concave function of $q$.

Scenario 2 when $q\in \left(s_2,s_3\right]$, the $\lambda$ of $\min \left\{q,\tilde{S}\right\}$ is:

$${\left(\min \left\{q,\tilde{S}\right\}\right)}_{\lambda }=\{\begin{array}{l}\left[L^{-1}\left(\lambda \right),q\right],\lambda \in \left[0,R\left(q\right)\right]\\ \left[L^{-1}\left(\lambda \right),R^{-1}\left(\lambda \right)\right],\lambda \in \left(R\left(q\right),1\right]\end{array}$$

(11)

At this point, the fuzzy expected profit of the power supplier is:

$$\begin{gathered} E\left({\tilde{\prod }}_{ESE}\right)=p_1\ast E\left[\min \left\{q,\tilde{S}\right\}\right]-c_{ev}\ast E\left[\min \left\{q,\tilde{S}\right\}\right]-c_{ef}\ast q \\ =\left(p_1-c_{ev}\right)\ast \left[\frac{1}{2}{\displaystyle {\int }_0^{R\left(q\right)}\left[L^{-1}\left(\lambda \right)+q\right]}d\lambda +\frac{1}{2}{\displaystyle {\int }_{R\left(q\right)}^1\left[q+q\right]}d\lambda \right]-c_{ef}\ast q \end{gathered}$$

(12)

With the same logic, the fuzzy expected profit of the power supplier against $q$ is the second derivative $\frac{d^{2}E\left({{\displaystyle \tilde{\prod }}}_{ESE}\right)}{d{q}^2}=\frac{1}{2}{p}_1{R}^{\prime }\left(q\right)<0$, thus, when $q\in \left[s_2,s_3\right]$, $E\left({{\displaystyle \tilde{\prod }}}_{ESE}\right)$ is related to the concave function of $q$.

In summary, the fuzzy expected profit of the power supplier is a concave function. According to the energy supply price provided by the electricity supplier to the charging pile operator, the optimal contract quantity of the power supplier is:

$$q_{{}_{ESE}}^{*}=\{\begin{array}{l}{L}^{-1}\left[\frac{2\left(p_1-c_{ev}-c_{ef}\right)}{p_1-c_{ev}}\right],q\in \left[s_1,s_2\right]\\ R^{-1}\left(\frac{2c_{ef}}{p_1-c_{ev}}\right),q\in \left(s_2,s_3\right]\end{array}$$

(13)

The charging pile operator follows the assumption of rational economic decision making and pursues the goal of maximizing profit. The fuzzy expected profit of the charging pile operator can be calculated as:

$$E\left({\tilde{\prod }}_{CPO}\right)=\{\begin{array}{l}\left(p_2-p_1-c_{cv}\right)\ast \left[\frac{1}{2}{\displaystyle {\int }_0^{L\left(q\right)}\left[L^{-1}\left(\lambda \right)+q\right]}d\lambda +\frac{1}{2}{\displaystyle {\int }_{L\left(q\right)}^1\left[q+q\right]}d\lambda \right]-c_{cf}\ast q,q\in \left[s_1,s_2\right]\\ \left(p_2-p_1-c_{cv}\right)\ast \left[\frac{1}{2}{\displaystyle {\int }_0^{R\left(q\right)}\left[L^{-1}\left(\lambda \right)+q\right]}d\lambda +\frac{1}{2}{\displaystyle {\int }_{R\left(q\right)}^1\left[L^{-1}\left(\lambda \right)+R^{-1}\left(\lambda \right)\right]}d\lambda \right]-c_{cf}\ast q,q\in \left(s_2,s_3\right]\end{array}$$

(14)

The fuzzy expected profit of the charging pile operator against $q$ is the second derivative $\frac{d^{2}E\left({{\displaystyle \tilde{\prod }}}_{CPO}\right)}{d{q}^2}=\{\begin{array}{c}-\frac{1}{2}\left(p_2-p_1-c_{cv}\right)L^{\prime }\left(q\right)<0,q\in \left[s_1,s_2\right]\\ \frac{1}{2}\left(p_2-p_1-c_{cv}\right)R^{\prime }\left(q\right)<0,q\in \left(s_2,s_3\right]\end{array}$, thus, the fuzzy expected profit of charging pile operator is also a concave function. The optimal contract quantity of the charging pile operator is:

$$q_{{}_{CPO}}^{*}=\{\begin{array}{l}{L}^{-1}\left[\frac{2\left(p_2-p_1-c_{cv}-c_{cf}\right)}{p_2-p_1-c_{cv}}\right],q\in \left[s_1,s_2\right]\\ R^{-1}\left(\frac{2c_{cf}}{p_2-p_1-c_{cv}}\right),q\in \left(s_2,s_3\right]\end{array}$$

(15)

As the new energy end user is the deciding factor, when $q\in \left[s_1,s_2\right]$, the fuzzy expected profit of end user is:

$$\begin{gathered} E\left({\tilde{\prod }}_{Users}\right)=\left(p_0-p_2\right)\ast E\left[\min \left\{q,\tilde{S}\right\}\right]-c_{uv}\ast E\left[\tilde{S}\right]+\xi \ast q \\ =\left(p_0-p_2\right)\ast \left[\frac{1}{2}{\displaystyle {\int }_0^{L\left(q\right)}\left[L^{-1}\left(\lambda \right)+q\right]}d\lambda +\frac{1}{2}{\displaystyle {\int }_{L\left(q\right)}^1\left[q+q\right]}d\lambda \right]-c_{uv}\ast \left[\frac{1}{2}{\displaystyle {\int }_0^1\left[L^{-1}\left(\lambda \right)+R^{-1}\left(\lambda \right)\right]}d\lambda \right]+\xi \ast q \end{gathered}$$

(16)

When $q\in \left(s_2,s_3\right]$, the fuzzy expected profit of the end user is:

$$\begin{gathered} E\left({\tilde{\prod }}_{Users}\right)=\left(p_0-p_2\right)\ast E\left[\min \left\{q,\tilde{S}\right\}\right]-c_{uv}\ast E\left[\tilde{S}\right]+\xi \ast q \\ =\left(p_0-p_2\right)\ast \left[\frac{1}{2}{\displaystyle {\int }_0^{R\left(q\right)}\left[L^{-1}\left(\lambda \right)+q\right]}d\lambda +\frac{1}{2}{\displaystyle {\int }_{R\left(q\right)}^1\left[q+q\right]}d\lambda \right]-c_{uv}\ast \left[\frac{1}{2}{\displaystyle {\int }_0^1\left[L^{-1}\left(\lambda \right)+R^{-1}\left(\lambda \right)\right]}d\lambda \right]+\xi \ast q \end{gathered}$$

(17)

The fuzzy expected profit of the new energy end users against $q$ is the second derivative $\frac{d^{2}E\left({{\displaystyle \tilde{\prod }}}_{Users}\right)}{d{q}^2}=\{\begin{array}{c}-\frac{1}{2}\left(p_0-p_2\right)L^{\prime }\left(q\right)<0,q\in \left[s_1,s_2\right]\\ \frac{1}{2}\left(p_0-p_2\right)R^{\prime }\left(q\right)<0,q\in \left(s_2,s_3\right]\end{array}$, thus, the fuzzy expected profit of the new energy end users is also a concave function. The optimal contract quantity of the new energy end user is:

$$q_{{}_{Users}}^{*}=\{\begin{array}{l}{L}^{-1}\left[\frac{2\left(p_0-p_2-\xi \right)}{p_0-p_2}\right],q\in \left[s_1,s_2\right]\\ R^{-1}\left(\frac{2\xi }{p_0-p_2}\right),q\in \left(s_2,s_3\right]\end{array}$$

(18)

In the new energy supply single-format service chain operation mode, end users as the direct consumers of new energy are the final determinants of effective demand, directly affecting the profit of the power supplier, charging pile operators, and themselves. Under the optimal decision conditions of end users, the fuzzy expected profits of end users, charging pile operators, and power suppliers are:

$$E{\left({\tilde{\prod }}_{Users}\right)}^{*}=\{\begin{array}{l}\left(p_0-p_2\right)\ast \frac{1}{2}{\displaystyle {\int }_0^{\frac{2\left(p_0-p_2-\xi \right)}{p_0-p_2}}{L}^{-1}\left(\lambda \right)}d\lambda -c_{uv}\ast \left[\frac{1}{2}{\displaystyle {\int }_0^1\left[L^{-1}\left(\lambda \right)+R^{-1}\left(\lambda \right)\right]}d\lambda \right]\\ +\xi \ast L^{-1}\left[\frac{2\left(p_0-p_2-\xi \right)}{p_0-p_2}\right],q\in \left[s_1,s_2\right]\\ \left(p_0-p_2\right)\ast \frac{1}{2}{\displaystyle {\int }_0^1{L}^{-1}\left(\lambda \right)}d\lambda +\left(p_0-p_2\right)\ast \frac{1}{2}{\displaystyle {\int }_{\frac{2\xi }{p_0-p_2}}^1{R}^{-1}\left(\lambda \right)}d\lambda -c_{uv}\ast \left[\frac{1}{2}{\displaystyle {\int }_0^1\left[L^{-1}\left(\lambda \right)+R^{-1}\left(\lambda \right)\right]}d\lambda \right]\\ +\xi \ast R^{-1}\left(\frac{2\xi }{p_0-p_2}\right),q\in \left(s_2,s_3\right]\end{array}$$

(19)

$$E{\left({\tilde{\prod }}_{CPO}\right)}^{*}=\{\begin{array}{l}\left(p_2-p_1-c_{cv}\right)\ast \left\{\frac{1}{2}{\displaystyle {\int }_0^{\frac{2\left(p_0-p_2-\xi \right)}{p_0-p_2}}{L}^{-1}\left(\lambda \right)}d\lambda -\frac{1}{2}{L}^{-1}\left[\frac{2\left(p_0-p_2-\xi \right)}{p_0-p_2}\right]\ast \frac{2\left(p_0-p_2-\xi \right)}{p_0-p_2}+L^{-1}\left[\frac{2\left(p_0-p_2-\xi \right)}{p_0-p_2}\right]\right\}\\ -c_{cf}\ast L^{-1}\left[\frac{2\left(p_0-p_2-\xi \right)}{p_0-p_2}\right],q\in \left[s_1,s_2\right]\\ \left(p_2-p_1-c_{cv}\right)\ast \left\{\frac{1}{2}{\displaystyle {\int }_0^1{L}^{-1}\left(\lambda \right)}d\lambda +\frac{1}{2}{R}^{-1}\left(\frac{2\xi }{p_0-p_2}\right)\ast \frac{2\xi }{p_0-p_2}+\frac{1}{2}{\displaystyle {\int }_{\frac{2\xi }{p_0-p_2}}^1{R}^{-1}\left(\lambda \right)}d\lambda \right\}\\ -c_{cf}\ast R^{-1}\left(\frac{2\xi }{p_0-p_2}\right),q\in \left(s_2,s_3\right]\end{array}$$

(20)

$$E{\left({\tilde{\prod }}_{ESE}\right)}^{*}=\{\begin{array}{l}\left(p_1-c_{ev}\right)\ast \left\{\frac{1}{2}{\displaystyle {\int }_0^{\frac{2\left(p_0-p_2-\xi \right)}{p_0-p_2}}{L}^{-1}\left(\lambda \right)}d\lambda -\frac{1}{2}{L}^{-1}\left[\frac{2\left(p_0-p_2-\xi \right)}{p_0-p_2}\right]\ast \frac{2\left(p_0-p_2-\xi \right)}{p_0-p_2}+L^{-1}\left[\frac{2\left(p_0-p_2-\xi \right)}{p_0-p_2}\right]\right\}\\ -c_{ef}\ast L^{-1}\left[\frac{2\left(p_0-p_2-\xi \right)}{p_0-p_2}\right],q\in \left[s_1,s_2\right]\\ \left(p_1-c_{ev}\right)\ast \left\{\frac{1}{2}{\displaystyle {\int }_0^1{L}^{-1}\left(\lambda \right)}d\lambda +\frac{1}{2}{R}^{-1}\left(\frac{2\xi }{p_0-p_2}\right)\ast \frac{2\xi }{p_0-p_2}+\frac{1}{2}{\displaystyle {\int }_{\frac{2\xi }{p_0-p_2}}^1{R}^{-1}\left(\lambda \right)}d\lambda \right\}\\ -c_{ef}\ast R^{-1}\left(\frac{2\xi }{p_0-p_2}\right),q\in \left(s_2,s_3\right]\end{array}$$

(21)

When the end users, charging pile operators, and power suppliers in the new energy supply single-format service chain make centralized decisions, the profits of the entire service chain can be expressed as:

$$\tilde{\prod }=\left(p_0-c_{ev}-c_{cv}\right)\ast \min \left\{q,\tilde{S}\right\}-\left(c_{ef}+c_{cf}-\xi \right)\ast q-c_{uv}\ast \tilde{S}$$

(22)

When the entire new energy supply single-format service chain has a fuzzy expected profit:

$$\mathrm{E}\left(\tilde{\prod }\right)=\{\begin{array}{l}\left(p_0-c_{ev}-c_{cv}\right)\ast \left\{\frac{1}{2}{\displaystyle {\int }_0^{L\left(q\right)}\left[L^{-1}\left(\lambda \right)+q\right]}d\lambda +\frac{1}{2}{\displaystyle {\int }_{L\left(q\right)}^1\left[q+q\right]}d\lambda \right\}-\left(c_{ef}+c_{cf}-\xi \right)\ast q\\ +c_{uv}\ast \frac{1}{2}{\displaystyle {\int }_0^1\left[L^{-1}\left(\lambda \right)+R^{-1}\left(\lambda \right)\right]}d\lambda ,q\in \left[s_1,s_2\right]\\ \left(p_0-c_{ev}-c_{cv}\right)\ast \left\{\frac{1}{2}{\displaystyle {\int }_0^{R\left(q\right)}\left[L^{-1}\left(\lambda \right)+q\right]}d\lambda +\frac{1}{2}{\displaystyle {\int }_{R\left(q\right)}^1\left[L^{-1}\left(\lambda \right)+R^{-1}\left(\lambda \right)\right]}d\lambda \right\}-\left(c_{ef}+c_{cf}-\xi \right)\ast q\\ +c_{uv}\ast \frac{1}{2}{\displaystyle {\int }_0^1\left[L^{-1}\left(\lambda \right)+R^{-1}\left(\lambda \right)\right]}d\lambda ,q\in \left(s_2,s_3\right]\end{array}$$

(23)

In both cases, the second derivative of the fuzzy expected profit against $q$ of the whole new energy supply single-format service chain is less than zero, which is a concave function. Therefore, the final contract quantity can be obtained as:

$$q^{*}=\{\begin{array}{l}{L}^{-1}\left[\frac{2\left(p_0-c_{ev}-c_{cv}-c_{ef}-c_{cf}+\xi \right)}{p_0-c_{ev}-c_{cv}}\right],q\in \left[s_1,s_2\right]\\ R^{-1}\left[\frac{2\left(c_{ef}+c_{cf}-\xi \right)}{p_0-c_{ev}-c_{cv}}\right],q\in \left(s_2,s_3\right]\end{array}$$

(24)

4. Analysis Results

4.1. Research Data

4.1.1. Research Data for the Fuzzy Demand Model

In order to further analyze the optimal contract quantity of the above-mentioned new energy demand in the multi-level new energy supply single-format service chain of power suppliers, charging pile operators, and end users, the actual data of electric vehicles in China from 2011 to 2018 [58] was collected. Then, five forecasting methods were applied to fit the actual data. The goodness of fit is shown in

Table 1. Comparisons of the goodness of fit of different models.

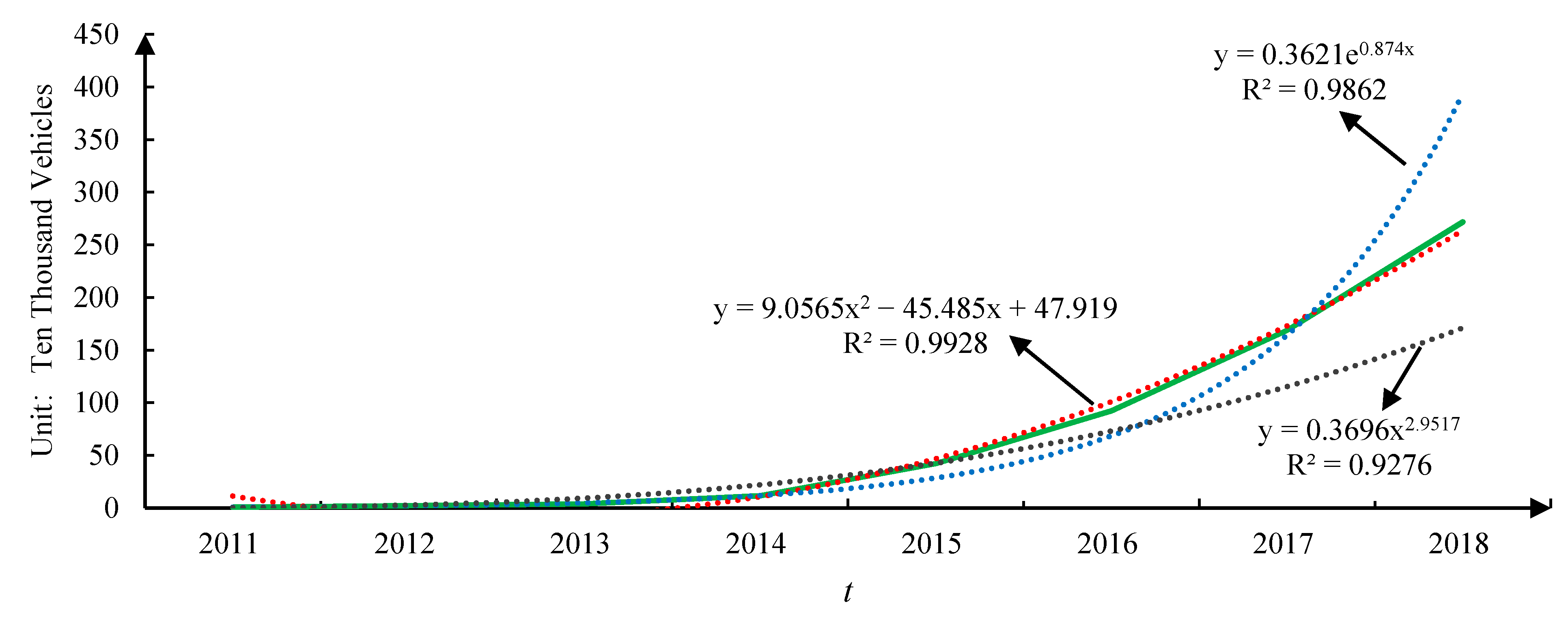
Goodness of Fitting Model	Polynomial Function	Exponential Function	Power Function	Linear Function	Logarithm Function
${\mathrm{R}}^2$	0.9928	0.9862	0.9276	0.7924	0.5501

.

Among the five methods in Table 1, the R² of the polynomial function, exponential function, and power function are all greater than 0.9, and the fitting effect is good, which can be used for the prediction in the next step. The fitting data of the three methods are compared with the actual data from 2011 to 2018. The results are shown in

Table 2. Comparison of polynomial function, exponential function, and power function.

Year	Actual Amount of Energy Vehicles (10,000)	Cumulative Amount of Energy Vehicles (10,000)	Polynomial Function		Exponential Function		Power Function
			Fitting Value (10,000)	Differences between the Fitting Value and Cumulative Amount (10,000)	Fitting Value (10,000)	Differences between the Fitting Value and Cumulative Amount (10,000)	Fitting Value (10,000)	Differences between the Fitting Value and Cumulative Amount (10,000)
2011	0.82	0.82	11.49	10.67	0.87	0.05	0.37	−0.45
2012	1.28	2.10	−6.83	−8.92	2.08	−0.02	2.86	0.76
2013	1.76	3.86	−7.03	−10.89	4.98	1.12	9.46	5.60
2014	7.75	11.61	10.88	−0.72	11.94	0.34	22.12	10.52
2015	30.60	42.21	46.91	4.70	28.62	−13.58	42.74	0.54
2016	50.07	92.28	101.04	8.77	68.59	−23.68	73.22	−19.06
2017	76.51	168.79	173.29	4.51	164.38	−4.41	115.40	−53.38
2018	102.98	271.77	263.66	−8.11	393.93	122.16	171.15	−100.61

.

According to Table 2, the fitting curve is shown in Figure 2.

In Figure 2, the green curve is the actual data, the red one is the fitting curve of the Polynomial Function, the blue one is the fitting curve of the Exponential Function, and the black one is the fitting curve of the Power Function. It can be seen that from Table 2 and Figure 2, the difference between the polynomial function and the actual data from 2011 to 2013 is a little large, while the difference from 2014 to 2018 is small, which reflects the long-term development trend of electric vehicles in China. Although the difference between the exponential function and the power function is small from 2011 to 2013, there is a big difference between 2014 and 2018, which is quite different from the actual situation. Therefore, the polynomial function is adopted in this study to forecast the energy vehicle stocks in China.

In this study, the service life of privately owned passenger vehicles is considered as 15 years [59]. It is assumed that they will be withdrawn after the service years. Through $t\in (0,15]$, the cumulative amount of energy vehicles before 2025 was predicted with the confidence level of 95%, as shown in Figure 3.

4.1.2. Research Data for the Profit Model

According to the data provided by the High-tech Lithium Battery Research Institute (GGII), the total installed capacity of electric vehicle power battery in China in 2018 is 56.89 GWh. As China’s electric vehicle tax exemption policy continues to 2020, the growth rate of new energy demand can reach 20% and it will decline after the tax exemption period. Assuming an annual growth rate of 10% [60], the energy demand for electric vehicles in China is shown in

Table 3. National new energy vehicle charging demand.

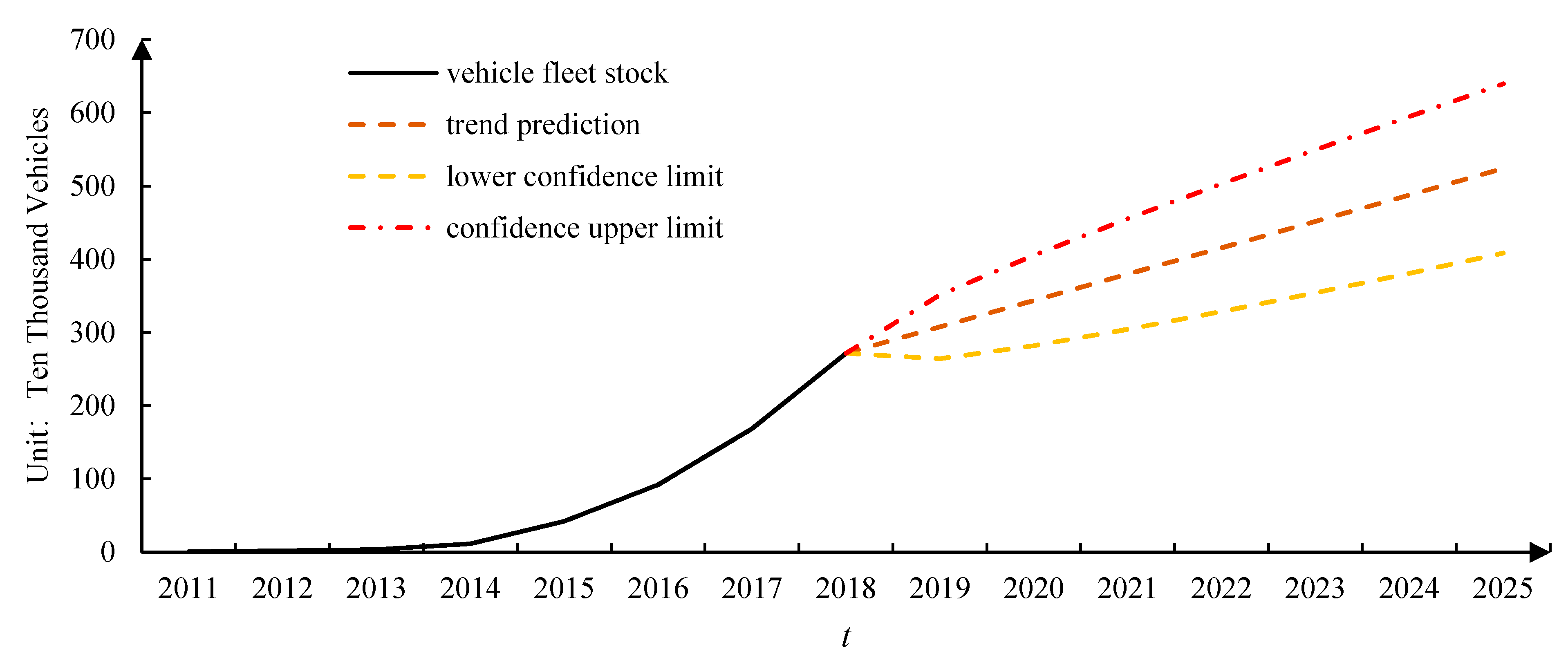
Demand	2019	2020	2021	2022	2023	2024	2025
$q$ (Unit: GWh)	68.40	82.08	90.29	99.32	109.25	120.17	132.19

.

The charging price of the mainstream charging pile is 1.6~1.8 ¥/kWh. In contrast, the average fuel consumption of a fuel vehicle with a displacement of 1.6L in the urban area is 9L per 100 km [61], and the price of gasoline is about 7 ¥/L.

Burning 1L of gasoline emits 1.69 kg of carbon dioxide [62]. The latest carbon trading price is about 70 ¥/ton [63]. For the convenience of calculation, the units of each variable are uniformly converted into ¥/kWh, as shown in

Table 4. New energy supply single-format service chain variable unit cost.

Variable	${\mathit{p}}_0$	${\mathit{p}}_1$	${\mathit{p}}_2$	$\mathit{\xi }$	${\mathit{c}}_{\mathit{e}\mathit{v}}$	${\mathit{c}}_{\mathit{e}\mathit{f}}$	${\mathit{c}}_{\mathit{c}\mathit{v}}$	${\mathit{c}}_{\mathit{c}\mathit{f}}$	${\mathit{c}}_{\mathit{u}\mathit{v}}$
Value (Yuan/kw.h)	2.1	0.78	1.7	0.08	0.14	0.22	0.16	0.24	0.6

.

4.2. Calculation Results

4.2.1. Calculation Results of the Fuzzy Demand Model

According to the prediction of the cumulative quantity of new energy vehicles in Figure 3, the average annual driving demand mileage of each vehicle as 15,000 km [61], and the average power consumption of new energy vehicles is 16 KWh every 100 km (using the Beiqi E150EV electric vehicles). The fuzzy demand for new energy in China from 2019-2025 is deduced. The results are shown in

Table 5. Fuzzy demand for national new energy vehicle charging capacity.

Fuzzy Demand	2019	2020	2021	2022	2023	2024	2025
$\tilde{S}=\left(s_1,s_2,s_3\right)$ (Unit: GWh)	(63.40, 73.87, 84.34)	(67.72, 82.51, 97.31)	(73.04, 91.16, 109.28)	(78.87, 99.81, 120.74)	(85.04, 108.45, 131.87)	(91.44, 117.10, 142.76)	(98.01, 125.74, 153.47)

.

4.2.2. Calculation Results of the Profit Model

Based on the inputs in Table 4 and Table 5, the contract number and profits of electricity suppliers, the charging pile operators, and the end users are calculated by (19)–(21). The results are shown in

Table 6. Relationship between demand quantity and optimal contract quantity.

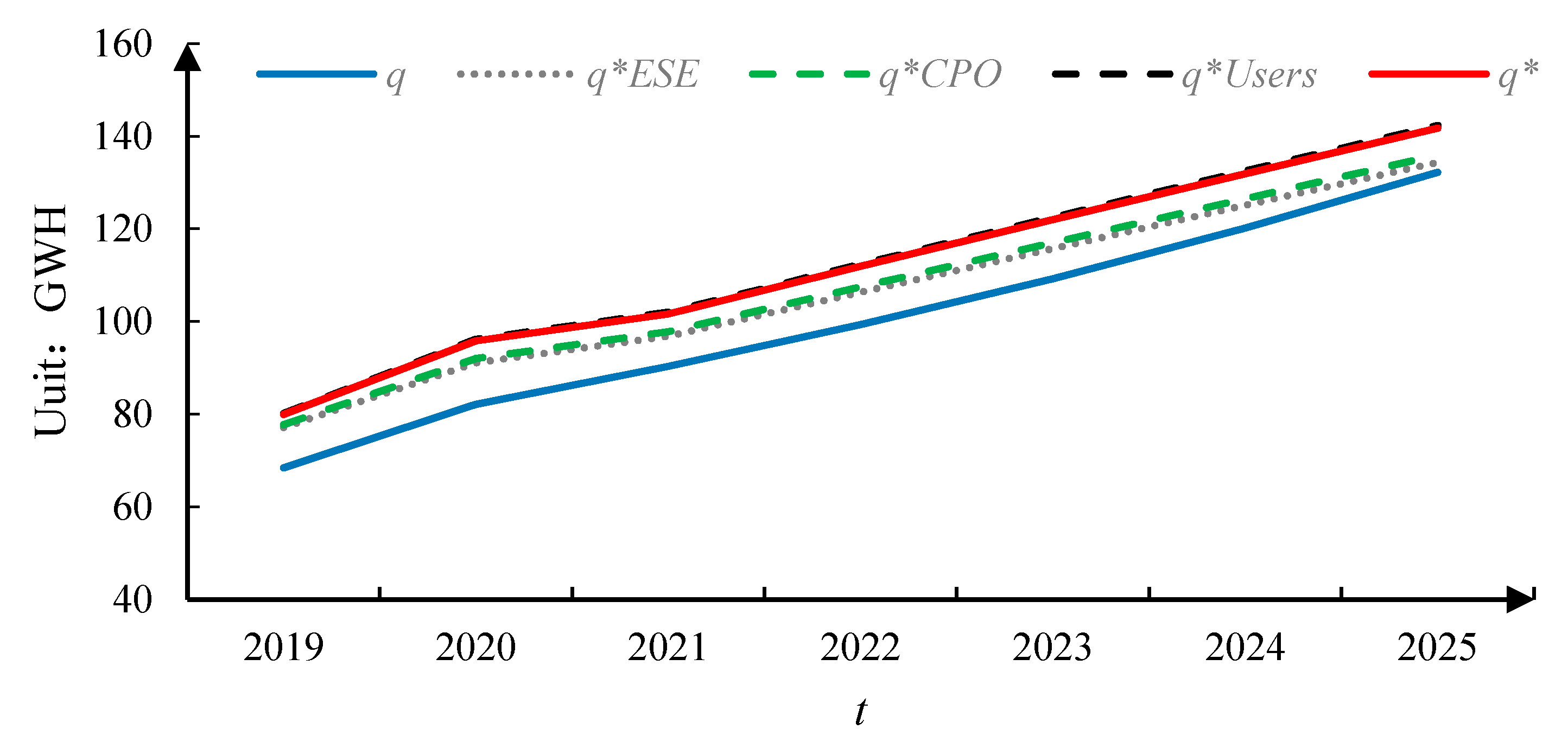
Variable	Unit	2019	2020	2021	2022	2023	2024	2025
$q$	GWh	68.40	82.08	90.29	99.32	109.25	120.17	132.19
$q_{{}_{ESE}}^{*}$	GWh	77.14	91.07	96.82	106.35	115.77	125.12	134.41
$q_{{}_{CPO}}^{*}$	GWh	77.73	92.06	97.84	107.52	117.08	126.55	135.96
$q_{{}_{Users}}^{*}$	GWh	80.15	96.18	102.03	112.37	122.50	132.50	142.38
$q^{*}$	GWh	79.92	95.79	101.63	111.91	121.98	131.93	141.76
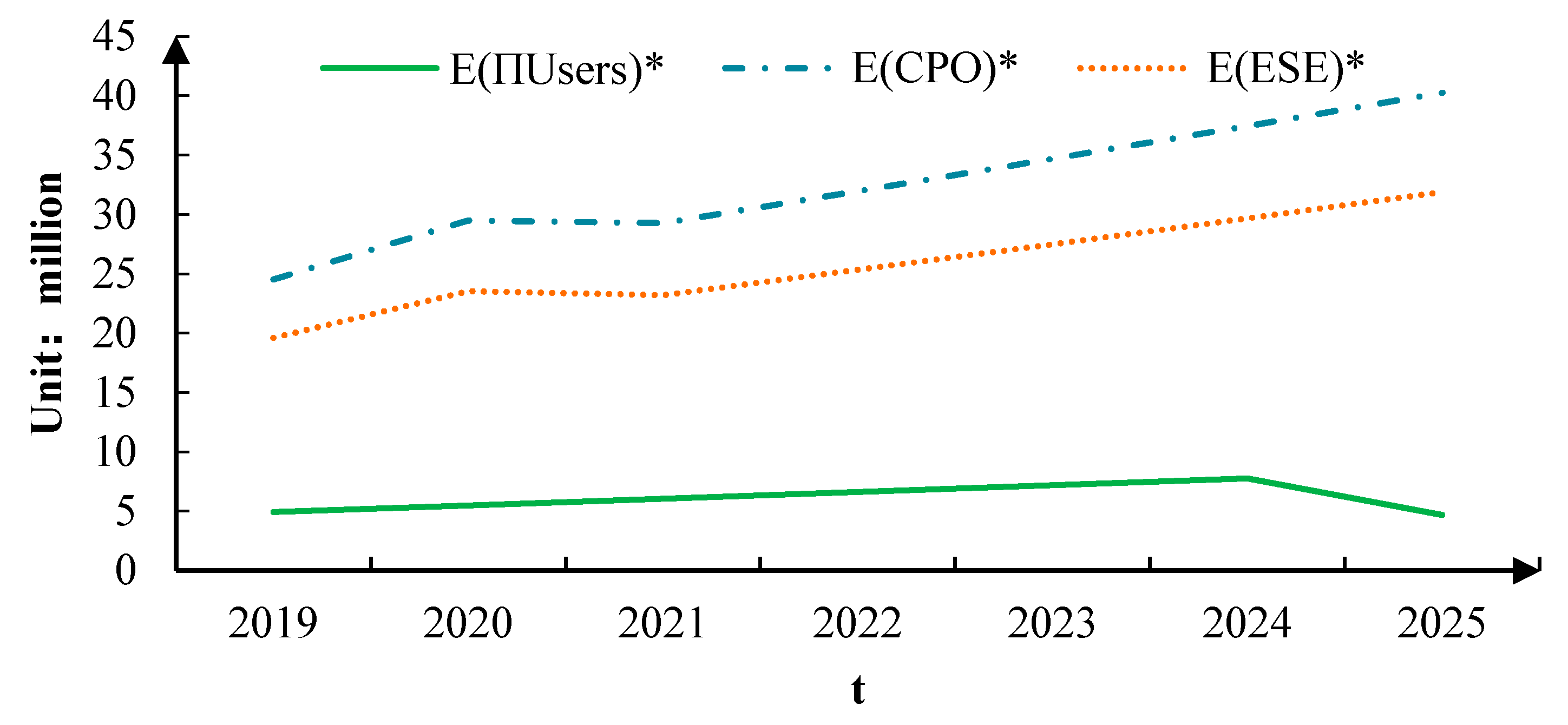
$E{\left({{\displaystyle \tilde{\prod }}}_{Users}\right)}^{*}$	1 × 106 Yuan	4.93	5.48	6.05	6.62	7.19	7.76	4.68
$E{\left({{\displaystyle \tilde{\prod }}}_{CPO}\right)}^{*}$	1 × 106 Yuan	24.53	29.50	29.28	31.98	34.71	37.47	40.26
$E{\left({{\displaystyle \tilde{\prod }}}_{ESE}\right)}^{*}$	1 × 106 Yuan	19.61	23.55	23.22	25.34	27.51	29.70	31.91

Note: “*” stands for the optimal solution.

. It is demonstrated that the number of the optimal contracts and fuzzy expected profits of the electricity supplier, the charging pile operator, and the end users change with the new energy demand, respectively.

5. Discussion

In order to investigate the impact of new energy demand to the contract number and expected profits of various stakeholders in the service chain, the optimal contract number between the new energy demand and the service chain is studied, and the relationship between new energy demand and the expected profit changes of each stakeholder in the service chain is analyzed in detail.

5.1. Changes of New Energy Demand and the Optimal Contract Number among the Main Entities of the Service Chain

As shown in Figure 4, as the effective demand for new energy sources increases, the number of optimal contracts for each participating entity in the service chain changes, and the optimal contract number of power suppliers, charging station operators, and end users is increasing. In the end, the optimal number of contracts for the end user is basically the same as that for the centralized decision-making of the entire service chain. According to this situation, the final contract quantity is slightly higher than the demand quantity, which can effectively promote the growth of the effective demand for new energy and catalyze the further promotion of new energy, which is in line with the strategic plan for new energy development in China.

The cultivation period of China’s new energy vehicle market begins with small-scale demonstration projects (such as the use of the Olympic Games and public transportation sectors). During this period, the demand for new energy is quite different from the optimal quantity of the entire service chain, which is mainly driven by government policies and financial support. With the development of new energy automobile industry, compared with the initial stage of market cultivation, the focus of government’s industrial support policy has shifted from merely technology research and development and investment to market expansion [21]. At this stage, the number of new energy vehicles is gradually increasing, and demand growth is accelerating, gradually approaching the optimal number of the whole service chain. At the same time, the subsidy policy continues to decline, the tax reduction policy is gradually cancelled, the construction and layout of charging facilities are constantly improved, shifting the whole service chain to be more market-oriented, and the new energy supply operation recognized by the end users has become an essential aspect in the increase of effective demand of new energy vehicles. At the same time, it is reflected in the end-user level and its gradual recognition of new energy. This process has strong synchronization with the improvement of industrial development maturity and the improvement of charging infrastructure. Therefore, the convenience of charging has become an important factor affecting the development speed and scale of new energy.

5.2. New Energy Demand and Changes in Expected Profit of Various Entities in the Service Chain

Figure 5 is a schematic diagram of the fuzzy expected profit of power suppliers, charging pile operators, and end users in the new energy supply single-format service chain. The fuzzy expected profits of each participating entity are increasing, and the growth rate of end users is significantly lower than other entities. In the new energy supply service chain, the initial investment of power suppliers and charging pile operators is relatively large, and the fuzzy expected profits of the latter are also significantly larger than the end users. The charging pile operators are responsible for the actual energy supply services, and the number of operators is much larger than power suppliers who are strictly related to the increase in demand. Therefore, the fuzzy expected profit of charging pile operators is higher than that of power suppliers. For the end user, its fuzzy expected profit shows a trend of slowly rising and then falling.

New energy supply infrastructure construction has achieved remarkable results, and China has become the country with the largest number of charging piles in the world. In this case, the construction investment of power suppliers and charging pile operators is reduced. With the continuous development of the new energy automobile industry and the rapid growth of energy demand, its profits can also grow steadily. However, the decline in the expected profit of end users may be related to two factors. On one hand, it is related to the change of total demand. The existing service chain can meet the needs of end users to a certain extent. However, when the demand exceeds a certain threshold, the scale and operation mode of the service chain need to be further improved. Otherwise, poor service experience and unfulfilled expectations may lead end users to other new energy supply methods (such as self-built household charging piles) to ensure their new energy demand. On the other hand, with the deepening of the global carbon emission trading mechanism and the further implementation of China’s new energy vehicle dual scoring policy, the carbon trading price in the new energy vehicle sector has shown an upward trend. The rising spillover gains are limited to the subject and length of this study and have not been explored and considered in depth.

6. Conclusions

Based on the new energy supply service chain and setting the new energy efficient demand of end users as a fuzzy variable, this paper establishes a multi-level new energy supply single-format service chain under the charging service mode and builds a new energy supply based on the demand changes with time. The fuzzy demand model and profit model of the single-format service chain are established, and the models are analyzed through the case study. In this service chain, the number of optimal contracts of the participating entities gradually increases, slightly higher than the demand.

With the development of the new energy automobile industry, the optimal contract number of end users is consistent with the optimal contract number in the centralized decision-making. The fuzzy profits of the participating entities increase steadily. The fuzzy profits of the power supplier and the charging pile operator are related to the number of groups and the actual business coverage; the fuzzy profit growth of the end users is lower than the power supplier and the charging pile operators. When the demand for new energy exceeds the demand threshold of the existing service chain, the charging pile operators need to further increase the scale and operation mode of the service chain. In general, the number of contracts developed in the new energy supply service chain has a good effect on the growth of new energy demand. In the future research, it is necessary to further measure the demand thresholds of different scales and operating modes of the service chain, and consider the changes in the fuzzy expected profits of end users under the change of carbon trading prices.