2.1. Research on Superhighways
At present, research on superhighways in China and abroad is still in its infancy. Our research team published several papers from 2016 to 2020 to conduct in-depth studies on the feasibility, safety, economy and traffic capacity of superhighways. In 2016, our research team studied the different stages of the development of new automobile technology and highway construction technology, demonstrated the feasibility of developing a superhighway, and conducted an in-depth study on the necessity of developing a superhighway [
1]. Subsequently, the team analyzed the driving characteristics of a superhighway in 2017, conducted an in-depth study on the capacity of the superhighway, and demonstrated the role of autonomous driving technology in improving the traffic capacity of the superhighway [
2]. The following year, to evaluate the economical efficiency of the superhighway, our research team conducted a comparative study on the travel expenses of superhighways and compared the single cost of traveling among civil aviation, ordinary highways, railways and other travel modes. The results showed that the single cost of traveling by superhighway is lower than that of an economy class ticket for civil aviation and is equivalent to a second-class seat for a high-speed railway and has certain economic advantages [
3,
4]. Additionally, the construction cost and use cost of a superhighway once again were studied by us in 2019, and the results showed that the comprehensive cost of a superhighway was higher than that of an ordinary highway and lower than that of a railway, and the economic feasibility of superhighways was again demonstrated [
5]. In 2020, to demonstrate the feasibility of superhighways from the perspective of safety, we studied a virtual track technology based on intelligent road buttons, which provided a strong guarantee for the safety of driving on a highway [
6]. In the same year, to demonstrate the safety alignment of superhighways, our research team studied the design theory of plane alignment, vertical alignment and cross-section alignment of superhighways based on the linear design theory of ordinary superhighways and the linear design of railways. Calculations and analysis showed that the safety of superhighways can be guaranteed by means of adopting plane curves with a large radius and relatively gentle longitudinal slope [
7].
Our team’s research on superhighways has aroused wide interest from domestic scholars. Zhao et al. established an obstacle identification model to analyze the curves of superhighways and studied the radius of the safety curve of superhighways by investigating the design of the curve of an existing highway and the problems [
8]. Chen et al. analyzed the advantages, disadvantages and external challenges of superhighways by means of SWOT (situation analysis based on internal and external competitive environment and competitive conditions) analysis during their construction and operation management, provided suggestions for the development of a superhighway, and demonstrated the advantages of developing a superhighway [
9]. Although some concepts of superhighways have been put forward in foreign countries, most of those studies have focused on the information superhighway, transportation of biochemical substances and other aspects, and a real superhighway has not yet been involved [
10,
11].
At present, the maximum speed limit of highways in more than 20 European countries has reached 130 km/h; in Italy it is 140 km/h, and in Texas it is 137 km/h (85 mile/h). There are 129,993 km of highway in Germany, approximately 2/3 of which have no speed limit [
12].
For example, 15 years ago, the speed limit of French motorways was set at 130 km/h. Long-term safe operation has provided rich experience for China’s construction of superhighways with design speed exceeding 120 km/h. Recently, due to the change of climate conditions in Europe, the French Citizens’ Climate Conference proposed to reduce the speed limit of motorways. However, this is only a drop in the ocean and cannot solve the problem fundamentally. In addition, with the rapid development of highway construction technology and automobile technology, autonomous driving technology has become increasingly mature and gradually industrialized. From Level 0 to Level 5, human intervention is less and less, the degree of intelligence is higher and higher, and the safety is more and more guaranteed. With the improvement of the level of automatic driving, safety hazards such as delayed reaction and wrong judgment caused by human physiological factors are less and less, or even eliminated, which greatly reduces the threat of adverse environment (such as rain and snow) to driving safety. Besides, Level 4 self-driving cars have entered the market, which can effectively guarantee the operation safety of superhighways. In late 1999, France established LAVIA (Limiteur s’Adaptant à la VItesse Autorisée), an intelligent speed adaptation (ISA) project. The generic term intelligent speed adaptation (ISA) includes a wide range of different technologies designed to improve road safety by reducing traffic speeds and homogenizing traffic flows within the limits of speed limits. It is estimated that a car equipped with such a speed adaptation system would reduce its injury rate under current conditions by 6 to 16 percent during use. The paper also makes a detailed analysis of the causes of fatal traffic accidents and concludes that overspeed (exceeding the speed limit) is an important cause of fatal traffic accidents. However, the “variable speed limit” system can be used to consider that speeds in certain parts of the road network should not be below the published speed limit, for example, at sharp turns, pedestrian crossings or collision black spots. The “dynamic speed limit” system takes further account of changes in weather and traffic conditions. The use of these systems can guarantee traffic safety caused by speeding [
13].
Studies have shown that, before 1997, the traffic death rate in France and the United States were fundamentally the same. Since 1997, the traffic death rate in France and the United States has decreased significantly. However, the traffic death rate in the United States is still much higher than that in France. Studies have speculated that Princess Diana died in Paris in 1997 as a result of a traffic accident caused by drunk drivers and speeding. Under pressure from public opinion, the French government has strengthened the formulation of traffic safety policies, such as making drunk driving illegal and implementing traffic light radar system. After 1997, the traffic death rate in France has been decreasing year by year. Although the United States and France both have similar vehicle engineering, road conditions and driver education, the United States did not adopt effective traffic policies after 1997 as France did, resulting in a much higher traffic death rate than France. This explains the importance of policy and traffic execution to traffic safety, which can guarantee the traffic safety problems caused by speeding to some extent [
14].
Therefore, from the perspective of highway construction technology, vehicle performance and foreign experience, conditions are ripe for the construction of superhighways with design speed exceeding 120 km/h in China.
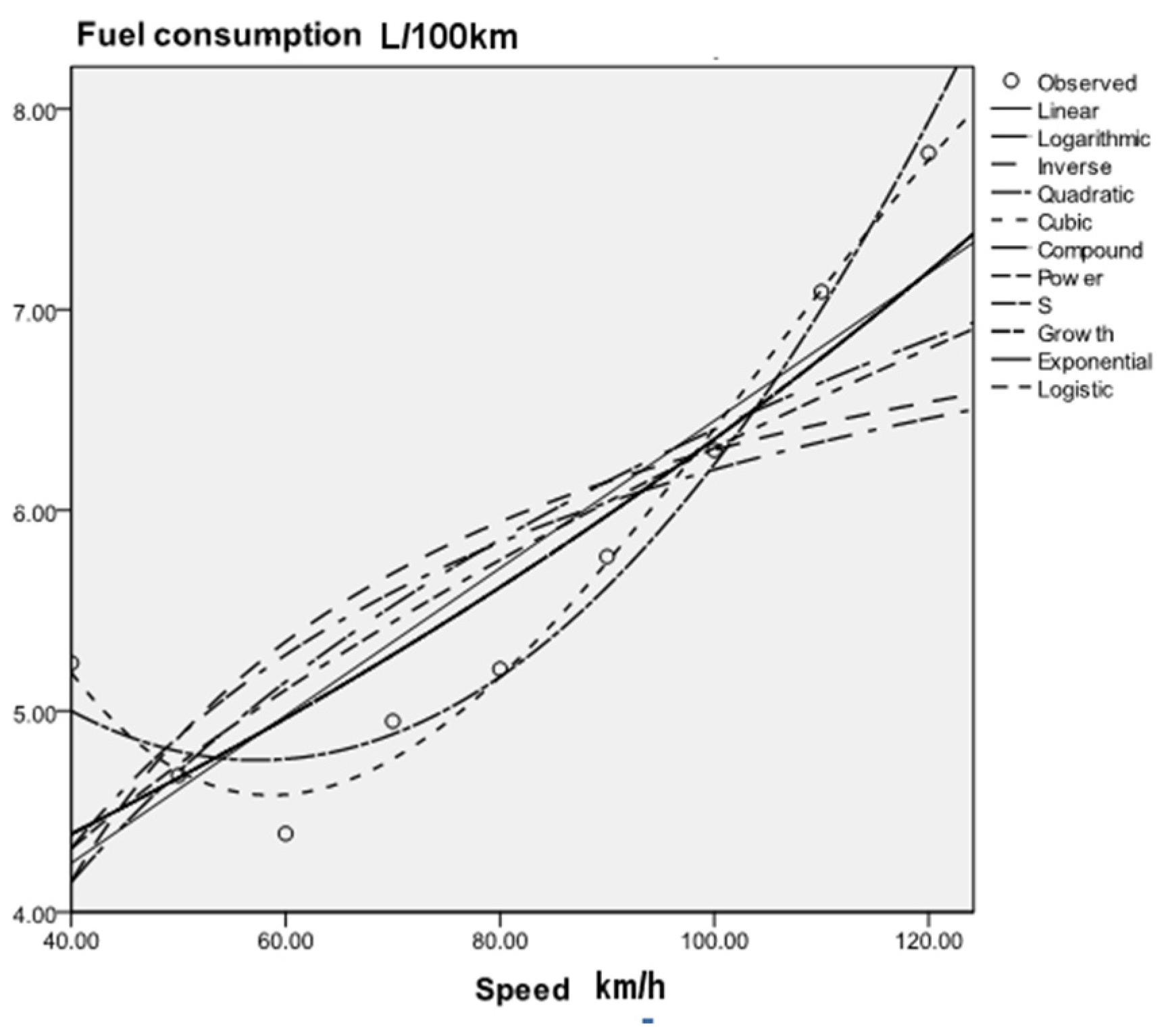
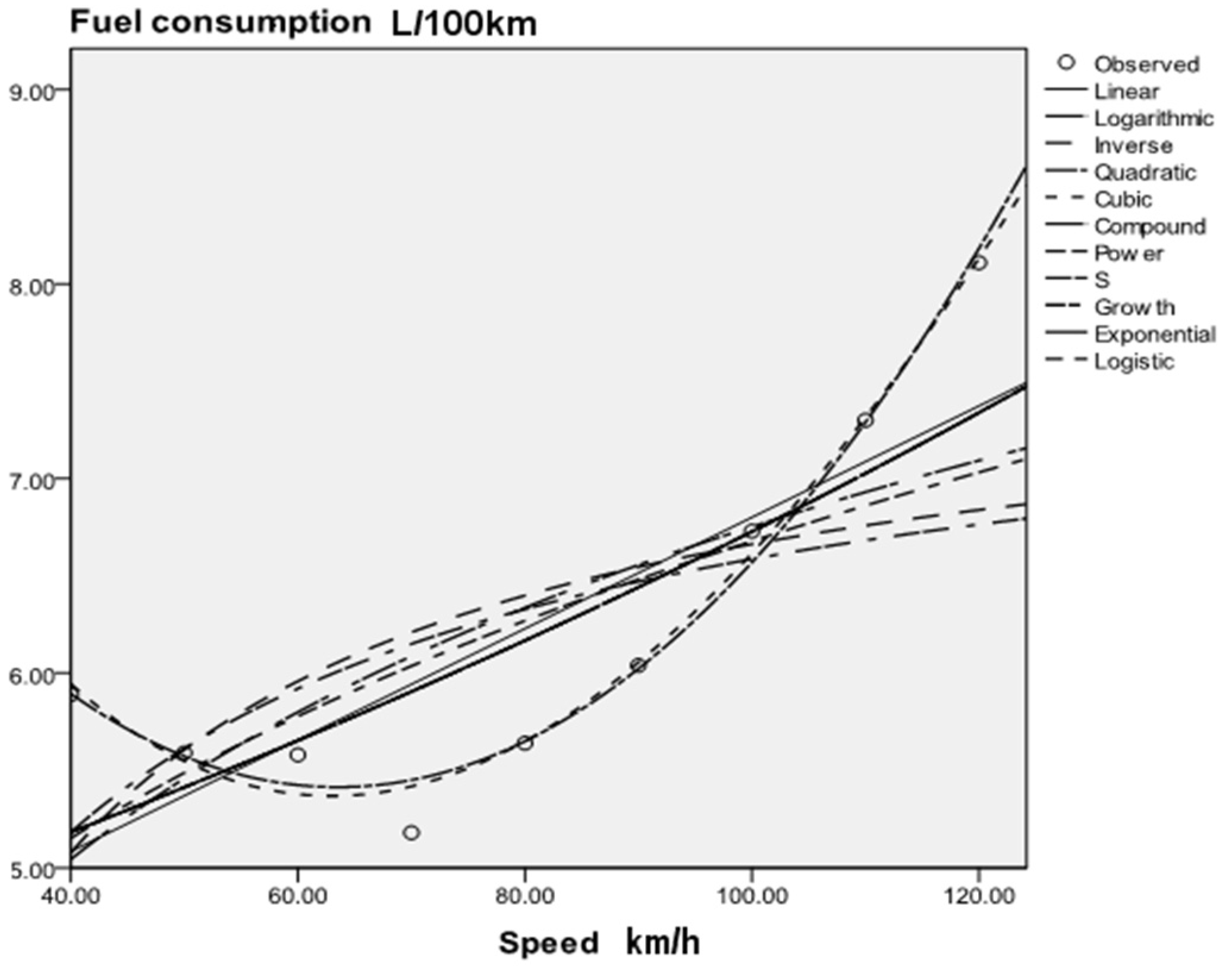
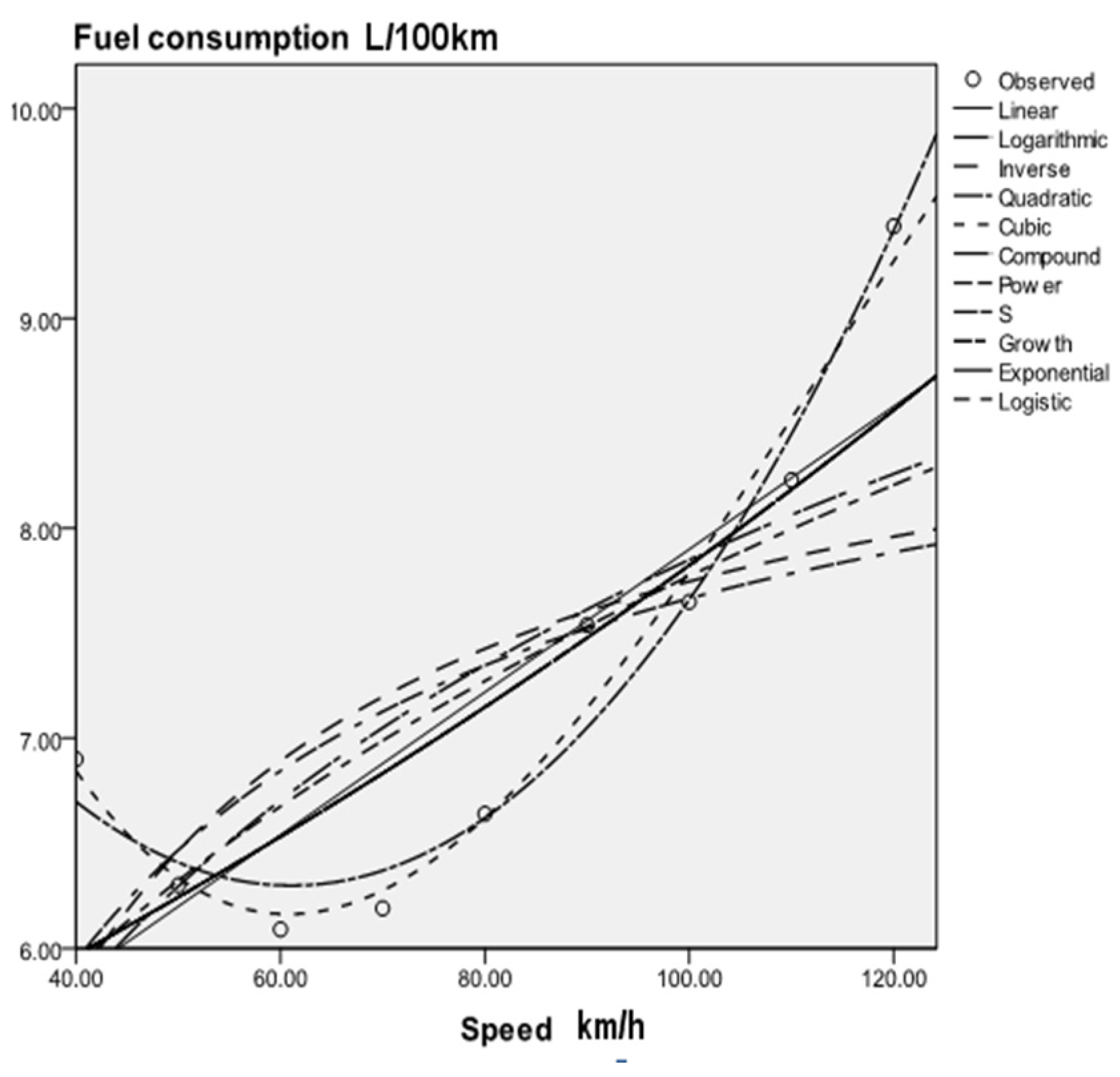
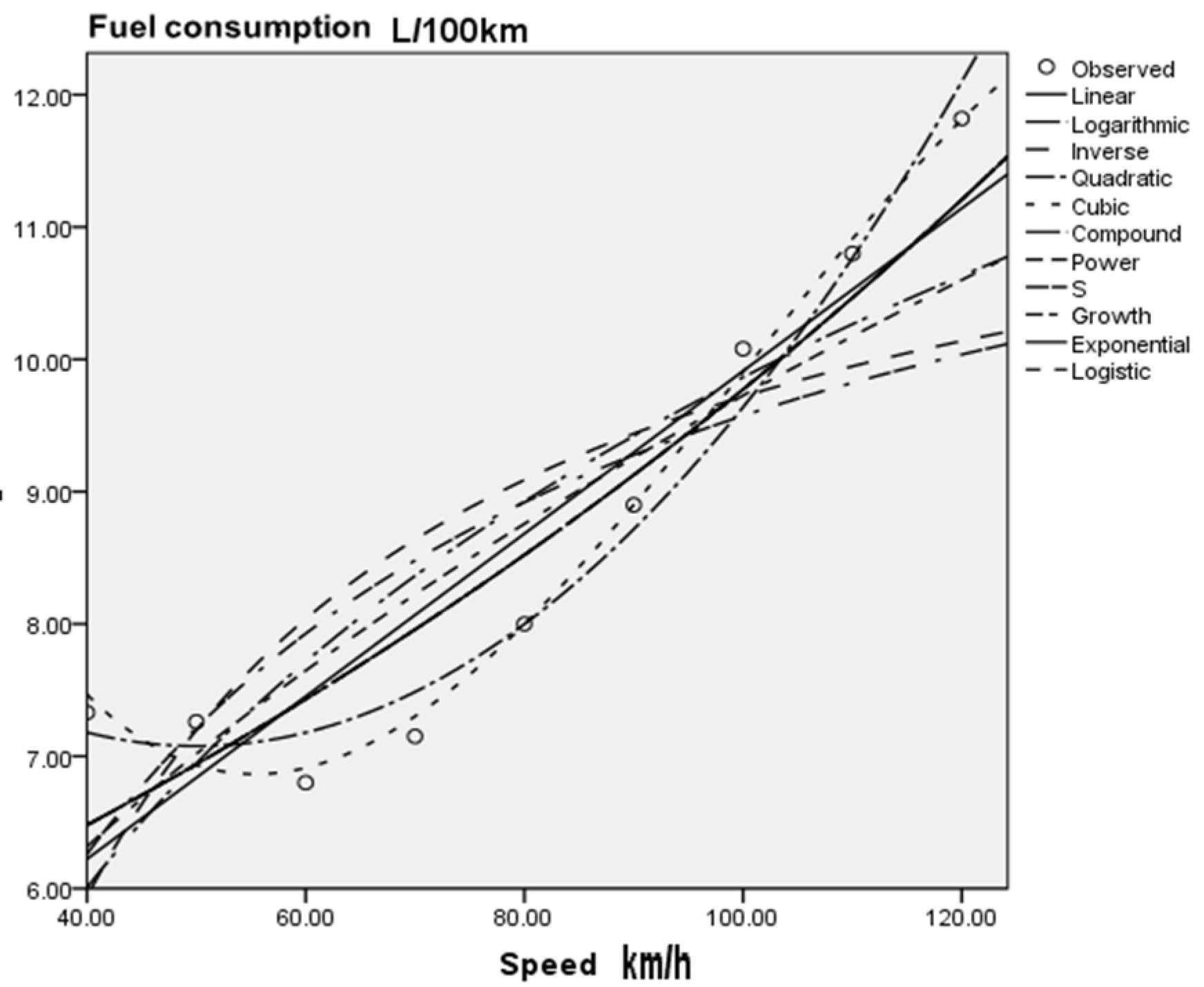
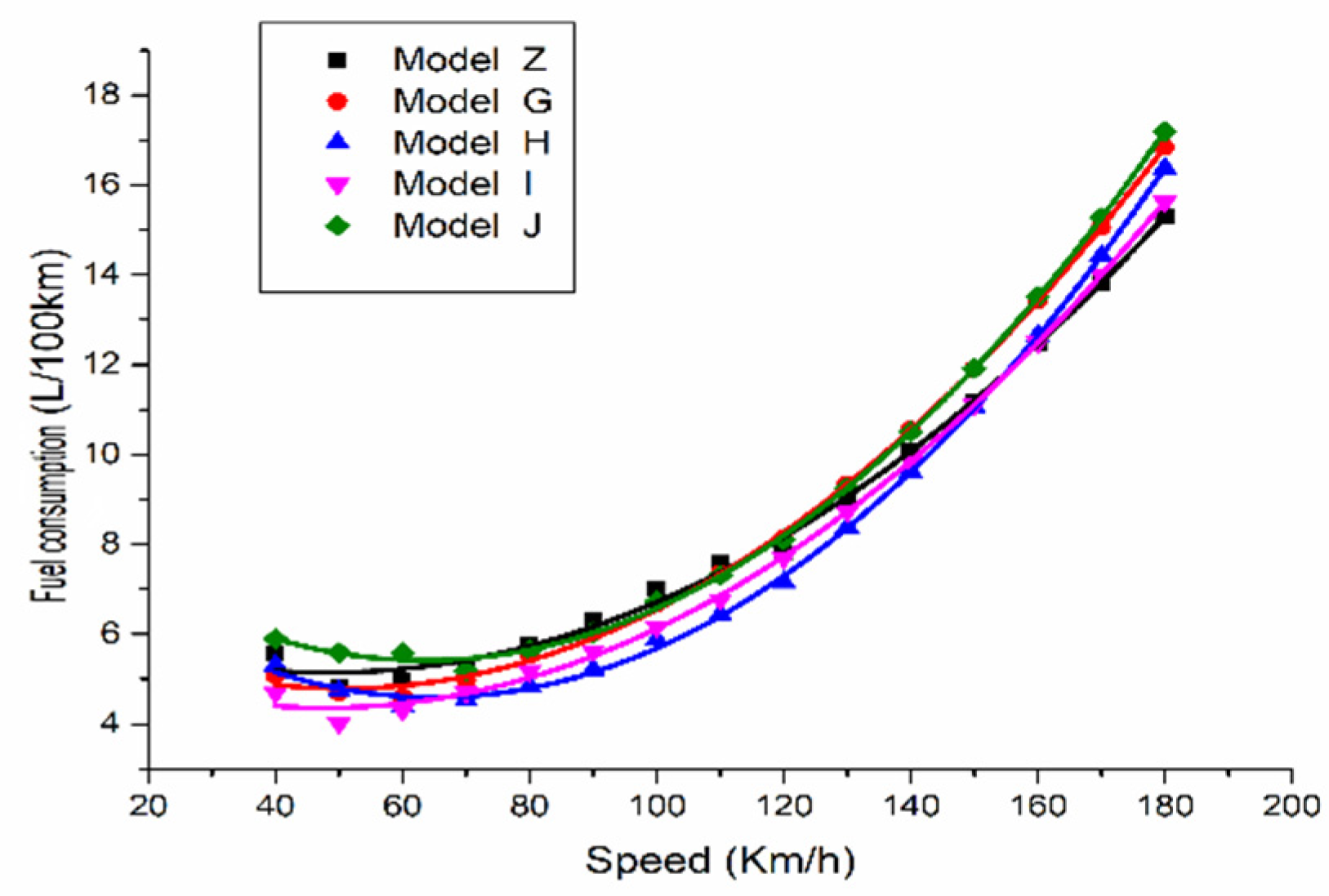
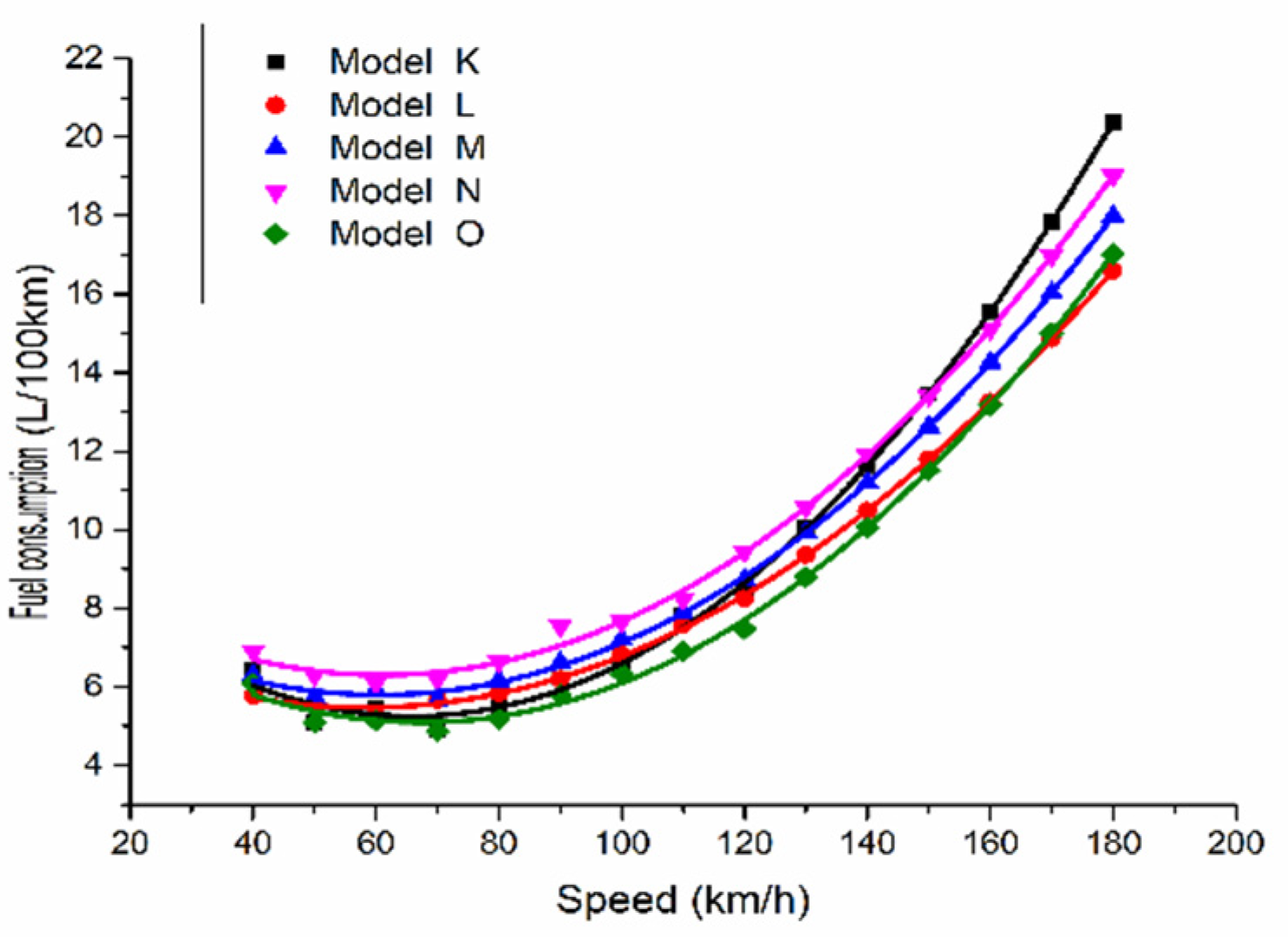
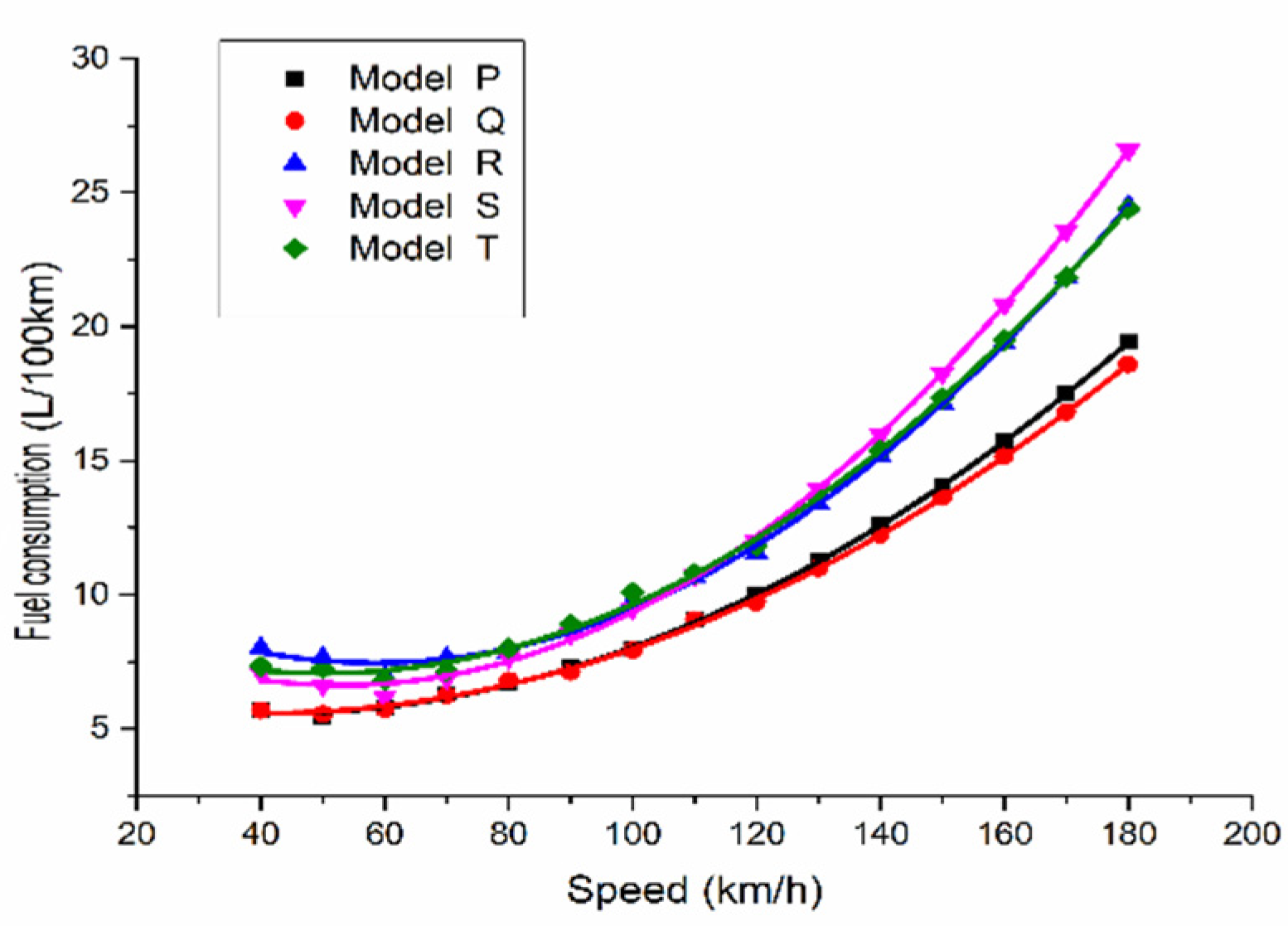
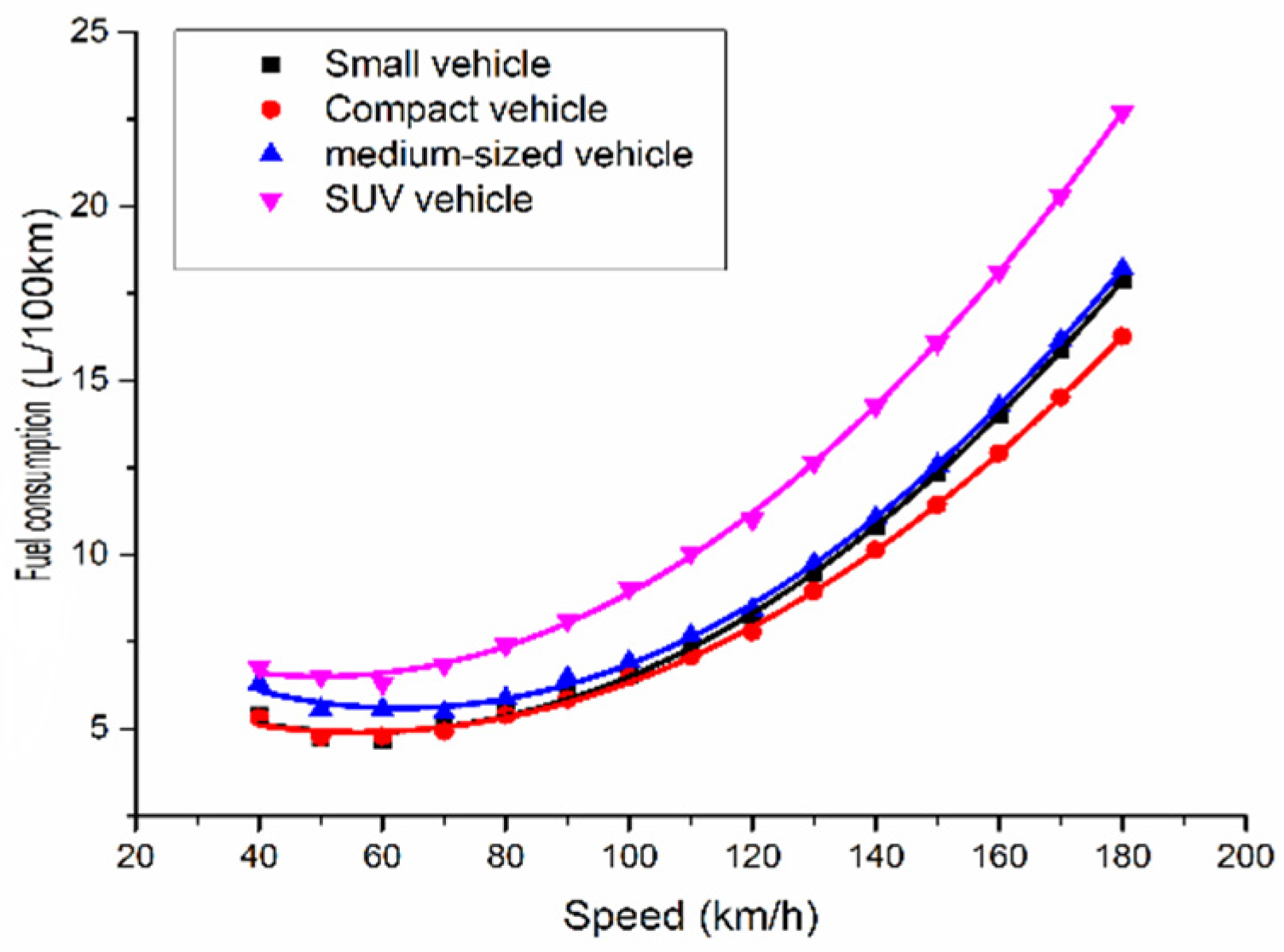
According to the current situation of highway development in foreign countries and the related research on superhighways in China, research on superhighways with design speeds over 120 km/h has a deep foundation, and the development prospects are quite considerable. The development of superhighways will bring opportunities and challenges. At present, the most serious problem in developing superhighways is safety and energy consumption. In this paper, through a comparative analysis of fuel consumption data of different models, a cubic curve model is established to provide a basis for prediction of fuel consumption on superhighways.
2.2. Research on Automobile Fuel Consumption
2.2.1. Research on Domestic Automobile Fuel Consumption
At present, a large amount of research has been conducted on the energy consumption of vehicles on highways in China and abroad. For example, Feng et al. studied the fuel consumption of commercial vehicles on mountain highways based on VSP (vehicle specific power) modeling and obtained the influence of vehicle weight on vehicle speed, which has a greater impact on fuel consumption [
15]. Jia et al. performed a comparative analysis of the evaluation index of fuel consumption of vehicles on highways, and the results showed that, when the driving speed is the same, the fuel consumption of vehicles on highways is lower than that of vehicles on ordinary roads [
16]. Peng et al. conducted an in-depth study on a fuel consumption model of automobiles on highways and modified the parameters of a traditional fuel consumption model by using experimental data to make the newly established fuel consumption model more accurate [
17]. Guo et al. established a multivariate linear regression fuel consumption prediction model by using the principle of multivariate statistical analysis, taking the unit fuel journey as the dependent variable and vehicle weight and horsepower as the independent variables by means of statistical analysis software and a method of curve fitting [
18,
19]. Zhang et al. put forward a method that can accurately evaluate the fuel consumption of vehicles by using the least squares method on the basis of fully considering many nonlinear factors affecting the fuel consumption, and the method can further reduce the impact of other factors on the model accuracy [
20].
The performance of the engine has the greatest impact on the fuel consumption of the vehicle at high speed. Generally speaking, the larger the displacement of the engine, the better the performance. The greater the output power, the better the dynamic performance of the vehicle. However, if the engine displacement is large, it may consume more fuel, and the fuel consumption of the car at high speed will also increase, especially for vehicles with a driving speed close to 200 km/h, such as Ruicheng CC and 2019 Honda Civic. In 2018, Ruicheng CC realized the release test at the speed of 200 km/h in the high ring runway. The car is equipped with ACC (adaptive cruise control) adaptive cruise, PAB (passenger airbag)active brake and LDW (lane departure warning)function, which makes the overall automatic driving level of the car to L2 level, which can ensure the safety of the vehicle under the premise of providing comfortable driving. In addition, the 1.5 T turbocharged engine equipped with Ruicheng CC has a maximum power of 156 HP (115 kW)/5500 rpm and a maximum torque of 225 nm/2000–4000 rpm, which makes the car have enough power to drive at high speed. From the perspective of driverless technology and engine performance, the driving safety of vehicles with a speed of more than 120 km/h can be guaranteed, and there is enough power for them to drive at high speed. Therefore, it is meaningful to study the fuel consumption of vehicles over 120 km/h. In addition, with the vigorous promotion of new energy vehicles, such as pure electric vehicles and hybrid electric vehicles, they have the common characteristics of clean, efficient, energy-saving and environmental protection. The popularization of new energy vehicles can offset the excessive energy consumption caused by ultra-high speed driving and can effectively solve the energy consumption problem caused by the development of superhighway.
Due to the differences in domestic and foreign traffic laws and regulations, driving habits of drivers, speed limits of vehicles, etc., many factors affecting vehicle driving are quite different, so research on the fuel consumption of driving vehicles in foreign countries is different from that in China. Many fruitful results have been achieved abroad in long-term research, and these research ideas and methods are worthy of our reference.
2.2.2. Research on Fuel Consumption of Foreign Automobiles
Westarp found that the parameters of many existing fuel consumption models were not applicable with a change in conditions in the research process, especially a change in speed [
21]. Therefore, a new model was proposed to represent the functional correlation between fuel consumption and speed, and the model was verified by actual collected data. Zhang et al. conducted research on the fuel consumption of hybrid electric vehicles, and a modified fuel consumption model was established based on the working principle of the internal combustion engine [
22]. Furthermore, the energy consumption of ground traffic flow under the hybrid model was further studied, and a quantitative analysis of fuel consumption was performed. Eugen et al. mainly studied the relationship between engine control and fuel consumption [
23]. The results showed that using a nonlinear model to control the engine operation can improve the fuel consumption efficiency, and a simulation analysis of the results was carried out. Lijun Hao et al. [
24] estimated the fuel economy of passenger cars in high-altitude areas through taxiing experiments. On the basis of this research, a reverse simulation method was used to build a model of internal combustion engines through the experimental data of engine torque and speed. The model was verified by simulations with actual data, and the simulation results showed that the error degree of the model is very small and that the model is feasible. Gunawan et al. thought deeply about the current problems of global warming and increasing greenhouse gases and concluded that automobile exhaust emissions account for 20% of greenhouse gas emissions [
25]. This paper mainly studied the influence of driving strategy on the fuel consumption of automobiles and performed a quantitative analysis of vehicle dynamics, and a correlation between braking distance and fuel consumption was obtained. Shahin et al. predicted additional fuel consumption by using an artificial neural network model and obtained a correlation among vehicle weight, fuel consumption and engine displacement through quantitative analysis [
26]. Maya et al. analyzed and studied energy policy. Through a comparison of fuel consumption data, the differences in fuel consumption and its characteristics were studied, fuel consumption control was carried out, and an actual fuel economy standard was established [
27]. Collier, Sonya et al. fully studied and analyzed data of transport trucks to estimate the average stroke fuel consumption [
28]. The relationship between vehicle models and fuel consumption was obtained by comparing different types of trucks.
Vehicle design, road geometry, road conditions, speed limit, driving mode and other important factors have a great impact on vehicle fuel consumption. For example, the design of vehicle shape and tires will make the vehicle subject to different degrees of air resistance and rolling resistance during driving, which will consume the energy generated by vehicle fuel [
29,
30]. When the road conditions are good, the work done by the car to overcome the road resistance will be reduced, which in turn will reduce the fuel consumption. Under the influence of engine performance, road conditions, load, wind direction, climate and usage, the vehicle will consume the least amount of fuel when driving within a certain speed range, which is the economic speed range. Generally speaking, the geometry of different roads will also have an impact on the fuel consumption of vehicle. When there are more uphill sections and turning sections, the vehicle must overcome the uphill resistance or brake to decelerate the turning to achieve the driving purpose, which will increase fuel consumption to a certain extent [
31].
In addition, there are many methods to predict the fuel consumption of passenger vehicles, such as artificial neural network method, multiple linear regression, least square method and simulation modeling method, etc. [
19,
20]. However, different methods have different advantages and disadvantages, which must be selected according to different vehicle types, different road conditions, and different driving modes, etc. Most importantly, the prediction results should be verified, and error analyzed, and necessary corrections should be made to ensure the accuracy of the prediction results.
In this paper, the fuel consumption data of different models are analyzed, curve fitting and modeling are carried out by SPSS software to predict the amount of fuel vehicles will consume at speeds over 120 km/h, and the fuel consumption curves of different models are compared.