Numerical Study of a Francis Turbine over Wide Operating Range: Some Practical Aspects of Verification

Abstract

Hydropower plays an essential role in maintaining energy flexibility. Modern designs focus on sustainability and robustness using different numerical tools. Automatic optimization of the turbines is widely used, including low, mini and micro head turbines. The numerical techniques are not always foolproof in the absence of experimental data, and hence accurate verification is a key component of automatic optimization processes. This work aims to investigate the newly designed Francis runner for flexible operation. Unsteady simulations at 80 operating points of the turbine were conducted. The numerical model consisted of 16 million nodes of hexahedral mesh. A SAS-SST (scale adaptive simulation-shear stress transport) model was enabled for resolving/modeling the turbulent flow. The selected time-step size was equivalent to one-degree angular rotation of the runner. Global parameters, such as efficiency, torque, head and flow rate were considered for proper verification and validation. (1) A complete hill diagram of the turbine was prepared and verified with the reference case. (2) The relative error in hydraulic efficiency was computed and the over trend was studied. This allowed us to investigate the consistency of the numerical model under extreme operating conditions, far away from the best efficiency point. (3) Unsteady fluctuations of runner output torque were studied to identify unstable regions and magnitude of torque oscillations.

1. Introduction

Flexibility of power generation is an important requirement for future turbine designs. The turbines need to operate outside the guaranteed region with more start–stop cycles and high-ramping rates. However, power generation at off-design load brings specific challenges, such as high-amplitude pressure pulsations, vortex breakdown, cavitation etc. Present day variable-speed operation of a hydro turbine is considered as an alternative option to meet fluctuating energy demand, as it allows a high-ramping rate. New design approaches are focusing on design optimization for the variable-speed operation including high, medium, low, mini and micro head turbines [1,2,3]. Furthermore, mini and micro hydro stations are good options for smart grid configurations. This will enable local flexibility of energy need and sustainability. One of the challenges for the very low head turbines is the lower efficiency. However, modern design approach and automatic optimization with proper verification will certainly be useful for improving the efficiency of very low head turbines.

Modern algorithms and tools allow designers to perform optimization with reduced effort. Numerical methods have played significant roles in design and development of hydro turbines over the last 50 years [4]. Presently, almost all turbine designs and the optimization are highly dependent on the numerical outcome. High quality results and the accurate prediction of physical phenomena are always a valuable input for the turbine designers. During the past few years, several verification approaches have been developed to quantify the numerical errors [5,6,7]. However, these approaches have certain limitations and require a customized solution for hydro turbines. The present work is the continuation of previous efforts initiated to study the practical aspects of accurate verification and validation of turbine simulations. During 2009–2014, the focus was the Francis-99 test case [8,9]. The reviewed parameters were passage modeling, component modeling (runner and draft tube separately), influence of boundary conditions, discretization techniques, turbulence models and time step sizes. Later (2014–2016), the work extended to other hydro turbines, and the data of several turbines were compiled [10]. The analysis underlined that the hybrid models with newly developed techniques of passage modeling (blade row) are able to predict turbine flow with reasonable accuracy. The gain in simulation speed is high; however, the accuracy related to flow periodicity, variable torque from each blade channel and flow asymmetry at runner outlet is expected to worsen, due to the assumption of periodical boundary type. This may be a compromise solution for the industry standard modeling of hydro turbines. The work also covered the fluid structure interactions and related numerical errors in hydro turbines [11,12]. Recently [13,14,15], a comprehensive study (including the compressibility effect) was conducted to develop a systematic verification and validation guide for the turbines. The conclusion was that more comprehensive study is needed to determine the precise trend and fit (systematic/random behavior) of numerical errors. In this paper, we focus on the complete hill diagram of a Francis turbine that allows credible quantification of numerical errors at several operating points and helps to investigate the systematic or random behavior of errors.

2. Test Case

A newly designed and optimized Francis runner was used for the verification and validation study, hereafter referred to as a HydroFlex runner. The specific speed ($N_{QE}$—see IEC 60193:1999-11, sub clause 1.3.3.12.11) of the turbine is 0.027. The runner is designed for flexible operations. Other components of the turbine, except for the runner, are the same as the Francis-99 runner [9]. The modeled turbine includes spiral casing with 14 stay vanes, 28 guide vanes, a runner with 17 blades and the elbow type draft tube. Detailed description of the test facility is presented in a previous publication [16].

Table 1. Boundary conditions and the numerical parameters enabled for the simulations. SAS-SST: scale adaptive simulation-shear stress transport.

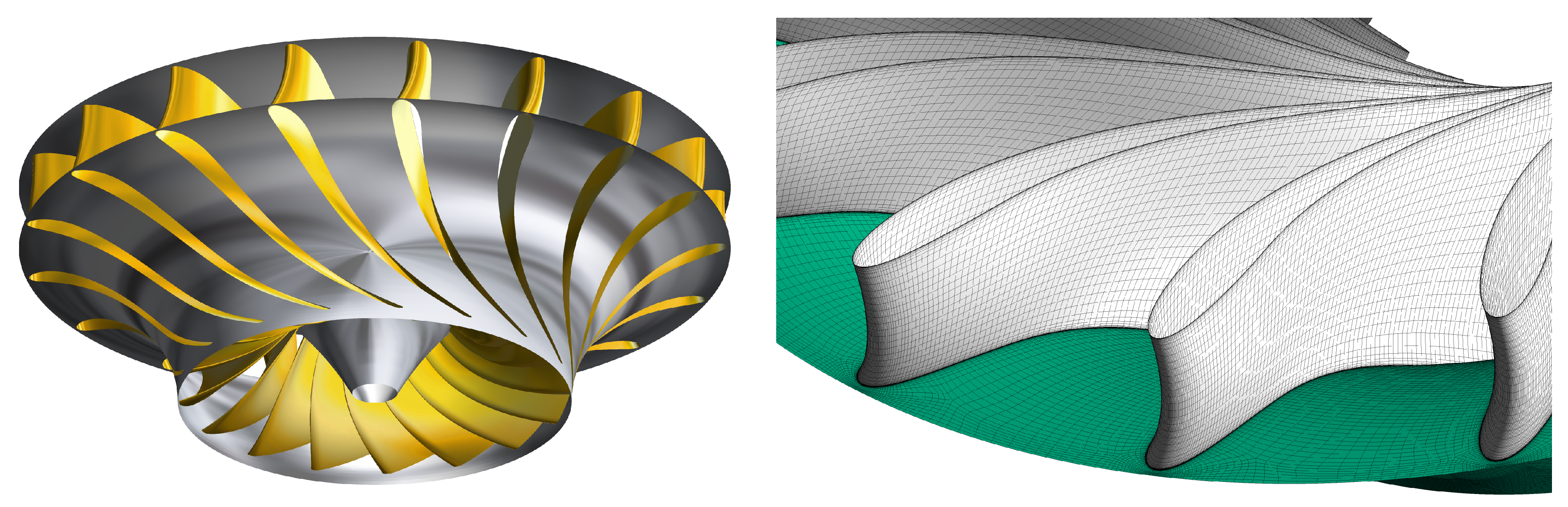
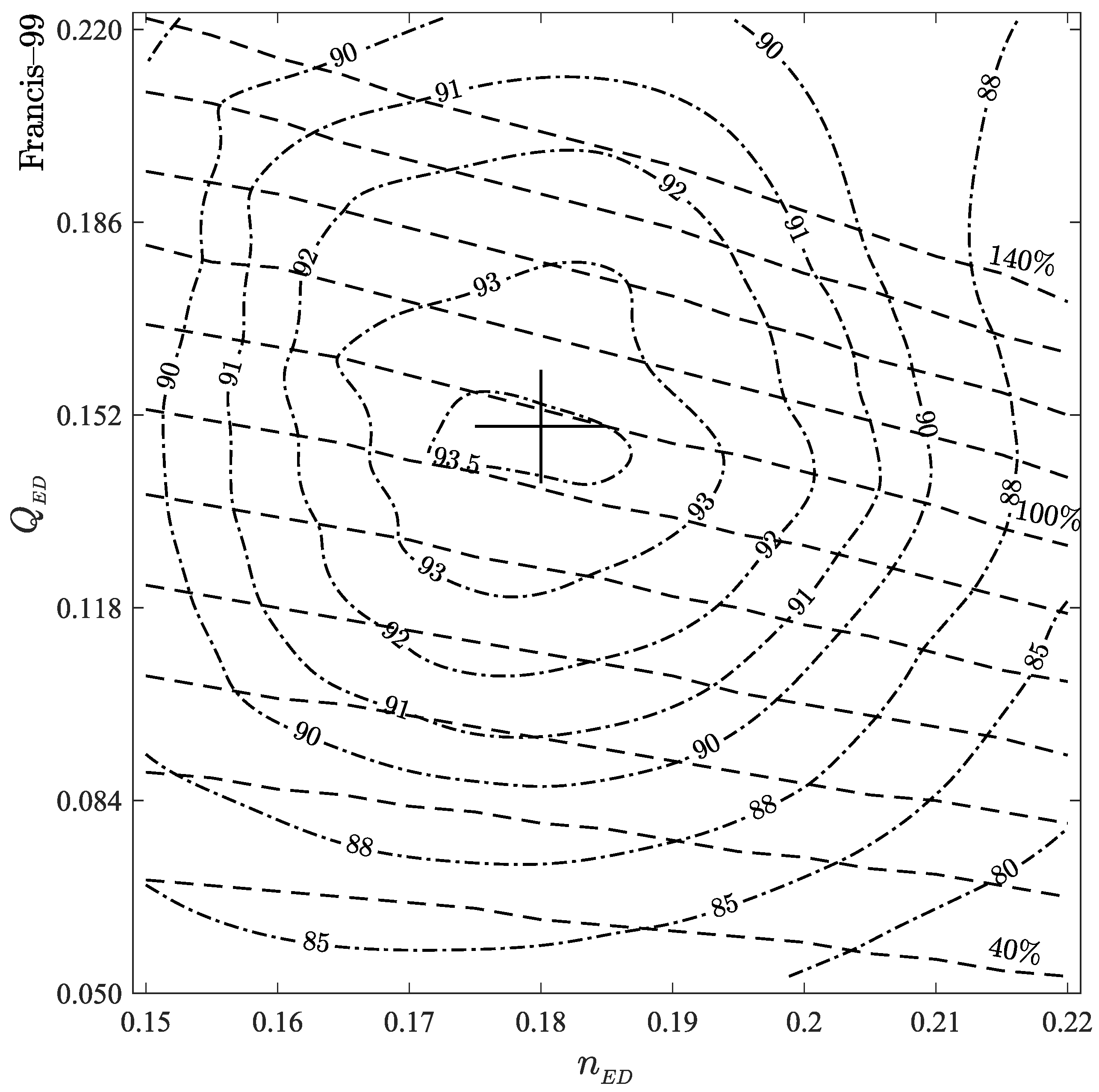
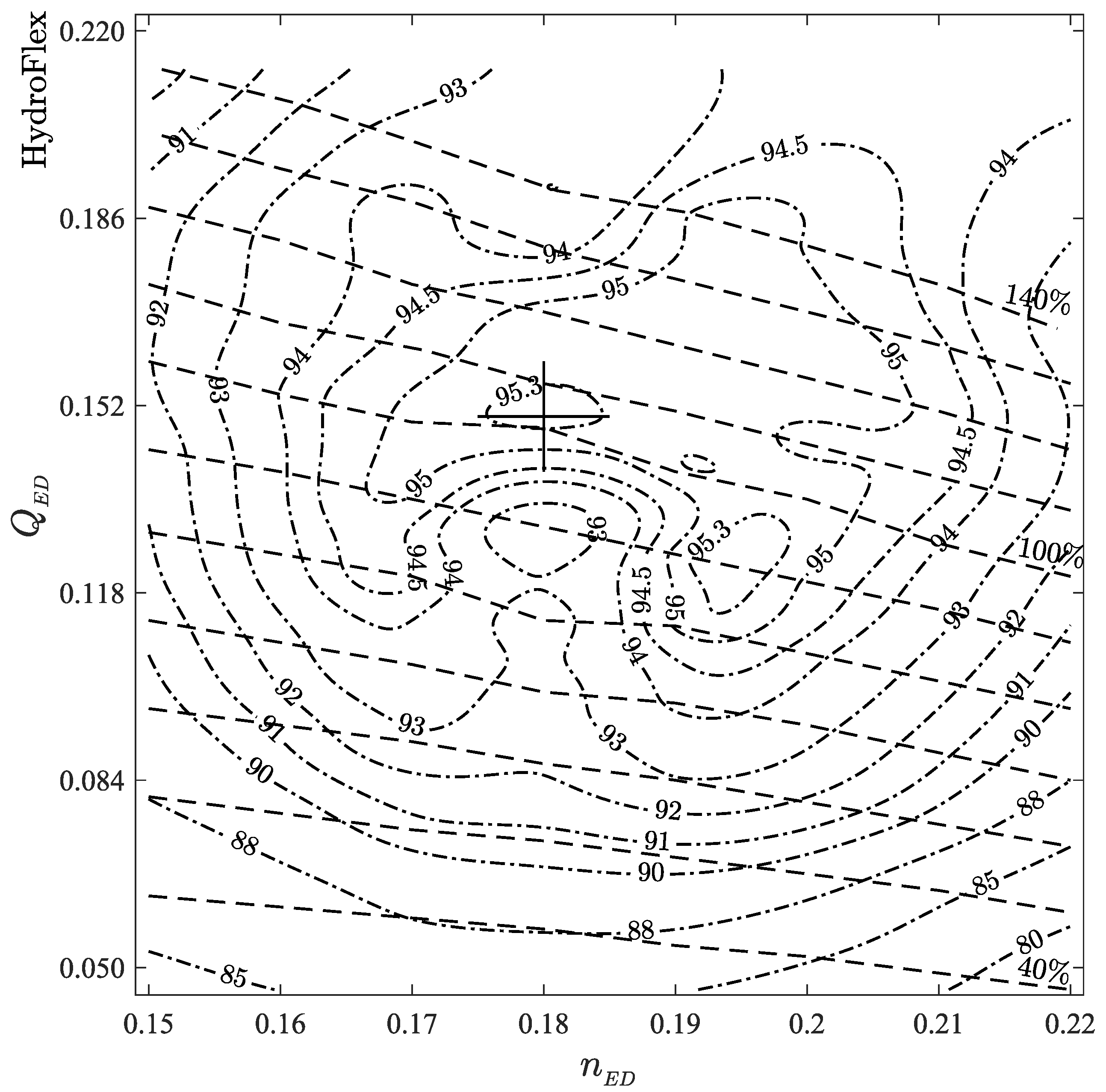
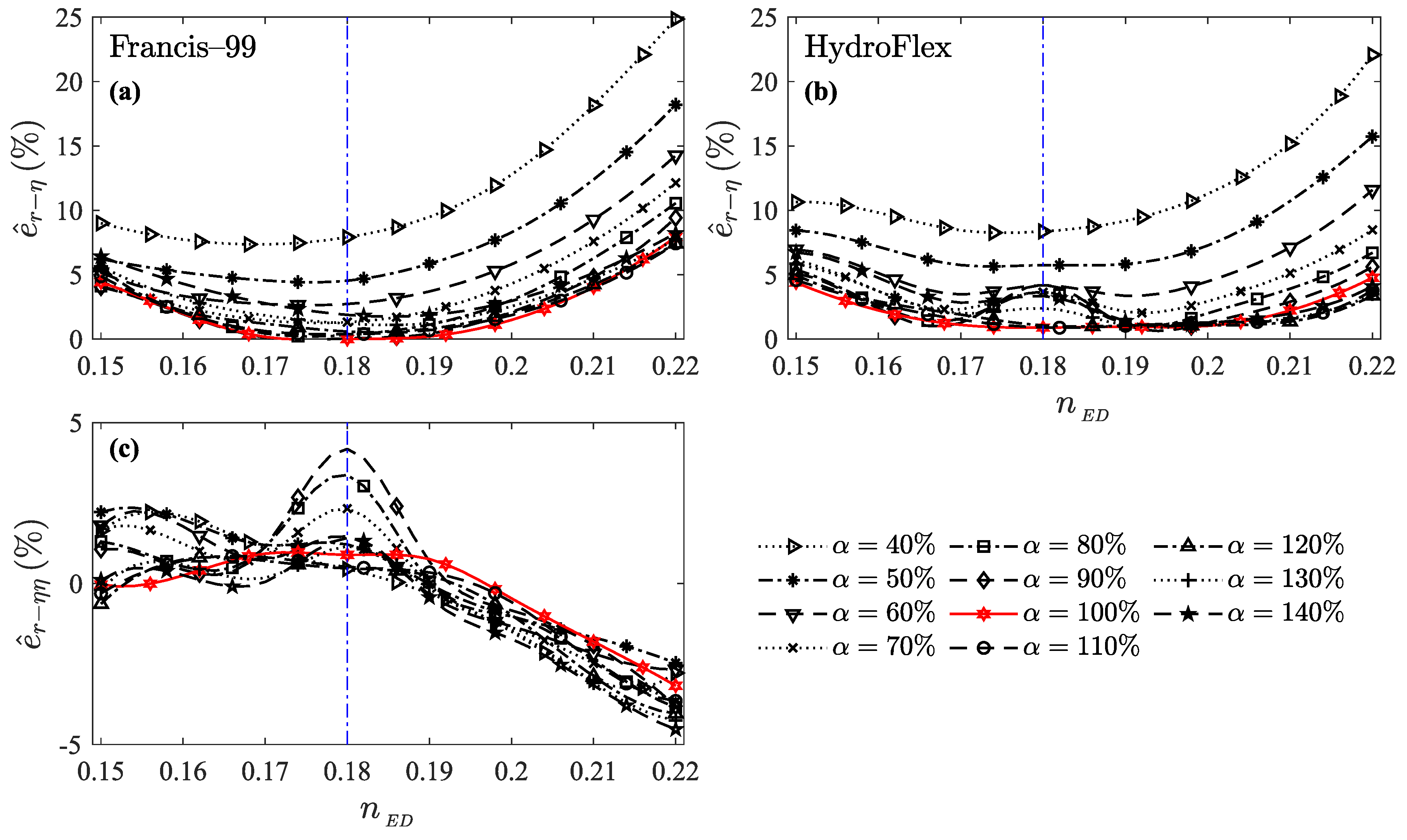
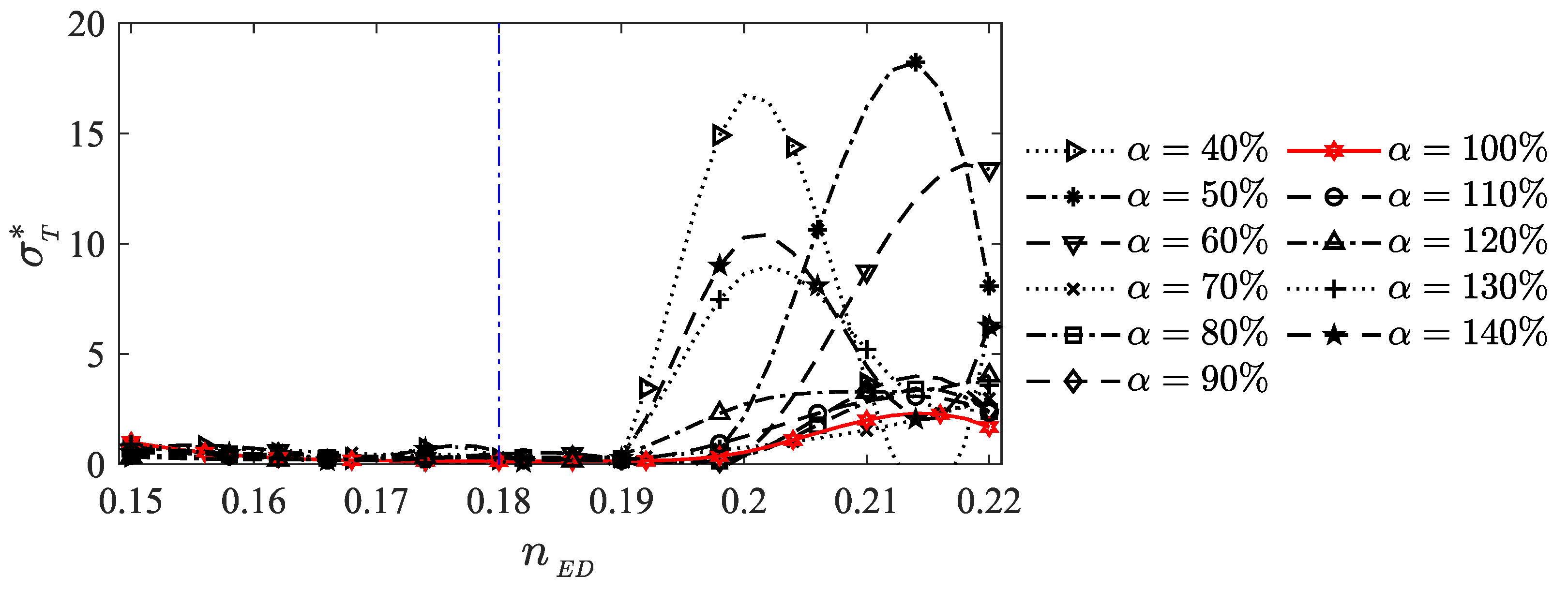
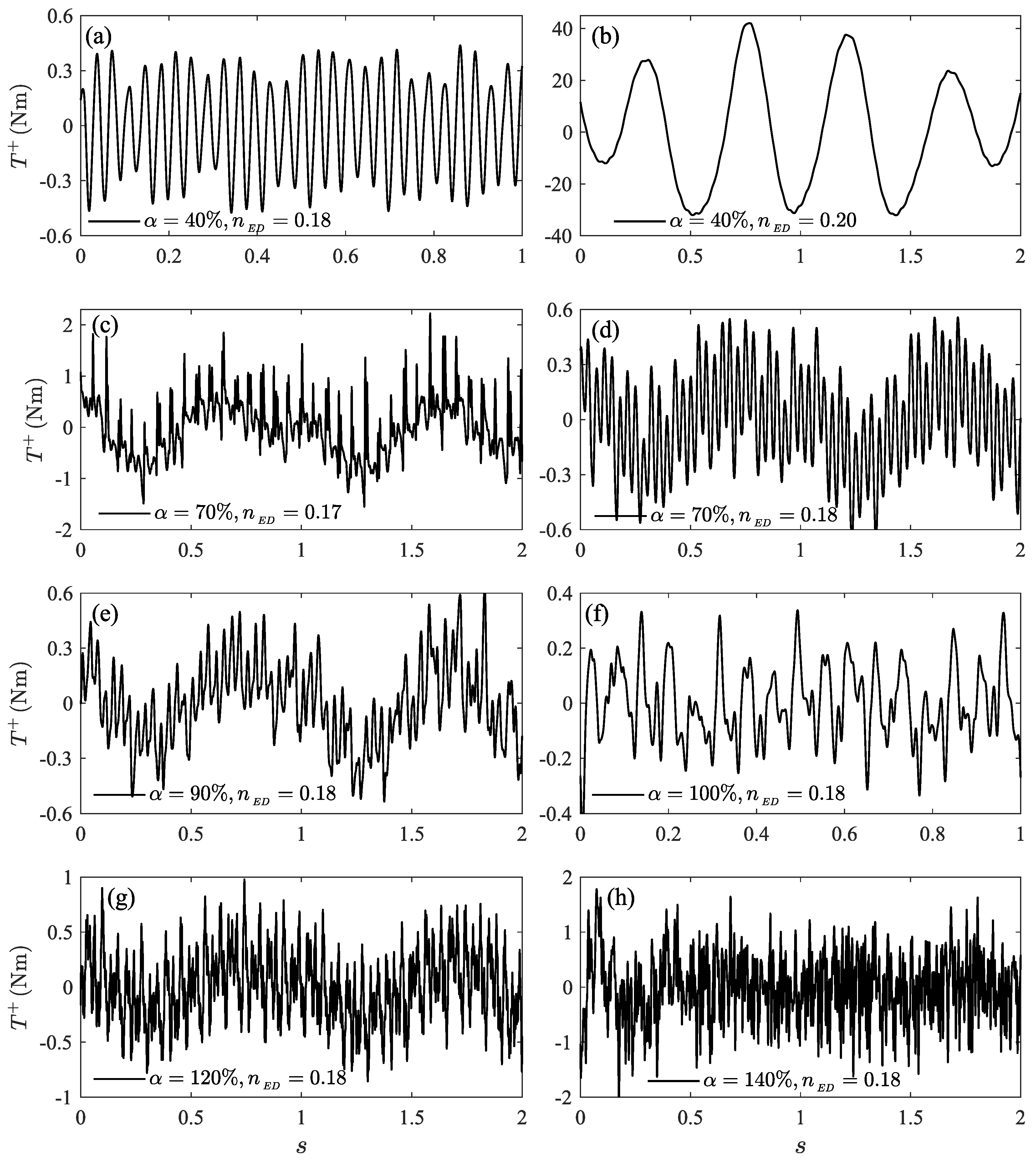
Parameters	Description
Mesh	spiral casing—3.56 million, guide vanes—4.75 million,
	runner—5.63 million, draft tube—2.9 million. $0.1<y^{+}<30$
Boundary types	Total pressure inlet and static pressure outlet
Turbulence model	SAS-SST
Advection scheme	High Resolution
Time marching scheme	Second order backward Euler
Time	Time step: 1° of runner rotation. Total time: three rotations

describes the boundary conditions and the numerical parameters enabled for the simulations. Figure 1 shows the geometry of the runner and the hexahedral mesh. The complete turbine includes around 16 million nodes (around four node points per cubic millimeter volume). Unsteady simulations at operating points (a total of 80 flow rate and speed combinations) were conducted.

3. Verification and Validation

The HydroFlex runner has geometrical parameters identical to the Francis-99 runner, e.g., the runner inlet and outlet diameters and the profiles of the crown and band seals are same. The other geometrical dimensions, such as blade, crown and band profiles, are based on optimization. Figure 2 shows the iso-efficiency hill diagram of the Francis-99 runner. The iso-efficiency hill diagram of a turbine represents the overall performance of the turbine for a wide range of operating conditions. Figure 3 shows the iso-efficiency hill diagram of the newly designed HydroFlex runner. The hill diagrams include guide vanes angular positions, and hydraulic efficiency on the axis of speed factor, $n_{ED}$ (indirect representation of turbine rotational speed) and discharge factor, $Q_{ED}$ (indirect representation of flow rate through the runner). The hill diagrams do not include runaway and no-load discharge characteristics. The hill diagram of the Francis-99 runner was prepared using available data of model acceptance tests in the laboratory. The best efficiency point is located at $n_{ED}=0.18, Q_{ED}=0.153$ and $\alpha =100\%$, and the hydraulic efficiency is ${93.52}^{\pm 0.16\%}$. The operating range for the Francis-99 runner is $n_{ED}=0.15-0.22$ and $Q_{ED}=0.05-0.22$. The experimental data of the model acceptance test of the Francis-99 runner in the laboratory were used to prescribe the boundary conditions for the HydroFlex runner. The numerical model of the HydroFlex runner predicted the maximum efficiency of 95.3%. It is important to note—all simulations are unsteady, and the data selected for the analysis were averaged over one complete rotation ($\phi ={360}^{\circ }$ or $s=1$) of the runner.

Since the blade profile of the HydroFlex runner is somewhat different from that of the Francis-99 runner, a direct validation can be misleading. The main purpose of using the Francis-99 runner is for relative comparison, as no experimental data of the HydroFlex runner are available. A relative (normalized) comparison with the maximum efficiency could be a good alternative. The HydroFlex runner was designed by keeping the best efficiency point at the same location (head, discharge and speed) as the Francis-99 runner. Additional peaks, apart from the best efficiency point, are believed to be numerical uncertainty. Figure 4 shows the relative deviation in hydraulic efficiency for both runners. The efficiency at all operating points of the Francis-99 runner was normalized by the maximum efficiency of 93.5%. The efficiency of the HydroFlex runner was normalized by the maximum efficiency of 95.3%. The speed factor, $n_{ED}$, of 0.18 represents the synchronous speed of the turbine. Model test data of the Francis-99 (Figure 4a) shows a deviation of 25%, which corresponds to deep part load conditions, i.e., a $40\%$ guide vane opening at the higher $n_{ED}$ side. In the case of the HydroFlex runner (Figure 4b), the trend of efficiency across the different $n_{ED}$ values is similar to the Francis-99 runner. Figure 4c shows the exact difference in efficiency values for the corresponding $n_{ED}$ and $Q_{ED}$. On the left side $(n_{ED}=0.15-0.17)$, the numerical model shows positive errors in the efficiency, whereas on the right side ($n_{ED}=0.18-0.22$), it shows negative errors in the efficiency. The numerical model seems to struggle with predicting the realistic flow phenomena at higher $n_{ED}$ values, although the simulations were unsteady in nature.

In this work, pressure-based boundary conditions were prescribed for all simulations; therefore, head values were predicted accurately, at 30^{±0.1 m}. However, the reduced numerical error and the minimized fluctuations in runner torque are very important as they reflect the global performance of the runner. Figure 5 shows the standard deviation of torque for the HydroFlex runner. The torque is normalized by the corresponding value at the maximum efficiency point. The standard deviation $\sigma$ corresponds to samples acquired during one complete rotation ($\phi ={360}^{\circ }$) of the runner. The deviation is high for some operating conditions, especially the 40%, 50%, 130% and 140% guide vane positions and $n_{ED}=0.19-0.22$. Unsteady torque fluctuations at some of these operating points are presented in Figure 6. The scale on the y-axis is different so as to preserve clarity in the high frequency fluctuations. The pattern of torque fluctuations across different operating conditions is quite interesting. Two operating points at 40% guide vane position, two operating points at 70% guide vane position and one operating point ($n_{ED}=0.18$) at each 90%, 100%, 120% and 140% guide vane positions are shown in the figure. Two operating points at 40%, which guide vane opening, show quite different behaviors. At $n_{ED}=0.18$, the amplitudes ($f\approx 3f_n$) of torque fluctuations are small; however, at $n_{ED}=0.20$, the amplitudes ($f=0.5f_n$) are predominantly high. While comparing the results at the same speed factor ($n_{ED}=0.18$), but different load/guide vane positions, the results are even more surprising, especially the frequency variation. Stochastic fluctuations are predominant at high load conditions and the 120% and 140% guide vane positions. At the location of maximum efficiency (Figure 6f), the amplitudes of torque fluctuations are moderate, and the frequency corresponds to the runner blades and the rotor–stator interactions. While comparing the signature of torque fluctuations, low frequency oscillations ($f=0.5-0.7$ Hz) were recorded at almost all operating points. Presently, it is unclear what causes such low frequency oscillations. This could be valuable to investigate in the future with longer simulation time, 20 – 25 revolutions of the runner, which would allow a large enough number of samples for spectral analysis and for examining the signature of low frequency fluctuations.

4. Conclusions

The present work focused on the numerical study of a newly designed Francis runner with a specific emphasis on verification. For many situations, especially automatic optimization, experimental data are not available to validate the numerical results. In such cases, relative verification is important with the reference case. For this work, we considered the Francis-99 runner as a reference case and optimized the new runner, HydroFlex, for flexible operations. The best efficiency point of the HydroFlex runner was maintained at the same location as the Francis-99 runner. The final optimized geometry of the HydroFlex runner was considered for the hill diagram simulations. The overall trend of efficiency variation across the $n_{ED}$ and $Q_{ED}$ values was found to be identical. This indicated that the numerical model performs consistently over the turbine operating range. However, the efficiency is a combination of several quantities, such as head, flow rate and torque, which can be misleading due to arithmetic cancellation of errors in these quantities. It is also important to examine the individual quantity, mainly torque, and its unsteady behavior over the hill diagram points. This will allow us to identify unstable regions. Only low frequency torque fluctuations exhibited at the 40% guide vane opening and $n_{ED}=0.20$ (see Figure 6b) were almost 100 times that of the best efficiency point. On the other hand, torque fluctuations at all other points were of high frequency. When examining the characteristics of torque closely, a quite interesting signature was observed along the synchronous speed line of the turbine ($n_{ED}=0.18$). It would be interesting to see a similar signature from the experiments in the future and validate the numerical results. Overall, investigations of unsteady torque fluctuations, in addition to efficiency, were found to be useful during the runner optimization process and the identification of the stable regions of turbine operation or the need for further optimization.

It is important to note that the simulations were unsteady, and that the computational domains carry 16 million nodes. For industry-scale simulations, such simulations may be expensive and time consuming. However, it will be worth to check a few operating conditions, especially along the synchronous speed, with unsteady simulations and scale-resolving models. This will help to identify the torque characteristics. The authors are also of the opinion that the appropriate method for one particular application depends on the expectations of the designer and available computational resources. The authors tend to favor hybrid models evolving continuously from the RANS (Reynolds-averaged Navier–Stokes) to the LES (large eddy simulation) mode. These models allow us to characterize the inter-blade vortices in the blade channels and vortex breakdown in the draft tube. Perhaps, the time has come to use a fully customized approach—a combination of steady RANS, unsteady RANS, SAS-SST, SBES (stress blended eddy simulation) and RANS-LES for selected points of the hill diagram.

Supplementary data of flow parameters for both runners are provided in the Appendix A.