Institutional Determinants of Budgetary Expenditures. A BMA-Based Re-Evaluation of Contemporary Theories for OECD Countries
Abstract
1. Introduction
2. Literature Review and Research Hypotheses
2.1. Institutions of Power Legitimacy
2.2. Institutions of Internal Power Relations
2.3. Rules of the Budgetary Process
2.4. Hypotheses
3. Materials and Methods
3.1. Data and Measurement
3.2. BMA—Bayesian Model Averaging
4. Analysis of the Results
4.1. Institutions of Power Legitimacy
4.2. Rules of the Budgetary Process
4.3. Other Institutional Variables and Controls
4.4. Strength of Influence and Robustness
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Description of All Variables Employed in Estimations
| Short Name | Explanation | Source |
|---|---|---|
| er_nat | Explained in Table 1 in the main text | [104] (IMF Fiscal rules dataset) |
| rr_nat | Explained in Table 1 in the main text | |
| bbr_nat | Explained in Table 1 in the main text | |
| dr_nat | Explained in Table 1 in the main text | |
| dr | Explained in Table 1 in the main text | |
| bbr | Explained in Table 1 in the main text | |
| cur_union | Dummy answering the question: Is country a member of currency union? 1—yes, 0—no | |
| advanced | Dummy answering the question: Country is on IMF the list of Advanced Economies—1, no—0 | |
| resour_rich | Dummy answering the question: Is the economy rich in natural resources? 1—yes, 0—no | |
| fed | Dummy answering the question: Is country a federation—1, otherwise—0 | |
| e_union | Dummy for EU members Yes—1, No—0 | |
| English_LE | According to “legal origins” concept one of possible legal systems: English Common Law | [105] |
| French_LE | According to “legal origins” concept: French Commercial Code, | |
| Socialist_LE | According to “legal origins” concept: Socialist/Communist Laws, | |
| German_LE | According to “legal origins” concept: German Commercial Code, | |
| elec_sys | Explained in Table 1 in the main text | [106] |
| reg_age | Current political regime durability in years (averages) | Polity IV project |
| checks_bal | Explained in Table 1 in the main text | [107] |
| closed_list | Explained in Table 1 in the main text | |
| gov_frac | Explained in Table 1 in the main text | |
| no_part | Explained in Table 1 in the main text | |
| yrs_elec | Explained in Table 1 in the main text | |
| dist_house | Explained in Table 1 in the main text | |
| elec_year | Dummy for parliamentary election year. Yes—1, No—0 | |
| ethnic_frac | Ethnic fractionalization. The variable reflect the probability that two randomly selected people from a given country will not share ethnicity, the higher the number the less probability of the two sharing that characteristic. | [108] |
| language_frac | Linguistic fractionalization. The variable reflect the probability that two randomly selected people from a given country will not share language, the higher the number the less probability of the two sharing that characteristic. | |
| religion_frac | Religious fractionalization. The variable reflect the probability that two randomly selected people from a given country will not share religion, the higher the number the less probability of the two sharing that characteristic. | |
| polcon3 | Explained in Table 1 in the main text | [109] |
| polcon5 | Explained in Table 1 in the main text | |
| vot_turn | Explained in Table 1 in the main text | [110] |
| pub_bal | Public fiscal net balance. Surplus (+)/Deficit (-) | IMF |
| bud_bal | Budgetary balance. Surplus (+)/Deficit (-) | |
| debt_pub | Gross General Government Debt % GDP | |
| gdpgr | GDP growth (%) | |
| unemployment | Official unemployment rate (%) | |
| inflation | Control for the inflation rate (%) | |
| COFOG_tot | Total central government expenditures (%GDP) - dependent variable | |
| x2009 | Control for first year after the financial crisis | Own |
| x2010 | Control for second year after the financial crisis |
Appendix B. Result for the RIC and Binomial-Beta, as Well as UIP and Dilution Prior
| Model Prior | Beta-Binomial | Dilution | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| g Prior | Risk Inflation Criterion | Unit Information Prior | ||||||||||
| Variable | PIP | PM | PSD | SPM | SPSD | P(+) | PIP | PM | PSD | SPM | SPSD | P(+) |
| er_nat | 1.000 | −2.519 | 0.493 | −0.176 | 0.034 | 0.000 | 1.000 | −2.62 | 0.477 | −0.183 | 0.033 | 0.000 |
| bbr_nat | 1.000 | 4.054 | 0.593 | 0.294 | 0.043 | 1.000 | 1.000 | 4.052 | 0.604 | 0.293 | 0.044 | 1.000 |
| English_LE | 1.000 | 11.639 | 1.187 | 0.675 | 0.069 | 1.000 | 1.000 | 11.372 | 1.044 | 0.659 | 0.061 | 1.000 |
| French_LE | 1.000 | 12.685 | 1.534 | 0.825 | 0.100 | 1.000 | 1.000 | 12.623 | 1.456 | 0.821 | 0.095 | 1.000 |
| Socialist_LE | 1.000 | 11.695 | 1.544 | 0.761 | 0.100 | 1.000 | 1.000 | 11.373 | 1.52 | 0.74 | 0.099 | 1.000 |
| elec_sys | 1.000 | 4.125 | 0.607 | 0.449 | 0.066 | 1.000 | 1.000 | 4.065 | 0.629 | 0.443 | 0.069 | 1.000 |
| cur_union | 1.000 | −8.26 | 0.766 | −0.598 | 0.055 | 0.000 | 1.000 | −8.264 | 0.772 | −0.598 | 0.056 | 0.000 |
| reg_age | 1.000 | 0.073 | 0.009 | 0.515 | 0.065 | 1.000 | 1.000 | 0.073 | 0.009 | 0.515 | 0.065 | 1.000 |
| checks_bal | 1.000 | −1.793 | 0.219 | −0.286 | 0.035 | 0.000 | 1.000 | −1.807 | 0.221 | −0.288 | 0.035 | 0.000 |
| closed_list | 1.000 | −6.046 | 0.814 | −0.438 | 0.059 | 0.000 | 1.000 | −6.092 | 0.827 | −0.441 | 0.060 | 0.000 |
| advanced | 1.000 | 5.356 | 0.828 | 0.285 | 0.044 | 1.000 | 1.000 | 5.219 | 0.828 | 0.277 | 0.044 | 1.000 |
| resour_rich | 1.000 | 9.990 | 1.401 | 0.284 | 0.040 | 1.000 | 1.000 | 10.002 | 1.403 | 0.284 | 0.040 | 1.000 |
| religion_frac | 1.000 | −10.079 | 1.533 | −0.322 | 0.049 | 0.000 | 1.000 | −10.405 | 1.448 | −0.332 | 0.046 | 0.000 |
| German_LE | 1.000 | 14.844 | 1.634 | 0.584 | 0.064 | 1.000 | 1.000 | 14.599 | 1.569 | 0.574 | 0.062 | 1.000 |
| ethnic_frac | 1.000 | −18.058 | 2.573 | −0.468 | 0.067 | 0.000 | 1.000 | −19.108 | 1.915 | −0.495 | 0.050 | 0.000 |
| polcon5 | 1.000 | −15.752 | 3.224 | −0.169 | 0.035 | 0.000 | 1.000 | −16.092 | 3.181 | −0.173 | 0.034 | 0.000 |
| fed | 1.000 | −5.309 | 1.187 | −0.308 | 0.069 | 0.000 | 0.997 | −4.919 | 1.250 | −0.285 | 0.072 | 0.000 |
| gov_frac | 0.995 | 9.971 | 1.914 | 0.368 | 0.071 | 1.000 | 0.991 | 10.114 | 1.668 | 0.374 | 0.062 | 1.000 |
| pub_bal | 0.933 | −0.582 | 0.176 | −0.417 | 0.126 | 0.000 | 0.907 | −0.579 | 0.195 | −0.415 | 0.140 | 0.000 |
| vot_turn | 0.823 | 0.058 | 0.035 | 0.103 | 0.062 | 1.000 | 0.672 | 0.044 | 0.036 | 0.078 | 0.063 | 1.000 |
| dr_nat | 0.779 | −1.33 | 0.863 | −0.081 | 0.053 | 0.000 | 0.791 | −1.439 | 0.889 | −0.088 | 0.054 | 0.000 |
| debt_pub | 0.555 | 0.017 | 0.017 | 0.068 | 0.071 | 1.000 | 0.427 | 0.013 | 0.017 | 0.054 | 0.070 | 1.000 |
| language_frac | 0.220 | −1.379 | 3.047 | −0.039 | 0.087 | 0.014 | 0.032 | −0.207 | 1.289 | −0.006 | 0.037 | 0.010 |
| polcon3 | 0.204 | 0.774 | 1.769 | 0.013 | 0.031 | 1.000 | 0.126 | 0.473 | 1.431 | 0.008 | 0.025 | 1.000 |
| no_part | 0.129 | 0.082 | 0.262 | 0.015 | 0.047 | 1.000 | 0.038 | 0.035 | 0.208 | 0.006 | 0.037 | 1.000 |
| bud_bal | 0.125 | −0.056 | 0.178 | −0.038 | 0.122 | 0.000 | 0.096 | −0.064 | 0.198 | −0.044 | 0.135 | 0.000 |
| gdpgr | 0.087 | −0.006 | 0.028 | −0.003 | 0.014 | 0.000 | 0.085 | −0.007 | 0.028 | −0.003 | 0.014 | 0.000 |
| yrs_elec | 0.082 | −0.014 | 0.059 | −0.002 | 0.010 | 0.000 | 0.096 | −0.015 | 0.062 | −0.003 | 0.011 | 0.000 |
| unemployment | 0.082 | −0.007 | 0.034 | −0.004 | 0.018 | 0.010 | 0.042 | −0.004 | 0.025 | −0.002 | 0.013 | 0.007 |
| dist_house | 0.077 | −0.001 | 0.007 | −0.004 | 0.022 | 0.121 | 0.023 | −0.000 | 0.003 | −0.001 | 0.011 | 0.029 |
| rr_nat | 0.062 | 0.050 | 0.284 | 0.003 | 0.014 | 1.000 | 0.026 | 0.016 | 0.167 | 0.001 | 0.008 | 0.995 |
| dr | 0.060 | 0.040 | 0.244 | 0.002 | 0.013 | 0.984 | 0.035 | 0.026 | 0.191 | 0.001 | 0.010 | 0.993 |
| x2009 | 0.050 | −0.025 | 0.200 | −0.001 | 0.008 | 0.019 | 0.061 | −0.027 | 0.209 | −0.001 | 0.008 | 0.023 |
| e_union | 0.045 | −0.015 | 0.224 | −0.001 | 0.012 | 0.292 | 0.013 | 0.000 | 0.104 | 0.000 | 0.006 | 0.430 |
| elec_year | 0.043 | 0.006 | 0.08 | 0.000 | 0.005 | 0.913 | 0.056 | 0.008 | 0.091 | 0.000 | 0.006 | 0.934 |
| x2010 | 0.042 | −0.007 | 0.125 | −0.000 | 0.005 | 0.010 | 0.051 | −0.009 | 0.140 | −0.000 | 0.006 | 0.017 |
| inflation | 0.040 | 0.001 | 0.022 | 0.000 | 0.006 | 0.807 | 0.040 | 0.001 | 0.022 | 0.000 | 0.006 | 0.936 |
| bbr | 0.039 | 0.010 | 0.167 | 0.000 | 0.007 | 0.914 | 0.028 | 0.008 | 0.139 | 0.000 | 0.006 | 0.968 |
| Burn-ins | 100,000 | |||||||||||
| Iterations | 1 m | |||||||||||
| Cor PMP | 0.9995 | 0.9996 | ||||||||||
Appendix C. Jointness Measures
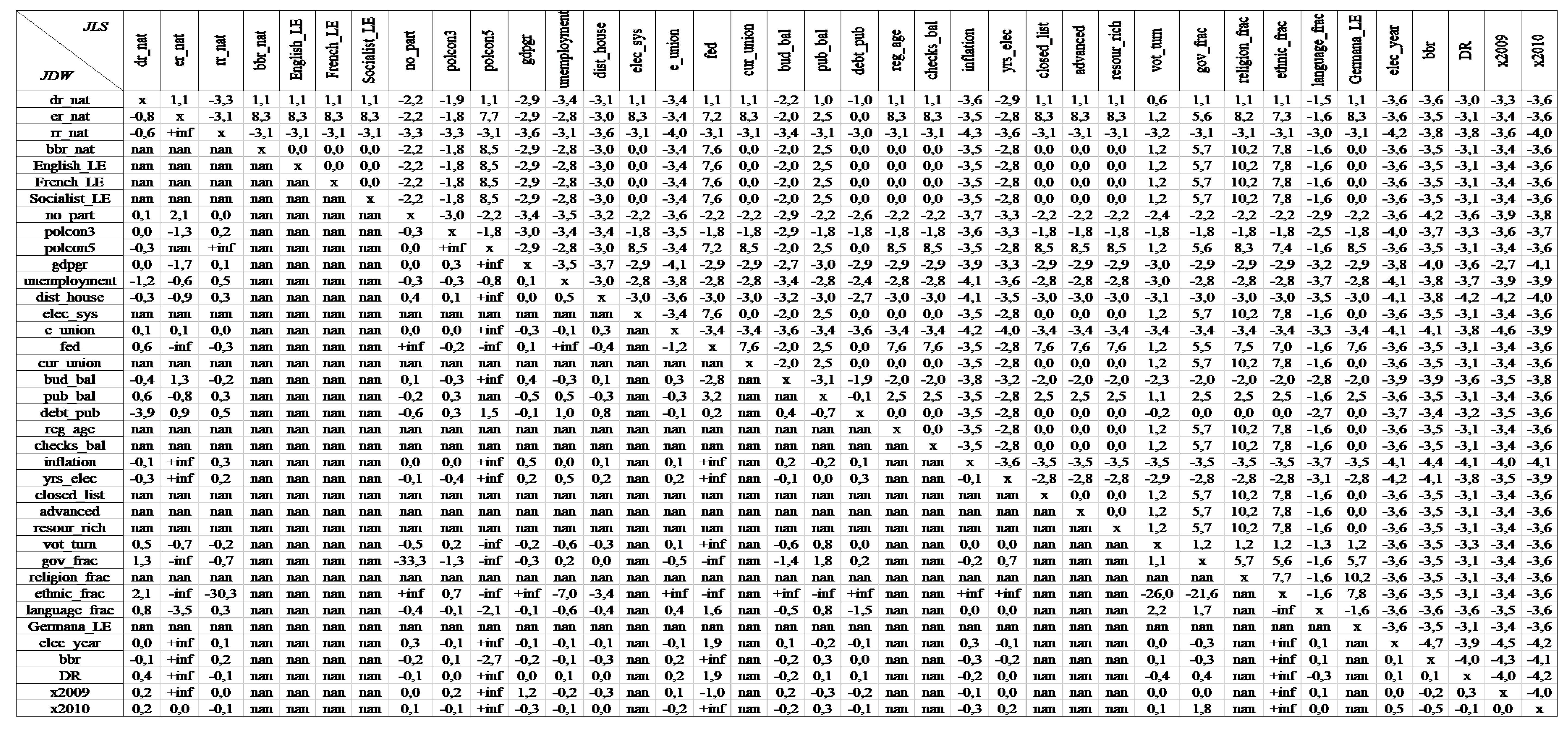
Appendix D. Overall and Country Specific Descriptive Statistics
| Variable | N | Min | Max | Avg | Std. Dev. |
|---|---|---|---|---|---|
| cen_gov_exp | 300 | 13.25 | 63.80 | 29.20 | 6.91 |
| pub_bal | 300 | −32.18 | 18.46 | −1.91 | 4.95 |
| bud_bal | 300 | −29.20 | 19.66 | −1.43 | 4.74 |
| debt_pub | 300 | 3.66 | 125.76 | 51.15 | 28.20 |
| gdpgr | 300 | −17.70 | 10.99 | 2.06 | 3.38 |
| unemployment | 300 | 2.20 | 25.00 | 7.86 | 3.68 |
| inflation | 300 | −2.75 | 14.03 | 2.75 | 1.87 |
| reg_age | 300 | 14.50 | 207.50 | 68.14 | 48.65 |
| ethnic_frac | 300 | 0.05 | 0.59 | 0.24 | 0.18 |
| religion_frac | 300 | 0.09 | 0.82 | 0.42 | 0.22 |
| language_frac | 300 | 0.02 | 0.64 | 0.26 | 0.20 |
| gov_frac | 300 | 0.00 | 0.83 | 0.37 | 0.26 |
| polcon3 | 300 | 0.12 | 0.72 | 0.47 | 0.12 |
| polcon5 | 300 | 0.34 | 0.89 | 0.77 | 0.07 |
| vot_turn | 300 | 40.57 | 94.85 | 71.01 | 12.26 |
| no_part | 300 | 1.00 | 6.00 | 2.53 | 1.24 |
| checks_bal | 300 | 2.00 | 8.00 | 4.27 | 1.10 |
| dist_house | 300 | 0.90 | 120.00 | 13.89 | 22.52 |
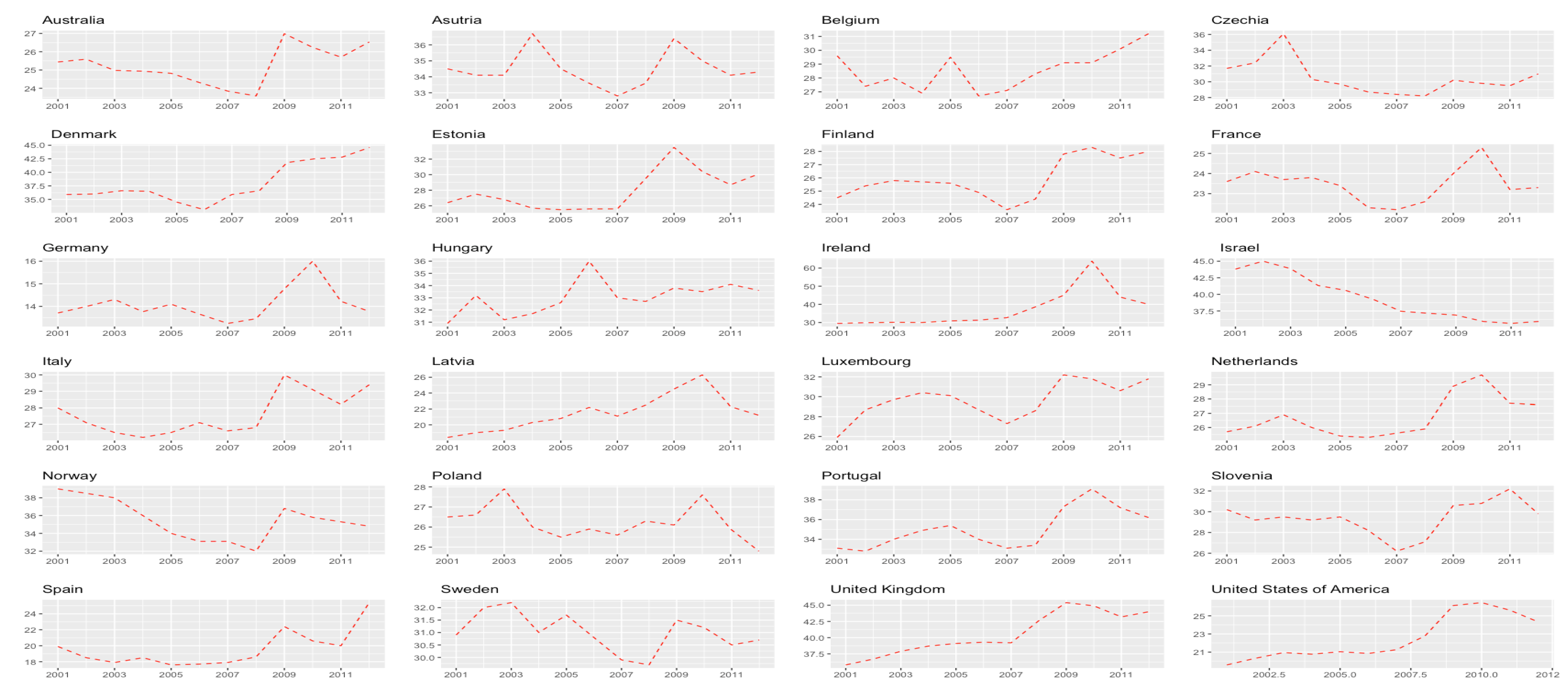
| Country avg. | Australia | Austria | Belgium | Bulgaria | Czech Republic | Denmark | Estonia | Finland | France | Germany | Hungary | Ireland | Israel |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| cen_gov_exp | 25.25 | 34.48 | 28.58 | 26.83 | 30.50 | 38.07 | 27.94 | 25.96 | 23.46 | 14.08 | 33.03 | 37.15 | 39.40 |
| pub_bal | −0.95 | −2.57 | −1.90 | 0.39 | −3.79 | 0.83 | 0.50 | 1.75 | −3.92 | −2.25 | −5.78 | −5.53 | −4.82 |
| bud_bal | −0.38 | −2.07 | −1.62 | 0.63 | −3.63 | 0.98 | 0.86 | 2.27 | −3.81 | −1.47 | −4.66 | −5.15 | −4.67 |
| debt_pub | 15.75 | 71.45 | 98.30 | 29.20 | 31.20 | 41.07 | 5.61 | 41.78 | 70.43 | 68.27 | 67.10 | 51.35 | 79.30 |
| gdpgr | 3.06 | 1.57 | 1.31 | 3.66 | 2.93 | 0.58 | 4.27 | 1.65 | 1.11 | 1.16 | 1.66 | 2.30 | 3.59 |
| unemployment | 5.33 | 4.41 | 7.75 | 11.14 | 7.00 | 5.38 | 10.11 | 8.13 | 9.04 | 8.39 | 8.08 | 7.71 | 10.07 |
| inflation | 2.83 | 2.08 | 2.21 | 5.12 | 2.47 | 2.09 | 4.19 | 1.97 | 1.91 | 1.70 | 5.24 | 2.33 | 2.26 |
| reg_age | 106.50 | 61.50 | 113.50 | 17.50 | 14.50 | 106.50 | 16.50 | 90.50 | 61.50 | 17.50 | 17.50 | 85.50 | 59.50 |
| ethnic_frac | 0.09 | 0.11 | 0.56 | 0.40 | 0.32 | 0.08 | 0.51 | 0.13 | 0.10 | 0.17 | 0.15 | 0.12 | 0.34 |
| religion_frac | 0.82 | 0.41 | 0.21 | 0.60 | 0.66 | 0.23 | 0.50 | 0.25 | 0.40 | 0.66 | 0.52 | 0.15 | 0.35 |
| language_frac | 0.33 | 0.15 | 0.54 | 0.30 | 0.32 | 0.10 | 0.49 | 0.14 | 0.12 | 0.16 | 0.03 | 0.03 | 0.55 |
| gov_frac | 0.16 | 0.44 | 0.80 | 0.41 | 0.36 | 0.48 | 0.61 | 0.64 | 0.18 | 0.40 | 0.14 | 0.18 | 0.70 |
| polcon3 | 0.44 | 0.49 | 0.71 | 0.48 | 0.46 | 0.31 | 0.53 | 0.54 | 0.51 | 0.46 | 0.37 | 0.46 | 0.58 |
| polcon5 | 0.86 | 0.75 | 0.89 | 0.61 | 0.74 | 0.73 | 0.77 | 0.77 | 0.87 | 0.85 | 0.74 | 0.76 | 0.78 |
| vot_turn | 94.29 | 80.71 | 90.71 | 61.01 | 62.62 | 86.63 | 60.21 | 66.02 | 60.41 | 76.10 | 66.88 | 65.56 | 65.05 |
| dist_house | 0.90 | 20.30 | 13.63 | 7.72 | 16.08 | 10.50 | 9.20 | 13.33 | 1.00 | 1.90 | 8.88 | 4.00 | 120.00 |
| no_part | 1.58 | 2.00 | 5.42 | 2.75 | 2.33 | 2.67 | 2.83 | 3.92 | 2.17 | 2.00 | 1.67 | 2.33 | 5.00 |
| checks_bal | 4.58 | 4.00 | 4.08 | 2.67 | 5.50 | 5.25 | 3.25 | 4.25 | 4.17 | 4.58 | 3.50 | 5.42 | 4.33 |
| French_LO | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| Socialist_LO | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| German_LO | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| English_LO | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| cur_union | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 0 |
| e_union | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| fed | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| advanced | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| resour_rich | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| elec_sys | 1 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 1 | 2 | 2 | 3 | 3 |
| closed_list | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| BBR | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| DR | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| BBR_nat | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 |
| DR_nat | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| RR_nat | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| ER_nat (2012) | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 |
| Country avg. | Italy | Latvia | Luxembourg | Netherlands | Norway | Poland | Portugal | Slovenia | Spain | Sweden | United Kingdom | United States | All |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| cen_gov_exp | 27.63 | 21.49 | 29.65 | 26.73 | 35.53 | 26.23 | 35.04 | 29.38 | 19.58 | 31.01 | 40.57 | 22.51 | 29.20 |
| pub_bal | −3.45 | −2.29 | 1.34 | −2.14 | 13.06 | −4.92 | −5.64 | −2.20 | −3.37 | 0.59 | −4.93 | −5.81 | −1.91 |
| bud_bal | −2.93 | −1.39 | 0.97 | −1.63 | 13.69 | −4.30 | −4.61 | −2.37 | −1.73 | 0.70 | −4.38 | −5.09 | −1.43 |
| debt_pub | 106.73 | 20.39 | 11.32 | 54.64 | 40.02 | 47.60 | 74.47 | 31.60 | 51.73 | 42.85 | 53.25 | 73.34 | 51.15 |
| gdpgr | 0.16 | 4.23 | 2.33 | 1.11 | 1.59 | 3.80 | 0.21 | 2.15 | 1.59 | 2.16 | 1.51 | 1.76 | 2.06 |
| unemployment | 8.07 | 11.86 | 4.27 | 4.09 | 3.57 | 13.55 | 8.46 | 6.47 | 13.87 | 7.11 | 6.09 | 6.51 | 7.86 |
| inflation | 2.41 | 5.03 | 2.68 | 2.22 | 1.82 | 2.79 | 2.44 | 3.60 | 2.84 | 1.77 | 2.41 | 2.37 | 2.75 |
| reg_age | 61.50 | 14.50 | 117.50 | 110.50 | 107.50 | 18.50 | 31.50 | 16.50 | 30.50 | 96.50 | 122.50 | 207.50 | 68.14 |
| ethnic_frac | 0.11 | 0.59 | 0.53 | 0.11 | 0.06 | 0.12 | 0.05 | 0.22 | 0.42 | 0.06 | 0.12 | 0.49 | 0.24 |
| religion_frac | 0.30 | 0.56 | 0.09 | 0.72 | 0.20 | 0.17 | 0.14 | 0.29 | 0.45 | 0.23 | 0.69 | 0.82 | 0.42 |
| language_frac | 0.11 | 0.58 | 0.64 | 0.51 | 0.07 | 0.05 | 0.02 | 0.22 | 0.41 | 0.20 | 0.05 | 0.25 | 0.26 |
| gov_frac | 0.11 | 0.63 | 0.48 | 0.58 | 0.48 | 0.29 | 0.08 | 0.56 | 0.01 | 0.52 | 0.04 | 0.00 | 0.37 |
| polcon3 | 0.40 | 0.51 | 0.51 | 0.56 | 0.53 | 0.46 | 0.38 | 0.40 | 0.37 | 0.45 | 0.38 | 0.40 | 0.47 |
| polcon5 | 0.68 | 0.77 | 0.77 | 0.76 | 0.77 | 0.74 | 0.74 | 0.75 | 0.85 | 0.76 | 0.74 | 0.85 | 0.77 |
| vot_turn | 81.43 | 65.35 | 90.14 | 78.26 | 76.43 | 48.27 | 61.84 | 64.51 | 72.72 | 81.97 | 61.80 | 56.44 | 71.01 |
| dist_house | 14.04 | 20.00 | 15.00 | 8.30 | 9.45 | 11.66 | 10.50 | 10.50 | 6.80 | 11.60 | 1.00 | 1.00 | 13.89 |
| no_part | 1.67 | 3.17 | 2.00 | 3.00 | 3.00 | 2.17 | 1.33 | 3.58 | 1.08 | 3.50 | 1.17 | 1.00 | 2.53 |
| checks_bal | 3.42 | 5.17 | 4.00 | 5.92 | 5.00 | 4.08 | 2.50 | 5.42 | 3.58 | 4.67 | 3.17 | 4.17 | 4.27 |
| French_LO | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0.28 |
| Socialist_LO | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0.28 |
| German_LO | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.08 |
| English_LO | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0.20 |
| cur_union | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0.52 |
| e_union | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0.82 |
| fed | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0.20 |
| advanced | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0.84 |
| resour_rich | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.04 |
| elec_sys | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 1 | 1 | 2.57 |
| closed_list | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 0.48 |
| BBR | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0.89 |
| DR | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0.83 |
| BBR_nat | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0.49 |
| DR_nat | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0.23 |
| RR_nat | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.14 |
| ER_nat (2012) | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0.50 |
Appendix E. Variable Inclusion over Posterior Probability Mass
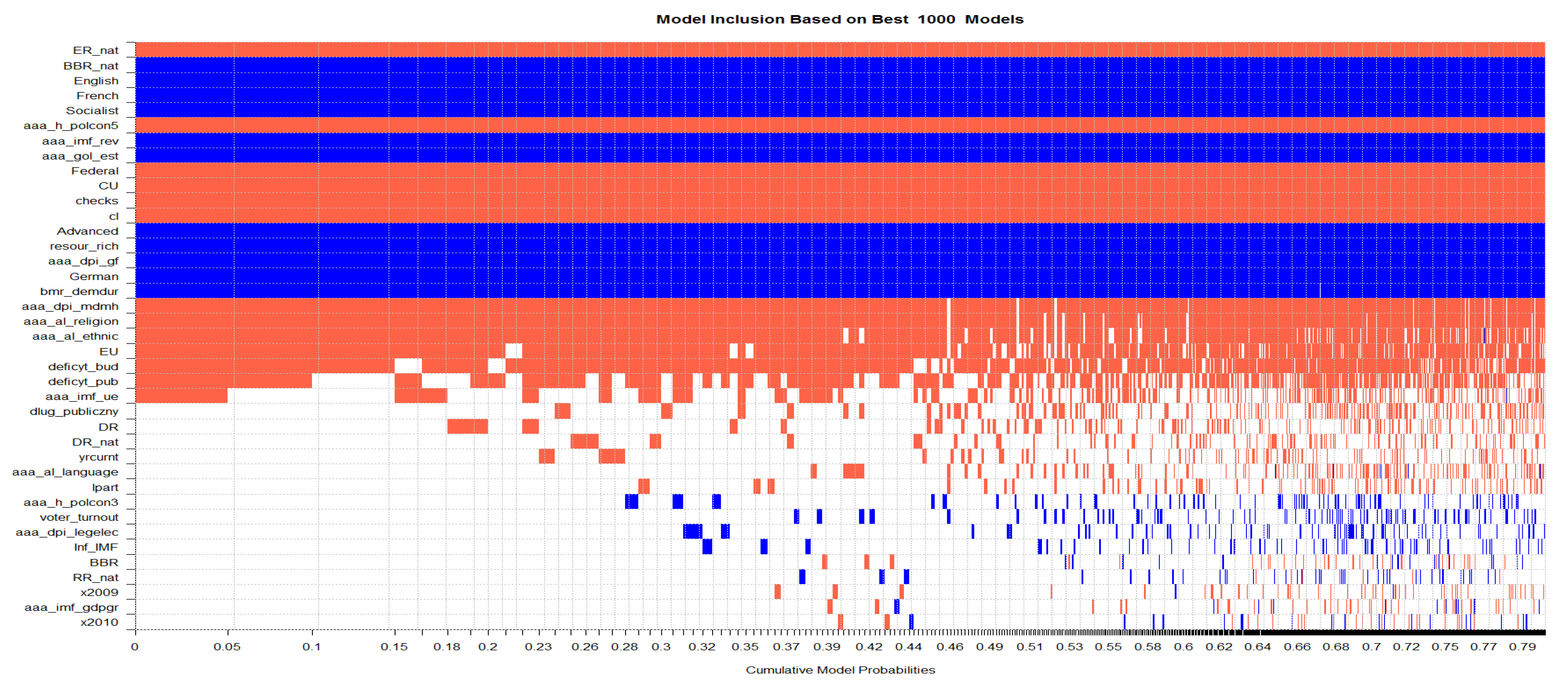
Appendix F. Variable Inclusion over Posterior Probability Mass
References
- Wagner, A. Three Extracts on Public Finance. In Classics in the Theory of Public Finance; Palgrave Macmillan: London, UK, 1958; pp. 1–15. [Google Scholar] [CrossRef]
- Afonso, A.; Huart, F.; Jalles, J.T.; Stanek, P. Assessing the sustainability of external imbalances in the European Union. World Econ. 2019, 42, 320–348. [Google Scholar] [CrossRef]
- Persson, T.; Tabellini, G. The Economic Effects of Constitutions: What Do The Data Say? MIT Press: London, UK, 2003. [Google Scholar]
- Wildavsky, A.B. The Politics of the Budgetary Process; Little, Brown: Boston, MA, USA, 1984; p. 323. [Google Scholar]
- Wagner, R.E. Fiscal Sociology and the Theory of Public Finance: An Exploratory Essay; Edward Elgar: Cheltenham, PA, USA, 2007; p. 228. [Google Scholar]
- Wagner, R.E. Deficits, Debt, and Democracy: Wrestling with Tragedy on the Fiscal Commons; Edward Elgar: Cheltenham, PA, USA, 2012; p. 194. [Google Scholar]
- Hardin, G. The Tragedy of the Commons. Science 1968, 162, 1243–1248. [Google Scholar] [PubMed]
- Buchanan, J.; Tullock, G. The Calculus of Consent; University of Michigan Press: Ann Arbor, MI, USA, 1962. [Google Scholar] [CrossRef]
- Możdżeń, M. Tragedia wspólnych zasobów w procesie politycznym. Public Gov. 2013, 2–3, 102–115. [Google Scholar] [CrossRef]
- Możdżeń, M. Instytucje Polityczne i Proces Budżetowy: Przeciwdziałanie Tragedii Wspólnych Zasobów Fiskalnych; Wydawnictwo Naukowe Scholar: Warsaw, Poland, 2018; p. 284. [Google Scholar]
- Poterba, J.; von Hagen, J. (Eds.) Fiscal Institutions and Fiscal Performance; University of Chicago Press: Chicago, IL, USA, 1999. [Google Scholar]
- Tsebelis, G. Veto Players: How Political Institutions Work; Princeton University Press: Princeton, NJ, USA, 2002; p. 317. [Google Scholar]
- Bueno de Mesquita, B.; Smith, A.; Siverson, R.M.; Morrow, J.D. The Logic of Political Survival; MIT Press: Cambridge, MA, USA, 2003; p. 536. [Google Scholar]
- Ehrlich, S.D. Access Points: An Institutional Theory of Policy Bias and Policy Complexity; Oxford University Press: New York, NY, USA, 2012; p. 208. [Google Scholar] [CrossRef]
- Alwasiak, S.; Lewandowska-Kalina, M.; Kalina, L.; Kowalewski, O.; Możdżeń, M.; Rybiński, K. What Determines State Capture in Poland? Manag. Bus. Adm. Cent. Eur. 2013, 21, 86–109. [Google Scholar] [CrossRef]
- Drazen, A.; Eslava, M. Electoral manipulation via voter-friendly spending: Theory and evidence. J. Dev. Econ. 2010, 92, 39–52. [Google Scholar] [CrossRef]
- Drazen, A. The Political Business Cycle after 25 Years. In NBER Macroeconomics Annual 2000; Bernanke, B.S., Rogoff, K., Eds.; MIT Press: Cambridge, MA, USA, 2001; Volume 15, pp. 75–138. [Google Scholar]
- Shi, M.; Svensson, J. Conditional Political Budget Cycles; Technical Report 3352; Centre for Economic Policy Research; SSRN: Rochester, NY, USA, 2002. [Google Scholar]
- Alwasiak, S.; Lewandowska-Kalina, M.; Kalina, L.; Kowalewski, O.; Możdżeń, M.; Rybiński, K. Interes publiczny a interesy grupowe w polskim ustawodawstwie. Ekonomista 2014, 3, 349–365. [Google Scholar]
- Foremny, D.; Freier, R.; Moessinger, M.D.; Yeter, M. Overlapping political budget cycles. Public Choice 2018, 177, 1–27. [Google Scholar] [CrossRef]
- Rogoff, K. Equilibrium Political Budget Cycles. Am. Econ. Rev. 1990, 80, 21–36. [Google Scholar] [CrossRef]
- Persson, T.; Tabellini, G. The size and scope of government: Comparative Politics with Rational Politicians. Eur. Econ. Rev. 1999, 43, 699–735. [Google Scholar] [CrossRef]
- Milesi-Ferretti, G.M.; Perotti, R.; Rostagno, M. Electoral Systems and Public Spending. Q. J. Econ. 2002, 117, 609–657. [Google Scholar] [CrossRef]
- Persson, T.; Tabellini, G. Political Institutions and Policy Outcomes: What are the Stylized Facts? Technical Report 412; Bank of Italy: Rome, Italy, 2001. [Google Scholar]
- Persson, T.; Tabellini, G. Constitutions and Economic Policy. J. Econ. Perspect. 2004, 18, 75–98. [Google Scholar] [CrossRef]
- Mink, M.; de Haan, J. Are there Political Budget Cycles in the Euro Area? Eur. Union Politics 2006, 7, 191–211. [Google Scholar] [CrossRef]
- Cusack, T.R. Partisan politics and public finance: Changes in public spending in the industrialized democracies, 1955–1989. Public Choice 1997, 91, 375–395. [Google Scholar] [CrossRef]
- Philips, A.Q. Seeing the forest through the trees: A meta-analysis of political budget cycles. Public Choice 2016, 168, 313–341. [Google Scholar] [CrossRef]
- Bee, C.A.; Moulton, S.R. Political budget cycles in U.S. municipalities. Econ. Gov. 2015, 16, 379–403. [Google Scholar] [CrossRef]
- Galli, E.; Rossi, S.P. Political Budget Cycles: The Case of the Western German Länder. Public Choice 2002, 110, 283–303. [Google Scholar] [CrossRef]
- Guillamón, M.D.; Bastida, F.; Benito, B. The electoral budget cycle on municipal police expenditure. Eur. J. Law Econ. 2013, 36, 447–469. [Google Scholar] [CrossRef]
- Vergne, C. Democracy, elections and allocation of public expenditures in developing countries. Eur. J. Political Econ. 2009, 25, 63–77. [Google Scholar] [CrossRef]
- Carey, J.M.; Shugart, M.S. Incentives to cultivate a personal vote: A rank ordering of electoral formulas. Elect. Stud. 1995, 14, 417–439. [Google Scholar] [CrossRef]
- Pfeil, F.C. Electoral System Change and Spending: Four Quantitative Case Studies; Technical Report 16/06; Walter Eucken Institut e.V.: Freiburg, Germany, 2016. [Google Scholar]
- Hallerberg, M.; Marier, P. Executive Authority, the Personal Vote, and Budget Discipline in Latin American and Caribbean Countries. Am. J. Political Sci. 2004, 48, 571. [Google Scholar] [CrossRef]
- Stratmann, T.; Okolski, G. Civic Participation and Government Spending; Technical Report No. 10-24; George Mason University Merkatus Center: Arlington, VA, USA, 2010. [Google Scholar]
- Von Hagen, J. Budgeting Procedures and Fiscal Performance in the European Communities; Technical Report 96; European Commission: Brussels, Belgium, 1992. [Google Scholar]
- Von Hagen, J.; Harden, I.J. Budget processes and commitment to fiscal discipline. Eur. Econ. Rev. 1995, 39, 771–779. [Google Scholar] [CrossRef]
- Hallerberg, M.; von Hagen, J. Electoral Institutions, Cabinet Negotiations, and Budget Deficits in the European Union. In Fiscal Institutions and Fiscal Performance; Poterba, J., von Hagen, J., Eds.; The University of Chicago Press: Chicago, IL, USA, 1999; pp. 209–232. [Google Scholar]
- Stienlet, G. Institutional Reforms and Belgian Fiscal Policy in the 90S. In Institutions, Politics, and Fiscal Policy; Strauch, J., von Hagen, J., Eds.; Kluwers Academic Publishers: New York, NY, USA, 2011; pp. 215–234. [Google Scholar] [CrossRef]
- Molander, P. Reforming Budgetary Institutions: Swedish Experiences. In Institutions, Politics, and Fiscal Policy; Strauch, R., von Hagen, J., Eds.; Kluwer Academic Publishers: New York, NY, USA, 2011; pp. 191–214. [Google Scholar] [CrossRef]
- Strauch, R. Budgetprozesse und Haushaltsdisziplin—Eine Analyse der US-Amerikanischen Staaten. Ph.D. Thesis, University of Bonn, Bonn, Germany, 1999. [Google Scholar]
- Dincecco, M. The political economy of fiscal prudence in historical perspective. Econ. Politics 2010, 22, 1–36. [Google Scholar] [CrossRef]
- Gleich, H.; Von Hagen, J. The Evolution of Budget Institutions: Evidence from Central and Eastern European Countries; Technical Report; University of Bonn, Center for European Integration Studies: Bonn, Germany, 2002. [Google Scholar]
- Hallerberg, M.; Yläoutinen, S. Political Power, Fiscal Institutions and Budgetary Outcomes in Central and Eastern Europe. J. Public Policy 2010, 30, 45–62. [Google Scholar] [CrossRef]
- Stein, E.; Talvi, E.; Grisanti, A. Institutional Arrangements and Fiscal Performance: The Latin American Experience. In Fiscal Institutions and Fiscal Performance; Poterba, J., von Hagen, J., Eds.; The University of Chicago Press: Chocago, IL, USA, 1999; pp. 103–134. [Google Scholar]
- Jones, M.P.; Sanguinetti, P.; Tommasi, M. Politics, Institutions, and Public-Sector Spending in the Argentine Provinces. In Fiscal Institutions and Fiscal Performance; Poterba, J., von Hagen, J., Eds.; The University of Chicago Press: Chiicago, IL, USA, 1999; pp. 135–150. [Google Scholar]
- Bawn, K. Money and Majorities in the Federal Republic of Germany: Evidence for a Veto Players Model of Government Spending. Am. J. Political Sci. 2007, 43, 707–736. [Google Scholar] [CrossRef]
- Keefer, P.; Knack, S. Boondoggles, rent-seeking, and political checks and balances: Public investment under unaccountable governments. Rev. Econ. Stat. 2007, 89, 566–572. [Google Scholar] [CrossRef]
- Brennan, G.; Buchanan, J.M. The Power to Tax: Analytical Foundations of a Fiscal Constitution; Cambridge University Press: Cambridge, UK, 1980; p. 231. [Google Scholar]
- Tiebout, C.M. A Pure Theory of Local Expenditures. J. Political Econ. 1956, 64, 416–424. [Google Scholar] [CrossRef]
- Weingast, B.R.; Shepsle, K.A.; Johnsen, C. The Political Economy of Benefits and Costs: A Neoclassical Approach to Distributive Politics. J. Political Econ. 1981, 89, 642–664. [Google Scholar] [CrossRef]
- Heinemann, F.; Moessinger, M.D.; Yeter, M. Do fiscal rules constrain fiscal policy? A meta-regression-analysis. Eur. J. Political Econ. 2018, 51. [Google Scholar] [CrossRef]
- Hallerberg, M. Domestic Budgets in a United Europe: Fiscal Governance from the end of Bretton Woods to EMU; Cornell University Press: New York, NY, USA, 2004; p. 245. [Google Scholar]
- Fatas, A.; Mihov, I. The Case for Restricting Fiscal Policy Discretion. Q. J. Econ. 2003, 118, 1419–1447. [Google Scholar] [CrossRef]
- Von Hagen, J.; Wolff, G.B. What do deficits tell us about debt? Empirical evidence on creative accounting with fiscal rules in the EU. J. Bank. Financ. 2006, 30, 3259–3279. [Google Scholar] [CrossRef]
- Shadbegian, R.J. Do tax and expenditure limitations affect the size and growth of state government? Contemp. Econ. Policy 1996, 14, 22–35. [Google Scholar] [CrossRef]
- Reuter, W.H. National numerical fiscal rules: Not complied with, but still effective? Eur. J. Political Econ. 2015, 39, 67–81. [Google Scholar] [CrossRef]
- Comiskey, M. Electoral Competition and the Growth of Public Spending in 13 Industrial Democracies, 1950 to 1983. Comp. Political Stud. 1993, 26, 350–374. [Google Scholar] [CrossRef]
- Levin, A.; Lin, C.F.; Chu, C.S.J. Unit root tests in panel data: Asymptotic and finite-sample properties. J. Econom. 2002, 108, 1–24. [Google Scholar] [CrossRef]
- Im, K.S.; Pesaran, M.H.; Shin, Y. Testing for unit roots in heterogeneous panels. J. Econom. 2003, 115, 53–74. [Google Scholar] [CrossRef]
- Pesaran, M.H. Bayes Factors. J. Appl. Econom. 2007, 22, 265–312. [Google Scholar] [CrossRef]
- Brock, W.A.; Durlauf, S.N. Growth empirics and reality. World Bank Econ. Rev. 2001, 15, 229–272. [Google Scholar] [CrossRef]
- Wooldridge, J.M. Econometric Analysis of Cross Section and Panel Data; MIT Press: Cambridge, MA, USA; London, UK, 2010; p. 1064. [Google Scholar]
- Zellner, A. On Assessing Prior Distributions and Bayesian Regression Analysis with g Prior Distributions. In Bayesian Inference and Decision Techniques: Essays in Honor of Bruno de Finetti. Studies in Bayesian Econometrics 6; Goel, P., Zellner, A., Eds.; Elsevier: New York, NY, USA, 1986; pp. 233–243. [Google Scholar]
- Fernández, C.; Ley, E.; Steel, M.F. Benchmark priors for Bayesian model averaging. J. Econom. 2001, 100, 381–427. [Google Scholar] [CrossRef]
- Kass, R.E.; Wasserman, L. A Reference Bayesian Test for Nested Hypotheses and its Relationship to the Schwarz Criterion. J. Am. Stat. Assoc. 1995, 90, 928. [Google Scholar] [CrossRef]
- Foster, D.P.; George, E.I. The Risk Inflation Criterion for Multiple Regression. Ann. Stat. 1994, 22, 1947–1975. [Google Scholar] [CrossRef]
- Ley, E.; Steel, M.F. On the effect of prior assumptions in Bayesian model averaging with applications to growth regression. J. Appl. Econom. 2009, 24, 651–674. [Google Scholar] [CrossRef]
- Ley, E.; Steel, M.F. Mixtures of g-priors for Bayesian model averaging with economic applications. J. Econom. 2012, 171, 251–266. [Google Scholar] [CrossRef]
- Feldkircher, M.; Zeugner, S. Benchmark Priors Revisited: On Adaptive Shrinkage and the Supermodel Effect in Bayesian Model Averaging; Technical Report 202; International Monetary Fund: Washington, DC, USA, 2009. [Google Scholar]
- Eicher, T.S.; Papageorgiou, C.; Raftery, A.E. Default priors and predictive performance in Bayesian model averaging, with application to growth determinants. J. Appl. Econom. 2011, 26, 30–55. [Google Scholar] [CrossRef]
- Sala-i Martin, X.; Doppelhofer, G.; Miller, R.I. Determinants of Long-Term Growth: A Bayesian Averaging of Classical Estimates (BACE) Approach. Am. Econ. Rev. 2004, 94, 813–835. [Google Scholar] [CrossRef]
- George, E.I. Dilution priors: Compensating for model space redundancy. In Borrowing Strength: Theory Powering Applications—A Festschrift for Lawrence D. Brown; Berger, J., Cai, T.J., Ohnstone, I., Eds.; Institute of Mathematical Statistics: Beachwood, OH, USA, 2010; pp. 158–165. [Google Scholar] [CrossRef]
- Madigan, D.; York, J.; Allard, D. Bayesian Graphical Models for Discrete Data. Int. Stat. Rev. 1995, 63, 215–223. [Google Scholar] [CrossRef]
- Doppelhofer, G.; Weeks, M. Jointness of growth determinants. J. Appl. Econom. 2009, 24, 209–244. [Google Scholar] [CrossRef]
- Kass, R.E.; Raftery, A.E. Bayes Factors. J. Am. Stat. Assoc. 1995, 90, 773–795. [Google Scholar] [CrossRef]
- Ley, E.; Steel, M.F. Jointness in Bayesian variable selection with applications to growth regression. J. Macroecon. 2007, 29, 476–493. [Google Scholar] [CrossRef]
- Blażejowski, M.; Kwiatkowski, J. Bayesian Model Averaging and Jointness Measures for gretl. J. Stat. Softw. 2015, 68, 1–24. [Google Scholar] [CrossRef]
- Beck, K. Bayesian model averaging and jointness measures: Theoretical framework and application to the gravity model of trade. Stat. Transition. New Ser. 2017, 18, 393–412. [Google Scholar] [CrossRef][Green Version]
- Beck, K. What drives business cycle synchronization? BMA results from the European Union. Balt. J. Econ. 2019, 19, 248–275. [Google Scholar] [CrossRef]
- Hofmarcher, P.; Crespo Cuaresma, J.; Grün, B.; Humer, S.; Moser, M. Bivariate joint measure in Bayesian Model Averaging: Solving the conundrum. J. Macroecon. 2018, 57, 150–165. [Google Scholar] [CrossRef]
- Hodler, R.; Luechinger, S.; Stutzer, A. The effects of voting costs on the democratic process and public finances. Am. Econ. J. Econ. Policy 2015, 7, 141–171. [Google Scholar] [CrossRef]
- Godefroy, R.; Henry, E. Voter turnout and fiscal policy. Eur. Econ. Rev. 2016, 89, 389–406. [Google Scholar] [CrossRef]
- Hoffman, M.; León, G.; Lombardi, M. Compulsory voting, turnout, and government spending: Evidence from Austria. J. Public Econ. 2017, 145, 103–115. [Google Scholar] [CrossRef]
- Parkinson, C.N.C.N. Parkinson’s Law, and Other Studies in Administration; Riverside Press: Cambridge, MA, USA, 1957; p. 112. [Google Scholar]
- Baumol, W.J.; Bowen, W.G. On the Performing Arts: The Anatomy of Their Economic Problems. Am. Econ. Rev. 1956, 55, 495–502. [Google Scholar] [CrossRef]
- Peacock, A.T.; Wiseman, J.; Peacock, A.T.; Wiseman, J. The Growth of Public Expenditure in the United Kingdom; Oxford University Press: London, UK, 1961. [Google Scholar]
- Roubini, N.; Sachs, J. Government Spending and Budget Deficits in the Industrial Economies; Technical Report; National Bureau of Economic Research: Cambridge, MA, USA, 1989. [Google Scholar] [CrossRef]
- Volkerink, B.; Haan, J.D. Fragmented Government Effects on Fiscal Policy: New Evidence. Public Choice 2001, 109, 221–242. [Google Scholar] [CrossRef]
- Brauninger, T. A partisan model of government expenditure. Public Choice 2005, 125, 409–429. [Google Scholar] [CrossRef]
- Esping-Andersen, G. The Three Worlds of Welfare Capitalism; Princeton University Press: Princeton, NJ, USA, 1990; p. 248. [Google Scholar]
- Iqbal, R.; Todi, P. The Nordic Model: Existence, Emergence and Sustainability. Procedia Econ. Financ. 2015, 30, 336–351. [Google Scholar] [CrossRef]
- Ossowski, R.; Halland, H. Fiscal Management in Resource-Rich Countries: Essentials for Economists, Public Finance Professionals, and Policy Makers; Technical Report; World Bank Studies: Washington, DC, USA, 2016. [Google Scholar] [CrossRef]
- Pierson, P. Increasing Returns, Path Dependence, and the Study of Politics. Am. Political Sci. Rev. 2000, 94, 251–267. [Google Scholar] [CrossRef]
- Buti, M.; Ejffinger, S.; Franco, D. Revisiting the Stability and Growth Pact: Grand Design or Internal Adjustment? Technical Report; Instituto Latinoamericano y del Caribe de Planificación Económica y Social: Santiago de Chile, Chile, 2003. [Google Scholar]
- BUITER, W.H. The ‘Sense and Nonsense of Maastricht’ Revisited: What Have we Learnt about Stabilization in EMU? JCMS J. Common Mark. Stud. 2006, 44, 687–710. [Google Scholar] [CrossRef]
- Alesina, A.; Glaeser, E. Fighting Poverty in the US and Europe: A World of Difference (Rodolfo DeBenedetti Lectures); Oxford University Press: New York, NY, USA, 2006. [Google Scholar]
- Stichnoth, H.; Van der Straeten, K. Ethnic diversity, public spending, and individual support for the welfare state: A review of the empirical literature. J. Econ. Surv. 2013, 27, 364–389. [Google Scholar] [CrossRef]
- Lora, E.; Olivera, M. Public debt and social expenditure: Friends or foes? Emerg. Mark. Rev. 2007, 8, 299–310. [Google Scholar] [CrossRef]
- Pasten, R.; Cover, J.P. The Political Economy of Unsustainable Fiscal Deficits. Cuad. Econ. 2010, 47, 169–189. [Google Scholar] [CrossRef][Green Version]
- Braşoveanu, L.O. Correlation Between Government and Economic Growth—Specific Features for 10 Nms. J. Knowl. Manag. Econ. Inf. Technol. 2012, 2, 1–14. [Google Scholar]
- Downs, A. An Economic Theory of Democracy; Harper: New York, NY, USA, 1957; p. 310. [Google Scholar]
- Schaechter, A.; Kinda, T.; Budina, N.; Weber, A. Fiscal Rules in Response to the Crisis–Toward the “Next-Generation” Rules. A New Dataset; Technical Report WP/12/187; International Monetary Fund: Washington, DC, USA, 2012. [Google Scholar]
- La Porta, R.; Lopez-De-Silanes, F.; Shleifer, A. Corporate Ownership Around the World. J. Financ. 1999, 54, 471–517. [Google Scholar] [CrossRef]
- Bormann, N.C.; Golder, M. Democratic Electoral Systems around the world, 1946–2011. Elect. Stud. 2013, 32, 360–369. [Google Scholar] [CrossRef]
- Beck, T.; Clarke, G.; Groff, A.; Keefer, P.; Walsh, P. New Tools in Comparative Political Economy: The Database of Political Institutions. World Bank Econ. Rev. 2001, 15, 165–176. [Google Scholar] [CrossRef]
- Alesina, A.; Devleeschauwer, A.; Easterly, W.; Kurlat, S.; Wacziarg, R. Fractionalization. J. Econ. Growth 2003, 8, 155–194. [Google Scholar] [CrossRef]
- Henisz, W. The Political Constraint Index (POLCON) Dataset. 2003. Available online: https://mgmt.wharton.upenn.edu/faculty/heniszpolcon/polcondataset/ (accessed on 13 May 2020).
- Reynolds, A.; Reilly, B.; Ellis, A.; José, W.; Cheibub, A.; Cox, K.; Lisheng, D.; Elklit, J.; Gallagher, M.; Hicken, A.; et al. Electoral System Design: The New International IDEA Handbook; Technical Report; IDEA: Stockholm, Sweden, 2005. [Google Scholar]
| Hypothesis | Variable Name | Variable Description |
|---|---|---|
| H1 | elec_sys | Electoral systems: 1. Majoritarian; 2. Mixed; 3. Proportional. |
| closed_list | Closed list variable is a dummy taking two values: If voters cannot choose individual candidates and vote for entire lists —1, otherwise—0 | |
| dist_house | Mean District Magnitude in House elections. Weighted average of the number of representatives elected in different size districts, if available. If not, the number of seats is divided by the number of districts (if both are known). | |
| H2 | vot_turn | Voter turnout in last parliamentary election (%) |
| H3 | yrs_elec | Years left in current parliamentary term |
| H4 | gov_frac | Government Fractionalization Index. The probability that two deputies picked at random from among the government parties will be of different parties (we understand that there are other methods to gauge electoral competition, such as introduced by [59]. However, we decided to use fractionalization as the most often used measure in these kind of studies). |
| no_part | Number of parties in the government | |
| H5 | checks_bal | The index of checks and balances equals 1, if the legislature is not chosen in competitive elections or in those in which only the executive has real power. For countries that do not meet this criterion (i.e., democratic states), one of the following conditions increases its value:
|
Additionally, in presidential systems the value is increased by 1 when:
| ||
| Polcon3 | Political constraints Index III. The index is composed from the following information: the number of independent branches of government with veto power over policy change, counting the executive and the presence of an elective lower and up https://www.overleaf.com/project/5d1da69847b47b3dfc826b40 per house in the legislature (more branches leading to more constraint); the extent of party alignment across branches of government, measured as the extent to which the same party or coalition of parties control each branch (decreasing the level of constraint); and the extent of preference heterogeneity within each legislative branch, measured as legislative fractionalization in the relevant house (increasing constraint for aligned executives, decreasing it for opposed executives). | |
| Polcon5 | Political constraints Index V. This index follows the same logic as Political Constraints Index III (Polcon3) but also includes two additional veto points: the judiciary and sub-federal entities | |
| H6 | er_nat | Existence of an expenditure rule at a central level. Yes—1, No—0 |
| rr_nat | Existence of a revenue rule at a central level. Yes—1, No—0 | |
| bbr_nat | Existence of a balance budget rule at a central level. Yes—1, No—0 | |
| dr_nat | Existence of a debt rule at a central level. Yes—1, No—0 | |
| dr | Existence of a debt rule at any level of government. Yes—1, No—0 | |
| bbr | Existence of a balance budget rule at any level of government. Yes—1, No—0 | |
| H7 | reg_age | Current political regime durability in years (averages) |
| Model Prior | Uniform | Dilution | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| g Prior | Unit Information Prior | Risk Inflation Criterion | ||||||||||
| VARIABLE | PIP | PM | PSD | SPM | SPSD | P(+) | PIP | PM | PSD | SPM | SPSD | P(+) |
| bbr_nat | 1.000 | 4.051 | 0.596 | 0.293 | 0.043 | 1.000 | 1.000 | 4.098 | 0.598 | 0.297 | 0.043 | 1.000 |
| English_LE | 1.000 | 11.710 | 1.220 | 0.679 | 0.071 | 1.000 | 1.000 | 11.340 | 1.009 | 0.657 | 0.058 | 1.000 |
| French_LE | 1.000 | 12.660 | 1.564 | 0.824 | 0.102 | 1.000 | 1.000 | 12.901 | 1.440 | 0.839 | 0.094 | 1.000 |
| Socialist_LE | 1.000 | 11.790 | 1.546 | 0.767 | 0.101 | 1.000 | 1.000 | 11.198 | 1.506 | 0.729 | 0.098 | 1.000 |
| elec_sys | 1.000 | 4.119 | 0.601 | 0.449 | 0.065 | 1.000 | 1.000 | 4.145 | 0.629 | 0.451 | 0.068 | 1.000 |
| cur_union | 1.000 | −8.231 | 0.772 | −0.596 | 0.056 | 0.000 | 1.000 | −8.415 | 0.769 | −0.609 | 0.056 | 0.000 |
| reg_age | 1.000 | 0.073 | 0.009 | 0.514 | 0.065 | 1.000 | 1.000 | 0.073 | 0.009 | 0.514 | 0.064 | 1.000 |
| checks_bal | 1.000 | −1.785 | 0.220 | −0.284 | 0.035 | 0.000 | 1.000 | −1.816 | 0.219 | −0.289 | 0.035 | 0.000 |
| closed_list | 1.000 | −5.998 | 0.806 | −0.434 | 0.058 | 0.000 | 1.000 | −6.217 | 0.826 | −0.450 | 0.060 | 0.000 |
| advanced | 1.000 | 5.371 | 0.831 | 0.285 | 0.044 | 1.000 | 1.000 | 5.224 | 0.824 | 0.278 | 0.044 | 1.000 |
| resour_rich | 1.000 | 9.931 | 1.424 | 0.282 | 0.040 | 1.000 | 1.000 | 10.051 | 1.384 | 0.285 | 0.039 | 1.000 |
| religion_frac | 1.000 | −10.005 | 1.557 | −0.319 | 0.050 | 0.000 | 1.000 | −10.453 | 1.430 | −0.334 | 0.046 | 0.000 |
| German_LE | 1.000 | 14.889 | 1.672 | 0.585 | 0.066 | 1.000 | 1.000 | 14.604 | 1.555 | 0.574 | 0.061 | 1.000 |
| fed | 1.000 | −5.424 | 1.154 | −0.314 | 0.067 | 0.000 | 0.993 | −4.627 | 1.277 | −0.268 | 0.074 | 0.000 |
| ethnic_frac | 1.000 | −17.659 | 2.688 | −0.458 | 0.070 | 0.000 | 1.000 | −19.496 | 1.805 | −0.505 | 0.047 | 0.000 |
| polcon5 | 1.000 | −15.661 | 3.269 | −0.168 | 0.035 | 0.000 | 1.000 | −16.384 | 3.133 | −0.176 | 0.034 | 0.000 |
| er_nat | 1.000 | −2.475 | 0.498 | −0.173 | 0.035 | 0.000 | 1.000 | −2.663 | 0.472 | −0.186 | 0.033 | 0.000 |
| gov_frac | 0.997 | 9.846 | 1.964 | 0.364 | 0.073 | 1.000 | 0.992 | 10.371 | 1.558 | 0.383 | 0.058 | 1.000 |
| pub_bal | 0.935 | −0.576 | 0.176 | −0.413 | 0.126 | 0.000 | 0.931 | −0.599 | 0.173 | −0.429 | 0.124 | 0.000 |
| vot_turn | 0.875 | 0.063 | 0.033 | 0.111 | 0.059 | 1.000 | 0.492 | 0.032 | 0.036 | 0.057 | 0.064 | 1.000 |
| dr_nat | 0.813 | −1.349 | 0.822 | −0.082 | 0.050 | 0.000 | 0.764 | −1.434 | 0.918 | −0.087 | 0.056 | 0.000 |
| debt_pub | 0.592 | 0.017 | 0.017 | 0.071 | 0.070 | 1.000 | 0.336 | 0.011 | 0.017 | 0.045 | 0.068 | 1.000 |
| language_frac | 0.276 | −1.724 | 3.321 | −0.049 | 0.094 | 0.014 | 0.015 | −0.096 | 0.879 | −0.003 | 0.025 | 0.008 |
| polcon3 | 0.263 | 0.998 | 1.954 | 0.017 | 0.034 | 1.000 | 0.062 | 0.231 | 1.023 | 0.004 | 0.018 | 1.000 |
| no_part | 0.164 | 0.097 | 0.274 | 0.017 | 0.049 | 1.000 | 0.024 | 0.027 | 0.197 | 0.005 | 0.035 | 1.000 |
| bud_bal | 0.146 | −0.058 | 0.177 | −0.040 | 0.121 | 0.000 | 0.070 | −0.047 | 0.174 | −0.032 | 0.119 | 0.000 |
| gdpgr | 0.124 | −0.010 | 0.034 | −0.005 | 0.017 | 0.000 | 0.044 | −0.003 | 0.020 | −0.002 | 0.010 | 0.000 |
| yrs_elec | 0.111 | −0.018 | 0.068 | −0.003 | 0.012 | 0.000 | 0.048 | −0.008 | 0.045 | −0.001 | 0.008 | 0.000 |
| dist_house | 0.109 | −0.002 | 0.008 | −0.006 | 0.027 | 0.135 | 0.010 | 0.000 | 0.002 | 0.000 | 0.007 | 0.023 |
| unemployment | 0.106 | −0.009 | 0.038 | −0.005 | 0.020 | 0.014 | 0.023 | −0.002 | 0.019 | −0.001 | 0.010 | 0.006 |
| rr_nat | 0.090 | 0.074 | 0.344 | 0.004 | 0.017 | 1.000 | 0.014 | 0.008 | 0.122 | 0.000 | 0.006 | 0.994 |
| dr | 0.086 | 0.056 | 0.291 | 0.003 | 0.016 | 0.978 | 0.016 | 0.012 | 0.132 | 0.001 | 0.007 | 0.995 |
| x2009 | 0.075 | −0.041 | 0.257 | −0.002 | 0.010 | 0.011 | 0.025 | −0.009 | 0.123 | 0.000 | 0.005 | 0.013 |
| e_union | 0.061 | −0.025 | 0.272 | −0.001 | 0.015 | 0.267 | 0.006 | 0.001 | 0.076 | 0.000 | 0.004 | 0.461 |
| elec_year | 0.061 | 0.009 | 0.096 | 0.001 | 0.006 | 0.907 | 0.027 | 0.004 | 0.062 | 0.000 | 0.004 | 0.971 |
| bbr | 0.060 | 0.014 | 0.212 | 0.001 | 0.009 | 0.892 | 0.012 | 0.004 | 0.092 | 0.000 | 0.004 | 0.984 |
| inflation | 0.057 | 0.001 | 0.026 | 0.000 | 0.007 | 0.795 | 0.020 | 0.001 | 0.015 | 0.000 | 0.004 | 0.973 |
| x2010 | 0.056 | −0.009 | 0.146 | 0.000 | 0.006 | 0.010 | 0.023 | −0.004 | 0.093 | 0.000 | 0.004 | 0.007 |
| Burn-ins | 100,000 | |||||||||||
| Iterations | 1 m | |||||||||||
| Cor PMP | 0.9987 | 0.9998 | ||||||||||
| NON_CU | CU | |
|---|---|---|
| 2001–2007 | 30.37% | 26.43% |
| 2008–2012 | 31.57% | 29.39% |
| Change | 3.96% | 11.18% |
| Hypothesis | Verdict |
|---|---|
| H1.States with a proportional electoral system are characterized by an average higher level of public spending (institutions of power legitimacy). | Not rejected |
| H2.States with a large size of winning coalition in relation to the size of the selectorate, are characterized by a higher level of public spending (institutions of power legitimacy). | Not rejected, but based on the value of PIP and SPM the link is very weak. |
| H3.There is no visible connection between the time left to the nearest elections and the volume of budget expenditures (institutions of power legitimacy). | Not rejected |
| H4.Governments with a large number of veto players are characterized by higher expenditures (institutions of internal power relations). | Not rejected |
| H5.Institutional checks and balances introducing independent counteracting forces to the institutions limiting government freedom of spending are generally effective (institutions of internal power relations). | Not rejected, but based on the value of SPM the link is not very strong. |
| H6.Fiscal rules, designed to stiffen the budget formation process, in practice have low effectiveness (rules of the budgetary process). | Analysis points towards rejection of H6. expenditure rule at the national level seems to suppress budget expenditures, but the influence of the rule, based on the value of SPM remains limited. |
| H7.The more robust the political system (the longer it is sustained) the higher the budgetary expenditures (institutions of power legitimacy/path dependence). | Not rejected |
| Framework | Fundamental Claim | Evaluation |
|---|---|---|
| Tragedy of the fiscal commons | The more actors with differing political bases are engaged in the budgetary process, the higher the public expenditures (and deficit) are | This claim is positively verified |
| Path dependence | Public expenditures rise incrementally in the long run | This claim is positively verified |
| Veto Players | The more veto players with different ideologies are engaged in the budgetary process, the more difficult it is to change expenditures | Institutional veto players which are weakly bound by the will of the voters decrease (and probably stabilize) public expenditures, while adding veto players of partisan nature increases expenditures. |
| Political Budget Cycle | Expenditures (and deficits) rise before important political elections | This claim is verified negatively |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Beck, K.; Możdżeń, M. Institutional Determinants of Budgetary Expenditures. A BMA-Based Re-Evaluation of Contemporary Theories for OECD Countries. Sustainability 2020, 12, 4104. https://doi.org/10.3390/su12104104
Beck K, Możdżeń M. Institutional Determinants of Budgetary Expenditures. A BMA-Based Re-Evaluation of Contemporary Theories for OECD Countries. Sustainability. 2020; 12(10):4104. https://doi.org/10.3390/su12104104
Chicago/Turabian StyleBeck, Krzysztof, and Michał Możdżeń. 2020. "Institutional Determinants of Budgetary Expenditures. A BMA-Based Re-Evaluation of Contemporary Theories for OECD Countries" Sustainability 12, no. 10: 4104. https://doi.org/10.3390/su12104104
APA StyleBeck, K., & Możdżeń, M. (2020). Institutional Determinants of Budgetary Expenditures. A BMA-Based Re-Evaluation of Contemporary Theories for OECD Countries. Sustainability, 12(10), 4104. https://doi.org/10.3390/su12104104





