Strategic Analysis of the Online Recycler’s Reselling Channel Selection: Agency or Self-Run

Abstract

With the rapid development of the internet, many WEEE (Waste Electrical and Electronic Equipment) online recyclers have emerged and developed. They improve recycling efficiency significantly and bring hope for sustainable development. Unfortunately, few works in the literature are concerned about it, with many questions still unanswered. The WEEE online recyclers always face a challenge with regard to how to strategically design their reselling channel structure in fact. In this paper, we examined this challenge by two decision models: agency and self-run. We derived the performance of the self-run model and agency model by backward induction and then examined the desirability from different stakeholders’ perspective. The results suggested that WEEE online recyclers prefer the self-run model to the agency model when the unit recycling cost is low and a conflict exists between the WEEE online recycler and e-retailer for the resale channel preference. Interestingly, the manufacturer shows consistent resale channel preference with the WEEE online recycler when the unit recycling cost is low. Our further analysis revealed that all players can agree on the agency model in a certain case. In addition, we found that the consumer surplus and the recovery ratio in the self-run model are always better than that in the agency model. Our work provides insight into the promotion of the WEEE online recycling industry and into the resale channel selection for online recyclers. The study also generates managerial insights for environmental sustainability.

1. Introduction

The rapid development of information technology and social economy has promoted the upgrading of electronic products, resulting in a huge amount of waste electrical and electronic equipment (WEEE) [1,2,3]. If no measures are taken to manage this WEEE, serious resource waste and environmental pollution will occur [4,5]. Although reverse logistics has been broadly favored by managers and researchers as an effective way to realize comprehensive and sustainable development, the rate of recycling in real life remains low due to inconveniences, high recycling cost, and confusing recycling systems [6,7]. In recent years, specific requirements in the field of environmental protection, such as reducing carbon emission, increasing recovery ratio, and improving the product lifetime, have become the driving force for sustainable development. Therefore, how to validly collect and dispose of WEEE has gradually become an urgent social problem worldwide [8,9,10,11,12].

Recently, with the rapid development of the internet, some companies, such as Aihuishou (www.aihuishou.com), Huishouge (www.huishouge.cn), and Yijiwang (www.58yiji.com), have emerged [13,14,15,16]. They collect WEEE from consumers by the online channel. Consumers can use smartphones or computers to return their used items to the WEEE online recycler within a few minutes, improving the recycling efficiency significantly [17,18,19]. Compared with traditional recycling, online recycling has many advantages due to its more transparent recovery price, smaller investment in building recycling stations, and more convenience for the consumer by relaxing the physical distance and space [20,21]. In addition, the WEEE online recycler’s professional data deletion service reduces consumer worry about leakage of private data stored in their digital products [21]. According to the data of Aihuishou, the total recycling amounts of WEEE have reached 11 million in 2017, with the number of users in China at more than 6 million and still increasing rapidly. It is an opportunity to improve resource utilization and promote sustainable development. For every one million cell phones recycled, we can recover 75 pounds of gold, 772 pounds of silver, 33 pounds of palladium, and 35,274 pounds of copper; cell phones also contain tin, zinc, and platinum. Moreover, recycling one million cell phones also can save enough energy to provide electricity to 185 U.S. households for a year (visit www.recyclemycell.com for more details). In other words, online recycling, which can integrate advantageous resources and avoid the recycling channel dispersion and less recycling quantity of the traditional recycling, is more environmental-friendly and sustainable. Therefore, in this paper, our research is based on the WEEE online recycling background.

The advent of online recycling brings a promising answer to the resource conservation and sustainable development of the environment. The WEEE online recycler, as a third-party remanufacturer, not only collects WEEE from consumers but also resells them after remanufacturing [22,23]. As a new industry, online recycling for WEEE has so far received very little attention in the literation. Scholars have made some preliminary studies on whether the recyclable dealer should open an online recycling channel [24,25,26,27]. However, how the WEEE online recycler operates its reselling business has been ignored by scholars. In real life, different WEEE online recyclers have different choices. For example, Gazelle (www.gazelle.com) combines the recycling and reselling business on its online platform, as well as Yijiwang and Love2recycle (www.love2recycle.fr). In this case, the WEEE online recycler must pay a certain cost to operate its reselling business. However, Aihuishou, Usell (www.usell.com), and Youdemai (www.youdemai.com) resell the collected products by JD (www.jd.com), Amazon (www.amazon.cn), and other e-retailers. Although the WEEE online recycler can transfer its operating cost to the e-retailer under this setting, a percentage of revenue has to be shared with the e-retailer as commission. Therefore, the underlying motivation for the WEEE online recycler to adopt which resale channel is unclear.

Online recycling has its typical structure characteristics, and proper mechanisms should be built to sustain its business operation and realize the sustainable development of the WEEE recycling industry. Motivated by the practices of the WEEE online recyclers, we considered that the online recycler has two options to resell the collected WEEE in this paper: resell them through its own online recycling platform (referred to as self-run model); or resell them through an e-retailer’s platform (referred to as agency model). Hence, we tried to answer these questions as follows: The key issue addressed in this paper is to determine which of the two reselling models (self-run and agency) is the better choice for the WEEE online recycler. To this end, we (1) derived the conditions under which the WEEE online recycler can choose an optimal resale channel; (2) examined the preference of the manufacturer and e-retailer for the resale channel, determining whether there is a situation under which all players can have a consistent preference for the resale channel; and (3) investigated the consumer surplus and the recovery ratio in the two models.

The above research questions include multiple decision makers, such as the manufacture, the e-retailer, and the WEEE online recycler, and each decision maker has its own choices (strategies). Moreover, they maximize their benefits through the choice (strategies), which are affected by each other. Game theory, which is a branch of applied mathematics to study multi-person decision making and search for the optimal decision under interactive condition [28,29], is an appropriate method for this study and has been widely used in previous studies [30,31,32,33]. Therefore, we used the game theory approach to develop two decision models (i.e., the agency model and self-run model) and then derived the performance of the two models by backward induction.

By comparing the results in the two reselling systems, we obtained several interesting findings. Intuitively, the WEEE online recycler prefers the self-run model to the agency model when the unit recycling cost is low. This is because a small unit recycling cost can help online recyclers compete with e-retailers by setting a lower retailing price. However, from the e-retailer’s perspective, when the unit recycling cost is low, the e-retailer prefers the agency model. Thus, there is a conflict between the WEEE online recycler and e-retailer for the resale channel preference. For the manufacturer, when the unit recycling cost is low, it prefers the self-run model. After examining the preferences of the WEEE online recycler, the e-retailer, and the manufacturer for the resale channel respectively, we are interested in exploring whether there is a region in which all players can have a consistent preference for the resale channel. We found that all players can agree on the agency model when the unit recycling cost is moderate. Moreover, from the perspectives of the consumer and environment, the self-run model is the better choice due to the lower retailing price and the higher recovery ratio. The above insights from the perspectives of enterprises, consumers, and environment will be able to not only supply a guideline for the enterprises but also provide a basis for the sustainable development of the environment. In addition, we were surprised to find that it is impossible to achieve supply chain coordination and environmental sustainability at the same time regarding the resale channel, which may require the guidance of government policy to promote sustainable development.

The remainder of the paper is organized as follows. After reviewing the relevant literature in Section 2, we provide the assumptions and notation in Section 3. Next, we introduce an agency model in which the WEEE online recycler resells collected products by an e-retailer and then we study the other case where the WEEE online recycler takes the resale business by itself in Section 4. Based on these analyses, a constructive comparison between agency model and self-run model is delivered in Section 5, and then the managerial insights were discussed in Section 6. The results were concluded in Section 7. All mathematical proofs can be found in the Appendix A.

2. Literature Review

This paper focuses on the resale channel choice of the WEEE online recyclers based on the reverse logistics supply chain. Thus, the related literature includes the fields of recycling operation and sales channel construction.

A growing stream of literature has focused on recycling channel selection and remanufacturing operation. Savaskan et al. [8] investigated the recycling issue early and compared three options for the recycling channel. Based on this, some scholars have studied the impact of retailer competition, cost structure, and recycling responsibility-sharing on recycling channel options [9,10,11]. With the deepening of research, an increasing number of scholars have turned their attention to third-party remanufacturers (TPRs) [12,30,31]; one of the interesting research questions concerning TPRs is who sells the remanufactured products. Wang et al. [32] considered two marketing channel structures of remanufactured products: (1) one that provides the remanufactured products to a manufacturer, and then the manufacturer sells both new products and the remanufactured products to customers, and (2) one that sells the remanufactured products directly to customers, finding that the customers’ acceptance for remanufactured products determines marketing channel selection. Moreover, Yan et al. [33] studied two options to market remanufactured products: marketing through the company’s e-channel or subcontracting the marketing operation to a third party. They found that both the original equipment manufacturers (OEM) and retailer prefer subcontracting to a third party. Zou et al. [34] extended Yan et al. [33]’s model to analyze the problem of marketing channel selection from the perspective of third-party remanufacturers. Our focus was completely different. First, we only focused on the online recycling channel, rather than comparing the pros and cons of multiple recycling channels. Second, instead of considering who performed the remanufacturing operations, we focused on the WEEE online recycler’s reselling business. Therefore, we built a self-run model and the agency model to distinguish the difference with the previous third-party remanufacturer (TPR) models.

Our work is also related to the rich stream of literature on the sales channel strategy: reselling or agency. Hagiu [35] demonstrated when the market intermediation should choose the “reselling” model or “agency selling” model under various channel structures. Hagiu and Wright [36] found that whether the marketplace or the reseller model is preferred depends on whether the independent supplier or the intermediary has more important information relevant to the optimal tailoring of marketing activities for each specific product. Based on this, Abhishek et al. [37] pointed out that the online intermediary prefers to use the marketplace model if the sales through the intermediary lead to a negative effect on the demand of the supplier’s traditional channel, and vice versa. At the same time, some researchers have considered the rationality of the supplier or traditional retailer selling by using online platforms. For example, Ryan et al. [38] considered a setting with a supplier who sells goods through its own direct sale website and has the option of selling its goods through an online platform. In a competitive supplier environment, Tian et al. [39] found that the order-fulfilment costs and upstream competition intensity are important factors affecting the online channel selection of suppliers. Regarding the traditional retailer, Bernstein et al. [40] studied how a traditional retailer sells its product online by using its own website or aligns with an e-retailer to reach the online market. Ru and Wang [41] considered a similar model in which a retailer sells its product through Amazon on a consignment basis with revenue sharing. Recently, Wang et al. [42] studied the problem of the retailer’s marketing channel selection, and the results suggested that a retailer that builds its online sale channel is not always good, but it emerges as a strategic necessity in some cases. Our paper differs from the aforementioned studies in the research objective. We studied the resale channel selection of the WEEE online recycler and combined the problem of channel selection with reverse logistics for the first time. Although our study considering the WEEE online recyclers that resell collected products through an e-retailer or by itself shows similarities with some studies [39,40,41], the key to our analysis is the change in the supply chain member’s operations caused by the WEEE online recycler’s selection of the resale channels.

Although the WEEE online recycling has become popular in recent years, the academic research on it is still at the initial stage [24,25,26,27]. In summary, the key issue of our paper (the resale channel selection of the WEEE online recycler) has not been thoroughly explored in the extant recycling channel selection, remanufacturing operation, and selling channel strategy literature. Thus, our findings regarding resale channel selection can also provide useful insights into reverse logistics research. In the next section, we describe our modeling framework.

3. Model Description

In this study, we considered a stylized supply chain comprising a manufacturer, an online recycler and an e-retailer. The e-retailer wholesales new products from the manufacturer, and then sells them to the consumer at a retailing price. The online recycler collects WEEE from the consumer, and then remanufactures and resells them in the consumer market. In Figure 1, we present two common resale channel structures as mentioned previously: resell the collected products by the e-retailer (agency model) or by itself (self-run model).

Our key assumptions concern the consumer preference, decision-making rule, cost of recycling, and reselling, etc. These assumptions we can find from the literature of reverse supply chain management (see, e.g., Savaskan et al. [8], Atasu et al. [10], Zou et al. [34], Örsdemir et al. [43], etc.). Here, we present the following set of assumptions but skip the detailed discussion on their justification. For convenience,

Table 1. Notation.

Symbol	Definition
ν	The consumer’s willingness-to-pay for the new product.
δ	The consumer value discount for the remanufactured product.
α	The WEEE online recycler shares $\alpha$ percentage of its revenue to the e-retailer as commission in the agency model.
$c_r$	The unit recycling cost of the online recycler for the used product.
$F$	In self-run model, the WEEE online recycler should pay a fixed cost to operate its resale business.
$p_n,p_o$	The unit retailing price of the new or remanufactured product.
$w$	The wholesale price of the new products set by the manufacturer.
$q_r$	Recycling quantity of the WEEE online recycler.
$q_n,q_o$	Sales of the new product or remanufactured product.
${\mathsf{\Pi }}_i\left(i=m,r,o\right)$	Profit function of the manufacturer, e-retailer, or online recycler.

summarizes the notation used in the model.

Assumption 1.

The inverse demand functions for new and remanufactured products are as follows:

$$p_n=1-q_n-\delta q_o;p_o=\delta \left(1-q_n-q_o\right)$$

(1)

Assumption 1 implies the consumer’s willingness-to-pay for the new product, $v$ is heterogeneous and distributed over the interval $\left[0,1\right]$ with a density of 1. Each consumer’s willingness-to-pay for the remanufactured product is a fraction $\delta \in \left(0,1\right)$ of that for the new one, and each customer buys at most one product that offers the most utility, as long as the net utility is positive. Thus, the linear inverse demand functions, Equation (1), can be derived from consumers’ utility functions. Assumption 1 has been widely used in previous studies (see, e.g., Atasu et al. [10], Örsdemir et al. [43], Xiong et al. [44], etc.).

Assumption 2.

To examine the resale channel selection of the WEEE online recycler without the distraction of the initial and terminal time-period effect, we developed a model of a steady-state period, implying that all players use the same strategies in every period after a ramp-up in the first period in an infinite horizon setting. In other words, we have $q_r\le q_n$ in the steady state period (similar to Agrawal et al. [31], Zou et al. [34], Xiong et al. [44]).

Assumption 3.

We assume that all collected products can be remanufactured and resold in the consumer market—that is $q_r=q_o$. This assumption can isolate the core research questions (i.e., selection of the resale channels) and simplifies the complexity of the problem to be analyzed (e.g.,Yan et al. [33], Xiong et al. [44], Jin et al. [45]).

Assumption 4.

We normalize the marginal sales cost of the new product and remanufactured product to zero. For simplicity, we also normalize the manufacturer’ unit production cost is zero. These assumptions have been widely used in other studies (e.g., Savaskan and Wassenhove [9], Ferguson and Toktay [30], Xiong et al. [44]).

Assumption 5.

Similar to the literature on the supply chain operation management (e.g., Yan et al. [33], Zou et al. [34], Jin et al. [45]), we assume that all players are risk-neutral and profit-seeking and have common knowledge of the demand and cost information. We also assume the game with the following sequence. The manufacturer sets the wholesale price first, and then the e-retailer and WEEE online recycler determine the sales for both new and remanufactured products simultaneously.

4. Models and Solutions

In the following analysis, subscript $i=\left\{m,r,o\right\}$ refers to the manufacturer, the e-retailer and the WEEE online recycler, respectively, and the superscript $j=\left\{a,s\right\}$ indicates the two types of resale channels, agency and self-run. Subscript $k=\left\{1,2,3\right\}$ indicates the scenario under which our analysis is proceeding. We first discuss the agency model (Section 4.1) and then discuss the self-run model (Section 4.2).

4.1. The Agency Model

In this subsection, we consider that the WEEE online recycler resells the collected product through the e-retailer. As in the practice of Amazon or JD, the WEEE online recycler can enter their online marketplace to resell remanufactured products and needs to share an allocation ratio $\alpha$ of its revenue with the e-retailer as commission. Moreover, we treat the allocation ratio as an exogenous variable. Much evidence exposes the common practice that e-retailers such as Amazon and JD serve several 3P-retailers. They cannot determine a revenue allocation ratio for every individual 3P-retailer, but announce a single ratio applicable to all relevant 3P-retailers. For example, Amazon sets 15% of the revenue allocation ratio for beauty, clothing, and outdoor and 8% for cell phone devices and consumer electronics. JD sets 1% of revenue allocation ratio for cell phone devices and 0.8% for computers. Accordingly, it is reasonable to assume the exogeneity of the revenue allocation ratio in this paper. Additionally, we find that the allocation ratio of e-retailers, such as Amazon and JD, is not more than $1/4$ practically. Thus, we set $\alpha \in \left(0,1/4\right)$, and this assumption will be held for the remainder of this paper. The profit functions of the manufacturer, e-retailer, and WEEE online recycler can be written as:

$$\{\begin{array}{l}\underset{w}{\max }{\mathsf{\Pi }}_m^a=w{q}_n\\ \underset{q_n}{\max }{\mathsf{\Pi }}_r^a=\left(p_n-w\right)q_n+\alpha p_o{q}_r\\ \underset{q_r}{\max }{\mathsf{\Pi }}_o^a=\left(1-\alpha \right)p_o{q}_r-c_r{q}_{r}s.t.q_n\ge q_r\ge 0\end{array}.$$

(2)

We solve the game with backward induction to guarantee the sub-game perfect equilibrium. For a given $w$, the e-retailer and WEEE online recycler determine $q_n$ and $q_r$ to maximize their profits simultaneously. The optimal sales decisions are characterized by the following Lemma 1.

Lemma 1.

In the agency model, for a given $w^a$, the e-retailer’s and online recycler’s optimal quantity responses are as follows:

(1) 

If $w^a<w_1^a$, then ${q_n^a}_1{\left(w^a\right)}^{\ast }=\frac{1-w^a}{2};{q_r^a}_1{\left(w^a\right)}^{\ast }=0$,

(2) 

If $w_1^a\le w^a\le w_2^a$, then $\{\begin{array}{l}{q_n^a}_2{\left(w^a\right)}^{\ast }=\frac{\left(2-\left(\alpha +1\right)\delta \right)\left(1-\alpha \right)+\left(\alpha +1\right)c_r+2w^a\left(\alpha -1\right)}{\left(4-\left(\alpha +1\right)\delta \right)\left(1-\alpha \right)}\\ {q_r^a}_2{\left(w^a\right)}^{\ast }=\frac{\delta \left(w^a+1\right)\left(1-\alpha \right)-2c_r}{\delta \left(1-\alpha \right)\left(4-\left(\alpha +1\right)\delta \right)}\end{array}$,

(3) 

Otherwise, ${q_n^a}_3{\left(w^a\right)}^{\ast }=q_{r3}^a{\left(w^a\right)}^{\ast }=\frac{1-w^a}{\delta \left(1+\alpha \right)+2}$.

Here, $w_1^a=\frac{2c_r+\delta \left(\alpha -1\right)}{\delta \left(1-\alpha \right)};w_2^a=\frac{\delta \left(1-\alpha \right)\left(1-\left(\alpha +1\right)\delta \right)+c_r\left(\left(\alpha +1\right)\delta +2\right)}{3\delta \left(1-\alpha \right)}$.

The economic intuition behind Lemma 1 is in line with intuition. If the wholesale price is sufficiently low, indicating the new product sold by the e-retailer has strong market competitiveness, the remanufactured product does not enter the market—i.e., scenario (1) of Lemma 1. If the wholesale price is moderate, this weakens the competitiveness of new products. Thus, the remanufactured product can gain some market share, and then the recycling product quantity is only a portion of the new product quantity—i.e., scenario (2) of Lemma 1. If the wholesale price is sufficiently high, the second-hand market is so large that the WEEE online recycler’s optimal response is to resell as many as possible, the recycling products quantity is bounded by the new product quantity sold by the e-retailer—i.e., scenario (3) of Lemma 1. We conclude from Lemma 1 that the resale decision of the WEEE online recycler is affected by the wholesale price of new products set by the manufacturer, and the manufacturer can collude with the e-retailer by setting a low wholesale price to prevent the WEEE online recycler from entering the consumer market [45]. From the point of sustainable development, a higher wholesale price is more conducive to increasing the amount of recycling. But the manufacturer and the e-retailer, which are rational and self-interested, are less likely to do so.

When setting $w^a$, the manufacturer does so with anticipation of the downstream quantity responses as shown in Lemma 1. Notably, the quantity equilibrium is contingent on the value of $w^a$, and the process to derive the manufacturer’s optimal wholesale price comprises two steps: (1) analyze the scenario in which the manufacturer induces the e-retailer and WEEE online recycler to choose a certain decision and (2) identify the global optimal solution by comparing the manufacturer’s profits in three scenarios. Let ${c_r^a}_1=\frac{3\delta \left(1-\alpha \right)}{4}$; $c_{r2}^a=\frac{\delta \left(6-\delta \left(1+\alpha \right)\right)\left(1-\alpha \right)}{8-\delta \left(1+\alpha \right)}$; $c_{r3}^a=\frac{\left(1-\alpha \right)\left({\left(\alpha +1\right)}^2{\delta }^2+\sqrt{A}-4\right)}{\left(1+\alpha \right)\left(\delta \left(1+\alpha \right)+2\right)},A=2\left(4-\delta \left(1+\alpha \right)\right)\left(2+\delta \left(1+\alpha \right)\right)$.

Proposition 1.

In the agency model, the manufacturer’s optimal wholesale price for the new product is as follows:

(1) 

${w_1^a}^{*}=\frac{1}{2}$, if $c_{r1}^a<c_r^a$;

(2) 

${w_2^a}^{*}=\frac{2c_r+\delta \left(\alpha -1\right)}{\delta \left(1-\alpha \right)}$, if $c_{r2}^a<c_r\le c_{r1}^a$;

(3) 

${w_3^a}^{*}=\frac{\left(2-\left(1+\alpha \right)\delta \right)\left(1-\alpha \right)+\left(\alpha +1\right)c_r}{4\left(1-\alpha \right)}$, If $c_{r3}^a<c_r\le c_{r2}^a$;

(4) 

${w_4^a}^{*}=\frac{1}{2}$, if $c_r^a\le c_{r3}^a$.

Proposition 1 illustrates that, if the unit recycling cost is sufficiently high, the manufacturer anticipates that the WEEE online recycler does not undertake the recycling business, and then the optimal wholesale price is a constant value. If the unit recycling cost is relatively high, the WEEE online recycler would be willing to enter the market because the resale is profitable. However, in this case, the manufacturer can price aggressively to deter the WEEE online recycler to enter the consumer market and the optimal wholesale price increases in $c_r$. If the unit recycling cost is relatively low, the manufacturer cannot prevent the WEEE online recycler from entering the market to sell remanufactured products; in this case, the manufacturer’s optimal wholesale price is also increasing in $c_r$. If the unit recycling cost is sufficiently low, the WEEE online recycler has the incentive to resell as many as possible. In this case, the optimal wholesale price is also a constant value and equal to that in scenario (1) of Proposition 1. The results are also illustrated in Figure 2. The insight behind this Proposition is that the WEEE online recycler should control its recycling cost as low as possible, so as to resell more remanufactured products and realize sustainable utilization of resources.

Substituting the optimal wholesale price back into Lemma 1 gives the optimal quantity; with the optimal price and optimal quantity, we have three players’ profits, as shown in

Table 2. Optimal profits in the agency model.

	${\mathit{c}}_{\mathit{r}}^{\mathit{a}}\le {{\mathit{c}}_{\mathit{r}}^{\mathit{a}}}_3$	${{\mathit{c}}_{\mathit{r}}^{\mathit{a}}}_3<{\mathit{c}}_{\mathit{r}}\le {{\mathit{c}}_{\mathit{r}}^{\mathit{a}}}_2$	${{\mathit{c}}_{\mathit{r}}^{\mathit{a}}}_2<{\mathit{c}}_{\mathit{r}}\le {{\mathit{c}}_{\mathit{r}}^{\mathit{a}}}_1$	${{\mathit{c}}_{\mathit{r}}^{\mathit{a}}}_1<{\mathit{c}}_{\mathit{r}}^{\mathit{a}}$
${\mathsf{\Pi }}_m^a$	$\frac{1}{4\left(2+\delta \left(1+\alpha \right)\right)}$	$\frac{{\left(c_r\left(1+\alpha \right)+\left(1-\alpha \right)\left(2-\delta \left(1+\alpha \right)\right)\right)}^2}{8{\left(1-\alpha \right)}^2\left(4-\delta \left(1+\alpha \right)\right)}$	$\frac{\left(2c_r+\delta \left(\alpha -1\right)\right)\left(\delta \left(1-\alpha \right)-c_r\right)}{{\delta }^2{\left(1-\alpha \right)}^2}$	$\frac{1}{8}$
${\mathsf{\Pi }}_r^a$	$\frac{2\alpha {\delta }^2\left(\alpha +1\right)+3\alpha \delta +1}{4{\left(2+\delta \left(1+\alpha \right)\right)}^2}$	$\frac{{\xi }_1{c}_r^2+{\xi }_2{c}_r+{\xi }_3}{16\delta {\left(1-\alpha \right)}^2{\left(4-\delta \left(1+\alpha \right)\right)}^2}$	$\frac{{\left(c_r+\delta \left(\alpha -1\right)\right)}^2}{{\delta }^2{\left(1-\alpha \right)}^2}$	$\frac{1}{16}$
${\mathsf{\Pi }}_o^a$	$\frac{{\xi }_4-\left(\left(\alpha +1\right)\delta +2\right)c_r}{2{\left(2+\delta \left(1+\alpha \right)\right)}^2}$	$\frac{{\left({\xi }_4+c_r\left(\left(\alpha +1\right)\delta -8\right)\right)}^2}{16\delta \left(1-\alpha \right){\left(4-\delta \left(1+\alpha \right)\right)}^2}$	$0$	$0$

$\begin{array}{l}{\xi }_1=\delta \left(\alpha +1\right)\left(4\left(5\alpha +1\right)-\alpha \delta \left(\alpha +1\right)\right)-64\alpha ;{\xi }_2=2\delta \left(1-\alpha \right)\left(2-\delta \left(1+\alpha \right)\right)\left(\alpha \delta \left(\alpha +1\right)+4\left(1-\alpha \right)\right)\\ {\xi }_3=\delta {\left(1-\alpha \right)}^2\left({3\alpha \delta }^3{\left(\alpha +1\right)}^2{+4\delta }^2\left(1-6\alpha \right)\left(1+\alpha \right)+44\alpha \delta +16\left(1-\delta \right)\right);{\xi }_4=\delta \left(1-\alpha \right)\left(\delta \left(1+\alpha \right)+1\right);{\xi }_5=\delta \left(1-\alpha \right)\left(6-\delta \left(1+\alpha \right)\right)\end{array}$.

.

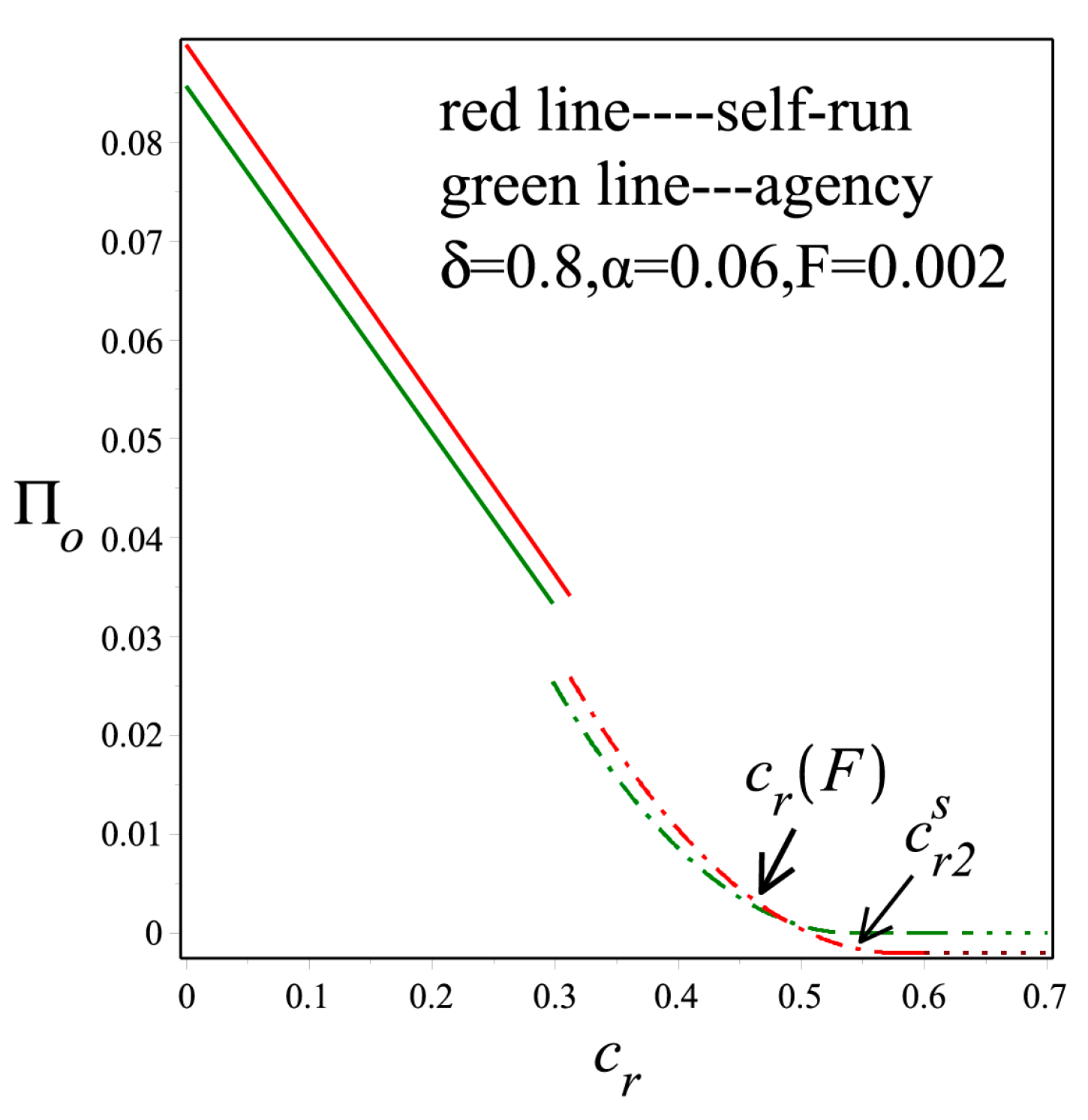
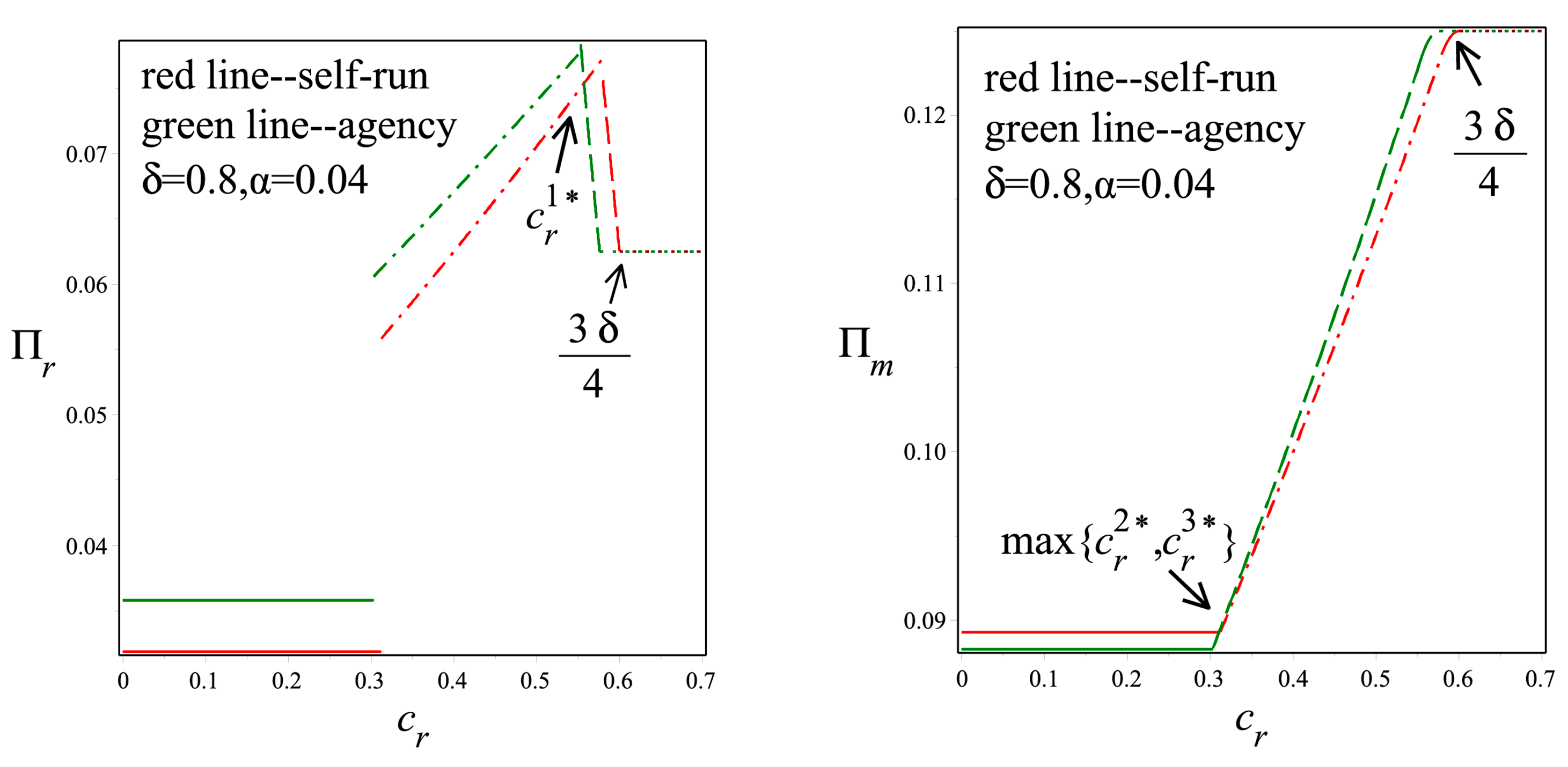
Clearly, we find that the optimal profit of the online recycler is decreasing in $c_r$, while the manufacturer’s is increasing in $c_r$. However, our finding towards the e-retailer is rather interesting: its profit is unimodal in $c_r$. In other words, as the unit recycling cost rises, the profit of the e-retailer is not always increasing. The results are also shown in Figure 3.

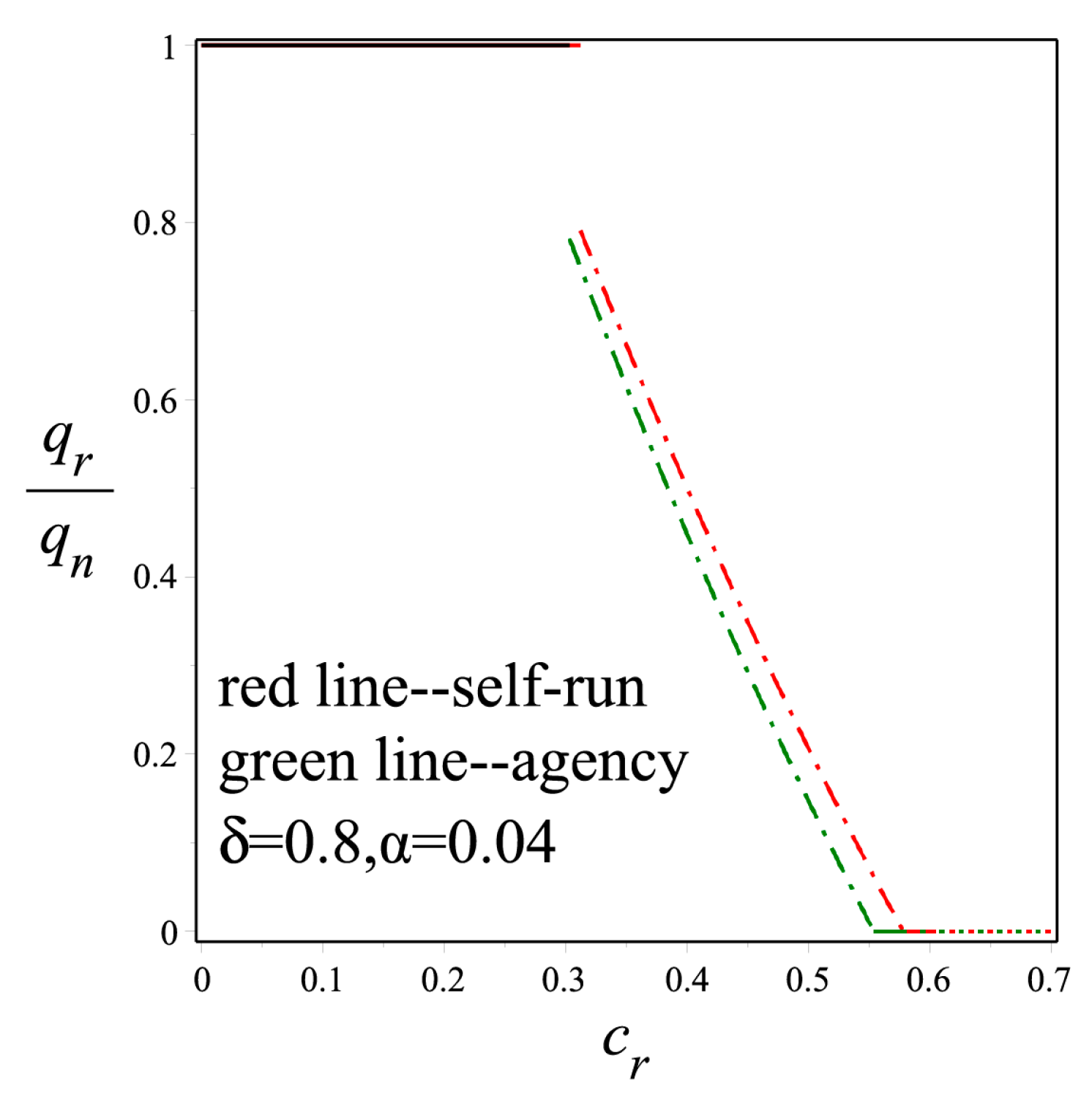
To understand the above findings, we further investigate how the quantity and retailing price change in $c_r$. As shown in Figure 4, interestingly, we find that $q_n^a$ is non-monotone in $c_r$. This is the key reason to explain why the profit of the e-retailer is unimodal in $c_r$. Regarding the manufacturer, a large wholesale price can make up the diminution of $q_n^a$ in some cases. Therefore, the profit of the manufacturer increases in $c_r$. For the WEEE online recycler, a large $c_r$ will increase its recycling cost and reduce the sales $q_r^a$ or retailing price $p_o^a$, leading to the decline of the online recycler’s profit. Compared with traditional recycling, the WEEE online recycler’s cost advantage has contribution to increase the recycling quantity and promote the sustainable development of the environment [22,23,24].

As a result, maintaining the recycling cost at a lower level is conducive to expanding the remanufactured market and improving the WEEE online recycler’s profit, but hurts the profits of the manufacturer and the e-retailer. In other words, although a lower recycling cost can help to promote the environmental sustainability, a coordinating and sustainable supply chain cannot be achieved.

4.2. The Self-Run Model

We consider the WEEE online recyclers (such as Gazelle and Yijiwang) resell the collected products through their own platform in this subsection. On the one hand, compared with the agency model, there is a stronger competition between the WEEE online recycler and e-retailer due to the lack of a revenue allocation ratio. On the other hand, undertaking the reselling business will make the WEEE online recycler pay a fixed cost $F$, which includes the labor cost, platform module construction, and platform maintenance cost.

At this time, the profit functions of the manufacturer, e-retailer, and WEEE online recycler can be expressed as follows:

$$\{\begin{array}{l}\underset{w}{\max }{\mathsf{\Pi }}_m^s=w{q}_n\\ \underset{q_n}{\max }{\mathsf{\Pi }}_r^s=\left(p_n-w\right)q_n\\ \underset{q_r}{\max }{\mathsf{\Pi }}_o^s=p_o{q}_r-c_r{q}_r-Fs.t.q_n\ge q_r\ge 0\end{array}.$$

(3)

Similar to the agency model, we solve the game with backward induction to guarantee the sub-game perfect equilibrium. According to Equations (1) and (2), we find that, if set $\alpha =0$ in Lemma 1, the optimal sales decision can be obtained in the self-run model. Similarly, we identify the manufacturer’s optimal decision in the second step as the following proposition. Let ${c_r^s}_1=\frac{3\delta }{4}$; ${c_r^s}_2=\frac{\delta \left(6-\delta \right)}{8-\delta }$; ${c_r^s}_3=\frac{\left({\delta }^2+\sqrt{2\left(4-\delta \right)\left(2+\delta \right)}-4\right)}{\delta +2}$.

Proposition 2.

In the self-run model, the manufacturer’s optimal wholesale price for the new product is as follows:

(1) 

$w_1^{s*}=\frac{1}{2}$, if $c_{r1}^s<c_r$;

(2) 

$w_2^{s*}=\frac{2c_r-\delta }{\delta }$, if $c_{r2}^s<c_r\le c_{r1}^s$;

(3) 

$w_3^{s*}=\frac{2-\delta +c_r}{4}$, if $c_{r3}^s<c_r\le c_{r2}^s$;

(4) 

$w_4^{s*}=\frac{1}{2}$ if $c_r^s\le c_{r3}^s$.

Proposition 2 shows that, similar to Proposition 1, with the decreasing unit recycling cost, the manufacturer will not be able to prevent the WEEE online recycler from reselling remanufactured products. The illustration of the wholesale price in the self-run model is also similar to Figure 2, and we will again find that the wholesale prices are constant (i.e., $w^s=1/2$) when the unit recycling cost is sufficiently high or low. In other cases, the wholesale price is increasing in $c_r$.

Substituting these optimal solutions back into Equation (2) gives the players’ optimal profits, as shown in

Table 3. Optimal profits in the self-run model.

	${\mathit{c}}_{\mathit{r}}^{\mathit{s}}\le {{\mathit{c}}_{\mathit{r}}^{\mathit{s}}}_3$	${{\mathit{c}}_{\mathit{r}}^{\mathit{s}}}_3<{\mathit{c}}_{\mathit{r}}\le {{\mathit{c}}_{\mathit{r}}^{\mathit{s}}}_2$	${{\mathit{c}}_{\mathit{r}}^{\mathit{s}}}_2<{\mathit{c}}_{\mathit{r}}\le {{\mathit{c}}_{\mathit{r}}^{\mathit{s}}}_1$	${{\mathit{c}}_{\mathit{r}}^{\mathit{s}}}_1<{\mathit{c}}_{\mathit{r}}^{\mathit{s}}$
${\mathsf{\Pi }}_m^s$	$\frac{1}{4\left(2+\delta \right)}$	$\frac{{\left(c_r+\left(2-\delta \right)\right)}^2}{8\left(4-\delta \right)}$	$\frac{\left(2c_r-\delta \right)\left(\delta -c_r\right)}{{\delta }^2}$	$\frac{1}{8}$
${\mathsf{\Pi }}_r^s$	$\frac{1}{4{\left(2+\delta \right)}^2}$	$\frac{{\left(c_r+2-\delta \right)}^2}{4{\left(4-\delta \right)}^2}$	$\frac{{\left(c_r-\delta \right)}^2}{{\delta }^2}$	$\frac{1}{16}$
${\mathsf{\Pi }}_o^s$	$\frac{\delta \left(1+\delta \right)-\left(\delta +2\right)c_r}{2{\left(2+\delta \right)}^2}-F$	$\frac{{\left(\delta \left(6-\delta \right)+c_r\left(\delta -8\right)\right)}^2}{16\delta {\left(4-\delta \right)}^2}-F$	$-F$	$-F$

.

The optimal profits in the self-run model change in $c_r$ are similar to those in the agency model. Again, we find that the manufacturer’s profit is increasing while the WEEE online recycler’s profit is decreasing in $c_r$, and the profit of the e-retailer is non-monotone in $c_r$. Compared with the agency model, the WEEE online recycler’s profit in the self-run model is smaller when the unit recycling cost is relatively high. This is because there is no market for the remanufactured products sold by the WEEE online recycler, resulting in the fixed cost (i.e., $F$) invested in the reselling business being irreparable.

5. Comparative Analysis

To find the optimal resale channel for the WEEE online recycler, we should analyze two reselling systems (i.e., agency and self-run) and then compare our results for these two systems.

Proposition 3.

Resale channel selection of the WEEE online recycler:

(1) 

if $0<c\le c_{r2}^s$ when $0<c_r\le c_r\left(F\right)$, ${\mathsf{\Pi }}_o^{s*}\ge {{\mathsf{\Pi }}_o^a}^{*}$; when $c_r\left(F\right)<c_r<c_{r2}^s$, ${\mathsf{\Pi }}_o^{s*}<{{\mathsf{\Pi }}_o^a}^{*}$. Thus, $c_r\left(F\right)$ is the unique solution to the equation ${{\mathsf{\Pi }}_{ok}^s}^{\ast }-{{\mathsf{\Pi }}_{ok}^a}^{\ast }=0$.

(2) 

if $c_{r2}^s<c_r$, ${\mathsf{\Pi }}_o^{s*}<{{\mathsf{\Pi }}_o^a}^{*}$.

This proposition reveals the WEEE online recycler’s resale channel strategy. The economic intuition behind this result is straightforward. On the one hand, if $0<c\le c_{r2}^s$, the WEEE online recycler reselling the remanufactured product by itself is better than through the e-retailer when the unit recycling cost is small. This is because when the unit recycling cost is small, the sales of the remanufactured product in the self-run model are larger than that in the agency model. On the other hand, if $c_{r2}^s<c_r$, there is no market for the remanufactured product in practice. In the self-run model, the WEEE online recycler cannot make up for the fixed cost invested in the resale business. Therefore, reselling by the e-retailer is a dominant strategy, although it also cannot obtain revenue in the agency model at this time. The results are also illustrated in Figure 5.

Proposition 4.

Resale channel preference of the e-retailer and the manufacturer:

(1) 

if $0<c_r\le c_r^{1*}$,${\mathsf{\Pi }}_r^{a*}\ge {\mathsf{\Pi }}_r^{s*}$; if $c_r^{1*}<c_r<\frac{3\delta }{4}$ ${{\mathsf{\Pi }}_r^a}^{*}<{\mathsf{\Pi }}_r^{s*}$; otherwise ${{\mathsf{\Pi }}_r^a}^{*}={\mathsf{\Pi }}_r^{s*}$. Where $c_r^{1*}=\frac{\delta \left(6-\delta \right)\left(1-\alpha \right)}{8-\delta \left(1+\alpha \right)}$.

(2) 

if $0<c_r\le \max \left\{c_r^{2*}{,c}_r^{3*}\right\}$, ${\mathsf{\Pi }}_m^{s*}\ge {\mathsf{\Pi }}_m^a$; if $\max \left\{c_r^{2*},c_r^{3*}\right\}<c_r<\frac{3\delta }{4}$, ${{\mathsf{\Pi }}_m^s}^{*}<{{\mathsf{\Pi }}_m^a}^{*}$; otherwise, ${{\mathsf{\Pi }}_m^s}^{*}={{\mathsf{\Pi }}_m^a}^{*}$. where $\{\begin{array}{l}{c}_r^{2*}=\frac{\left(1-\alpha \right)\left({\delta }^2\left(\alpha +1\right)+2\alpha \delta -4+\sqrt{2\left(\delta +2\right)\left(4-\delta \left(1+\alpha \right)\right)}\right)}{\left(2+\delta \right)\left(1+\alpha \right)}\\ {c_r^3}^{*}=\frac{\left(1-\alpha \right)\left({14\delta -16-2\delta }^2\left(\alpha +1\right)+6\alpha \delta +\sqrt{\left(4-\delta \right){\left(4-\delta \left(1+\alpha \right)\right)}^3}\right)}{{\alpha }^2\delta -2\alpha \delta -3\delta +16}\end{array}$.

From the perspective of the e-retailer, we find that, if the unit recycling cost is small—i.e., $0<c_r<{c_r^1}^{\ast }$—the e-retailer has the incentive to allow the WEEE online recycler to enter its online marketplace to resell the collected product. The driving force behind this result is that the e-retailer can obtain more commission from the WEEE online recycler under this situation. If the unit recycling cost is moderate—i.e., ${c_r^1}^{\ast }\le c_r<\frac{3\delta }{4}$—the e-retailer hopes the WEEE online recycler resells the remanufactured product by itself. A large unit recycling cost makes the online recycler lose its competitive advantage in the consumer market, resulting in the remanufactured product being withdrawn from the market gradually. For the manufacturer, if the unit recycling cost is small, i.e. $0<c_r<\max \left\{{c_r^2}^{\ast },{c_r^3}^{\ast }\right\}$, the wholesale price in the self-run is larger than that in the agency model, resulting in the manufacturer obtaining more profit in the self-run model. Under the condition, i.e., $\max \left\{{c_r^2}^{\ast },{c_r^3}^{\ast }\right\}\le c_r<\frac{3\delta }{4}$, the wholesale price in the agency model is larger. If the unit recycling cost is sufficiently high, the WEEE online recycler will no longer participate in recycling and reselling, and there is no difference between the two models. The results are also illustrated in Figure 6.

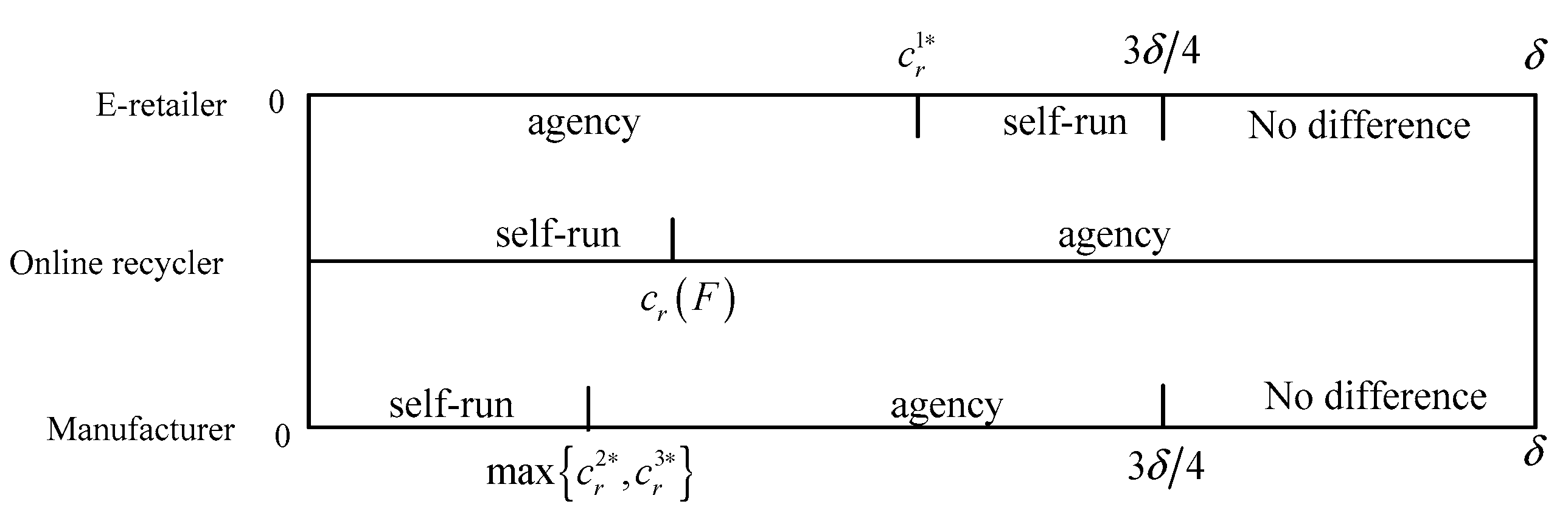
Proposition 5.

If $\max \left\{c_r\left(F\right),{c_r^2}^{\ast },{c_r^3}^{\ast }\right\}<c_r<{c_r^1}^{\ast }$, all the players have a consistent resale channel preference (i.e., agency model).

According to the above analysis, we find that, in a certain interval, i.e., $\max \left\{c_r\left(F\right),{c_r^2}^{\ast },{c_r^3}^{\ast }\right\}<c_r<{c_r^1}^{\ast }$ the manufacturer, e-retailer, and WEEE online recycler have the same preference for the resale channel (as shown in Figure 7). Under this particular condition, the WEEE online recycler can obtain more revenue by setting a higher retailing price for the remanufactured product. For the manufacturer and e-retailer, the wholesale price, retailing price, and sales of the new product in the agency model are higher than that in the self-run model. Therefore, they have a consistent preference for the resale channel in this case. As is known to all, ensure all players to be profitable is a basis for maintaining a coordinating and sustainable supply chain. A consistent choice can effectively avoid channel conflict and promote coordinating development of the supply chain.

Proposition 6.

The consumer surplus and the recovery ratio in the self-run model are always better than that in the agency model.

Comparing the consumer surplus and the recovery ratio between the self-run model and agency model, we find that the consumer surplus and the recovery ratio in the self-run model are always better than that in the agency model, as shown in Figure 8 and Figure 9. Interestingly, we take a closer look at the retailing price and the sales for the new and remanufactured products in two models, finding that the retailing prices in the self-run model are lower than that in the agency model. This is the key reason to explain why the consumer surplus in the self-run model is better. On the other hand, the amount of recycling in the self-run model is larger than that in the agency model. As a result, the recovery ratio in the self-run model is better. Extracting the managerial insights, in the self-run model, a lower retailing price will result in boosting the consumer surplus and a higher recovery ratio is conducive to resource conservation and improving product utilization. Therefore, from the perspective of consumers and the environment, the WEEE online recycler reselling the collected products by itself can accelerate the sustainable development of the economy and environment.

6. Discussion and Revelation

In this section, we would like to discuss the potential conflict revealed by the above results from the perspectives of supply chain coordination and environmental sustainability, and then we give some policy advice.

Firstly, we set up two resale models (i.e., agency model and self-run model) based on the WEEE online recycling background, and then solve the equilibrium solutions of the two models by backwards induction, respectively. The results imply that a smaller recycling cost can help to expand the sales of remanufactured products and improve the profit of the WEEE online recycler, which will boost the WEEE recycling industry and promote sustainable development. But there is a threat to the manufacturer and the retailer, because the remanufactured will erode the market of new products. As a response, the manufacturer and the e-retailer will conspire to set a low retailing price to prevent the WEEE online recycler from taking resale business (Proposition 1). There is a conflict between the WEEE online recycler and the forward supply chain. In other words, it is impossible to achieve supply chain coordination and environmental sustainability at the same time.

Next, we compare the two resale models from the perspectives of enterprises, consumers, and environment. Making a profit is a basis to the sustainable operation of the supply chain, and all the players, which are rational and self-interested, have their own preference for the resale channel (Proposition 3 and Proposition 4). Fortunately, we found that in a certain case, all players can agree with the agency model (Proposition 5), which implies that the supply chain can achieve coordinated operation. Moreover, we also found that the consumer surplus and recovery ratio in the self-run model is better than that in the agency model (Proposition 6), which indicates that the self-run model is more acceptable to consumers and is more conducive to resource conservation and environmental protection. At this time, we found that there is still a conflict between the supply chain coordination and sustainable development regarding the preference of resale channels.

Finally, to achieve the sustainable development and promote the supply chain coordination, the government needs to make efforts at this point. The government policy has an important role to ensure the recycling industry develops in a healthy way. For instance, the EPR (extended producer responsibility) policy—which refers to the responsibility of the producer extending not only to the production process, but also to the whole life cycle of the product, especially the recovery—has been implemented in many countries around the world. This policy can avoid the collusion between the manufacturer and the e-retailer to drive the WEEE online recycler out of the market, and encourage the recycler to increase the recycling quantity. As we all know, a suitable policy can achieve coordination between enterprises’ profits and environmental protection. In other words, we still have a long way to go on the road to achieve sustainable development.

7. Conclusions

Although recycling is an important measure to manage environmental pollution and resource shortage, the recycling rate is still low in real life. However, with the development of the internet, the rise in the WEEE online recycling industry may help to solve this dilemma. Compared to traditional recycling, the WEEE online recycling in O2O (online and offline) has many advantages due to its more transparent recovery price, smaller investment in building recycle stations, and convenience. Moreover, a key feature of online recyclers is that they not only collect the WEEE but also resell the remanufactured ones in the consumer market. However, how to construct the resale channel is the challenge for the WEEE online recycler in real life. Motivated by this, we established two reselling models (self-run and agency) to answer some questions, such as which resale channel the WEEE online recycler prefers, which model the manufacturer and e-retailer would prefer, and which model can generate more consumer surplus and higher recovery ratio.

To our knowledge, our study is the first to investigate resale channel selection with reverse logistics. We analyzed the performance of two resale channels and examined their desirability from different stakeholder perspectives. The analytical results confirmed that the manufacturer can collude with the e-retailer to resist the WEEE online recycler undertaking the resale business by setting a low wholesale price when the unit recycling cost is small. This finding is consistent with traditional wisdom (Jin et al. [45]). Our comparison of the profits of the WEEE online recycler in the two models suggests that the online recycler prefers the self-run model to the agency model when the unit recycling cost is low intuitively. However, from the e-retailer perspective, when the unit recycling cost is low, the e-retailer prefers the agency model; when the unit recycling cost is high, the e-retailer prefers the self-run model. A low unit recycling cost gives the online recycler more advantage than the e-retailer in the consumer market. If the WEEE online recycler undertakes the resale business by itself, the profit of the e-retailer will be hurt at this time, creating a conflict between the online recycler and e-retailer. For the manufacturer, when the unit recycling cost is low, the manufacturer prefers the self-run model; when the unit recycling cost is high, the manufacturer prefers the agency model. This result demonstrated that the manufacturer is more likely to have a consistent resale channel preference toward the WEEE online recycler than the e-retailer. This is because, when the unit recycling cost is low, the online recycler adopts the self-run model to conduct a fierce price war with the e-retailer, increasing the sales of new products and boosting the profits of the manufacturer. On further study, we found that all players can agree on the agency model in a certain case. Moreover, we also examined the consumer surplus and the recovery ratio in two models, and the result suggests that the consumer surplus and the recovery ratio in the self-run model are always better than that in the agency model due to lower retailing price and larger amount of recycling.

We believe our study makes three substantive contributions to the body of knowledge in the field of WEEE online recycling. First, in terms of the research questions and the research method, we provide the first economic analysis of the resale channel strategy for the collected products under the WEEE online recycling background by the game theory method. It forms a crucial modeling element for future research. Second, in terms of the research findings, our analyses provide a useful tool and guideline to access different resale channel models in different scenarios, and have important and timely implications for all stakeholders. Third, from a policy maker’s perspective, some regulations should be issued to effectively alleviate the conflict between corporate profit and environmental sustainability, so as to achieve coordination among the enterprises, consumers, and the environment. Certainly, our work is limited and can be extended in many aspects. First, Assumption 3 can be relaxed, considering the manufacturer can buy the collected products from the WEEE online recycler to remanufacture with a transfer price. Second, the manufacturer or e-retailer may participate in recycling to compete with the WEEE online recycler. Third, there may be information asymmetry between the WEEE online recycler and consumer regarding the reselling product’s quality.