Factors Contributing to Efficient Forest Production in the Region of the Three-North Shelter Forest Program, China
Abstract
1. Introduction
2. Study Area and Materials
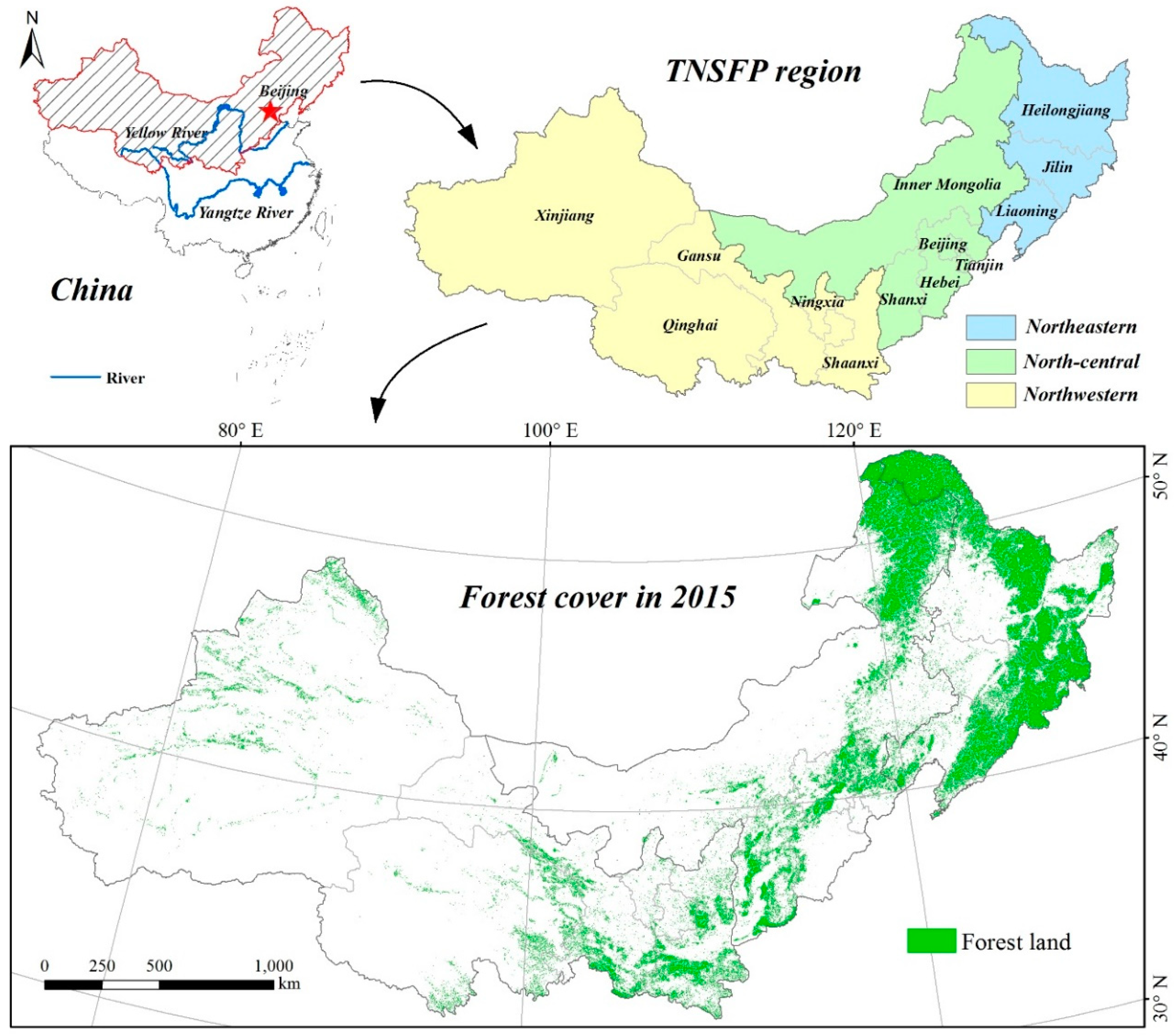
2.1. Study Area
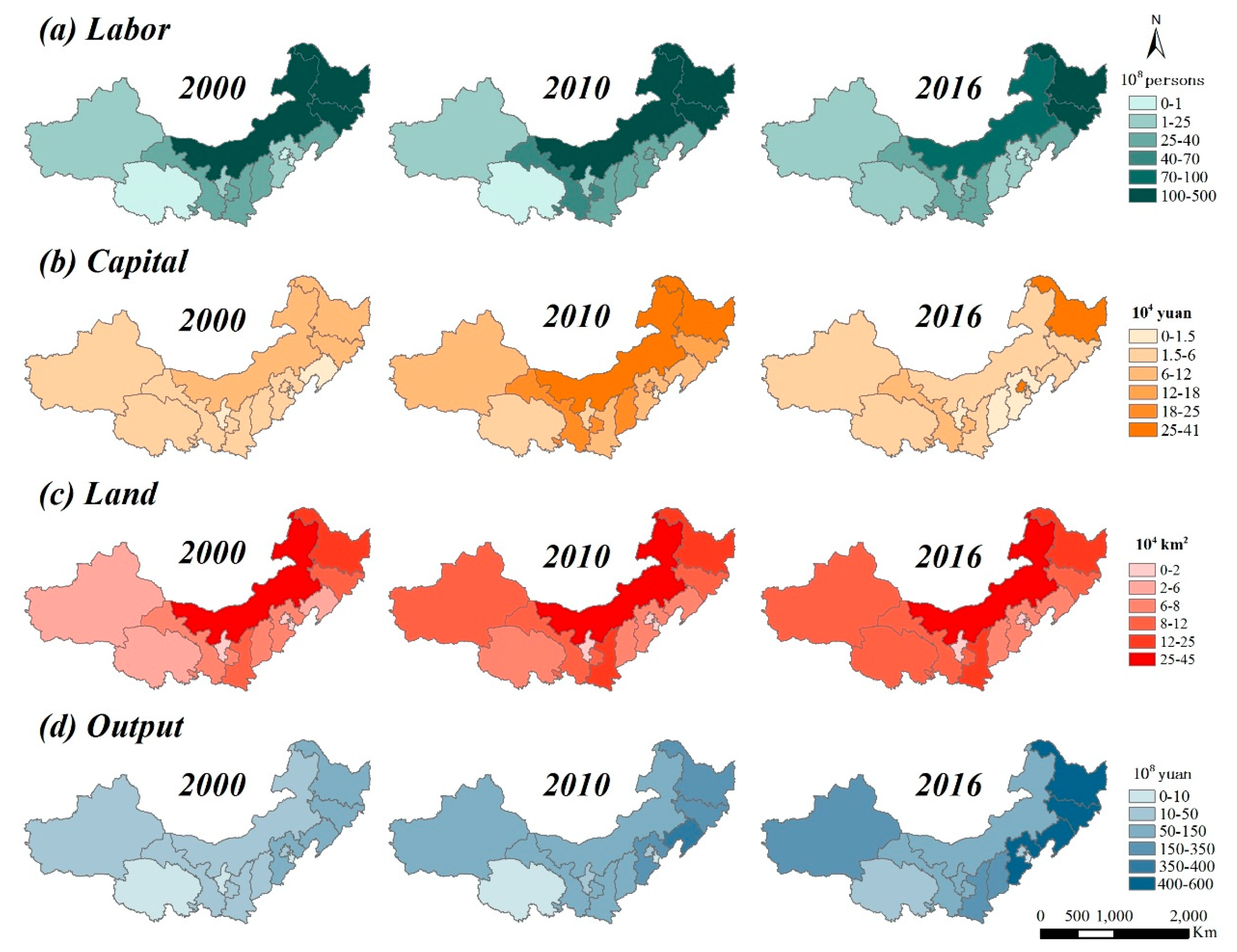
2.2. Data Preparation
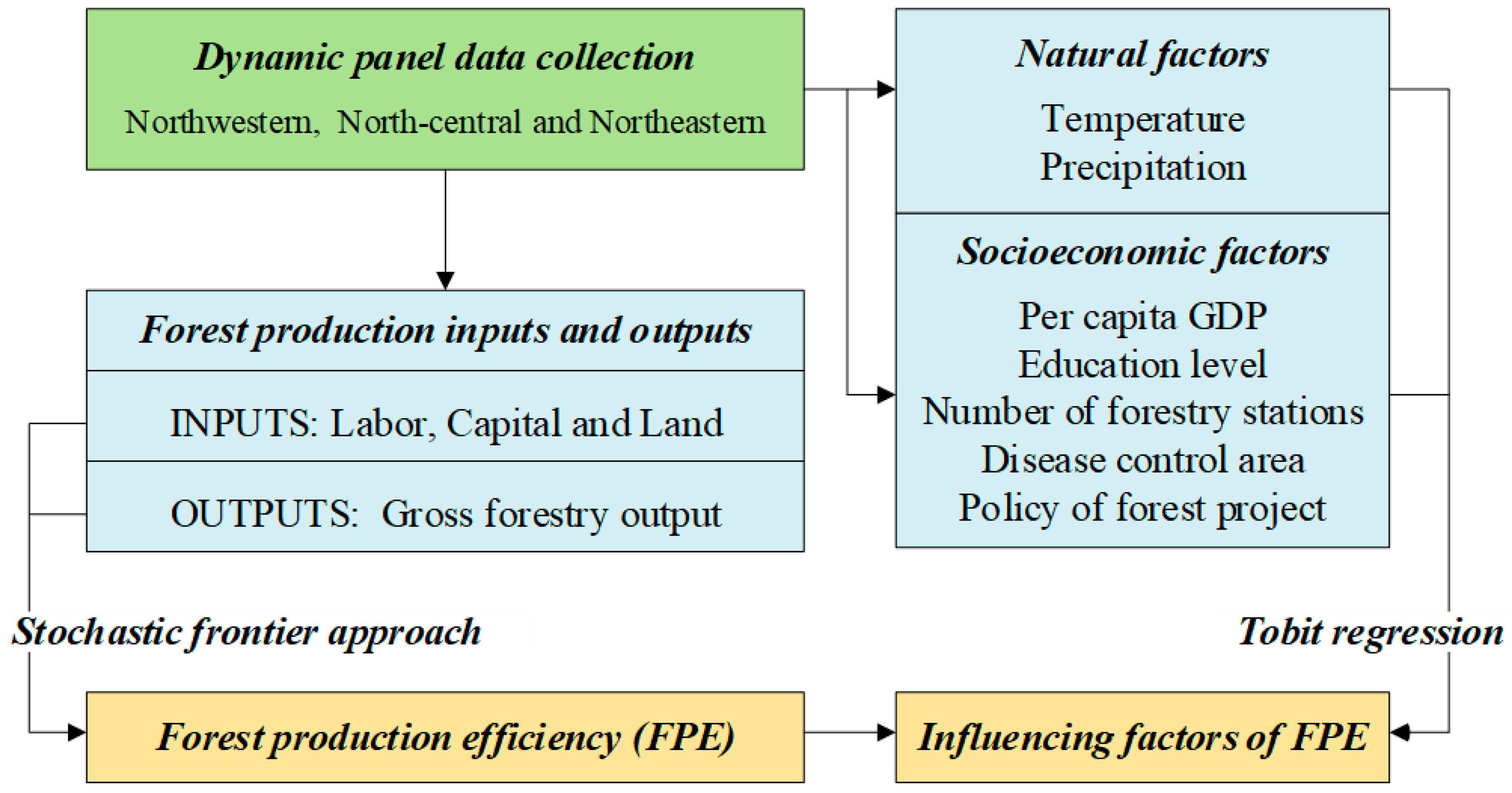
3. Methods
3.1. Parameter Estimation of FPE
3.2. Influencing Factor Analysis of FPE
4. Results and Analysis
4.1. The Estimation Function for Forest Production Efficiency
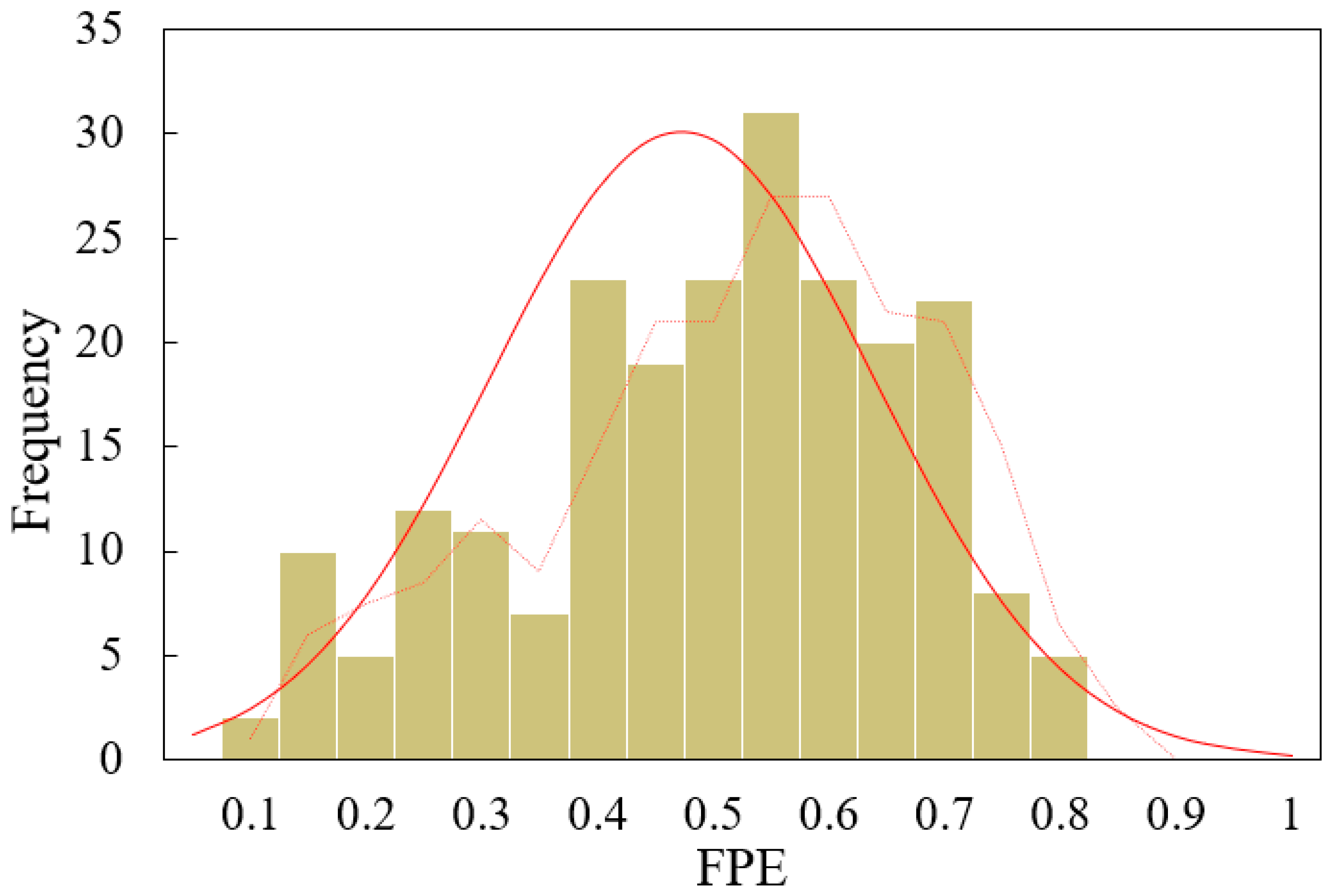
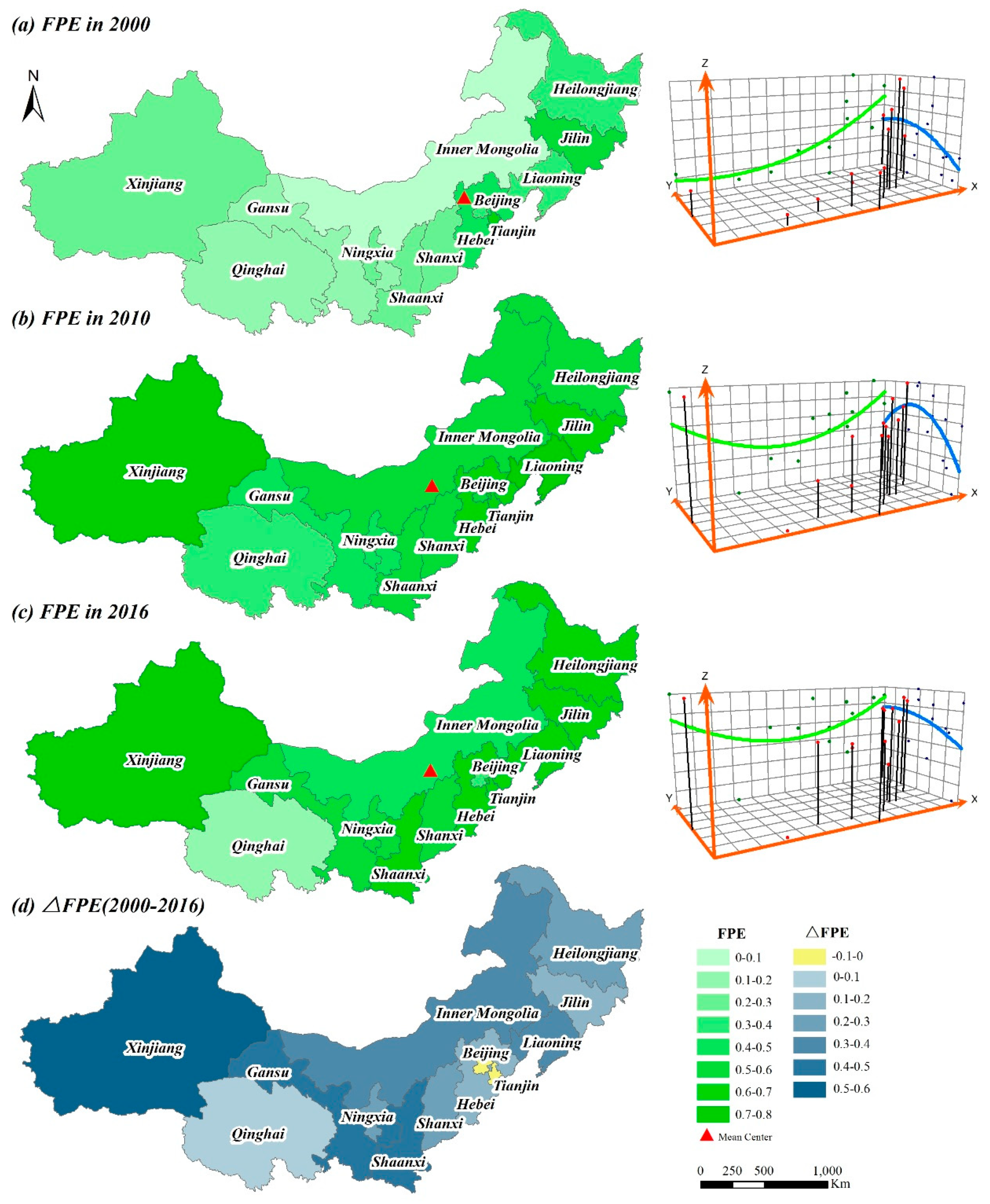
4.2. Spatial and Temporal Variations of Forest Production Efficiency
4.3. Influencing Factors of Forest Production Efficiency
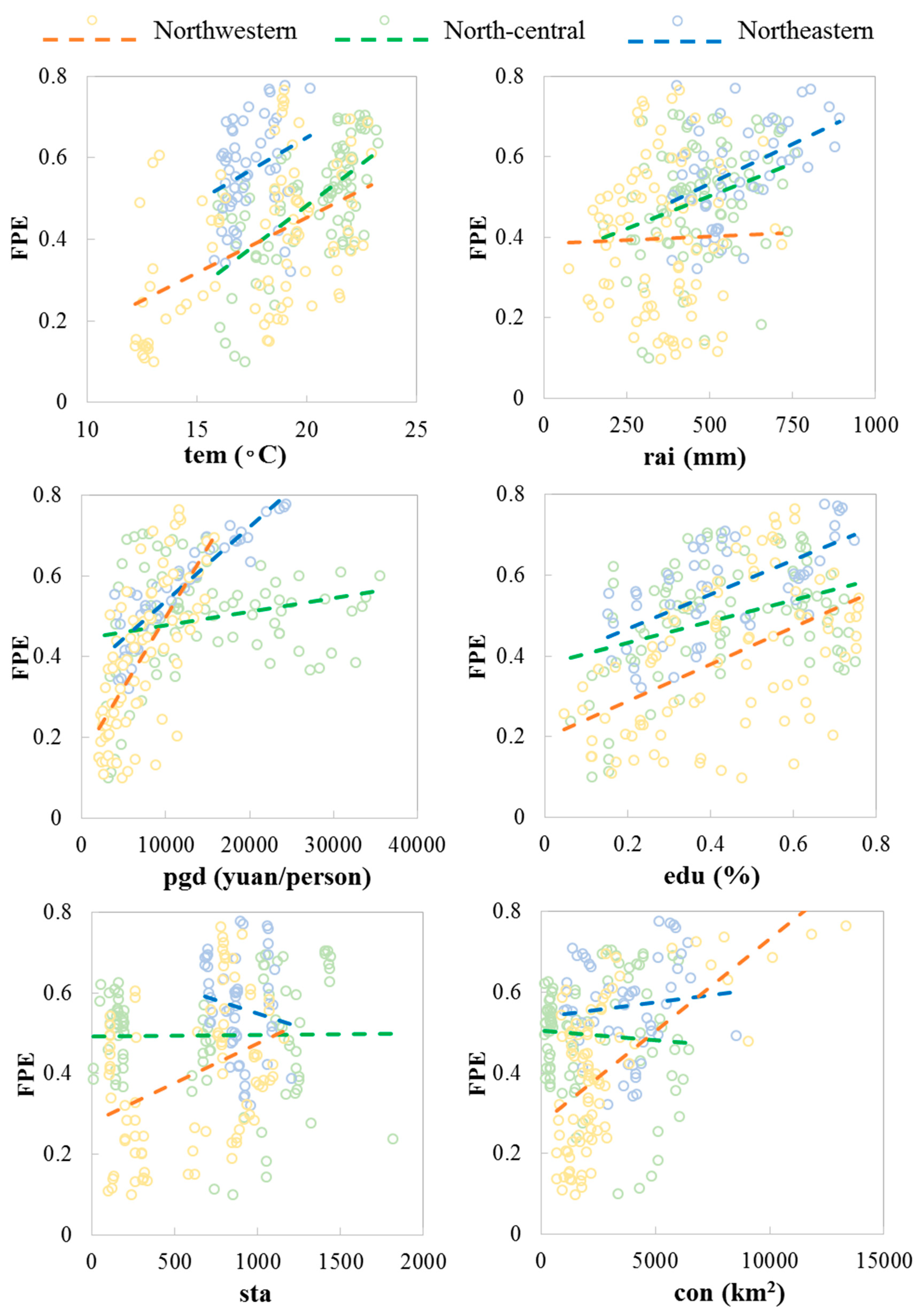
4.4. Analyzing the Influencing Factors of Forest Production Efficiency in the Three Sub-Regions
5. Conclusions and Discussion
Author Contributions
Funding
Conflicts of Interest
Appendix A

References
- Ali, A. Forest stand structure and functioning: Current knowledge and future challenges. Ecol. Indic. 2019, 98, 665–677. [Google Scholar] [CrossRef]
- Jåstad, E.O.; Bolkesjø, T.F.; Trømborg, E.; Rørstad, P.K. Large-scale forest-based biofuel production in the Nordic forest sector: Effects on the economics of forestry and forest industries. Energy Convers. Manag. 2019, 184, 374–388. [Google Scholar] [CrossRef]
- Hua, F.; Wang, X.; Zheng, X.; Fisher, B.; Wang, L.; Zhu, J.; Tang, Y.; Yu, D.W.; Wilcove, D.S. Opportunities for biodiversity gains under the world’s largest reforestation programme. Nat. Commun. 2016, 7, 12717. [Google Scholar] [CrossRef] [PubMed]
- Adami, M.; Theodor Rudorff, B.F.; Freitas, R.M.; Aguiar, D.A.; Sugawara, L.M.; Mello, M.P. Remote Sensing Time Series to Evaluate Direct Land Use Change of Recent Expanded Sugarcane Crop in Brazil. Sustainability 2012, 4, 574–585. [Google Scholar] [CrossRef]
- Chen, W.; Xu, D.; Liu, J. The forest resources input–output model: An application in China. Ecol. Indic. 2015, 51, 87–97. [Google Scholar] [CrossRef]
- Chen, J.; Wu, Y.; Song, M.; Zhu, Z. Stochastic frontier analysis of productive efficiency in China’s Forestry Industry. J. For. Econ. 2017, 28, 87–95. [Google Scholar] [CrossRef]
- Eggers, J.; Holmgren, S.; Nordstrom, E.-M.; Lamas, T.; Lind, T.; Ohman, K. Balancing different forest values: Evaluation of forest management scenarios in a multi-criteria decision analysis framework. For. Policy Econ. 2019, 103, 55–69. [Google Scholar] [CrossRef]
- Djurfeldt, G.; Hall, O.; Jirstrom, M.; Bustos, M.A.; Holmquist, B.; Nasrin, S. Using panel survey and remote sensing data to explain yield gaps for maize in sub-Saharan Africa. J. Land Use Sci. 2018, 13, 344–357. [Google Scholar] [CrossRef]
- Mwalupaso, G.E.; Wang, S.; Rahman, S.; Alavo, E.J.-P.; Tian, X. Agricultural Informatization and Technical Efficiency in Maize Production in Zambia. Sustainability 2019, 11, 2451. [Google Scholar] [CrossRef]
- Lin, B.; Wang, X. Carbon emissions from energy intensive industry in China: Evidence from the iron & steel industry. Renew. Sustain. Energy Rev. 2015, 47, 746–754. [Google Scholar]
- Zhan, J.; Zhang, F.; Jia, S.; Chu, X.; Li, Y. Spatial Pattern of Regional Urbanization Efficiency: An Empirical Study of Shanghai. Comput. Econ. 2018, 52, 1277–1291. [Google Scholar] [CrossRef]
- Fall, F.; Akim, A.-M.; Wassongma, H. DEA and SFA research on the efficiency of microfinance institutions: A meta-analysis. World Dev. 2018, 107, 176–188. [Google Scholar] [CrossRef]
- Zhu, Q.; Wu, J.; Song, M. Efficiency evaluation based on data envelopment analysis in the big data context. Comput. Oper. Res. 2018, 98, 291–300. [Google Scholar] [CrossRef]
- Reinhard, S.; Knox Lovell, C.A.; Thijssen, G.J. Environmental efficiency with multiple environmentally detrimental variables; estimated with SFA and DEA. Eur. J. Oper. Res. 2000, 121, 287–303. [Google Scholar] [CrossRef]
- Lee, J.Y. Comparing SFA and DEA methods on measuring production efficiency for forest and paper companies. For. Prod. J. 2005, 55, 51–56. [Google Scholar]
- Kuosmanen, T.; Saastamoinen, A.; Sipiläinen, T. What is the best practice for benchmark regulation of electricity distribution? Comparison of DEA, SFA and StoNED methods. Energy Policy 2013, 61, 740–750. [Google Scholar] [CrossRef]
- Bai, Y.; Deng, X.; Zhang, Y.; Wang, C.; Liu, Y. Does climate adaptation of vulnerable households to extreme events benefit livestock production? J. Clean. Prod. 2019, 210, 358–365. [Google Scholar] [CrossRef]
- Makridou, G.; Andriosopoulos, K.; Doumpos, M.; Zopounidis, C. Measuring the efficiency of energy-intensive industries across European countries. Energy Policy 2016, 88, 573–583. [Google Scholar] [CrossRef]
- Li, N.; Jiang, Y.; Mu, H.; Yu, Z. Efficiency evaluation and improvement potential for the Chinese agricultural sector at the provincial level based on data envelopment analysis (DEA). Energy 2018, 164, 1145–1160. [Google Scholar] [CrossRef]
- Jia, S.; Wang, C.; Li, Y.; Zhang, F.; Liu, W. The urbanization efficiency in Chengdu City: An estimation based on a three-stage DEA model. Phys. Chem. Earth Parts A/B/C 2017, 101, 59–69. [Google Scholar] [CrossRef]
- Angulo-Meza, L.; González-Araya, M.; Iriarte, A.; Rebolledo-Leiva, R.; Soares de Mello, J.C. A multiobjective DEA model to assess the eco-efficiency of agricultural practices within the CF + DEA method. Comp. Electron. Agric. 2019, 161, 151–161. [Google Scholar] [CrossRef]
- Gidion, D.K.; Hong, J.; Adams, M.Z.A.; Khoveyni, M. Network DEA models for assessing urban water utility efficiency. Util. Policy 2019, 57, 48–58. [Google Scholar] [CrossRef]
- Wanke, P.; Abul Kalam Azad, M.; Emrouznejad, A.; Antunes, J. A dynamic network DEA model for accounting and financial indicators: A case of efficiency in MENA banking. Int. Rev. Econ. Financ. 2019, 61, 52–68. [Google Scholar] [CrossRef]
- Wang, J.; Wang, S.; Li, S.; Cai, Q.; Gao, S. Evaluating the energy-environment efficiency and its determinants in Guangdong using a slack-based measure with environmental undesirable outputs and panel data model. Sci. Total Environ. 2019, 663, 878–888. [Google Scholar] [CrossRef]
- Deng, X.; Gibson, J. Improving eco-efficiency for the sustainable agricultural production: A case study in Shandong, China. Technol. Forecast. Soc. Chang. 2019, 144, 394–400. [Google Scholar] [CrossRef]
- Musaba, E.; Bwacha, I. Technical efficiency of small scale maize production in Masaiti district, Zambia: A stochastic frontier approach. J. Ecol. Sustain. Dev. 2014, 5, 104–111. [Google Scholar]
- Katuwal, H.; Calkin, D.E.; Hand, M.S. Production and efficiency of large wildland fire suppression effort: A stochastic frontier analysis. J. Environ. Manag. 2016, 166, 227–236. [Google Scholar] [CrossRef]
- Xiong, L.; Wang, F.; Cheng, B.; Yu, C. Identifying factors influencing the forestry production efficiency in Northwest China. Resour. Conserv. Recycl. 2018, 130, 12–19. [Google Scholar] [CrossRef]
- Wang, P.; Deng, X.; Jiang, S. Global warming, grain production and its efficiency: Case study of major grain production region. Ecol. Indic. 2018, 105, 563–570. [Google Scholar] [CrossRef]
- Du, K.R.; Lin, B.Q. International comparison of total-factor energy productivity growth: A parametric Malmquist index approach. Energy 2017, 118, 481–488. [Google Scholar] [CrossRef]
- Lin, B.Q.; Zheng, Q.Y. Energy efficiency evolution of China’s paper industry. J. Clean. Prod. 2017, 140, 1105–1117. [Google Scholar] [CrossRef]
- Jin, G.; Li, Z.; Deng, X.; Yang, J.; Chen, D.; Li, W. An analysis of spatiotemporal patterns in Chinese agricultural productivity between 2004 and 2014. Ecol. Indic. 2019, 105, 591–600. [Google Scholar] [CrossRef]
- Wingate, V.R.; Phinn, S.R.; Kuhn, N. Mapping precipitation-corrected NDVI trends across Namibia. Sci. Total Environ. 2019, 684, 96–112. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Zhan, J.; Zhao, F.; Yan, H.; Zhang, F.; Wei, X. Impacts of urbanization-induced land-use changes on ecosystem services: A case study of the Pearl River Delta Metropolitan Region, China. Ecol. Indic. 2019, 98, 228–238. [Google Scholar] [CrossRef]
- Deng, X.; Huang, J.; Rozelle, S.; Uchida, E. Cultivated land conversion and potential agricultural productivity in China. Land Use Policy 2006, 23, 372–384. [Google Scholar] [CrossRef]
- China Year Books. China Forest Statistical Yearbook; China Forestry Press: Beijing, China, 2017. [Google Scholar]
- Duan, H.; Yan, C.; Tsunekawa, A.; Song, X.; Li, S.; Xie, J. Assessing vegetation dynamics in the Three-North Shelter Forest region of China using AVHRR NDVI data. Environ. Earth Sci. 2011, 64, 1011–1020. [Google Scholar] [CrossRef]
- Chu, X.; Zhan, J.; Li, Z.; Zhang, F.; Qi, W. Assessment on forest carbon sequestration in the Three-North Shelterbelt Program region, China. J. Clean. Prod. 2019, 215, 382–389. [Google Scholar] [CrossRef]
- Debreu, G. The Coefficient of Resource Utilization. Econometrica 1951, 19, 273–292. [Google Scholar] [CrossRef]
- Farrell, M.J. The Measurement of Productive Efficiency. J. Royal Stat. Soc. Ser. a-Gen. 1957, 120, 253–290. [Google Scholar] [CrossRef]
- Battese, G.E.; Coelli, T.J. Frontier production functions, technical efficiency and panel data: With application to paddy farmers in India. J. Prod. Anal. 1992, 3, 153–169. [Google Scholar] [CrossRef]
- Amemiya, T. Regression analysis when the dependent variable is truncated normal. Econom. J. Econom. Soc. 1973, 41, 997–1016. [Google Scholar] [CrossRef]
- Peltonen-Sainio, P.; Pirinen, P.; Mäkelä, H.M.; Ojanen, H.; Venäläinen, A. Spatial and temporal variation in weather events critical for boreal agriculture: II Precipitation. Agric. Food Sci. 2016, 25, 57–70. [Google Scholar] [CrossRef]
- Tobin, J. Estimation of relationships for limited dependent variables. Econom. J. Econom. Soc. 1958, 26, 24–36. [Google Scholar] [CrossRef]
- Peterson, E.B. Estimating cover of an invasive grass (Bromus tectorum) using tobit regression and phenology derived from two dates of Landsat ETM plus data. Int. J. Remote Sens. 2005, 26, 2491–2507. [Google Scholar] [CrossRef]


| Variables | Unit | Abbr. | Obs. | Mean | Std. Dev | Min. | Max. | |
|---|---|---|---|---|---|---|---|---|
| Input | Labor | 104 | L | 221 | 62,737.78 | 91,446.81 | 735.00 | 470,317.00 |
| Capital | 104 yuan | K | 221 | 77,482.55 | 85,302.16 | 343.59 | 484,956.00 | |
| Land | km2 | T | 221 | 98,249.17 | 105,839.60 | 1330.00 | 440,361.00 | |
| Output | Gross forestry output | 104 yuan | Y | 221 | 1,241,460.00 | 1,539,604.00 | 8231.24 | 6,600,000.00 |
| Factors | Average temperature for the period April–October | 102 °C | tem | 221 | 0.1866 | 0.0275 | 0.12 | 0.23 |
| Total annual rainfall | 103 mm | rai | 221 | 0.4514 | 0.1594 | 0.07 | 0.89 | |
| Per capita GDP | 104 yuan/person | pgd | 221 | 1.0982 | 0.7358 | 0.20 | 3.55 | |
| Education levels of forestry employees | % | edu | 221 | 0.4322 | 0.1904 | 0.05 | 0.76 | |
| Number of forest technology stations in townships | 102 | sta | 221 | 7.0121 | 3.9793 | 0.09 | 18.15 | |
| Disease and pest control areas | 103 km2 | con | 221 | 2.7484 | 2.2020 | 0.12 | 13.34 | |
| Natural Forest Protection Program (Yes = 1, No = 0) | - | pol | 221 | 0.6923 | 0.4626 | 0 | 1 | |
| Number of Obs. = 221 | Wald chi2(9) = 289.67 | ||||||
|---|---|---|---|---|---|---|---|
| Log Likelihood = −327.24 | Prob > chi2 = 0.0000 | ||||||
| Coefficient | Variable | Coef. Value | Std. Err. | z | p-Value | [95% Conf. Interval] | |
| β0 | _cons | −10.3848 *** | 3.9973 | −2.60 | 0.009 | −18.2193 | −2.5503 |
| βl | lnL | −1.4921 | 1.7952 | −0.83 | 0.406 | −5.0106 | 2.0264 |
| βk | lnK | 1.6790 *** | 0.5746 | 2.92 | 0.003 | 0.5528 | 2.8052 |
| βt | lnT | 3.6556 ** | 1.7022 | 2.15 | 0.032 | 0.3194 | 6.9919 |
| βll | lnLlnL | −1.0713 *** | 0.1697 | −6.31 | 0.000 | −1.4040 | −0.7387 |
| βkk | lnKlnK | 0.0208 | 0.0376 | 0.55 | 0.580 | −0.0529 | 0.0945 |
| βtt | lnTlnT | −0.8223 *** | 0.1575 | −5.22 | 0.000 | −1.1309 | −0.5136 |
| βlk | lnLlnK | 0.3295 ** | 0.1626 | 2.03 | 0.043 | 0.0109 | 0.6481 |
| βlt | lnLlnT | 1.9217 *** | 0.3020 | 6.36 | 0.000 | 1.3297 | 2.5136 |
| βkt | lnKlnT | −0.5185 *** | 0.1331 | −3.90 | 0.000 | −0.7794 | −0.2577 |
| No. | Variables | Adjusted t | p-Value |
|---|---|---|---|
| 1 | lab | −2.8934 *** | 0.0019 |
| 2 | cap | −2.4056 *** | 0.0081 |
| 3 | lan | −1.5803 * | 0.0570 |
| 4 | tem | −4.5568 *** | 0.0000 |
| 5 | rai | −7.2397 *** | 0.0000 |
| 6 | pgd | −2.8716 *** | 0.0020 |
| 7 | edu | −4.0350 *** | 0.0000 |
| 8 | con | −4.5640 *** | 0.0000 |
| 9 | sta | −4.9882 *** | 0.0000 |
| 10 | pol | - | - |
| FPE | Tobit1 | Tobit2 | Tobit3 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Coef. | Std. Err. | t | p-Value | Coef. | Std. Err. | t | p-Value | Coef. | Std. Err. | t | p-Value | |
| lab | 0.0002 | 0.0001 | 1.4600 | 0.1460 | 0.0003 *** | 0.0001 | 3.1700 | 0.0020 | 0.0004 *** | 0.0001 | 3.5500 | 0.0000 |
| cap | −8.70 × 10−4 | 0.0013 | −0.6700 | 0.5020 | −0.0019 * | 0.0011 | −1.7600 | 0.0810 | −0.0021 ** | 0.0010 | −2.0500 | 0.0420 |
| lan | −4.46 × 10−5 | 0.0011 | −0.0400 | 0.9680 | −0.0058 *** | 0.0011 | −5.3600 | 0.0000 | −0.0050 *** | 0.0011 | −4.6700 | 0.0000 |
| tem | 2.5271 *** | 0.3718 | 6.8000 | 0.0000 | 1.4476 *** | 0.3440 | 4.2100 | 0.0000 | ||||
| rai | 0.3319 *** | 0.0612 | 5.4300 | 0.0000 | 0.0800 | 0.0591 | 1.3500 | 0.1780 | ||||
| pgd | 0.1138 *** | 0.0165 | 6.8900 | 0.0000 | 0.0882 *** | 0.0181 | 4.8700 | 0.0000 | ||||
| edu | 0.1554 *** | 0.0587 | 2.6500 | 0.0090 | 0.2120 *** | 0.0591 | 3.5800 | 0.0000 | ||||
| sta | 0.0180 *** | 0.0024 | 7.6300 | 0.0000 | 0.0149 *** | 0.0025 | 6.0600 | 0.0000 | ||||
| con | 0.0205 *** | 0.0048 | 4.2800 | 0.0000 | 0.0190 *** | 0.0046 | 4.1000 | 0.0000 | ||||
| pol | −0.0331 | 0.0215 | −1.5300 | 0.1260 | 0.0064 | 0.0232 | 0.2800 | 0.7810 | ||||
| _cons | −0.1539 ** | 0.0741 | −2.0800 | 0.0390 | 0.1720 *** | 0.0331 | 5.2000 | 0.0000 | −0.1412 * | 0.0825 | −1.7100 | 0.0890 |
| /sigma | 0.1393 | 0.0066 | 0.1085 | 0.0052 | 0.1044 | 0.0050 | ||||||
| Log likelihood = 122.0705 | Log likelihood = 177.32173 | Log likelihood = 185.86889 | ||||||||||
| Pro > chi2 = 0.0000 | Pro > chi2 = 0.0000 | Pro > chi2 = 0.0000 | ||||||||||
| LR chi2 (7) = 77.56 | LR chi2(6) = 188.06 | LR chi2 (3) = 205.16 | ||||||||||
| Pseudo R2 = −0.4656 | Pseudo R2 = −1.1289 | Pseudo R2 = −1.2316 | ||||||||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Chu, X.; Zhan, J.; Wang, P.; Zhang, F.; Xin, Z. Factors Contributing to Efficient Forest Production in the Region of the Three-North Shelter Forest Program, China. Sustainability 2020, 12, 302. https://doi.org/10.3390/su12010302
Wang C, Chu X, Zhan J, Wang P, Zhang F, Xin Z. Factors Contributing to Efficient Forest Production in the Region of the Three-North Shelter Forest Program, China. Sustainability. 2020; 12(1):302. https://doi.org/10.3390/su12010302
Chicago/Turabian StyleWang, Chao, Xi Chu, Jinyan Zhan, Pei Wang, Fan Zhang, and Zhongling Xin. 2020. "Factors Contributing to Efficient Forest Production in the Region of the Three-North Shelter Forest Program, China" Sustainability 12, no. 1: 302. https://doi.org/10.3390/su12010302
APA StyleWang, C., Chu, X., Zhan, J., Wang, P., Zhang, F., & Xin, Z. (2020). Factors Contributing to Efficient Forest Production in the Region of the Three-North Shelter Forest Program, China. Sustainability, 12(1), 302. https://doi.org/10.3390/su12010302







