Uncertainty Problems in Image Change Detection
Abstract
1. Introduction
2. Materials and Methods
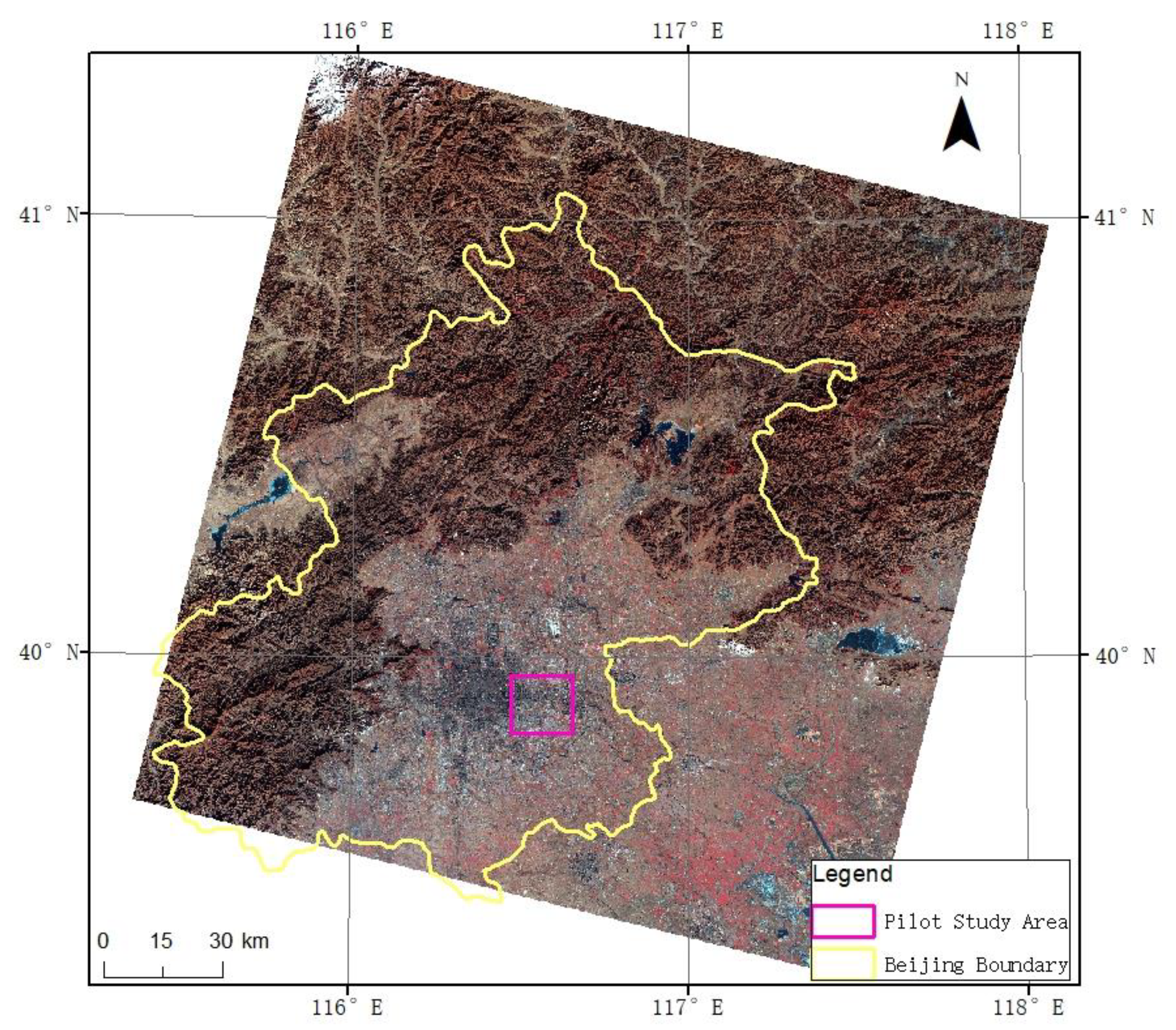
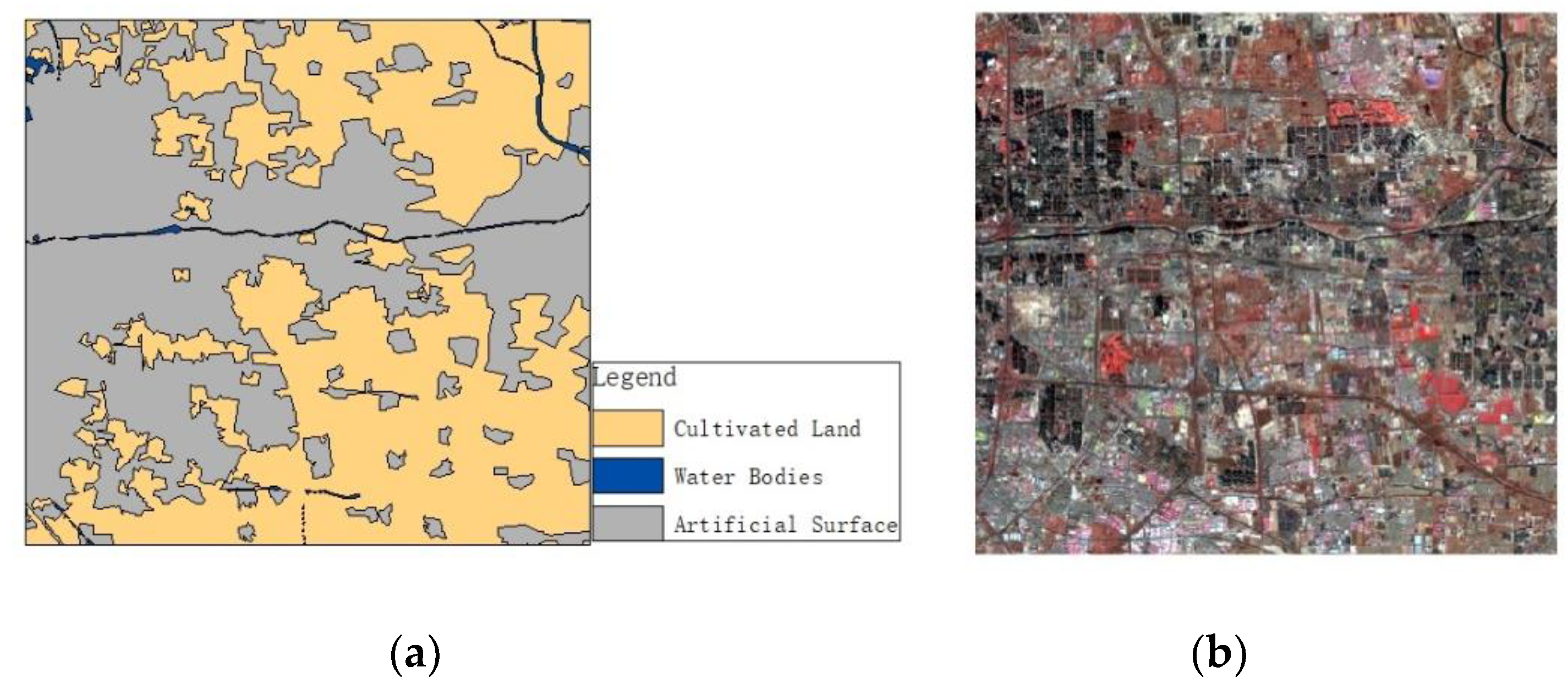
2.1. Study Area and Data
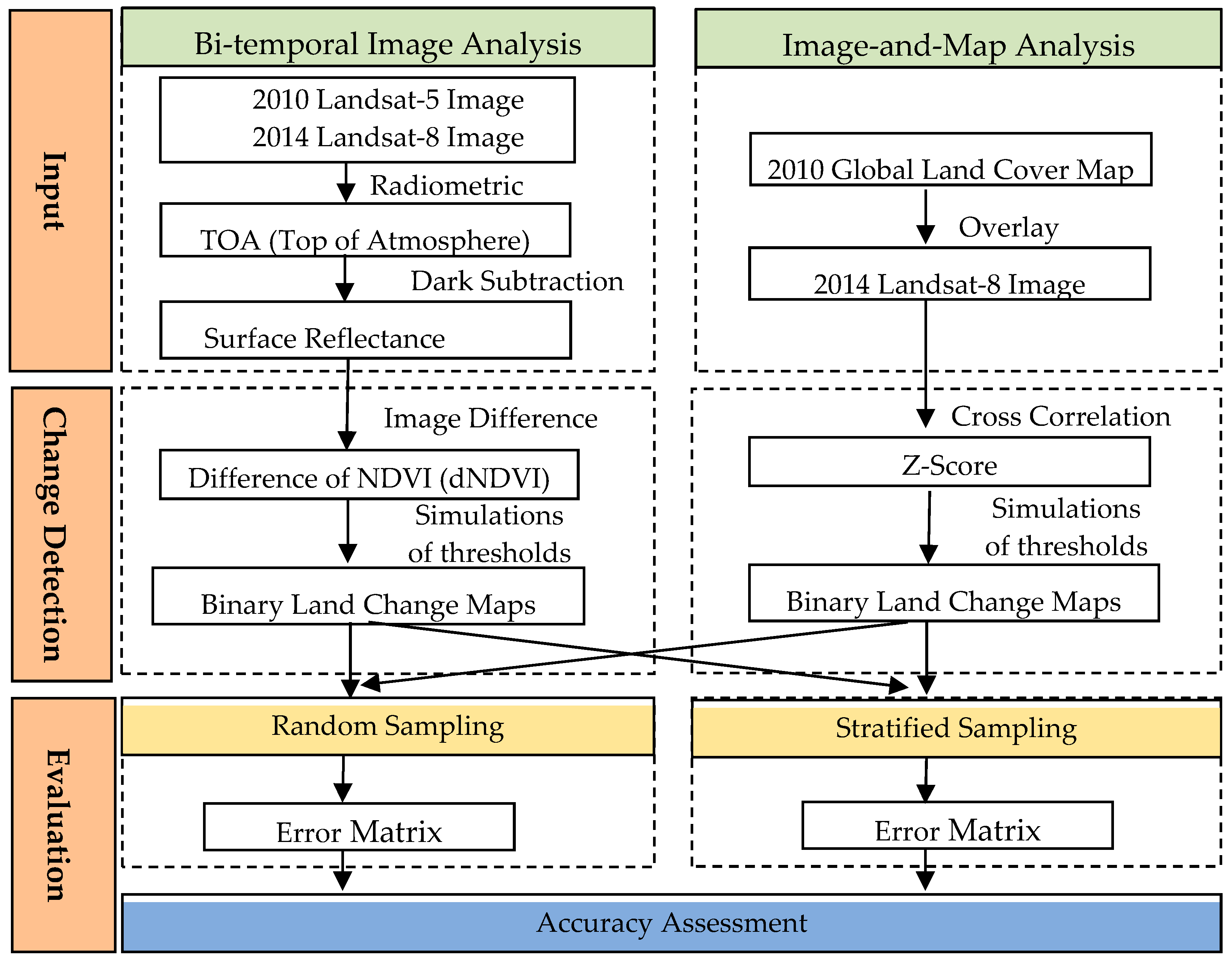
2.2. Methodology
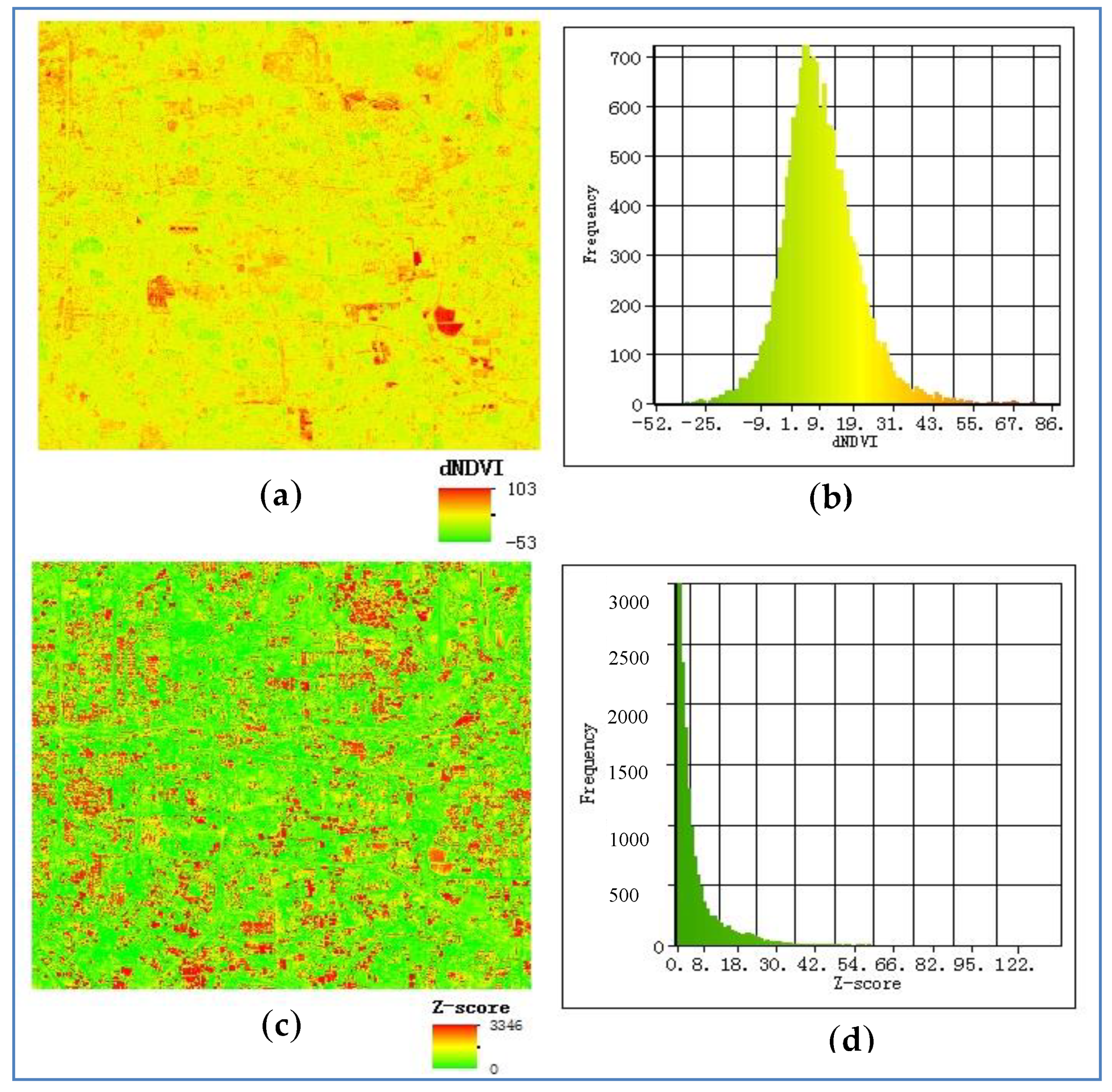
2.2.1. Change Variables
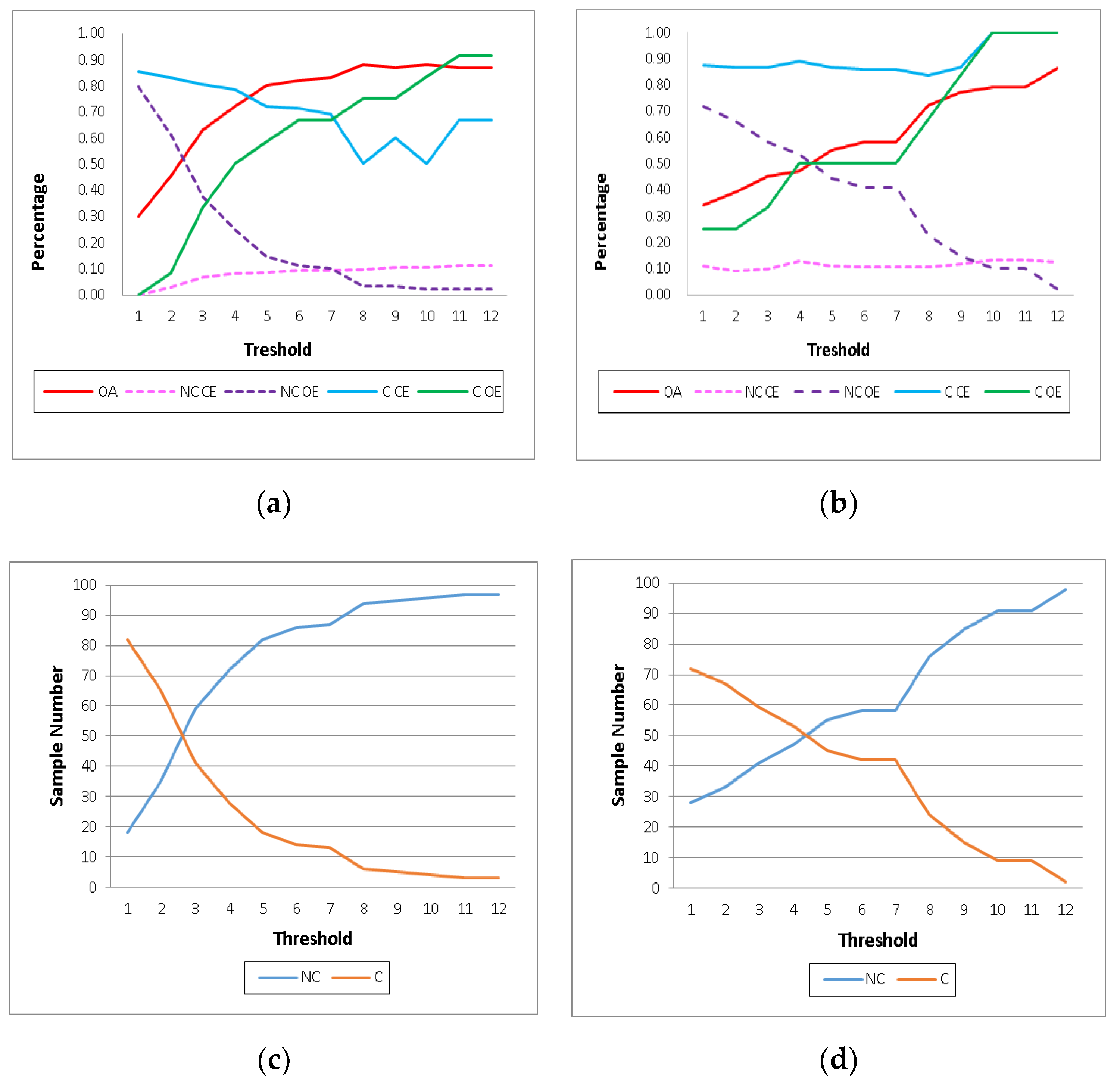
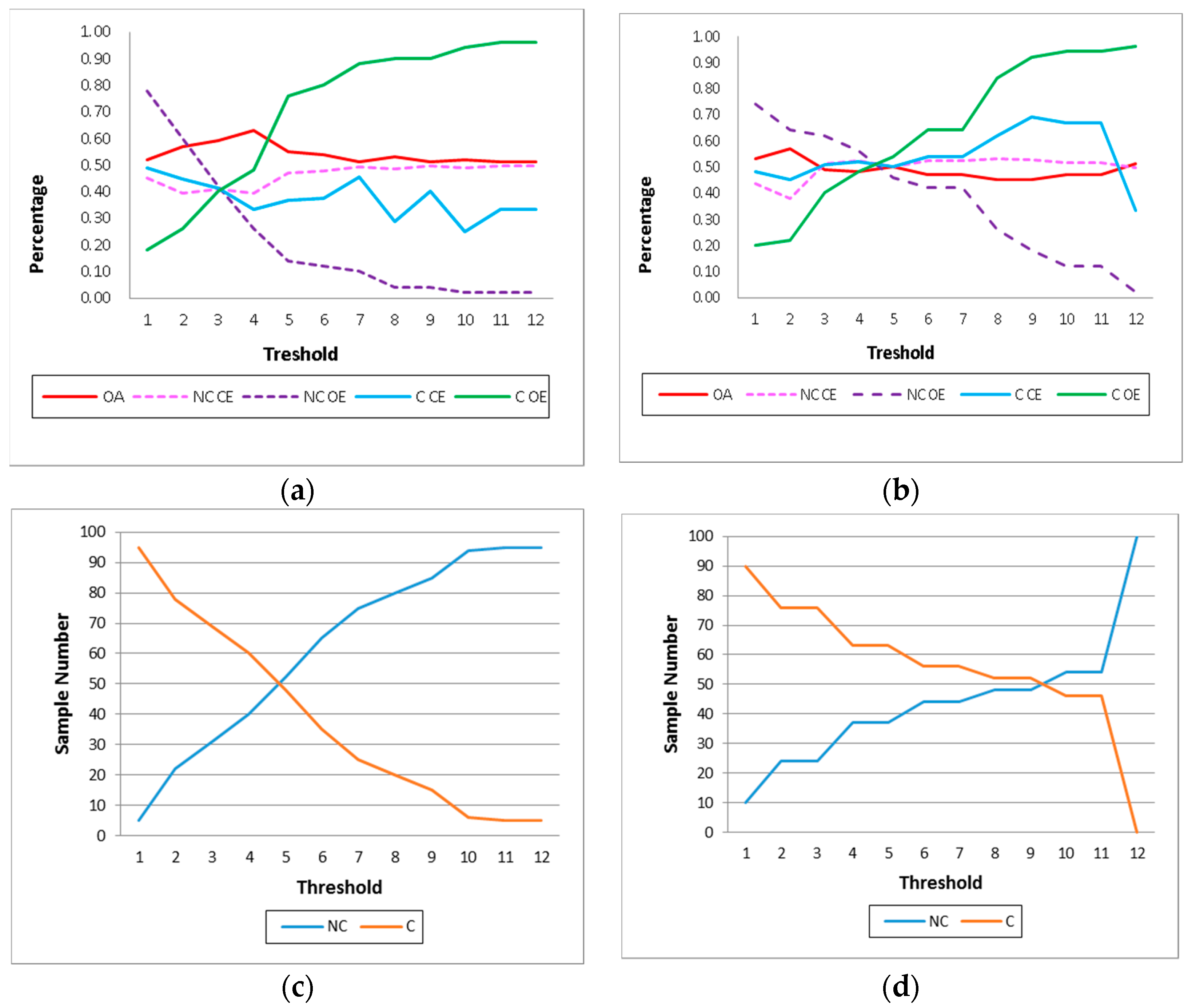
2.2.2. Sampling and Accuracy Assessments
3. Results
4. Discussion
4.1. Bi-Temporal Image Analysis Versus Image-and-Map Analysis
4.2. Random Sampling Versus Stratified Sampling
4.3. Thresholding and Sensitivity Analysis
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Liu, J.; Zhang, Z.; Zhuang, D.; Wang, Y.; Zhou, W.; Zhang, S.; Li, R.; Jiang, N.; Wu, S. A study on the spatial-temporal dynamic changes of land-useand driving forces analyses of China in the 1990s. Geogr. Res. 2003, 22, 1–12. [Google Scholar] [CrossRef]
- Fry, J.; Xian, G.Z.; Jin, S.; Dewitz, J.; Homer, C.G.; Yang, L.; Barnes, C.A.; Herold, N.D.; Wickham, J.D. Completion of the 2006 national land cover database for the conterminous united states. Photogramm. Eng. Remote Sens. 2011, 77, 858–864. [Google Scholar]
- Zhang, Z.; Wang, X.; Zhao, X.; Liu, B.; Yi, L.; Zuo, L.; Wen, Q.; Liu, F.; Xu, J.; Hu, S. A 2010 update of National Land Use/Cover Database of China at 1: 100000 scale using medium spatial resolution satellite images. Remote Sens. Environ. 2014, 149, 142–154. [Google Scholar] [CrossRef]
- Xian, G.; Homer, C.G.; Fry, J. Updating the 2001 National Land Cover Database land cover classification to 2006 by using Landsat imagery change detection methods. Remote Sens. Environ. 2009, 113, 1133–1147. [Google Scholar] [CrossRef]
- Jin, S.; Yang, L.; Danielson, P.; Homer, C.; Fry, J.; Xian, G. A comprehensive change detection method for updating the National Land Cover Database to circa 2011. Remote Sens. Environ. 2013, 132, 159–175. [Google Scholar] [CrossRef]
- Xian, G.; Homer, C. Updating the 2001 National Land Cover Database Impervious Surface Products to 2006 using Landsat Imagery Change Detection Methods. Remote Sens. Environ. 2010, 114, 1676–1686. [Google Scholar] [CrossRef]
- Song, X.; Hansen, M.C.; Stehman, S.V.; Potapov, P.V.; Tyukavina, A.; Vermote, E.F.; Townshend, J.R. Global land change from 1982 to 2016. Nature 2018, 560, 639–643. [Google Scholar] [CrossRef]
- MRLC. Available online: http://www.mrlc.gov/nlcd (accessed on 3 December 2019).
- Singh, A. Review article digital change detection techniques using remotely-sensed data. Int. J. Remote Sens. 1989, 10, 989–1003. [Google Scholar] [CrossRef]
- Blaschke, T. Towards a framework for change detection based on image objects. Göttinger Geogr. Abh. 2005, 113, 1–9. [Google Scholar]
- Jensen, J.R. Introductory Digital Image Processing: A Remote-Sensing Perspective; Pearson Education, Inc.: Glenview, IL, USA, 2016. [Google Scholar] [CrossRef]
- Lu, D.; Mausel, P.; Brondizio, E.; Moran, E. Change detection techniques. Int. J. Remote Sens. 2004, 25, 2365–2401. [Google Scholar] [CrossRef]
- Radke, R.J.; Andra, S.; Al-Kofahi, O.; Roysam, B. Image change detection algorithms: A systematic survey. IEEE Trans. Image Process. 2005, 14, 294–307. [Google Scholar] [CrossRef] [PubMed]
- Ridd, M.K.; Liu, J. A Comparison of Four Algorithms for Change Detection in an Urban Environment. Remote Sens. Environ. 1998, 63, 95–100. [Google Scholar] [CrossRef]
- Tewkesbury, A.P.; Comber, A.J.; Tate, N.J.; Lamb, A.; Fisher, P.F. A critical synthesis of remotely sensed optical image change detection techniques. Remote Sens. Environ. 2015, 160, 1–14. [Google Scholar] [CrossRef]
- Civco, D.L.; Hurd, J.D.; Wilson, E.H.; Song, M.; Zhang, Z. A comparison of land use and land cover change detection methods. In Proceedings of the ASPRS-ACSM Annual Conference, Washington, DC, USA, 22–26 April 2002. [Google Scholar]
- Canty, M.J. Image Analysis, Classification and Change Detection in Remote Sensing: With algorithms for ENVI/IDL and Python; CRC Press: Florida, FL, USA, 2014. [Google Scholar]
- Hussain, M.; Chen, D.; Cheng, A.; Wei, H.; Stanley, D. Change detection from remotely sensed images: From pixel-based to object-based approaches. ISPRS J. Photogramm. Remote Sens. 2013, 80, 91–106. [Google Scholar] [CrossRef]
- Koeln, G.; Bissonnette, J. Cross-correlation analysis: Mapping landcover change with a historic landcover database and a recent, single-date multispectral image. In Proceedings of the 2000 ASPRS Annual Convention, Washington, DC, USA, 1–5 May 2000. [Google Scholar]
- Tarantino, C.; Adamo, M.; Lucas, R.; Blonda, P. Detection of changes in semi-natural grasslands by cross correlation analysis with WorldView-2 images and new Landsat 8 data. Remote Sens. Environ. 2016, 175, 65–72. [Google Scholar] [CrossRef] [PubMed]
- Hamby, D. A review of techniques for parameter sensitivity analysis of environmental models. Environ. Monit. Assess. 1994, 32, 135–154. [Google Scholar] [CrossRef]
- VanderWeele, T.J.; Tchetgen, E.J.T.; Halloran, M.E. Interference and sensitivity analysis. Stat. Sci. 2014, 29, 687. [Google Scholar] [CrossRef]
- Plewe, B. The Nature of Uncertainty in Historical Geographic Information. Trans. GIS 2002, 6, 431–456. [Google Scholar] [CrossRef]
- Hao, M.; Shi, W.; Deng, K.; Zhang, H.; He, P. An object-based change detection approach using uncertainty analysis for VHR images. J. Sens. 2016, 2016. [Google Scholar] [CrossRef]
- Patil, G.; Taillie, C. Modeling and interpreting the accuracy assessment error matrix for a doubly classified map. Environ. Ecol. Stat. 2003, 10, 357–373. [Google Scholar] [CrossRef]
- Zhu, Z.; Woodcock, C.E. Continuous change detection and classification of land cover using all available Landsat data. Remote Sens. Environ. 2014, 144, 152–171. [Google Scholar] [CrossRef]
- Dronova, I.; Gong, P.; Wang, L. Object-based analysis and change detection of major wetland cover types and their classification uncertainty during the low water period at Poyang Lake, China. Remote Sens. Environ. 2011, 115, 3220–3236. [Google Scholar] [CrossRef]
- Song, C.; Woodcock, C.E. Monitoring forest succession with multitemporal Landsat images: Factors of uncertainty. IEEE Trans. Geosci. Remote Sens. 2003, 41, 2557–2567. [Google Scholar] [CrossRef]
- Stehman, S.V. Estimating area from an accuracy assessment error matrix. Remote Sens. Environ. 2013, 132, 202–211. [Google Scholar] [CrossRef]
- Olofsson, P.; Foody, G.M.; Herold, M.; Stehman, S.V.; Woodcock, C.E.; Wulder, M.A. Good practices for estimating area and assessing accuracy of land change. Remote Sens. Environ. 2014, 148, 42–57. [Google Scholar] [CrossRef]
- Coppin, P.; Lambin, E.; Jonckheere, I.; Muys, B. Digital change detection methods in natural ecosystem monitoring: A review. In Analysis of Multi-Temporal Remote Sensing Images; World Scientific: Singapore, 2002; pp. 3–36. [Google Scholar]
- Rosin, P.L.; Ioannidis, E. Evaluation of global image thresholding for change detection. Pattern Recognit. Lett. 2003, 24, 2345–2356. [Google Scholar] [CrossRef]
- Rosin, P. Thresholding for change detection. In Proceedings of the Sixth International Conference on Computer Vision, Bombay, India, 4–7 January 1998; pp. 274–279. [Google Scholar]
- Wang, J.; Stein, A.; Gao, B.; Ge, Y. A review of spatial sampling. Spat. Stat. 2012, 2, 1–14. [Google Scholar] [CrossRef]
- Stats. Available online: http://www.stats.gov.cn/ (accessed on 5 October 2016).
- USGS. Available online: http://glovis.usgs.gov/ (accessed on 20 October 2016).
- Siewe, S.S. Change Detection Analysis of the Landuse and Landcover of the Fort Cobb Reservoir Watershed; Oklahoma State University: Stillwater, OK, USA, 2007. [Google Scholar]
- GlobaLand30. Available online: http://www.globallandcover.com/ (accessed on 10 June 2016).
- Li, H.; Song, W. Expansion of Rural Settlements on High-Quality Arable Land in Tongzhou District in Beijing, China. Sustainability 2019, 11, 5153. [Google Scholar] [CrossRef]
- Van Oort, P. Interpreting the change detection error matrix. Remote Sens. Environ. 2007, 108, 1–8. [Google Scholar] [CrossRef]
- Couclelis, H. The Certainty of Uncertainty: GIS and the Limits of Geographic Knowledge. Trans. GIS 2003, 7, 165–175. [Google Scholar] [CrossRef]
- Mowrer, H.T. Accuracy (re)assurance: Selling uncertainty assessment to the uncertain. In Spatial Accuracy Assessment: Land Information Uncertainty in Natural Resources; Jaton, K.L.A.A., Ed.; Ann Arbor Press: Chelsea, MI, USA, 1999. [Google Scholar]
- Thompson, S.K. Sampling, 3rd ed.; Wiley: Hoboken, HN, USA, 2012. [Google Scholar]
- Hansen, M.C.; Loveland, T.R. A review of large area monitoring of land cover change using Landsat data. Remote Sens. Environ. 2012, 122, 66–74. [Google Scholar] [CrossRef]
- Boori, M.S.; Amaro, V.E. Land use change detection for environmental management: Using multi-temporal, satellite data in the Apodi Valley of northeastern Brazil. Appl. GIS 2010, 6, 1–15. [Google Scholar] [CrossRef]
- Heckman, J.J. Sample selection bias as a specification error. Econom. J. Econom. Soc. 1979, 153–161. [Google Scholar] [CrossRef]
- Rogerson, P.A.; Delmelle, E.; Batta, R.; Akella, M.; Blatt, A.; Wilson, G. Optimal Sampling Design for Variables with Varying Spatial Importance. Geogr. Anal. 2004, 36, 177–194. [Google Scholar] [CrossRef]
- Biagini, F.; Campanino, M. Elements of Probability and Statistics: An. Introduction to Probability with de Finetti’s Approach and to Bayesian Statistics; Springer: New York, NY, USA, 2016. [Google Scholar]
- Harris, R.; Jarvis, C. Statistics for Geography and Environmental Science, 1st ed.; Routledge: London, UK, 2014. [Google Scholar] [CrossRef]
- Bruzzone, L.; Prieto, D.F. Automatic analysis of the difference image for unsupervised change detection. IEEE Trans. Geosci. Remote Sens. 2000, 38, 1171–1182. [Google Scholar] [CrossRef]
- Teng, S.; Chen, Y.; Cheng, K.; Lo, H. Hypothesis-test-based landcover change detection using multi-temporal satellite images–A comparative study. Adv. Space Res. 2008, 41, 1744–1754. [Google Scholar] [CrossRef]
- Burt, J.E.; Barber, G.M.; Rigby, D.L. Elementary Statistics for Geographers; Guilford Press: New York, NY, USA, 2009. [Google Scholar]
- Hwang, C.L.; Lin, M.J. Group Decision Making Under Multiple Criteria: Methods and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Saltelli, A.; Tarantola, S.; Campolongo, F.; Ratto, M. Sensitivity Analysis in Practice: A Guide to Assessing Scientific Models; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2004. [Google Scholar] [CrossRef]
- Seebach, L.; Strobl, P.; Vogt, P.; Mehl, W.; San-Miguel-Ayanz, J. Enhancing post-classification change detection through morphological post-processing–a sensitivity analysis. Int. J. Remote Sens. 2013, 34, 7145–7162. [Google Scholar] [CrossRef]
- Verburg, P.H.; Tabeau, A.; Hatna, E. Assessing spatial uncertainties of land allocation using a scenario approach and sensitivity analysis: A study for land use in Europe. J. Environ. Manag. 2013, 127, S132–S144. [Google Scholar] [CrossRef]
- Chen, Y.; Yu, J.; Khan, S. Spatial sensitivity analysis of multi-criteria weights in GIS-based land suitability evaluation. Environ. Model. Softw. 2010, 25, 1582–1591. [Google Scholar] [CrossRef]
- Iman, R.L.; Helton, J.C. An investigation of uncertainty and sensitivity analysis techniques for computer models. Risk Anal. 1988, 8, 71–90. [Google Scholar] [CrossRef]
- Christopher, F.H.; Patil, S.R. Identification and review of sensitivity analysis methods. Risk Anal. 2002, 22, 553–578. [Google Scholar] [CrossRef]
- Saltelli, A.; Annoni, P. How to avoid a perfunctory sensitivity analysis. Environ. Model. Softw. 2010, 25, 1508–1517. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Hall-Beyer, M.; Wu, C.; Fang, W.; Nsengiyumva, W. Uncertainty Problems in Image Change Detection. Sustainability 2020, 12, 274. https://doi.org/10.3390/su12010274
Wang W, Hall-Beyer M, Wu C, Fang W, Nsengiyumva W. Uncertainty Problems in Image Change Detection. Sustainability. 2020; 12(1):274. https://doi.org/10.3390/su12010274
Chicago/Turabian StyleWang, Wenyu, Mryka Hall-Beyer, Changshan Wu, Weihua Fang, and Walter Nsengiyumva. 2020. "Uncertainty Problems in Image Change Detection" Sustainability 12, no. 1: 274. https://doi.org/10.3390/su12010274
APA StyleWang, W., Hall-Beyer, M., Wu, C., Fang, W., & Nsengiyumva, W. (2020). Uncertainty Problems in Image Change Detection. Sustainability, 12(1), 274. https://doi.org/10.3390/su12010274






