Uncertainty Problems in Image Change Detection
Abstract
:1. Introduction
2. Materials and Methods
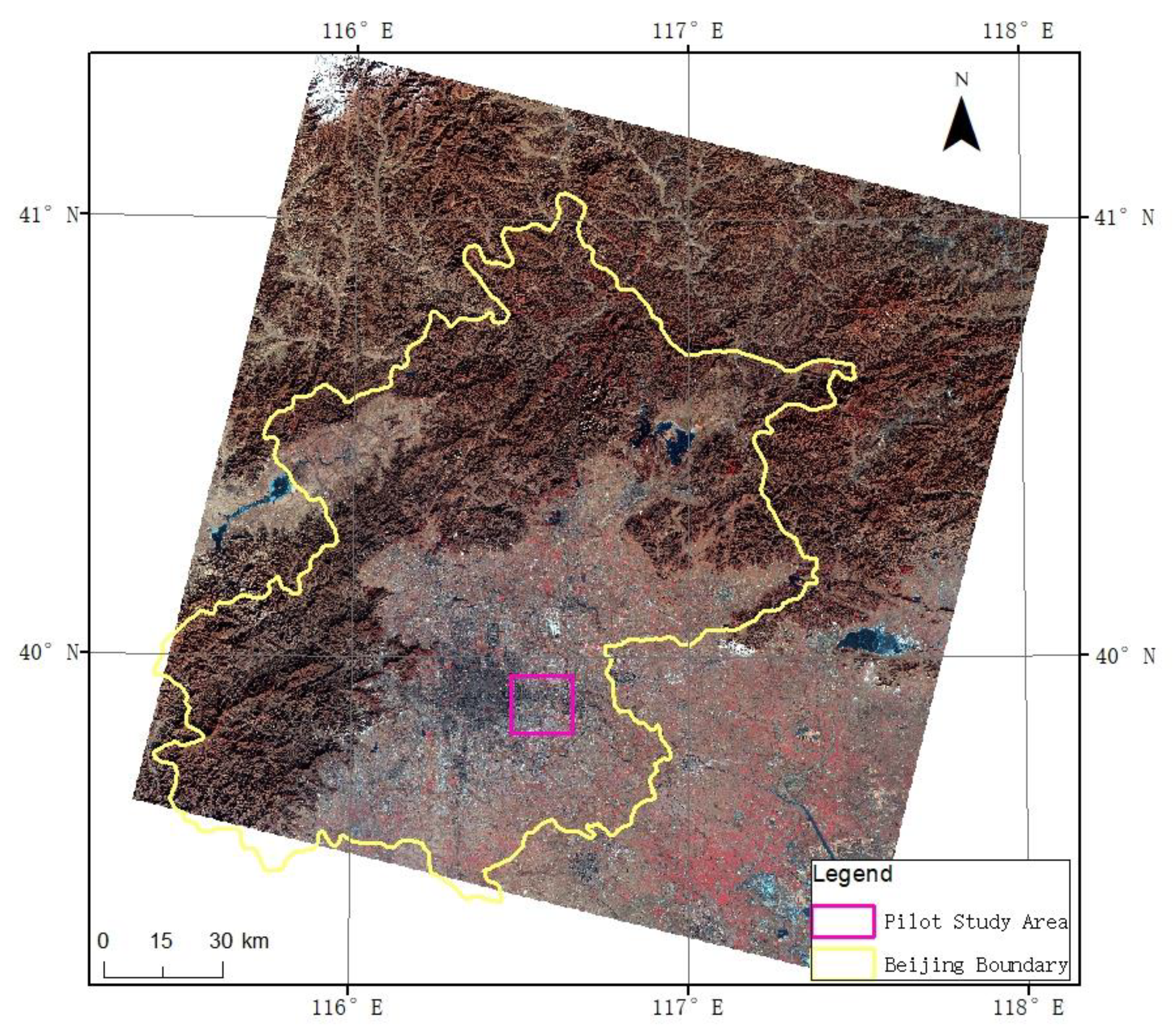
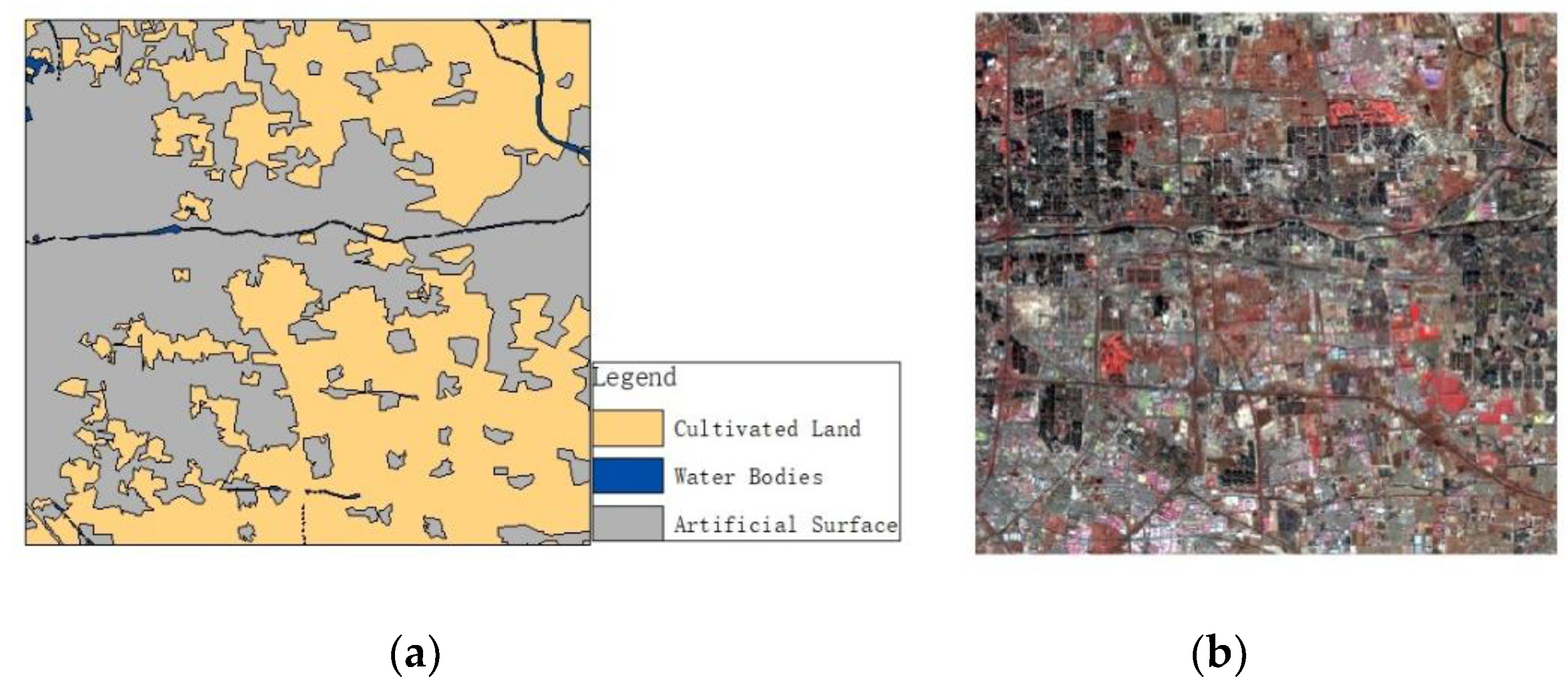
2.1. Study Area and Data
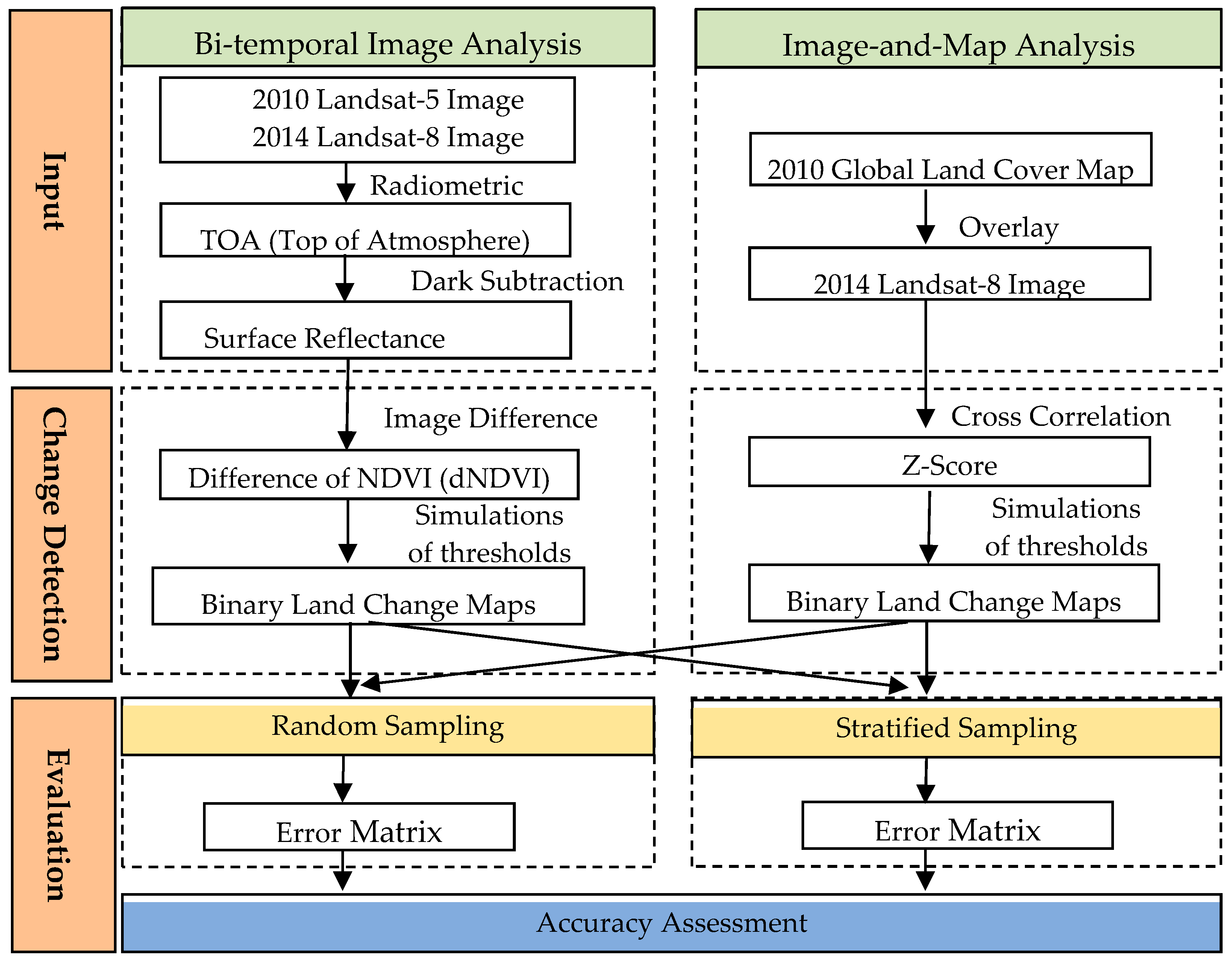
2.2. Methodology
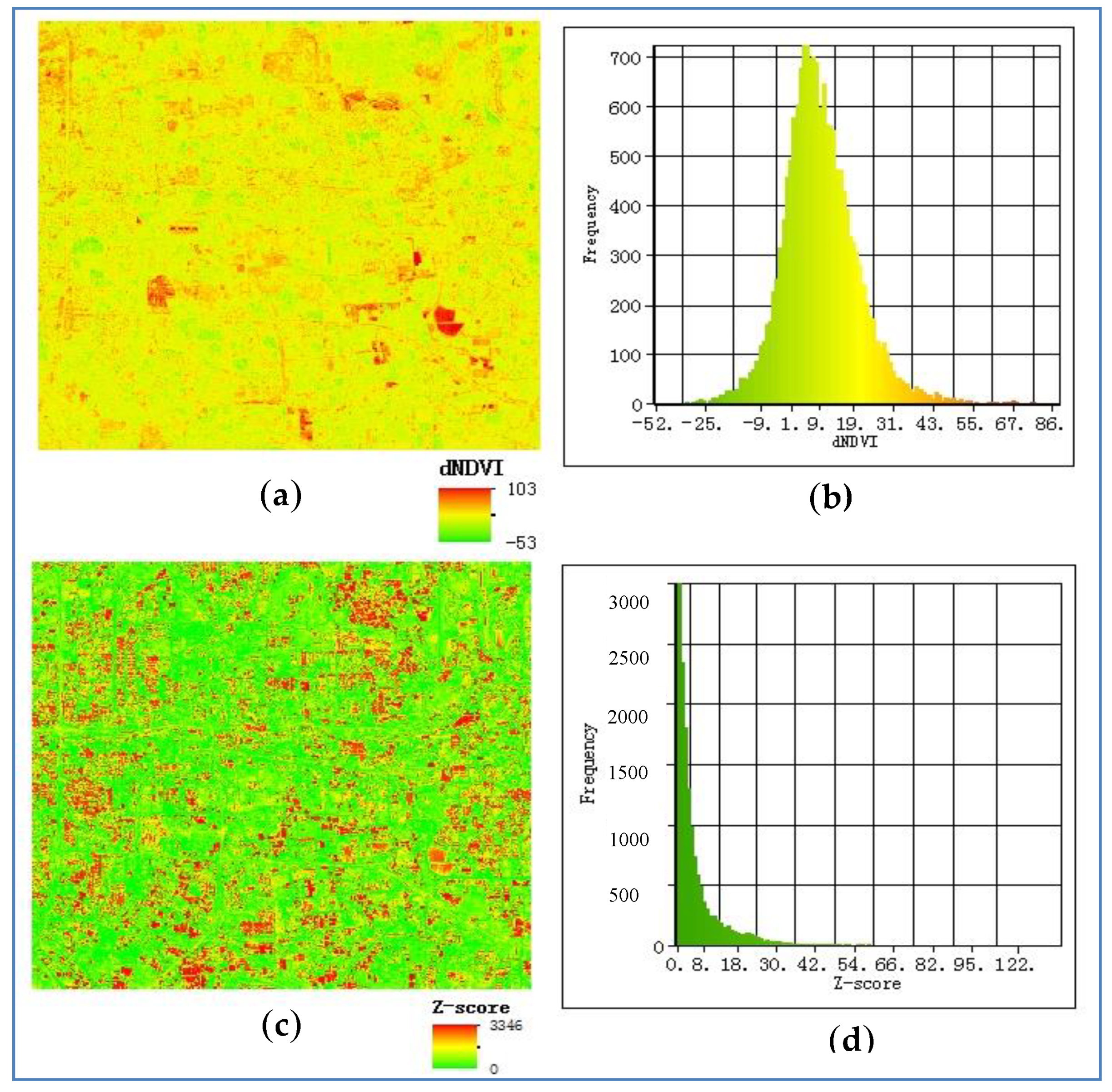
2.2.1. Change Variables
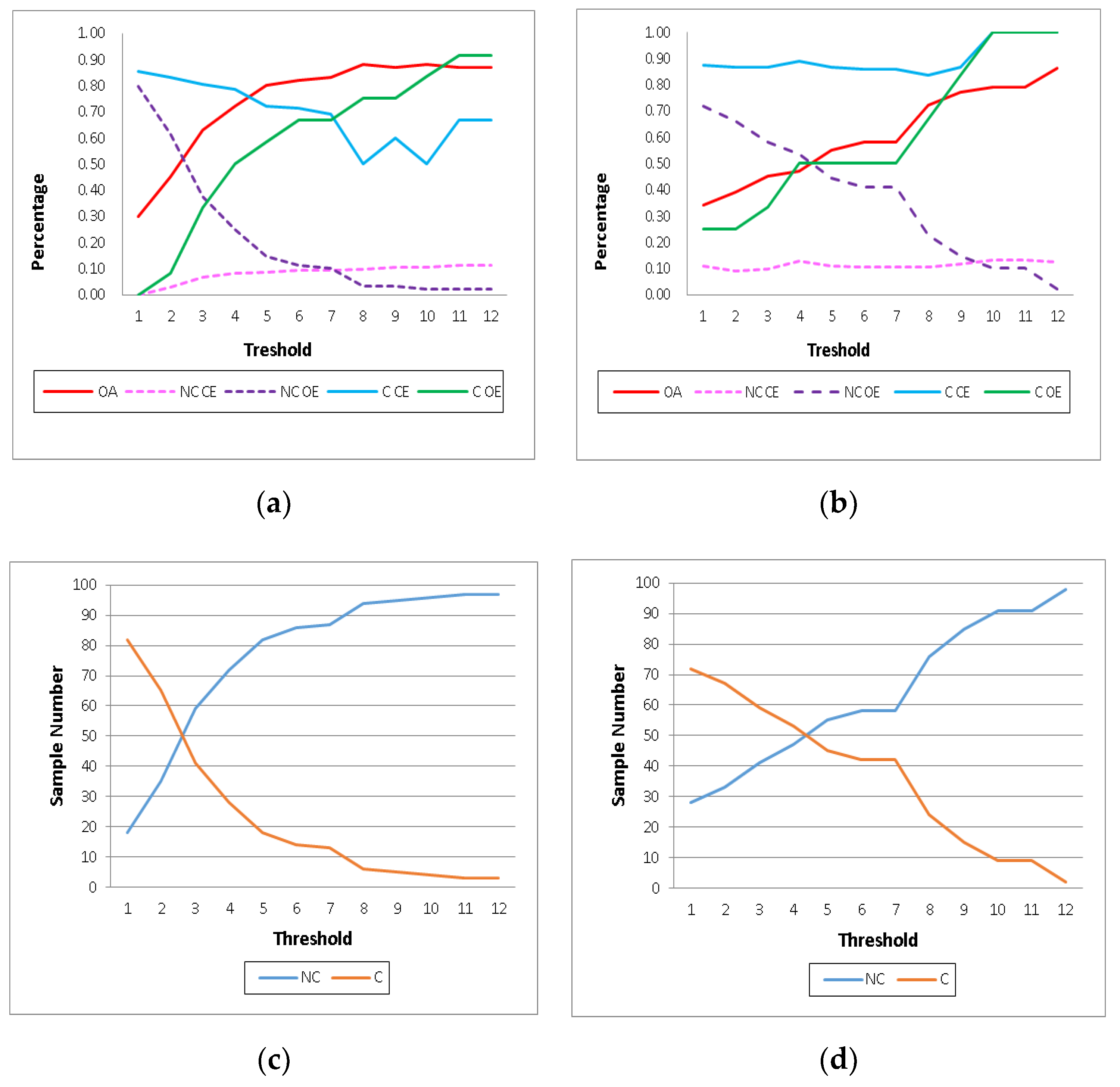
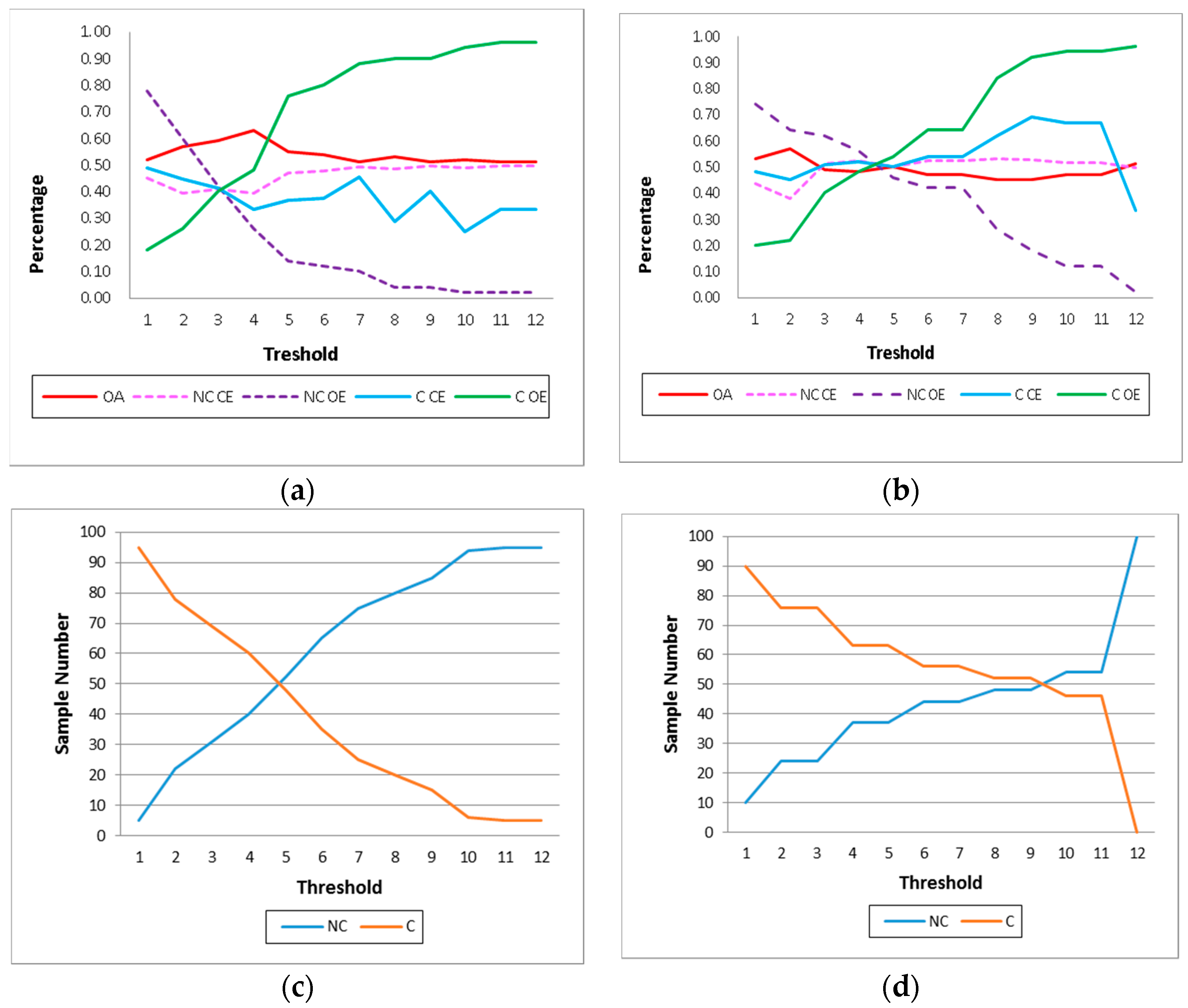
2.2.2. Sampling and Accuracy Assessments
3. Results
4. Discussion
4.1. Bi-Temporal Image Analysis Versus Image-and-Map Analysis
4.2. Random Sampling Versus Stratified Sampling
4.3. Thresholding and Sensitivity Analysis
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Liu, J.; Zhang, Z.; Zhuang, D.; Wang, Y.; Zhou, W.; Zhang, S.; Li, R.; Jiang, N.; Wu, S. A study on the spatial-temporal dynamic changes of land-useand driving forces analyses of China in the 1990s. Geogr. Res. 2003, 22, 1–12. [Google Scholar] [CrossRef]
- Fry, J.; Xian, G.Z.; Jin, S.; Dewitz, J.; Homer, C.G.; Yang, L.; Barnes, C.A.; Herold, N.D.; Wickham, J.D. Completion of the 2006 national land cover database for the conterminous united states. Photogramm. Eng. Remote Sens. 2011, 77, 858–864. [Google Scholar]
- Zhang, Z.; Wang, X.; Zhao, X.; Liu, B.; Yi, L.; Zuo, L.; Wen, Q.; Liu, F.; Xu, J.; Hu, S. A 2010 update of National Land Use/Cover Database of China at 1: 100000 scale using medium spatial resolution satellite images. Remote Sens. Environ. 2014, 149, 142–154. [Google Scholar] [CrossRef]
- Xian, G.; Homer, C.G.; Fry, J. Updating the 2001 National Land Cover Database land cover classification to 2006 by using Landsat imagery change detection methods. Remote Sens. Environ. 2009, 113, 1133–1147. [Google Scholar] [CrossRef] [Green Version]
- Jin, S.; Yang, L.; Danielson, P.; Homer, C.; Fry, J.; Xian, G. A comprehensive change detection method for updating the National Land Cover Database to circa 2011. Remote Sens. Environ. 2013, 132, 159–175. [Google Scholar] [CrossRef] [Green Version]
- Xian, G.; Homer, C. Updating the 2001 National Land Cover Database Impervious Surface Products to 2006 using Landsat Imagery Change Detection Methods. Remote Sens. Environ. 2010, 114, 1676–1686. [Google Scholar] [CrossRef]
- Song, X.; Hansen, M.C.; Stehman, S.V.; Potapov, P.V.; Tyukavina, A.; Vermote, E.F.; Townshend, J.R. Global land change from 1982 to 2016. Nature 2018, 560, 639–643. [Google Scholar] [CrossRef]
- MRLC. Available online: http://www.mrlc.gov/nlcd (accessed on 3 December 2019).
- Singh, A. Review article digital change detection techniques using remotely-sensed data. Int. J. Remote Sens. 1989, 10, 989–1003. [Google Scholar] [CrossRef] [Green Version]
- Blaschke, T. Towards a framework for change detection based on image objects. Göttinger Geogr. Abh. 2005, 113, 1–9. [Google Scholar]
- Jensen, J.R. Introductory Digital Image Processing: A Remote-Sensing Perspective; Pearson Education, Inc.: Glenview, IL, USA, 2016. [Google Scholar] [CrossRef]
- Lu, D.; Mausel, P.; Brondizio, E.; Moran, E. Change detection techniques. Int. J. Remote Sens. 2004, 25, 2365–2401. [Google Scholar] [CrossRef]
- Radke, R.J.; Andra, S.; Al-Kofahi, O.; Roysam, B. Image change detection algorithms: A systematic survey. IEEE Trans. Image Process. 2005, 14, 294–307. [Google Scholar] [CrossRef] [PubMed]
- Ridd, M.K.; Liu, J. A Comparison of Four Algorithms for Change Detection in an Urban Environment. Remote Sens. Environ. 1998, 63, 95–100. [Google Scholar] [CrossRef]
- Tewkesbury, A.P.; Comber, A.J.; Tate, N.J.; Lamb, A.; Fisher, P.F. A critical synthesis of remotely sensed optical image change detection techniques. Remote Sens. Environ. 2015, 160, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Civco, D.L.; Hurd, J.D.; Wilson, E.H.; Song, M.; Zhang, Z. A comparison of land use and land cover change detection methods. In Proceedings of the ASPRS-ACSM Annual Conference, Washington, DC, USA, 22–26 April 2002. [Google Scholar]
- Canty, M.J. Image Analysis, Classification and Change Detection in Remote Sensing: With algorithms for ENVI/IDL and Python; CRC Press: Florida, FL, USA, 2014. [Google Scholar]
- Hussain, M.; Chen, D.; Cheng, A.; Wei, H.; Stanley, D. Change detection from remotely sensed images: From pixel-based to object-based approaches. ISPRS J. Photogramm. Remote Sens. 2013, 80, 91–106. [Google Scholar] [CrossRef]
- Koeln, G.; Bissonnette, J. Cross-correlation analysis: Mapping landcover change with a historic landcover database and a recent, single-date multispectral image. In Proceedings of the 2000 ASPRS Annual Convention, Washington, DC, USA, 1–5 May 2000. [Google Scholar]
- Tarantino, C.; Adamo, M.; Lucas, R.; Blonda, P. Detection of changes in semi-natural grasslands by cross correlation analysis with WorldView-2 images and new Landsat 8 data. Remote Sens. Environ. 2016, 175, 65–72. [Google Scholar] [CrossRef] [PubMed]
- Hamby, D. A review of techniques for parameter sensitivity analysis of environmental models. Environ. Monit. Assess. 1994, 32, 135–154. [Google Scholar] [CrossRef]
- VanderWeele, T.J.; Tchetgen, E.J.T.; Halloran, M.E. Interference and sensitivity analysis. Stat. Sci. 2014, 29, 687. [Google Scholar] [CrossRef]
- Plewe, B. The Nature of Uncertainty in Historical Geographic Information. Trans. GIS 2002, 6, 431–456. [Google Scholar] [CrossRef]
- Hao, M.; Shi, W.; Deng, K.; Zhang, H.; He, P. An object-based change detection approach using uncertainty analysis for VHR images. J. Sens. 2016, 2016. [Google Scholar] [CrossRef]
- Patil, G.; Taillie, C. Modeling and interpreting the accuracy assessment error matrix for a doubly classified map. Environ. Ecol. Stat. 2003, 10, 357–373. [Google Scholar] [CrossRef]
- Zhu, Z.; Woodcock, C.E. Continuous change detection and classification of land cover using all available Landsat data. Remote Sens. Environ. 2014, 144, 152–171. [Google Scholar] [CrossRef] [Green Version]
- Dronova, I.; Gong, P.; Wang, L. Object-based analysis and change detection of major wetland cover types and their classification uncertainty during the low water period at Poyang Lake, China. Remote Sens. Environ. 2011, 115, 3220–3236. [Google Scholar] [CrossRef]
- Song, C.; Woodcock, C.E. Monitoring forest succession with multitemporal Landsat images: Factors of uncertainty. IEEE Trans. Geosci. Remote Sens. 2003, 41, 2557–2567. [Google Scholar] [CrossRef]
- Stehman, S.V. Estimating area from an accuracy assessment error matrix. Remote Sens. Environ. 2013, 132, 202–211. [Google Scholar] [CrossRef]
- Olofsson, P.; Foody, G.M.; Herold, M.; Stehman, S.V.; Woodcock, C.E.; Wulder, M.A. Good practices for estimating area and assessing accuracy of land change. Remote Sens. Environ. 2014, 148, 42–57. [Google Scholar] [CrossRef]
- Coppin, P.; Lambin, E.; Jonckheere, I.; Muys, B. Digital change detection methods in natural ecosystem monitoring: A review. In Analysis of Multi-Temporal Remote Sensing Images; World Scientific: Singapore, 2002; pp. 3–36. [Google Scholar]
- Rosin, P.L.; Ioannidis, E. Evaluation of global image thresholding for change detection. Pattern Recognit. Lett. 2003, 24, 2345–2356. [Google Scholar] [CrossRef] [Green Version]
- Rosin, P. Thresholding for change detection. In Proceedings of the Sixth International Conference on Computer Vision, Bombay, India, 4–7 January 1998; pp. 274–279. [Google Scholar]
- Wang, J.; Stein, A.; Gao, B.; Ge, Y. A review of spatial sampling. Spat. Stat. 2012, 2, 1–14. [Google Scholar] [CrossRef]
- Stats. Available online: http://www.stats.gov.cn/ (accessed on 5 October 2016).
- USGS. Available online: http://glovis.usgs.gov/ (accessed on 20 October 2016).
- Siewe, S.S. Change Detection Analysis of the Landuse and Landcover of the Fort Cobb Reservoir Watershed; Oklahoma State University: Stillwater, OK, USA, 2007. [Google Scholar]
- GlobaLand30. Available online: http://www.globallandcover.com/ (accessed on 10 June 2016).
- Li, H.; Song, W. Expansion of Rural Settlements on High-Quality Arable Land in Tongzhou District in Beijing, China. Sustainability 2019, 11, 5153. [Google Scholar] [CrossRef] [Green Version]
- Van Oort, P. Interpreting the change detection error matrix. Remote Sens. Environ. 2007, 108, 1–8. [Google Scholar] [CrossRef]
- Couclelis, H. The Certainty of Uncertainty: GIS and the Limits of Geographic Knowledge. Trans. GIS 2003, 7, 165–175. [Google Scholar] [CrossRef]
- Mowrer, H.T. Accuracy (re)assurance: Selling uncertainty assessment to the uncertain. In Spatial Accuracy Assessment: Land Information Uncertainty in Natural Resources; Jaton, K.L.A.A., Ed.; Ann Arbor Press: Chelsea, MI, USA, 1999. [Google Scholar]
- Thompson, S.K. Sampling, 3rd ed.; Wiley: Hoboken, HN, USA, 2012. [Google Scholar]
- Hansen, M.C.; Loveland, T.R. A review of large area monitoring of land cover change using Landsat data. Remote Sens. Environ. 2012, 122, 66–74. [Google Scholar] [CrossRef]
- Boori, M.S.; Amaro, V.E. Land use change detection for environmental management: Using multi-temporal, satellite data in the Apodi Valley of northeastern Brazil. Appl. GIS 2010, 6, 1–15. [Google Scholar] [CrossRef]
- Heckman, J.J. Sample selection bias as a specification error. Econom. J. Econom. Soc. 1979, 153–161. [Google Scholar] [CrossRef]
- Rogerson, P.A.; Delmelle, E.; Batta, R.; Akella, M.; Blatt, A.; Wilson, G. Optimal Sampling Design for Variables with Varying Spatial Importance. Geogr. Anal. 2004, 36, 177–194. [Google Scholar] [CrossRef]
- Biagini, F.; Campanino, M. Elements of Probability and Statistics: An. Introduction to Probability with de Finetti’s Approach and to Bayesian Statistics; Springer: New York, NY, USA, 2016. [Google Scholar]
- Harris, R.; Jarvis, C. Statistics for Geography and Environmental Science, 1st ed.; Routledge: London, UK, 2014. [Google Scholar] [CrossRef]
- Bruzzone, L.; Prieto, D.F. Automatic analysis of the difference image for unsupervised change detection. IEEE Trans. Geosci. Remote Sens. 2000, 38, 1171–1182. [Google Scholar] [CrossRef] [Green Version]
- Teng, S.; Chen, Y.; Cheng, K.; Lo, H. Hypothesis-test-based landcover change detection using multi-temporal satellite images–A comparative study. Adv. Space Res. 2008, 41, 1744–1754. [Google Scholar] [CrossRef]
- Burt, J.E.; Barber, G.M.; Rigby, D.L. Elementary Statistics for Geographers; Guilford Press: New York, NY, USA, 2009. [Google Scholar]
- Hwang, C.L.; Lin, M.J. Group Decision Making Under Multiple Criteria: Methods and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Saltelli, A.; Tarantola, S.; Campolongo, F.; Ratto, M. Sensitivity Analysis in Practice: A Guide to Assessing Scientific Models; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2004. [Google Scholar] [CrossRef]
- Seebach, L.; Strobl, P.; Vogt, P.; Mehl, W.; San-Miguel-Ayanz, J. Enhancing post-classification change detection through morphological post-processing–a sensitivity analysis. Int. J. Remote Sens. 2013, 34, 7145–7162. [Google Scholar] [CrossRef]
- Verburg, P.H.; Tabeau, A.; Hatna, E. Assessing spatial uncertainties of land allocation using a scenario approach and sensitivity analysis: A study for land use in Europe. J. Environ. Manag. 2013, 127, S132–S144. [Google Scholar] [CrossRef]
- Chen, Y.; Yu, J.; Khan, S. Spatial sensitivity analysis of multi-criteria weights in GIS-based land suitability evaluation. Environ. Model. Softw. 2010, 25, 1582–1591. [Google Scholar] [CrossRef]
- Iman, R.L.; Helton, J.C. An investigation of uncertainty and sensitivity analysis techniques for computer models. Risk Anal. 1988, 8, 71–90. [Google Scholar] [CrossRef]
- Christopher, F.H.; Patil, S.R. Identification and review of sensitivity analysis methods. Risk Anal. 2002, 22, 553–578. [Google Scholar] [CrossRef]
- Saltelli, A.; Annoni, P. How to avoid a perfunctory sensitivity analysis. Environ. Model. Softw. 2010, 25, 1508–1517. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Hall-Beyer, M.; Wu, C.; Fang, W.; Nsengiyumva, W. Uncertainty Problems in Image Change Detection. Sustainability 2020, 12, 274. https://doi.org/10.3390/su12010274
Wang W, Hall-Beyer M, Wu C, Fang W, Nsengiyumva W. Uncertainty Problems in Image Change Detection. Sustainability. 2020; 12(1):274. https://doi.org/10.3390/su12010274
Chicago/Turabian StyleWang, Wenyu, Mryka Hall-Beyer, Changshan Wu, Weihua Fang, and Walter Nsengiyumva. 2020. "Uncertainty Problems in Image Change Detection" Sustainability 12, no. 1: 274. https://doi.org/10.3390/su12010274
APA StyleWang, W., Hall-Beyer, M., Wu, C., Fang, W., & Nsengiyumva, W. (2020). Uncertainty Problems in Image Change Detection. Sustainability, 12(1), 274. https://doi.org/10.3390/su12010274






