Abstract
One of the main problems related to the excavation of dog headings in coal beds is the emission of methane during this process. To prevent the occurrence of dangerous concentration levels of this gas, it is necessary to use an appropriate ventilation system. The operation effectiveness of such a system depends on a number of mining, geological, technical and organizational factors. One of them includes the size and permeability of the fractures zone formed around the excavated dog heading. The primary objective of the paper is to determine the influence of this zone on the ventilation parameters, including the concentration and distribution of methane in the excavated dog heading. In order to achieve the assumed objective, multivariate model-based tests were carried out, which reproduce a real-world dog heading. Literature data and test results in actual conditions were used to determine the size and permeability of the fractures zone around the excavated heading. These data served as the basis to develop a model of the region under analysis and adopt boundary conditions. The analyses were carried out for four permeability values of the fractures zone and for two volumetric flow rates of the air stream supplied to the heading. The results were used to determine the influence of the fractures zone on the distribution and concentration of methane in the heading under analysis. The model-based tests were performed using ANSYS Fluent software. The idea to take into account the fractures zone around the heading represents a new approach to the analysis of ventilation parameters in underground mine headings. The results clearly indicate that this zone affects the ventilation parameters in the heading, including the distribution and concentration of methane. The knowledge obtained from the tests should be used to optimize the ventilation process of dog headings. All authors have read and agreed to the published version of the manuscript.
1. Introduction
In the global underground coal mining, hundreds of kilometers of dog headings are mined (excavated) every year. In most cases, those are preparatory headings for the fundamental process of coal exploitation. Depending on the geological conditions of the particular headings, they are mined either in the waste rock or in coal. In recent years, in Polish hard coal mines, those headings are primarily mined in coal beds with high methane-bearing capacity [1,2,3,4,5].
During the mining process related to mined (excavated), dog headings are usually “the blind”. The dog heading has one connection with the main airways in underground ventilation systems (Figure 1). This makes it very difficult to properly ventilate them, especially because in the face of such heading and along their entire length, there are employees who operate the mining machinery and machines that protect the heading. The presence of the crew and the highly specialist, and hence very expensive, equipment makes it necessary to provide adequate ventilation to such headings. The ventilation system must ensure proper temperature and chemical composition of air, so that the employees could freely and safely perform their work [6,7,8,9,10,11,12,13,14,15].
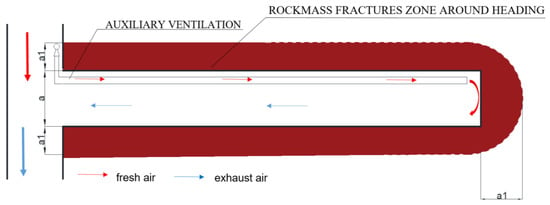
Figure 1.
A scheme of the excavated dog heading with the demarcated fractures zone, where a is The width of dog heading and a1 is range of the fractures zone in sidewalls (own study based on [16,17]).
In terms of chemical composition, one of the most significant tasks of the ventilation system is to prevent the occurrence of dangerous methane concentration levels in those headings [7,8,9,10,11,12,13,14,15]. Unfortunately, the coal beds currently excavated in Poland contain high methane deposits. As a result, the dog headings mined in those coal beds are susceptible to high methane emissions. To guarantee working safety for the crew and proper effectiveness of the excavation process, dangerous methane concentration levels are not acceptable in such headings. This is because they may lead to the combustion and/or explosion of this gas. Both of these phenomena are amongst the most dangerous in the mining industry, posing a serious threat to working crews and equipment alike [18,19,20].
To prevent dangerous accumulation of methane and ensure proper composition of the atmosphere in excavated dog headings, a ventilation system with an air duct is commonly used to supply fresh air to the face of the headings (Figure 1). The parameters of the air supplied are selected depending on the geometric parameters of each heading, the temperature, as well as the anticipated level of methane emission.
During the excavation of dog headings, methane is emitted into such headings from the exposed (mined) body of coal, sidewalls, roof and floor, mainly in the form of free methane present in the crevices and cracks of coal and released during the mining process, as well as methane adsorbed in micro-pores with a diameter less than 2 mm. Methane also occurs as a gas dissolved in the water present in coal and held by weak Van der Waals bonds on the coal surface [21,22,23,24]. In terms of adequate ventilation of dog headings, the most crucial point to consider is the emission of methane from the crevices and as a result of desorption, which occurs in the decompressed part of the rock mass. The excavation of dog headings in coal beds changes the pressure distribution in the surrounding rock mass, reduces methane pressure and changes gas permeability, as well as partially degasses the body of coal adjacent to the heading. As a result of these processes, the excavated headings are supplied not only with the free methane present in the voids of the rock mass, but also with the methane adsorbed in the coal bed [25,26,27,28].
Consequently, methane is released into the heading from the mined face, the excavated coal and the cracked rock mass around the heading. If the height of the heading is equal to the thickness of the coal bed, methane is released from the cracks in sidewalls. On the other hand, when the thickness of the coal bed is greater, this zone may also encompass the roof and the floor [24].
However, there is no doubt that the cracks forming around the excavated dog heading affect the process of its ventilation. These cracks create a discontinuity zone in the rock mass, which forms as a result of mining operations, and whose size depends on a number of factors. The main ones include the size of the excavated heading, the manner and speed of excavation, the type of support used, the geomechanical parameters of the rocks and geological conditions [28,29,30]. All these factors determine the intensity and extent of the fractures zone (the formation of crevices) around the dog heading [16,17].
From the perspective of ventilation, the fractures zone forming around the dog heading constitutes a porous and permeable medium. The parameters of this medium, and especially its permeability, depend on numerous factors and affect the ventilation parameters in the heading.
It is therefore reasonable during the examination of the ventilation parameters in the dog heading to take into account the fractures zone around it, as a porous medium that takes active part in this process. Disturbing the original balance present in this zone increases its porosity and permeability compared to the original state of the rock mass [28,29,30]. This, in turn, leads to increased gas permeability of the rocks surrounding the dog heading, through which methane migration occurs, and activates the process of methane desorption from coal [16,17,25,26,27,28].
It is therefore reasonable to state that the size and parameters of this zone, especially those concerning permeability, influence the ventilation process in the excavated dog heading.
Literature review indicates that this problem has not been thoroughly examined so far. This is because the ventilation analyses have failed to take into consideration the fractures zone as a porous medium during the determination of ventilation parameters in dog headings, despite the fact that the issue of determining those parameters in mine headings and tunnels has been discussed in numerous publications. Those publications also revolve around the very dangerous aspects of methane.
Papers discussing the examination of processes related to the flow of air as well as the mixture of air and methane through dog headings have been presented in a number of publications. They encompassed the findings from analyses conducted both in real-world conditions [31,32] and in laboratory settings [33,34], as well as the results of model-based tests [7,9,35,36,37,38,39,40,41,42,43].
The papers which are particularly interesting in this regard are those presenting the results of numerical research related with methane concentration in excavated dog headings. This is because they make it possible to determine of airflow parameters related with ventilation processes, the measurement of which in real underground coal mine conditions is difficult, or in certain cases-impossible.
Particular potential in this regard is offered by research using numerical simulations based on Computational Fluid Dynamics (CFD) [7,9,35,36,37,38,39,40,41,42,43,44]. Currently, this method is more and more frequently applied to analyzing phenomena related to ventilation of dog headings. This is proved by the papers [35,36,37,38,39,40,41,42,43] which present the results of model-based tests related to the ventilation of excavated mine headings.
The paper by [35], amongst others, presents the calculation results for the gas concentration and velocity fields in headings of various lengths and with different fan locations in the cross-section of the heading. The results of these tests corroborated the thesis about the essential influence of the adopted description of boundary conditions on the precision of the numerical reproduction of the actual flow.
Kurnia, Sasmito and Mujumdar in paper [7] presented the results of methane concentration in mining heading. They observed that the concentration of methane depends on location of methane sources and the number of sources from which methane flows [7].
Kurnia Sasmito and Mujumdar in the paper [38] proposed a new ventilation system. In the next step, they evaluated this system with Computational Fluid Dynamics (CFD) method. The main aim paper was numerical research with the goal of reducing the energy cost while maintaining methane concentration in the mining heading below the safe level.
Sasimoto et al. [39] conducted numerical analyses whose purpose was to examine the behavior of the flow of air-methane mixture in the ‘‘room and pillar’’. For this purpose, they compared several turbulence models, and then compared the results obtained with experimental data. The results of their analyses indicate that the Spalart-Allmaras one-equation turbulence model is suitable for proper prediction of the behavior of the flowing mixture of air and mining gases in underground mine headings.
Wala et al. in the paper [40] validated the numerical research results (with use Computational Fluid Dynamics simulation) with experimental data for designing ventilation systems for underground coal mine. In the paper by Wala et al. [41] the results of experimental and numerical studies of methane concentration distribution were compared.
In a Computational Fluid Dynamics simulation on air and methane mixture recirculation in auxiliary ventilation system in mining excavation, Torano et al. [43] found higher methane distribution than the safe levels in some places of excavation zones due to presence of dead zones.
The works discussed explain a considerable part of the phenomena related to the flow of air, the release of methane into the excavated dog headings and its distribution. These works, like many others, most frequently assumed that methane is released into the dog heading from a given point [7] or from a surface [35] only from the face area.
In actual fact, this process occurs in a slightly different manner. This particularly concerns headings excavated in coal. Practical experience shows, as mentioned before, that methane is released into the excavated dog heading not only from the exposed (mined) body of coal, but also from the sidewalls, roof and floor of the heading. This results from the formation of crevices and cracks in the rock mass around the excavated heading during its excavation. The resultant fractures zone is a porous and permeable medium and should therefore also be considered during the analysis of the ventilation parameters in those headings.
A literature review demonstrates that ventilation analyses in dog headings fail to take into consideration the influence of the fractures zone around them. No attention was therefore given to methane, which is emitted from this zone to the heading. It can therefore be assumed that the analyses of ventilation parameters conducted in dog headings to date have failed to take into consideration the fractures zone around those headings.
As a result, it is reasonable to carry out research to determine the influence of the fractures zone around the excavated dog heading on the concentration and distribution of methane in this heading. This new approach to analyzing ventilation parameters in dog headings will make it possible to conduct a more comprehensive analysis of the ventilation process occurring in such headings.
In order to determine the influence of the fractures zone around the excavated dog heading on the ventilation parameters in this heading, multivariate model-based tests were carried out for the actual layout of mine headings in one of the underground coal mines. The tests involved reproducing the actual dog heading being excavated, by retaining its geometric and ventilation parameters, as well as taking into consideration the geological conditions. The literature data and the mining/geological information from the mine served as the basis to determine the size of the fractures zone around the excavated heading and the permeability value for this zone. The permeability of the fractures zone was determined on the basis of the strength of the rocks that formed the zone [28,29,30].
Since model-based tests create major opportunities for multivariate analyses, they were conducted for four (one actual and three assumed) different permeability values of the fractures zone, as well as for two different volumetric flow rates of the fresh air stream supplied through a pipeline to the face of the excavated heading.
The main aim of the research was to determine to what extent is the distribution of methane concentration in the excavated dog heading affected by taking into consideration the fractures zone around this heading. This zone was assumed to represent a porous and permeable medium. The analyses also involved determining how the permeability of this zone affects the distribution and concentration methane in the heading. The focus on determining the distribution of methane concentration is due to the fact that methane represents the greatest risk in the process of excavating mine headings, including dog headings [6,7,8,9,10,11,12,13].
The numerical analysis was conducted using Computational Fluid Dynamics (CFD). The simulations were performed in ANSYS Fluent 18.2 software.
2. Materials and Methods
2.1. Area of Research
The numerical analysis was conducted for the real dog heading excavated in one of the deep underground coal mines located in the Upper Silesian Coal Basin area. This coal mine is located in the southern part of Poland (Figure 2). It is one of the largest mines in Poland, where approximately 10,000 m of dog headings were mined in 2018.
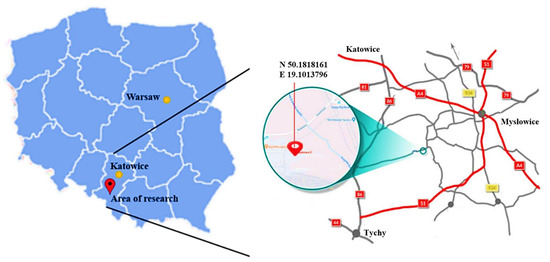
Figure 2.
Location of the Upper Silesian Coal Basin area where the research was conducted (own study based on [9,45]).
This mine is classified as very dangerous, especially due to the methane hazard. It is exposed to all the natural risks related to underground coal exploitation.
According to Polish regulations in this coal mine occur following threats: methane (4th category), rock burst (1st and 2nd degree), water (1st and 2nd degree), and dust explosion (class A and B) [46].
The regulations in Poland require that the exploited coal seams or their parts be classified into a one of four methane hazard category (where first category of methane hazard is lowest, while fourth category is highest) [46].
Moreover, according to Polish legal regulations, mine headings in methane fields are classified to one of the three degrees of methane explosion hazard (degree “a”—no hazard of methane explosion; degree “b” of methane explosion hazard, if in normal ventilation conditions the concentration of methane in air higher than 1.0% is excluded; and degree “c” of methane explosion hazard, if even in normal ventilation conditions the concentration of methane in air can be higher than 1.0%) [47].
Moreover, if the methane concentration level exceeds 3%, the mining crew is evacuated from the heading. As a result, tests related to the analysis of methane-bearing capacity are of crucial importance for this mine. This is because the provision of adequate ventilation conditions determines both the safety and the effectiveness of the exploitation process [47].
Description of the Excavated Dog Heading under Analysis
The dog heading under analysis was ventilated by means of a duct line ventilation system. Approximately 310 m3/min. of fresh air was supplied to the heading via the forcing air duct. The flow of methane to the heading area amounted to approx. 4.5 m3CH4/min. The scheme of the heading and air distribution, indicating the measurement points where methane sensors were located, is presented in Figure 3. The cross-section area of the excavated heading amounted to 14.8 m2. The numerical analysis was conducted for a heading with a length of 70 m.

Figure 3.
A scheme of the heading indicating the distribution of air and the measurement points where methane sensors were located (own study).
2.2. Methods
The numerical analysis was conducted for a 3D model of the dog heading under analysis, using Computational Fluid Dynamics and the finite volume method. Computational Fluid Dynamics method is used for analyzing processes related with the air flows or other gases flows and fluids, the heat and mass transfer and the process of combustion [7,9,35,36,37,38,39,40,41,42,43,44,48].
The study made use of the ANSYS Fluent 18.2 software [49]. The methodology for conducting research by means of this software encompasses development of a mathematical model, adoption of cell-zones and boundary conditions, calculations and analysis of the research results. The stages of the research methodology are briefly presented in the next sections.
2.2.1. Mathematical Models
Governing Equations
The flow of the mixture of air stream and mining gases, including methane, is described by the conservation equations. The conservation equations include mass, momentum, energy and species transport equations in following form [7,38,39,50]:
where ρ is the density of air or another gas (kg/m3), U is the gas velocity (m/s), p is pressure (Pa), τ is the viscous stress tensor (Pa), g is gravity acceleration (m∙s−2), cp is the heat of the gas, keff is the effective gas thermal conductivity, T is the temperature (K), ωi is the mass fraction N2, O2 and CH4, μt is turbulent viscosity (Pa·s), Di,eff is the effective diffusivity of N2, O2 and CH4 (m2/s), Sct is the turbulent Schmidt number (0.7), Prt is the Prandtl number.
Model of Turbulence
The stream of the air and methane mixture flowing through mine headings, including the excavated dog heading, is of a turbulent nature. It is necessary for the model to take into account the complex structure of flow turbulence due to the significant intensification of all the transportation processes occurring in turbulent flows [51,52].
The flow turbulence in the analyses concerning the flow of air and methane mixture through mine headings was described using the so-called RANS approach (Reynold-Averaged Navier-Stokes).
According to Reynolds’ hypothesis, the instantaneous values of all the physical quantities characterizing the flow at a given point of the flow field are an aggregate of the quantities averaged in time and the constituent of fluctuation (turbulence), which is a random function of time and space. The application of this concept to the Navier–Stokes equations transforms them into the form known as the Reynolds equation.
The Navier-Stokes equations in the Reynold Averaged Navier-Stokes (RANS) approach have the following form [7,38,39,50]:
The Reynolds stresses are related to the mean velocity gradients in the Boussinesq hypothesis [7,38,39,50]:
Based on the Boussinesq hypothesis, the k−ω model (two equations), k−ε model (in several form; two equations) and the Spalart-Allmaras model (one equation), are provided in the ANSYS Fluent 18.2 software. These models vary from each other in method of determining the turbulent viscosity μt.
The turbulence model k-ε in the standard variation is most commonly used. The kinetic turbulent energy (k) and the kinetic turbulent energy (ε) equations in the k–ε standard approach model have the following form [49]:
where σk, σε are turbulent Prandtl numbers for k and ε, Gb is the generation of turbulence kinetic energy, C1ε, C2ερ, C3ε are constant, Gk is the generation of turbulence kinetic energy, YM is contribution of the fluctuating dilatation in compressible turbulence to the overall dissipation rate, Sk, Sε are user-defined source terms.
Constitutive Equations
A species air-methane mixture occurs in the mines air in the underground headings. The interaction between eg. the oxygen, methane or water vapor is captured in the density of mixture, which follows incompressible ideal gas in the following form [39]:
where R is the universal gas constant and M is the mixture molar mass.
Mixture molar mass occur the following form [39]:
where Mi is the molar mass of oxygen, methane, water vapor or nitrogen.
Nitrogen mass fraction can be determined from:
The air–methane mixture viscosity can be determined from equation [39]:
where xi, and xj, are the mole fraction of species i and j, respectively, and [39]:
The mole fractions of species are related to the mass fractions of species according to [39]:
The methane concentration in mixture is presented as percentage of methane concentration (where CH4 is equal to ωCH4 × 100%).
2.3. Demarcation of the Fractures Zone Around the Excavated Dog Heading
The layered nature of the carboniferous rock mass, in combination with its lithological features, makes its structure discontinuous [53]. Its natural and inherent feature is porosity. In an intact rock mass, solid bodies, liquids and gases retain a relative balance of pressure and temperature. Creating a heading in such a rock mass leads to the disturbance of this balance. One of the consequences of disturbing this balance in the event of excavating a dog heading is the formation of the fractures zone around it [16,17,27,28,54,55,56,57,58,59]. As mentioned in the introduction, this zone is an area where the rocks have become less compact, thereby leading to discontinuities in the form of crevices and cracks. The size and density of these crevices depend on a number of mining and geological factors as well as technical and organizational considerations related to the process of heading excavation. The factors that significantly affect the size of the fractures zone include, amongst others, the geometry of the heading, the methods of its excavation, the resistance of rocks in which the heading is excavated, and the depth of deposit. The fractures zone forming around the excavated heading usually allows the flow of gases and liquids, creating a permeable porous medium.
In the case at hand, the formation of crevices in the fractures zone around the heading excavated in a methane-rich coal bed additionally turns this zone a degassing area, i.e., an area of methane desorption [60]. Generally, this process involves release of methane particles from micro-crevices as a result of pressure changes. The heading excavated in a methane-filled coal bed is therefore surrounded on all sides by the degassing zone (the desorption zone) [16,17] (Figure 1). Therefore, it was assumed that the desorption area overlapped the fractures zone of the rock mass (coal) around the heading under analysis.
There were numerous studies concerning the determination of the fractures zone, the results of which were presented in the papers [27,28,54,55,56,57]. The interest in determining this zone mainly arises from the fact that its size is very important while choosing the support protecting a given heading against the deformative action of the rock mass [4,5]. However, the impact of this zone has so far not been accounted for in ventilation issues.
In the case at hand, the fractures zone around the excavated dog heading was determined on the basis of the study results presented in the paper [54]. It was assumed that the test results presented in the paper are reliable and referred to the specificity of Polish underground coal mines. In terms of rock resistance, geometry of the heading under analysis and the depth of its excavation, they correspond to the parameters of the heading analyzed and the bed in which it is excavated.
The size of the fractures zone was determined by means of the summary developed in the paper [16,17], which is presented in Table 1. The size of the fractures zone around the excavated heading, presented in Table 1, corresponds to the size of dimension a1 indicated in Figure 1.

Table 1.
The size of the fractures zone of the rock mass in the sidewalls of the dog heading with a cross section area of 14.8 m2 [16,17].
In the case of the analyzed heading excavated in a coal bed at the depth of 875 m, with the tensile strength of the coal equal to 11.5 MPa, it was assumed that the width of the fractures zone would be equal to 2 m.
Taking into consideration the tensile strength of the coal present around the excavated heading, the heading’s permeability was also determined and amounted to 3.55308·10−8 m2. The permeability of this zone was determined from the equations thoroughly described in the paper [61].
2.4. Model of Undeground Dog Heading
The important role for the reliability of the results obtained from model-based tests is played by the precision of the model, which should reproduce the actual dog heading and the conditions therein in the best manner possible.
For this goal, a geometric model was developed for the excavated dog heading and for the fractures zone around it. This model incorporated an air duct forcing fresh air into the face of the excavated dog heading, a belt conveyor and a roadheader (in the form of simplified geometry). The geometric model of the heading under analysis, along with the fractures zone and the heading equipment, is presented in Figure 4.
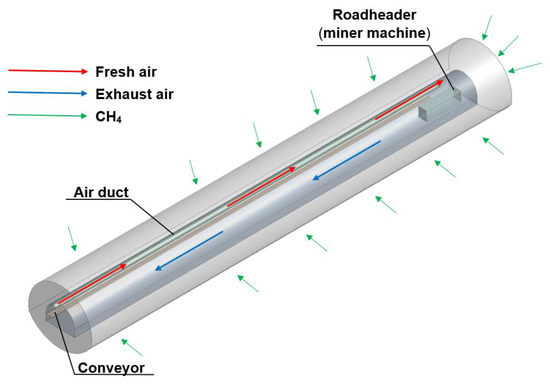
Figure 4.
The geometric model of the heading under analysis, along with the fractures zone and the heading equipment [own study].
Next, discretization of the model was performed, involving generation of a triangular mesh. The mesh consisted of 91,656,136 elements, whose size amounted to 0.05 m (for the part of the model reflecting the air duct and the conveyor, the size of the mesh was 0.01 m). Fragment of the discrete model of the heading is presented in Figure 5.

Figure 5.
A fragment of the discrete model of the heading under analysis [own study].
The sensitivity analysis revealed that the mesh made of elements not exceeding the size of 0.05 m is sufficient to obtain correct calculations. Further densification of the mesh significantly increased the duration of calculations, without leading to any significant improvement of their precision.
The next stage of the works involved determination of the boundary conditions and the model surrounding. The mining parameters of the excavated heading are presented in Table 2.

Table 2.
The mining parameters of dog heading.
Table 3 presents the permeability values of the fractures zone adopted for the calculations for the variants under analysis. The first variant corresponds to the permeability of the actual fractures zone around the heading in question. The second variant adopted a higher value for this permeability, whereas the third and fourth variants—lower values.

Table 3.
The permeability values of the fractures zone adopted for the analysis.
The ANSYS Fluent 18.2 software was employed for all numerical analysis of methane concentration. The pressure—velocity coupling and scheme Coupled algorithm, and the second-order upwind discretization method were used to solve the mathematical equation. The model thus developed, along with the simplifications adopted, was subjected to a numerical analysis.
3. Results
The analyses performed provided a series of interesting results related to the flow of the air and methane mixture within the dog heading under analysis. It was particularly important to determine the influence of various permeability values of the fractures zone (desorption zone) and the volumetric flow rate of the fresh air supplied on the distribution of methane concentration in the excavated dog heading.
The first stage of the analyses involved determining the trajectories of air flow through the excavated dog heading for all the analyzed permeability values of the fractures zone. This is because the manner in which the air stream (supplied through a forcing air duct) flows through the heading significantly affects the sites of local accumulations of methane in this heading. Since the manner in which the air stream flows does not demonstrate significant changes for the variants under analysis, Figure 6 presents the trajectories of the air flow in the heading under analysis for a fractures zone with permeability of 3.55308·10−8 m2. This variant reflects the parameters present in the actual heading.
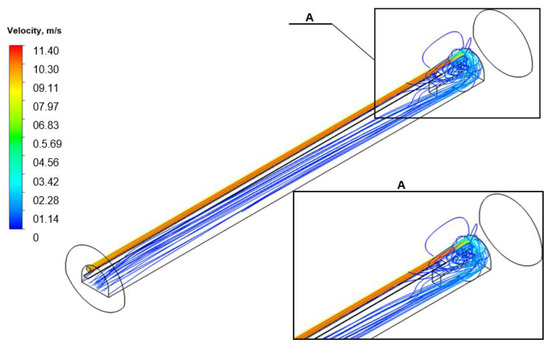
Figure 6.
The trajectories of the air stream flows through the excavated dog heading.
The analysis of the determined trajectories clearly indicates that the greatest flow disturbances occur in the face area of the excavated heading (the mining area). Flowing out of the air duct, the air stream hits the excavated body of coal. After bouncing off, it flows through the entire length of the heading. This leads to the formation of a gyrating flow and recirculation of air in the mine face area. The air stream hitting the coal body results in large curvatures of the current line.
The trajectories presented also indicate that, as a result of taking into account the fractures zone around the excavated heading, small amounts of air pushed into the face of the excavated dog heading may migrate to this zone. This phenomenon should be regarded as dangerous since it may disturb the ventilation process of this heading and lead to low-temperature oxidation of coal in the cracked sidewall area. This, in turn, may cause an endogenous fire to arise [44,62,63]. This is confirmed by the statistics related to spontaneous combustion of coal in the roof and sidewalls of excavated dog headings [64].
The phenomenon of air migration from the dog heading into the fractures zone also leads to reduction of the amount of methane directly released from the front of the excavated face into the heading. The zone with the most intense release of methane from the fractures zone into the excavated dog heading is located at the roof of the heading along approximately 15–20 m, counting from the front of the excavated face (surface). This is confirmed by the results obtained for the release of methane from the fractures zone (the desorption zone) into the excavated dog heading (Figure 7).

Figure 7.
The distribution of methane emission into the excavated dog heading from the fractures zone.
As already mentioned, the analyses were carried out for four different permeability values of the fractures zone and for two volumetric flow rates of the fresh air stream supplied to the heading through an air duct. Therefore, the results obtained were presented with reference to both volumetric flow rates.
3.1. The Results of the Analysis of Methane Distribution and Concentration in the Excavated Dog Heading for the Volumetric Flow Rate of Fresh Air Amounting to 301.44 m3/min
The distributions of methane concentration in vertical sections of the excavated dog heading are presented in Figure 8. They are presented in cross-sections of the heading located every 5.0 m from the exposed surface of excavation (for 14 sections). They include the results for the actual (the first variant) and the three additional permeability values of the fractures zone.
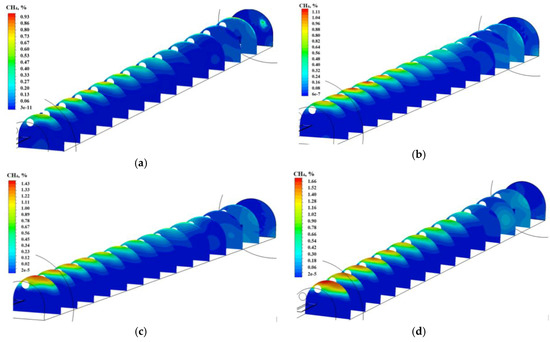
Figure 8.
The concentration and distribution of methane in the vertical planes of the excavated dog heading for different permeability values of the fractures (desorption) zones ((a)—permeability equal to 3.55308·10−8 m2; (b)—permeability equal to 6.37053·10−8 m2; (c)—permeability equal to 1.05197·10−7 m2; (d)—permeability equal to 1.32935·10−7 m2).
It was assumed, according to the results presented in the papers [16,17], that methane is released into this heading along its entire length from the fractures (desorption) zone.
Analyzing the distributions obtained, one can conclude that the permeability of the fractures zone around the excavated dog heading significantly affects the distribution and concentration of methane in this heading. The greater the permeability of the fractures zone, the more methane can be released into the excavated dog heading. Importantly, this release does not only occur from the excavated surface of the heading, but also from the roof and sidewalls.
The analyses conducted showed that the distributions and concentrations of methane in the face area (the mining zone) for the permeability variants under analysis are very similar. With the increasing distance from the mine face area, the methane concentration levels at the roof of the heading become higher. The results obtained confirm that a particularly dangerous place due to the accumulation of methane is the roof zone of the excavated heading.
The distribution of methane concentration in the horizontal section of the excavated dog heading at the height of 2.0 m from the floor for the analyzed permeability variants of the fractures (desorption) zone are presented in Figure 9. Due to the fact that the reserved flow phenomenon occurred during the calculations in the area of the “outlet” boundary condition, the distributions of methane in the distance of up to 5 m from this boundary condition should be deemed as subject to a high calculation error.
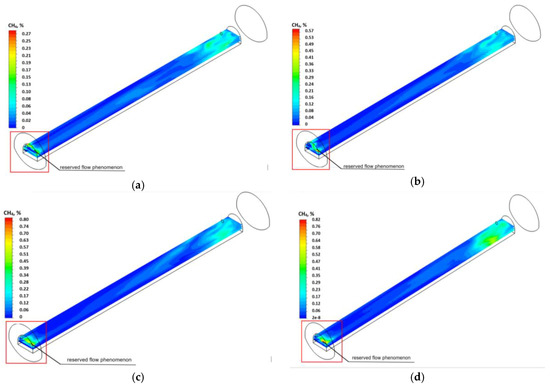
Figure 9.
The concentration and distribution of methane in the horizontal plane at the height of 2.0 m from the floor of the excavated dog heading for different permeability values of the desorption zone ((a)—permeability equal to 3.55308·10−8 m2; (b)—permeability equal to 6.37053·10−8 m2; (c)—permeability equal to 1.05197·10−7 m2; (d)—permeability equal to 1.32935·10−7 m2).
The changing methane concentration values along the entire length of the heading under analysis could be determined thanks to reading out their values from the measurement lines, whose location is shown in Figure 10. This Figure also indicates the measurement points that correspond to the location of the automatic methanometry sensors in the actual heading (according to the Polish regulations in force).
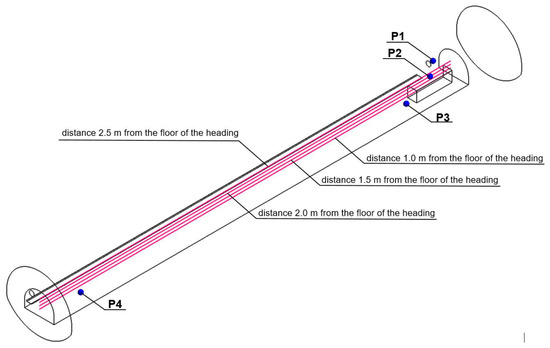
Figure 10.
The distribution of measurement points and lines in the heading under analysis.
Figure 11, Figure 12, Figure 13 and Figure 14 present the methane concentration values along the measurement lines for the analyzed permeability variants of the fractures zone (methane desorption). The results for the measurement lines situated at the heights of 1.0 and 1.5 m from the floor show discontinuities in the reading of methane concentration values due to the presence of a roadheader in this place.
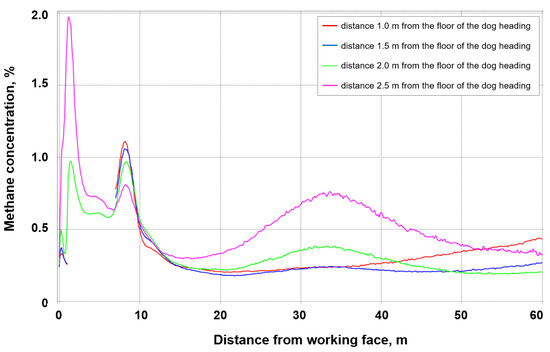
Figure 11.
The concentration and distribution of methane along the measurement lines in the heading with a fractures zone with permeability of 3.55308·10−8 m2.
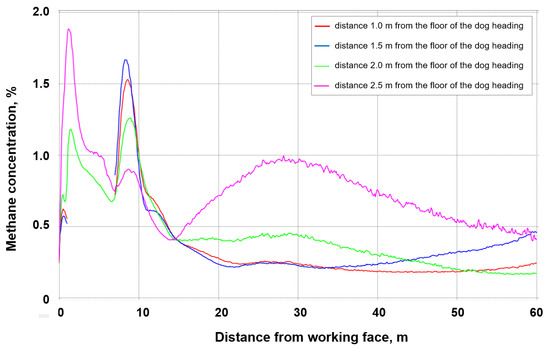
Figure 12.
The concentration and distribution of methane along the measurement lines in the heading with a fractures zone with permeability of 6.37053·10−8 m2.
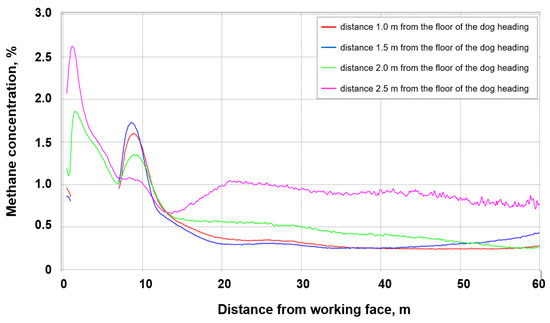
Figure 13.
The concentration and distribution of methane along the measurement lines in the heading with a fractures zone with permeability of 1.05197·10−7 m2.
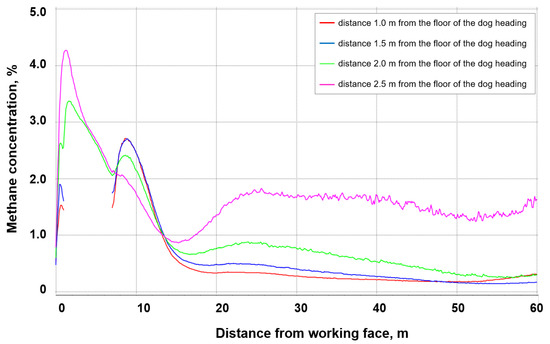
Figure 14.
The concentration and distribution of methane along the measurement lines in the heading with a fractures zone with permeability of 1.32935·10−7 m2.
Analyzing the results obtained, it can be concluded that the highest methane concentration levels are present at the height of 2.0 m from the floor of the excavated heading, along its entire length.
For all the permeability variants of the fractures zone (methane desorption), the concentration of methane decreases along with an increase in the distance from the mined surface to approx. 20th meter of the heading. Around the 20th m, the trend changes and then the methane concentration level decreases again around the 30th m. This increase particularly concerns the measurement line situated at a distance of 2.0 m from the floor of the heading.
For each of the variants, and especially for the first and second ones, there is a significant increase in methane concentration for the highest measurement line (2.5 m from the floor), at a distance of approx. 20–30 m from the face of the heading. This results from the stabilization of methane flow, which—as a gas lighter than air—moves towards the roof of the heading.
This may be explained by the fact that, in the case of low permeability of the fractures zone for these variants, a zone is formed which is characterized by a significantly more intense recirculation flow (the rock mass is less permeable, and the air more intensely hits the sidewalls and face of the working front, thereby forming more vortices). The phenomena of recirculation may lead to the formation of a zone with poorer air exchange and locally increased methane concentration.
3.2. The Results of the Analysis of Methane Distribution and Concentration in the Excavated Dog Heading for the Volumetric Flow rate of Fresh Air Amounting to 361.73 m3/min
Figure 15 shows the distributions of methane concentration in the excavated dog heading on vertical planes located every 5.0 m along the heading, for the volumetric flow rate of air amounting to 361.73 m3/min.
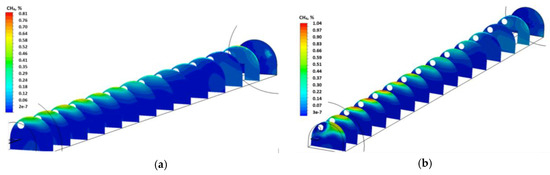
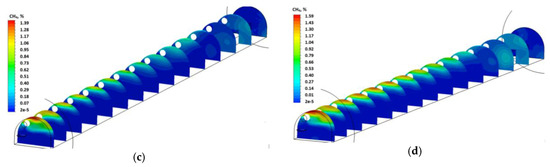
Figure 15.
The concentration and distribution of methane in the vertical planes of the excavated dog heading for different permeability values of the fractures (desorption) zones ((a)—permeability equal to 3.55308·10−8 m2; (b)—permeability equal to 6.37053·10−8 m2; (c)—permeability equal to 1.05197·10−7 m2; (d)—permeability equal to 1.32935·10−7 m2).
Analyzing the distributions presented, it can be concluded that an increase in the volumetric flow rate of the fresh air stream supplied to the excavated dog heading decreases the concentration of methane in this heading. An increase in this rate by 61.29 m3/min. (i.e., approx. 20%) reduced the value of methane concentration by approx. 0.2% for variants 1 and 2, and by approx. 0.4% for variants 3 and 4.
The distribution of methane concentration in the horizontal section of the excavated dog heading at the height of 2.0 m from the floor of the heading for the analyzed permeability variants of the fractures zone are presented in Figure 16. As in the preceding case, the reserved flow phenomenon occurred during the calculations in the area of the “outlet” boundary condition.
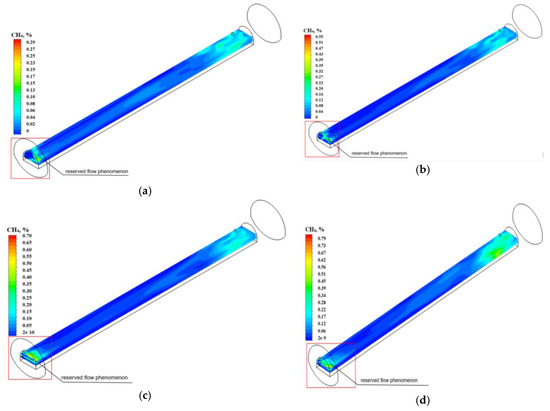
Figure 16.
The concentration and distribution of methane in the horizontal plane at the height of 2.0 m from the floor of the excavated dog heading for different permeability values of the desorption zone ((a)—permeability equal to 3.55308·10−8 m2; (b)—permeability equal to 6.37053·10−8 m2; (c)—permeability equal to 1.05197·10−7 m2; (d)—permeability equal to 1.32935·10−7 m2).
The distributions presented in Figure 16 make it possible to determine the level of methane distribution in mixture with air. A definitely greater accumulation of methane occurs in the face area of the heading, but for higher permeability values of the fractures zone, there are higher concentrations of methane. They also stretch across a larger area.
Figure 17, Figure 18, Figure 19 and Figure 20 present the methane concentration values along the measurement lines for the analyzed permeability variants of the fractures zone (methane desorption). The results for the measurement lines situated at the heights of 1.0 and 1.5 m from the floor show discontinuities in the reading of methane concentration values due to the presence of a roadheader in this place.
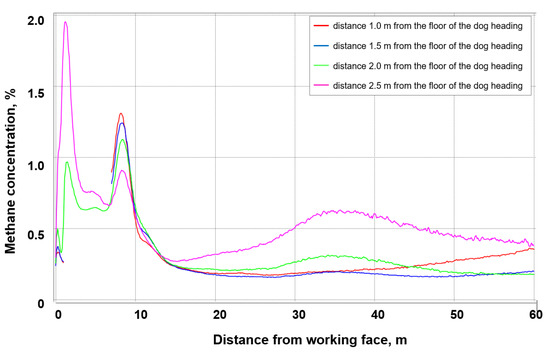
Figure 17.
The concentration and distribution of methane along the measurement lines in the heading with a fractures zone with permeability of 3.55308·10−8 m2.
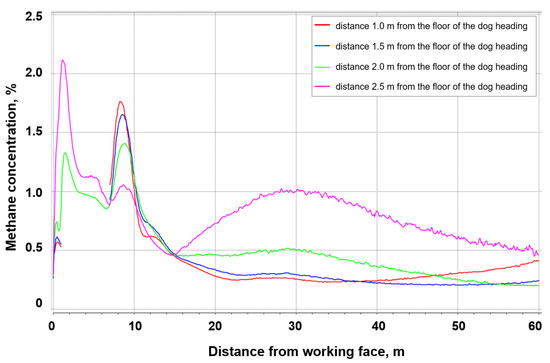
Figure 18.
The concentration and distribution of methane along the measurement lines in the heading with a fractures zone with permeability of 6.37053·10−8 m2.
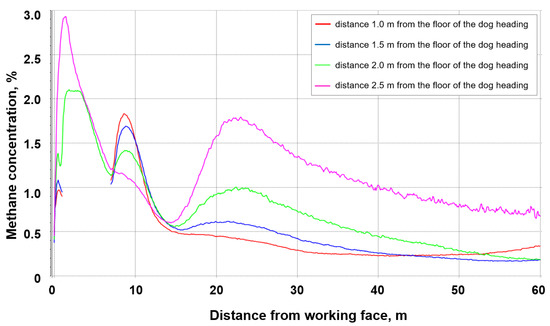
Figure 19.
The concentration and distribution of methane along the measurement lines in the heading with a fractures zone with permeability of 1.05197·10−7 m2.
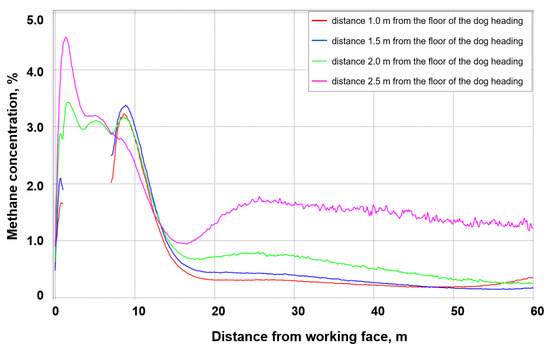
Figure 20.
The concentration and distribution of methane along the measurement lines in the heading with a fractures zone with permeability of 1.32935·10−7 m2.
3.3. Comparison of the Simulation Results and Measurement in Actual Conditions
The precision of the calculation results was assessed by comparing them with the results of measurements performed in real-world underground conditions at the control points. Methane concentration levels in underground coal mines in Poland are measured on a local basis, only in places (points) specified in relevant law regulations.
The location of the control points in the numerical model corresponded to the location of the automatic methanometry sensors (Figure 10).
The comparison of the methane concentration values obtained from the measurements in real conditions and those determined through numerical analysis, for the first variant (corresponds to the parameters of the actual heading), is presented in Table 4.

Table 4.
The comparison of the methane concentration values obtained from the measurements points in underground conditions and those determined from numerical analysis, for the permeability of the fractures zone equal 3.55308·10−8 m2.
The relative error between the values of methane concentration levels from the measurements points in coal mine and those obtained through the numerical research ranges from 2.56% (for the measurement point P2) to 13.21% (for the measurement point P3).
Given that the measurement accuracy of the automatic methanometry sensor is 0.1%, it can be assumed that the model developed, which is nevertheless a kind of simplified reproduction of the actual heading and fractures zone, shows great convergence with the measurement results in real underground coal mines conditions. This shows that the real system under analysis has been well reproduced in the numerical model.
4. Discussion
The methodology developed, the analyses conducted and the results obtained made it possible to determine how the permeability of the fractures zone around the dog heading affects the concentration and distribution of methane in this heading. The analyses were conducted for four permeability values of the fractures zone around the analyzed heading and for two volumetric flow rates of the air supplied to the excavated heading.
Based on the results obtained, it can be concluded that the higher the permeability of the fractures zone in the rock mass around the excavated heading, the more methane migrates from the rock mass into the heading, thereby leading to higher concentrations of this gas. This is due to the fact that the more cracks there are in the rock mass, the more voids it has, so methane can freely migrate into the heading.
Another important point is that large permeability of the fractures zone has practically no influence on the concentration and distribution of methane in the face area of the excavated dog heading (in the area of excavating the front of the heading). This impact is particularly important beyond the mine face area, at a distance of approx. 20–25 m from the front of the face.
The analyses conducted also demonstrated that the higher the permeability of the fractures zone is, the more air can migrate from the heading itself into the rock mass of this zone. The migration of air from the heading into the fractures zone leads to losses in the volumetric flow rate of the air in the heading. As a result, there is less air to reduce (dilute) the concentration of methane in this heading.
The analyses also led to a conclusion that, besides the permeability of the fractures zone in the rock mass, the concentration and distribution of methane in the excavated dog heading is also affected by the height of the volumetric flow rate of the air. For the same values of the volumetric flow rate of air and different permeability values of the fractures zone around the heading, the concentration and distribution of methane decreases along with the decreasing permeability of the fractures zone.
It is also important to note that the oxygen-rich air migrating from the heading into the fractures zone (inside the rock mass) may cause a highly dangerous phenomenon, i.e., low-temperature coal oxidation, which leads to spontaneous combustion of coal. This phenomenon is very common in the roof and sidewalls of excavated headings [62].
In the Authors’ opinion, the results obtained should be widely used for the identification of places in headings where dangerous methane concentrations may accumulate.
In practice, based on such a prognosis, it is possible to choose relevant ventilation parameters of the air stream supplied through a forcing air duct in order to ensure the safety of the mining operations in progress. Choosing the optimum amount of air to be supplied into the heading will help to reduce the concentration of methane to the acceptable limits. This is all the more important because the amount of air supplied to the heading is also related to the costs for the enterprise. It is therefore reasonable to optimize the amount of air supplied.
The results presented should also be used to properly localize the sensors of automatic methanometry. They should be located in areas where the highest methane concentrations are expected. The results obtained indicate that these areas should be practically selected for each heading individually. This is because a change in the heading’s geometry, as well as in the mining and geological conditions in which the heading is made, affects the different distributions of methane concentration.
The overall conclusion is that, for ensuring the safety of excavating dog headings, it is necessary to take into account the fractures zone and the methane desorption zone in forecasting the distribution and concentration of methane in excavated dog headings and other mine headings.
5. Conclusions
The analysis of the actual condition of the rock mass in which mine headings are excavated, unambiguously demonstrates that areas of cracked rock mass form around those headings are a result of the operations performed. The formation of cracks in these zones turns them into porous and permeable media, which may take active part in ventilation processes. These zones may be the source of gas emissions into mine headings. On the other hand, the stream of fresh air may also migrate back to these zones. In both cases, this may disturb the ventilation process of mine headings.
However, the presence of these zones is unquestionable, and their size and permeability depend on a number of factors. In this context, it was therefore reasonable to determine the influence of such a zone present around the excavated dog heading and its permeability on the distribution and concentration of methane in this heading.
In order to determine this impact, a methodology of model-based tests was developed which took into account the presence of such a zone. This new approach to the analysis of ventilation parameters in excavated dog headings made it possible to determine the impact of the fractures zone (methane desorption) on those parameters.
The results clearly indicate that the fractures zones around mine headings have an influence on the ventilation parameters in those headings. The paper presented focuses on analyzing the concentration of methane in the excavated heading and, in this respect, the results obtained confirmed this influence. It is reasonable to broaden the analysis by other ventilation parameters, which is definitely possible thanks to the methodology developed. This is because the results obtained indicate that the impact of the fractures zones and their properties should also be taken into account in other ventilation analyses.
This particularly concerns endogenous fires, whose foci are very often located exactly in the fractures zones of the rock mass around mine headings. Taking these zones into consideration also seems reasonable in other cases, for example during analyses of the distribution of air and air conditioning system, as well as exogenous fires. The method developed made it possible to extend the analyses in this respect and may also be applied to other analyses.
It should also be borne in mind that a very significant influence on the quality of the results obtained is exerted by good identification of the mining, geological and organizational conditions in which the headings are made. In this respect, it is reasonable to make a wider use of automation systems for registering the physical and chemical parameters of the stream of gases flowing through a given heading. It also seems necessary to conduct analyses concerning the determination of permeability for the rocks forming the porous medium around excavated mine headings.
The undeniable success of the works conducted is therefore a significant extension of the knowledge in the field of ventilation of mine headings and tunnel excavations. The methodology developed and the results obtain indicate a new direction for carrying out ventilation analyses in order to ensure optimum working conditions in underground headings. As can be seen, these analyses require a much broader view of the aerological phenomena in the mining industry than before, especially due to the need to take account of, amongst others, the issues related to rock mass mechanics and geotechnical science.
Funding
This article was financed by statutory research (SUBB) of the Faculty of Mining, Safety Engineering and Industrial Automation of the Silesian University of Technology no. 06/030/BKM_19/0048.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Brodny, J. Determining the working characteristic of a friction joint in a yielding support. Arch. Min. Sci. 2010, 55, 733–746. [Google Scholar]
- Brodny, J. Tests of friction joints in mining yielding supports under dynamic load. Arch. Min. Sci. 2011, 56, 303–318. [Google Scholar]
- Brodny, J. Analysis of operation of new construction of the frictional joint with the resistance wedge. Arch. Min. Sci. 2012, 57, 209–227. [Google Scholar]
- Szurgacz, D.; Brodny, J. Tests of Geometry of the Powered Roof Support Section. Energies 2019, 12, 3945. [Google Scholar] [CrossRef]
- Szurgacz, D.; Brodny, J. Analysis of the Influence of Dynamic Load on the Work Parameters of a Powered Roof Support’s Hydraulic Leg. Sustainability 2019, 11, 2570. [Google Scholar] [CrossRef]
- Branny, M.; Filipek, W. Numerical simulation of ventilation of blind drifts with a force- exhaust overlap system in the condition of methan and dust hazards. Arch. Min. Sci. 2008, 53, 221–234. [Google Scholar]
- Kurnia, J.C.; Sasmito, A.P.; Mujumdar, A.S. CFD simulation of methane dispersion and innovative methane management in underground mining faces. Appl. Math. Model. 2014, 38, 3467–3484. [Google Scholar] [CrossRef]
- Brodny, J.; Tutak, M. Forecasting the distribution of methane concentration levels in mine headings by means of model-based tests and in-situ measurements. Arch. Control Sci. 2019, 29, 25–39. [Google Scholar]
- Tutak, M.; Brodny, J. Analysis of the impact of auxiliary ventilation equipment on the distribution and concentration of methane in the tailgate. Energies 2018, 11, 3076. [Google Scholar] [CrossRef]
- Tutak, M.; Brodny, J. Predicting Methane Concentration in Longwall Regions Using Artificial Neural Networks. Int. J. Environ. Res. Public Health 2019, 16, 1406. [Google Scholar] [CrossRef]
- Felka, D.; Brodny, J. Application of Neural-Fuzzy System in Prediction of Methane Hazard. In Proceedings of the International Conference on Intelligent Systems in Production Engineering and Maintenance, Wroclaw, Poland, 28–29 September 2017; Springer: Berlin/Heidelberg, Germany, 2017; pp. 151–160. [Google Scholar]
- Felka, D.; Małachowski, M.; Wróbel, Ł.; Brodny, J. Fuzzy modelling of the methane hazard rate. Beyond databases, architectures and structures. Paving the road to smart data processing and analysis. In Proceedings of the 15th International Conference, BDAS 2019, Ustroń, Poland, 28–31 May 2019; Kozielski, S., Mrozek, D., Kasprowski, P., Małysiak-Mrozek, B., Kostrzewa, D., Eds.; Springer: Cham, Switzerland, 2019; pp. 303–331. [Google Scholar]
- Felka, D.; Brodny, J. Forecasting of methane hazard state in the exploitation wall using neural-fuzzy system. In Proceedings of the Mechatronics 2017—Ideas for Industrial Applications, Gliwice, Poland, 13–15 September 2017; Świder, J., Kciuk, S., Trojnacki, M., Eds.; Springer: Berlin, Germany, 2019; pp. 119–133. [Google Scholar]
- Xiu, Z.; Nie, W.; Yan, J.; Chen, D.; Cai, P.; Liu, Q.; Du, T.; Yang, B. Numerical simulation study on dust pollution characteristics and optimal dust control air flow rates during coal mine production. J. Clean. Prod. 2019, 119197. [Google Scholar] [CrossRef]
- Szlązak, N.; Borowski, D. Badania wydzielania metanu do wyrobisk chodnikowych drążonych kombajnami w pokładach węgla. Górnictwo i Geoinżynieria 2006, 30, 45–56. [Google Scholar]
- Koptoń, H. Method of prognosing absolute methane content in dog headings driven with heading machine in coal mines. Res. Rep. Min. Environ. 2009, 3, 53–72. [Google Scholar]
- Koptoń, H. Mathematical model of prediction of methane emissions into a drift crossing a coal seam. Res. Rep. Min. Environ. 2011, 4, 51–64. [Google Scholar]
- Sanmiquel-Pera, L.; Bascompta, M.; Anticoi, H.F. Analysis of a Historical Accident in a Spanish Coal Mine. Int. J. Environ. Res. Public Health 2019, 16, 3615. [Google Scholar] [CrossRef]
- Log, T.; Pedersen, W.B. A Common Risk Classification Concept for Safety Related Gas Leaks and Fugitive Emissions? Energies 2019, 12, 4063. [Google Scholar] [CrossRef]
- Guo, W.; Guo, M.; Tan, Y.; Bai, E.; Zhao, G. Sustainable Development of Resources and the Environment: Mining-Induced Eco-Geological Environmental Damage and Mitigation Measures—A Case Study in the Henan Coal Mining Area, China. Sustainability 2019, 11, 4366. [Google Scholar] [CrossRef]
- Bumb, A.C.; McKee, C.R.; Bumb, A.C.; McKee, C.R. Gas-Well Testing in the Presence of Desorption for Coalbed Methane and Devonian Shale. Soc. Pet. Eng. 1988. [Google Scholar] [CrossRef]
- Hagoort, J. Fundamentals of Gas Reservoir Engineering; Elsevier: Amsterdam, The Netherlands, 1988. [Google Scholar]
- Harpalani, S.; Schraufnagel, A.R. Nfluence of Matrix Shrinkage and Compressibility on Gas Production from Coalbed Methane Reservoirs’. Soc. Pet. Eng. 1990. [Google Scholar] [CrossRef]
- Moore, T. Coalbed methane: A review. Int. J. Coal Geol. 2012, 101, 36–81. [Google Scholar] [CrossRef]
- Alexeev, A.D.; Feldman, E.P.; Vasilenko, T.A. Methane desorption from a coal-bed. Fuel 2007, 86, 2574–2580. [Google Scholar] [CrossRef]
- Stączek, A.; Simka, A. Boundary index of intensity gas desorption from coal characterizing state threat metanew and reproaches of methane and rocks. Res. Rep. Min. Environ. 2004, 3, 123–142. [Google Scholar]
- Zhao, D.; Gao, T.; Ma, Y.; Feng, Z. Methane Desorption Characteristics of Coal at Different Water Injection Pressures Based on Pore Size Distribution Law. Energies 2018, 11, 2345. [Google Scholar] [CrossRef]
- Prusek, S. Modification of parameters in the Hoek-Brown failure criterion for gate road deformation prediction by means of numerical modeling. Glückauf 2008, 9, 529–534. [Google Scholar]
- Prusek, S.; Walantek, A. Wielkość strefy zniszczenia górotworu wokół wyrobiska korytarzowego w oparciu o kryteria Hoeka-Browna. Prace Naukowe GIG Seria Konferencje 2005, 49, 13–24. [Google Scholar]
- Małkowski, P.; Ostrowski, Ł.; Brodny, J. Analysis of Young’s modulus for Carboniferous sedimentary rocks and its relationship with uniaxial compressive strength using different methods of modulus determination. J. Sustain. Min. 2018, 17, 145–157. [Google Scholar] [CrossRef]
- Janus, J.; Krawczyk, J.; Kruczkowski, J. Comparing numerical simulations with the results of measurements of velocity field distributions in gallery cross-sections. Prace Instytutu Mechaniki Górotworu PAN 2011, 13, 165–182. [Google Scholar]
- Dziurzyński, W.; Gawor, M.; Pałka, T. Graphical presentation of the airflow velocity profile in mine workings. Przegląd Górniczy 2015, 71, 26–33. [Google Scholar]
- Jaszczur, M.; Nowak, R.; Szmyd, J.; Branny, M.; Wodziak, W. Experimental validation of the transport phenomena in T-shape channel flow. J. Phys. Conf. Ser. 2012, 395, 012037. [Google Scholar] [CrossRef]
- Szmyd, J.; Branny, M.; Karch, M.; Wodziak, W.; Jaszczur, M.; Nowak, R. Experimental and Numerical Analysis of the Air Flow in T-Shape Channel Flow. Arch. Min. Sci. 2013, 58, 333–348. [Google Scholar]
- Branny, M.; Jaszczur, M.; Wodziak, W.; Szmyd, J. Experimental and numerical analysis of air flow in a dead-end channel. J. Phys. Conf. Ser. 2016, 745, 032045. [Google Scholar] [CrossRef]
- Herdeen, J.; Sullivan, P. The application of CFD for evaluation of dust suppression and auxiliary ventilation systems used with continuous miners. In Proceedings of the 6th US Mine Ventilation Symposium, Salt Lake City, UT, USA, 21–23 June 1993; SME: Littleton, CO, USA, 1993; pp. 293–297. [Google Scholar]
- Branny, M. Numerical simulation of airflow in blind headings ventilated with jet fans. Arch. Min. Sci. 2003, 48, 425–443. [Google Scholar]
- Kurnia, J.C.; Sasmito, A.P.; Mujumdar, A.S. Simulation of a novel intermittent ventilation system for underground mines. Tunn. Undergr. Space Technol. 2014, 42, 206–215. [Google Scholar] [CrossRef]
- Sasmito, A.P.; Birgersson, E.; Hung, C.; Mujumdar, A.S. Some approaches to improve ventilation system in underground coal mines environment—A computational fluid dynamic study. Tunn. Undergr. Space Technol. 2013, 34, 82–95. [Google Scholar] [CrossRef]
- Wala, A.M.; Vytla, S.; Taylor, C.D.; Huang, G. Mine face ventilation: A comparison of CFD results against benchmark experiments for the CFD code validation. Min. Eng. 2007, 59, 49–57. [Google Scholar]
- Wala, M.A.; Jacob, J.; Turner, D. Experimental study of mine face ventilation system for validation of numerical models. In Mine Ventilation, Proceedings of the North American/Ninth US Mine Ventilation Symposium, Kingston, ON, Canada, 8–12 June 2002; De Souza, E., Ed.; Swets & Zeitlinger: Lisse, The Netherlands, 2002; pp. 191–196. [Google Scholar]
- Wala, M.A.; Stoltz, J.; Jacob, J. Numerical and experimental study of a mine face ventilation system for CFD code validation. In Proceedings of the Seventh International Mine Ventilation Congress, Cracow, Poland, 17–22 June 2001; Wasilewski, S., Ed.; pp. 411–417. [Google Scholar]
- Toraño, J.; Torno, S.; Menendez, M.; Gent, M.; Velasco, J. Models of methane behaviour in auxiliary ventilation of underground coal mining. Int. J. Coal Geol. 2009, 80, 35–43. [Google Scholar] [CrossRef]
- Brodny, J.; Tutak, M. Determination of the Zone with a Particularly High Risk of Endogenous Fires in the Goaves of a Longwall with Caving. J. Appl. Fluid Mech. 2018, 3, 545–553. [Google Scholar] [CrossRef]
- Polska Grupa Górnicza. Available online: https://www.pgg.pl (accessed on 5 November 2019).
- Ordinance of the Minister of Environment on Natural Hazards in Mining Company of 29 January 2013. Available online: http://prawo.sejm.gov.pl/isap.nsf/download.xsp/WDU20130000230/O/D20130230.pdf (accessed on 5 November 2019).
- Ordinance of the Minister of Energy on Detailed Requirements for Conducting Underground Mining Operations of 23 November 2016. Available online: http://www.dziennikustaw.gov.pl/du/2017/1118/1 (accessed on 5 November 2019).
- Veersteg, K.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics. The Finite Volumne Method; Pearson Education: London, UK, 2007. [Google Scholar]
- Ansys Theory Guide. 2011. Available online: http://www.pmt.usp.br/academic/martoran/notasmodelosgrad/ANSYS%20Fluent%20Users%20Guide.pdf (accessed on 15 November 2019).
- Kurnia, J.C.; Xu, P.; Sasmito, A. A novel concept of enhanced gas recovery strategy from ventilation air methane in underground coal mines e A computational investigation. J. Nat. Gas Sci. Eng. 2016, 35, 661–672. [Google Scholar] [CrossRef]
- Tuliszka–Sznitko, E. Wybrane Zagadnienia z Mechaniki Płynów Wirujących; WPP: Poznań, Poland, 2011. [Google Scholar]
- Bogusławski, A.; Drobniak, S.; Tyliszczak, A. Turbulencja–od Losowości do Determinizmu. Instytut Maszyn Cieplnych; Politechnika Częstochowska: Częstochowa, Poland, 2008. [Google Scholar]
- Brady, B.; Brown, E. Rock Mechanics for Underground Mining, 3rd ed.; Springer: Dordrecht, The Netherlands, 2004. [Google Scholar]
- Prusek, S.; Walentek, A. Numerical Modelling the Failure Zone in the Rock Mass around a Heading Based on the Hoek-Brown Criterion; Szkoła Podzemnoj Razrabotki: Dnepropetrowsk, Ukraine, 2007; pp. 95–105. [Google Scholar]
- Kabiesz, J.; Patyńska, R. Investigation of the range and intensity of fracture zones around the passageway galleries. Górnictwo i Geoinżynieria 2009, 33, 263–282. [Google Scholar]
- Małkowski, P.; Niedbalski, Z.; Majcherczyk, T. Roadways’ convergence based on numerical calculation and its verification by “in-situ” research. Górnictwo i Geoinżynieria 2008, 32, 199–215. [Google Scholar]
- Majcherczyk, T.; Małkowski, P. The influence of longwall’s front upon the magnitude of fractures around the working adjacent to the longwall. Wiadomości Górnicze 2003, 54, 20–29. [Google Scholar]
- Barton, N.; Lien, R.; Lunde, J. Engineering clasification of rock masses for the design of tunnel support. Rock Mech. 1974, 6, 189–236. [Google Scholar] [CrossRef]
- Deere, D.U. Technical Description of Rock Cores for Engineering Purpose. Rock Mech. Eng. Geol. 1963, 1, 16–22. [Google Scholar]
- Tarnowski, J. Prognoza gazowości wyrobisk chodnikowych drążonych w pokładach małej i średniej miąższości. Archiwum Górnictwa 1987, 32, 53–72. [Google Scholar]
- Szlązak, J. The determination of a co-efficient of longwall gob permeability. Arch. Min. Sci. 2001, 46, 451–468. [Google Scholar]
- Szurgacz, D.; Sobik, L.; Brodny, J. Integrated method of reducing the threat of endogenous fires in hard coal mines. E3S Web Conf. 2019, 105, 01013. [Google Scholar] [CrossRef]
- Tutak, M.; Brodny, J. Determination of Particular Endogenous Fires Hazard Zones in Goaf with Caving of Longwall. IOP Conf. Ser. Earth Environ. Sci. 2017, 95, 042026. [Google Scholar] [CrossRef]
- State Mining Authority. Available online: http://www.wug.gov.pl/bhp/stan_bhp_w_gornictwie (accessed on 15 November 2019).
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).