Performance Evaluation of Major Asian Airline Companies Using DEA Window Model and Grey Theory
Abstract
1. Introduction
2. Literature Review
2.1. Data Envelopment Analysis
2.2. Grey Forecasting
3. Methodology
3.1. The Selection of DMUs
3.2. The Selection of Inputs and Outputs Variables
- Total Assets: This input variable refers to the sum of all cash, investments, furniture, fixtures, equipment, receivables, intangibles, and any other items of value owned by a person or a business entity.
- Operating expenses: This input variable refers to expenses required to carry out an organization’s day-to-day activities. Relevant items include payroll, sales commissions, employee benefits and pension contributions, transportation and travel, amortization and depreciation, rent, repairs, and taxes. These items are not directly associated with production.
- Fleet: Refers to the number of operating airplanes of an airline company.
- Available seat kilometers (ASKs): This output variable refers to the number of seats available for sale multiplied by the kilometers flown.
- Revenue passenger kilometers (RPKs): This output variable is calculated by multiplying the number of revenue-paying passengers aboard the planes by the distance traveled.
3.3. Malmquist Productivity Index
3.4. DEA Window Model
3.5. GM (1,1)
3.6. Measurement of Forecasting Accuracy
4. Empirical Study Results
4.1. Data Collection
4.2. Pearson Correlation Test
4.3. Grey Forecasting
X(1)(2) = X(0)(1) + X(0)(2) = 402
X(1)(3) = X(0)(1) + X(0)(2) + X(0)(3) = 619
X(1)(4) = X(0)(1) + X(0)(2) + X(0)(3) + X(0)(4) = 855
X(1)(5) = X(0)(1) + X(0)(2) + X(0)(3) + X(0)(4) + X(0)(5) = 1099
4.4. Evaluation of the Forecast Accuracy
4.5. DEA Window Analysis
4.5.1. DEA Window of the Whole Time Period
4.5.2. DEA Window of 3-Year Period
4.6. Performance Evaluation
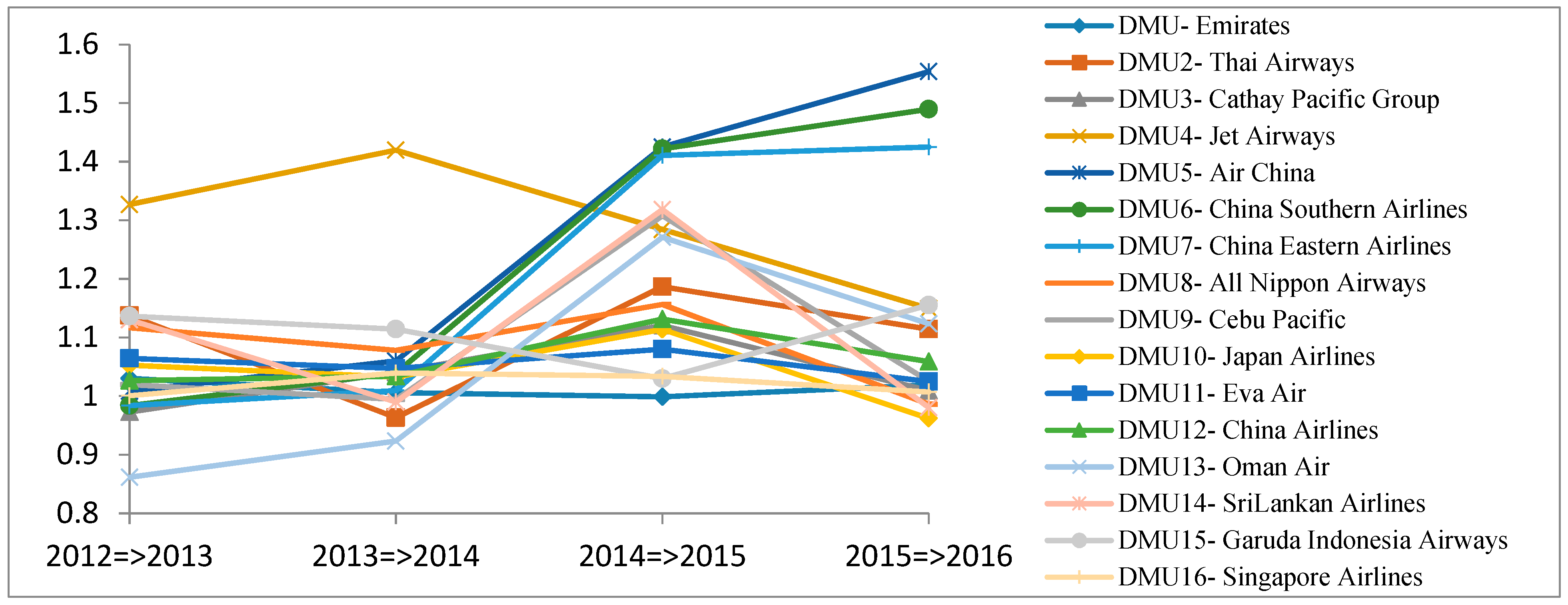
4.6.1. Efficiency Change Index
4.6.2. Technological Change Index
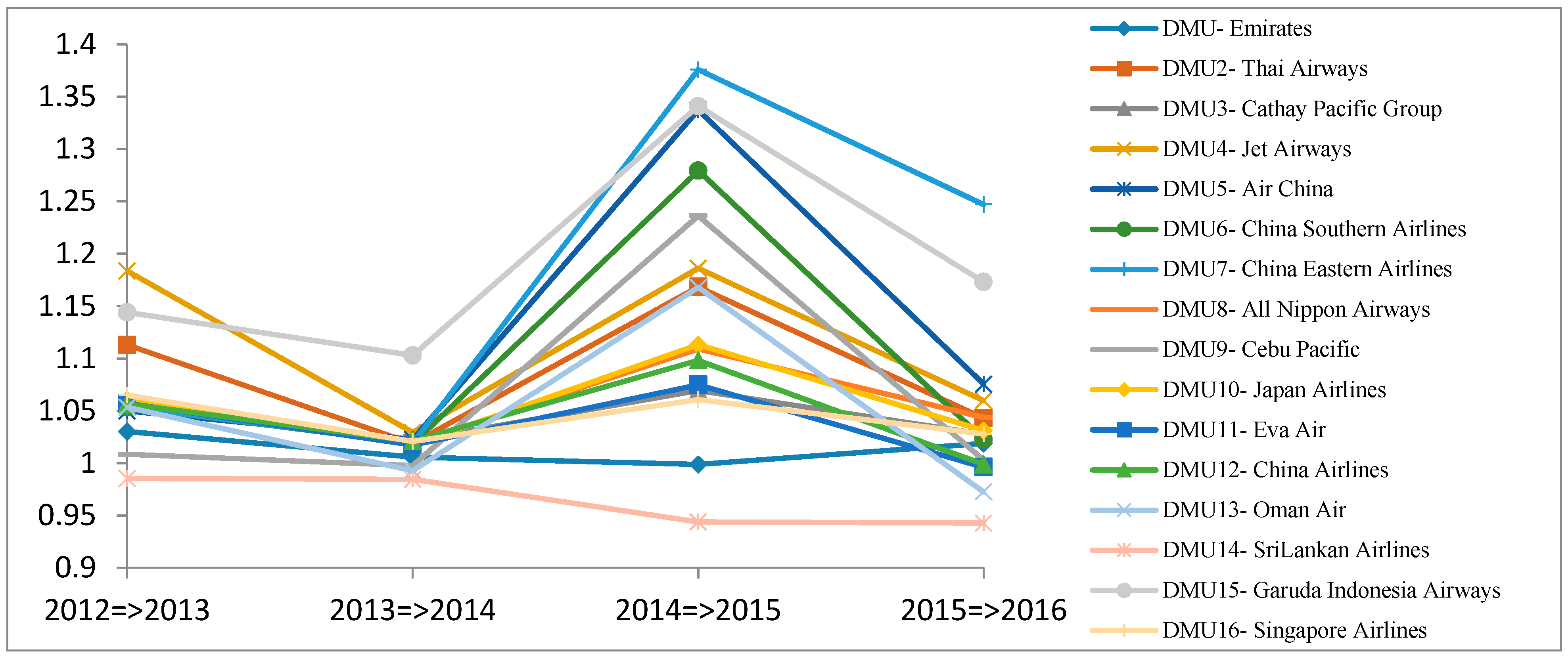
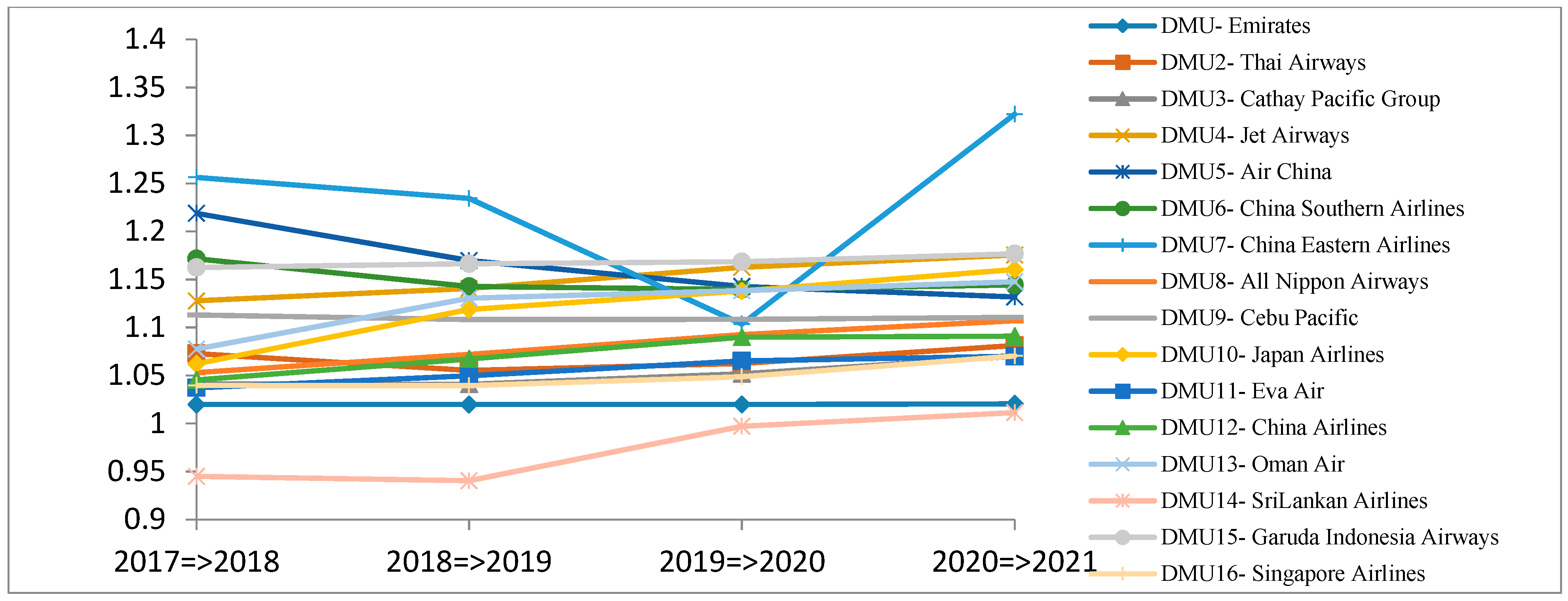
4.6.3. Malmquist Productivity Index
5. Conclusions and Future Research Direction
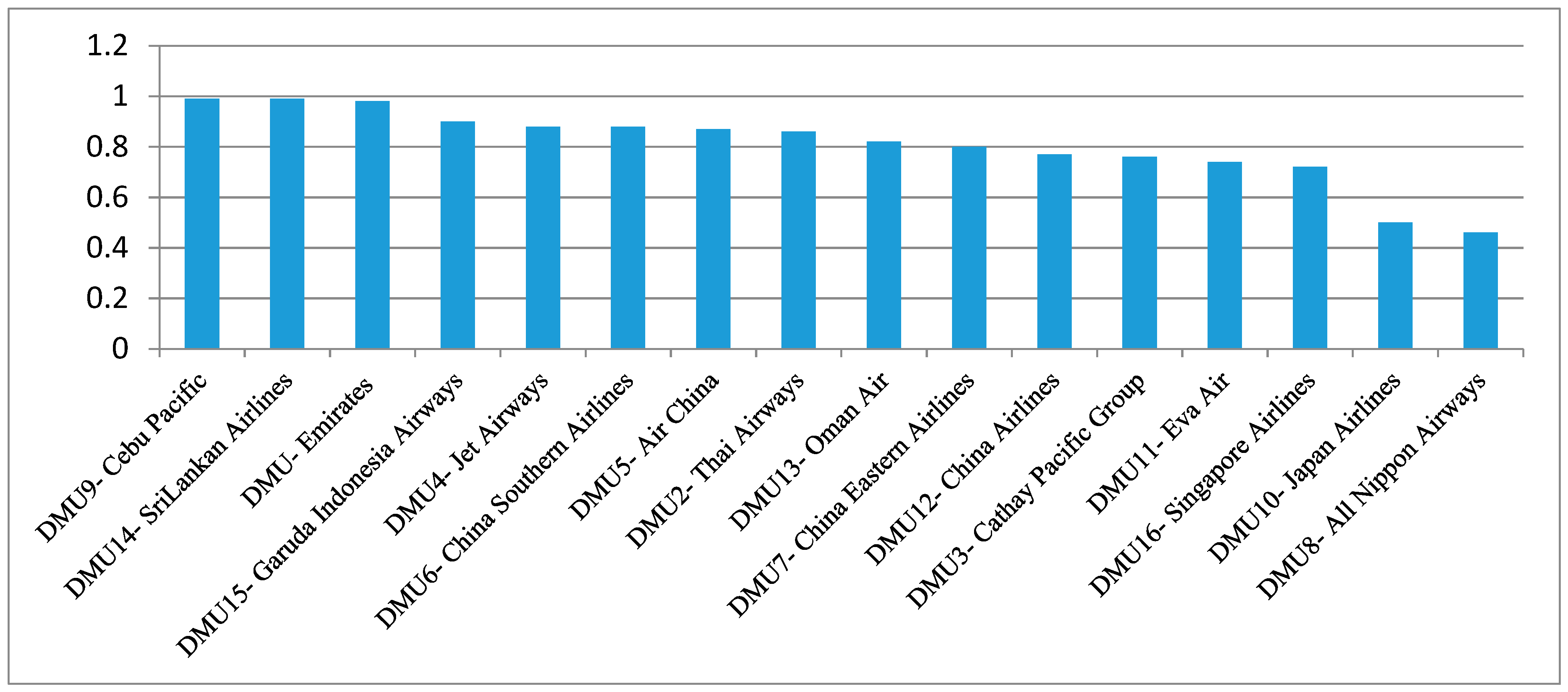
- The DEA Window analysis showed that DMUs performed differently for the time period of 2012 to 2016. Specifically, airline companies, including Emirates, Cebu Pacific, and Sri Lankan Airlines, are in the 1st group with leading performance. Airline companies Thai Airways, Jet Airways, Air China, China Southern Airlines, China Eastern Airlines, Oman Air, Garuda Indonesia, and Cathay Pacific are in the 2nd group, followed by the 3rd group that includes Singapore Airlines, Japan Airlines, and All Nippon Airway. Singapore Airlines and Cathay Pacific used to perform well in the Asia air transport industry, but they have lost their leading positions.
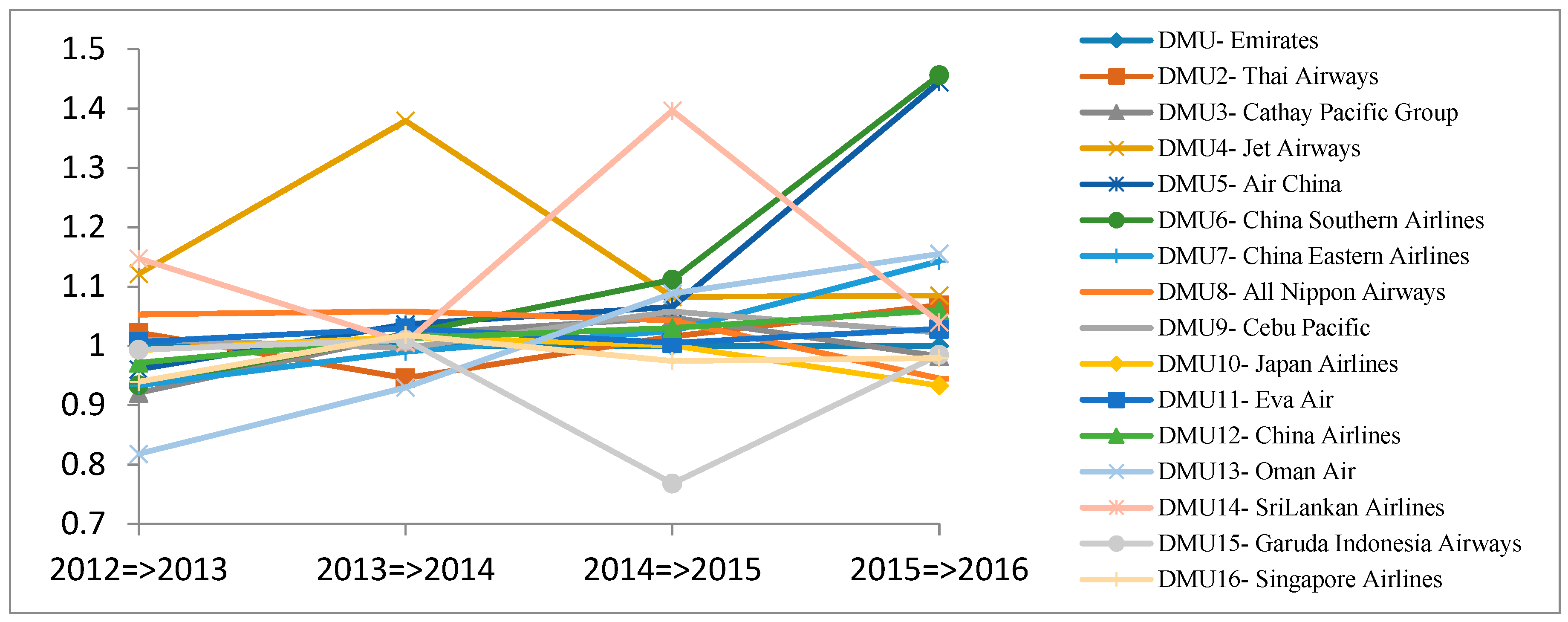
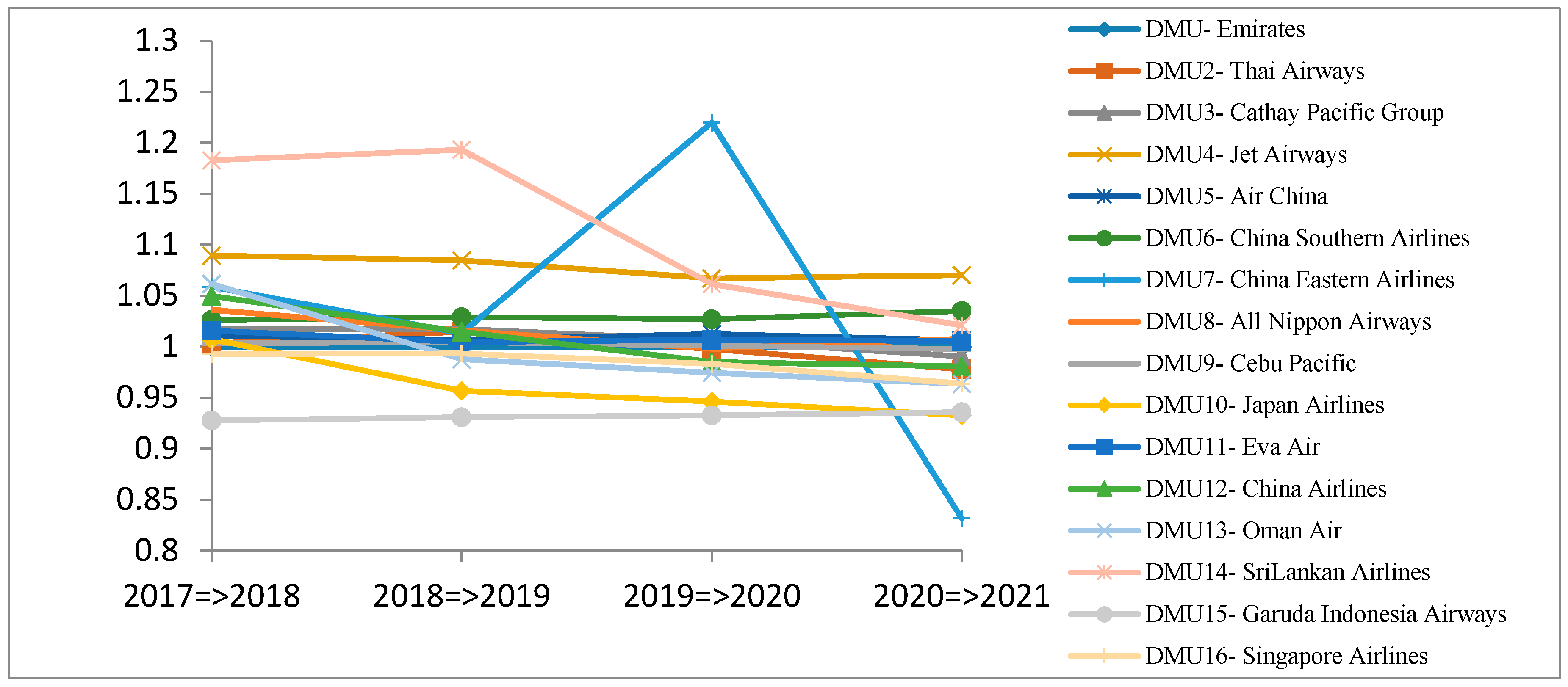
- The Efficiency change indexes (catch-up effect) showed that Air China, China Southern Airlines, China Eastern Airlines, Eva Air, China Airlines, and Oman Air improved their efficiency for the time period 2012 to 2016. Especially, Air China, China, China Eastern Airlines, Eva Air, China Airlines, and Oman Air had a noticeable improvement. Meanwhile, All Nippon Airways and Japan Airlines had declined efficiency. In the time period 2017 to 2021 most airline companies are expected to have declined efficiency; especially China Eastern Airlines and Sir Lanka Airlines, which will experience a dramatic dip on their efficiency.
- The Technological change indexes (Frontier-shift effect) showed that these DMUs failed to improve their technological capabilities in the time period 2012 to 2016. In the time period 2017 to 2021 most of the DMUs are expected to have a stable Technological Change Index, excluding China Eastern Airlines that will have a declined Technological change index in the time period 2017 to 2020, which then recovers in 2021.
- The MPIs showed that Cathay Pacific Group, China Southern Airlines, China Eastern Airlines and Oman Air performed poorly in the first time period 2012 to 2013, but improved their performance in following years from 2013 to 2016. In 2016, airline companies China Southern Airlines, China Eastern Airlines, and Oman Air had greatly improved their MPIs in 2016, while airline companies All Nippon Airways, Japan Airlines, and Sri Lankan Airlines had a declined MPI. In the time period 2017 to 2021, all airline companies are expected to improve their productivity as their MPIs ≥1.
Author Contributions
Funding
Conflicts of Interest
References
- Cederholm, T. The Global Airline Industry Contributes to Economic Development. Available online: https://finance.yahoo.com/news/global-airline-industry-contributes-economic-174012431.html (accessed on 6 November 2017).
- Domínguez, G. Asia’s Aviation Industry Flying High. Available online: http://www.dw.com/en/asias-aviation-industry-flying-high/a-19049866 (accessed on 6 November 2017).
- Boeing Commercial Airplanes. Current Market Outlook 2017–2036. Available online: http://www.boeing.com/resources/boeingdotcom/commercial/market/current-market-outlook-2017/assets/downloads/2017-cmo-6-19.pdf (accessed on 6 November 2017).
- Recio, A. Asia Pacific: The World’s Fastest Growing Aviation Market. Available online: https://knect365.com/gad/article/9a586c65-a7e0-4b8d-85a5-4409bc2fc613/asia-pacific-the-worlds-fastest-growing-aviation-market (accessed on 6 November 2017).
- Welford, R.; Roeth, H.; Bal, S. Airlines in Asia; Issues for Responsible Investors; Responsible Research Pte Ltd.: Singapore, Singapore, 2010. [Google Scholar]
- Distexhe, V.; Perelman, S. Technical Efficiency and Productivity Growth in an Era of Deregulation: The Case of Airlines. Swiss J. Econ. Stat. 1994, 130, 669–689. [Google Scholar]
- Barbot, C.; Costa, A.; Sochirca, E. Airlines performance in the new market context: A comparative productivity and efficiency analysis. J. Air Transp. Manag. 2008, 14, 270–274. [Google Scholar] [CrossRef]
- Barros, C.P.; Peypoch, N. An evaluation of European Airlines’ operational performance. Int. J. Prod. Econ. 2009, 122, 525–533. [Google Scholar] [CrossRef]
- Merkert, R.; Hensher, D.A. The impact of strategic management and fleet planning on airline efficiency: A random effects Tobit model based on DEA efficiency scores. Transp. Res. Part A Policy Pract. 2011, 45, 686–695. [Google Scholar] [CrossRef]
- Assaf, A.G.; Josiassen, A. European vs. U.S. airlines: Performance comparison in a dynamic market. Tour. Manag. 2012, 33, 317–326. [Google Scholar] [CrossRef]
- Arjomandi, A.; Seufert, J.H. An evaluation of the world’s major airlines’ technical and environmental performance. Econ. Model. 2014, 41, 133–144. [Google Scholar] [CrossRef]
- Lee, B.L.; Worthington, A.C. Technical efficiency of mainstream airlines and low cost carriers: New evidence using bootstrap data envelopment analysis truncated. J. Air Transp. Manag. 2014, 38, 15–20. [Google Scholar] [CrossRef]
- Lozano, S.; Gutiérrez, E. A slacks-based network DEA efficiency analysis of European airlines. Transp. Plan. Technol. 2014, 37, 623–637. [Google Scholar] [CrossRef]
- Mallikarjun, S. Efficiency of US airlines: A strategic operating model. J. Air Transp. Manag. 2015, 43, 46–56. [Google Scholar] [CrossRef]
- Tavassoli, M.; Faramarzi, G.R.; Farzipoor Saen, R. Efficiency and effectiveness in airline performance using a SBM-NDEA model in the presence of shared input. J. Air Transp. Manag. 2014, 34, 146–153. [Google Scholar] [CrossRef]
- Deng, J.L. Control problems of Grey Systems. Syst. Control Lett. 1982, 5, 288–294. [Google Scholar]
- Liu, S.; Yang, Y.; Xie, N.; Forrest, J. New progress of Grey System Theory in the new millennium. Grey Syst. Theory Appl. 2016, 6, 2–31. [Google Scholar] [CrossRef]
- Hsu, L. Using improved grey forecasting models to forecast the output of opto-electronics industry. Expert Syst. Appl. 2011, 38, 13879–13885. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, X. Applying the Grey Forecasting Model to the Energy Supply Management Engineering. Syst. Eng. Procedia 2012, 5, 179–184. [Google Scholar] [CrossRef]
- Hamzacebi, C.; Es, H.A. Forecasting the annual electricity consumption of Turkey using an optimized grey model. Energy 2014, 70, 165–171. [Google Scholar] [CrossRef]
- Shaikh, F.; Ji, Q.; Shaikh, P.H.; Mirjat, N.H.; Uqaili, M.A. Forecasting China’s natural gas demand based on optimised nonlinear grey models. Energy 2017, 140, 941–951. [Google Scholar] [CrossRef]
- Liu, S.; Forrest, J. The current developing status on Grey System Theory. J. Grey Syst. 2007, 2, 111–123. [Google Scholar]
- Fethi, M.D.; Jackson, P.M.; Weyman-Jones, T.G. European Airlines: A Stochastic DEA Study of Efficiency with Market Liberalization; Efficiency and Productivity Research Unit, University of Leicester: Leicester, UK, 2001; pp. 1–4. [Google Scholar]
- Rashmi, M. Benchmarking the Operating Efficiency of U.S. Airlines Using DEA. In Proceedings of the Asia Pacific Decisions Sciences Institute’s Annual Meetings, Boston, MA, USA, 19–22 November 2011. [Google Scholar]
- Gramani, M.C. Efficiency decomposition approach: A cross-country airline analysis. Expert Syst. Appl. 2012, 39, 5815–5819. [Google Scholar] [CrossRef]
- Żółtaszek, A.; Pisarek, R. Effectiveness of National Airlines in Europe—The DEA Approach. Folia Oeconomica Stetin. 2016, 16. [Google Scholar] [CrossRef]
- Lee, B.L.; Worthington, A.C. The Relative Efficiency of International, Domestic, and Budget Airlines: Nonparametric Evidence; Griffith University: Brisbane, Australia, 2010. [Google Scholar]
- Jain, R.K.; Natarajan, R. A DEA study of airlines in India. Asia Pac. Manag. Rev. 2015, 20, 285–292. [Google Scholar] [CrossRef]
- Merkert, R.; Williams, G. Determinants of European PSO airline efficiency—Evidence from a semi-parametric approach. J. Air Transp. Manag. 2013, 29, 11–16. [Google Scholar] [CrossRef]
- Fickling, D. The Decline and Fall of Asia’s Airline Enterprises. Available online: https://www.bloomberg.com/gadfly/articles/2017-01-19/ominous-fading-of-air-power-in-hong-kong-and-singapore (accessed on 6 November 2017).
- Layne, N. After Bankruptcy and Makeover, Japan Airlines Returns. Available online: https://www.reuters.com/article/us-japanairlines-ipo/after-bankruptcy-and-makeover-japan-airlines-returns-idUSBRE88H1AP20120918 (accessed on 6 November 2017).
| No | Airline Company | Country | DMU Code |
|---|---|---|---|
| 1 | Emirates | United Arab Emirates | DMU |
| 2 | Thai Airways | Thailand | DMU2 |
| 3 | Cathay Pacific Group | Hong Kong | DMU3 |
| 4 | Jet Airways | India | DMU4 |
| 5 | Air China | China | DMU5 |
| 6 | China Southern Airlines | China | DMU6 |
| 7 | China Eastern Airlines | China | DMU7 |
| 8 | All Nippon Airways | Japan | DMU8 |
| 9 | Cebu Pacific | Philippines | DMU9 |
| 10 | Japan Airlines | Japan | DMU10 |
| 11 | Eva Air | Taiwan | DMU11 |
| 12 | China Airlines | Taiwan | DMU12 |
| 13 | Oman Air | Oman | DMU13 |
| 14 | Sri Lankan Airlines | Sri Lankan | DMU14 |
| 15 | Garuda Indonesia Airways | Indonesia | DMU15 |
| 16 | Singapore Airlines | Singapore | DMU16 |
| Previous Researches | Input Variable | Output Variable |
|---|---|---|
| Fethi et al. [23] | ATK (available tone kilometer), operating cost Nonflight assets | RPK (revenue passenger kilometer), Non passenger revenue |
| Rashmi, M. [24] | Operating cost as percentage of revenue Fixed assets turnover ratio | Passenger Load Factor |
| Gramani, M.C. [25] | Aircraft Fuel, Wages Salaries Benefits Cost per available seatmate | Flight Revenue Flight Income |
| Barbot et al. [7] | Labor (number of core business workers) Fleet (number of operating aircraft) Fuel (in gallons consumed) | ASK (available seat kilometer) RPK (revenue passenger kilometer) RTK (revenue ton kilometers) |
| Żółtaszek & Pisarek [26] | Fleet Number of employee Number of destinations | Total revenue Number of passenger Load factor |
| Lee & Worthington [27] | ATK Operating cost Nonflight assets | RPK Non passenger revenue |
| Jain & Natarajan (2015) [28] | Total Available ton kilometer (ATKM) Operating cost | RPK Non Passenger revenue |
| Assaf & Josiassen [10] | Staff number Total Assets Fuel Operating expenses | RPK Incidental revenues |
| Merkert and Williams [29] | ASK FTE | RPK Realized Departures |
| Fleet | Total Asset | Operating Expenses | RPK | ASK | |
|---|---|---|---|---|---|
| Fleet | 1 | 0.766713 | 0.727115 | 0.724468 | 0.729144 |
| Total Asset | 0.766713 | 1 | 0.967721 | 0.883336 | 0.902239 |
| Operating expenses | 0.727115 | 0.967721 | 1 | 0.896062 | 0.920124 |
| RPK | 0.724468 | 0.883336 | 0.896062 | 1 | 0.997899 |
| ASK | 0.729144 | 0.902239 | 0.920124 | 0.997899 | 1 |
| Fleet | Total Asset | Operating Expenses | RPK | ASK | |
|---|---|---|---|---|---|
| Fleet | 1 | 0.795090 | 0.712596 | 0.704832 | 0.707295 |
| Total Asset | 0.795090 | 1 | 0.952161 | 0.900676 | 0.909052 |
| Operating expenses | 0.712596 | 0.952161 | 1 | 0.916749 | 0.935786 |
| RPK | 0.704832 | 0.900676 | 0.916749 | 1 | 0.997813 |
| ASK | 0.707295 | 0.909052 | 0.935786 | 0.997813 | 1 |
| Fleet | Total Asset | Operating Expenses | RPK | ASK | |
|---|---|---|---|---|---|
| Fleet | 1 | 0.819426 | 0.705601 | 0.705590 | 0.719359 |
| Total Asset | 0.819426 | 1 | 0.958505 | 0.922943 | 0.924216 |
| Operating expenses | 0.705601 | 0.958505 | 1 | 0.937495 | 0.945536 |
| RPK | 0.705590 | 0.922943 | 0.937495 | 1 | 0.995516 |
| ASK | 0.719359 | 0.924216 | 0.945536 | 0.995516 | 1 |
| Fleet | Total Asset | Operating Expenses | RPK | ASK | |
|---|---|---|---|---|---|
| Fleet | 1 | 0.808687 | 0.697654 | 0.729319 | 0.714401 |
| Total Asset | 0.808687 | 1 | 0.958421 | 0.942910 | 0.936114 |
| Operating expenses | 0.697654 | 0.958421 | 1 | 0.940155 | 0.945504 |
| RPK | 0.729319 | 0.942910 | 0.940155 | 1 | 0.99780 |
| ASK | 0.714401 | 0.936114 | 0.945504 | 0.99780 | 1 |
| Fleet | Total Asset | Operating Expenses | RPK | ASK | |
|---|---|---|---|---|---|
| Fleet | 1 | 0.790132 | 0.654574 | 0.739650 | 0.713132 |
| Total Asset | 0.790132 | 1 | 0.951402 | 0.936297 | 0.926245 |
| Operating expenses | 0.654574 | 0.951402 | 1 | 0.928332 | 0.935735 |
| RPK | 0.739650 | 0.936297 | 0.928332 | 1 | 0.997681 |
| ASK | 0.713132 | 0.926245 | 0.935735 | 0.997681 | 1 |
| DMU | Input Variables | Output Variables | |||
|---|---|---|---|---|---|
| Fleet (N) | Total Asset (M) | Operating Expenses (M) | RPK (M) | ASK (M) | |
| 2012 | 197 | 25,810 | 19,132 | 188,618 | 236,645 |
| 2013 | 205 | 27,663 | 21,339 | 215,353 | 271,133 |
| 2014 | 217 | 30,319 | 22,577 | 235,498 | 295,740 |
| 2015 | 236 | 32,446 | 20,885 | 255,176 | 333,726 |
| 2016 | 244 | 33,095 | 22,496 | 276,608 | 368,102 |
| k (year) | Ẍ(1)(k) | Value | Ẍ(0)(k) | Value |
|---|---|---|---|---|
| 0 (2012) | Ẍ(1)(0) | 197 | Ẍ(0)(0) | 197 |
| 1 (2013) | Ẍ(1)(1) | 402.549 | Ẍ(0)(1) | 205.549 |
| 2 (2014) | Ẍ(1)(2) | 620.8188 | Ẍ(0)(2) | 218.2698 |
| 3 (2015) | Ẍ(1)(3) | 852.5966 | Ẍ(0)(3) | 231.7778 |
| 4 (2016) | Ẍ(1)(4) | 1098.718 | Ẍ(0)(4) | 246.1219 |
| 5 (2017) | Ẍ(1)(5) | 1360.072 | Ẍ(0)(5) | 261.3536 |
| 6 (2018) | Ẍ(1)(6) | 1637.6 | Ẍ(0)(6) | 277.528 |
| 7 (2019) | Ẍ(1)(7) | 1932.303 | Ẍ(0)(7) | 294.7034 |
| 8 (2020) | Ẍ(1)(8) | 2245.245 | Ẍ(0)(8) | 312.9417 |
| 9 (2021) | Ẍ(1)(9) | 2577.554 | Ẍ(0)(9) | 332.3087 |
| DMU | Average MAPE | DMU | Average MAPE |
|---|---|---|---|
| DMU | 0.264% | DMU9 | 0.370% |
| DMU2 | 0.202% | DMU10 | 0.161% |
| DMU3 | 0.136% | DMU11 | 0.393% |
| DMU4 | 0.295% | DMU12 | 0.256% |
| DMU5 | 0.266% | DMU13 | 0.454% |
| DMU6 | 0.263% | DMU14 | 0.327% |
| DMU7 | 0.341% | DMU15 | 0.318% |
| DMU8 | 0.261% | DMU16 | 0.350% |
| DMU | 2012 | 2013 | 2014 | 2015 | 2016 | Average | Rank |
|---|---|---|---|---|---|---|---|
| DMU | 0.86087 | 0.93750 | 0.96418 | 0.99010 | 1 | 0.95053 | 3 |
| DMU2 | 0.71509 | 0.75317 | 0.72810 | 0.83631 | 0.92865 | 0.79226 | 8 |
| DMU3 | 0.63944 | 0.64499 | 0.66169 | 0.77884 | 0.80489 | 0.70597 | 13 |
| DMU4 | 0.60787 | 0.65282 | 0.75102 | 0.97636 | 1 | 0.79761 | 6 |
| DMU5 | 0.66655 | 0.69015 | 0.73300 | 0.88035 | 0.99459 | 0.79293 | 7 |
| DMU6 | 0.69301 | 0.69677 | 0.73283 | 0.90591 | 1 | 0.80570 | 4 |
| DMU7 | 0.63906 | 0.63079 | 0.66623 | 0.80734 | 0.93072 | 0.73483 | 11 |
| DMU8 | 0.34404 | 0.37457 | 0.41181 | 0.49835 | 0.48914 | 0.42358 | 16 |
| DMU9 | 0.99999 | 0.99999 | 0.88483 | 1 | 1 | 0.97696 | 2 |
| DMU10 | 0.40257 | 0.42807 | 0.44737 | 0.51833 | 0.49747 | 0.45876 | 15 |
| DMU11 | 0.71147 | 0.71166 | 0.67782 | 0.76469 | 0.79001 | 0.73113 | 12 |
| DMU12 | 0.74181 | 0.70856 | 0.67111 | 0.78235 | 0.83201 | 0.74717 | 10 |
| DMU13 | 0.83861 | 0.75311 | 0.71826 | 0.79151 | 0.82447 | 0.78519 | 9 |
| DMU14 | 0.95531 | 0.99999 | 1 | 1 | 1 | 0.99106 | 1 |
| DMU15 | 0.67835 | 0.72651 | 0.76804 | 0.87253 | 0.96227 | 0.80154 | 5 |
| DMU16 | 0.73829 | 0.71510 | 0.67015 | 0.67498 | 0.68741 | 0.69719 | 14 |
| Windows | Years |
|---|---|
| 1st Window | 2012–2014 |
| 2nd Window | 2013–2015 |
| 3rd Window | 2014–-2016 |
| DMU | 2012 | 2013 | 2014 | 2015 | 2016 | Average | Rank |
|---|---|---|---|---|---|---|---|
| Emirates | 0.94 | 1.00 | 1.00 | ||||
| 0.98 | 1.00 | 1.00 | |||||
| 0.96 | 0.99 | 1.00 | |||||
| Average | 0.94 | 0.99 | 0.99 | 1.00 | 1.00 | 0.98 | 3 |
| Thai Airways | 0.86 | 0.92 | 0.89 | ||||
| 0.79 | 0.76 | 0.87 | |||||
| 0.73 | 0.84 | 0.93 | |||||
| Average | 0.86 | 0.85 | 0.79 | 0.85 | 0.93 | 0.86 | 8 |
| Cathay Pacific Group | 0.77 | 0.78 | 0.80 | ||||
| 0.66 | 0.67 | 0.79 | |||||
| 0.66 | 0.78 | 0.80 | |||||
| Average | 0.77 | 0.72 | 0.71 | 0.79 | 0.80 | 0.76 | 11 |
| Jet Airways | 0.78 | 0.86 | 1.00 | ||||
| 0.73 | 0.83 | 1.00 | |||||
| 0.75 | 0.98 | 1.00 | |||||
| Average | 0.78 | 0.79 | 0.86 | 0.99 | 1.00 | 0.88 | 5 |
| Air China | 0.84 | 0.87 | 0.92 | ||||
| 0.73 | 0.78 | 0.95 | |||||
| 0.73 | 0.88 | 0.99 | |||||
| Average | 0.84 | 0.80 | 0.81 | 0.92 | 0.99 | 0.87 | 7 |
| China Southern Airlines | 0.83 | 0.87 | 0.93 | ||||
| 0.73 | 0.78 | 0.98 | |||||
| 0.73 | 0.91 | 1.00 | |||||
| Average | 0.83 | 0.80 | 0.81 | 0.94 | 1.00 | 0.88 | 6 |
| China Eastern Airlines | 0.77 | 0.77 | 0.85 | ||||
| 0.65 | 0.71 | 0.88 | |||||
| 0.67 | 0.81 | 0.93 | |||||
| Average | 0.77 | 0.71 | 0.74 | 0.84 | 0.93 | 0.80 | 10 |
| All Nippon Airways | 0.42 | 0.46 | 0.51 | ||||
| 0.39 | 0.43 | 0.52 | |||||
| 0.41 | 0.50 | 0.49 | |||||
| Average | 0.42 | 0.43 | 0.45 | 0.51 | 0.49 | 0.46 | 16 |
| Cebu Pacific | 1.00 | 1.00 | 1.00 | ||||
| 1.00 | 0.89 | 1.00 | |||||
| 0.91 | 1.00 | 1.00 | |||||
| Average | 1.00 | 1.00 | 0.93 | 1.00 | 1.00 | 0.99 | 2 |
| Japan Airlines | 0.49 | 0.53 | 0.55 | ||||
| 0.47 | 0.47 | 0.54 | |||||
| 0.45 | 0.52 | 0.50 | |||||
| Average | 0.49 | 0.50 | 0.49 | 0.53 | 0.50 | 0.50 | 15 |
| Eva Air | 0.73 | 0.72 | 0.75 | ||||
| 0.72 | 0.69 | 0.77 | |||||
| 0.68 | 0.76 | 0.79 | |||||
| Average | 0.73 | 0.72 | 0.71 | 0.77 | 0.79 | 0.74 | 13 |
| China Airlines | 0.77 | 0.74 | 0.79 | ||||
| 0.73 | 0.68 | 0.79 | |||||
| 0.67 | 0.78 | 0.83 | |||||
| Average | 0.77 | 0.74 | 0.71 | 0.79 | 0.83 | 0.77 | 12 |
| Oman Air | 0.93 | 0.84 | 0.80 | ||||
| 0.76 | 0.72 | 0.80 | |||||
| 0.73 | 0.79 | 0.82 | |||||
| Average | 0.93 | 0.80 | 0.75 | 0.80 | 0.82 | 0.82 | 9 |
| SriLankan Airlines | 0.96 | 1.00 | 1.00 | ||||
| 1.00 | 1.00 | 1.00 | |||||
| 1.00 | 1.00 | 1.00 | |||||
| Average | 0.96 | 1.00 | 1.00 | 1.00 | 1.00 | 0.99 | 1 |
| Garuda Indonesia Airways | 0.88 | 0.95 | 1.00 | ||||
| 0.78 | 0.93 | 0.93 | |||||
| 0.77 | 0.87 | 0.96 | |||||
| Average | 0.88 | 0.86 | 0.90 | 0.90 | 0.96 | 0.90 | 4 |
| Singapore Airlines | 0.77 | 0.75 | 0.73 | ||||
| 0.74 | 0.69 | 0.70 | |||||
| 0.67 | 0.67 | 0.69 | |||||
| Average | 0.77 | 0.74 | 0.70 | 0.69 | 0.69 | 0.72 | 14 |
| DMU | 2012–2013 | 2013–2014 | 2014–2015 | 2015–2016 | Average |
|---|---|---|---|---|---|
| DMU | 1 | 1 | 1 | 1 | 1 |
| DMU2 | 1.022144 | 0.945607 | 1.015684 | 1.068443 | 1.01296 |
| DMU3 | 0.920699 | 1.018862 | 1.047909 | 0.982322 | 0.99244 |
| DMU4 | 1.121351 | 1.379235 | 1.082651 | 1.084630 | 1.16696 |
| DMU5 | 0.960345 | 1.036379 | 1.065577 | 1.444541 | 1.12671 |
| DMU6 | 0.933864 | 1.020124 | 1.111289 | 1.456444 | 1.13043 |
| DMU7 | 0.933364 | 0.990430 | 1.025294 | 1.142754 | 1.02296 |
| DMU8 | 1.052998 | 1.058232 | 1.042745 | 0.945054 | 1.02475 |
| DMU9 | 1.011201 | 0.996441 | 1.057971 | 1.022223 | 1.02195 |
| DMU10 | 0.992907 | 1.014996 | 1.000655 | 0.932986 | 0.98538 |
| DMU11 | 1.006890 | 1.029436 | 1.004832 | 1.028759 | 1.01747 |
| DMU12 | 0.971682 | 1.012760 | 1.030212 | 1.059947 | 1.01865 |
| DMU13 | 0.817895 | 0.929828 | 1.088509 | 1.155010 | 0.99781 |
| DMU14 | 1.147281 | 1.005244 | 1.396500 | 1.039999 | 1.14725 |
| DMU15 | 0.993408 | 1.010125 | 0.768008 | 0.984767 | 0.93907 |
| DMU16 | 0.939675 | 1.018399 | 0.974501 | 0.979387 | 0.97799 |
| DMU | 2012–2013 | 2013–2014 | 2014–2015 | 2015–2016 | Average |
|---|---|---|---|---|---|
| DMU | 1.030308 | 1.005838 | 0.998817 | 1.018876 | 1.01345 |
| DMU2 | 1.112939 | 1.018684 | 1.168310 | 1.042989 | 1.08573 |
| DMU3 | 1.056719 | 1.021641 | 1.069319 | 1.027652 | 1.04383 |
| DMU4 | 1.183521 | 1.029377 | 1.186115 | 1.059748 | 1.11469 |
| DMU5 | 1.049983 | 1.022626 | 1.337322 | 1.075550 | 1.12137 |
| DMU6 | 1.053584 | 1.018625 | 1.279385 | 1.022795 | 1.09359 |
| DMU7 | 1.053960 | 1.018991 | 1.375833 | 1.247085 | 1.17396 |
| DMU8 | 1.060404 | 1.018654 | 1.109026 | 1.043595 | 1.05792 |
| DMU9 | 1.008379 | 0.997715 | 1.236168 | 1.002991 | 1.06131 |
| DMU10 | 1.060398 | 1.017276 | 1.113167 | 1.031216 | 1.05551 |
| DMU11 | 1.057101 | 1.017305 | 1.074853 | 0.996026 | 1.03632 |
| DMU12 | 1.056490 | 1.020859 | 1.098148 | 0.998859 | 1.04358 |
| DMU13 | 1.053349 | 0.992803 | 1.167868 | 0.972591 | 1.04665 |
| DMU14 | 0.985295 | 0.984564 | 0.943874 | 0.942748 | 0.96412 |
| DMU15 | 1.143990 | 1.102972 | 1.341016 | 1.173203 | 1.19029 |
| DMU16 | 1.064881 | 1.020747 | 1.060730 | 1.028048 | 1.04360 |
| DMU | 2012–2013 | 2013–2014 | 2014–2015 | 2015–2016 | Average |
|---|---|---|---|---|---|
| DMU | 1.030308 | 1.005838 | 0.998817 | 1.018876 | 1.01345 |
| DMU2 | 1.137584 | 0.963275 | 1.186634 | 1.114373 | 1.10046 |
| DMU3 | 0.972920 | 1.040911 | 1.120549 | 1.009486 | 1.03596 |
| DMU4 | 1.327143 | 1.419753 | 1.284148 | 1.149435 | 1.29512 |
| DMU5 | 1.008346 | 1.059828 | 1.425019 | 1.553675 | 1.26171 |
| DMU6 | 0.983904 | 1.039124 | 1.421766 | 1.489644 | 1.23360 |
| DMU7 | 0.983728 | 1.009239 | 1.410633 | 1.425112 | 1.20717 |
| DMU8 | 1.116603 | 1.077972 | 1.156431 | 0.986254 | 1.08431 |
| DMU9 | 1.019674 | 0.994165 | 1.307830 | 1.025280 | 1.08673 |
| DMU10 | 1.052876 | 1.032531 | 1.113897 | 0.962110 | 1.04035 |
| DMU11 | 1.064385 | 1.047250 | 1.080047 | 1.024671 | 1.05408 |
| DMU12 | 1.026573 | 1.033884 | 1.131325 | 1.058738 | 1.06263 |
| DMU13 | 0.861529 | 0.923136 | 1.271235 | 1.123352 | 1.04481 |
| DMU14 | 1.130409 | 0.989726 | 1.318121 | 0.980457 | 1.10467 |
| DMU15 | 1.136449 | 1.114140 | 1.029911 | 1.155331 | 1.10895 |
| DMU16 | 1.000641 | 1.039527 | 1.033682 | 1.006857 | 1.02017 |
| Average | 1.053317 | 1.049394 | 1.205628 | 1.130228 | 1.10964 |
| DMU | 2017–2018 | 2018–2019 | 2019–2020 | 2020–2021 | Average |
|---|---|---|---|---|---|
| DMU | 1.019948 | 1.019883 | 1.019828 | 1.020415 | 1.020019 |
| DMU2 | 1.076143 | 1.070901 | 1.060145 | 1.057297 | 1.066121 |
| DMU3 | 1.059506 | 1.059120 | 1.058745 | 1.059874 | 1.059311 |
| DMU4 | 1.228791 | 1.237375 | 1.240584 | 1.257866 | 1.241154 |
| DMU5 | 1.232024 | 1.177755 | 1.157005 | 1.139002 | 1.176446 |
| DMU6 | 1.202669 | 1.175979 | 1.170434 | 1.184397 | 1.183370 |
| DMU7 | 1.330209 | 1.251003 | 1.346116 | 1.099687 | 1.256754 |
| DMU8 | 1.091076 | 1.089263 | 1.090702 | 1.115797 | 1.096709 |
| DMU9 | 1.116606 | 1.113391 | 1.109818 | 1.108030 | 1.111961 |
| DMU10 | 1.070202 | 1.070493 | 1.076761 | 1.082520 | 1.074994 |
| DMU11 | 1.053492 | 1.054542 | 1.072725 | 1.076058 | 1.064204 |
| DMU12 | 1.097660 | 1.083014 | 1.073699 | 1.070021 | 1.081098 |
| DMU13 | 1.143971 | 1.116903 | 1.109269 | 1.105917 | 1.119015 |
| DMU14 | 1.117836 | 1.122267 | 1.058430 | 1.032547 | 1.082770 |
| DMU15 | 1.078566 | 1.085943 | 1.090054 | 1.101419 | 1.088996 |
| DMU16 | 1.032213 | 1.032688 | 1.031053 | 1.031685 | 1.031910 |
| Average | 1.121932 | 1.110032 | 1.110335 | 1.096408 | 1.109677 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.-N.; Tsai, T.-T.; Hsu, H.-P.; Nguyen, L.-H. Performance Evaluation of Major Asian Airline Companies Using DEA Window Model and Grey Theory. Sustainability 2019, 11, 2701. https://doi.org/10.3390/su11092701
Wang C-N, Tsai T-T, Hsu H-P, Nguyen L-H. Performance Evaluation of Major Asian Airline Companies Using DEA Window Model and Grey Theory. Sustainability. 2019; 11(9):2701. https://doi.org/10.3390/su11092701
Chicago/Turabian StyleWang, Chia-Nan, Tsang-Ta Tsai, Hsien-Pin Hsu, and Le-Hoang Nguyen. 2019. "Performance Evaluation of Major Asian Airline Companies Using DEA Window Model and Grey Theory" Sustainability 11, no. 9: 2701. https://doi.org/10.3390/su11092701
APA StyleWang, C.-N., Tsai, T.-T., Hsu, H.-P., & Nguyen, L.-H. (2019). Performance Evaluation of Major Asian Airline Companies Using DEA Window Model and Grey Theory. Sustainability, 11(9), 2701. https://doi.org/10.3390/su11092701





