Abstract
The New Zealand housing sector is experiencing rapid growth that has a significant impact on society, the economy, and the environment. In line with the growth, the housing market for both residential and business purposes has been booming, as have house prices. To sustain the housing development, it is critical to accurately monitor and predict housing prices so as to support the decision-making process in the housing sector. This study is devoted to applying a mathematical method to predict housing prices. The forecasting performance of two types of models: autoregressive integrated moving average (ARIMA) and multiple linear regression (MLR) analysis are compared. The ARIMA and regression models are developed based on a training-validation sample method. The results show that the ARIMA model generally performs better than the regression model. However, the regression model explores, to some extent, the significant correlations between house prices in New Zealand and the macro-economic conditions.
1. Introduction
As climate change has become a hot issue, many countries have begun to pay greater attention to sustainable development. Sustainable urban development includes sustainability in social, economic, and environmental facets [1,2,3]. As one of the most critical sectors in urban development, housing construction is one of the largest consumers of resources (e.g., water, mineral, and fossil fuel) and one of the largest producers of pollution. Therefore, it potentially plays an important role in sustainability. In New Zealand, the housing sector is experiencing rapid growth that has a significant impact on society, the economy, and the environment. Following the growth, the housing market for both residential and business purposes has been booming, as have house prices, especially in Auckland [4]. The stretched housing valuations can lead to an overbuild of housing that wastes resources and increases household indebtedness, which decreases wealth. According to [5], the further expansion of the building sector beyond the adaptive capacity of the economy may waste resources. In fact, the uncontrollable housing prices may have a negative effect on the long-term macro-economic development. The boom-and-bust cycles in housing prices may significantly harm economic stability, which became evident during the Subprime Mortgage Crisis of 2007/2008 [6]. During times of economic growth, an increasing demand for housing pushes up investment in residential properties and employment, and thus reinforces aggregate demand. In the reverse phase, falling employment and income decreases demand for housing, weakens residential investment and reduces prices.
Furthermore, housing prices in New Zealand, especially in Auckland, are amongst the highest in the world. As the largest city in New Zealand, Auckland currently has significant housing affordability challenges [7]. The affordability issue for first-time buyers strongly impacts the quality of life in urban populations. In addition, the housing market plays an important role in New Zealand’s economy and its financial system, and the ratio of the value of housing to total household assets is higher than in other advanced economies [8]. Housing debt is nearly 30 percent of the value of housing stock, and mortgages account for more than half of total bank lending in New Zealand; this poses a significant risk to the housing market and the New Zealand banking system [4]. This will bring both financial imbalances in New Zealand’s economy and macro-economic effects from the correction of these imbalances.
Under such circumstances, it is meaningful to further explore the trend of housing prices in New Zealand. This study aims to provide an effective method to model the house prices in Auckland. The method will allow for properly monitoring housing prices to help assess the sustainability of the housing market and properly controlling the sector so as to improve the performance of the housing sector in sustainable urban development. Additionally, the method and analysis may assist government administration in better understanding the trend of housing prices in New Zealand so they can, accordingly, formulate policies on sustainable urban planning.
Both autoregressive integrated moving average (ARIMA) and multiple linear regression (MLR) are applied to model the house prices of Auckland and compare their forecasting performance to identify which model better fit the price trend. Owing to the merits of the ARIMA technique, it is preferred over structural models of residential property markets, particularly for short-term forecasts. The ARIMA model comprises three important components: the degree of integration (the number of differences requested to obtain a stationary series), lagged values of the variable of interest (the auto-regressive component), and lagged values of the error term (the moving average component) [9]. Furthermore, the multiple linear regression analysis can also help to explore the relationship between the house price in Auckland and the macro-economic indicators such as mortgage rate, employment, and population.
The study is structured as follows. Section 2 presents the literature review. Section 3 introduces ARIMA forecasting methods and multiple linear regression (MLR) analysis. The application of the ARIMA approach on Auckland housing prices is presented in Section 4. Section 5 illustrates the implementation of multiple regression analysis on Auckland house prices. The comparison of the two methods is presented in Section 6. The discussion and conclusion are shown in the final section.
2. Literature Review
2.1. Sustainability in Housing Construction
Sustainable development satisfies the requirements of the current generation but does not satisfy the needs of future generations [10,11]. In this study, sustainable development is defined as development that supports social, economic, and environmental requirements. The purpose is that development should make efforts to generate integral quality associated with social, economic, and environmental performance [12]. According to [13], sustainability is an intersection of three different pillars: economic, environmental, and social. During building development, economic sustainability is usually adequately addressed [14,15]. Environmental sustainability is more likely to increase the developmental costs of a building project because of the use of green materials to reduce CO2 emissions [16]. Social sustainability is usually evaluated based on cost, such as housing affordability. Incorporating sustainability considerations into usually drive building costs slightly higher [17]. However, many life cycle benefits can be expected, including facilitated communication, better amenities, and reduced energy bills.
Housing sector plays a key role in the process of the nation’s economy and society. The housing construction is particularly significant within this context since it consumes a large amount of natural resources and produces waste [18]. Sustainable development is a growing subject among decision-makers, policy-makers, and researchers. There has therefore been an increasing need for sustainable development in this sector. Although sustainability has been regarded as a strategy for project development, there is still a lack of current sustainability indicators. To improve sustainability, certain measures should be introduced. Therefore, it is necessary to provide a common concept of sustainable construction at least provide a clue to correctly monitor the construction to support sustainable development.
2.2. Housing Security in Sustainable Urban Development
According to [19,20], housing insecurity is one of the main challenges to achieve sustainable urban development. If the housing prices are unaffordable by most citizens, it is excruciating and significantly impacts living quality [21,22,23]. A large proportion of household income is taken by housing properties, and the high housing prices limit the access of city population to the good living environment [24]. The unequal resources distribution, inadequate regional development, and political issues significantly affect socio satisfaction [25,26]. The economic limitation on access to housing should be properly dealing with so that policy to improve equity and equality in access to housing should be adopted [27].
2.3. Housing Prices in the Economy
Rapid urban development and growth has become a global issue [28] so that the increase in urban population is anticipated. Meanwhile, the economic growth is stimulated and employment opportunities and a variety of services are provided [29]. New Zealand is experiencing a housing market boom [30]. The rapid growth in housing prices has driven household debt to a very high level. The booming also attracts a large amount of investment in this sector, and it also generates a large number of job opportunities. This sector contributes significantly to urban development. Moreover, the rapid development in this sector can also significantly affect other sectors such as material suppliers and financial services. For example, the rapid growth sector requires a lot of construction materials and frequent money transactions. Following the booming in this sector, the housing prices also have a great increase.
Although the booming contributes greatly to economic development and living standards, it is also likely to harm the economy in the long term and pose risks on the bank and financial sector. The booming housing sector pushes up the house prices that cause many problems including a property bubble, unaffordable housing, and waste of resources. The rapid development in the housing sector can attract more investment and resources into it, in the long run, this may hinder the development of other sectors. Moreover, the increasing housing prices, the easing of fiscal regulations, and bank competition encourage mortgage growth. The far beyond fundamentals housing prices may cause distortions in the economy and financial risks, as the 2008 Financial Crisis. Evidence from the boom and bust cycles of the housing market in some advanced economies indicates that the boom market is always followed by a severe correction [31,32]. A severe housing market correction could impose a raft of challenges for the financial system and broader economy as the banks are heavily exposed to housing with mortgages accounting for 55 percent of total assets [33].
2.4. The Influencing Factors of Housing Prices
Due to the complex relationships between socio-economic factors and housing prices, some variables are considered in this study to better estimate house prices. In fact, house prices are influenced by many factors. The aim of this study is not to comprehensively investigate all these indicators. In fact, there is no single agreement in the literature on a set of macro-economic indicators for predicting models of house prices [34]. It is beyond the scope of this study to discuss the impacts of all the fundamental factors on housing prices in New Zealand. Thus, this paper incorporates four indicators for use in a multiple linear regression model: employment, mortgage rate, population, and CO2 emissions.
The authors of [15] revealed that housing prices are associated with population, employment rate, financial deepening, interest rate, and real income. Housing prices respond to the availability of mortgage loans and a change in mortgage rate, based on different empirical studies and research [35,36,37,38]. In [39], the study developed a model in which the mortgage rate, developers, and lenders interacted to produce the volatility in house prices. According to [40], the importance of understanding the fluctuations in house prices has been emphasized. As well, the close relationship between employment and housing prices has been revealed. The studies that supposedly identify the key determinants of house price volatility found that economic indicators such as employment, net migration, and income growth can significantly impact house prices [41,42]. Reference [43] explored that a linkage between rises in population density and increasing levels of house prices. The findings are also supported by [44,45]. Thus, the determinants of housing prices are sensitive to a country’s economic conditions and policy and should be examined within a specific macro-economic context. This means that it is necessary to investigate the determinants of housing prices in the New Zealand macroeconomic context.
2.4.1. Housing Prices
Because of the high proportion of home ownership in New Zealand, a large proportion of household wealth is associated with housing prices [33]. The rise in housing prices also increases the balance sheet and borrowing and lending power of firms and individuals. This facilitates a general expansion in spending as well as an expansion in spending on the construction of appreciating buildings. However, a housing downturn also can affect the commercial property market by decreasing the value of land and buildings that commercial property developers might use as collateral when borrowing [46]. The cheap and easy credit conditions have no effects on housing supply but will increase the demand for housing, thereby pushing up house prices. The rising housing prices will increase inflation and then impose upward pressure on interest rates and the exchange rate thus having a negative effect on exporters. This will introduce risks both to the economy and the financial system in New Zealand.
2.4.2. Mortgage Rate
The bank sector in New Zealand was heavily regulated and access to mortgage money was relatively limited before 1984 [47]. As the report tells, the mortgage terms and conditions were fairly stringently controlled by conservative restrictions on loan-to-value ratio (the ratio of the mortgage to the property value) and mortgage repayment to income (the ration of mortgage repayment to gross income). Following the world-wide deregulation in bank sectors in the 1980s, credit constraints have been largely relaxed. Following this trend, residential mortgages account for a large proportion of lending portfolios. It is possible to consider that the mortgage rate can influence housing prices. However, the reality is that it usually influences only the younger buyers who require the loan to cover the purchase but not the investors. The investment property market is more determined by the real interest rate. For example, the rise in mortgage rates makes first-time buyers delay their purchasing plan, but the rent growth encourages the investors to input more in residential properties.
2.4.3. Employment and Population
The employed people are those who during the reference week worked for one hour or more for pay or profit in the context of an employee/employer relationship or self-employment, worked without pay for one hour or more in work which contributed directly to the operation of a farm, business, or professional practice owned or operated by a relative, had a job but were not at work due to their own illness or injury, personal or family responsibilities, bad weather or mechanical breakdown, direct involvement in an industrial dispute, or on leave or on holiday [48].
Rising employment increases the demand for housing since those householders who are employed earn an increased income, which makes the purchase of property more affordable. Moreover, according to [49], employment is an indicator of the level of economic activity. Thanks to the presence of the increased employment, some households decide to purchase a house. At the same time, banks are also more than pleased to issue a new mortgage in this kind of context. All these factors induce a rise in demand for housing.
Population trends are usually considered as an important driver of housing price fluctuations as population change results in a changing demand for housing [50]. Rapid population growth increases the demand for housing, whilst the spending of an increased population might decrease the funds available for housing supply. Moreover, housing prices also influence the selection of residential location. In the long run, housing prices tend to follow the demand for, and the number of, dwellings in a particular area.
2.4.4. Environmental Indicator
Environmental sustainability in the building sector usually corresponds to issues such as climate change and CO2 emissions [51]. Various methods can be adopted to support environmental sustainability, such as green materials, sustainable technologies, and renewable energy. Environmental sustainability is important for building development in New Zealand, as policies and regulations are required [52,53]. Hence, the project should be properly planned to avoid any violations.
Auckland, the largest city in New Zealand with a population of 1.5 million, is facing a housing affordability challenge [54]. A shortage of 20,000–30,000 houses and an annual need of 13,000 new houses is expected in the next 30 years [55]. To mitigate this problem, the central and local government have attempted to build more houses for meeting the demand. Moreover, demand has increased because of demographic change and international migration, which impose great pressure on environmental sustainability, such as climate change.
Anthropogenic climate change is mainly caused by CO2 emissions and increased population, which are major challenges for urban sustainable development [56]. The building sector is one of the largest contributors to energy consumption and CO2 emissions [57,58]. The existing literature explored the significant relationship between energy consumption and CO2 emissions [59,60]. Hence, CO2 emissions is selected as the environmental indicator of environmental sustainability. This study links CO2 emissions (the environmental indicator) to housing prices by assuming a relationship exists between housing prices and environmental sustainability.
3. Research Methodology
3.1. Data
A time series is a set of observations obtained by measuring a single variable regularly over a period of time and the variable was observed at regular, known intervals over a certain length of time. Thus, the form of the data for a typical time series is a single sequence or list of observations representing measurements taken at regular intervals. A total of four time series were employed in this study. The applied data series are the indices of house prices in New Zealand, the mortgage rate indices, the employment, the population and the CO2 emissions indices. Quarterly data from 1989: Q4 to 2018: Q4 were obtained from Statistics New Zealand and the Reserve Bank of New Zealand. The sources are reasonable and reliable as they are statutory boards under the auspices of the New Zealand government. The home price index is seen as an efficient and accurate means of tracking changes in residential property values over time. The analysis only focuses on New Zealand, as it displays a variety of volatility patterns and trend growth.
3.2. Forecasting Methods
There are two basic forecasting methods: qualitative methods and quantitative methods [61]. Qualitative methods are those that usually adopt subjectively experts’ opinions to predict future events. Since the assumption of forecasting is that the data pattern will persist in future, the changes in the data pattern will not be identified, thereby such changes are often predicted by qualitative methods. The commonly used qualitative forecasting techniques, judgmental forecasting methods, include subjective curve fitting, Delphi method, and technological comparisons [61,62].
There are two main group quantitative forecasting methods—univariate models and causal models [63]. A univariate model usually utilizes the past values of a time series to predict their future values. A causal forecasting model is usually an endeavor to build a statistical model that describes the relationship between the predicted time series and the related variables. The causal model can identify the variables related to the predicted time series and evaluate the impacts on the series, but it is more difficult to develop than a univariate model, and the accuracy of prediction for the time series is highly dependent on the related variables.
Forecasting methods include Autoregressive Integrated Moving Average (ARIMA) models [64,65], Generalized Autoregressive Conditional Heteroskedasticity (GARCH) models [66,67,68,69], and Vector Auto-Regression (VAR) models [70,71]. Also, artificial intelligence methods such as Support Vector Machine (SVM) [72] and Artificial Neural Networks (ANNs) [73] are used. Recently, researchers attempted to adopt several forecasting methods to take advantage of every method for more accurate forecasts.
In this study, the ARIMA model, the multiple liner regression model, and the ANNs model are all adopted to produce more accurate forecasts. The ARIMA method is used by considering the potentially time-varying determinants of house prices. The study also uses the multiple linear regression method to incorporate the factors that influence housing prices in the forecasting model. Taking into account the possibility of non-linear model fitting, the ANN model is adopted.
3.3. ARIMA
The autoregressive integrated moving average (ARIMA) method, developed by [74], is one of the most noted models for time series data prediction and is often used in various fields [75]. ARIMA models can be considered to be a time series forecasting method since they are reliable, and easy to use and interpret [76,77]. The ARIMA method has been developed from the auto-regressive model (AR), the moving average model (MA) and the combination of the AR and MA, and the ARMA model, introduced in 1926, 1937, and 1938, respectively [78]. Compared with the early AR, MA, and ARMA models, the ARIMA model is more flexible in application and more accurate in the quality of the simulative or predictive results. According to existing literature, ARIMA is a high precision model for time series data.
The ARIMA model can approximately characterize the stochastic nature of the data with the aid of auto-correlation function and partial auto-correlation function, and discover the information, such as trend, random variation, periodic component, cyclic patterns, and serial correlation. If a time series is generated from an ARIMA process, it should have some theoretical auto-correlation properties. Firstly, we should ensure that the analysis data is stationary. A stationary time series has the property that its statistical characters such as the mean and the auto-correlation structure are constant over time. After the series has been identified as stationary, it is appropriate to estimate its best fit AR and MA parameters according to its partial auto-correlation (PAC) function and auto-correlation (AC) function, respectively. The last step of model building is the diagnostic checking.
The research divides the time series into an estimation period and a validation period. The analysis develops a model on the basis of the observations in the estimation period and then tests it to see how well it works in the validation period. By undertaking the model to make predictions for points we already know (the points in the validation period), we get an idea of how well the model does at forecasting. Once we are satisfied that the model does an adequate job of forecasting, we can redefine the estimation period to include the validation cases, and then build the final model. In the ARIMA (p, d, q) model, p is the number of auto-regressive terms in AR processes, q is the number of lagged forecast errors in MA processes, d is the number of differences of the component [79]. It is convenient to express it in Equation (1); where indicating the p-th degree polynomials, indicating the q-th degree polynomials, B representing backward shift operator, d representing a non-negative integer.
3.4. Multiple Linear Regression Analysis
Regression analysis is a statistical methodology that relates a variable of interest (dependent variable) to one or more predictors (independent variables) [61]. The developed model can be used to describe, predict, and control the dependent variable on the basis of the independent variables. Multiple linear regression is a widely used analysis method to build the relationship between depend variables and several independent variables. The general model is expressed as in Equation (2), where (i = 1,2, …, n) indicating regression coefficients and representing regression analysis error.
Approaches to cost estimation based on statistics and linear regression analysis have been developed since the 1970s [63]. Regression analysis is a very powerful statistical tool that can be used as both an analytical and predictive technique in examining the contribution of potential new items to the overall estimate reliability, although it is not appropriate when describing non-linear relationships, which are multidimensional, consisting of a multiple input and output problem.
3.5. ANNs Modelling
The artificial neutral networks (ANNs) modelling employs the architecture of a neutral network, which have a powerful leaning mechanism for modelling complex relationships [80,81]. Several types of ANN models are available, one of the main is multilayer perceptron [82]. An ANN model is composed of the input layer, the hidden layer or layers, and the output layer. The basic elements in the layers are called neurons or nodes and they are connected by links. Each link in the ANN model carries a weight that can be used to calculate the weighted sum of all the input variables from the input layer. The weighted sum of the input variable is expressed as shown in Equation (3):
where is the summation at neutron i, n is the number of hidden neutrons, l is layer, is the value of the input variable i at the neutron j, and is the weight of the link between the input variable i and the neutron j.
The activation function is used to create the output, which is defined in Equation (4). The output for layer l will become input for the subsequent layer l + 1.
where is the output at layer l and is the activation function.
After feeding the input variables into the network, a set of hidden nodes in the hidden layer is used to calculate a weighed sum according to the inputs from the previous layer. The weighted sum at every node is calculated based on the linking weights and the values of the input variables mapped on the node. Then, the result passes through to the activation function to produce the output. For nodes in the subsequent layer, the input variables are a mixture of the nodes with different weights. The input variables are aggregated and recombined layer-by-layer to fit the outputs, which is helpful in modelling complex patterns. The network is developed based on hidden layers, hidden nodes, and the weighted linking of the nodes. The activation function typically includes linear function, sigmoid function, and tangent function. The selection of the type of activation function is based on model performance. The ANNs method use several hidden layers with a non-linear modelling node to form a neutral network that can be used to model the underlying relationship between input and output variables. The structure of the ANN model is shown in Figure 1.
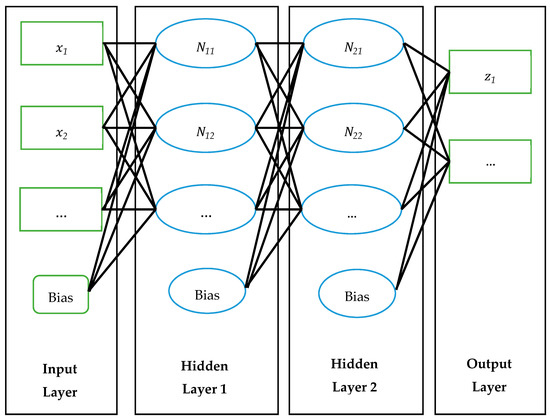
Figure 1.
The structure of the Artificial Neural Networks (ANNs).
It is difficult to choose a suitable number of hidden layers and hidden nodes for an ANN model. In general, the number of nodes is regarded to be one- to three-times the number of input nodes. During model training or the learning process, the weights of the links and the types of activation function can be modified based on a training rule [81]. The purpose of ANN training is to enable ANNs to learn the relationship between the inputs and output so that an ANN can successfully map the links between inputs and output. During the training process, the optimal weight matrix W and the bias matrix b are obtained and are used to calculate an accurate estimate of output. The optimization algorithms include scaled conjugate gradient and gradient descent. When training the ANN model, the training data of the input variables are standardized. The input variables are standardized using Equation (5):
where is the standardized input variable series i, is the input variable series i, and is the mean of the input variable series .
4. ARIMA Model
4.1. Examination of Time Series Stationarity
At the outset it was suggested that all analyses be performed with the housing prices data from 1989: Q4 to 2014: Q4 so that the data from 2015: Q1 to 2018: Q4 could be used as a check on the validity of the model. Classical ARIMA models describe stationary time series. Thus, the first in ARIMA models is to determine whether the data series is stationary. A plot of the observed values of housing prices series can help to determine whether the data series is stationary. If the values seem to fluctuate with constant variation around a constant mean, it is reasonable to believe that the series is stationary. The 101 house prices indices are plotted in Figure 2. It should be noticed from Figure 1 that the original values of the series is obviously with an upward trend, and thus it would seem that these values are non-stationary.
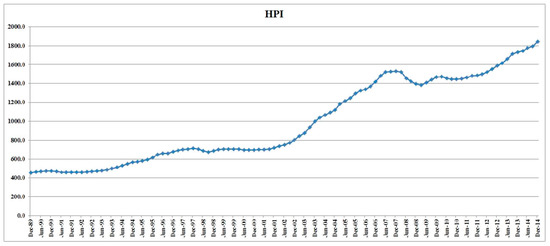
Figure 2.
A plot of the time series for the house price index.
As the time series is non-stationary, a first difference of the non-stationary time series values can be used. Moreover, sample auto-correlation is used to determine whether the first differences series is stationary by observing the behavior of sample auto-correlation (SAC). The SAC of the first difference house prices series is shown in Figure 3. It can be seen from Figure 3 that the SAC of the series values dies down fairly quickly, and then the series values should be considered stationary.
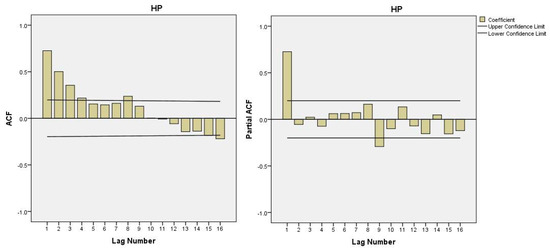
Figure 3.
Autocorrelation function (ACF) and partial autocorrelation function (PACF) plots of the differenced time series for the house price index.
4.2. Model Identification
Sample auto-correlation (SAC) and sample partial auto-correlation (SPAC) are usually adopted to identify the type of model from many Box–Jenkins models [61]. The SPAC of the time series values are shown in Figure 2. It should be noticed that after the first lag, the SPAC of the series values drop down very quickly, while the SAC of the series values decrease in a relatively steady fashion as shown in Figure 2. Therefore, it can be tentatively concluded that the time series values are described by the auto-regressive model of order 1.
4.3. Estimation
After having tentatively identified a model to describe the house prices series, it is time now to estimate the value of the model parameters. The least square estimate technique was used in ARIMA parameter estimation. The parameters of the ARIMA models are listed in Table 1. For the first order auto-regressive model there is no invertibility requirement, but it must satisfy the stationary condition that the absolute value of the auto-regressive parameter is less than 1. According to the t-value and sig-value, the parameter of ARIMA (1, 1, 0) is the optimal model for housing prices in Auckland.

Table 1.
Autoregressive integrated moving average (ARIMA) models parameter estimates.
4.4. Diagnostic Checking
Analyzing the residuals obtained from the model in some manner is a good way to check the adequacy of an overall ARIMA model [61]. In this study, RSAC denotes the sample auto-correlation function of the residuals and RSPAC denotes the sample partial auto-correlation function of the residuals. The Box–Ljung statistic for the residuals is used to check the adequacy of the overall model. It is supposed that the modeling process can account for the relationship between the observations of the time series. If these relationships are all described by the model, the residuals should be unrelated, and thus the auto-correlations of the residuals should be small. The Q value of the ARIMA (1, 1, 0) is less than Chi-Square Q value (27.767 < 28.869), identifying that the model is adequate.
4.5. Forecasting
After various diagnostics have been done to check the adequacy of the tentative model, it can be assumed that the ARIMA (1, 1, 0) for the house prices in Auckland is a qualified model. This also implies that the model can be used to forecast future time series values. In the previous section, the model is estimated on a sample of data from 1989: Q4 to 2014: Q4. In this section, the out-of-sample period is used (forecast: 2015: Q1-2018: Q4). The ARIMA model is a dynamic forecasting model so that lags are automatically obtained from previous forecasts.
5. Multiple Regression Analysis
5.1. The General Multiple Linear Model
The multiple linear regression analysis employs more than one independent variable to build the relationship between dependent variable and independent variables. The particular variable that the study is interested in and modelled is called a dependent variable. A set of other variables that might be useful in predicting or modelling the dependent variable are the predictors or the independent variables. In this study, the house price is a dependent variable and the employment, mortgage, population, and CO2 emissions are independent variables.
5.2. Multicollinearity Checking
Multicollinearity among independent variables tends to reduce the accuracy of the regression analysis results. Multicollinearity can be defined as being when the independent variables are related to each other and thus to some extent contribute redundant information for the description and prediction of the dependent variable can cause the t statistics to make individual independent variables look unimportant when they really are important [61]. The correlation analysis between the predictors can be used to test the seriousness of multicollinearity. The more significant correlation between the predictors is, the more severe the multicollinearity that exists. The correlation analysis is conducted by Statistical Package for the Social Sciences (SPSS). The SPSS output of the correlation analysis is presented in Table 2. It also can be seen from Table 2, there is no strong correlation between the independent variables.

Table 2.
Predictor correlations.
5.3. Model Adequacy Testing
An F-test is usually used to determine the independent variables or predictors which significantly influence the dependent variable. If the F parameter obtained from the model is greater than the corresponding point scale of F distribution, it is safe to conclude that at least one of the independent variables significantly influences the dependent variable. The F test result of the regression model is far greater than the corresponding point scale of F distribution (181.5 > 2.76).
Therefore, the study can check the t-test further to decide which predictors are significant. If the t-value of the parameter is greater than the corresponding point scale of t distribution, it is suggested that the parameter is significant. As the result shows in Table 3, all the parameters in the model are greater than the corresponding point scale of t distribution (1.96). Therefore, the study suggested that all the predictors are significant to the dependent variable.

Table 3.
Multiple linear regression analysis results.
5.4. Diagnostic Checking
The residuals of the regression model are the difference between the observed values of the dependent variable and the estimated values of the dependent variable obtained by regression model. The residuals are assumed to be independently normally distributed with zero mean and constant variance. Examination of the residuals plots is a simple and effective way to check the assumptions. Residuals plots will present when violations in assumptions exist. If the histogram fits the normal distributed curve and the points scatter around the 45° tangent line in normal distributed probability plots, it can be concluded that the residual series are normally distributed. As is shown in Figure 4, the normal curve looks reasonably bell-shaped and symmetrical about zero and the points scatter around the 45° tangent line. It can be concluded that the normal distribution assumption approximately satisfies the house prices regression model.
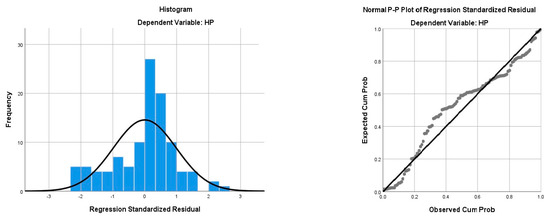
Figure 4.
Residual analysis in multiple regression model.
5.5. MLR Forecasting
Forecasting property prices is an important task in much economic decision making. Multiple linear regressions technique can also be used for time series forecasting. This study will investigate the accuracy of performance multiple linear regressions (MLR) model for forecasting future house prices (from 2015: Q1 to 2018: Q4). Consider the regression model for house prices in New Zealand, if the values of the four predictors during the forecasting period are known, the regression model can be used to predict New Zealand’s house prices. The observed values of the house prices and the predictions of these values are shown in Table 4.

Table 4.
The final ANN model summary.
6. ANNs
The optimal numbers of hidden layers and nodes are based on a variety of factors such as the number of input and output variables, size of the training dataset, the complexity of the problem, and the activation function. The ANN model, with few hidden layers and nodes, is unable to capture the relationship between input and output variables. In contrast, if too many hidden layers and nodes are included in the ANN model, the model tends to over-fit and fails to produce adequate outputs. Thus, the model training process is required to obtain a suitable ANNs model.
ANNs models were trained using MAPE to select a suitable number of hidden layers or hidden nodes and the activation functions. In this study, as shown in Figure 5, the neutral network with four layers was used because the application of two hidden layers are suitable for this case. This neutral network consists of four layers. The first layer is input variables. For this study, the four input variables are employment, mortgage rate, population, and CO2 emissions. The second and third layers are known as hidden layers. There are three nodes in the first hidden layer, two nodes in the second hidden layer. The last layer is output layer, while house price (HP) was used as the output variable. Sigmoid function was used as the activation function to model the non-linearity in the hidden layer. Scaled conjugate gradient was used as the optimization algorithm.
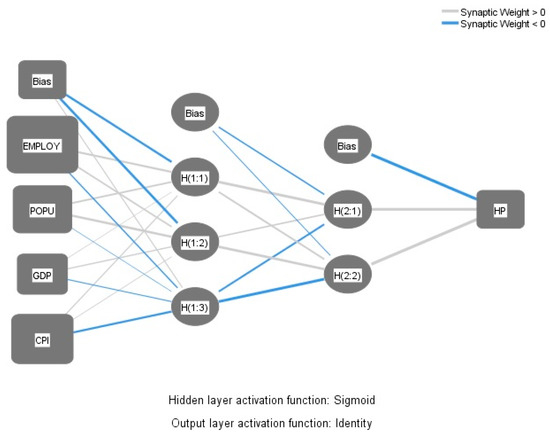
Figure 5.
The final ANN model for housing prices with four input variables.
The final ANNs results are shown in Table 4. The value of sum of squares error (SSE) is 0.529, which is lower than other ANNs models and is acceptable. The sum of squares error (SSE) of the testing section is much less than that of the training part (0.121 < 0.529), indicating that the model obtained from training is qualified. The results suggest that the final ANNs model is able to model the underlying relationships between the input variables and output variable. Therefore, the final ANN model is satisfactory and can be used to estimate house prices, given the input variables. The results of predicted values and residuals are shown in Figure 6, indicating the final ANN model is acceptable. Because the predicted values scatter around the 45° tangent line and residuals are around the horizontal line.
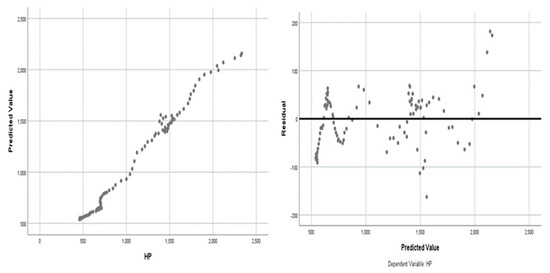
Figure 6.
The ANN model fit results.
7. Models Comparison
The error measures such as RMSE, MAE, and MAPE obtained with ARIMA, multiple linear regression, and ANN models are shown in Table 5. It can be seen from Table 5 that the ARIMA model performs better than the multiple linear regression model for the forecasting of house prices in Auckland. However, the advantage of the regression model is that it able to express the secular trend in a mathematical equation which allows objective extrapolation into past, present, and future. ARIMA models were compared to select the most appropriate one. ARIMA (1, 1, 0) was found to be performing best than others.

Table 5.
Forecasting and comparison results of the two models.
Although the forecasting performance of the regression model is not as accurate as the ARIMA model, the regression model still provides more useful information about the relationship between house prices and some important economic indicators. As for the four important indicators in this study, the regression model explored that all four can significantly influence house prices in New Zealand. That can be supported by the results of an F test and t test. The regression model provides a framework to analyze the effects of exogenous influences and key policy decisions on house prices. According to the regression model, house prices in New Zealand are determined positively by employment, population, and CO2 emissions, but they are negatively influenced by mortgages.
8. Discussion and Conclusions
The housing sector has an essential role in sustainable urban development. The dynamics in housing prices can help in adjusting related policies to improve sustainable urban development. The prediction of housing prices provides clues to monitor the rapidly expanding sector and its impacts on the sustainability. In terms of social impact, the housing sector boom improves the living conditions and social standards of the public such as sufficient social housing, healthcare, sports, and leisure facilities. However, the stretched housing valuation also increases household indebtedness, and thus decreases homeowners’ wealth and consumption capability. On the economic aspect, the rapid increase in housing prices during 2001–2012 in New Zealand led to the housing sector boom and the increased investment in property [33]. The rapid increased investment in this sector may mislead the market, and thus misallocate resources. The mismanagement of resources causes significant losses every year. In fact, while the housing sector has made a great contribution to economic development, the building construction consumes numerous resources and produces waste and pollution. Although laws and regulations impose many constraints on the construction industry to minimize its environmental impact, a tool that provides a comprehensive assessment of the environmental impact is lacking. This may be an area for further studies.
The study evaluated three different statistical techniques for the forecasting of house prices in New Zealand. They all show satisfactory results for in-sample estimation, but the ARIMA model performed better in out-of-sample forecasting than regression analysis. Performance measures, namely root mean square error (RMSE), mean absolute error (MAE), and mean absolute percentage error (MAPE), have been adopted for comparison. The assessment of the ARIMA models indicated that the ARIMA (1, 1, 0) model produced better results in- and out-of-sample. This suggests that house prices might be characterized as the combination of a non-stationary stochastic growth component and a stationary cyclical component over the past two decades. Given the merits of the ARIMA method, property researchers and investors should incorporate this modeling technique to evaluate the national housing market. Central bank can apply the ARIMA technique on forecasting national house price inflation to evaluate the speculative bubbles.
Furthermore, a regression model is found to be useful in explaining the relationships between the housing prices in New Zealand and the macro-economic climate. This offers additional evidence of the close linkage between the economic conditions and housing prices. The regression model describes the relationship between the house prices in New Zealand and four economic indicators including employment, mortgage rate, population, and CO2 emissions. The house prices interact with the four predictors, and thus a change of house prices can be traced through employment, mortgage population, and CO2 emissions. It is found that these four indicators have significant impacts on housing prices in New Zealand. The model also revealed the positive relationship between population and house prices.
The final ANNs model was developed and successfully trained to estimate housing prices using 72 datasets. The final ANNs model consists of an input layer with four input variables, two hidden layers with five hidden nodes, and an output layer with an output variable. The application of Sigmoid as an activation function in the hidden layers of the ANNs model minimize the estimated error, indicated by MAPE. The developed ANNs model cannot generate estimated house prices as accurate as the other two forecasting methods. The results indicate that ARIMA method is still the best fit model for New Zealand’s housing price. The results also indicate that the non-linear relationship between the housing prices with the four input variables such as employment, mortgage rate, population, and CO2 emissions are not evident.
Although sustainability is gaining considerable attention and has been formulating policies or regulations, there is a shortage of sustainability indicators to guide decision makers. This study, therefore, introduces housing prices as a performance indicator of sustainability to support sustainable development. This study contributes to urban administration by improving understanding of the movement of housing prices in New Zealand so that housing affordability policies can be adjusted to enhance sustainable development. The proposed forecasting method can help in monitoring housing prices to guide the housing market to orderly and reasonably allocate resources. This study can be used as a useful reference for taking sustainability into consideration by policy makers, which helps to achieve sustainable development.
Author Contributions
Conceptualization, L.Z. and J.M.; methodology, L.Z.; software, Z.L.; validation, L.Z., Z.L.; writing—original draft preparation, L.Z.; writing—review and editing, J.M.; supervision, J.M.; project administration, J.M.; funding acquisition, L.Z.
Funding
This research was funded by China Scholarship Council, grant number 201206130069, Massey University, grant number 09166424, and The APC was funded by the both grants.
Acknowledgments
The authors would like to thank the China Scholarship Council (CSC) for its support through the research project and also the Massey University. The authors would like to thank Reserve Bank of New Zealand and Ministry of Business, Innovation, and Employment for providing data to conduct this research. In addition, I would like to thank all practitioners who contributed to this project.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Liu, H.; Zhou, G.; Wennersten, R.; Frostell, B. Analysis of sustainable urban development approaches in China. Habitat Int. 2014, 41, 24–32. [Google Scholar] [CrossRef]
- Nuzir, F.A.; Dewanckera, B.J. Understanding the role of education facilities in sustainable urban development: A case study of KSRP, Kitakyushu, Japan. Procedia Environ. Sci. 2014, 20, 632–641. [Google Scholar] [CrossRef]
- Wang, N.; Wei, K.; Sun, H. The whole life project management approach to sustainability. ASCE J. Manag. Eng. 2014, 30, 246–255. [Google Scholar] [CrossRef]
- RBNZ. Household Debt: A Cross-Country Perspective; Reserve Bank of New Zealand: Wellington, New Zealand, 2014.
- Giang, D.T.H.; Pheng, L.S. Role of construction in economic development: Review of key concepts in the past 40 years. Habitat Int. 2011, 35, 118–125. [Google Scholar] [CrossRef]
- Risse, M.; Kern, M. Forecasting house-price growth in the Euro area with dynamic model averaging. N. Am. J. Econ. Financ. 2016, 38, 70–85. [Google Scholar] [CrossRef]
- Preval, N.; Randal, E.; Chapman, R.; Moores, J.; Howden-Chapman, P. Streamlining urban housing development: Are there environmental sustainability impacts? Cities 2016, 55, 101–112. [Google Scholar] [CrossRef]
- RBNZ. Update on the New Zealand Housing Market; Reserve Bank of New Zealand: Wellington, New Zealand, 2014.
- Brockwell, P.J. Introduction to Time Series and Forecasting, 3rd ed.; Springer: London, UK, 2016. [Google Scholar]
- Golubchikov, O.; Badyina, A. Sustainable housing for sustainable cities: A policy framework for developing countries. In United Nations Human Settlements Programme; French, M., Ed.; UN-HABITAT: Nairobi, Kenya, 2012. [Google Scholar]
- Lin, Y.; Zhang, X.; Geertman, S. Toward smart governance and social sustainability for Chinese migrant communities. J. Clean. Prod. 2015, 107, 389–399. [Google Scholar] [CrossRef]
- Roufechaei, K.M.; Bakar, A.H.A.; Tabassi, A.A. Energy-efficient design for sustainable housing development. J. Clean. Prod. 2014, 65, 380–388. [Google Scholar] [CrossRef]
- Elkington, J. Cannibals with Forks: The Triple Bottomline of 21-st Century Business; New Society Publishers: Gabriola, BC, Canada, 1998. [Google Scholar]
- Pullen, S.; Zillante, G.; Arman, M.; Wilson, L.; Zuo, J.; Chileshe, N. Ecocents Living: Affordable and Sustainable Housing for South Australia; University of South Australia: Adelaide, Australia, 2009. [Google Scholar]
- Winston, N.; Montserrat, P.E. Sustainable housing in the urban context: International sustainable development indicator sets and housing. Soc. Indic. Res. 2007, 87, 211–221. [Google Scholar] [CrossRef]
- Pullen, S.; Arman, M.; Zillante, G.; Zuo, J.; Chileshe, N.; Wilson, L. Developing an assessment framework for affordable and sustainable housing. Australas. J. Constr. Econ. Build. 2010, 10, 48–64. [Google Scholar]
- Coimbra, J.; Almeida, M. Challenges and benefits of building sustainable cooperative housing. Build. Environ. 2013, 62, 9–17. [Google Scholar] [CrossRef][Green Version]
- Wang, N. The role of the construction industry in China’s sustainable urban development. Habitat Int. 2014, 44, 442–450. [Google Scholar] [CrossRef]
- Roy, A. Urban informality: The production of space and practice of planning. In The Oxford Handbook of Urban Planning; Oxford University Press: Oxford, UK, 2012. [Google Scholar]
- UN-Habitat. Informal Settlements; UN-Habitat: New York, NY, USA, 2015. [Google Scholar]
- Inam, A. Informality and Urbanism; UN-Habitat: New York, NY, USA, 2015. [Google Scholar]
- Lai, L.W. Squatting by the privileged? A Hong Kong study on the innovations and ambiguity of property rights of irregular development. Habitat Int. 2015, 50, 317–325. [Google Scholar] [CrossRef]
- Nwokoro, I.; Lawanson, T.; Ebuethi, O.; Fadare, S.; Agwu, J.; Soyinka, O. Socioeconomic dynamics and environmental health outcomes in informal settlements of Port Harcourt, Nigeria. J. Constr. Proj. Manag. Innov. 2015, 5, 1064–1081. [Google Scholar]
- Campos, R.B.A.; Guilhoto, J.J. The socioeconomic impact of low-income housing programs: An interregional input-output model for the state of Sao Paulo and the rest of Brazil. Habitat Int. 2017, 65, 59–69. [Google Scholar] [CrossRef]
- Soyinka, O. Assessment of Spatial Development Indicators vis-a-vis Smart Growth Potential in Lagos Metropolis; University of Lagos: Lagos, Nigeria, 2014. [Google Scholar]
- Lawanson, T.; Fadare, S. Environment and health disparities in urban communities: Focus on Eti Osa, Nigeria. City Cult. Soc. 2015, 6, 43–52. [Google Scholar] [CrossRef]
- Soyinka, O.; Siu, K.W.M. Urban informality, housing insecurity, and social exclusion; concept and case study assessment for sustainable urban development. City Cult. Soc. 2018, 15, 23–36. [Google Scholar] [CrossRef]
- Pouriyeh, A.; Khorasani, N.; Lotfi, F.H.; Farshchi, P. Efficiency evaluation of urban development in Yazd City, Central Iran using data envelopment analysis. Environ. Monit. Assess. 2016, 188, 618. [Google Scholar] [CrossRef]
- Hosseini, A.; Pourahmad, A.; Pajoohan, M. Assessment of institutions in sustainable urban-management effects on sustainable development of Tehran: Learning from a developing country. J. Urban Plan. Dev. 2015, 142, 05015009. [Google Scholar] [CrossRef]
- Crawford, G.W.; Rosenblatt, E.L. Efficient mortgage default option exercise: Evidence from loan loss severity. J. Real Estate Res. 1995, 10, 543–555. [Google Scholar]
- Bordo, M.D.; Landon-Lane, J. What explains house price booms? History and empirical evidence. Macroecon. Anal. Int. Financ. 2014, 23, 1–36. [Google Scholar]
- Pitros, C.; Arayic, Y. Housing cycles in the UK: A historical and empirical investigation. Prop. Manag. 2017, 35, 89–108. [Google Scholar] [CrossRef]
- RBNZ. Housing Risks Require a Broad Policy Response; Reserve Bank of New Zealand: Wellington, New Zealand, 2016.
- Gallin, J. The long run relationship between house prices and income: Evidence from local housing markets. Real Estate Econ. 2006, 34, 417–438. [Google Scholar] [CrossRef]
- Agnello, L.; Schuknecht, L. Booms and busts in housing markets: Determinants and implications. J. Hous. Econ. 2011, 20, 171–190. [Google Scholar] [CrossRef]
- Apergis, N. Housing prices and macroeconomic factors: Prospects within the European Monetary Union. Int. Real Estate Rev. 2003, 6, 63–74. [Google Scholar]
- Panagiotidis, T.; Printzis, P. On the macroeconomic determinants of the housing market policy in Greece: A VECM approach. Int. Econ. Econ. Policy 2015, 13, 388–409. [Google Scholar]
- Xu, L.; Tang, B. On the determinants of UK house prices. Int. J. Econ. Res. 2014, 5, 57–64. [Google Scholar]
- Spiegel, M. Housing return and construction cycles. Real Estate Econ. 2001, 29, 521–551. [Google Scholar] [CrossRef]
- Evenson, B. House-Price Variation across Local Housing Markets: A Supply-Side View; University of Nevada: Las Vegas, Nevada, 2004. [Google Scholar]
- Johnes, G.; Hyclark, T. House prices, migration, and regional labor markets. J. Hous. Econ. 1994, 3, 312–329. [Google Scholar] [CrossRef]
- Johnes, G.; Hyclark, T. House prices and regional labor markets. Ann. Reg. Sci. Urban Econ. 1999, 33, 33–49. [Google Scholar] [CrossRef]
- Miles, D. Population density, house prices and mortgage design. Scott. J. Political Econ. 2012, 59, 444–466. [Google Scholar] [CrossRef]
- Levin, E.; Montagnoli, A.; Wright, R.E. Demographic change and the housing market: Evidence from a comparison of Scotland and England. Urban Stud. 2009, 46, 27–43. [Google Scholar] [CrossRef]
- Malpezzi, S.; Maclennan, D. The long-run price elasticity of supply of new residential construction in the United States and the United Kingdom. J. Hous. Econ. 2001, 10, 278–306. [Google Scholar] [CrossRef]
- Kragh-Sorenson, K.; Solheim, H. What Do Banks Lose Money on during Crises? Norges Bank: Oslo, Norway, 2014. [Google Scholar]
- RBNZ. Delivering Sound and Innovative Financial Services for New Zealand; Reserve Bank of New Zealand: Wellington, New Zealand, 2007.
- Gans, J.; King, S.; Stonecash, R.; Byford, M.; Libich, J.; Mankiw, N.G. Principles of Economics: Australia and New Zealand; Cengage Learning: Victoria, Australia, 2014. [Google Scholar]
- Cameron, G.; Muellbauer, J. Earnings, Unemployment, and Hous-ing in Britain. J. Appl. Econ. 2001, 16, 203–220. [Google Scholar] [CrossRef]
- Mulder, C.H. Population and housing. Demogr. Res. 2006, 15, 401–412. [Google Scholar] [CrossRef]
- Carvalho, J.P.; Bragança, L.; Mateus, R. Optimising building sustainability assessment using BIM. Autom. Constr. 2019, 102, 170–182. [Google Scholar] [CrossRef]
- EPA. Emissions Trading Scheme Report; Environmental Protection Authority: Addis Ababa, Ethiopia, 2017.
- EPA. Synthetic Greenhouse Gas Levy Report; Environmental Protection Authority: Addis Ababa, Ethiopia, 2017.
- Murphy, L. The politics of land supply and affordable housing: Auckland’s housing accord and special housing areas. Urban Stud. 2016, 53, 2530–3547. [Google Scholar] [CrossRef]
- Auckland Council. Auckland Housing Accord; Auckland Ciuncil: Auckland, New Zealand, 2013.
- Chapman, R. Time of Useful Consciousness: Acting Urgently on Climate Change; Bridget Williams Books: Wellington, New Zealand, 2015. [Google Scholar]
- Song, X.; Lu, Y.; Shen, L.; Shi, X. Will China’s building sector participate in emission trading system? Insights from modelling an owner’s optimal carbon reduction strategies. Energy Policy 2018, 118, 232–244. [Google Scholar] [CrossRef]
- Zuo, J.; Zhao, Z.Y. Green building researchecurrent status and future agenda: A review. Renew. Sustain. Energy Rev. 2014, 30, 271–281. [Google Scholar] [CrossRef]
- Islam, H.; Jollands, M.; Setunge, S. Life cycle assessment and life cycle cost implication of residential buildings-A review. Renew. Sustain. Energy Rev. 2015, 42, 129–140. [Google Scholar] [CrossRef]
- Ibn-Mohammed, T.; Greenough, R.; Taylor, S.; Ozawa-Meida, L.; Acquaye, A. Operational vs. embodied emissions in buildings-A review of current trends. Energy Build. 2013, 66, 232–245. [Google Scholar] [CrossRef]
- Bowerman, B.L.; O’Connell, R.T.; Koehler, A.B. Forecasting, Time Series, and Regression; Thomson Learning Inc.: Glendale, CA, USA, 2005. [Google Scholar]
- Armstrong, J. Principles of Forecasting; Kluwer Academic: Boston, MA, USA, 2001. [Google Scholar]
- Pindyck, R.S. Econometric Models and Economic Forecasts, 3rd ed.; McGraw-Hill: New York, NY, USA, 1991. [Google Scholar]
- Ahmed, R.A.; Shabri, A.B. Daily crude oil price forecasting model using ARIMA, generalized autoregressive conditional heteroscedastic and support vector machines. Am. J. Appl. Sci. 2014, 11, 425–432. [Google Scholar] [CrossRef]
- Zhao, C.L.; Wang, B. Forecasting Crude Oil Price with an Autoregressive Integrated Moving Average (ARIMA) Model: Fuzzy Information & Engineering and Operations Research & Management; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Narayan, P.K.; Narayan, S. Modelling oil price volatility. Energy Policy 2007, 35, 6549–6553. [Google Scholar] [CrossRef]
- Wei, Y.; Wang, Y.D.; Huang, D.S. Forecasting crude oil market volatility: Further evidence using GARCH-class models. Energy Econ. 2010, 32, 1477–1484. [Google Scholar] [CrossRef]
- Wang, Y.D.; Wu, C.F.; Wei, Y. Can GARCH-classmodels capture longmemory inWTI crude oil markets? Econ. Model. 2011, 28, 921–927. [Google Scholar] [CrossRef]
- Wang, Y.D.; Wu, C.F. Forecasting energymarket volatility using GARCHmodels: Can multivariate models beat univariate models? Energy Econ. 2012, 34, 2167–2181. [Google Scholar] [CrossRef]
- Zhao, L.; Cheng, L.; Wan, Y.; Zhang, H.; Zhang, Z. A VAR-SVM model for crude oil price forecasting. Int. J. Glob. Energy Issues 2015, 38, 126–144. [Google Scholar] [CrossRef]
- Gupta, R.; Wohar, M. Forecasting oil and stock returns with a Qual VAR using over 150 years off data. Energy Econ. 2017, 62, 181–186. [Google Scholar] [CrossRef]
- Fan, L.; Pan, S.; Li, Z.; Li, H. An ICA-based support vector regression scheme for forecasting crude oil prices. Technol. Forecast. Soc. Chang. 2016, 112, 245–253. [Google Scholar] [CrossRef]
- Mostafa, M.M.; El-Masry, A.A. Oil price forecasting using gene expression programming and artificial neural networks. Econ. Model. 2016, 54, 40–53. [Google Scholar] [CrossRef]
- Box, G.E.P.; Jenkins, G.M. Time Series Analysis Forecasting and Control; Wiley: Hoboken, NJ, USA, 1976. [Google Scholar]
- Terrell, D.; Fomby, T.B. Econometric Analysis of Financial and Economic Time Series; Elsevier JAI: Boston, MA, USA, 2006. [Google Scholar]
- Aasim; Singh, S.N.; Mohapatra, A. Repeated wavelet transform based ARIMA model for very short-term wind speed forecasting. Renew. Energy 2019, 136, 758–768. [Google Scholar] [CrossRef]
- Drachal, K. Forecasting spot oil price in a dynamic model averaging framework—Have the determinants changed over time? Energy Econ. 2016, 60, 35–46. [Google Scholar] [CrossRef]
- Pena, D.; Tiao, G.C.; Tsay, R.S. A Course in Time Series Analysis; John Wiley & Sons: New York, NY, USA, 2001. [Google Scholar]
- Pankratz, A. Forecasting with Univariate Box-Jenkins Models; John Wiley & Sons: New York, NY, USA, 1983. [Google Scholar]
- Gallant, S.I. Neural Network Learning and Expert Systems; The MIT Press: Cambridge, MA, USA, 1993. [Google Scholar]
- Singh, K.P.; Basant, A.; Malik, A.; Jain, G. Artificial neural network modeling of the river water quality—A case study. Ecol. Model. 2009. [Google Scholar] [CrossRef]
- Sharma, S. Artificial Neural Network Model; Data Science Central: Seattle, WA, USA, 2017. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).