A Two-Sided Matching Model for Task Distribution in Ridesharing: A Sustainable Operations Perspective
Abstract
1. Introduction
2. Literature Review
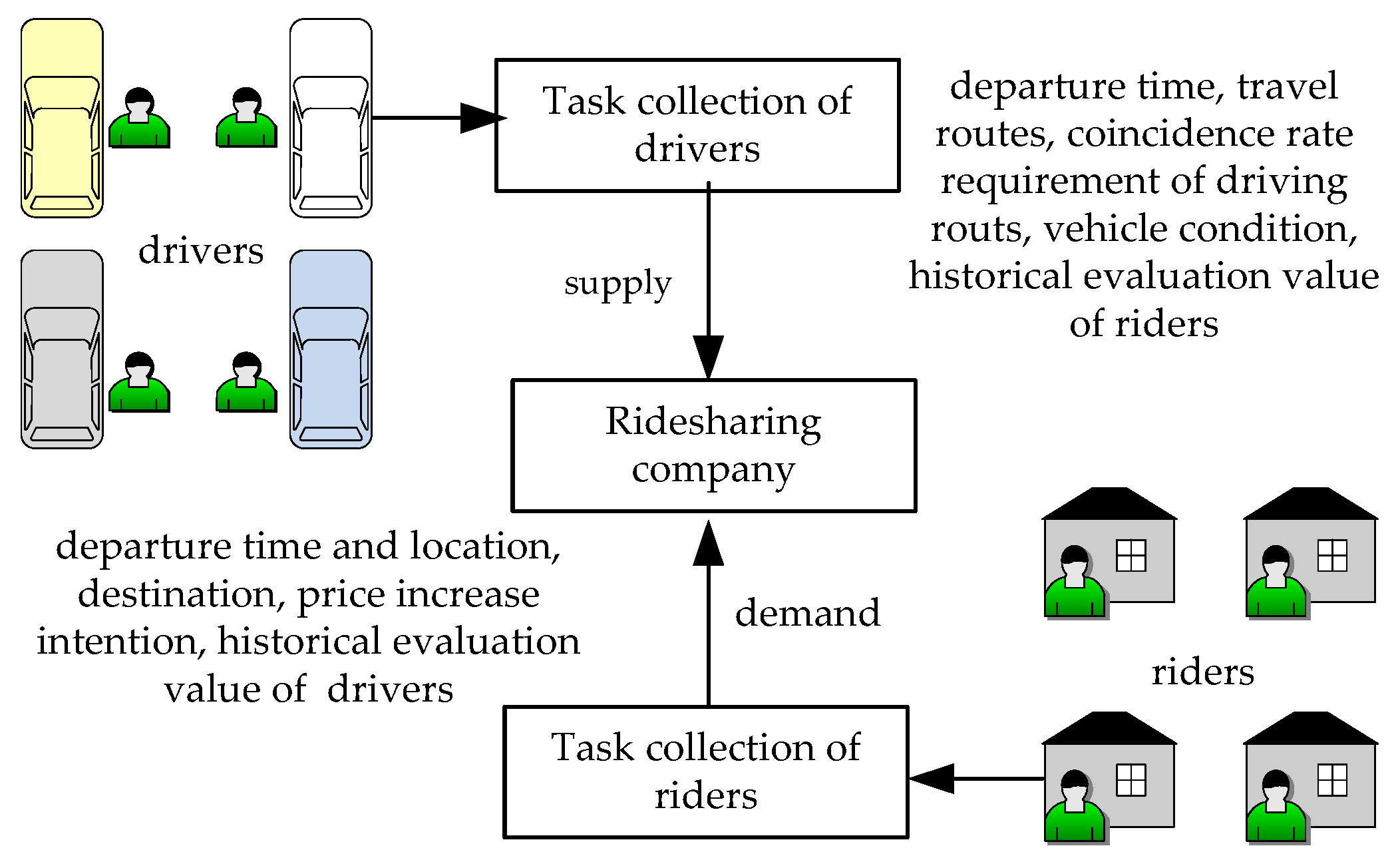
3. Problem Description
3.1. Description of the Notations
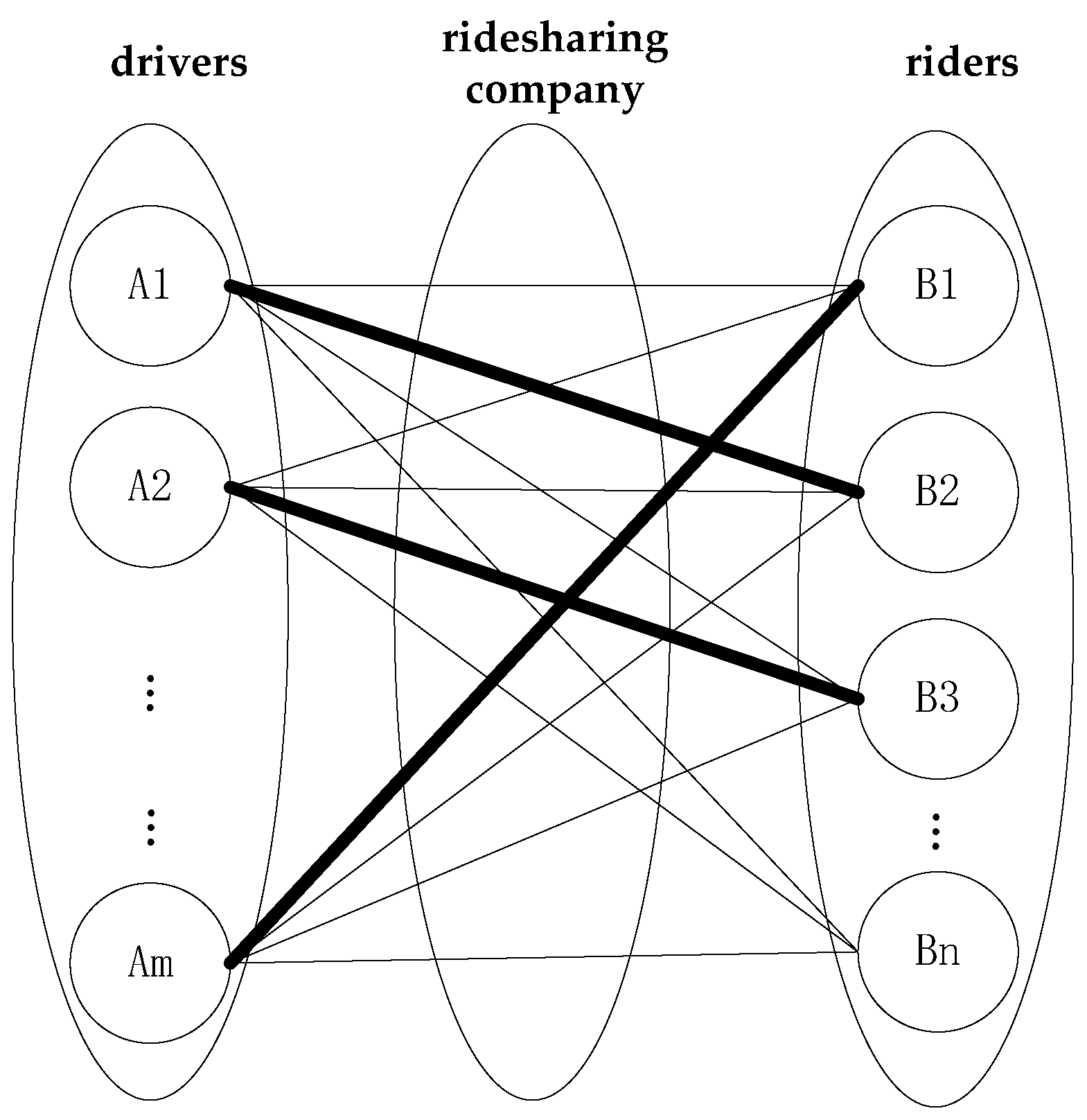
3.2. One-to-One Two-Sided Matching
3.3. The Benchmark of the Two-Sided Matching Scheme
4. Two-Sided Matching Decision Model Formulation
4.1. Characterization of Two-Sided Matching Relationships
4.1.1. The Comprehensive Evaluation Vector and Matrix Regarding Matching Scheme
4.1.2. The Comprehensive Evaluation Mean Vector for Historical Matching Scheme
4.2. Establishment of Perception Function of Both Sides Based on Prospect Theory
4.2.1. Determination of Reference point
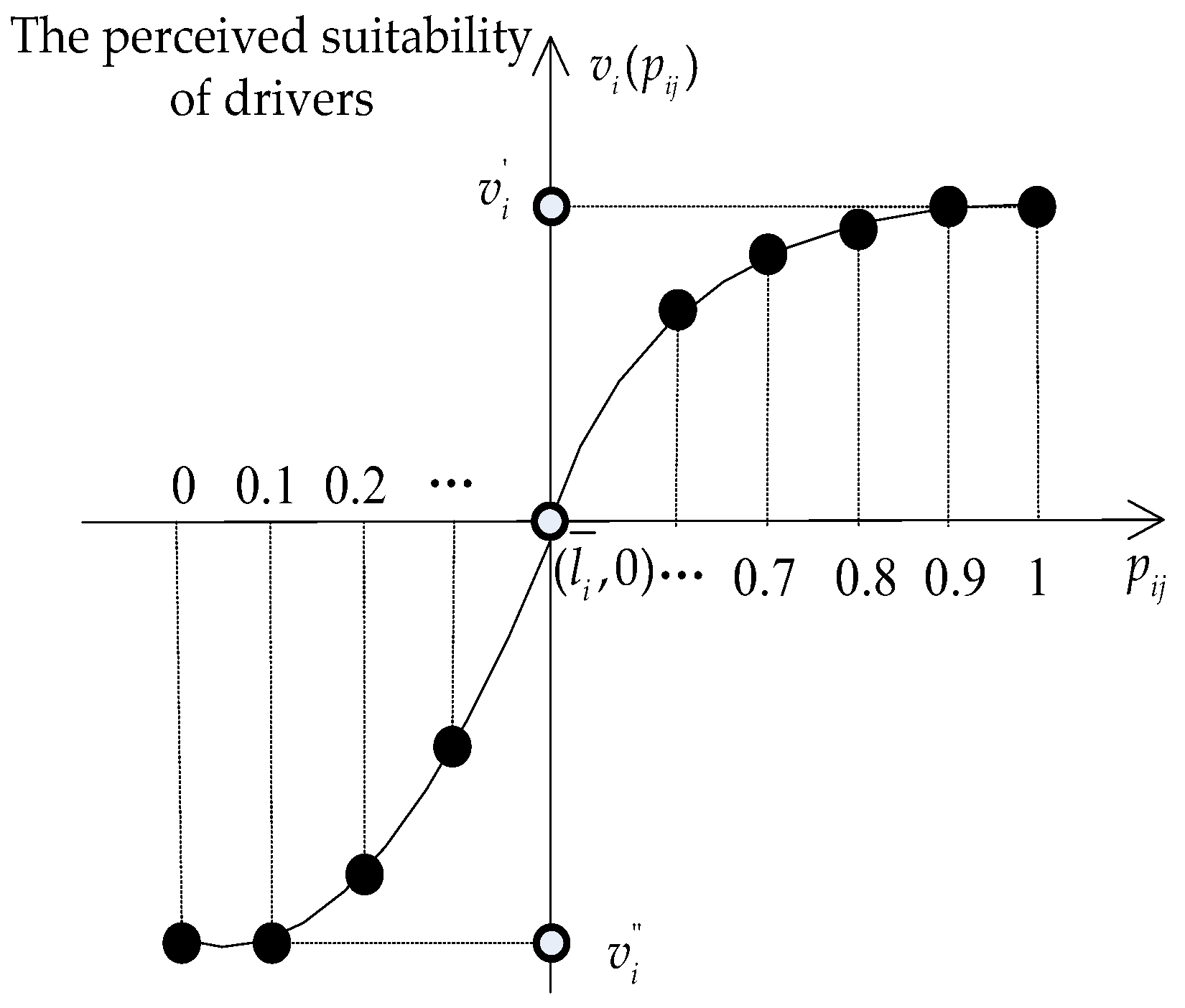
4.2.2. The Perception Function of the Drivers
- ①
- The origin (the reference point) measures the comprehensive evaluation value regarding the perceived suitability of the drivers equal to their historical evaluation mean, in which .
- ②
- In the first quadrant curve (yield curve), it measures the comprehensive evaluation value regarding the perceived suitability of drivers to the matching scheme. As the comprehensive evaluation value of the matching objects (riders) increases, the perceived suitability of the drivers to the matching scheme increases. Due to the “marginal diminishing effect”, the growth rate of perceived suitability gradually declines, and the perceived suitability of drivers gets the upper limit .
- ③
- The third quadrant curve (loss curve) measures whether drivers think the matching scheme is unreasonable, which is in the state of “loss”. Combined with “loss-averse”, as the comprehensive evaluation value of the matching object decreases, the suitability of drivers to the matching scheme decreases obviously, and the loss aversion coefficient is set. The perceived suitability of drivers would get the lower limit .where and are power parameters related to gains and losses, respectively, and 0 ≤ , 1 ≤ , and is the risk-aversion parameter, which has the characteristic of being steeper for losses than for gains, where > 1 [38].
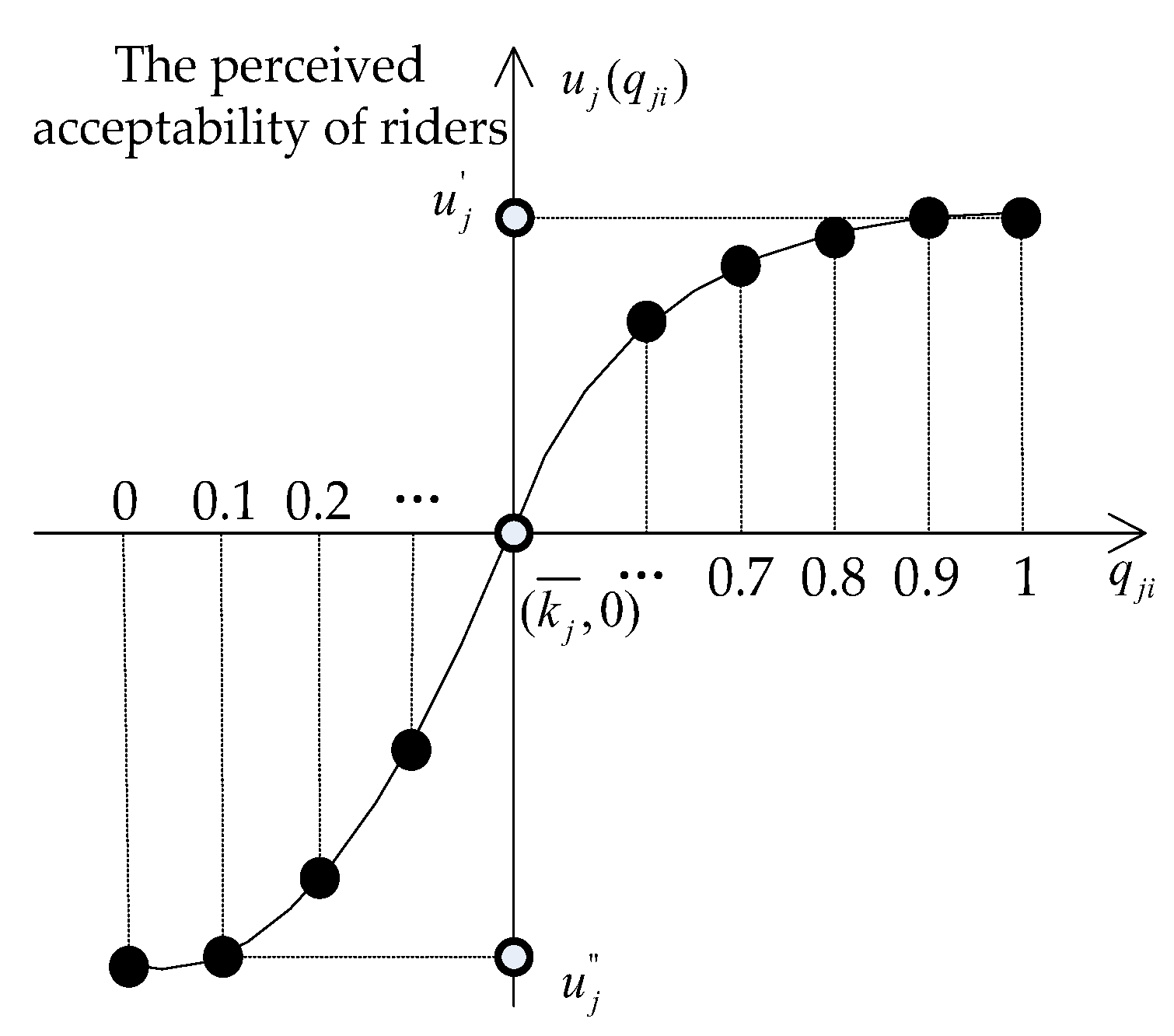
4.2.3. The Perception Function of Riders
4.3. A Two-Sided Matching Decision Model Considering Psychological Perceived Behavior.
5. The Numerical Example
5.1. Description of the Test Data
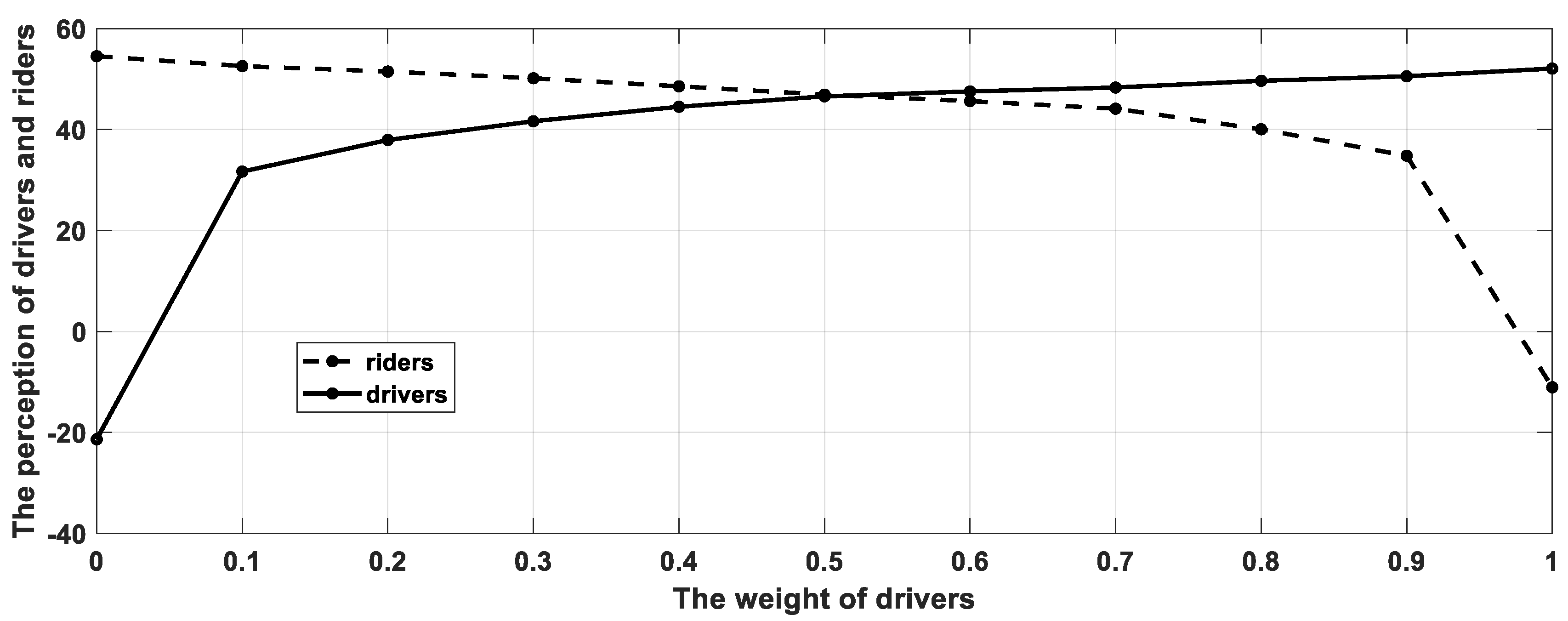
5.2. Analysis of the Weights Assigned to Different Objectives
- ①
- Both drivers and riders can get a better comprehensive perception when their perception of matching scheme is taken into consideration;
- ②
- With the improvement of the weight of the perception regarding one side, the weight of the perception regarding the other side can be correspondingly decreased. Causing the integral perception of the weight increase side in the matching scheme is improved, and the integral perception of the weight reduction side is decreased;
- ③
- The perception of the matching scheme regarding the other objects decreases rapidly based on only optimizing the perception of one object. For example, DiDi’s Hitch business was used to encourage drivers to provide sharing services by adopting the task distribute mode of priority dispatching for drivers. The results of this approach have proved to be a failure.
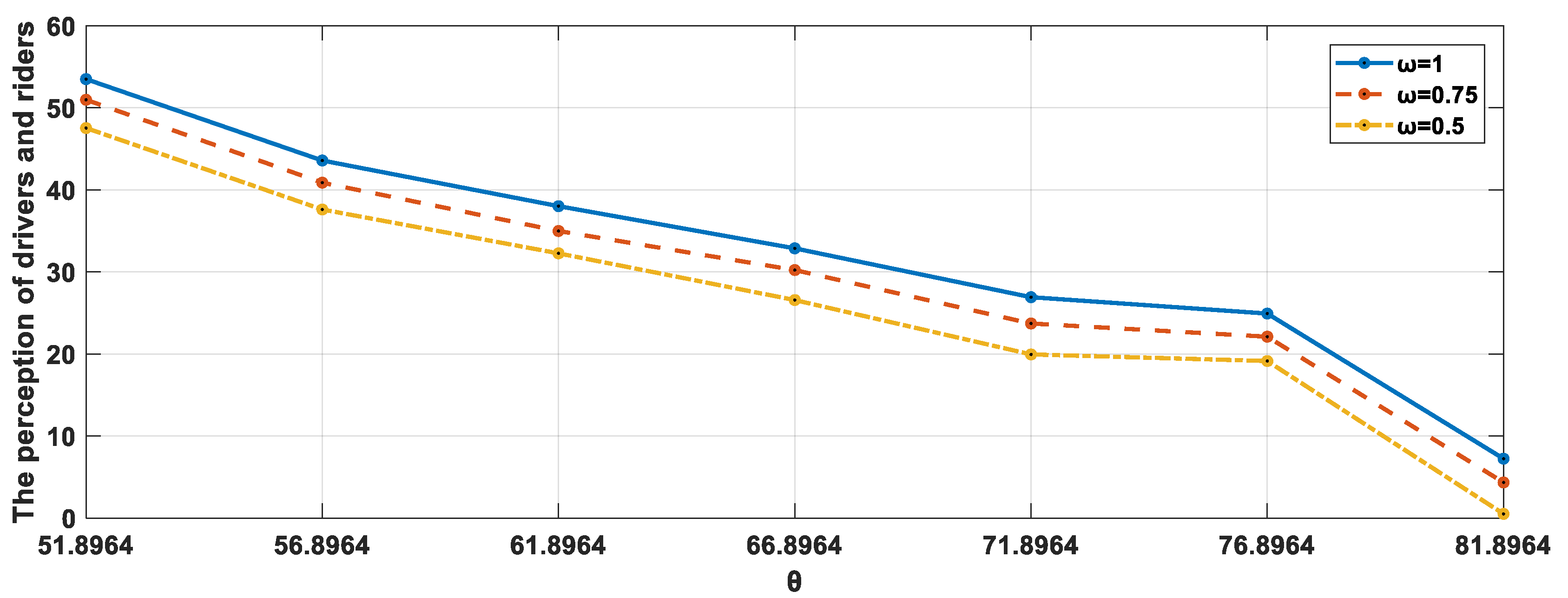
5.3. Analysis of Multi-Objective Weight Setting and Managerial Insights Under Unbalanced Supply-Demand
6. Conclusions and Future Works
Author Contributions
Funding
Conflicts of Interest
References
- Furuhata, M.; Dessouky, M.; Ordónez, F.; Brunet, M.E.; Wang, X.; Koenig, S. Ridesharing: The state-of-the-art and future directions. Transp. Res. Part B Methodol. 2013, 57, 28–46. [Google Scholar] [CrossRef]
- DiDi Hitch. Available online: https://www.didiglobal.com/about-special/milestone (accessed on 14 January 2019).
- Greenwood, B.N.; Wattal, S. Show Me the Way to Go Home: An Empirical Investigation of Ride-Sharing and Alcohol Related Motor Vehicle Fatalities. MIS Q. 2017, 41, 163–187. [Google Scholar] [CrossRef]
- Hello Hitch. Available online: http://www.hellobike.com/newsDetail.html?guid=23d15d7acb124fa1997e14d8b5796272 (accessed on 22 February 2019).
- Pelzer, D.; Xiao, J.J.; Zehe, D.; Lees, M.H.; Knoll, A.C.; Aydt, H. A partition-based match making algorithm for dynamic Ridesahring. IEEE Trans. Intell. Transp. Syst. 2015, 16, 2587–2598. [Google Scholar] [CrossRef]
- Barann, B.; Beverungen, D.; Müllerc, O. An open-data approach for quantifying the potential of taxi ridesahring. Decis. Support Syst. 2017, 99, 86–95. [Google Scholar] [CrossRef]
- Lee, A.; Savelsbergh, M. Dynamic Ridesharing: Is there a role for dedicated drivers? Transp. Res. Part B 2015, 81, 483–497. [Google Scholar] [CrossRef]
- Rayle, L.; Dai, D.; Chan, N.; Cervero, R.; Shaheen, S. Just a better taxi? A survey-based comparison of taxis, transit, and ridesourcing services in San Francisco. Transp. Policy 2016, 45, 168–178. [Google Scholar] [CrossRef]
- Chan, N.D.; Shaheen, S.A. Ridesharing in North America: Past, Present, and Future. Transp. Rev. 2012, 32, 93–112. [Google Scholar] [CrossRef]
- Carter, C.R.; Rogers, D.S. A framework of sustainable supply chain management: Moving toward new theory. Int. J. Phys. Distrib. Logist. Manag. 2008, 38, 360–387. [Google Scholar] [CrossRef]
- Schreieck, M.; Safetli, H.; Siddiqui, S.A.; Pflügler, C.; Wiesche, M.; Krcmar, H. A matching algorithm for dynamic ridesharing. Ridesharing Transp. Res. Procedia 2016, 19, 272–285. [Google Scholar] [CrossRef]
- Seuring, S. Integrated chain management and supply chain management comparative analysis and illustrative cases. J. Clean. Prod. 2004, 12, 1059–1071. [Google Scholar] [CrossRef]
- Hong, Z.; Chen, Y.; Mahmassani, H.S.; Xu, S. Commuter ride-sharing using topology-based vehicle trajectory clustering: Methodology, application and impact evaluation. Transp. Res. C Emerg. Technol. 2017, 85, 573–590. [Google Scholar] [CrossRef]
- Agatz, N.; Erera, A.; Savelsbergh, M.; Wang, X. Optimization for dynamic ride-sharing: A review. Eur. J. Oper. Res. 2012, 223, 295–303. [Google Scholar] [CrossRef]
- Nourinejad, M.; Roorda, M.J. Agent based model for dynamic ridesharing. Transp. Res. Part C 2016, 64, 117–132\. [Google Scholar] [CrossRef]
- Wang, X.L.; Yang, H.; Zhu, D.L. Driver-rider cost-sharing strategies and equilibria in a ridesharing program. Transp. Sci. 2018, 52, 868–881. [Google Scholar] [CrossRef]
- Ma, R.; Zhang, H.M. The morning commute problem with ridesharing and dynamic parking charges. Transp. Res. Part B Methodol. 2017, 106, 345–374. [Google Scholar] [CrossRef]
- Liu, Y.; Li, Y.Y. Pricing scheme design of ridesharing program in morning commute problem. Transp. Res. Part C Emerg. Technol. 2017, 79, 156–177. [Google Scholar] [CrossRef]
- Mallus, M.; Colistra, G.; Atzori, L.; Murroni, M.; Pilloni, V. Dynamic Carpooling in Urban Areas: Design and Experimentation with a Multi-Objective Route Matching Algorithm. Sustainability 2017, 9, 254. [Google Scholar] [CrossRef]
- Yousaf, J.; Li, J.Z.; Chen, L.; Tang, J.; Dai, X.W. Generalized multipath planning model for ride-sharing systems. Front. Comput. Sci. 2014, 8, 100–118. [Google Scholar] [CrossRef]
- Lee, H.L.; Tang, C.S. Socially and Environmentally Responsible Value Chain Innovations: New Operations Management Research Opportunities. Manag. Sci. 2017, 64, 983–996. [Google Scholar] [CrossRef]
- Jaehn, F. Sustainable Operations. Eur. J. Oper. Res. 2016, 253, 243–264. [Google Scholar] [CrossRef]
- Cao, C.; Li, C.; Yang, Q.; Zhang, F. Multi-Objective Optimization Model of Emergency Organization Allocation for Sustainable Disaster Supply Chain. Sustainability 2017, 9, 2103. [Google Scholar] [CrossRef]
- Cao, C.; Li, C.; Yang, Q.; Liu, Y.; Qu, T. A novel multi-objective programming model of relief distribution for sustainable disaster supply chain in large-scale natural disasters. J. Clean. Prod. 2018, 174, 1422–1435. [Google Scholar] [CrossRef]
- Gale, D.; Shapley, L.S. College Admissions and the Stability of Marriage. Am. Math. Mon. 1962, 69, 9. [Google Scholar] [CrossRef]
- Korkmaz, I.; Gokcen, H.; Çetinyokuş, T. An analytic hierarchy process and two-sided matching based decision support system for military personnel assignment. Inf. Sci. 2008, 178, 2915–2927. [Google Scholar] [CrossRef]
- Cheng, Y.; Tao, F.; Zhao, D.; Zhang, L. Modeling of manufacturing service supply–demand matching hypernetwork in service-oriented manufacturing systems. Robot. Comput. Manuf. 2017, 45, 59–72. [Google Scholar] [CrossRef]
- Uetake, K.; Watanabe, Y. Entry by Merger: Estimates from a Two-Sided Matching Model with Externalities. SSRN Electron. J. 2012. [Google Scholar] [CrossRef]
- Liang, R.; Wu, C.; Sheng, Z.; Wang, X. Multi-Criterion Two-Sided Matching of Public–Private Partnership Infrastructure Projects: Criteria and Methods. Sustainability 2018, 10, 1178. [Google Scholar] [CrossRef]
- Vecchioa, G.; Tricarico, L. “May the Force move you”: Roles and actors of information sharing devices in urban mobility. Cities 2018. [Google Scholar] [CrossRef]
- Fan, Z.P.; Li, M.Y.; Zhang, X. Satisfied Two-Sided Matching: A Method Considering Elation and Disappointment of Agent. Soft Computing 2018, 22, 7227. [Google Scholar] [CrossRef]
- Chen, X.; Li, Z.; Fan, Z.-P.; Zhou, X.; Zhang, X. Matching demanders and suppliers in knowledge service: A method based on fuzzy axiomatic design. Inf. Sci. 2016, 346, 130–145. [Google Scholar] [CrossRef]
- Echenique, F.; Lee, S.; Shum, M.; Yenmez, M.B. The Revealed Preference Theory of Stable and Extremal Stable Matchings. Econometrica 2013, 81, 153–171. [Google Scholar] [CrossRef][Green Version]
- Zhong, L.W.; Bai, Y.Q. Equivalence of two-sided stable matching. J. Comb. Optim. 2018, 36, 1380–1387. [Google Scholar] [CrossRef]
- Kahneman, D.; Tversky, A. Prospect theory: An analysis of decision under risk. Estudios De Psicología Stud. Psychol. 1987, 8, 95–124. [Google Scholar] [CrossRef]
- Fulga, C. Portfolio optimization under loss aversion. Eur. J. Oper. Res. 2016, 251, 310–322. [Google Scholar] [CrossRef]
- Tan, C.Q.; Lp, W.H.; Chen, X.H. Stochastic multiple criteria decision making with aspiration level based on prospect stochastic dominance. Knowl.-Based Syst. 2014, 70, 231–241. [Google Scholar] [CrossRef]
- Wang, L.; Wang, Y.-M.; Martínez, L. A group decision method based on prospect theory for emergency situations. Inf. Sci. 2017, 418, 119–135. [Google Scholar] [CrossRef]
- Guan, G.H.; Liang, Z.X. Optimal management of DC pension plan under loss aversion and Value-at-Risk constraints. Insur. Math. Econ. 2016, 69, 224–237. [Google Scholar] [CrossRef]
- Liu, P.; Jin, F.; Zhang, X.; Su, Y.; Wang, M. Research on the multi-attribute decision-making under risk with interval probability based on prospect theory and the uncertain linguistic variables. Knowl.-Based Syst. 2011, 24, 554–561. [Google Scholar] [CrossRef]
- Lovelock, C.; Wirtz, J.; Tang, C. Uber: Competing as Market Leader in the US versus Being a Distant Second in China; World Scientific Pub Co. Pte Lt.: Singapore, 2016; pp. 626–632. [Google Scholar]
- Kong, D.C.; Jiang, Y.P.; Liang, H.M. Stable Matching with Fairness for Two-sided Agents. J. Syst. Manag. 2015, 24, 397–404. [Google Scholar]
- Herbawi, W.; Weber, M. The ridematching problem with time windows in dynamic ridesharing: A model and a genetic algorithm. In Proceedings of the 2012 IEEE Congress on Evolutionary Computation (CEC), Brisbane, QLD, Australia, 10–15 June 2012; pp. 1–8. [Google Scholar]
- D’Agostino, R.B. Tests for the Normal Distribution. Goodness-of-Fit-Techniques; Routledge: Abingdon-on-Thames, UK, 2017; pp. 367–420. [Google Scholar]
- Tversky, A.; Kahneman, D. Advances in prospect theory: Cumulative representation of uncertainty. J. Risk Uncertain. 1992, 5, 297–323. [Google Scholar] [CrossRef]
| Reference | Year | Main Objectives | ||
|---|---|---|---|---|
| Economic | Social Cost | Environment | ||
| Hong et al. | 2017 | √ | √ | |
| Nourinejad et al. | 2016 | √ | ||
| Barann et al. | 2017 | √ | √ | |
| Pelzer et al. | 2015 | √ | ||
| Wang et al. | 2018 | √ | ||
| Ma et al. | 2017 | √ | ||
| Lee et al. | 2015 | √ | ||
| Liu et al. | 2017 | √ | ||
| Mallus et al. | 2017 | √ | √ | |
| Yousaf et al. | 2014 | √ | √ | |
| Notation | Description |
|---|---|
| The number of drivers | |
| The number of riders | |
| Set of drivers, where , denotes driver , and , where | |
| Set of riders, where , denotes rider , and ,where | |
| The comprehensive evaluation vector regarding the perceived suitability of to potential matching schemes provided by riders, where , denotes the comprehensive evaluation value regarding the perceived suitability of to potential matching scheme provided by | |
| The comprehensive evaluation matrix regarding the perceived suitability of potential drivers to potential matching schemes provided by riders, where | |
| The comprehensive evaluation vector regarding the perceived acceptability of to potential matching schemes provided by drivers, where , denotes the comprehensive evaluation value regarding the perceived acceptability of to potential matching scheme provided by | |
| The comprehensive evaluation matrix regarding the perceived acceptability of potential riders to potential matching schemes provided by drivers, where | |
| The historical evaluation mean regarding the perceived suitability of to historical matching scheme | |
| The comprehensive evaluation value regarding the perceived suitability of to historical matching scheme , , where , denotes the numbers of success matching scheme | |
| The historical evaluation mean vector regarding the perceived suitability of drivers to historical matching scheme, where | |
| The historical evaluation mean regarding the perceived acceptability of to historical matching scheme | |
| The comprehensive evaluation value regarding the perceived acceptability of , to historical matching scheme , , where , denotes the numbers of matching scheme | |
| The historical evaluation mean vector regarding the perceived acceptability of riders to historical matching scheme, where | |
| The perception function of to matching scheme | |
| The perception function of to matching scheme |
| Operation Time (s) | |||||
|---|---|---|---|---|---|
| (50,50) | 28.7921 | −20.4788 | −18.1376 | 31.4482 | 0.1596 |
| (100,100) | 45.2423 | −25.4568 | −21.3699 | 44.1580 | 0.2456 |
| (150,150) | 79.3023 | −33.0059 | −31.4955 | 76.4522 | 0.5130 |
| (200,200) | 105.3567 | −44.2357 | −52.2579 | 109.2479 | 1.3174 |
| (250,250) | 123.2316 | −46.8948 | −61.9862 | 129.0581 | 2.3250 |
| (300,300) | 153.0194 | −74.3257 | −89.2357 | 159.3575 | 2.9516 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Q.; Liu, J.; Liu, X.; Cao, C.; Zhang, W. A Two-Sided Matching Model for Task Distribution in Ridesharing: A Sustainable Operations Perspective. Sustainability 2019, 11, 2187. https://doi.org/10.3390/su11072187
Yang Q, Liu J, Liu X, Cao C, Zhang W. A Two-Sided Matching Model for Task Distribution in Ridesharing: A Sustainable Operations Perspective. Sustainability. 2019; 11(7):2187. https://doi.org/10.3390/su11072187
Chicago/Turabian StyleYang, Qin, Jinfeng Liu, Xing Liu, Cejun Cao, and Wei Zhang. 2019. "A Two-Sided Matching Model for Task Distribution in Ridesharing: A Sustainable Operations Perspective" Sustainability 11, no. 7: 2187. https://doi.org/10.3390/su11072187
APA StyleYang, Q., Liu, J., Liu, X., Cao, C., & Zhang, W. (2019). A Two-Sided Matching Model for Task Distribution in Ridesharing: A Sustainable Operations Perspective. Sustainability, 11(7), 2187. https://doi.org/10.3390/su11072187





