Livelihoods Strategies and Household Resilience to Food Insecurity: A Case Study from Rural Tunisia
Abstract
1. Introduction
2. Materials and Methods
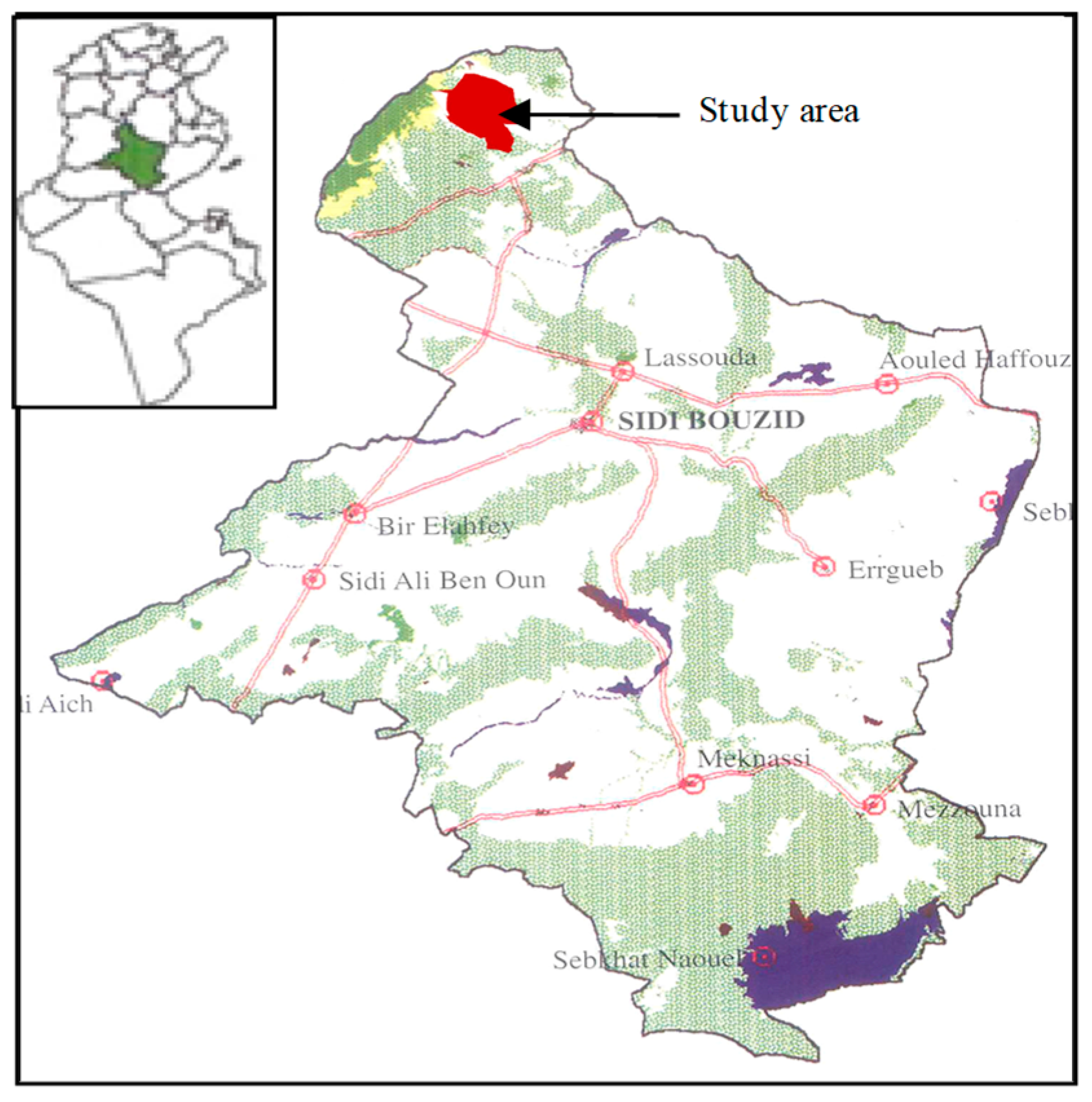
2.1. Study Area
2.2. Data Collection and Analysis Procedure
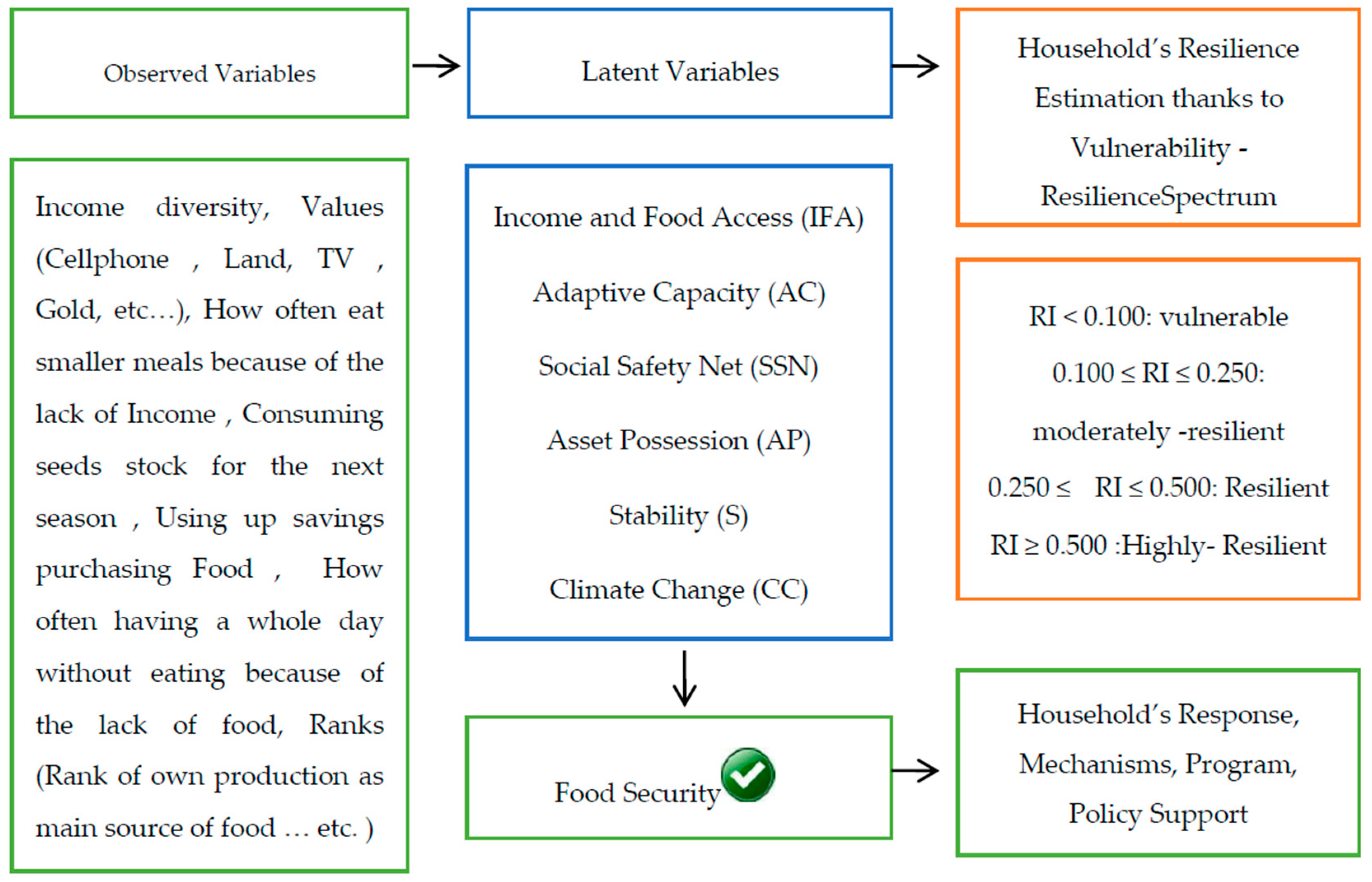
2.3. Empirical Model
3. Results and Discussion
3.1. Estimation of the Latent Indicators
3.1.1. Income and Food Access (IFA)
- Total income per day per person (TIPDPP). This is a continuous included observed variable measuring the IFA. Its calculation is based on the different sources of income (livestock income, crop income, and other income)
- Storage after harvest (SAH). The quantity of grain held in stock (quintals (1 quintal = 100 kg))
- Diversity (D). This measure is based on the number of days/month, on average, that the household consumes certain items, such as wheat, barley, other cereal (rice, sorghum, millet, maize, etc.), roots and tubers (potatoes and sweet potatoes), legumes, sugar or sugar products, groundnuts or cashew nuts, etc.
- Index adaptation strategy (IAS). This was estimated from the average number of coping strategies available to the household when it lacks food—purchasing food on credit to overcome daily food insecurity, borrowing food, seeking help from relatives or the community, adults eating less so that children can eat more, consuming seeds saved for next season, etc. Its value lies between 0 and 1 where 0 equates to no coping strategy and 1 equates to a maximum of 11 coping strategies
- Food access (FA). This is a continuous observed variable that was estimated as an average of the responses to six questions that sought to understand the household’s ability to access food. Its values lie between 0 and 3. The question was concerned mainly with different aspects of the households’ abilities to access food. The questions addressed such issues as:
- How often was the household worried that it would not have enough food to eat for the month?
- How often was the household unable to eat its preferred food because of a lack of income?
- How often did the household eat fewer meals per day because of not having enough food?
3.1.2. Adaptive Capacity (AC)
- Anticipate and respond to changes
- Minimize, cope with, and recover from the consequences of change
- Take advantage of new opportunities.
- In our study, the included observed variables estimating AC are all continuous variables.
- Income diversity (ID): with values between a minimum of 1 and a maximum of 5
- Available coping strategies (ACS): with values ranging from 0 to 16
- Number of off-farm incomes (NOFI): with values ranging from 0 to 10
- Number of house assets (NHA): with values ranging between 1 and 22.
3.1.3. Social Safety Net (SSN)
- Member of a social organization or association (MSOA): (Yes/No).
- Borrow food or get help from a relative or the community (BFHRC): (Yes/No).
- Send the children to live with relatives (SCLR): (Yes/No).
- Accept food aid from an international organization (AFAIO): (Yes/No).
- Borrow money from relatives or neighbors (BMRN): (Yes/No).
- Level of participation, contribution and policy making (LPCPM): (Yes/No).
3.1.4. Assets Possession (AP)
- Total owned land (ha) (TOwLH): This is an interesting variable, knowing that only 2.9% in Zoghmar, and only 7.6% in Selta are landless farmers
- Herd size (HS): was included because it is an also an intriguing observed variable. Given the lack of water resources, the system of production is mostly dependent on raising livestock, and therefore, the practice of sheep herding [10]
- House value (HVal): Amount in Tunisian dinars
- Value of agricultural assets (AA): Amount in Tunisian dinars
- Value of non-agricultural assets (NAA): Amount in Tunisian dinars.
3.1.5. Stability (S)
- Farming experience (FExp)
- Number of households off-farm (NHHOF)
- Family size (FS)
- Number of members of the household studying in superior school or university (NSup)
- Number of females in the household (NFem)
3.1.6. Climate Change (CC)
- Observed drought (OD): (Yes/No)
- Observed flood (OF): (Yes/No)
- Observed hail storms (OHS): (Yes/No)
- Observed timely rains (OTR): (Yes/No)
- Observed dry spells (ODS): (Yes/No)
- Observed temperature fluctuations – highs (OTFH): (Yes/No)
- Observed temperature fluctuation – lows (OTFL): (Yes/No)
- Observed changes in soil salinity (OCSS): (Yes/No)
3.2. Estimating an Overall Resilience Index (RI)
- Vulnerable (RI < 0.100) with all values coded 0;
- Moderately resilient (0.100 ≤ RI < 0.250) with all values coded 1
- Resilient (0.250 ≤RI < 0.500) with all values coded 2
- Highly resilient (RI ≥0.500) with all values coded 3. The results (Table 8) shows that 64.4% of the surveyed households were vulnerable, while 35.6% were resilient to different degrees (10.4% moderately, 13.6% resilient, and 11.6% highly).
3.3. Relative Importance of the Latent Dimensions of Household Resilience
4. Concluding Remarks and Policy Implications
Author Contributions
Acknowledgments
Conflicts of Interest
References
- World Bank. Tunisia in a Changing Climate: Assessment and Actions for Increased Resilience and Development. A World Bank Study; Verner, D., Ed.; World Bank: Washington, DC, USA, 2013; ISBN 978-0-8213-9857-9. [Google Scholar]
- Institut National de la Statistique (INS). 2015. Available online: http://www.ins.tn/fr/p%C3%A9riode-de-r%C3%A9ference/2015 (accessed on 12 December 2018).
- Stambouli, T.; Hammami, R.; Ouissi, A.; Ben Alaya, A.; Laajili-Ghezal, L. Virtual water balance estimation in Tunisia. J. New Sci. 2017, 31, 1783–1793. [Google Scholar]
- Verner, D.; Treguer, D.O.; Redwood, J.; Christensen, J.; Mcdonnell, R.; Elbert, C.; Konishi, Y. Climate Variability, Drought, and Drought Management in Tunisia’s Agricultural Sector; World Bank Group: Washington, DC, USA, 2018; 114p. [Google Scholar]
- Alexander, D.E. Resilience and disaster risk reduction: An etymological journey. Nat. Hazards Earth Syst. Sci. 2013, 13, 2707–2716. Available online: https://www.nat-hazards-earth-syst-sci.net/13/2707/2013/nhess-13-2707-2013.pdf (accessed on 12 December 2018). [CrossRef]
- Jones, L.; Tanner, T. Measuring ‘Subjective Resilience’: Using Peoples’ Perceptions to Quantify Household Resilience; Working Paper 423; Overseas Development Institute: London, UK, 2015. [Google Scholar]
- Ciani, F. A Resilience-Based Approach to Food Insecurity: The Impact of Hurricane Mitch on Rural Household in Nicaragua. Ph.D. Thesis, University of Florence, Gainesville, FL, USA, 2012. [Google Scholar]
- Errico, M.; Pietrelli, R.; Romano, D. Household resilience to food insecurity: Evidence from Tanzania and Uganda. In Proceedings of the 90th Annual Conference of the Agricultural Economics Society, Coventry, UK, 4–6 April 2016; Available online: https://ageconsearch.umn.edu/record/236350/files/marco_d_errico%20upload.pdf (accessed on 12 December 2018).
- Alinovi, L.; Mane, E.; Romano, D. Towards the Measurement of Household Resilience to Food Insecurity: An Application to Palestinian Households. 2008. Available online: http://www.stats.gov.cn/english/ICAS/papers../P020071017475481721768.pdf (accessed on 12 December 2018).
- Dhraief, M.Z.; Oueslati, M.; Daly, H.; Bedhiaf, S.; Dhehibi, B.; Kassam, S.; Aw-Hassan, A. Analysis Report of the Baseline Survey for the CRP DS Project in Sidi Bouzid Site; ICRDA: Beirut, Lebanon, 2015; 123p. [Google Scholar]
- Béné, C.; Headey, D.; Haddad, L.; Grebmer, K.V. Is resilience a useful concept in the context of food security and nutrition programs? Some conceptual and practical considerations. Food Secur. 2016, 8, 123–138. [Google Scholar] [CrossRef]
- Bizikova, L.; Tyler, S.; Moench, M.; Keller, M.; Echeverria, D. Climate resilience and food security in Central America: A practical framework. Clim. Dev. 2015. [Google Scholar] [CrossRef]
- Frankenberger, T. Enhancing Resilience to Food Security Shocks in Africa, TANGO International TOPS Knowledge Sharing Meeting, Washington, DC, USA, 2012. Available online: http://www.fsnnetwork.org/sites/default/files/resilience_ppt.pptx (accessed on 12 December 2018).
- Guyu, F.D.; Muluneh, W. Household resilience to seasonal food insecurity: Dimensions and magnitudes in the “Green Famine” belt of Ethiopia. Appl. Sci. Rep. 2015, 3, 125–143. [Google Scholar]
- Boukary, A.G.; Diaw, A.; Wünscher, T. Factors Affecting rural households’ resilience to food insecurity in Niger. Sustainability 2016, 8, 181. [Google Scholar] [CrossRef]
- Burton, C.G. The Development of Matrices for Community Resilience to Natural Disasters. Ph.D. Thesis, University of South Carolina, Columbia, SC, USA, 2012, unpublished. [Google Scholar]
- Alinovi, L.; Mane, E.; Romano, E. Measuring Household Resilience to Food Insecurity: Application to Palestinian Household. 2009. Available online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.175.7411&rep=rep1&type=pdf (accessed on 10 October 2018).
- Nelli, N. The Resilience of Rural Ethiopian Livelihoods: A Case Study from Hararghe Zone, Eastern Ethiopia. Master’s Thesis, University of Jyväskylä, Jyväskylän yliopisto, Finland, 2011. Available online: https://jyx.jyu.fi/bitstream/handle/123456789/37212/URN%3aNBN%3afi%3ajyu-201201161033.pdf?sequence=1&isAllowed=y (accessed on 12 December 2018).
- Bartlett, M.S. Properties of sufficiency and statistical tests. Proc. R. Stat. Soc. 1937, 160, 268–282. [Google Scholar]
- Cramer, L.; Forch, W.; Mutie, L.; Thornton, F.K. Connecting women, connecting men: How communities and organizations interact to strengthen adaptive capacity and food security in the face of climate change. Gend. Technol. Dev. 2016, 20, 169–199. [Google Scholar] [CrossRef]
- McClanahan, T.R.; Allison, E.H.; Cinner, J.E. Managing fisheries for human and food security. Fish Fish. J. 2013, 16. [Google Scholar] [CrossRef]
- Mathers, N.; Fox, N.; Hunn, A. Surveys and Questionnaires, The NIHR Research Design Service for Yorkshire and the Humber. 2009. Available online: https://www.rds-yh.nihr.ac.uk/wp-content/uploads/2013/05/12_Surveys_and_Questionnaires_Revision_2009.pdf (accessed on 12 December 2018).
- DiStefano, C.; Zhu, M.; Mindrila, D. Understanding and using factor scores: Considerations for the applied researchers. Pract. Assess. Res. Eval. 2009, 14, 1–11. [Google Scholar]
- Elloumi, M.; Véronique, A.; Selmi, S. Policies and strategies of livestock farmers in Sidi Bouzid Governorate (central Tunisia). Afr. Contemp. 2016, 219, 63–79. [Google Scholar] [CrossRef]
| Indicators of IFA | Communalities | Factors and Their Loads | Corr. IFA | ||
|---|---|---|---|---|---|
| Initial | Extraction | 1 | 2 | ||
| FA | 1.000 | 0.597 | 0.726 | 0.263 | 0.585** |
| TIPDPP | 1.000 | 0.465 | 0.647 | 0.217 | 0.505** |
| IAS | 1.000 | 0.515 | 0.630 | 0.343 | 0.608** |
| SAH | 1.000 | 0.655 | −0.366 | 0.722 | 0.450** |
| D | 1.000 | 0.626 | −0.425 | 0.667 | 0.374** |
| Eigenvalues | Total Variance (%) Cumulative (%) | 1.591 | 1.312 | ||
| 33.141 | 23.997 | ||||
| 33.141 | 57.138 | ||||
| KMO test of sampling adequacy = 0.598 Bartlett’s test of sphericity is significant at p = 0.000; chi-square = 82.320 Extraction method: principal component analysis **: Correlation is significant at the 0.01 level | |||||
| Indicators of AC | Communalities | Factors and Their Loads | Corr. AC | ||
|---|---|---|---|---|---|
| Initials | Extraction | 1 | 2 | ||
| NHA | 1.000 | 0.572 | 0.755 | 0.627** | |
| ID | 1.000 | 0.366 | 0.605 | 0.460** | |
| NOFI | 1.000 | 0.776 | 0.413 | 0.778 | 0.803** |
| ACS | 1.000 | 0.705 | −0.509 | 0.668 | 0.006 |
| Eigenvalues | Total Variance (%) Cumulative (%) | 1.350 | 1.062 | ||
| 34.122 | 26.378 | ||||
| 34.122 | 60.501 | ||||
| KMO test of sampling adequacy = 0.524 Bartlett’s test of sphericity is significant at p = 0.000; chi-square = 28.798 Extraction method: principal component analysis **: Correlation is significant at the 0.01 level | |||||
| Indicators of SSN | Factors and Their Loads | Corr. SSN | ||
|---|---|---|---|---|
| 1 | 2 | |||
| BFHRC | 0.802 | −0.254 | 0.471** | |
| SCLR | 0.687 | 0.060 | 0.576** | |
| BMRN | 0.546 | 0.492 | 0.734** | |
| AFAIO | 0.209 | 0.759 | 0.635** | |
| LPCPM | −0.364 | 0.640 | 0.112 | |
| MSOA | 0.256 | −0.124 | 0.124 | |
| Eigenvalues | Total | 1.655 | 1.312 | Total Cronbach’s alpha = 0.796 |
| Variance (%) | 27.588 | 21.864 | ||
| Cumulative (%) | 27.588 | 49.452 | ||
| Cronbach’s alpha | 0.475 | 0.285 | ||
| Indicators of AP | Communalities | Factors and Their Loads | Corr. AP | ||
|---|---|---|---|---|---|
| Initials | Extraction | 1 | 2 | ||
| TOwLH | 1.000 | 0.504 | 0.756 | 0.217 | 0.439** |
| HS | 1.000 | 0.619 | 0.695 | 0.270 | 0.759** |
| HVal | 1.000 | 0.644 | 0.665 | −0.248 | 0.352** |
| AA | 1.000 | 0.562 | 0.799 | 0.602** | |
| NAA | 1.000 | 0.555 | 0.281 | 0.695 | 0.734** |
| Eigenvalues | Total Variance (%) Cumulative (%) | 1.793 | 1.092 | ||
| 35.865 | 21.834 | ||||
| 35.865 | 57.699 | ||||
| KMO test of sampling adequacy = 0.566 Bartlett’s test of sphericity is significant at p = 0.000; chi-square = 114.417 Extraction method: principal component analysis **: Correlation is significant at the level of 0.01 | |||||
| Indicators of S | Communalities | Factors and Their Loads | Corr. S | ||
|---|---|---|---|---|---|
| Initials | Extraction | 1 | 2 | ||
| FS | 1.000 | 0.846 | 0.920 | 0.854** | |
| NFem | 1.000 | 0.782 | 0.883 | 0.547** | |
| NSup | 1.000 | 0.583 | 0.599 | −0.473 | 0.302** |
| FExp | 1.000 | 0.689 | 0.160 | 0.814 | 0.420** |
| NHHOF | 1.000 | 0.378 | 0.422 | 0.447 | 0.621** |
| Eigenvalues | Total Variance (%) Cumulative (%) | 2.146 | 1.234 | ||
| 43.772 | 21.775 | ||||
| 43.772 | 65.547 | ||||
| KMO test of sampling adequacy = 0.595 Bartlett’s test of sphericity is significant at p = 0.000; chi-square = 334.863 Extraction method: principal component analysis **: Correlation is significant at the 0.01 level (2-tailed) | |||||
| Indicators of CC | Factors and Their Loads | Corr. CC | |||
|---|---|---|---|---|---|
| 1 | 2 | 3 | |||
| OTR | 0.816 | −0.099 | −0.096 | 0.628** | |
| ODS | 0.705 | 0.388 | 0.026 | 0.760** | |
| OTFL | 0.655 | 0.139 | −0.177 | 0.552** | |
| OTFH | 0.661 | 0.353 | 0.050 | 0.717** | |
| OHS | 0.583 | −0.069 | 0.407 | 0.616** | |
| OCSS | 0.400 | −0.597 | 0.078 | 0.144* | |
| OF | −0.350 | 0.693 | 0.291 | 0.064 | |
| OD | −0.027 | −0.158 | 0.886 | 0.228** | |
| Eigenvalues | Total | 2.652 | 1.170 | 1.085 | Total Cronbach’s alpha = 0.910a |
| Variance (%) | 33.149 | 14.624 | 13.565 | ||
| Cumulative (%) | 33.149 | 47.773 | 61.338 | ||
| Cronbach’s alpha | 0.712 | 0.166 | 0.090 | ||
| A: the total Cronbach’s alpha value is based on the total eigenvalue **correlation is significant at the 0.01 level | |||||
| Variable | Factors and Their Loads | Correlation With (RI) | ||
|---|---|---|---|---|
| 1 | 2 | 3 | ||
| S | 0.756 | 0.172 | 0.446 | 0.457** |
| AC | 0.684 | 0.475 | 0.293 | 0.690** |
| AP | 0.583 | −0.568 | 0.009 | |
| IFA | −0.328 | 0.761 | −0.161 | 0.594** |
| SSN | −0.501 | 0.594 | 0.344 | 0.501** |
| CC | −0.172 | −0.617 | 0.506 | −0.517** |
| Eigenvalue | 1.614 | 1.453 | 1.498 | |
| Variance (%) | 29.455 | 26,124 | 16,798 | |
| Cumulative (%) | 29.455 | 55.579 | 72.377 | |
| KMO test of sampling adequacy = 0.541 Bartlett’s test of sphericity is significant at p = 0.000; chi-square = 203.538 Extraction method: principal component analysis **: Correlation is significant at the 0.01 level (2-tailed) | ||||
| N | Proportion (%) | Cumulative Proportion (%) | |
|---|---|---|---|
| Vulnerable (RI < 0.100) | 161 | 64.4 | 64.4 |
| Moderately resilient (0.100 ≤ RI < 0.250) | 26 | 10.4 | 74.8 |
| Resilient (0.250 ≤ RI < 0.500) | 34 | 13.6 | 88.4 |
| Highly resilient (RI ≥ 0.500) | 29 | 11.6 | 100.0 |
| Total | 250 | 100.0 |
| N1 | Selta sub-District (%) | N2 | Zoghmar Sub-District (%) | |
|---|---|---|---|---|
| Vulnerable | 91 | 62.8 | 70 | 66.7 |
| Moderately resilient | 16 | 11.0 | 10 | 9.5 |
| Resilient | 24 | 16.6 | 10 | 9.5 |
| Highly resilient | 14 | 9.7 | 15 | 14.3 |
| Total | 145 | 100.0 | 105 | 100.0 |
| Model Summary | ||||
|---|---|---|---|---|
| Model | R | R2 | Adjusted R2 | Std. error of the estimate |
| 1 | 0.966a | 0.933 | 0.932 | 0.11488 |
| a. Predictors: (constant), CC, AP, SSN, IFA, AC | ||||
| Latent Variables | Unstandardized Coefficients | Standardized Coefficients β | t | Sig. | Collinearity Statistics | ||
|---|---|---|---|---|---|---|---|
| B | Std. error | Tolerance | VIF | ||||
| Constant | −0.000 | 0.007 | 0.000 | 1,000 | 0.760 | 1.316 | |
| IFA | 0.754 | 0.044 | 0.328 | 17.324 | 0.000 | 0.922 | 1.084 |
| AC | 1.255 | 0.035 | 0.614 | 35.689 | 0.000 | 0.877 | 1.140 |
| CC | −0.966 | 0.060 | −0.283 | −16.061 | 0.000 | 0.762 | 1.312 |
| SSN | 0.843 | 0.047 | 0.337 | 17.840 | 0.000 | 0.876 | 1.142 |
| AP | −0.073 | 0.037 | −0.035 | −1.968 | 0.050 | 0.760 | 1.316 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dhraief, M.Z.; Dhehibi, B.; Daly Hassen, H.; Zlaoui, M.; Khatoui, C.; Jemni, S.; Jebali, O.; Rekik, M. Livelihoods Strategies and Household Resilience to Food Insecurity: A Case Study from Rural Tunisia. Sustainability 2019, 11, 907. https://doi.org/10.3390/su11030907
Dhraief MZ, Dhehibi B, Daly Hassen H, Zlaoui M, Khatoui C, Jemni S, Jebali O, Rekik M. Livelihoods Strategies and Household Resilience to Food Insecurity: A Case Study from Rural Tunisia. Sustainability. 2019; 11(3):907. https://doi.org/10.3390/su11030907
Chicago/Turabian StyleDhraief, Mohamed Zied, Boubaker Dhehibi, Hamed Daly Hassen, Meriem Zlaoui, Chaima Khatoui, Sondes Jemni, Ouessama Jebali, and Mourad Rekik. 2019. "Livelihoods Strategies and Household Resilience to Food Insecurity: A Case Study from Rural Tunisia" Sustainability 11, no. 3: 907. https://doi.org/10.3390/su11030907
APA StyleDhraief, M. Z., Dhehibi, B., Daly Hassen, H., Zlaoui, M., Khatoui, C., Jemni, S., Jebali, O., & Rekik, M. (2019). Livelihoods Strategies and Household Resilience to Food Insecurity: A Case Study from Rural Tunisia. Sustainability, 11(3), 907. https://doi.org/10.3390/su11030907





