Particle Deposition Characteristics and Efficiency in Duct Air Flow over a Backward-Facing Step: Analysis of Influencing Factors
Abstract
:1. Introduction
2. Numerical Methodology
2.1. 2D Air-Particle Two-Phase Models
2.2. Modification of Turbulent Velocity Fluctuation
2.3. Fully Developed Inlet Conditions
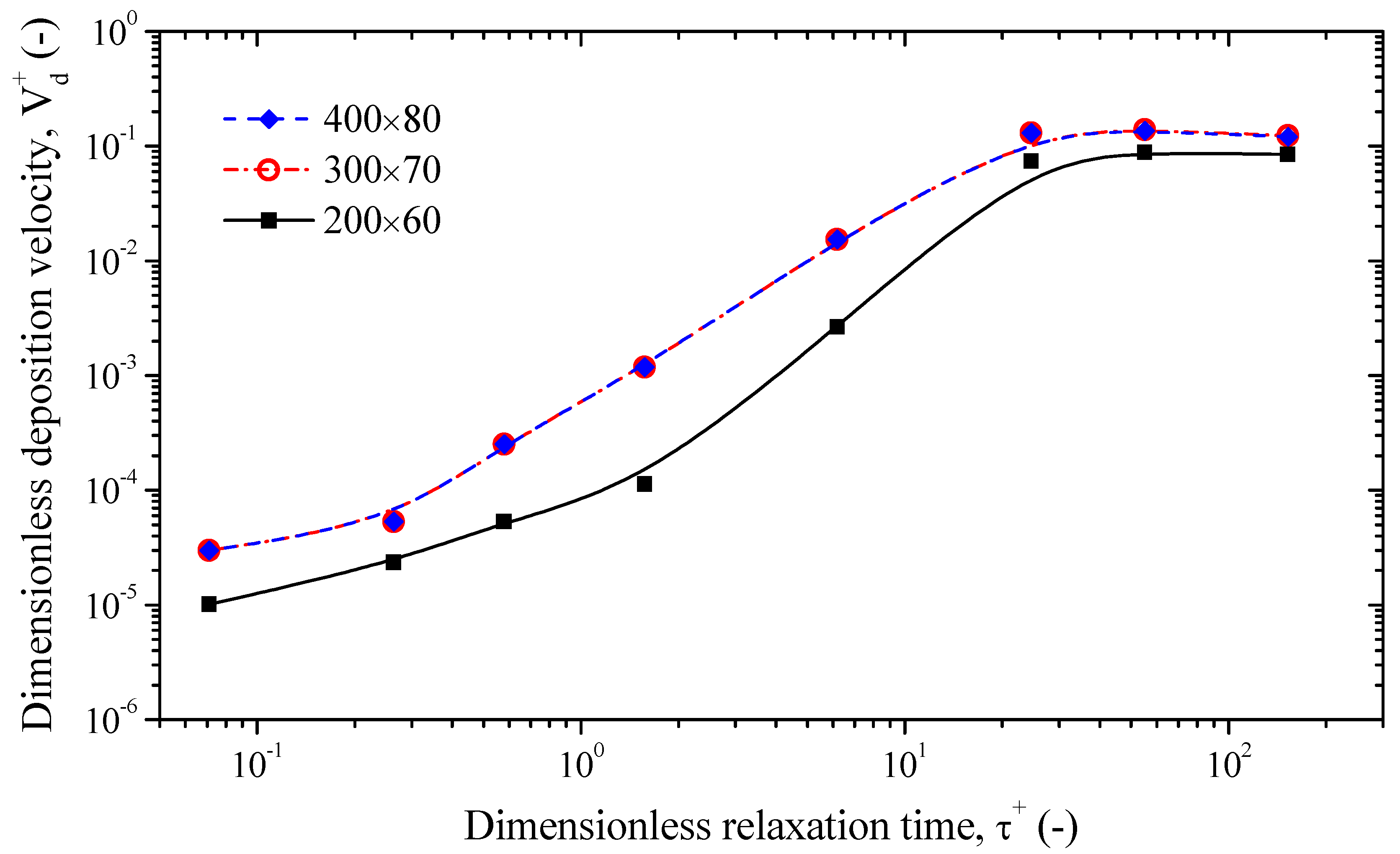
3. Computational Cases and Grid Independence Test
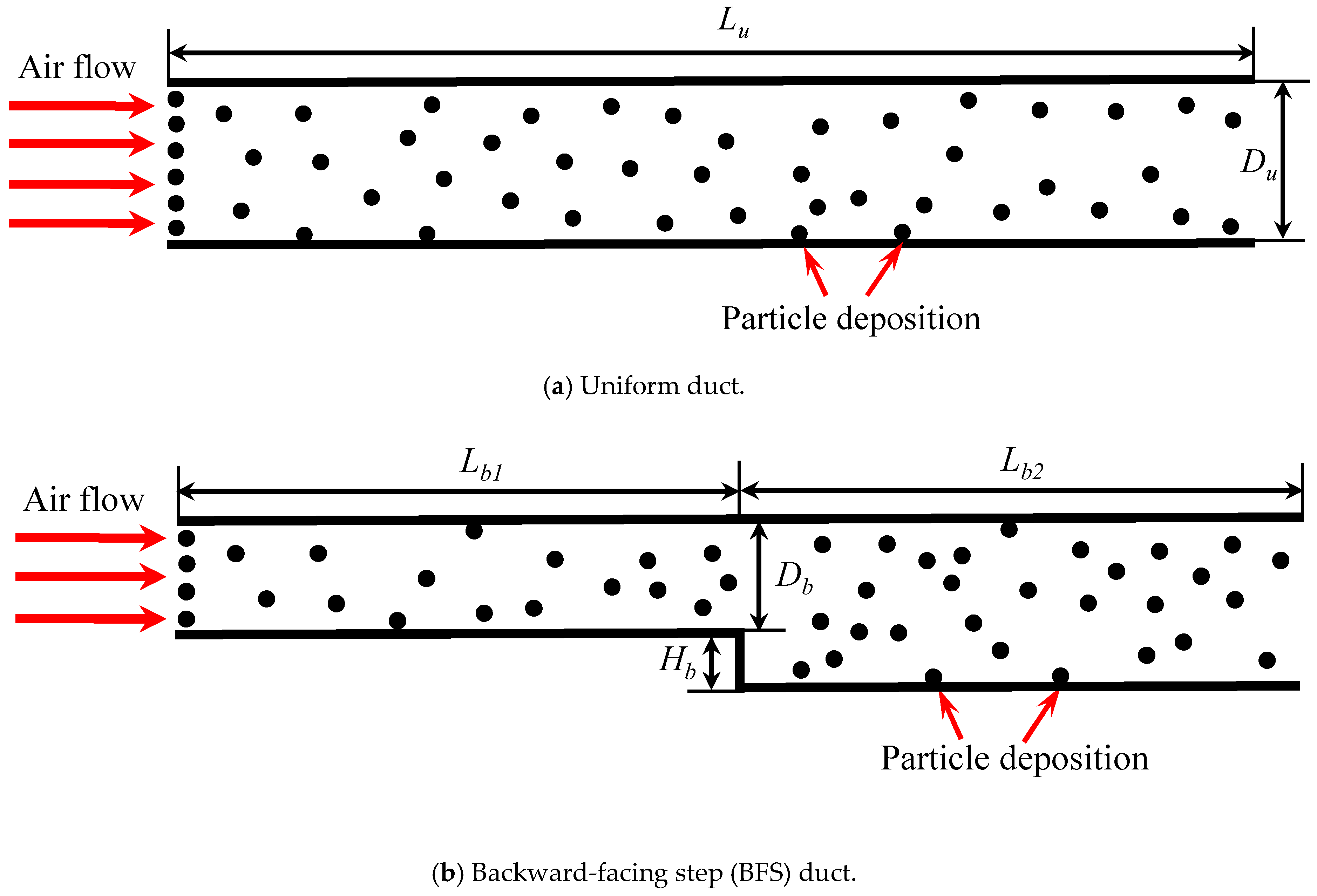
3.1. Computational Geometry
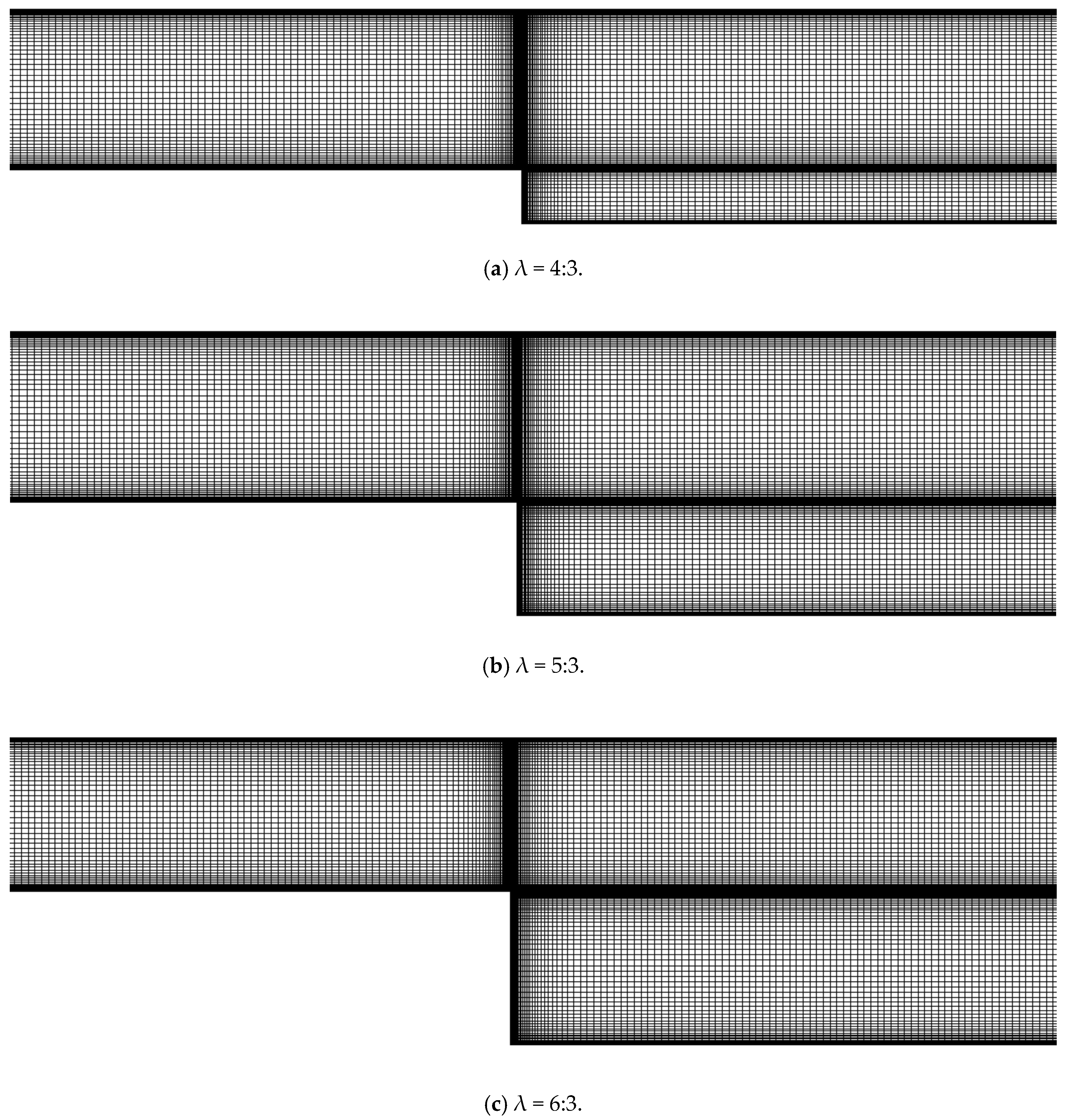
3.2. Structural Mesh
4. Results and Discussions
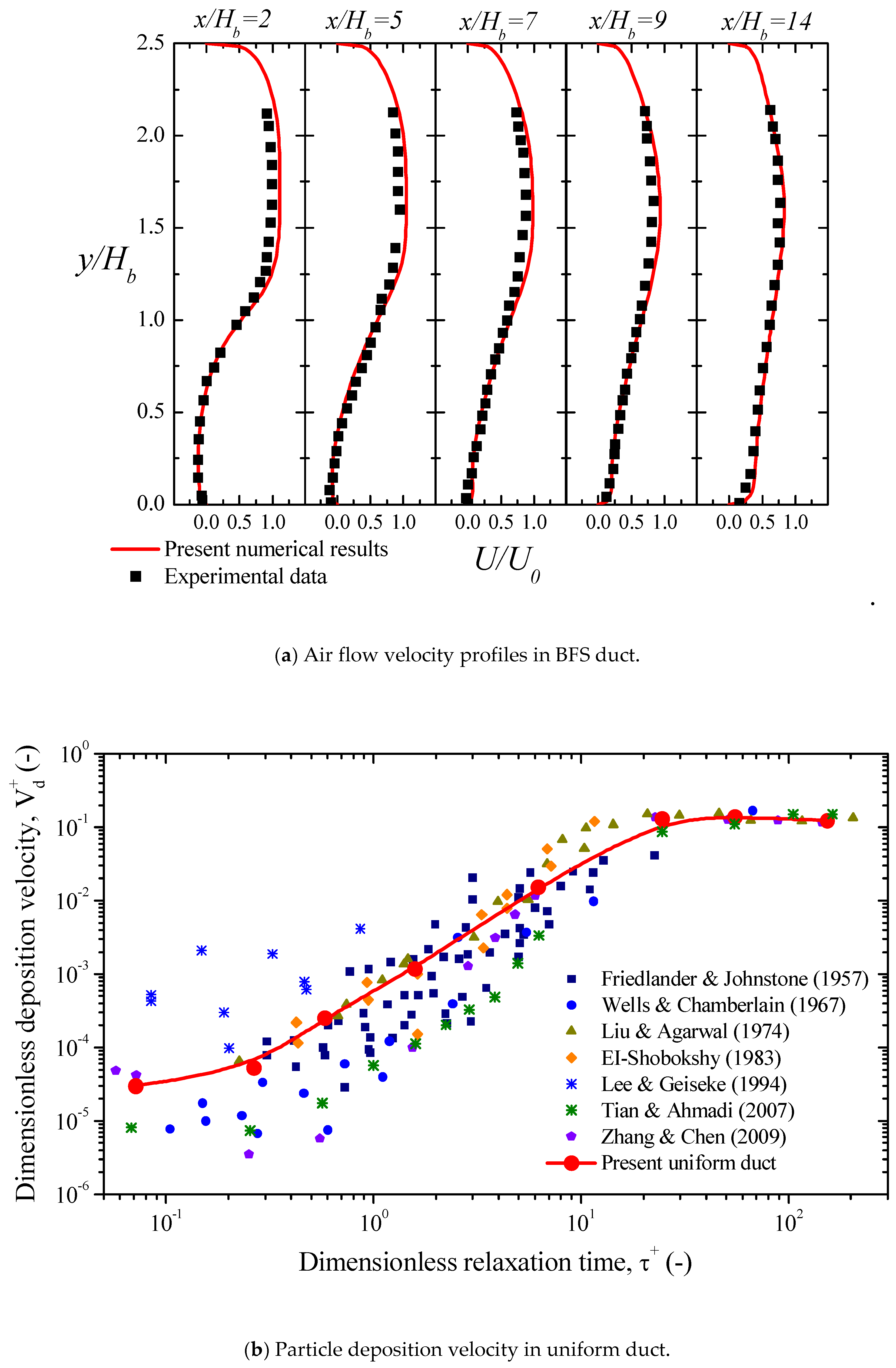
4.1. Numerical Validation
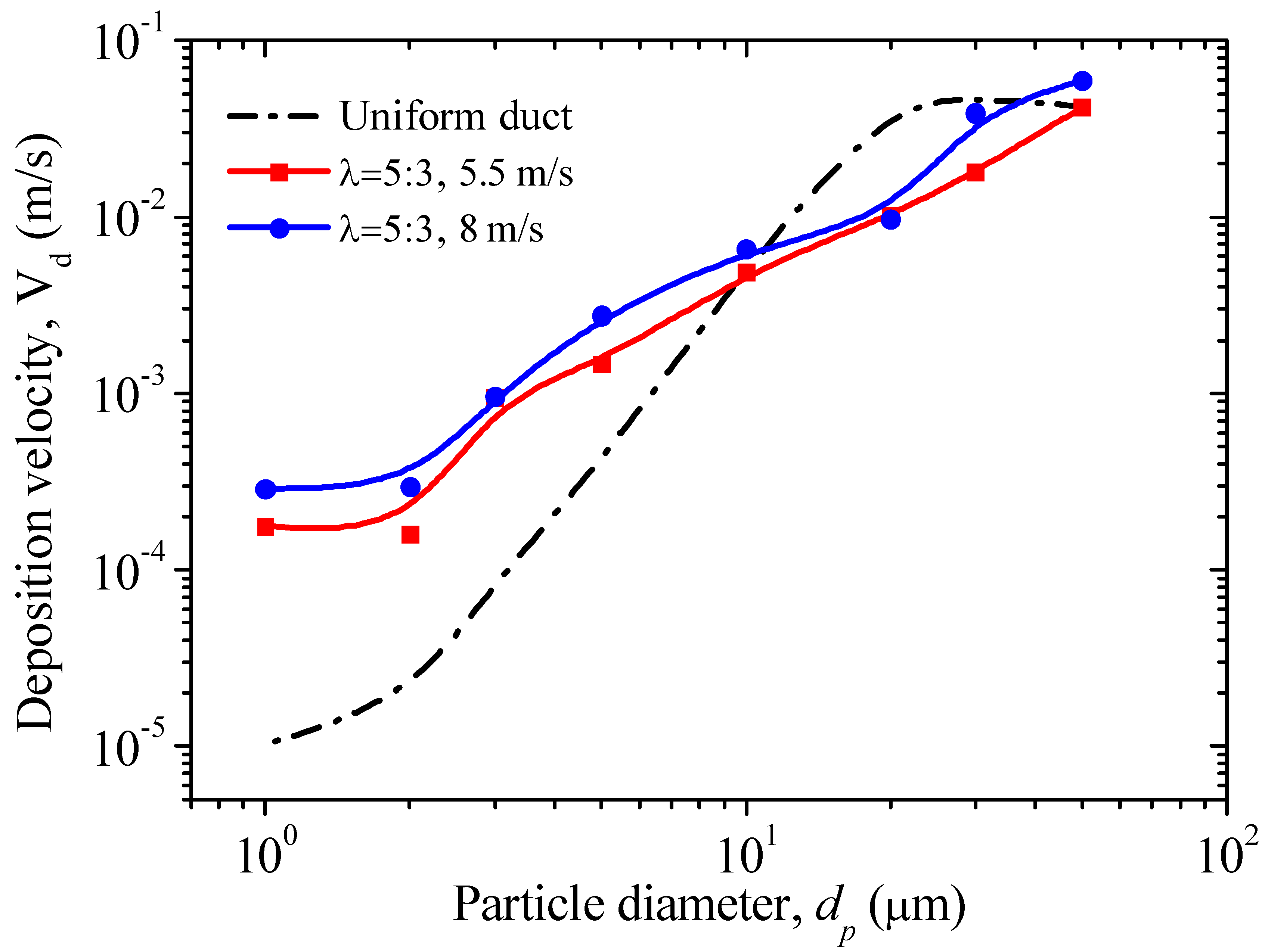
4.2. Particle Deposition Velocity in BFS Flow
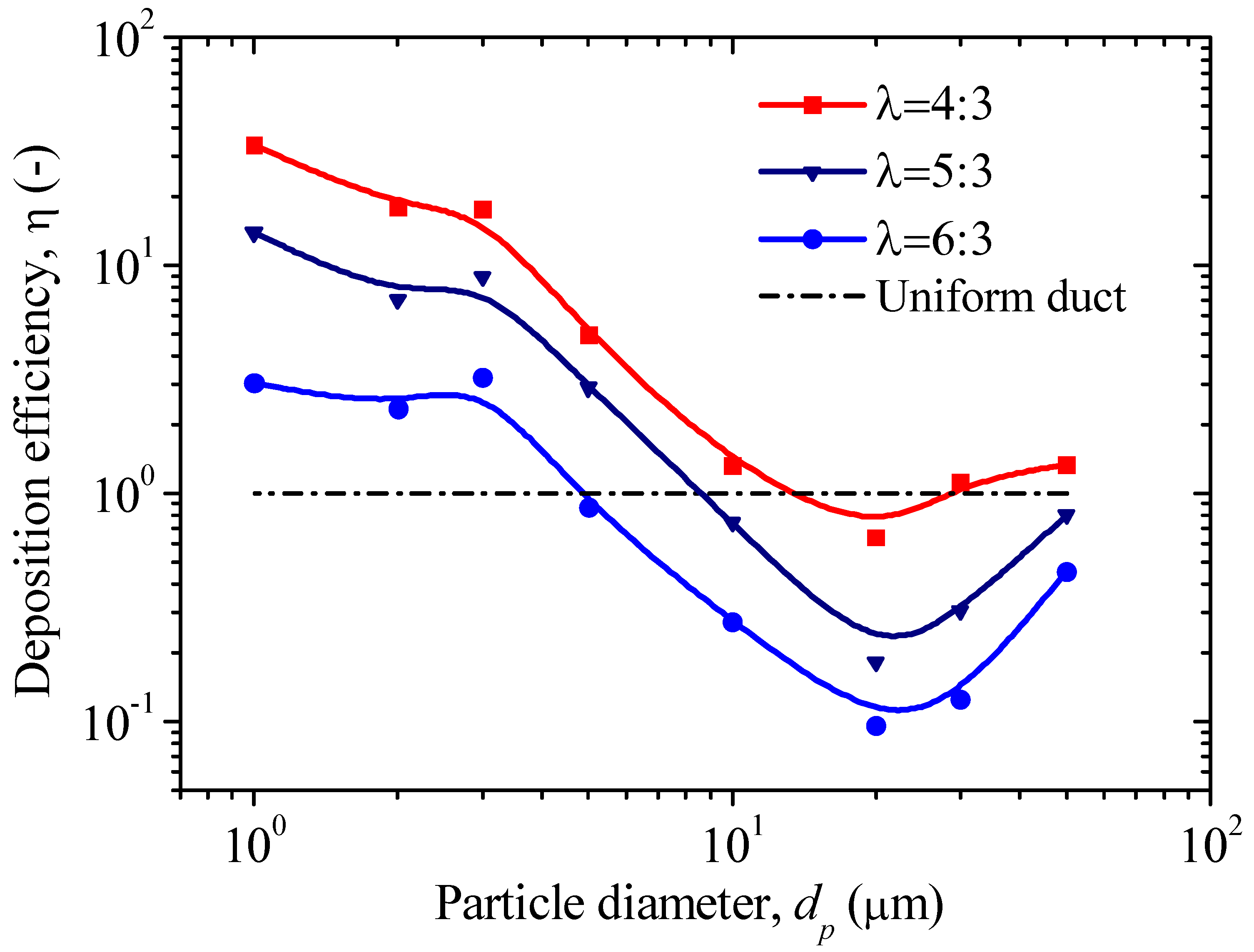
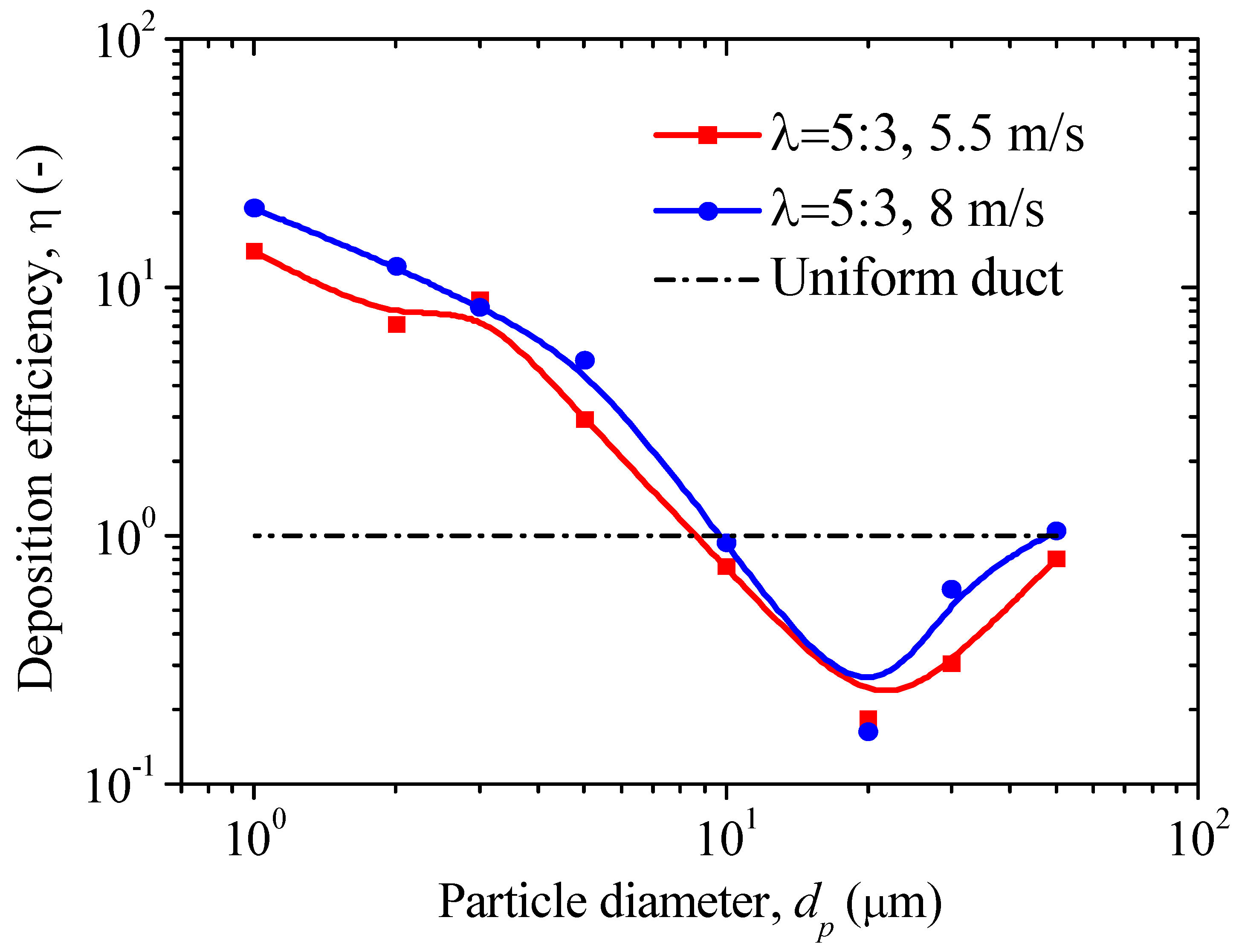
4.3. Particle Deposition Efficiency in BFS Flow
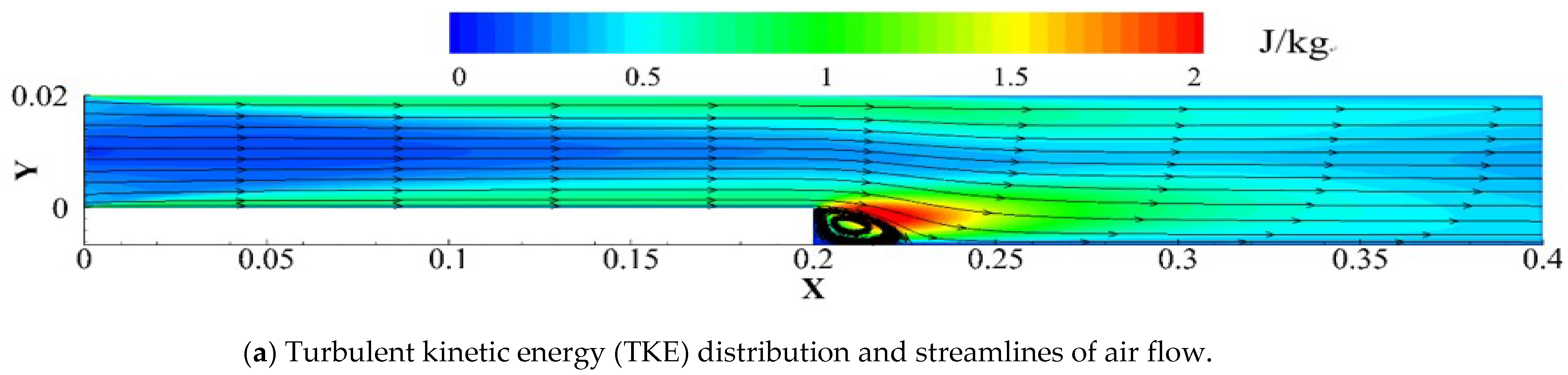
4.4. Particle Deposition Mechanisms in BFS Flow
4.5. Limitations of the Study
5. Conclusions
- Deposition velocity in a BFS duct monotonically increases when the particle diameter increases. Deposition velocity in a BFS duct is higher for small particles but lower for large particles, compared with a uniform duct. Moreover, deposition velocity decreases as the expansion ratio increases. Deposition rates in BFS ducts are enhanced by higher air velocity, but deposition characteristics are not altered by different flow velocities.
- The deposition efficiency of a BFS duct first decreases and then increases as the particle size increases. Compared with a uniform duct, the deposition efficiency of a BFS duct is higher for small particles but lower for large particles. Higher particle deposition efficiency can be obtained by BFS with a smaller expansion ratio. The maximum deposition efficiency can reach 33.6 for 1-μm particles when the BFS expansion ratio is 4:3.
- Compared with a uniform duct, the deposition rates of large particles in a BFS duct are reduced because of the increased deposition distance. However, BFS could increase the deposition efficiency of small particles because a separation vortex is produced by BFS and the TKE is much more intense in the turbulent eddy areas. The trajectories of small particles can fill in whole flow fields of a BFS duct. However, the particle free zone occurs for 50-μm particles in a BFS duct, and the particle free zone is enlarged when the duct expansion ratio increases.
Author Contributions
Funding
Conflicts of Interest
References
- Huang, J.; Zhang, L. Numerical simulation of micro-particle deposition in a realistic human upper respiratory tract model during transient breathing cycle. Particuology 2011, 9, 424–431. [Google Scholar] [CrossRef]
- Zhu, C.; Wang, D.; Lin, C.H. Jet dispersion and deposition of charged particles in confined chambers. Particuology 2010, 8, 28–36. [Google Scholar] [CrossRef]
- Gao, N.P.; Niu, J.L. Modeling particle dispersion and deposition in indoor environments. Atmos. Environ. 2007, 41, 3862–3876. [Google Scholar] [CrossRef]
- Lu, H.; Lu, L. Investigation of particle deposition efficiency enhancement in turbulent duct air flow by surface ribs with hybrid-size ribs. Indoor Built Environ. 2017, 26, 608–620. [Google Scholar]
- Lu, H.; Lu, L.; Jiang, Y. Numerical simulation of particle deposition in duct air flows with uniform, expanding or contracting cross-section. Energy Build. 2016, 128, 867–875. [Google Scholar] [CrossRef]
- Zhou, B.; Zhao, B.; Tan, Z.C. How particle resuspension from inner surfaces of ventilation ducts affects indoor air quality-a modeling analysis. Aerosol Sci. Technol. 2011, 45, 996–1009. [Google Scholar] [CrossRef]
- Jin, H.H.; Fan, J.R.; Zeng, M.J.; Cen, K.F. Large eddy simulation of inhaled particle deposition within the human upper respiratory tract. J. Aerosol Sci. 2007, 38, 257–268. [Google Scholar] [CrossRef]
- Sajjadi, H.; Salmanzadeh, M.; Ahmadi, G.; Jafari, S. Lattice Boltzmann method and RANS approach for simulation of turbulent flows and particle transport and deposition. Particuology 2017, 30, 62–72. [Google Scholar] [CrossRef]
- Piskunov, V.N. Parameterization of Aerosol Dry Deposition Velocities onto Smooth and Rough Surfaces. J. Aerosol Sci. 2009, 40, 664–679. [Google Scholar] [CrossRef]
- Jin, H.H.; He, C.; Lu, L.; Fan, J.R. Numerical Investigation of the Wall Effect on Airborne Particle Dispersion in a Test Chamber. Aerosol Air Qual. Res. 2013, 13, 786–794. [Google Scholar] [CrossRef]
- Tu, J.Y.; Yeoh, G.H.; Morsi, Y.S.; Yang, W. A study of particle rebounding characteristics of a gas–particle flow over a curved wall surface. Aerosol Sci. Technol. 2004, 38, 739–755. [Google Scholar] [CrossRef]
- Guha, A. A Unified Eulerian Theory of Turbulent Deposition to Smooth and Rough Surface. J. Aerosol Sci. 1997, 28, 1517–1537. [Google Scholar] [CrossRef]
- Hussein, T.; Smolik, J.; Kerminen, V.; Kulmala, M. Modeling Dry Deposition of Aerosol Particles onto Rough Surfaces. Aerosol Sci. Technol. 2012, 46, 44–59. [Google Scholar] [CrossRef] [Green Version]
- Sippola, M.R.; Nazaroff, W.W. Experiment measuring particle deposition from fully developed turbulent flow in ventilation ducts. Aerosol Sci. Technol. 2004, 38, 914–925. [Google Scholar] [CrossRef]
- Lai, A.C.K.; Nazaroff, W.W. Modelling Indoor Particle Deposition from Turbulent Flow onto Smooth Surfaces. J. Aerosol Sci. 2000, 31, 463–476. [Google Scholar] [CrossRef]
- Sun, K.; Lu, L.; Jiang, H. A numerical study of bend-induced particle deposition in and behind duct bends. Build. Environ. 2012, 52, 77–87. [Google Scholar] [CrossRef]
- Zhang, J.; Li, A. Study on particle deposition in vertical square ventilation duct flows by different models. Energy Convers. Manag. 2008, 49, 1008–1018. [Google Scholar] [CrossRef]
- Zhao, B.; Wu, J. Modeling Particle Deposition from Fully Developed Turbulent Flow in Ventilation Duct. Atmos. Environ. 2006, 40, 457–466. [Google Scholar] [CrossRef]
- Yao, J.; Fairweather, M. Particle deposition in turbulent duct flows. Chem. Eng. Sci. 2012, 84, 781–800. [Google Scholar] [CrossRef]
- Zhao, B.; Chen, J.J. Numerical analysis of particle deposition in ventilation duct. Build. Environ. 2006, 41, 710–718. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, Q. Prediction of particle deposition onto indoor surfaces by CFD with a modified Lagrangian method. Atmos. Environ. 2009, 43, 319–328. [Google Scholar] [CrossRef] [Green Version]
- Tian, L.; Ahmadi, G. Particle deposition in turbulent duct flows-comparisons of different model predictions. J. Aerosol Sci. 2007, 38, 377–397. [Google Scholar] [CrossRef]
- Gao, N.P.; Niu, J.L.; He, Q.B.; Zhu, T.; Wu, J.Z. Using RANS turbulence models and Lagrangian approach to predict particle deposition in turbulent channel flows. Build. Environ. 2012, 48, 206–214. [Google Scholar] [CrossRef]
- Haber, S.; Yitzhak, D.; Tsuda, A. Characteristics of particle transport in an expanding or contracting alveolated tube. J. Appl. Physiol. 2003, 95, 657–671. [Google Scholar] [CrossRef] [PubMed]
- Lee, D.Y.; Lee, J.W. Characteristics of particle transport in an expanding or contracting alveolated tube. J. Aerosol Sci. 2003, 34, 1193–1215. [Google Scholar] [CrossRef]
- Li, A.; Ahmadi, G.; Bayer, R.G.; Gaynes, M.A. Aerosol particle deposition in an obstructed turbulent duct flow. J. Aerosol Sci. 1994, 25, 91–112. [Google Scholar] [CrossRef]
- Iacono, G.I.; Tucker, P.; Reynolds, A. Predictions for particle deposition from LES of ribbed channel flow. Int. J. Heat Fluid Flow 2005, 26, 558–568. [Google Scholar] [CrossRef]
- Benedetto, A.; Russo, P.; Sanchirico, R.; Sarli, V. CFD simulations of turbulent fluid flow and dust dispersion in the 20 L explosion vessel. AIChE J. 2013, 59, 2485–2496. [Google Scholar] [CrossRef]
- Sarli, V.; Russo, P.; Sanchirico, R.; Benedetto, A. CFD simulations of dust dispersion in the 20 L vessel: Effect of nominal dust concentration. J. Loss Prev. Process Ind. 2014, 27, 8–12. [Google Scholar] [CrossRef]
- Sarli, V.; Russo, P.; Sanchirico, R.; Di Benedetto, A. CFD simulations of the effect of dust diameter on the dispersion in the 20 L bomb. Chem. Eng. Trans. 2013, 31, 727–732. [Google Scholar]
- Lu, H.; Lu, L. Effects of rib spacing and height on particle deposition in ribbed duct air flows. Build. Environ. 2015, 92, 317–327. [Google Scholar] [CrossRef]
- Lu, H.; Lu, L. CFD investigation on particle deposition in aligned and staggered ribbed duct air flows. Appl. Therm. Eng. 2016, 93, 697–706. [Google Scholar] [CrossRef]
- Lu, H.; Lu, L. A numerical study of particle deposition in ribbed duct flow with different rib shapes. Build. Environ. 2015, 94, 43–53. [Google Scholar] [CrossRef]
- FLUENT Inc. FLUENT 12.0 User’s Guide; FLUENT Inc.: Lebanon, NH, USA, 2009. [Google Scholar]
- Kim, J.; Moin, P.; Moser, R. Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 1987, 177, 133–166. [Google Scholar] [CrossRef]
- Lu, H.; Lu, L. Numerical investigation on particle deposition enhancement in duct air flow by ribbed wall. Build. Environ. 2015, 85, 61–72. [Google Scholar] [CrossRef]
- Fessler, J.R.; Eaton, J.K. Turbulence modification by particles in a backward-facing step flow. J. Fluid Mech. 1999, 394, 97–117. [Google Scholar] [CrossRef]
- Wells, A.C.; Chamberlain, A.C. Transport of small particles to vertical surfaces. Br. J. Appl. Phys. 1967, 18, 1793–1799. [Google Scholar] [CrossRef]
- Liu, B.Y.H.; Agarwal, J.K. Experimental observation of aerosol deposition in turbulent flow. J. Aerosol Sci. 1974, 5, 145–155. [Google Scholar] [CrossRef]
- El-Shobokshy, M.S. Experimental measurements of aerosol deposition to smooth and rough surfaces. Atmos. Environ. 1983, 17, 639–644. [Google Scholar] [CrossRef]
- Friedlander, S.K.; Johnstone, H.F. Deposition of suspended particles from turbulent gas streams. Ind. Eng. Chem. 1957, 49, 1151–1156. [Google Scholar] [CrossRef]
- Lee, K.W.; Gieseke, J.A. Deposition of particles in turbulent pipe flows. J. Aerosol Sci. 1994, 25, 699–709. [Google Scholar] [CrossRef]






© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, H.; Zhang, L.-z. Particle Deposition Characteristics and Efficiency in Duct Air Flow over a Backward-Facing Step: Analysis of Influencing Factors. Sustainability 2019, 11, 751. https://doi.org/10.3390/su11030751
Lu H, Zhang L-z. Particle Deposition Characteristics and Efficiency in Duct Air Flow over a Backward-Facing Step: Analysis of Influencing Factors. Sustainability. 2019; 11(3):751. https://doi.org/10.3390/su11030751
Chicago/Turabian StyleLu, Hao, and Li-zhi Zhang. 2019. "Particle Deposition Characteristics and Efficiency in Duct Air Flow over a Backward-Facing Step: Analysis of Influencing Factors" Sustainability 11, no. 3: 751. https://doi.org/10.3390/su11030751
APA StyleLu, H., & Zhang, L.-z. (2019). Particle Deposition Characteristics and Efficiency in Duct Air Flow over a Backward-Facing Step: Analysis of Influencing Factors. Sustainability, 11(3), 751. https://doi.org/10.3390/su11030751



