An Empirical Comparison of Machine-Learning Methods on Bank Client Credit Assessments
Abstract
:1. Introduction
- The distribution of SCF data and FICO credit scores may be slightly different. Therefore, we resampled several times from the test dataset to generate equivalent distribution matching FICO credit scores.
- The estimated PD for the overall population of FICO credit scores is not necessarily the same as for those who have debt in sampled SCF data. To avoid this issue, Arezzo [31] introduced the response-based sampling schemes in the context of binary response models with a sample selection. This study, however, did not use this due to the lack of data. Instead, we grouped the clients into eight ratings the same as FICO credit scores based on their estimated PD to compute the average PD on each credit rating. It may reduce the bias.
2. Materials and Methods
2.1. Materials
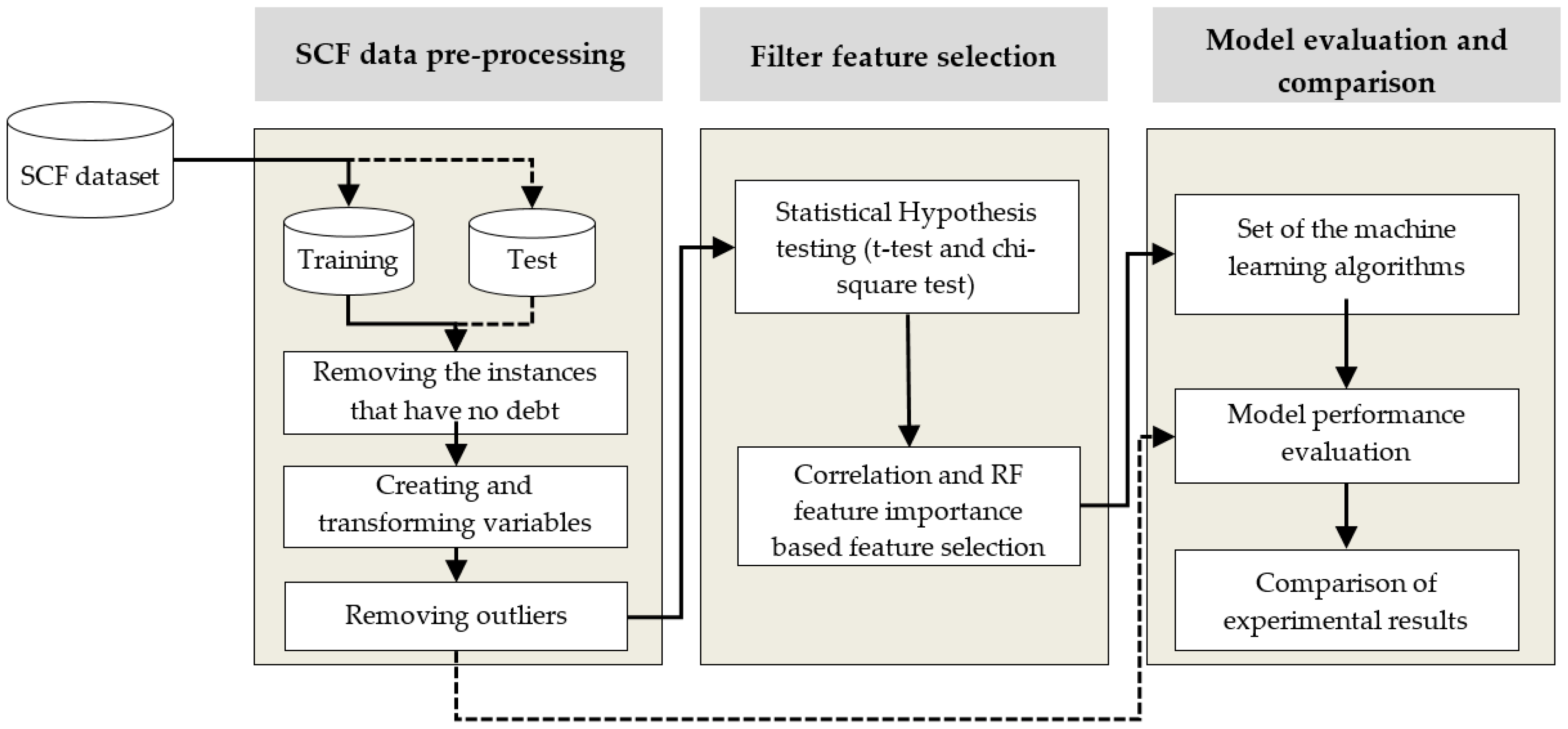
2.1.1. Proposed Framework
2.1.2. SCF Dataset
2.1.3. A Strategy for Comparing FICO Credit Scores and Machine-Learning Models
2.2. Methods
2.2.1. Feature-Selection Algorithms
- Compute random forest importance measure using the training set.
- To assess the empirical distribution of each variable’s random forest importance measure under the null hypothesis, this method permutes each variable separately and several times.
- The p-value is assessed for each variable by means of the empirical distributions and the random forest importance measures.
- Choose the variables with p-value adjusted by Bonferroni-Adjustment lower than a certain threshold.
2.2.2. Machine-Learning Approaches
2.2.3. A Cumulative Expected Credit Loss
3. Results
3.1. Data Pre-Processing and Experimental Setup
3.1.1. Data Pre-Processing
3.1.2. Experimental Setup
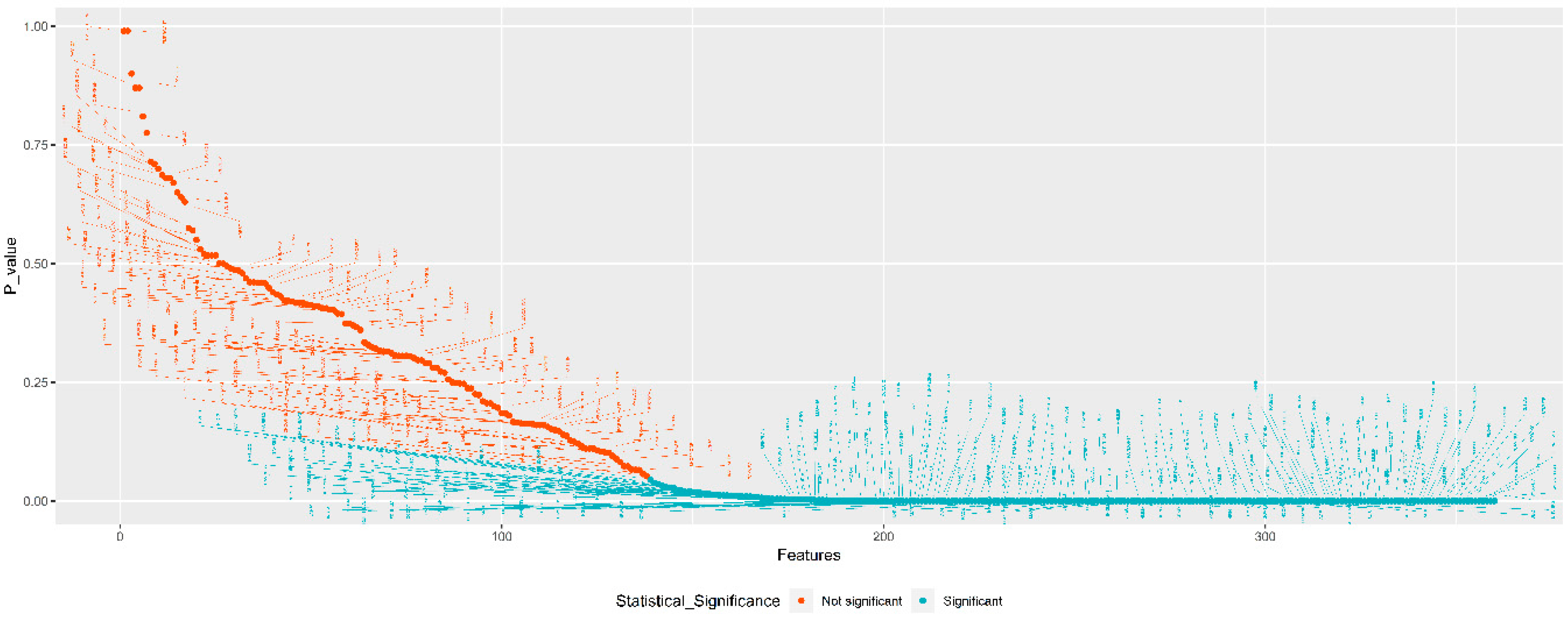
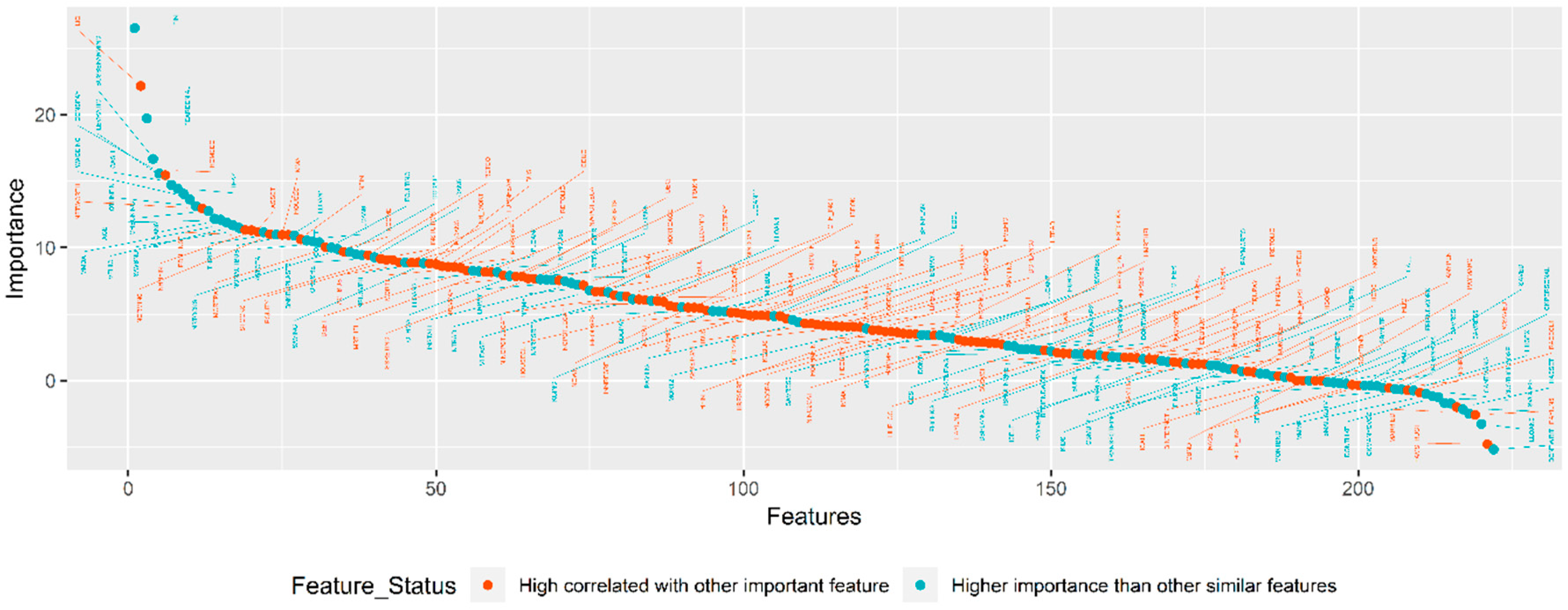
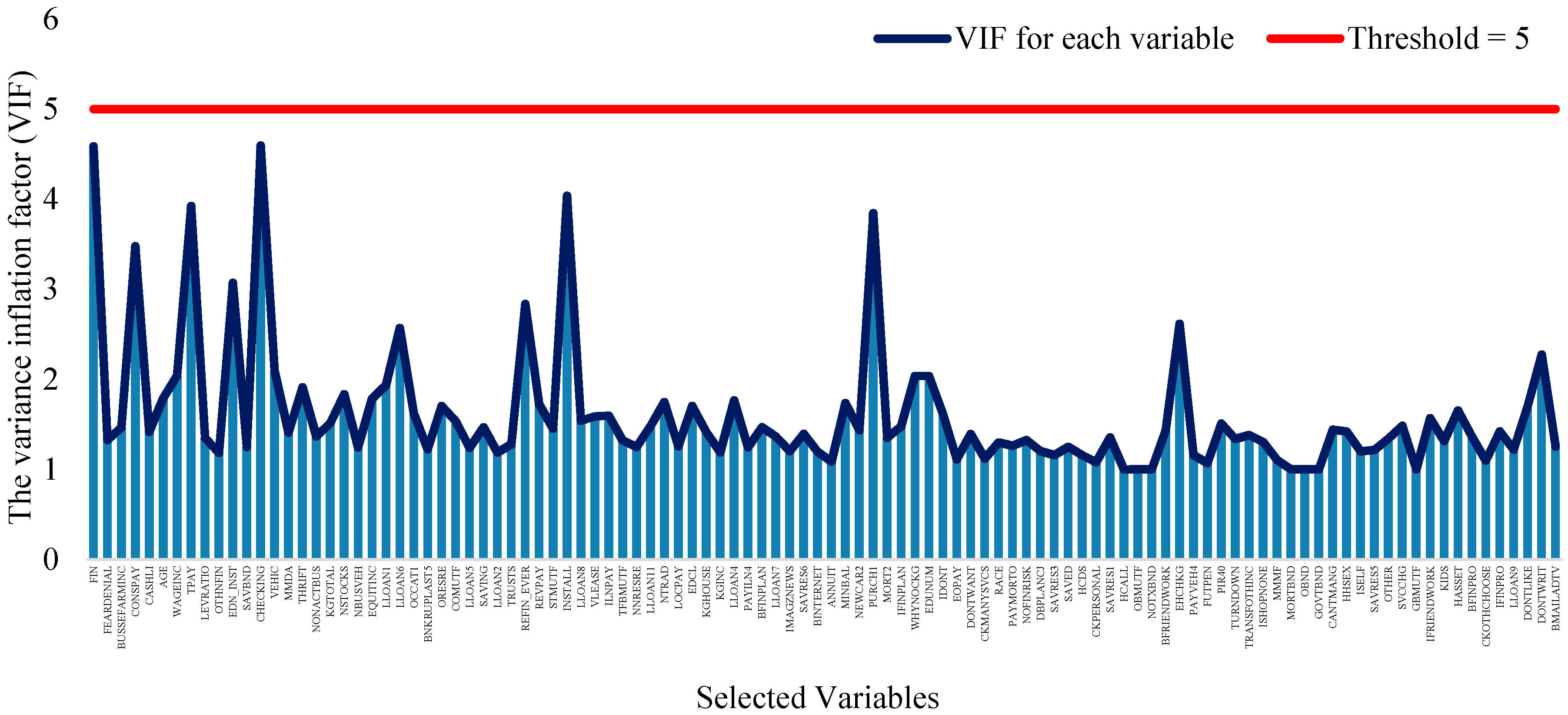
3.2. The Results of Feature-Selection Algorithms
3.2.1. TSFFS Algorithm
3.2.2. NAP Algorithm
3.3. Comparison of the Machine-Learning Algorithms
3.3.1. Evaluation Results
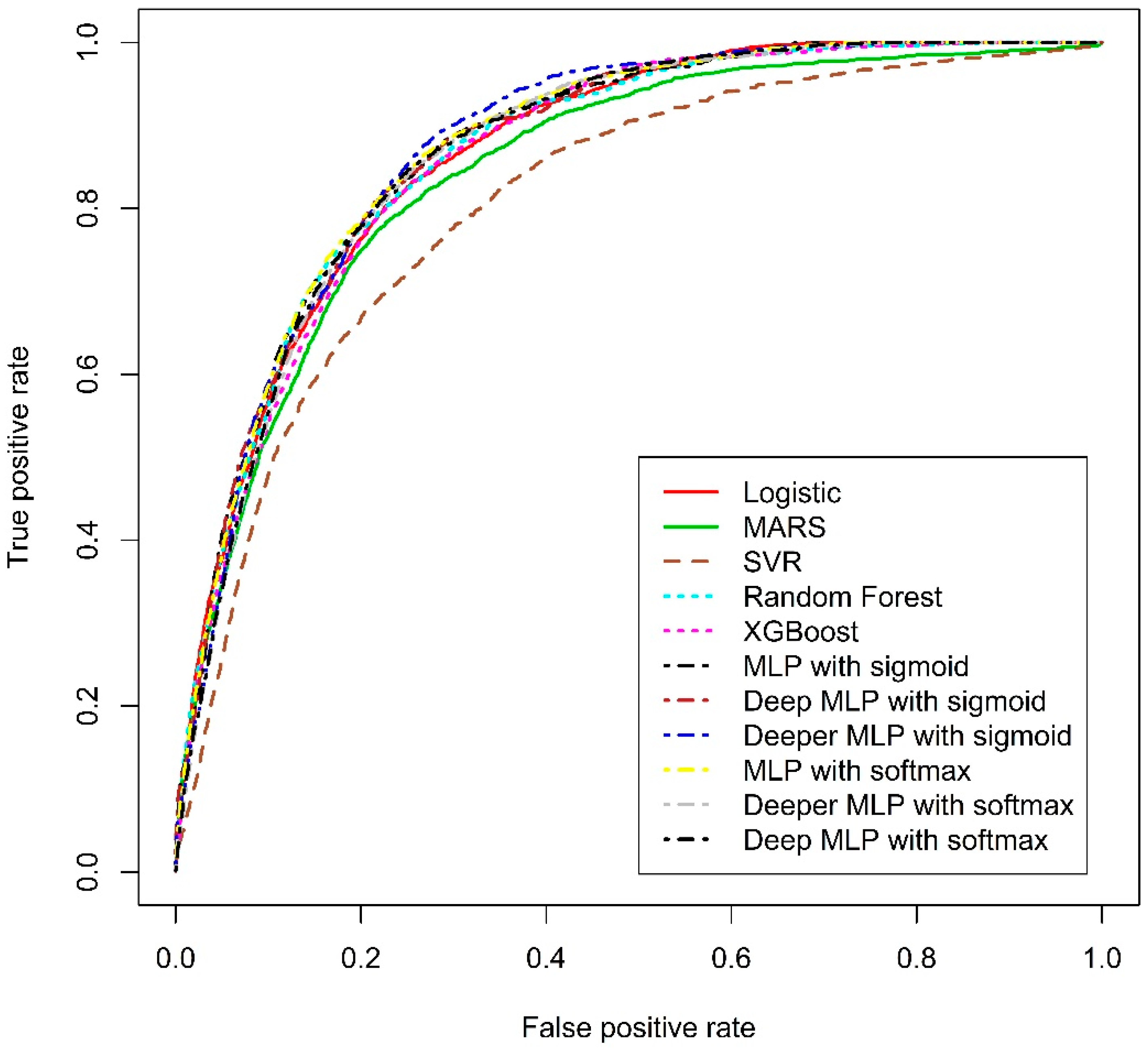
3.3.2. ROC Curve Analysis
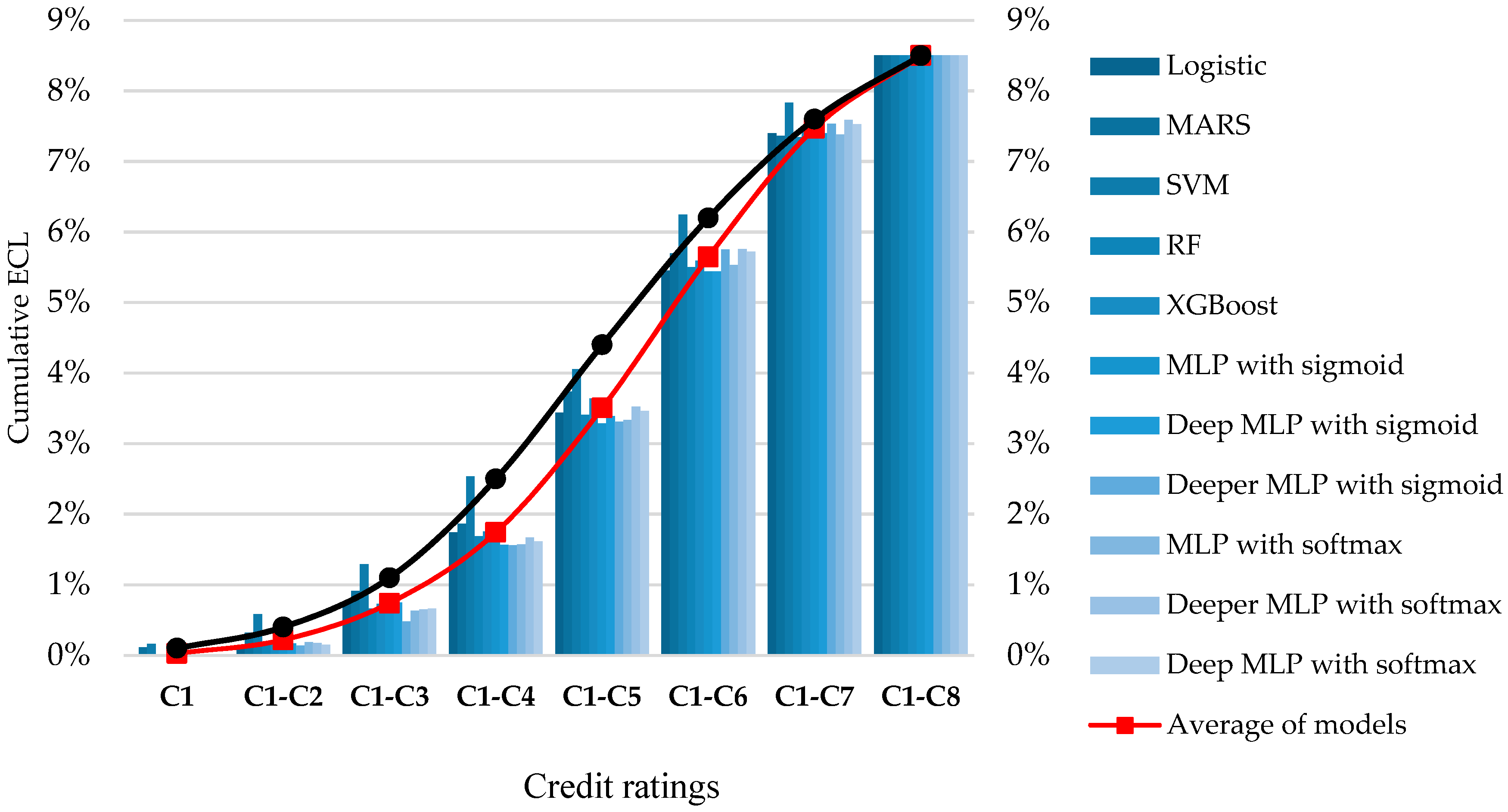
3.4. Empirical Comparison of Machine-Learning Models between FICO
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| ANN | Artificial Neural Network |
| AUC | Area Under the Curve |
| CART | Classification and Regression Tree |
| CBR | Case Based Reasoning |
| CV | Cross-Validation |
| EAD | Exposure at Default |
| ECL | Expected Credit Loss |
| FPR | False Positive Rate |
| GA | Genetic Algorithms |
| GCV | Generalized Cross-Validation |
| GS | Grid Search |
| IFRS | International Financial Reported Standards |
| LATE | Delinquent Debt Repayment Variable |
| LGD | Loss Given Default |
| LR | Logistic Regression |
| MARS | Multivariate Adaptive Regression Splines |
| MLP | Multilayer Perceptron |
| NAP | Random Forest-Based New Approach |
| PD | Probability of Default |
| RBF | Radial Basis Function |
| RF | Random Forest |
| ROC | Receiver Operating Characteristic |
| SCF | Survey of Consumer Finances |
| SVM | Support Vector Machine |
| TPR | True Positive Rate |
| VIF | Variance Inflation Factor |
| XGBoost | Extreme Gradient Boosting |
References
- Chang, H.; Park, M.A. Smart e-Form for Effective Business Communication in the Financial Industry. Bus. Commun. Res. Pract. 2018, 1, 95–101. [Google Scholar] [CrossRef]
- Altman, E.I. Financial ratios, discriminant analysis and the prediction of corporate bankruptcy. J. Financ. 1968, 23, 589–609. [Google Scholar] [CrossRef]
- West, D. Neural network credit scoring models. Comput. Oper. Res. 2000, 27, 1131–1152. [Google Scholar] [CrossRef]
- Huang, Z.; Chen, H.; Hsu, C.J.; Chen, W.H.; Wu, S. Credit rating analysis with support vector machines and neural networks: A market comparative study. Decis. Support Syst. 2004, 37, 543–558. [Google Scholar] [CrossRef]
- Thomas, L.C. A survey of credit and behavioural scoring: Forecasting financial risk of lending to consumers. Int. J. Forecast. 2000, 16, 149–172. [Google Scholar] [CrossRef]
- Orgler, Y.E. A credit scoring model for commercial loans. J. Money Credit Bank. 1970, 2, 435–445. [Google Scholar] [CrossRef]
- Hoffmann, F.; Baesens, B.; Mues, C.; Van Gestel, T.; Vanthienen, J. Inferring descriptive and approximate fuzzy rules for credit scoring using evolutionary algorithms. Eur. J. Oper. Res. 2007, 177, 540–555. [Google Scholar] [CrossRef]
- Oreski, S.; Oreski, G. Genetic algorithm-based heuristic for feature selection in credit risk assessment. Expert Syst. Appl. 2014, 41, 2052–2064. [Google Scholar] [CrossRef]
- Giudici, P. Bayesian data mining, with application to benchmarking and credit scoring. Appl. Stoch. Models Bus. Ind. 2001, 17, 69–81. [Google Scholar] [CrossRef]
- Lee, T.S.; Chiu, C.C.; Lu, C.J.; Chen, I.F. Credit scoring using the hybrid neural discriminant technique. Expert Syst. Appl. 2002, 23, 245–254. [Google Scholar] [CrossRef]
- Lee, T.S.; Chen, I.F. A two-stage hybrid credit scoring model using artificial neural networks and multivariate adaptive regression splines. Expert Syst. Appl. 2005, 28, 743–752. [Google Scholar] [CrossRef]
- Wang, G.; Ma, J.; Huang, L.; Xu, K. Two credit scoring models based on dual strategy ensemble trees. Knowl. Based Syst. 2012, 26, 61–68. [Google Scholar] [CrossRef]
- Liu, Y.; Schumann, M. Data mining feature selection for credit scoring models. J. Oper. Res. Soc. 2005, 56, 1099–1108. [Google Scholar] [CrossRef]
- Bellotti, T.; Crook, J. Support vector machines for credit scoring and discovery of significant features. Expert Syst. Appl. 2009, 36, 3302–3308. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.M.; Huang, Y.F. Evolutionary-based feature selection approaches with new criteria for data mining: A case study of credit approval data. Expert Syst. Appl. 2009, 36, 5900–5908. [Google Scholar] [CrossRef]
- Chen, F.L.; Li, F.C. Combination of feature selection approaches with SVM in credit scoring. Expert Syst. Appl. 2010, 37, 4902–4909. [Google Scholar] [CrossRef]
- Waad, B.; Ghazi, B.M.; Mohamed, L. A three-stage feature selection using quadratic programming for credit scoring. Appl. Artif. Intell. 2013, 27, 721–742. [Google Scholar] [CrossRef]
- Yeh, I.C.; Lien, C.H. The comparisons of data mining techniques for the predictive accuracy of probability of default of credit card clients. Expert Syst. Appl. 2009, 36, 2473–2480. [Google Scholar] [CrossRef]
- Kieso, D.E.; Weygandt, J.J.; Warfield, T.D. Intermediate Accounting: IFRS Edition; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Basel Committee. Basel III: A Global Regulatory Framework for More Resilient Banks and Banking Systems; Basel Committee: Basel, Switzerland, 2010. [Google Scholar]
- Asuncion, A.; Newman, D. UCI Machine Learning Repository. Available online: http://www.ics.uci.edu/~mlearn/MLRepository.html (accessed on 1 November 2018).
- Louzada, F.; Ara, A.; Fernandes, G.B. Classification methods applied to credit scoring: Systematic review and overall comparison. Comput. Oper. Res. 2016, 21, 117–134. [Google Scholar] [CrossRef] [Green Version]
- Xia, Y.; Liu, C.; Li, Y.; Liu, N. A boosted decision tree approach using Bayesian hyper-parameter optimization for credit scoring. Expert Syst. Appl. 2017, 78, 225–241. [Google Scholar] [CrossRef]
- Chen, Q.; Tsai, S.B.; Zhai, Y.; Chu, C.C.; Zhou, J.; Li, G.; Hsu, C.F. An Empirical Research on Bank Client Credit Assessments. Sustainability 2018, 10, 1406. [Google Scholar] [CrossRef]
- Dinh, T.H.; Kleimeier, S. A credit scoring model for Vietnam’s retail banking market. Int. Rev. Financ. Anal. 2007, 16, 471–495. [Google Scholar] [CrossRef]
- Jacobson, T.; Roszbach, K. Bank lending policy, credit scoring and value-at-risk. J. Bank. Financ. 2003, 27, 615–633. [Google Scholar] [CrossRef] [Green Version]
- Zhou, G.; Zhang, Y.; Luo, S. P2P Network Lending, Loss Given Default and Credit Risks. Sustainability 2018, 10, 1010. [Google Scholar] [CrossRef]
- Bucks, B.K.; Kennickell, A.B.; Moore, K.B. Recent changes in US family finances: Evidence from the 2001 and 2004 Survey of Consumer Finances. Fed. Res. Bull. 2006, A1, 92. [Google Scholar]
- Zhang, T.; DeVaney, S.A. Determinants of consumer’s debt repayment patterns. Consum. Interest Annu. 1990, 45, 65–70. [Google Scholar]
- Board of Governors of the Federal Reserve System (US). Report to the Congress on Credit Scoring and its Effects on the Availability and Affordability of Credit, Board of Governors of the Federal Reserve System. Available online: https://www.federalreserve.gov/boarddocs/rptcongress/creditscore/creditscore.pdf (accessed on 26 January 2019).
- Arezzo, M.F.; Guagnano, G. Response-Based Sampling for Binary Choice Models with Sample Selection. Econometrics 2018, 6, 12. [Google Scholar] [CrossRef]
- Cox, D.R. The regression analysis of binary sequences. J. R. Stat. Soc. Ser. B Stat. Methodol. 1958, 20, 215–242. [Google Scholar] [CrossRef]
- Friedman, J.H. Multivariate adaptive regression splines. Ann. Stat. 1991, 33, 1–67. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef] [Green Version]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. arXiv, 2016; arXiv:1603.02754. [Google Scholar]
- Rosenblatt, F. The perceptron: A probabilistic model for information storage and organization in the brain. Psychol. Rev. 1958, 65, 386. [Google Scholar] [CrossRef] [PubMed]
- Hapfelmeier, A.; Ulm, K. A new variable selection approach using random forests. Comput. Stat. Data Anal. 2013, 60, 50–69. [Google Scholar] [CrossRef]
- Hand, D.J.; Anagnostopoulos, C. A better Beta for the H measure of classification performance. Pattern Recognit. Lett. 2014, 40, 41–46. [Google Scholar] [CrossRef]
- Volareviþ, H.; Varoviþ, M. Internal model for ifrs 9-expected credit losses calculation. Ekonomski Pregled 2018, 69, 269–297. [Google Scholar] [CrossRef]
- DeVaney, S.A.; Lytton, R.H. Household insolvency: A review of household debt repayment, delinquency, and bankruptcy. Financ. Serv. Rev. 1995, 4, 137–156. [Google Scholar] [CrossRef] [Green Version]
- Sengupta, R.; Bhardwaj, G. Credit scoring and loan default. Int. Rev. Financ. 2015, 15, 139–167. [Google Scholar] [CrossRef]
- Welch, B.L. The significance of the difference between two means when the population variances are unequal. Biometrika 1938, 29, 350–362. [Google Scholar] [CrossRef]
- Bhapkar, V.P. A note on the equivalence of two test criteria for hypotheses in categorical data. J. Am. Stat. Assoc. 1966, 61, 228–235. [Google Scholar] [CrossRef]
- Farrar, D.E.; Glauber, R.R. Multicollinearity in regression analysis: The problem revisited. Rev. Econ. Stat. 1967, 92–107. [Google Scholar] [CrossRef]
- Belsley, D.A. A guide to using the collinearity diagnostics. Comput. Sci. Econ. Manag. 1991, 4, 33–50. [Google Scholar]
- Lessmann, S.; Baesens, B.; Seow, H.V.; Thomas, L.C. Benchmarking state-of-the-art classification algorithms for credit scoring: An update of research. Eur. J. Oper. Res. 2015, 247, 124–136. [Google Scholar] [CrossRef] [Green Version]
- Kim, Y.S.; Sohn, S.Y. Managing loan customers using misclassification patterns of credit scoring model. Expert Syst. Appl. 2004, 26, 567–573. [Google Scholar] [CrossRef]
- Van Gestel, T.; Baesens, B.; Van Dijcke, P.; Suykens, J.; Garcia, J.; Alderweireld, T. Linear and nonlinear credit scoring by combining logistic regression and support vector machines. J. Credit Risk 2005, 1. [Google Scholar] [CrossRef]
- Vellido, A.; Martín-Guerrero, J.D.; Lisboa, P.J. Making machine learning models interpretable. ESANN 2012, 12, 163–172. [Google Scholar]
- De Gooijer, J.G.; Ray, B.; Kräger, H. Forecasting exchange rates using TSMARS. J. Int. Money Financ. 1998, 17, 513–534. [Google Scholar] [CrossRef] [Green Version]
- Kuhnert, P.M.; Do, K.A.; McClure, R. Combining non-parametric models with logistic regression: An application to motor vehicle injury data. Comput. Stat. Data Anal. 2000, 34, 371–386. [Google Scholar] [CrossRef]
- Chuang, C.L.; Lin, R.H. Constructing a reassigning credit scoring model. Expert Syst. Appl. 2009, 36, 1685–1694. [Google Scholar] [CrossRef]
- Huang, C.L.; Chen, M.C.; Wang, C.J. Credit scoring with a data mining approach based on support vector machines. Expert Syst. Appl. 2007, 33, 847–856. [Google Scholar] [CrossRef] [Green Version]
- Han, L.; Han, L.; Zhao, H. Orthogonal support vector machine for credit scoring. Eng. Appl. Artif. Intell. 2013, 26, 848–862. [Google Scholar] [CrossRef]
- Shi, J.; Xu, B. Credit scoring by fuzzy support vector machines with a novel membership function. J. Risk Financ. Manag. 2016, 9, 13. [Google Scholar] [CrossRef]
- Bennett, K.P.; Mangasarian, O.L. Robust linear programming discrimination of two linearly inseparable sets. Optim. Methods Softw. 1992, 1, 23–34. [Google Scholar] [CrossRef] [Green Version]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef] [Green Version]
- Schapire, R.E. The strength of weak learnability. Mach. Learn. 1990, 5, 197–227. [Google Scholar] [CrossRef] [Green Version]
- Wolpert, D.H. Stacked generalization. Neural Netw. 1992, 5, 241–259. [Google Scholar] [CrossRef] [Green Version]
- Kruppa, J.; Schwarz, A.; Arminger, G.; Ziegler, A. Consumer credit risk: Individual probability estimates using machine learning. Expert Syst. Appl. 2013, 40, 5125–5131. [Google Scholar] [CrossRef]
- Koutanaei, F.N.; Sajedi, H.; Khanbabaei, M. A hybrid data mining model of feature selection algorithms and ensemble learning classifiers for credit scoring. J. Retail. Consum. Serv. 2015, 27, 11–23. [Google Scholar] [CrossRef]
- Ala’raj, M.; Abbod, M.F. Classifiers consensus system approach for credit scoring. Knowl. Based Syst. 2016, 104, 89–105. [Google Scholar] [CrossRef] [Green Version]
- Breiman, L. Classification and Regression Trees; Routledge: London, UK, 2017. [Google Scholar]
- Su-lin, P.A. Study on Credit Scoring Model and Forecasting Based on Probabilistic Neural Network. Syst. Eng.-Theory Pract. 2005, 5, 006. [Google Scholar]
- Lisboa, P.J.; Etchells, T.A.; Jarman, I.H.; Arsene, C.T.; Aung, M.H.; Eleuteri, A.; Taktak, A.F.; Ambrogi, F.; Boracchi, P.; Biganzoli, E. Partial logistic artificial neural network for competing risks regularized with automatic relevance determination. IEEE Trans. Neural Netw. 2009, 20, 1403–1416. [Google Scholar] [CrossRef] [PubMed]
- Marcano-Cedeno, A.; Marin-De-La-Barcena, A.; Jiménez-Trillo, J.; Pinuela, J.A.; Andina, D. Artificial metaplasticity neural network applied to credit scoring. Int. J. Neural Syst. 2011, 21, 311–317. [Google Scholar] [CrossRef]
- Chuang, C.L.; Huang, S.T. A hybrid neural network approach for credit scoring. Expert Syst. 2011, 28, 185–196. [Google Scholar] [CrossRef]
- Abdou, H.; Pointon, J.; El-Masry, A. Neural nets versus conventional techniques in credit scoring in Egyptian banking. Expert Syst. Appl. 2008, 35, 1275–1292. [Google Scholar] [CrossRef] [Green Version]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv, 2014; arXiv:1412.6980. [Google Scholar]
- Ruder, S. An overview of gradient descent optimization algorithms. arXiv, 2016; arXiv:1609.04747. [Google Scholar]
- Girosi, F.; Jones, M.; Poggio, T. Regularization theory and neural networks architectures. Neural Comput. 1995, 7, 219–269. [Google Scholar] [CrossRef]
- Alam, M.; Hao, C.; Carling, K. Review of the literature on credit risk modeling: Development of the past 10 years. Banks Bank Syst. 2010, 5, 43–60. [Google Scholar]
- Dixon, W.J. Processing data for outliers. Biometrics 1953, 9, 74–89. [Google Scholar] [CrossRef]
- Romanski, P.; Kotthoff, L.; Kotthoff, M.L. Package ‘FSelector’. 2013. Available online: http://cran/r-project. org/web/packages/FSelector/index. html (accessed on 16 May 2018).
- Dimitriadou, E.; Hornik, K.; Leisch, F.; Meyer, D.; Weingessel, A.; Leisch, M.F. Package ‘e1071’. R Software package. 2009. Available online: http://cran.rproject.org/web/packages/e1071/index.html (accessed on 21 January 2019).
- Liaw, A.; Wiener, M. The randomforest package. R News 2002, 2, 18–22. [Google Scholar]
- Chen, T.; He, T.; Benesty, M. Xgboost: Extreme Gradient Boosting. R package Version. Available online: https://cran.r-project.org/web/packages/xgboost/vignettes/xgboostPresentation.html (accessed on 9 June 2018).
- Arnold, T. kerasR: R Interface to the Keras Deep Learning Library. Computer Software Manual (R Package Version 0.6. 1). Available online: https://CRAN.R-project.org/package=kerasR (accessed on 22 November 2018).
- Sing, T.; Sander, O.; Beerenwinkel, N.; Lengauer, T. ROCR: Visualizing classifier performance in R. Bioinformatics 2005, 21, 3940–3941. [Google Scholar] [CrossRef]
- O’brien, R.M. A caution regarding rules of thumb for variance inflation factors. Qual. Quant. 2007, 41, 673–690. [Google Scholar] [CrossRef]

| Datasets | Good Instances | Bad Instances | Total Instances | Total Variables |
|---|---|---|---|---|
| Training (SCF-1998) | 4113 | 192 | 4305 | 345 |
| Test (SCF-2001) | 4245 | 197 | 4442 | 345 |
| Credit Rating | FICO Score | The Percent of Population (%) | The Probability of Default (%) | Interest Rate |
|---|---|---|---|---|
| C1 | 800 or more | 13 | 1 | 5.99 |
| C2 | 750–799 | 27 | 1 | 5.99 |
| C3 | 700–749 | 18 | 4.4 | 6.21 |
| C4 | 650–699 | 15 | 8.9 | 6.49 |
| C5 | 600–649 | 12 | 15.8 | 7.30 |
| C6 | 550–599 | 8 | 22.5 | 8.94 |
| C7 | 500–549 | 5 | 28.4 | 9.56 |
| C8 | Less than 499 | 2 | 41 | - |
| Datasets No. | Good Instances | Bad Instances | Total Instances | Total Variables |
|---|---|---|---|---|
| Training (SCF-1998) | 2889 | 187 | 3076 | 361 |
| Test (SCF-2001) | 2924 | 193 | 3117 | 361 |
| Method | Parameters | Symbol | Search Space |
|---|---|---|---|
| Support Vector Machine | Gamma | 0.001, 0.01, 0.1 | |
| Cost | 10, 100, 1000 | ||
| Epsilon | 0.05, 0.15, 0.3, 0.5 | ||
| Random Forest | Number of features randomly sampled | 3, 6, 9, 12, 15, 18, 21 | |
| Minimum size of terminal nodes | 50, 80, 110 | ||
| Number of tree | 500, 1500, 2500 | ||
| XGBoost | Maximum tree depth | 2, 4, 6, 8 | |
| Minimum child weight | 1, 2, 3, 4 | ||
| Early stop round | 100 | ||
| Maximum epoch number | epoch | 500 | |
| Learning rate | 0.1 | ||
| Number of boost | N | 60 | |
| Maximum delta step | 0.4,0.6,0.8,1 | ||
| Subsample ratio | 0.9,0.95,1 | ||
| Column subsample ratio | 0.9,0.95,1 | ||
| Gamma | 0, 0.001 |
| FS | Machine Learning Models | AUC | H-Measure | TPR | FPR | Accuracy |
|---|---|---|---|---|---|---|
| TSFFS | Logistic | 0.8507 | 0.3880 | 0.7668 | 0.2031 | 0.7950 |
| MARS | 0.8283 | 0.3591 | 0.7005 | 0.1834 | 0.8094 | |
| SVM | 0.7841 | 0.2429 | 0.4793 | 0.1396 | 0.8368 | |
| RF | 0.8544 | 0.4039 | 0.8534 | 0.2709 | 0.7368 | |
| XGBoost | 0.8587 | 0.3897 | 0.6192 | 0.1361 | 0.8487 | |
| MLP with sigmoid | 0.8681 | 0.4336 | 0.8259 | 0.2108 | 0.7914 | |
| Deep MLP with sigmoid | 0.8657 | 0.4232 | 0.8135 | 0.2103 | 0.7911 | |
| Deeper MLP with sigmoid | 0.8581 | 0.3952 | 0.7528 | 0.1915 | 0.8051 | |
| MLP with softmax | 0.8672 | 0.4243 | 0.8389 | 0.2324 | 0.7720 | |
| Deeper MLP with softmax | 0.8637 | 0.4155 | 0.7917 | 0.2115 | 0.7887 | |
| Deep MLP with softmax | 0.8631 | 0.4128 | 0.8135 | 0.2175 | 0.7844 | |
| NAP | Logistic | 0.8667 | 0.4151 | 0.7762 | 0.2090 | 0.7901 |
| MARS | 0.8462 | 0.3868 | 0.7166 | 0.1815 | 0.8122 | |
| SVM | 0.8083 | 0.3097 | 0.8788 | 0.4394 | 0.5803 | |
| RF | 0.8682 | 0.4214 | 0.8497 | 0.2765 | 0.7313 | |
| XGBoost | 0.8633 | 0.3987 | 0.5824 | 0.1163 | 0.8650 | |
| MLP with sigmoid | 0.8726 | 0.4256 | 0.8171 | 0.2337 | 0.7695 | |
| Deep MLP with sigmoid | 0.8718 | 0.4233 | 0.8228 | 0.2303 | 0.7730 | |
| Deeper MLP with sigmoid | 0.8748 | 0.4298 | 0.8306 | 0.2318 | 0.7720 | |
| MLP with softmax | 0.8742 | 0.4311 | 0.8358 | 0.2417 | 0.7631 | |
| Deeper MLP with softmax | 0.8664 | 0.4126 | 0.8140 | 0.2285 | 0.7742 | |
| Deep MLP with softmax | 0.8682 | 0.4172 | 0.8161 | 0.2303 | 0.7725 |
| FS | ML Models | C1 | C1–C2 | C1–C3 | C1–C4 | C1–C5 | C1–C6 | C1–C7 | C1–C8 |
|---|---|---|---|---|---|---|---|---|---|
| TSFFS | Logistic | 0.04% | 0.33% | 0.75% | 1.75% | 3.89% | 6.09% | 7.72% | 8.50% |
| MARS | 0.26% | 0.47% | 0.95% | 1.98% | 3.93% | 6.05% | 7.67% | 8.50% | |
| SVM | 0.04% | 0.64% | 1.63% | 3.05% | 4.76% | 6.59% | 7.95% | 8.50% | |
| RF | 0.02% | 0.35% | 0.85% | 1.56% | 3.72% | 5.90% | 7.51% | 8.50% | |
| XGBoost | 0.01% | 0.16% | 0.69% | 1.78% | 3.78% | 5.89% | 7.65% | 8.50% | |
| MLP with sigmoid | 0.04% | 0.27% | 0.66% | 1.41% | 3.45% | 5.81% | 7.63% | 8.50% | |
| Deep MLP with sigmoid | 0.00% | 0.23% | 0.74% | 1.50% | 3.50% | 5.67% | 7.61% | 8.50% | |
| Deeper MLP with sigmoid | 0.00% | 0.26% | 0.78% | 1.73% | 3.80% | 5.84% | 7.58% | 8.50% | |
| MLP with softmax | 0.00% | 0.26% | 0.68% | 1.55% | 3.38% | 5.69% | 7.67% | 8.50% | |
| Deeper MLP with softmax | 0.00% | 0.25% | 0.66% | 1.61% | 3.61% | 5.72% | 7.63% | 8.50% | |
| Deep MLP with softmax | 0.00% | 0.26% | 0.70% | 1.59% | 3.52% | 5.79% | 7.65% | 8.50% | |
| Average of models | 0.04% | 0.32% | 0.83% | 1.77% | 3.76% | 5.91% | 7.66% | 8.50% | |
| NAP | Logistic | 0.00% | 0.15% | 0.73% | 1.74% | 3.44% | 5.45% | 7.40% | 8.50% |
| MARS | 0.11% | 0.32% | 0.91% | 1.86% | 3.74% | 5.70% | 7.36% | 8.50% | |
| SVM | 0.16% | 0.59% | 1.29% | 2.53% | 4.05% | 6.25% | 7.83% | 8.50% | |
| RF | 0.01% | 0.19% | 0.66% | 1.68% | 3.41% | 5.50% | 7.34% | 8.50% | |
| XGBoost | 0.01% | 0.15% | 0.73% | 1.75% | 3.64% | 5.59% | 7.46% | 8.50% | |
| MLP with sigmoid | 0.00% | 0.21% | 0.64% | 1.65% | 3.29% | 5.44% | 7.37% | 8.50% | |
| Deep MLP with sigmoid | 0.00% | 0.17% | 0.75% | 1.56% | 3.39% | 5.44% | 7.40% | 8.50% | |
| Deeper MLP with sigmoid | 0.00% | 0.14% | 0.48% | 1.56% | 3.31% | 5.75% | 7.53% | 8.50% | |
| MLP with softmax | 0.00% | 0.19% | 0.63% | 1.57% | 3.33% | 5.53% | 7.38% | 8.50% | |
| Deeper MLP with softmax | 0.00% | 0.18% | 0.65% | 1.67% | 3.52% | 5.75% | 7.59% | 8.50% | |
| Deep MLP with softmax | 0.00% | 0.15% | 0.67% | 1.61% | 3.46% | 5.72% | 7.53% | 8.50% | |
| Average of models | 0.03% | 0.22% | 0.74% | 1.74% | 3.51% | 5.65% | 7.47% | 8.50% | |
| FICO | 0.10% | 0.40% | 1.10% | 2.50% | 4.40% | 6.20% | 7.60% | 8.50% | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Munkhdalai, L.; Munkhdalai, T.; Namsrai, O.-E.; Lee, J.Y.; Ryu, K.H. An Empirical Comparison of Machine-Learning Methods on Bank Client Credit Assessments. Sustainability 2019, 11, 699. https://doi.org/10.3390/su11030699
Munkhdalai L, Munkhdalai T, Namsrai O-E, Lee JY, Ryu KH. An Empirical Comparison of Machine-Learning Methods on Bank Client Credit Assessments. Sustainability. 2019; 11(3):699. https://doi.org/10.3390/su11030699
Chicago/Turabian StyleMunkhdalai, Lkhagvadorj, Tsendsuren Munkhdalai, Oyun-Erdene Namsrai, Jong Yun Lee, and Keun Ho Ryu. 2019. "An Empirical Comparison of Machine-Learning Methods on Bank Client Credit Assessments" Sustainability 11, no. 3: 699. https://doi.org/10.3390/su11030699
APA StyleMunkhdalai, L., Munkhdalai, T., Namsrai, O.-E., Lee, J. Y., & Ryu, K. H. (2019). An Empirical Comparison of Machine-Learning Methods on Bank Client Credit Assessments. Sustainability, 11(3), 699. https://doi.org/10.3390/su11030699







