Abstract
This study examines the risks and profitability of low-volatility investing in the Korean Securities Dealers Automated Quotations (KOSDAQ) market during the 2001–2017 period. We chose the KOSDAQ market because noise trading is dominant and stocks are likely to be mispriced. We, therefore, expected that low-volatility investing could generate robust profits on the KOSDAQ market, unlike investing on the KOSPI market. Our empirical results support our prediction. Several risk metrics also indicated that this strategy can be implemented in practice. Furthermore, our findings suggest that the idiosyncratic volatility anomaly can be magnified by the mispricing effects of noise trading.
1. Introduction
The efficient market hypothesis, despite being so well known, is often unable to explain realized stock returns. During the last decade, one of the most hotly debated anomalies has been the idiosyncratic volatility (IVOL) puzzle, first reported by Ang et al. [1,2], where stocks with high IVOL yield lower future returns. Both academics and practitioners have been intrigued by the finding that higher IVOL stocks yield lower returns in subsequent periods, but the two sides have attempted to deal with this issue from different perspectives. On the one hand, academics have tried to reconcile the phenomenon with theory; researchers who advocate the rational asset pricing theory introduce a new risk factor, and those who advocate the behavioral finance theory attribute the anomaly to investors’ irrational behaviors. On the other hand, practitioners have paid attention to developing a trading strategy to exploit the potential returns generated by the anomaly. Like the latter approach, the purpose of this study is to examine if the strategy exploiting the IVOL anomaly (typically referred to as “low-volatility investing” by practitioners) is implementable in one “small and medium-sized enterprise” (SME) stock market, KOSDAQ.
While previous studies on the IVOL puzzle in Korea have focused on stocks listed in the Korea Composite Stock Price Index (KOSPI)—the major exchange board of the Korean stock market—few studies have examined it in the context of the KOSDAQ market. This study fills that gap. We present the differences between the KOSPI and KOSDAQ markets relating to the IVOL anomaly, suggesting that the KOSDAQ market would be an ideal environment to conduct low-volatility investing. We then examine if the strategy can be implemented in practice by analyzing its risks and the robustness of its profitability. The main focus of this study is the viability of such a strategy from a practical point of view.
We focus on the KOSDAQ market because retail investors account for the majority of investors in this exchange. Dorn and Huberman [3], Han and Kumar [4], and Kumar [5] argue that speculative trading by retail investors can result in overvalued asset prices that subsequently drop to rational levels because retail investors tend to hold stocks with lottery-like features such as high IVOL. Although it is known that low-volatility investing is unable to generate a robust profit on the KOSPI market [6], we expect that it will be able to produce significant profits on the KOSDAQ market where the retail trading proportion is dominant. The KOSDAQ market can be the ideal environment for analyzing the impact of mispricing by retail investors.
Our study is interesting in that we link a theoretical prediction to a practical investing strategy. Based on the behavioral theories arguing that the idiosyncratic risk puzzle may be due to mispricing by noise traders such as individual investors [7,8,9], we have chosen a special market—KOSDAQ— the market most aggressively traded by individual investors and where, due to Korean market regulations, the classification of investors of a trade is possible. As predicted, we confirm that this market shows different characteristics relating to the idiosyncratic risk puzzle compared to the KOSPI market, where noise trading is relatively less prevalent. We then find evidence that low-volatility investing is profitable and can be implemented.
Our empirical analysis is organized into four main parts. The first part provides an explanation of the unique features of KOSDAQ associated with the IVOL anomaly by comparing it with KOSPI. In the second part, we examine the degree to which IVOL trading strategies are profitable on KOSDAQ and provide an explanation for why its profitability is persistent for a long time. The third part provides some risk metrics to measure the riskiness of the strategy. To implement a trading strategy in practice, risk management remains important even if the strategy can, on average, generate profit over time. Finally, robustness checks confirm that our findings are robust to various “L/M/N” strategies (discussed in further detail later in this paper) and the use of different numbers of portfolios.
2. Literature Review and Hypothesis Development
2.1. Related Literature
The idiosyncratic volatility puzzle was first found by Ang et al. [1,2]. In the U.S. market, stocks with high IVOL earn low returns, and stocks with low IVOL earn high returns in the following month [1]. Ang et al. [2] found further evidence in international markets that was very consistent with previous findings. Since then, vast empirical studies, with a various set of assets or in different countries, have found similar results and supported the finding of Ang et al. [1,2]. For example, Cao and Han [10] showed that IVOL matters in explaining option returns, while Nartea et al. [11] added evidence in southeast Asian stock markets, and Umutlu [12] defined global idiosyncratic risk and provided similar results.
These findings on IVOL are indeed a puzzle in view of the classical or rational asset pricing theory. The capital asset pricing model (CAPM), the inception of the classical theory, predicts that systematic risk or beta is the only determinant of expected return on a stock and that idiosyncratic risk, which is uncorrelated with systematic risk, does not affect the expected return [13,14]. Therefore, CAPM expects idiosyncratic volatility not to be associated with future returns and the empirical finding that high IVOL stocks earn low returns in the future cannot be reconciled with CAPM.
The intertemporal capital asset pricing model (ICAPM), a more advanced model of CAPM, allows for more factors in addition to the market return, implying that a risk is priced if it affects the future opportunity set of investments [15]. Therefore, if IVOL is a proxy of some missing factors which offer hedge opportunity, it can be negatively priced. In line with this logic, Chabi-Yo [16] and Chen and Petkova [17] have provided risk-based explanations for the IVOL puzzle. Chabi-Yo [16] related IVOL to the comovement of the asset volatility with the market return. Using a linear stochastic discount factor approach, he showed that non-systematic coskewness is negatively priced. Chen and Petkova [17] argue that IVOL is a proxy of aggregate volatility risk. They decomposed market volatility into average variance and average correlation to show that high IVOL stocks have a positive loading to average variance. Consequently, they argue that a negative price of risk is required for bearing high IVOL, providing a risk-based explanation for the IVOL puzzle.
Despite such risk-based explanations, many papers have provided findings which fortify the IVOL puzzle. Specifically, Hou and Loh [18] showed that Chen and Petkova’s [17] explanation only accounts for 1% of the puzzle. Rather, they argue that behavioral explanations are more appealing.
One model on which behavioral approaches are based is Merton’s [19] theory. The model suggests that idiosyncratic risk matters if investors hold only a small number of assets because of the lack of information and some market constraints. While CAPM assumes that investors always hold well-diversified portfolios by distributing their wealth to the risk-free asset and the market portfolio, Merton [19] disproved this assumption and developed his model. However, even this model cannot explain the IVOL puzzle because it predicts a positive relation between IVOL and the expected return. When investors hold incompletely-diversified portfolios, they request a positive premium for the risk. Although Goyal and Santa-Clara [20] have found empirical evidence that supports this model, their approach is based on a time-series analysis of aggregate variables, not a cross-sectional study. This stream of literature still cannot explain the negative cross-sectional relation.
Recent behavioral explanations relate the puzzle to mispricing of noise traders. Some papers [3,4,5,21] have argued that retail investors, typically unskilled and noise traders, have a strong preference toward stocks with lottery-like property and cause overpricing. Han and Kumar [4] found evidence that stocks with a high retail trading proportion are overpriced. Bali et al. [21] reported that stocks with a high maximum return in the past earn low future returns because stocks with high maximum returns are lottery-like stocks. They also argued that high IVOL is also a lottery-like feature, and hence, high demand for high IVOL stocks are overpriced. The price-correction process results in the negative relation between IVOL and future returns. Similarly, Nagel [22] has also supported the explanation with evidence that the negative IVOL relation is stronger for stocks with low institutional ownership. Moreover, Hou and Loh [18] showed that using their own methodology, 80% of the IVOL puzzle is attributed to investors’ lottery preferences and market frictions.
The most recent behavioral explanation was provided by Stambaugh et al. [7]. They explained the IVOL puzzle as a result of arbitrage risk with arbitrage asymmetry. Noise trading results in high IVOL, which cannot be neutralized for systematic factors, and increases arbitrage risk; short-selling is typically more expensive. Consequently, the negative IVOL effect is stronger among overpriced stocks. They provided further evidence, consistent with previous explanations, that the IVOL puzzle has something to do with market sentiment and institutional ownership.
2.2. Hypothesis Development
Inspired by these studies, we examine (i) whether the IVOL puzzle is more significant for KOSDAQ stocks than KOSPI stocks and (ii) whether IVOL investing is implementable in the KOSDAQ universe in terms of profitability and risk.
KOSDAQ stocks are mainly traded by retail investors, as shown in Figure 1, which shows retail trading proportions (RTP) for KOSPI and KOSDAQ from 2001 to 2017. On average, the RTP were 93.1% in KOSDAQ and 55.9% in KOSPI. Compared to KOSPI, the participation of retail investors in KOSDAQ was very high. As we will show, the high RTP is associated with the high IVOL of KOSDAQ, which is one of the lottery-like features preferred by speculative retail investors.
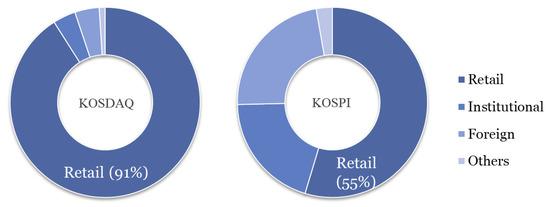
Figure 1.
Retail Trading Proportion (RTP): Korean Securities Dealers Automated Quotations (KOSDAQ) vs. Korea Composite Stock Price Index (KOSPI).
Therefore, if the IVOL anomaly is due to mispricing by speculative retail investors [3,4,5,7,8,9,21], stocks listed in KOSDAQ, the exchange most aggressively traded by individual investors, will exhibit a more significant IVOL anomaly compared to those listed in KOSPI. In addition, we also expect that IVOL trading strategies generate sustainable profits. While Miller [23] argues that it is difficult for underpricing to persist because skilled investors will try to exploit the mispricing, we hypothesize that underpricing can persist in a market where the proportion of trades by naïve investors is extremely high.
3. Methodology
We covered all the common stocks listed on KOSDAQ from January 2001 to December 2017 and obtained data from FnGuide. In order to estimate IVOL for an individual stock, daily stock returns for the past 12 months were required, so we used data from February 2000. We excluded observations from the sample that satisfied the following criteria: First, data 15 days prior to delisting were excluded. Second, observations for which trading volume and trading money (dollar value) were simultaneously recorded as zero were excluded. In accordance with these criteria, 67,408 samples were excluded, which corresponded to approximately 1.6% of the sample. Finally, 1772 stocks (1304 listed stocks and 468 delisted stocks) in KOSDAQ were included in the sample. The number of firm-day observations was 4,062,072.
To estimate IVOL, we employed the KOSDAQ index returns for the market return and the CD-91 rates for the risk-free rate. Following [24], we computed the returns in the size-factor mimicking portfolio (SMB) and value-factor mimicking portfolio (HML), using the SIZE × BM portfolio returns obtained from FnGuide. Stock returns were calculated using the dividend-adjusted price. Monthly IVOL was calculated as the standard deviation of the excess return residuals from the following time-series regression:
where is the stock return, is the risk-free rate, MKT is the market factor, SMB is the size factor, and HML is the value factor as in Fama and French [24]. Specifically, MKT was calculated as the KOSDAQ index return in excess of the Korean commercial deposit rate with a maturity of 91 days (91-day CD rate). Similar to Fama and French’s general approach, small–minus–big (SMB) is the return of the smallest 50% stocks minus the return on the biggest 50% stocks, ranked by market capitalization. High–minus–low (HML) is the return of the portfolio that goes long at the top 30% of firms and short at the bottom 30% of firms, ranked by the ratio of book equity to market equity.
In the recent literature, Carhart [25] has included the momentum factor and Fama and French [26] have considered the investment and operating profitability factors in addition to the existing three factors. Although it is well-known that the new models with more factors can better explain the cross-section of stock returns, we found no significant difference in our main results associated with IVOL profits when we used other models. Since the Fama–French three-factor model has been used most widely in the IVOL literature [1,2,7], we chose this model as our factor model to estimate IVOLs. Following Ang et al. [1], we used prior one-month, three-month, or 12-month daily return data at the end of each month. When calculating IVOL, at least 15, 50, and 120 trading-day observations were required; if the observations were insufficient, we excluded the data.
Our portfolio analysis proceeded as follows. As described earlier, at the end of each month, we computed the IVOL of each stock as the standard deviation of the residuals of the regression in (1), utilizing the daily excess returns of the past one-, three-, or twelve months. Then, we sorted all firms into quintile or decile portfolios, based on their IVOLs. Then, we computed future returns on the portfolios.
When constructing portfolios and computing future returns, we employed the “L/M/N” strategy suggested by Ang et al. [1]. The “L/M/N” strategy refers to a trading strategy involving the estimation of IVOL for L months, waiting for M months before investing, and holding portfolios for N months. For example, for a 3/1/1 strategy, we estimate IVOLs using data for three months and wait for one month to avoid market microstructure issues. Then we buy and hold a portfolio for the next month. In the main analysis, we focused on a one-month future return (or N = 1) with various L (1, 3, 12) and M (0, 1). Then, in robustness checks, we extended N up to 12 (or a year) to test how long the profit would persist.
The IVOL anomaly was tested by the statistical significance of the average return and Fama–French alpha (FF-) of long–short portfolios. The long–short portfolio is a portfolio which goes long in stocks with low IVOL and short in stocks with high IVOL. For example, in a quintile portfolio analysis, the long–short portfolio return is the return on the portfolio that takes long on Portfolio 1 (the lowest IVOL) and takes short on Portfolio 5 (the highest IVOL). FF- is estimated by the regression intercept of (1) with a dependent variable of the long–short portfolio return. We tested if the average returns or FF-s were significantly negative for various L/M/N strategies.
4. Results
4.1. Why KOSDAQ?
Table 1 shows the characteristics of IVOL-sorted quintile portfolios for stocks listed on KOSDAQ (Panel A) and KOSPI (Panel B). At the end of each month, we sorted stocks into quintiles based on their IVOLs that were estimated using daily data one month prior to the formation date. IVOL (%) is the IVOL computed by the standard deviation of the excess return residuals of the Fama–French three-factor model, where the KOSDAQ and KOSPI indices are used as the market factors in the KOSDAQ and KOSPI markets, respectively. RET (%) is the monthly excess return in the month following the formation date, where the CD-91 rate is used as the risk-free rate. ME (10 billion KRW) is the total market value of each portfolio in the formation month. RTP (%) is the retail trading proportion of each portfolio calculated as (BUY + SELL) / (TradeVolume2), where BUY, SELL, and NET (billion KRW) are the total trading volumes bought, sold, and net-bought, respectively, by retail investors in the portfolio formation month. ILLIQ () is the illiquidity of stocks measured using the methodology of Amihud [27], while TURN is the turnover rate measured as the trading volume over a month divided by the number of shares outstanding, and PRICE (KRW) is the closing price at the formation date. Portfolio characteristics including IVOL, RET, ILLIQ, TURN, and PRICE were calculated using value-weighted (VW) averages of firm-level counterparts. The other characteristics such as ME, RTP, BUY, SELL, and NET were calculated directly at the portfolio level. All reported values are monthly averages during the sample period. To clarify some features, Figure 2 and Figure 3 plot RET, RTP, and IVOL.

Table 1.
Characteristics of quintile portfolios sorted by idiosyncratic volatility (IVOL): KOSDAQ vs. KOSPI.
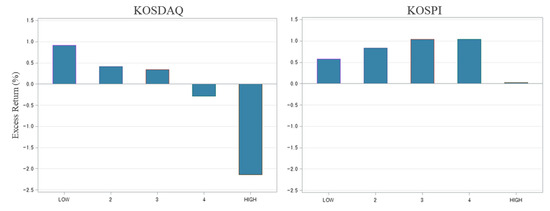
Figure 2.
IVOL-return relationship: KOSDAQ vs. KOSPI.
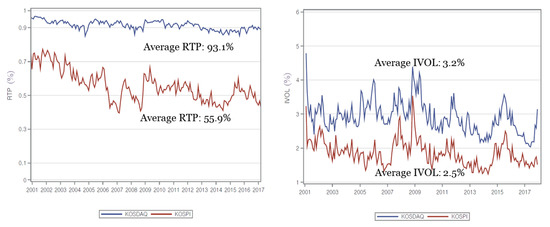
Figure 3.
Time-series of average RTP and average IVOL: KOSDAQ vs. KOSPI.
Table 1 shows several distinct features of the KOSDAQ market compared to the KOSPI market (see also Figure 2 and Figure 3). First, on average, IVOLs were higher in the KOSDAQ market, ranging from 1.45% for the lowest-IVOL quintile to 5.93% for the highest-IVOL quintile.
Second, the relation between market capitalization and IVOL was dissimilar between KOSDAQ and KOSPI. In the KOSPI market, small firms were mostly allocated to the highest quintile and the pattern was clearly negative; there was a negative relation between size and IVOL. However, this was not true for KOSDAQ, although the highest quintile had the smallest market capitalization. Therefore, we see that the IVOL anomaly in KOSDAQ is not a result of the size effect.
Third, the effect of retail trading on asset prices seemed to be stronger in the KOSDAQ market. While retail trading was more prevalent in the higher-IVOL portfolios for both markets, the overall level of RTP was much higher in the KOSDAQ market, consistent with the earlier market-level evidence. More interestingly, the sign of net trading volume was the opposite of the sign of excess returns in the KOSDAQ market. That is, future returns tended to be positive (negative) for portfolios that individual investors net-sell (net-buy). This evidence also supports our hypothesis that the trading of retail investors affects asset prices, and the influence is stronger on the KOSDAQ market because of the heavy participation of individual investors in this market.
Table 2 shows the future excess returns of IVOL-sorted quintile portfolios for stocks listed on KOSDAQ or KOSPI. At the end of each month, we sorted stocks listed on a market (KOSDAQ or KOSPI) into quintiles based on their IVOLs, estimated using daily data for the one-, three-, or 12-month period prior to the formation date. The results for each estimation window are reported in each panel as indicated. IVOL was computed using the standard deviation of the excess return residuals of the Fama–French three-factor model, where KOSDAQ and KOSPI indices are used as market factors in the KOSDAQ and KOSPI market, respectively. As represented by RET (%), we computed monthly value-weighed (VW) returns in excess of the risk-free rate in the month following the formation date. We define market share as the portion of the market capitalization of a firm or a portfolio in the entire market. SHR is the market share of each portfolio in each investigated market. We constructed quintile portfolios using two break points: (i) Each portfolio should have the same number of stocks or (ii) each portfolio should have equal market shares of 20%. Table 2 exhibits the two portfolio returns and SHR in each column. At the bottom of each panel, returns on long–short strategies (denoted by 1–5) and their risk-adjusted returns (denoted by FF-) of the Fama–French three-factor model are reported. To save space, we have only reported the results of the long–short portfolio returns and risk-adjusted returns for the three- and 12-month-windows in Panels B and C. All values are monthly averages during the sample period from January 2001 to December 2017. All t-statistics in parentheses were computed using the Newey and West [28] corrected standard errors.

Table 2.
Excess returns on IVOL-sorted portfolios: KOSDAQ vs. KOSPI.
Panel A of Table 2 shows that the cross-sectional relationship between IVOL and future returns was statistically significant and negative in the KOSDAQ market, suggesting that the investment strategy of buying low-IVOL stocks and selling high-IVOL stocks would earn profits. The long–short strategy earned 3.06% per month with a t-statistic of 5.25; it had a corresponding alpha of 2.51% with a t-statistic of 4.29 after adjusting for the Fama–French three risk factors. In contrast, stocks on the KOSPI market did not exhibit such a relationship with statistical significance, which is consistent with our findings in previous studies using KOSPI stocks. The relationship was negative (the Fama–French alpha of the long–short strategy was 0.83% per month) but not statistically significant (t-statistic = 1.27). Panels B and C repeat the same analysis with three- and twelve-month IVOLs, respectively. We have only reported average return and FF- to save space. The results are qualitatively similar with those in Panel A. Thus, the main finding is not sensitive to the selection of the window length of IVOL estimation.
What creates this difference between the two markets? One sharp contrast is the distribution of market shares of the quintile portfolios. When we constructed portfolios, each of which had an equal number of constituents, the market shares of quintile portfolios in both markets decreased with the size of IVOL. However, the KOSDAQ market had rather similar market values (ranging from 13% to 24%) compared to the KOSPI market where the market share of the highest quintile dropped dramatically (from 35% to 5%). This implies that the negative IVOL-return relation in the KOSPI market might be entirely due to a characteristic of small caps in the 5th quintile portfolio. The last two columns provide further evidence; to control for the effect of that characteristic, we sorted the firms by IVOL again but each portfolio was required to have an equal market share. We see that in the KOSPI market, the negative relation disappears (and even becomes positive); the raw return is −0.48% with a t-statistic of −1.05 and the alpha is 0.19% with a t-statistic of 0.41. In contrast, the statistically significant negative relation remains in the KOSDAQ market after controlling for market share; the magnitude of the profit decreases.
Another distinct feature in the KOSDAQ market is the return pattern across IVOL quintiles. Compared with the KOSPI market, KOSDAQ exhibited a “clearer” negative relation between IVOL and future returns. Table 2 shows that future excess returns on quintiles exhibited a monotonically decreasing trend with IVOL in KOSDAQ. However, such a pattern was not shown in the KOSPI market; the highest IVOL portfolio earned lower returns than the lowest IVOL portfolio, but average returns increased up to the 4th quintile portfolio. In other words, the IVOL anomaly in KOSPI was merely driven by low returns on the 5th quintile portfolio in which small-cap firms were included. In contrast, the IVOL anomaly in KOSDAQ was more prominent and profitable because the decreasing pattern of returns was present across the entire range of IVOL-sorted portfolios.
Motivated by these findings about the KOSDAQ market, we have examined whether low-volatility investing strategies can be carried out on the KOSDAQ market from the perspective of their risks and profits, in the following sections.
4.2. Profitability of Low-Volatility Investing
We analyzed the profitability of low-volatility investing on the KOSDAQ market with reference to excess returns and risk-adjusted returns. Table 3 shows the average future returns on the long leg and the short leg and the spread of the long and short legs; the long (short) leg is the lowest (highest) quintile portfolio based on the magnitude of IVOL. An “L/M/N” strategy refers to a trading strategy involving the estimation of IVOL for L months, waiting for M months before investing, and holding portfolios for N months. For example, for a 3/1/1 strategy, we estimate IVOLs using data for three months (L = 3) and wait for one month (M = 1) to avoid market microstructure issues. Then we buy and hold a portfolio for the next month (N = 1). Average future returns were calculated in terms of excess returns (Panel A) or in terms of risk-adjusted returns using the Fama–French three-factor model (Panel B). Both equal-weight (EW) and value-weight (VW) returns are presented. All t-statistics in parentheses were computed using Newey–West corrected standard errors.

Table 3.
Average returns on long–short strategies (quintiles).
In Table 3, it is worth noting that the long–short strategies generated economically and statistically significant returns in the following month. For example, Panel A of Table 3 shows that the 12/0/1 strategy yielded the highest VW return of 3.29% (t-statistic = 5.75) and the 1/0/1 strategy yielded the highest EW return of 2.99% per month (t-statistic = 4.98). Panel B of Table 3 confirms that such profitability remained even after controlling for the Fama–French three factors. The alphas were 2.59% for 12/0/1 (VW) and 2.54% for 1/0/1 (EW) strategies, which were slightly lower than their raw excess return counterparts; statistical significance also dropped slightly, but the 1% significance level remained. While the weighting scheme did not significantly affect the result, VW returns generally earned slightly more. Similarly, the one-month wait was not crucial; by and large, profits declined when we waited for one month before investing regardless of the weighting scheme and the length of the estimation window. Overall, in the KOSDAQ market, a low-volatility investment strategy that buys stocks in the lowest-IVOL quintile and sells stocks in the highest-IVOL quintile can generate statistically significant alphas that are robust to weighting and various L/M/N strategies.
An in-depth analysis into the long and short legs provided more interesting implications. As seen previously, both VW and EW strategies yielded statistically significant future returns. The sources of the profitability, however, differed depending on the weighting scheme. Specifically, average returns on the long (short) leg were statistically significant at the 1–5% level only in the EW (VW) scheme. Moreover, the magnitudes of the returns and the alphas were higher on the long (short) leg for the EW (VW) scheme. This implies that while EW long–short strategies earn most of their profit from the long portfolio, VW long-short strategies earn most of their profit from the short portfolio. These two facts reveal that the source of profits is different for EW and VW strategies.
How can we explain our results? The results of the short leg are not very surprising because they can be explained by the growing corpus of literature on the limits of arbitrage [22,29,30,31,32,33]. The short leg includes stocks with high IVOL. As evidenced by Table 1, RTP in the short leg was higher than in the long leg, and we hypothesize that this is because retail traders prefer high-IVOL stocks in order to entertain high incomes and overcome limited leverage. The investment amount of retail investors is typically much smaller than that of institutional investors. Also, because of their creditworthiness, retail investors cannot exploit a leverage as much as they want to. Consequently, retail investors have a strong preference for volatility or IVOL. As a result, the short leg is overpriced and subsequently yields negative returns. Even in a competitive and rational market, such abnormal returns can continue to be earned if there exist short-sale constraints. In actuality, it is difficult for short-selling to be carried out by individual investors because of regulations in the KOSDAQ market.
We find the results of the long leg interesting. They are somewhat surprising at two points. First, is it possible for stocks that are “less preferred” by retail investors to be underpriced? In a completely competitive market, a low proportion of unskilled investors means a high proportion of skilled traders. Therefore, if a stock is less preferred by retail investors, it will be correctly priced by skilled traders.
We argue that the high RTP of the KOSDAQ market is the key to the first question. As mentioned earlier, the KOSDAQ market is mainly driven by unskilled retail investors, compared to the KOSPI market; at the market level, the trading volume attributable to foreign and institutional investors—commonly regarded as skilled investors—is very small in the KOSDAQ market. Therefore, low-IVOL stocks that are “less preferred” by retail investors can remain underpriced. As shown in Table 1, the RTP of stocks in the lowest-IVOL quintile was as high as 82%, although this was lower than the RTP of stocks in the highest-IVOL quintile (97%). In other words, low-IVOL stocks were less preferred by retail investors, which does not necessarily mean that skilled investors correctly priced those stocks. Thus, the “less-preference” of unskilled investors can lead to underpricing in the KOSDAQ market where the influence of individual investor trades cannot be ignored. In Table 1, the NET values also support our argument. Net buying by retail investors led to negative returns and net selling led to positive returns in the KOSDAQ market, showing opposite signs between NET and RET in all quintiles. This was not found in the KOSPI market where the influence of retail investors was relatively weaker. In unreported results, we confirm that the same phenomenon occurs for decile portfolios.
Second, why do the statistically significant (e.g., at a 1% level) abnormal returns on the long leg persist? Even if low-IVOL stocks can be underpriced, arbitrageurs would exploit the anomaly and the risk-adjusted returns should ultimately be insignificant, both economically and statistically.
Market friction such as trading costs can answer the second question. We argue that trading costs are too high for skilled arbitrageurs to exploit anomaly, and accordingly the KOSDAQ market remains inefficient for several reasons. First, even though the long leg includes large stocks, the total market capitalization of the long leg is only 20 trillion won, which is 0.07 times the long leg of the KOSPI market (approximately 260 trillion won). Second, stocks in the lowest-IVOL quintile (long leg) are more liquid than those in the highest-IVOL quintile (short leg) in KOSDAQ, but they are still illiquid compared to stocks in KOSPI. As measured by Amihud’s illiquidity variable (ILLIQ) in Table 1, the long leg illiquidity was 12.39 in the KOSDAQ market and 0.25 in the KOSPI market. A large volume of trading would impact prices so significantly that the seemingly profitable anomaly would be unable to generate any profit. Other liquidity measures such as turnover (TURN) and price per share (PRICE) also support our argument that the long leg of KOSDAQ is not attractive to skilled traders with large amounts of funding. Therefore, even if the long leg appears to continue to earn abnormal returns, they are not easily earned because those stocks are small caps, illiquid, and subsequently accompanied by high costs.
4.3. Risks of Low-Volatility Investing
Even if the average returns are highly profitable, asset managers cannot ignore the risks of the portfolios that they manage. We, therefore, now analyze the risks of IVOL trading strategies. Considering that short-only strategies are not common in practice, we have focused on studying long-only and long–short strategies.
The first dimension of risk we have evaluated is maximum drawdown (MDD), the maximum loss of portfolio value in percent during the entire investment period [34]. If a strategy experiences significant drops in its portfolio value during its term, it is difficult for investors to endure such periods even though the portfolio eventually generates a high return. These significant drops can result in substantial flows of money out of the fund. For this reason, particular attention should be paid to managing a drawdown.
Table 4 shows the MDD for each L/M/N strategy. We found that long–short strategies are less risky than long-only strategies in terms of MDD. For example, while the 1/0/1 EW long-only strategy exhibited an MDD of −50.42%, the MDD of the corresponding long–short strategy was only −32.09%. This means that if an investor invested in this fund, he/she would have experienced a 32.09% loss in money invested during the sample period. While it is true that 32% is not a small loss, considering the fact that the sample period includes a financial crisis during which the KOSDAQ index experienced an MDD of −68.5%, this long–short low-volatility investing strategy can be quite attractive as a defensive strategy.

Table 4.
Risks of low-volatility investing.
Another dimension of risk is covariance with existing risk factors such as market, size, and value. A low covariance is preferred because it can provide the advantage of diversification. Covariance is typically estimated by factor loadings (OLS betas). As can be seen in Table 4, the long-only strategies had a market beta of less than one—ranging from 0.78 to 0.88—depending on weight and L/M/N. Therefore, the long-only low-volatility investing strategy can be a defensive strategy. The long–short portfolio reduced its market beta nearly to zero. In EW cases, it ranged from −0.07 to −0.02; VW cases had a slightly higher exposure, ranging from −0.15 to −0.08. This finding suggests that low-volatility investing can offer a diversification opportunity to mitigate market risk.
Practitioners and academics are also interested in where the premium originates. To investigate the sources of the premiums, we decomposed the profit (average excess return) into four components using the Fama–French three-factor model: The market risk premium (), the size premium (), the value premium (), and an unexplained premium (FF-).
Long-only strategies generally earn their premiums from the alpha, which means that most of the premiums cannot be explained by the Fama–French model. For example, the 1/0/1 EW portfolio earned a premium of 1.74% per month on average, of which 1.28% was alpha. Only 0.46% was due to the three types of risk factors. Among the three sources, the value premium accounted for most of the factor premiums, amounting to 0.42%. Compared to long-only investing, the premiums on the long–short portfolios were far less accounted for by the Fama–French model. Out of the excess return of 2.99%, 2.54% was alpha for the 1/0/1 EW strategy. As with the long-only investing strategy, it was the value premium that accounted for most of the factor premiums. All in all, low-volatility investing has low exposure to traditional risk factors, resulting in a small factor risk premium. Although the factor risk premium is small, the value premium comprises a significant portion of the factor risk premium.
4.4. Robustness Checks
In this section, we test whether our main findings on the profitability of IVOL strategies are robust to a different number of portfolios and to longer holding periods. For the first robustness check, we constructed decile portfolios based on the magnitude of IVOL (in contrast to the quintile portfolios constructed in the main analysis earlier) and repeated the main analysis of Table 3. The results are presented in Table 5 and confirm that our main findings in the quintile analysis remain intact even when we sort into deciles. First, the long–short portfolios earned economically and statistically significant profits both in EW and VW schemes. For example, for the 1/0/1 strategy, the EW (VW) profit was 4.15% (4.00%) per month. This was also true for risk-adjusted returns in Panel B, although their magnitudes reduced slightly to 3.59% and 3.33% for EW and VW, respectively. Second, the profit sources of the long–short portfolios were different. Looking at t-statistics, while VW portfolios earned profits from the short leg, EW portfolios earned from the long leg. For the 1/0/1 strategy, for example, the VW short leg had a t-statistic of -4.03, but its long leg showed a t-statistic of 1.39. The opposite argument is true for the EW portfolio. Therefore, we can see that the EW low-volatility strategy earns profits from undervalued stocks, while the VW strategy earns profits from overvalued stocks.

Table 5.
Average returns on long–short strategies (deciles).
The second robustness check was whether the strategy remained profitable for longer holding periods. In the earlier main analysis, we only investigated profits for one-month holding periods (i.e., strategies with N = 1). We now extended N to examine the returns for three-, six-, and 12-month holding periods. This examination allowed us to not only carry out a robustness check, but to also see how long the profitability persisted. Table 6 presents the results. We confirm that the profitability remained unchanged when we used holding periods longer than one month. In the earlier result, EW profit was 4.15% for the one month holding period. In Table 6, the three-, six-, and 12-month holding periods generated 2.27% 2.31%, and 2.04% returns, respectively. Although the economical magnitude reduced as the holding period was extended, we confirm that IVOL investing was still profitable. More interestingly, the profitability persisted for up to 12 months: Both the economical and statistical significance did not weaken over the 12-month holding period. For example, the 1/0/12 excess returns were 2.04% (t = 4.21) and 1.77% (t = 4.38) for the EW and VW portfolios, respectively. These findings are important for practical purposes. In practice, trading costs such as taxes, fees, and bid/ask spreads significantly reduce the net profit. Frequent rebalancing causes higher trading costs and lowers net profit. Some studies have argued that factor investing cannot make profits after considering costs [35,36,37]. Therefore, the finding that low-volatility investing in the KOSDAQ market produces significant profits even for the 12-month holding period implies that trading costs are not a big concern for this investment strategy.

Table 6.
Average returns on long–short strategies (holding periods over one month)
5. Conclusions
So far, we have examined the risks and profitability of IVOL trading in KOSDAQ. Based on the fact that retail investor trading accounts for a substantial portion of the total trading in KOSDAQ, we expected that the IVOL anomaly would become more profitable in KOSDAQ if the phenomenon was due to mispricing by speculative retail traders. The results are consistent with our prediction. The long–short trading strategy generated approximately a 3% return per month. Separate analyses on each leg revealed that the EW IVOL long–short strategy is one that exploits “underpriced” stocks, while the VW strategy is one that exploits “overpriced” stocks. Practically, even though the long leg appears to be very profitable, it is not easy for institutional investors to realize the abnormal returns because of market friction. However, market friction such as trading costs has less of an impact on retail investors. The IVOL long-only strategy may help astute retail investors make profits in KOSDAQ.
Our findings are important in several aspects. In a practical point of view, our research suggests that KOSDAQ stocks can be a good universe of IVOL investing, although practitioners have paid less attention to SME stocks. In terms of risk metrics, IVOL investing is implementable. This can give an important implication to practitioners such as arbitrage traders and asset managers.
From a theoretical perspective, we have provided additional evidence that the IVOL puzzle is associated with noise trading and mispricing. With a hypothesis that mispricing is more severe for SMEs where retail trading is highly dominant, we have shown that the IVOL puzzle is more significant for KOSDAQ stocks than KOSPI stocks. This finding can also contribute to the literature by providing indirect out-of-sample evidence. Consistent with the empirical evidence from the U.S. market [7,8], we have also confirmed the hypothesis that the idiosyncratic risk puzzle is related to mispricing in another market. Furthermore, while Miller [23] has hypothesized that it is difficult for underpricing to persist because skilled investors will try to exploit the mispricing, we have provided evidence that underpricing can persist in a market where the proportion of trades by naïve investors is extremely high.
Author Contributions
The authors contributed to this paper as follows. J.K.: Software, formal analysis, investigation, data curation, writing—original draft preparation; Y.J.P.: Methodology, validation, writing—review and editing, supervision, project administration.
Funding
This research was supported by the Hallym University Research Fund, HRF-201902-006.
Acknowledgments
We thank Youngkyung Ok for excellent research assistance.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ang, A.; Hodrick, R.J.; Xing, Y.; Zhang, X. The cross-section of volatility and expected returns. J. Financ. 2006, 61, 259–299. [Google Scholar] [CrossRef]
- Ang, A.; Hodrick, R.J.; Xing, Y.; Zhang, X. High idiosyncratic volatility and low returns: International and further US evidence. J. Financ. Econ. 2009, 91, 1–23. [Google Scholar] [CrossRef]
- Dorn, D.; Huberman, G. Preferred risk habitat of individual investors. J. Financ. Econ. 2010, 97, 155–173. [Google Scholar] [CrossRef]
- Han, B.; Kumar, A. Speculative retail trading and asset prices. J. Financ. Quant. Anal. 2013, 48, 377–404. [Google Scholar] [CrossRef]
- Kumar, A. Who gambles in the stock market? J. Financ. 2009, 64, 1889–1933. [Google Scholar] [CrossRef]
- Ok, Y.; An, S.; Kim, J. Robustness of idiosyncratic volatility puzzle in the Korean stock market. Korean J. Financ. Stud. 2018, 47, 635–671. [Google Scholar] [CrossRef]
- Stambaugh, R.F.; Yu, J.; Yuan, Y. Arbitrage asymmetry and the idiosyncratic volatility puzzle. J. Financ. 2015, 70, 1903–1948. [Google Scholar] [CrossRef]
- Stambaugh, R.F.; Yu, J.; Yuan, Y. The short of it: Investor sentiment and anomalies. J. Financ. Econ. 2012, 104, 288–302. [Google Scholar] [CrossRef]
- Aabo, T.; Pantzalis, C.; Park, J.C. Idiosyncratic volatility: An indicator of noise trading? J. Bank. Financ. 2017, 75, 136–151. [Google Scholar] [CrossRef]
- Cao, J.; Han, B. Cross section of option returns and idiosyncratic stock volatility. J. Financ. Econ. 2013, 108, 231–249. [Google Scholar] [CrossRef]
- Nartea, G.V.; Ward, B.D.; Yao, L.J. Idiosyncratic volatility and cross-sectional stock returns in Southeast Asian stock markets. Account. Financ. 2011, 51, 1031–1054. [Google Scholar] [CrossRef]
- Umutlu, M. Idiosyncratic volatility and expected returns at the global level. Financ. Anal. J. 2015, 71, 58–71. [Google Scholar] [CrossRef]
- Sharpe, W.F. Capital asset prices: A theory of market equilibrium under conditions of risk. J. Financ. 1964, 19, 425–442. [Google Scholar]
- Lintner, J. The valuation of risk assets and the selection of risky investments in stock portfolios and capital budgets. Rev. Econ. Stat. 1965, 47, 13–37. [Google Scholar] [CrossRef]
- Merton, R.C. An intertemporal capital asset pricing model. Econom. J. Econom. Soc. 1973, 41, 867–887. [Google Scholar] [CrossRef]
- Chabi-Yo, F. Explaining the idiosyncratic volatility puzzle using Stochastic Discount Factors. J. Bank. Financ. 2011, 35, 1971–1983. [Google Scholar] [CrossRef]
- Chen, Z.; Petkova, R. Does idiosyncratic volatility proxy for risk exposure? Rev. Financ. Stud. 2012, 25, 2745–2787. [Google Scholar] [CrossRef]
- Hou, K.; Loh, R.K. Have we solved the idiosyncratic volatility puzzle? J. Financ. Econ. 2016, 121, 167–194. [Google Scholar] [CrossRef]
- Merton, R.C. A simple model of capital market equilibrium with incomplete information. J. Financ. 1987, 42, 483–510. [Google Scholar] [CrossRef]
- Goyal, A.; Santa-Clara, P. Idiosyncratic risk matters! J. Financ. 2003, 58, 975–1008. [Google Scholar] [CrossRef]
- Bali, T.G.; Cakici, N.; Whitelaw, R.F. Maxing out: Stocks as lotteries and the cross-section of expected returns. J. Financ. Econ. 2011, 99, 427–446. [Google Scholar] [CrossRef]
- Nagel, S. Short sales, institutional investors and the cross-section of stock returns. J. Financ. Econ. 2005, 78, 277–309. [Google Scholar] [CrossRef]
- Miller, E.M. Risk, uncertainty, and divergence of opinion. J. Financ. 1977, 32, 1151–1168. [Google Scholar] [CrossRef]
- Fama, E.F.; French, K.R. Common risk factors in the returns on stocks and bonds. J. Financ. Econ. 1993, 33, 3–56. [Google Scholar] [CrossRef]
- Carhart, M.M. On persistence in mutual fund performance. J. Financ. 1997, 52, 57–82. [Google Scholar] [CrossRef]
- Fama, E.F.; French, K.R. A five-factor asset pricing model. J. Financ. Econ. 2015, 116, 1–22. [Google Scholar] [CrossRef]
- Amihud, Y. Illiquidity and stock returns: Cross-section and time-series effects. J. Financ. Mark. 2002, 5, 31–56. [Google Scholar] [CrossRef]
- Newey, W.; West, K. A simple, positive semi-definite, heteroskedasticity and autocorrelation consistent covariance matrix. Econometrica 1987, 55, 703–708. [Google Scholar] [CrossRef]
- Beber, A.; Pagano, M. Short-selling bans around the world: Evidence from the 2007–09 crisis. J. Financ. 2013, 68, 343–381. [Google Scholar] [CrossRef]
- Brav, A.; Heaton, J.B.; Li, S. The limits of the limits of arbitrage. Rev. Financ. 2010, 14, 157–187. [Google Scholar] [CrossRef]
- Jones, C.M.; Lamont, O.A. Short-sale constraints and stock returns. J. Financ. Econ. 2002, 66, 207–239. [Google Scholar] [CrossRef]
- Lam, F.Y.E.C.; Wei, K.C.J. Limits-to-arbitrage, investment frictions, and the asset growth anomaly. J. Financ. Econ. 2011, 102, 127–149. [Google Scholar] [CrossRef]
- Shleifer, A.; Vishny, R.W. The limits of arbitrage. J. Financ. 1997, 52, 35–55. [Google Scholar] [CrossRef]
- Grossman, S.J.; Zhou, Z. Optimal investment strategies for controlling drawdowns. Math. Financ. 1993, 3, 241–276. [Google Scholar] [CrossRef]
- Hasbrouck, J. Trading costs and returns for U.S. equities: Estimating effective costs from daily data. J. Financ. 2009, 64, 1445–1477. [Google Scholar] [CrossRef]
- Korajczyk, R.A.; Sadka, R. Are momentum profits robust to trading costs? J. Financ. 2004, 59, 1039–1082. [Google Scholar] [CrossRef]
- Novy-Marx, R.; Velikov, M. A taxonomy of anomalies and their trading costs. Rev. Financ. Stud. 2016, 29, 104–147. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).