1. Introduction
Dockless shared-bike services have emerged with technological improvements. Users are exempt from searching for a fixed dock location to borrow or return a dockless shared-bike. The dockless shared-bike services have attracted a significant number of users as they provide an effective solution to “the last kilometer” problem. Many bike-sharing companies emerged to gain profit from this huge market, and each has been producing and launching more and more bicycles to attract users. However, excessive shared-bikes have been placed everywhere in many urban cities in China and occupy roadway space. A study has pointed out that the rapid growth of dockless bike share programs in China is mainly “supply-driven by operators” rather than by “user demand” or “triggered by government policy” [
1]. The promotion of the bike-sharing service is also raising questions about profitability, wide-spread bike vandalism and theft, and growing government regulation [
1]. Managing the size of a shared-bike fleet has been a problem for bike-sharing companies and transportation management departments. Therefore, it is essential to understand the trip pattern for shared-bikes and to develop a method to estimate the demand for shared-bikes.
Various studies have been conducted to explore the travel behavior and trip pattern of shared-bikes, including both docked bikes [
2,
3,
4] and station-free dockless bikes. A study explored bike-sharing trip data from eight cities in the United States and analyzed the distributions of trip distance and trip duration for bike-sharing trips for commuting and touristic purposes [
5]. A study in Minnesota examined factors that influences shared-bike uses with a six-year panel data set of members’ bike-share trips, the finding suggests that the effects of distance are heterogeneous and vary with different built-environment contexts based on a quasi-experimental research, members live in areas with higher population density and a higher percentage of retail land use tended to increase their bike-share use, and improvements in physical accessibility may not result in practically meaningful changes in the frequency of use in all cases [
2]. Another study carried out in Shenzhen indicated that the bike trip pattern is found to be different in the central city and the suburban area [
6]. Several studies utilized deep learning methods to estimate short-term shared-bikes trip volumes [
7,
8,
9,
10,
11]. One study proposes a novel graph convolutional neural network with data-driven graph filter (GCNN-DDGF) model that can learn hidden heterogeneous pairwise correlations between stations to predict station-level hourly demand in a large-scale bike-sharing network [
8]. Another study developed a dynamic demand forecasting model for station-free bike-sharing using long short-term memory neural networks (LSTM NNs) at the TAZ (Traffic Analysis Zone) level for different time intervals [
9]. However, these previous studies relied on historical data and failed to incorporate spatial factors which are found to be important.
With the increasing popularity of smartphones and tablets with location-based service (LBS) features, location-based social networking (LBSN) services have attracted increasing number of users to broadcast their locations and activities through their LBSN applications. The easy availability and wide range of applications have made the LBSN data valuable for researchers in various fields to better understand different aspects of mobility and urban activity patterns. The LBSN data has been used by transportation researchers in land-use type identification [
12,
13], urban travel demand estimation [
14,
15], passenger flow prediction [
16], trip purposes inference [
11,
17,
18,
19] and etc. For instance, one study explored the spatiality of destinations and social network influence on travelers’ destination choice in Chicago [
17]; another study used a topic modeling method to infer individual activity patterns using location-based social network data [
18]; and another study conducted in Florida proposed a method to build individual-level tourist travel demand models [
19]. Some other researches explored methods to estimate aggregated travel demand with location-based social network data. For example one study developed a microscopic long-distance travel demand model and analyzed the sensitivity to the implementation of a new high speed rail corridor in Ontario, Canada [
15]; another study proposed a combined clustering, regression, and gravity model to estimate an origin-destination (OD) matrix for non-commuting trips based on Foursquare user check-in data in the Chicago urban area [
14], and the research established a linear relationship between check-ins at different categories of venues and trip productions and attractions. The location-based social network data could also be used as a data source to extract urban land-use information. One study utilized time distribution frequency of Twitter check-in activity to attain the land-use function in Makassar City, Indonesia [
13]; and another study in New York City used data mining techniques to infer land use types [
12]. Those studies have manifested the potential of using location-based social network data in urban land use inference, and also reveals the hidden linkage between the human activity pattern and the underlying urban land-use pattern.
The purpose of our research is to provide a method to estimate shared-bike demand for transportation management departments and shared service providers to manage a reasonable size of a shared-bike fleet in a metropolitan area. The location-based social network data is proved by many previous researchers to be a useful data source for extracting various human activity pattern. This paper proposes a novel dockless shared-bike demand estimation method that utilizes location-based social network check-in data. The rest of the paper is organized as follows.
Section 2 introduces the data-processing procedures and some preliminary data analysis. In
Section 3, ordinary least square, geographically weighted regression (GWR), and semiparametric geographically weighted regression (SGWR) models are applied and compared to establish the dockless shared-bike trip estimation model. In
Section 4, a case study is conducted in Nanjing using real-world data from the leading shared-bike business company Mobike and location-based social network Weibo.
Section 5 concludes the paper.
2. Data Collection and Preliminary Analysis
Our case study is conducted in Nanjing, which is the capital city in Jiangsu Province. The population of Nanjing is estimated as 8 million, and the GDP is among one of the most prosperous provinces in China. The city is home to 30 university campuses and more than 800,000 university students. The research area is within the central part of the city and covers approximately 850 square kilometers, 25 kilometers long from east to west, and 34 kilometers long from north to south, as shown in
Figure 1.
The shared-bike data used in our research is from the Mobike company. Mobike [
20] is the lead company in bike sharing services in China, which was founded in Shanghai in 2016 and their novel dockless shared-bike services expanded rapidly. By the end of 2017, their membership had grown to 200 million world-wide [
21]. Nanjing was among the first 12 cities where Mobike launched bikes, therefore the market penetration rate is very high. Mobike users can use a mobile app and scanning a QR (Quick Response) code on the mobike to unlock it. After the journey, users can leave mobikes anywhere in public and pay a little money for the use. A mobike is equipped with a built-in Global Positioning System (GPS) chip, enabling the users to find the locations of the nearest mobikes on their mobile phone.
We use an automated program to collect bike location data continuously through the Mobike application programming interface (API). The API provide access to the locations of all the mobikes within 1km distance from a certain location. The program is able to collect bike locations within the study area every 10 minutes. A bike trip can be identified by comparing the location of each mobike between consecutive time periods. The data was collected in 11–13 November 2017. As indicated in
Figure 2a, there are about 100,000 mobikes available for the users to unlock in the research area. The use of mobikes peaks at 7–8AM and 5–6PM, which coincides with the peak hours when people leave for work in the morning and went back home in the afternoon.
Figure 2b displayed the trip length distribution statistics, which suggests most of the trips are under 1 km.
The LBSN data used in this research are from Weibo, one of the leading LBSN service provider in China. Weibo has attracted more than 376 million registered users by September 2017. The Weibo applications use the built-in GPS to obtain a user’s current location and render a list of nearby places for the user to confirm the name of the place when they “check-in” at a location.
Weibo provides API [
22] for check-in information at each venue. The check-in data are publicly accessible, including the locations, the service types, and the historical total check-in counts, etc.; 6463 venues are collected in the research area with total check ins of 3.48 million in history. The locations of the venues are displayed in
Figure 1b, which suggests good spatial coverage in the central area of the city. The service types of the Weibo POIs (points of interest) are labeled with 272 detailed categories. In order to facilitate future studies, we further grouped these categories into 9 classifications: residence, work, entertainment, school, transportation facilities, tour attractions, shop and services, food and others, which are the most commonly used types for trip analyses in transportation planning. The “Others” category contains POI labeled as district names or street names, from which we cannot infer the specific land-use type. The user created personal tags are also classified as others. As indicated in
Table 1, the “School” venue category receives the largest number of average daily check-ins while the “Work” venues have the lowest daily check-ins, which suggest a users’ preference to check-in varies with different venue categories.
3. Methodology
This paper adopted a geographically weighted regression model framework to develop dockless shared-bike trip demand estimation model. Spatial correlation exists in many transportation phenomena, and the geographically weighted regression model framework has been used in various research to explore the spatial variation in association between trip demand for various trip purposes or traveler groups, traffic events, crashes and other explanatory variables such as the built-environment attributes, social-economical attributes, population, etc. For instance, one study used a geographically weighted Poisson regression model to examine the effects of the built-environment on students’ metro ridership in Nanjing [
23]; one study uses geographically weighted regressions to examine the implications of location and attitudinal characteristics for travel behavior in Chengdu [
24]; another research developed zonal crash prediction models within the geographically weighted generalized linear model framework in order to explore the spatial variations in association with the number of crashes causing injuries and other explanatory variables in Belgium [
25]; another study utilized GWR models to identify whether there are spatially varying relationships between walking, bicycling, traffic counts and ambient built-environment attributes including socioeconomic characteristics, transit accessibility indices, land use attributes and characteristics of intersections and roadway networks [
26].
The methodology framework of our research is illustrated in
Figure 3. The check in data are grouped into 8 venue categories to be used as determinant variables of the shared-bike trip prediction model. Since users are only able to find shared-bikes within 1km radius range from their app, we divided the research area into 1 km * 1 km grids, producing 850 zones. A venue can only reside in one grid while check ins at a venue could reflect activities within a much larger area than 1 km
2, therefore we use kriging interpolation method to estimate the activities in the neighboring grid. In addition to check ins at eight venue categories, we also consider total check in and distance to the subway station as candidate determinant variables. In this study, we evaluated three methods including the conventional ordinary least squares (OLS) regression model, GWR and SGWR to establish the prediction model of shared-bike trips, which are discussed in the following sections:
3.1. Ordinary Least Squares (OLS) Model
We firstly use the traditional OLS model explore the relationship between shared-bike uses and number of check ins at different venue types in a zone, the form of the OLS model [
27] is:
where
is the response variable at a certain location
and
is a row vector of explanatory variables at location i,
is a column vector of regression coefficients, and
is the random error for zone i. The first element of the equation
is the intercept.
The model parameters of the OLS model are estimated globally for the entire study area, and the relationships between the dependent variable and the explanatory variables are considered to be stationary over space. However, in reality, especially in the transportation engineering field, the influence of each explanatory variable on the response variable may vary in space.
3.2. Geographically Weighted Regression (GWR) Model
GWR is a linear formulation which models spatially varying relationships by incorporating geo-coordinates into the model. The general form of the GWR equation is given as [
28]:
where:
represent dependent variable at location
represent independent variable at location
represent the error term at location
represent the geographical location (geo-coordinates) of location
represent the weighing parameter for location for independent variable
The most commonly used weighting functions include Gaussian function and bi-square function, which are defined as follows:
Bi-square function,
where
is the Euclidean distance between observations
i and j, and b is the bandwidth.
In practice, the results of GWR are relatively insensitive to the choice of weighting function, but they are sensitive to the bandwidth of the particular weighting function. There are two weighting schemes in the choice of bandwidth: one is a constant bandwidth (a fixed kernel) and the other one is a variable bandwidth (an adaptive kernel). In an adaptive kernel, the bandwidth may change from location to location. The bandwidth will be larger in case of sparsely distributed data than densely distributed data. This flexibility could induce a more accurate model, therefore we adopt the adaptive kernel method with bi-square function in our study [
29].
In the calibration of the adaptive kernel, we use the number of data points as the bandwidth. Adjusting the bandwidth changes the number of degrees of freedom in the model. The Akaike information criterion (AIC) method provides a trade-off between goodness-of-fit and the degree of freedom to optimize the bandwidth. Fotheringham defined the AICc equation for GWR as [
28]:
where n is the local sample size (according to bandwidth);
is the estimated standard deviation of the error term; and tr(S) represents the trace of the hat matrix S. The hat matrix denotes the projection matrix from the observed y to the fitted values.
Preference is given to lower values of AICc since they indicate a closer fit to the data. The function minimization procedure uses the Golden Section method. The AIC criterion provides not only a framework for bandwidth selection, but also one for choosing models. Typically, the AIC value may be presented in relative form, by subtracting the lowest AIC value from each of the raw AIC values. When the AIC values for two models differ by more than 3, the two models are considered significantly different [
23].
3.3. Semiparametric Geographically Weighted Regression (SGWR) Model
GWR is not always appropriate if some of the variables do not exhibit spatial non-stationarity and can be held constant. An important extension of GWR is its semiparametric formation by mixing globally fixed and geographically varying coefficients. We used a SGWR model after testing for spatial variability of all variables. In SGWR, some contributing factors that have no spatial variability will generate a global parameter, while others with spatial variability will produce a local parameter. The SGWR is defined as [
27]:
are the global coefficients and are the local coefficient functions, are the independent global variables associated with fixed coefficients and are the independent local variables associated with geographically varying coefficients.
For testing the geographical variability of the kth local variable, a model comparison is carried out between the original GWR and a switched model with the kth coefficient fixed. If the switched GWR model outperforms the original GWR model in terms of AICc, we can judge that the kth coefficient should be fixed. This procedure is repeated for each of the remaining local variables until no improvement can be gained by transforming into the global variable.
4. Results
We aggregated the LBSN check ins and the shared-bike uses data by 1km*1km grids, resulting in 850 (25*34) zones in the study area.
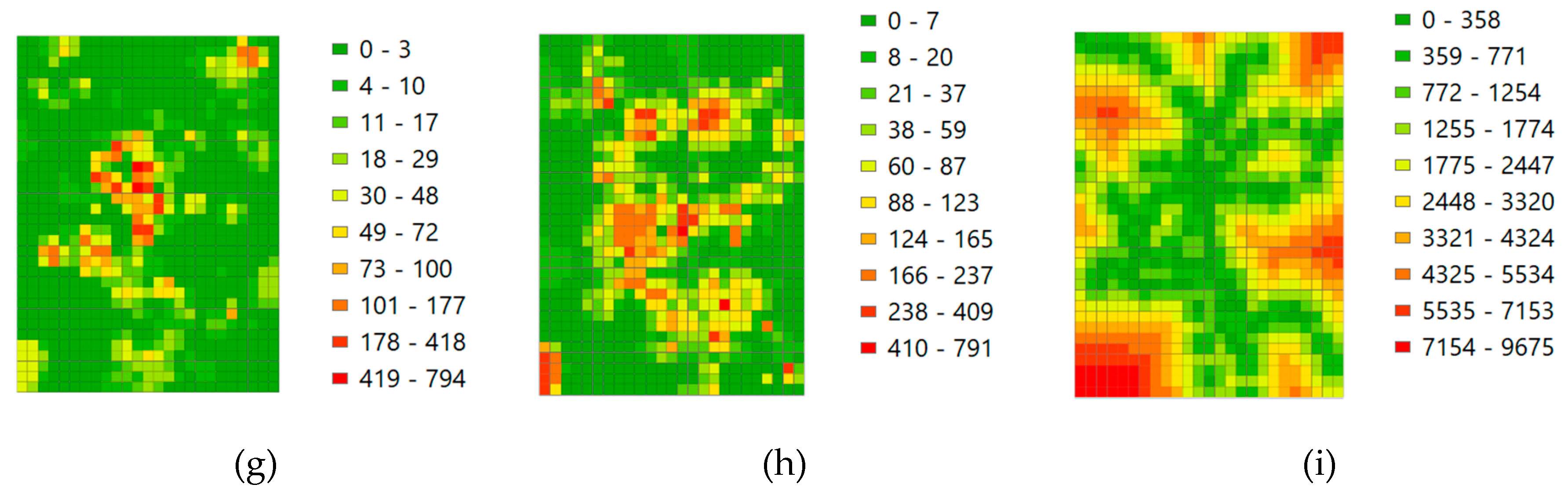
Figure 4 illustrates the heatmap of the average daily check ins and the mobike uses. We used the natural breaks (Jenks) method to classify the values into 10 groups. As indicated in the heatmap, both the check ins and mobike uses are concentrated in the center area of the city. It can also be found that in the upper left corner of the map, there is a hot spot for mobike use but this suggests a low value for check ins. The place is a newly developed area, which may not be adequately reflected in the LBSN data.
In this study, a total of 10 variables were considered as potential mobike use predictor. The number of total check ins is accounted as one of the prospective predictors. As found in previous research, users’ preference of checking in varies greatly at different venue types [
14]. Therefore, the number of check ins of the 8 major venue categories are also considered as potential predictors of mobike trips, including transportation facilities, residence, work, entertainment, school, tour attractions, shop and services, and food. In addition, the distance to the nearest subway station is taken into consideration since many people use shared-bike as a last mile transportation solution to transfer between public transportation system and their destination places. As shown in
Figure 5, the number of check ins of the 8 venue categories and the distance from the centroid of the zone to the nearest subway station (in meters) are color coded in the 850 zones using the natural breaks (Jenks) method. Shop, food and entertainment venues are mostly concentrated in the center area, most check ins at transportation facilities are in the two railway stations.
Firstly, we use OLS method to examine the significance of each variable. All of the independent variables are standardized by z-score transformation so that each variable has zero mean and one standard deviation. It is useful for interpreting estimated coefficients under the same metric.
Table 2 lists the significance test of the explanatory variables of the OLS model. In addition, we performed a Koenker (BP) test and examined the correlation between these variables in pairs plots (See
Appendix A). The result of the BP test is statistically significant, therefore we use the robust probability column to determine if a coefficient is significant or not. Of the covariates, only total check ins, campus and transportation facilities are not significant (at significance level 0.05) in the model; therefore, only the other 7 variables are considered in the following analysis. In addition, the result suggested that coefficients associated with transportation facilities, tour attractions and distance to the nearest subway station are negative indicating that a decrease of Mobike use may be associated with an increase of activities in transportation facilities, tour attractions and distance to the nearest subway station.
We used the OLS, GWR, SGWR methods to establish the methods to establish the prediction model of mobike uses with location-based social network data. Several commonly used evaluation criteria including R-square, adjusted R-square, classic Akaike’s information criterion (AIC), and AICc are calculated as in
Table 3. The OLS method is the most widely used method in building models with several parameters since the model is relatively simple, and the meaning of the coefficients are relatively easy-to-interpret. The adjusted R
2 of the OLS model is calculated as 0.464452, which indicate approximately 47% of the variations in the number of mobike uses could be explained the 6 categories of check ins and the distance to the subway.
The OLS model failed to account for the non-stationarity of the influence of check ins in different areas and needs to be explored using GWR. The adjusted R2 of the GWR model is 0.696865, which is a significant improvement of the prediction accuracy from OLS. GWR may not be appropriate if some of the variables do not exhibit spatial non-stationarity. In SGWR, contributing factors that have no spatial variability will generate a global parameter, while others with spatial variability will produce a local parameter.
After the geographically variability test, we found that switching the tour and residence variable into fixed global variable would not significantly change the AICc (the value changed is less than 3), the remaining local variables includes shop, food, entertainment, work and distance to subway. The adjusted R2 of the SGWR model is 0.71166, which is better than GWR. In addition, the lower value of AICc confirms the advantage of SGWR model.
We further examined the local R2 using heat map to compare the performance of GWR and SGWR model on a zonal basis. As indicated in
Figure 6, both models perform well in the city center where shared-bike uses are higher.
To further evaluate the performances of the results of the three models, the residuals are plotted in
Figure 7. In addition, the Moran’s index method is used to inspect the spatial autocorrelation of the residuals. The results of the spatial autocorrelation test are listed in
Table 4, which suggests the pattern of the residuals of SGWR did not appear to be significantly different than random, while the residuals of the OLS and GWR model appeared to be clustered. The result of the spatial autocorrelation test also suggest the SGWR model perform better than the other two models.
Based on the above evaluations, we adopted the SGWR model to further examine the influences of each variable on shared-bike use. There are two global terms of the SGWR model: tour and residence, and the coefficients are 0.0326 and 0.1334 respectively. Their coefficients are both positive which indicates positive influences of touring activities and residential activities on the shared-bike use.
Figure 8a illustrated the spatial variations of the average coefficients and
Figure 8b displays the t-statistics of the local variables of the SGWR model, where the red indicates a positive association between the variable and the shared-bike use, and the green color indicates negative association between the variable and the shared-bike use. The figure suggests the effect of the subway station is very strong in attracting shared-bike use. With the distance closer to a subway station, the shared-bike uses will increase. The influence of dinning places is generally positive in most of the area which indicate the increase of dining activities may induce more shared-bike use. The influence of shopping activities appears to be negative in the central area where shopping places are densely distributed while in the suburban area where shopping places are sparse the influence turns out to be positive. The effect of the entertainment places on shared-bike use presents significant variations, while in the central area the trend is still generally positive. The effect of working places exhibits positive in the central area where office buildings are densely distributed while in the southern part of the city, most of the working places are factories which are sparsely distributed. The increased commuting distance in the southern area may induce people to choose personal vehicles over the shared-bikes.
5. Conclusions
In this study, we proposed a data-driven method to estimate urban shared-bike uses with location-based social networking data. A total of 10 variables were considered as potential Mobike use predictors, seven variables including residence, work, entertainment, tour attractions, shop, services, and food, and the distance to the nearest subway station were selected to develop the models. We compared OLS, GWR and SGWR models and the results indicated that the SGWR models were able to better explain the variation in the data and to predict shared-bike use with smaller errors than the ordinary linear regression models and GWR models. To investigate the predictive powers of various predictors over the space, statistics such local r-square and local parameter estimates were examined and mapped to assess the usefulness of SGWR methods.
The analysis presented here can help us understand the demand pattern of shared-bike use and help to address a series of questions both for urban transportation management department and the shared-bike service providers. i.e., how many shared-bikes should be launched in a certain place? In what kind of places should the shared-bikes be launched to maximize the benefit? How to distribute new shared-bikes in different places in a city? Our method of estimating shared-bike demand using LBSN data could be applied in large metropolitan areas where the use of LBSN services is popular to calculate recommended number of shared-bikes in various traffic analysis zones, eliminating superfluous shared-bikes and help improve the quality of urban transportation environment.
In small cities where the LBSN service is not widely used, shared-bike demand would be difficult to quantify and an estimation maybe biased. However, our findings could still be useful in guiding the allocation of the shared-bikes given the land use type information in a certain area. As indicated in our previous analysis, more shared-bikes should be launched in the central area rather than in the suburban area. In addition, the shared-bike should be launched more in residential areas, places near to a subway station, and commercial areas with a lot of shopping and dining places.
For future studies, if more data would be available, we could further this research to establish dynamic shared-bike trip prediction model. In addition, we could incorporate more datasets into our methodological framework such as traffic volume, subway volume, and origin–destination demand, etc. Furthermore, we could investigate the transferability of this methodology if the datasets of other cities could be obtained.