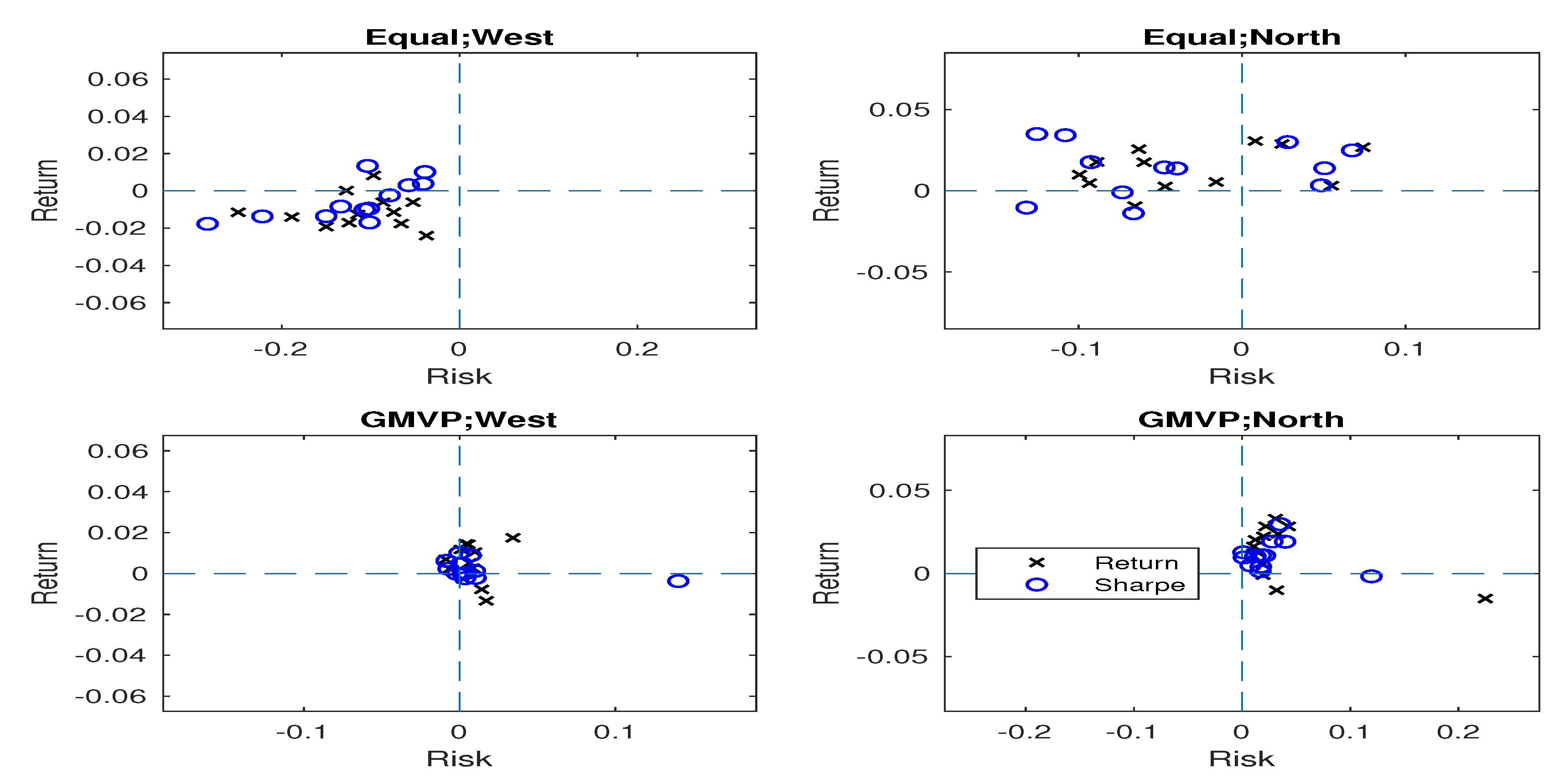
Figure 1.
Positions of the proposed portfolios based on the benchmark portfolio when 12 real datasets were used. The circle and cross points indicate the portfolios using Sharpe ratio and mean return as criterion functions, respectively. As the 12 datasets are considered for the equally-weighted and GMVP portfolios, each subplot consists of points.
Figure 1.
Positions of the proposed portfolios based on the benchmark portfolio when 12 real datasets were used. The circle and cross points indicate the portfolios using Sharpe ratio and mean return as criterion functions, respectively. As the 12 datasets are considered for the equally-weighted and GMVP portfolios, each subplot consists of points.
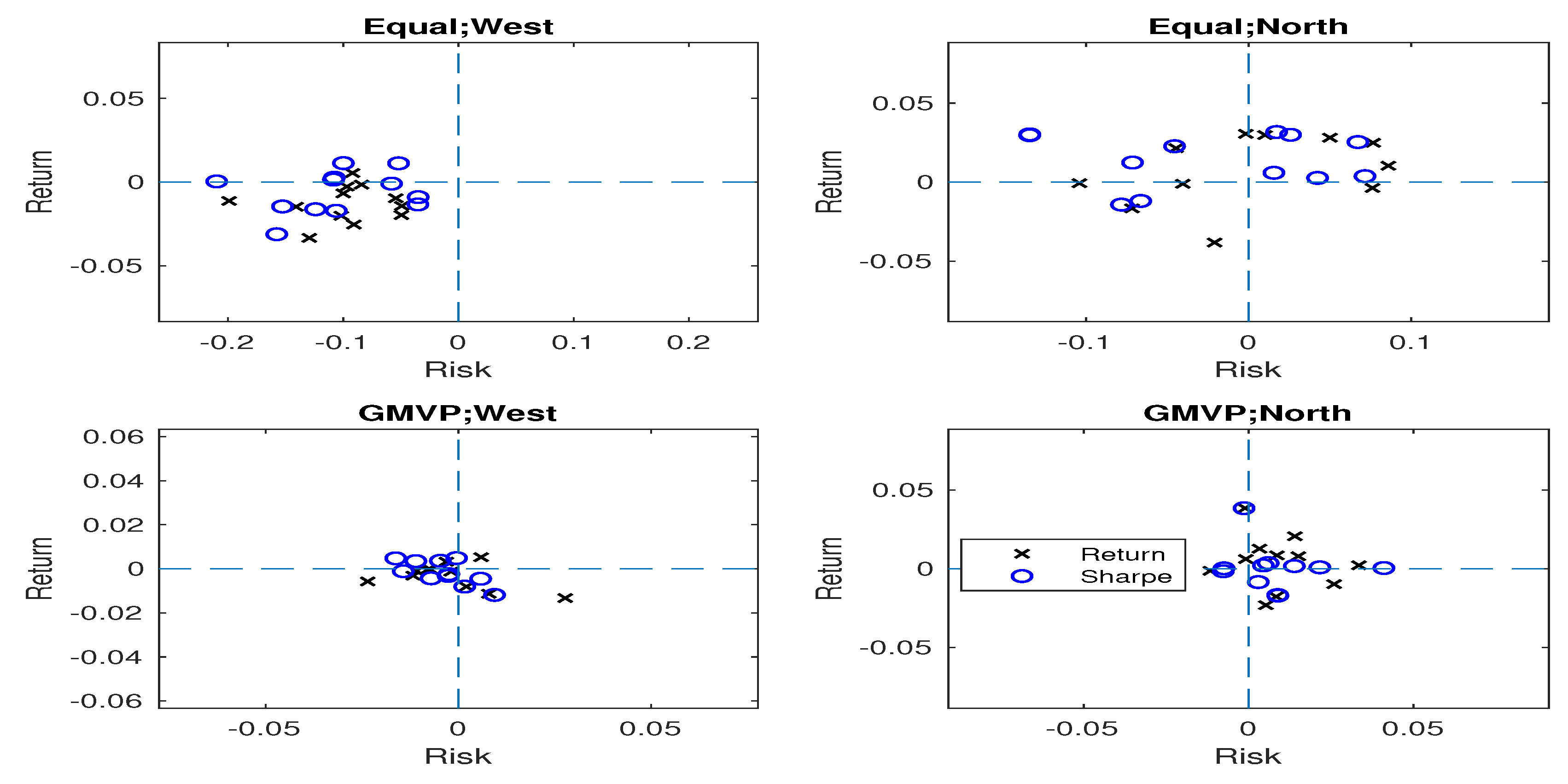
Figure 2.
Positions of the proposed portfolios based on the benchmark portfolio when the partially simulated data were considered. The circle and cross points indicate the portfolios using Sharpe ratio and mean return as criterion functions, respectively. As the 12 datasets are considered for the equally-weighted and GMVP portfolios, each subplot consists of points.
Figure 2.
Positions of the proposed portfolios based on the benchmark portfolio when the partially simulated data were considered. The circle and cross points indicate the portfolios using Sharpe ratio and mean return as criterion functions, respectively. As the 12 datasets are considered for the equally-weighted and GMVP portfolios, each subplot consists of points.
Table 1.
Comparison between contributions of different authors in terms of optimization, parameter selection, and performance measures.
Table 1.
Comparison between contributions of different authors in terms of optimization, parameter selection, and performance measures.
| Method | Optimization | Parameter Selection | Performances |
|---|
| Return | Risk | Sparsity | Stability | Cross-validation | Fixed | Return | Skewness | Turnovers | Sharpe Ratio |
|---|
| Proposed west selection | | ✓ | ✓ | ✓ | ✓ | | ✓ | ✓ | ✓ | ✓ |
| Proposed north selection | ✓ | ✓ | ✓ | ✓ | ✓ | | ✓ | ✓ | ✓ | ✓ |
| Lobo et al. [14] | ✓ | ✓ | | ✓ | | ✓ | ✓ | | | |
| DeMiguel et al. [15] | | ✓ | ✓ | | ✓ | | | | ✓ | ✓ |
| Brodie et al. [16] | ✓ | ✓ | ✓ | | | ✓ | ✓ | | | ✓ |
| Xing et al. [18] | | ✓ | ✓ | ✓ | ✓ | | ✓ | | ✓ | ✓ |
| Roll [24] | ✓ | ✓ | | | | ✓ | ✓ | | | |
| Jorion [25] | ✓ | ✓ | | | | ✓ | ✓ | | | ✓ |
| Shen et al. [26] | | ✓ | ✓ | ✓ | ✓ | | ✓ | | ✓ | ✓ |
| Ruiz-Torrubiano and Suárez [41] | ✓ | ✓ | | | | ✓ | ✓ | | | |
| Gilli and Kellezi [42] | ✓ | ✓ | ✓ | | | ✓ | ✓ | | ✓ | |
| Beasley et al. [43] | ✓ | ✓ | | | | ✓ | ✓ | | | |
| Ni and Wang [44] | ✓ | ✓ | | | | ✓ | ✓ | | ✓ | |
| Hodder, Jackwerth, and Kolokolova [28] | ✓ | ✓ | | | | ✓ | ✓ | ✓ | ✓ | ✓ |
| Kuosmanen [29] | ✓ | ✓ | | | | ✓ | ✓ | ✓ | ✓ | ✓ |
| Luedtke [30] | ✓ | ✓ | ✓ | | | ✓ | ✓ | | ✓ | |
| Bruni et al. [31] | ✓ | ✓ | ✓ | | | ✓ | ✓ | | | ✓ |
| Fábián et al. [32] | ✓ | ✓ | ✓ | | | ✓ | ✓ | ✓ | | |
| Guastaroba and Speranza [33] | ✓ | ✓ | ✓ | | | ✓ | ✓ | | | |
Table 2.
Portfolio selection methods, cross-validation performance measures, and abbreviations.
Table 2.
Portfolio selection methods, cross-validation performance measures, and abbreviations.
| Method | Cross-Validation Criterion | Abbreviation |
|---|
| West selection | Mean return | W-R |
| Sharpe ratio | W-S |
| North selection | Mean return | N-R |
| Sharpe ratio | N-S |
Table 3.
Average monthly returns of the proposed portfolios and benchmark for the 12 real datasets case. The two benchmark portfolios, equally-weighted portfolio and GMVP, were considered when constructing the portfolios, respectively. The differences of mean returns between proposed portfolios and benchmark are also given in parenthesis. “Bench” represents the benchmark, and “W-R” (“N-R”) and “W-S” (“N-S”) represent the west (north) portfolios using the mean return and Sharpe ratio as criterion functions in the cross validation, respectively.
Table 3.
Average monthly returns of the proposed portfolios and benchmark for the 12 real datasets case. The two benchmark portfolios, equally-weighted portfolio and GMVP, were considered when constructing the portfolios, respectively. The differences of mean returns between proposed portfolios and benchmark are also given in parenthesis. “Bench” represents the benchmark, and “W-R” (“N-R”) and “W-S” (“N-S”) represent the west (north) portfolios using the mean return and Sharpe ratio as criterion functions in the cross validation, respectively.
| Data | Equally-Weighted | GMVP |
|---|
| Bench | W-R | W-S | N-R | N-S | Bench | W-R | W-S | N-R | N-S |
|---|
| DOW30 | 0.129 | 0.114 | 0.110 | 0.149 | 0.138 | 0.107 | 0.102 | 0.105 | 0.107 | 0.113 |
| | | (−0.015) | (−0.019) | (0.020) | (0.009) | | (−0.005) | (−0.002) | (0.000) | (0.006) |
| DAX30 | 0.117 | 0.098 | 0.106 | 0.122 | 0.120 | 0.101 | 0.105 | 0.105 | 0.108 | 0.115 |
| | | (−0.019) | (−0.011) | (0.005) | (0.003) | | (0.004) | (0.004) | (0.007) | (0.014) |
| FTSE100 | 0.135 | 0.134 | 0.123 | 0.159 | 0.160 | 0.125 | 0.133 | 0.132 | 0.144 | 0.151 |
| | | (−0.001) | (−0.012) | (0.024) | (0.025) | | (0.008) | (0.007) | (0.019) | (0.026) |
| SP100 | 0.128 | 0.120 | 0.136 | 0.133 | 0.158 | 0.112 | 0.112 | 0.111 | 0.127 | 0.117 |
| | | (−0.008) | (0.008) | (0.005) | (0.030) | | (0.000) | (−0.001) | (0.015) | (0.005) |
| FTSE250 | 0.145 | 0.119 | 0.146 | 0.147 | 0.149 | 0.158 | 0.143 | 0.154 | 0.143 | 0.157 |
| | | (−0.026) | (0.001) | (0.002) | (0.004) | | (−0.015) | (−0.004) | (−0.015) | (−0.001) |
| SP500 | 0.143 | 0.130 | 0.144 | 0.143 | 0.172 | 0.074 | 0.077 | 0.072 | 0.097 | 0.073 |
| | | (−0.013) | (0.001) | (0.001) | (0.029) | | (0.003) | (−0.002) | (0.023) | (−0.001) |
| Hang Seng | 0.038 | 0.022 | 0.022 | 0.059 | 0.057 | 0.060 | 0.061 | 0.061 | 0.088 | 0.066 |
| | | (−0.016) | (−0.016) | (0.021) | (0.019) | | (0.001) | (0.001) | (0.028) | (0.006) |
| FF49 | 0.118 | 0.125 | 0.130 | 0.131 | 0.131 | 0.109 | 0.109 | 0.103 | 0.110 | 0.111 |
| | | (0.007) | (0.012) | (0.013) | (0.013) | | (0.001) | (−0.006) | (0.001) | (0.002) |
| NASDAQ100 | 0.170 | 0.151 | 0.159 | 0.196 | 0.179 | 0.113 | 0.129 | 0.109 | 0.136 | 0.127 |
| | | (−0.019) | (−0.011) | (0.026) | (0.009) | | (0.016) | (−0.004) | (0.023) | (0.014) |
| Euro Stoxx50 | 0.093 | 0.085 | 0.088 | 0.091 | 0.093 | 0.101 | 0.111 | 0.099 | 0.103 | 0.102 |
| | | (−0.008) | (−0.005) | (−0.002) | (0.000) | | (0.010) | (−0.002) | (0.002) | (0.001) |
| NASDAQ3000 | 0.149 | 0.128 | 0.133 | 0.161 | 0.158 | 0.077 | 0.089 | 0.080 | 0.094 | 0.081 |
| | | (−0.021) | (−0.016) | (0.012) | (0.009) | | (0.012) | (0.003) | (0.017) | (0.004) |
| RUSSELL2000 | 0.146 | 0.133 | 0.127 | 0.147 | 0.131 | 0.060 | 0.073 | 0.068 | 0.072 | 0.068 |
| | | (−0.013) | (−0.019) | (0.001) | (−0.015) | | (0.013) | (0.008) | (0.012) | (0.008) |
Table 4.
Average monthly returns of the proposed portfolios and benchmark when partially simulated data were considered.
Table 4.
Average monthly returns of the proposed portfolios and benchmark when partially simulated data were considered.
| Data | Equally-Weighted | GMVP |
|---|
| Bench | W-R | W-S | N-R | N-S | Bench | W-R | W-S | N-R | N-S |
|---|
| DOW30 | 0.127 | 0.107 | 0.111 | 0.157 | 0.158 | 0.102 | 0.100 | 0.099 | 0.110 | 0.104 |
| | | (−0.020) | (−0.016) | (0.030) | (0.031) | | (−0.002 ) | (−0.003) | (0.008) | (0.002) |
| DAX30 | 0.113 | 0.098 | 0.098 | 0.096 | 0.101 | 0.094 | 0.086 | 0.086 | 0.102 | 0.096 |
| | | (−0.015) | (−0.015) | (−0.017) | (−0.012) | | (−0.008) | (−0.008) | (0.008) | (0.002) |
| FTSE100 | 0.127 | 0.124 | 0.128 | 0.155 | 0.157 | 0.133 | 0.136 | 0.137 | 0.145 | 0.136 |
| | | (−0.003) | (0.001) | (0.028) | (0.030) | | (0.003) | (0.004) | (0.012) | (0.003) |
| SP100 | 0.125 | 0.111 | 0.116 | 0.124 | 0.155 | 0.109 | 0.114 | 0.106 | 0.115 | 0.101 |
| | | (−0.014) | (−0.009) | (−0.001) | (0.030) | | (0.005) | (−0.003) | (0.006) | (−0.008) |
| FTSE250 | 0.137 | 0.127 | 0.136 | 0.136 | 0.149 | 0.144 | 0.131 | 0.140 | 0.135 | 0.145 |
| | | (−0.010) | (−0.001) | (−0.001) | (0.012) | | (−0.013) | (−0.004) | (−0.009) | (0.001) |
| SP500 | 0.125 | 0.105 | 0.112 | 0.124 | 0.155 | 0.109 | 0.114 | 0.106 | 0.115 | 0.101 |
| | | (−0.020) | (−0.013) | (−0.001) | (0.030) | | (0.005) | (−0.003) | (0.006) | (−0.008) |
| Hang Seng | 0.026 | 0.015 | 0.026 | 0.051 | 0.051 | 0.076 | 0.065 | 0.065 | 0.097 | 0.077 |
| | | (−0.011) | (0.000) | (0.025) | (0.025) | | (−0.011) | (−0.011) | (0.021) | (0.001) |
| FF49 | 0.095 | 0.101 | 0.107 | 0.117 | 0.118 | 0.708 | 0.698 | 0.697 | 1.092 | 1.092 |
| | | (0.006) | (0.012) | (0.022) | (0.023) | | (−0.010) | (−0.011) | (0.384) | (0.384) |
| NASDAQ100 | 0.164 | 0.139 | 0.147 | 0.194 | 0.170 | 0.130 | 0.127 | 0.134 | 0.107 | 0.130 |
| | | (−0.025) | (−0.017) | (0.030) | (0.006) | | (−0.003) | (0.004) | (−0.023) | (0.000) |
| Euro Stoxx50 | 0.089 | 0.087 | 0.100 | 0.085 | 0.091 | 0.105 | 0.105 | 0.101 | 0.104 | 0.104 |
| | | (−0.002) | (0.011) | (−0.004) | (0.002) | | (0.000) | (−0.004) | (−0.001) | (−0.001) |
| NASDAQ3000 | 0.191 | 0.184 | 0.193 | 0.201 | 0.195 | 0.157 | 0.157 | 0.161 | 0.159 | 0.140 |
| | | (−0.007) | (0.002) | (0.010) | (0.004) | | (0.000) | (0.004) | (0.002) | (−0.017) |
| RUSSELL2000 | 0.174 | 0.140 | 0.143 | 0.136 | 0.160 | 0.159 | 0.153 | 0.162 | 0.141 | 0.142 |
| | | (−0.034) | (−0.031) | (−0.038) | (−0.014) | | (−0.006) | (0.003) | (−0.018) | (−0.017) |
Table 5.
Average monthly returns of the proposed portfolios and benchmark over six different evaluation periods when completely simulated data were considered. The two benchmark portfolios, equally-weighted portfolio and GMVP, were considered when constructing the proposed portfolios, respectively, and was used in simulation, where p represents the number of static components in the simulation model.
Table 5.
Average monthly returns of the proposed portfolios and benchmark over six different evaluation periods when completely simulated data were considered. The two benchmark portfolios, equally-weighted portfolio and GMVP, were considered when constructing the proposed portfolios, respectively, and was used in simulation, where p represents the number of static components in the simulation model.
| Case | Evaluation Period | Equally-Weighted | GMVP |
|---|
| Bench | W-R | W-S | N-R | N-S | Bench | W-R | W-S | N-R | N-S |
|---|
| 1–5000 | 0.597 | 0.603 | 0.533 | 0.674 | 0.653 | 0.002 | 0.033 | 0.024 | 0.043 | 0.036 |
| | | (0.006) | (−0.064) | (0.077) | (0.056) | | (0.031) | (0.022) | (0.041) | (0.034) |
| 1–1000 | 0.027 | 0.089 | 0.084 | 0.060 | 0.092 | −0.002 | −0.006 | 0.016 | 0.006 | 0.014 |
| | | (0.062) | (0.057) | (0.033) | (0.065) | | (−0.004) | (0.018) | (0.008) | (0.016) |
| 1001–2000 | −0.508 | −0.287 | −0.360 | −0.242 | −0.395 | −0.002 | −0.005 | −0.003 | 0.009 | 0.017 |
| | | (0.221) | (0.148) | (0.266) | (0.113) | | (−0.003) | (−0.001) | (0.011) | (0.019) |
| 2001–3000 | 1.219 | 1.057 | 0.943 | 1.108 | 1.122 | 0.006 | 0.055 | 0.022 | 0.063 | 0.047 |
| | | (−0.162) | (−0.276) | (−0.111) | (−0.097) | | (0.049) | (0.016) | (0.057) | (0.041) |
| 3001–4000 | 1.482 | 1.385 | 1.259 | 1.443 | 1.448 | 0.007 | 0.072 | 0.045 | 0.076 | 0.056 |
| | | (−0.097) | (−0.223) | (−0.039) | (−0.034) | | (0.065) | (0.038) | (0.069) | (0.049) |
| 4001–5000 | 0.752 | 0.757 | 0.720 | 0.971 | 0.967 | 0.003 | 0.049 | 0.037 | 0.058 | 0.045 |
| | | (0.005) | (−0.032) | (0.219) | (0.215) | | (0.046) | (0.034) | (0.055) | (0.042) |
| 1–5000 | 0.497 | 0.558 | 0.540 | 0.542 | 0.574 | 0.001 | 0.030 | 0.013 | 0.032 | 0.016 |
| | | (0.061) | (0.043) | (0.045) | (0.077) | | (0.029) | (0.012) | (0.031) | (0.015) |
| 1–1000 | −0.972 | −0.710 | −0.696 | −0.937 | −0.896 | −0.001 | −0.007 | −0.012 | −0.016 | −0.021 |
| | | (0.262) | (0.276) | (0.035) | (0.076) | | (−0.006) | (−0.011) | (−0.015) | (−0.020) |
| 1001–2000 | 0.364 | 0.429 | 0.443 | 0.400 | 0.455 | 0.001 | −0.003 | 0.011 | 0.015 | 0.016 |
| | | (0.065) | (0.079) | (0.036) | (0.091) | | (−0.004) | (0.010) | (0.014) | (0.015) |
| 2001–3000 | 1.541 | 1.527 | 1.369 | 1.502 | 1.556 | 0.002 | 0.068 | 0.034 | 0.070 | 0.042 |
| | | (−0.014) | (−0.172) | (−0.039) | (0.015) | | (0.066) | (0.032) | (0.068) | (0.040) |
| 3001–4000 | 1.420 | 1.346 | 1.225 | 1.529 | 1.509 | 0.002 | 0.083 | 0.029 | 0.081 | 0.030 |
| | | (−0.074) | (−0.195) | (0.109) | (0.089) | | (0.081) | (0.027) | (0.079) | (0.028) |
| 4001–5000 | 0.166 | 0.230 | 0.375 | 0.242 | 0.276 | 0.001 | 0.011 | 0.005 | 0.010 | 0.014 |
| | | (0.064) | (0.209) | (0.076) | (0.110) | | (0.010) | (0.004) | (0.009) | (0.013) |
Table 6.
Kurtosis of the proposed portfolio when 12 real datasets were considered. The two benchmark portfolios, equally-weighted portfolio and GMVP, were considered when constructing the proposed portfolios, respectively. Kurtosis of any univariate normal distribution is 3. A higher kurtosis indicates infrequent extreme outliers or deviations in returns. “W-R” (“N-R”) and “W-S” (“N-S”) represent the west (north) portfolios using the mean return and Sharpe ratio as criterion functions in the cross validation, respectively.
Table 6.
Kurtosis of the proposed portfolio when 12 real datasets were considered. The two benchmark portfolios, equally-weighted portfolio and GMVP, were considered when constructing the proposed portfolios, respectively. Kurtosis of any univariate normal distribution is 3. A higher kurtosis indicates infrequent extreme outliers or deviations in returns. “W-R” (“N-R”) and “W-S” (“N-S”) represent the west (north) portfolios using the mean return and Sharpe ratio as criterion functions in the cross validation, respectively.
| Data | Equally-Weighted | GMVP |
|---|
| W-R | W-S | N-R | N-S | W-R | W-S | N-R | N-S |
|---|
| DOW30 | 2.55 | 2.61 | 2.49 | 2.50 | 1.99 | 1.99 | 2.01 | 1.93 |
| DAX30 | 2.57 | 2.51 | 2.30 | 2.24 | 2.87 | 2.97 | 2.91 | 2.88 |
| FTSE100 | 2.95 | 2.96 | 2.77 | 2.76 | 2.46 | 2.40 | 2.43 | 2.40 |
| SP100 | 2.46 | 2.29 | 2.30 | 2.20 | 2.31 | 2.29 | 2.03 | 2.16 |
| FTSE250 | 3.03 | 2.88 | 3.05 | 2.99 | 2.05 | 2.10 | 2.46 | 2.13 |
| SP500 | 2.18 | 2.38 | 2.25 | 2.20 | 2.51 | 2.24 | 2.10 | 2.12 |
| Hang Seng | 2.43 | 2.46 | 2.45 | 2.33 | 2.48 | 2.42 | 2.16 | 2.31 |
| FF49 | 2.66 | 2.82 | 2.99 | 3.09 | 2.25 | 2.29 | 2.19 | 2.32 |
| NASDAQ100 | 2.51 | 2.30 | 2.68 | 2.66 | 2.32 | 2.39 | 2.40 | 2.46 |
| Euro Stoxx50 | 2.52 | 2.64 | 2.57 | 2.59 | 2.22 | 2.38 | 2.35 | 2.38 |
| NASDAQ3000 | 1.93 | 2.32 | 2.20 | 1.98 | 1.93 | 2.32 | 2.20 | 1.98 |
| RUSSELL2000 | 2.45 | 2.29 | 1.97 | 1.93 | 2.45 | 2.29 | 1.97 | 1.93 |
Table 7.
Kurtosis of the proposed portfolio when partially simulated data were considered.
Table 7.
Kurtosis of the proposed portfolio when partially simulated data were considered.
| Data | Equally-Weighted | GMVP |
|---|
| W-R | W-S | N-R | N-S | W-R | W-S | N-R | N-S |
|---|
| DOW30 | 2.47 | 2.53 | 2.56 | 2.57 | 2.03 | 2.01 | 2.01 | 2.02 |
| DAX30 | 2.58 | 2.49 | 2.18 | 2.24 | 3.33 | 3.32 | 3.06 | 2.97 |
| FTSE100 | 2.90 | 2.99 | 2.81 | 2.91 | 2.57 | 2.30 | 2.34 | 2.39 |
| SP100 | 2.52 | 2.54 | 2.44 | 2.18 | 2.33 | 2.29 | 2.23 | 2.17 |
| FTSE250 | 3.07 | 3.13 | 2.74 | 3.01 | 2.19 | 2.22 | 2.34 | 2.21 |
| SP500 | 2.46 | 2.46 | 2.44 | 2.18 | 2.33 | 2.29 | 2.23 | 2.17 |
| Hang Seng | 2.47 | 2.46 | 2.34 | 2.31 | 2.81 | 2.79 | 2.48 | 2.51 |
| FF49 | 2.81 | 2.67 | 2.73 | 2.75 | 2.70 | 2.76 | 2.65 | 2.68 |
| NASDAQ100 | 2.38 | 2.35 | 2.69 | 2.72 | 2.41 | 2.25 | 2.41 | 2.22 |
| Euro Stoxx50 | 2.40 | 2.43 | 2.41 | 2.33 | 2.22 | 2.25 | 2.34 | 2.20 |
| NASDAQ3000 | 2.16 | 2.05 | 1.94 | 1.99 | 2.17 | 2.19 | 2.38 | 2.23 |
| RUSSELL2000 | 2.09 | 2.21 | 1.98 | 2.06 | 2.38 | 2.39 | 2.24 | 2.20 |
Table 8.
Kurtosis of the proposed portfolio over six different evaluation periods when completely simulated data were considered.
Table 8.
Kurtosis of the proposed portfolio over six different evaluation periods when completely simulated data were considered.
| Case | Evaluation Period (T) | Equally-Weighted | GMVP |
|---|
| W-R | W-S | N-R | N-S | W-R | W-S | N-R | N-S |
|---|
| 1–5000 | 2.91 | 2.76 | 2.91 | 2.83 | 3.05 | 2.85 | 3.50 | 3.21 |
| 1–1000 | 2.11 | 2.29 | 2.19 | 2.27 | 3.34 | 2.87 | 2.90 | 2.56 |
| 1001–2000 | 2.13 | 2.31 | 2.82 | 2.68 | 3.56 | 3.50 | 3.12 | 3.33 |
| 2001–3000 | 2.14 | 2.11 | 1.91 | 1.93 | 2.07 | 2.80 | 2.07 | 1.96 |
| 3001–4000 | 3.24 | 3.14 | 2.92 | 2.83 | 3.03 | 3.65 | 2.78 | 2.74 |
| 4001–5000 | 2.82 | 2.53 | 2.86 | 2.83 | 3.66 | 3.55 | 3.29 | 3.39 |
| 1–5000 | 2.89 | 2.85 | 2.81 | 2.82 | 3.95 | 3.72 | 3.60 | 3.09 |
| 1–1000 | 1.91 | 1.89 | 1.89 | 1.90 | 2.34 | 2.98 | 3.30 | 3.66 |
| 1001–2000 | 2.57 | 2.57 | 2.79 | 2.84 | 3.48 | 2.90 | 3.01 | 2.97 |
| 2001–3000 | 2.66 | 2.49 | 2.54 | 2.64 | 3.40 | 3.24 | 3.18 | 3.56 |
| 3001–4000 | 2.48 | 2.88 | 2.54 | 2.55 | 2.53 | 3.58 | 2.59 | 3.51 |
| 4001–5000 | 2.83 | 2.73 | 2.52 | 2.55 | 3.01 | 2.94 | 2.78 | 3.30 |
Table 9.
Sparsity of the proposed portfolios and benchmark portfolios when 12 real datasets were used. Two benchmark portfolios, equally-weighted portfolio and GMVP, were considered when constructing the proposed portfolios, respectively. “Bench” represents the benchmark, and “W-R” (“N-R”) and “W-S” (“N-S”) represent the west (north) portfolios using the mean return and Sharpe ratio as criterion functions in the cross validation, respectively.
Table 9.
Sparsity of the proposed portfolios and benchmark portfolios when 12 real datasets were used. Two benchmark portfolios, equally-weighted portfolio and GMVP, were considered when constructing the proposed portfolios, respectively. “Bench” represents the benchmark, and “W-R” (“N-R”) and “W-S” (“N-S”) represent the west (north) portfolios using the mean return and Sharpe ratio as criterion functions in the cross validation, respectively.
| Data | Equally-Weighted | GMVP |
|---|
| W-R | W-S | N-R | N-S | W-R | W-S | N-R | N-S |
|---|
| DOW30 | 0.05 | 0.05 | 0.08 | 0.08 | 0.03 | 0.03 | 0.06 | 0.05 |
| DAX30 | 0.06 | 0.07 | 0.08 | 0.08 | 0.04 | 0.04 | 0.07 | 0.06 |
| FTSE100 | 0.02 | 0.03 | 0.03 | 0.03 | 0.01 | 0.01 | 0.02 | 0.03 |
| SP100 | 0.02 | 0.02 | 0.02 | 0.02 | 0.01 | 0.01 | 0.03 | 0.03 |
| FTSE250 | 0.14 | 0.10 | 0.04 | 0.07 | 0.07 | 0.08 | 0.13 | 0.10 |
| SP500 | 0.02 | 0.02 | 0.02 | 0.03 | 0.01 | 0.01 | 0.02 | 0.02 |
| Hang Seng | 0.04 | 0.04 | 0.04 | 0.04 | 0.02 | 0.02 | 0.03 | 0.03 |
| FF49 | 0.07 | 0.09 | 0.05 | 0.05 | 0.12 | 0.07 | 0.07 | 0.06 |
| NASDAQ100 | 0.04 | 0.04 | 0.02 | 0.03 | 0.01 | 0.01 | 0.02 | 0.03 |
| Euro Stoxx50 | 0.03 | 0.03 | 0.04 | 0.04 | 0.02 | 0.02 | 0.04 | 0.04 |
| NASDAQ3000 | 0.04 | 0.03 | 0.03 | 0.03 | 0.07 | 0.06 | 0.06 | 0.03 |
| RUSSELL2000 | 0.04 | 0.02 | 0.05 | 0.04 | 0.07 | 0.06 | 0.07 | 0.05 |
Table 10.
Sparsity of the proposed portfolios and benchmark when partially simulated data were considered.
Table 10.
Sparsity of the proposed portfolios and benchmark when partially simulated data were considered.
| Data | Equally-Weighted | GMVP |
|---|
| W-R | W-S | N-R | N-S | W-R | W-S | N-R | N-S |
|---|
| DOW30 | 0.03 | 0.04 | 0.06 | 0.07 | 0.03 | 0.03 | 0.04 | 0.04 |
| DAX30 | 0.05 | 0.05 | 0.06 | 0.06 | 0.03 | 0.03 | 0.06 | 0.05 |
| FTSE100 | 0.02 | 0.03 | 0.03 | 0.02 | 0.01 | 0.01 | 0.02 | 0.02 |
| SP100 | 0.02 | 0.02 | 0.02 | 0.02 | 0.01 | 0.01 | 0.02 | 0.02 |
| FTSE250 | 0.02 | 0.02 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 |
| SP500 | 0.02 | 0.02 | 0.02 | 0.02 | 0.01 | 0.01 | 0.02 | 0.02 |
| Hang Seng | 0.04 | 0.03 | 0.03 | 0.04 | 0.02 | 0.02 | 0.03 | 0.03 |
| FF49 | 0.06 | 0.07 | 0.03 | 0.03 | 0.09 | 0.16 | 0.09 | 0.09 |
| NASDAQ100 | 0.03 | 0.03 | 0.02 | 0.02 | 0.01 | 0.01 | 0.02 | 0.02 |
| Euro Stoxx50 | 0.03 | 0.02 | 0.03 | 0.03 | 0.02 | 0.02 | 0.03 | 0.03 |
| NASDAQ3000 | 0.03 | 0.04 | 0.01 | 0.02 | 0.01 | 0.01 | 0.01 | 0.01 |
| RUSSELL2000 | 0.02 | 0.02 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 |
Table 11.
Sparsity of the proposed portfolios and benchmark over six different evaluation periods when completely simulated data were considered.
Table 11.
Sparsity of the proposed portfolios and benchmark over six different evaluation periods when completely simulated data were considered.
| Case | Evaluation Period | Equally-Weighted | GMVP |
|---|
| W-R | W-S | N-R | N-S | W-R | W-S | N-R | N-S |
|---|
| 1–5000 | 0.10 | 0.07 | 0.07 | 0.10 | 0.11 | 0.10 | 0.07 | 0.09 |
| 1–1000 | 0.07 | 0.18 | 0.08 | 0.21 | 0.12 | 0.07 | 0.06 | 0.07 |
| 1001–2000 | 0.04 | 0.11 | 0.07 | 0.09 | 0.11 | 0.12 | 0.06 | 0.05 |
| 2001–3000 | 0.12 | 0.06 | 0.10 | 0.14 | 0.10 | 0.11 | 0.08 | 0.06 |
| 3001–4000 | 0.12 | 0.06 | 0.09 | 0.16 | 0.10 | 0.12 | 0.08 | 0.15 |
| 4001–5000 | 0.17 | 0.17 | 0.10 | 0.09 | 0.09 | 0.10 | 0.08 | 0.10 |
| 1–5000 | 0.16 | 0.13 | 0.19 | 0.14 | 0.04 | 0.02 | 0.02 | 0.02 |
| 1–1000 | 0.04 | 0.07 | 0.06 | 0.01 | 0.07 | 0.02 | 0.02 | 0.02 |
| 1001–2000 | 0.05 | 0.05 | 0.09 | 0.04 | 0.06 | 0.02 | 0.02 | 0.02 |
| 2001–3000 | 0.09 | 0.16 | 0.11 | 0.17 | 0.02 | 0.03 | 0.02 | 0.02 |
| 3001–4000 | 0.11 | 0.15 | 0.13 | 0.21 | 0.03 | 0.03 | 0.02 | 0.03 |
| 4001–5000 | 0.07 | 0.03 | 0.16 | 0.26 | 0.04 | 0.02 | 0.02 | 0.03 |
Table 12.
Stability of the proposed portfolios and benchmark portfolios for the 12 real datasets case. The two benchmark portfolios, equally-weighted portfolio and GMVP, were considered when constructing the proposed portfolios, respectively. “Bench” represents the benchmark, and “W-R” (“N-R”) and “W-S” (“N-S”) represent the west (north) portfolios using the mean return and Sharpe ratio as criterion functions in the cross validation, respectively.
Table 12.
Stability of the proposed portfolios and benchmark portfolios for the 12 real datasets case. The two benchmark portfolios, equally-weighted portfolio and GMVP, were considered when constructing the proposed portfolios, respectively. “Bench” represents the benchmark, and “W-R” (“N-R”) and “W-S” (“N-S”) represent the west (north) portfolios using the mean return and Sharpe ratio as criterion functions in the cross validation, respectively.
| Data | Equally-Weighted | GMVP |
|---|
| W-R | W-S | N-R | N-S | W-R | W-S | N-R | N-S |
|---|
| DOW30 | 0.03 | 0.04 | 0.09 | 0.08 | 0.01 | 0.01 | 0.05 | 0.05 |
| DAX30 | 0.04 | 0.06 | 0.10 | 0.08 | 0.01 | 0.01 | 0.05 | 0.05 |
| FTSE100 | 0.02 | 0.03 | 0.04 | 0.03 | 0.01 | 0.01 | 0.02 | 0.04 |
| SP100 | 0.01 | 0.02 | 0.02 | 0.02 | 0.01 | 0.01 | 0.03 | 0.03 |
| FTSE250 | 0.02 | 0.02 | 0.03 | 0.03 | 0.02 | 0.02 | 0.03 | 0.02 |
| SP500 | 0.02 | 0.02 | 0.02 | 0.03 | 0.01 | 0.01 | 0.01 | 0.02 |
| Hang Seng | 0.04 | 0.03 | 0.04 | 0.04 | 0.01 | 0.01 | 0.02 | 0.03 |
| FF49 | 0.08 | 0.02 | 0.06 | 0.06 | 0.12 | 0.09 | 0.10 | 0.08 |
| NASDAQ100 | 0.04 | 0.05 | 0.02 | 0.03 | 0.01 | 0.01 | 0.02 | 0.04 |
| Euro Stoxx50 | 0.03 | 0.03 | 0.05 | 0.05 | 0.04 | 0.03 | 0.02 | 0.07 |
| NASDAQ3000 | 0.04 | 0.04 | 0.02 | 0.03 | 0.04 | 0.03 | 0.03 | 0.03 |
| RUSSELL2000 | 0.05 | 0.02 | 0.02 | 0.01 | 0.02 | 0.02 | 0.02 | 0.02 |
Table 13.
Stability of the proposed portfolios and benchmark when partially simulated data were considered.
Table 13.
Stability of the proposed portfolios and benchmark when partially simulated data were considered.
| Data | Equally-Weighted | GMVP |
|---|
| W-R | W-S | N-R | N-S | W-R | W-S | N-R | N-S |
|---|
| DOW30 | 0.02 | 0.03 | 0.07 | 0.08 | 0.02 | 0.01 | 0.04 | 0.04 |
| DAX30 | 0.04 | 0.04 | 0.07 | 0.07 | 0.02 | 0.01 | 0.06 | 0.05 |
| FTSE100 | 0.02 | 0.03 | 0.03 | 0.03 | 0.01 | 0.01 | 0.03 | 0.02 |
| SP100 | 0.01 | 0.02 | 0.02 | 0.02 | 0.02 | 0.01 | 0.02 | 0.02 |
| FTSE250 | 0.02 | 0.02 | 0.02 | 0.02 | 0.01 | 0.01 | 0.01 | 0.02 |
| SP500 | 0.01 | 0.02 | 0.02 | 0.02 | 0.01 | 0.01 | 0.02 | 0.02 |
| Hang Seng | 0.04 | 0.02 | 0.03 | 0.04 | 0.01 | 0.01 | 0.02 | 0.02 |
| FF49 | 0.07 | 0.07 | 0.03 | 0.03 | 0.06 | 0.09 | 0.06 | 0.06 |
| NASDAQ100 | 0.04 | 0.04 | 0.02 | 0.03 | 0.01 | 0.01 | 0.01 | 0.02 |
| Euro Stoxx50 | 0.03 | 0.02 | 0.04 | 0.04 | 0.01 | 0.02 | 0.04 | 0.03 |
| NASDAQ3000 | 0.03 | 0.06 | 0.01 | 0.02 | 0.01 | 0.01 | 0.01 | 0.01 |
| RUSSELL2000 | 0.02 | 0.02 | 0.02 | 0.02 | 0.01 | 0.01 | 0.01 | 0.02 |
Table 14.
Stability of the proposed portfolios and benchmark over six different evaluation periods when completely simulated data were considered.
Table 14.
Stability of the proposed portfolios and benchmark over six different evaluation periods when completely simulated data were considered.
| Case | Evaluation Period | Equally-Weighted | GMVP |
|---|
| W-R | W-S | N-R | N-S | W-R | W-S | N-R | N-S |
|---|
| 1–5000 | 0.13 | 0.07 | 0.06 | 0.06 | 0.07 | 0.07 | 0.05 | 0.07 |
| 1–1000 | 0.07 | 0.05 | 0.06 | 0.06 | 0.07 | 0.06 | 0.06 | 0.05 |
| 1001–2000 | 0.04 | 0.13 | 0.08 | 0.10 | 0.10 | 0.08 | 0.05 | 0.04 |
| 2001–3000 | 0.05 | 0.08 | 0.10 | 0.04 | 0.06 | 0.08 | 0.05 | 0.05 |
| 3001–4000 | 0.05 | 0.06 | 0.12 | 0.06 | 0.04 | 0.06 | 0.04 | 0.11 |
| 4001–5000 | 0.08 | 0.07 | 0.10 | 0.04 | 0.06 | 0.06 | 0.05 | 0.11 |
| 1–5000 | 0.12 | 0.13 | 0.16 | 0.10 | 0.03 | 0.01 | 0.01 | 0.01 |
| 1–1000 | 0.06 | 0.09 | 0.06 | 0.01 | 0.06 | 0.01 | 0.01 | 0.01 |
| 1001–2000 | 0.06 | 0.06 | 0.08 | 0.07 | 0.07 | 0.01 | 0.01 | 0.01 |
| 2001–3000 | 0.05 | 0.11 | 0.05 | 0.07 | 0.01 | 0.01 | 0.01 | 0.01 |
| 3001–4000 | 0.10 | 0.05 | 0.06 | 0.08 | 0.01 | 0.02 | 0.01 | 0.01 |
| 4001–5000 | 0.10 | 0.05 | 0.10 | 0.10 | 0.03 | 0.01 | 0.01 | 0.01 |
Table 15.
Turnover of the proposed portfolio when 12 real datasets were considered. The two benchmark portfolios, equally-weighted portfolio and GMVP, were considered when constructing the proposed portfolios, respectively. “W-R” (“N-R”) and “W-S” (“N-S”) represent the west (north) portfolios using the mean return and Sharpe ratio as criterion functions in the cross validation, respectively.
Table 15.
Turnover of the proposed portfolio when 12 real datasets were considered. The two benchmark portfolios, equally-weighted portfolio and GMVP, were considered when constructing the proposed portfolios, respectively. “W-R” (“N-R”) and “W-S” (“N-S”) represent the west (north) portfolios using the mean return and Sharpe ratio as criterion functions in the cross validation, respectively.
| Data | Equally-Weighted | GMVP |
|---|
| W-R | W-S | N-R | N-S | W-R | W-S | N-R | N-S |
|---|
| DOW30 | 0.09 | 0.13 | 0.18 | 0.23 | 0.05 | 0.05 | 0.07 | 0.07 |
| DAX30 | 0.11 | 0.11 | 0.23 | 0.16 | 0.02 | 0.03 | 0.10 | 0.10 |
| FTSE100 | 0.09 | 0.10 | 0.14 | 0.15 | 0.03 | 0.04 | 0.07 | 0.12 |
| SP100 | 0.08 | 0.12 | 0.13 | 0.12 | 0.03 | 0.05 | 0.08 | 0.10 |
| FTSE250 | 0.13 | 0.09 | 0.12 | 0.13 | 0.06 | 0.04 | 0.07 | 0.08 |
| SP500 | 0.10 | 0.12 | 0.14 | 0.16 | 0.02 | 0.01 | 0.03 | 0.02 |
| Hang Seng | 0.11 | 0.09 | 0.12 | 0.15 | 0.03 | 0.04 | 0.05 | 0.06 |
| FF49 | 0.15 | 0.08 | 0.13 | 0.08 | 0.15 | 0.14 | 0.13 | 0.11 |
| NASDAQ100 | 0.19 | 0.19 | 0.11 | 0.13 | 0.03 | 0.02 | 0.06 | 0.09 |
| Euro Stoxx50 | 0.09 | 0.09 | 0.13 | 0.17 | 0.04 | 0.03 | 0.09 | 0.10 |
| NASDAQ3000 | 0.12 | 0.03 | 0.03 | 0.01 | 0.12 | 0.03 | 0.03 | 0.01 |
| RUSSELL2000 | 0.20 | 0.01 | 0.03 | 0.01 | 0.20 | 0.01 | 0.03 | 0.01 |
Table 16.
Turnover of the proposed portfolio when partially simulated data were considered.
Table 16.
Turnover of the proposed portfolio when partially simulated data were considered.
| Data | Equally-Weighted | GMVP |
|---|
| W-R | W-S | N-R | N-S | W-R | W-S | N-R | N-S |
|---|
| DOW30 | 0.10 | 0.12 | 0.18 | 0.23 | 0.04 | 0.04 | 0.04 | 0.06 |
| DAX30 | 0.11 | 0.09 | 0.12 | 0.14 | 0.02 | 0.02 | 0.06 | 0.06 |
| FTSE100 | 0.09 | 0.12 | 0.11 | 0.11 | 0.03 | 0.05 | 0.06 | 0.06 |
| SP100 | 0.10 | 0.10 | 0.14 | 0.13 | 0.03 | 0.04 | 0.05 | 0.07 |
| FTSE250 | 0.09 | 0.09 | 0.14 | 0.12 | 0.04 | 0.03 | 0.06 | 0.07 |
| SP500 | 0.09 | 0.10 | 0.08 | 0.13 | 0.03 | 0.04 | 0.05 | 0.07 |
| Hang Seng | 0.15 | 0.07 | 0.11 | 0.15 | 0.04 | 0.05 | 0.04 | 0.07 |
| FF49 | 0.16 | 0.10 | 0.08 | 0.07 | 0.10 | 0.08 | 0.13 | 0.09 |
| NASDAQ100 | 0.12 | 0.12 | 0.12 | 0.10 | 0.03 | 0.04 | 0.06 | 0.07 |
| Euro Stoxx50 | 0.11 | 0.09 | 0.17 | 0.18 | 0.03 | 0.04 | 0.06 | 0.06 |
| NASDAQ3000 | 0.14 | 0.23 | 0.09 | 0.12 | 0.03 | 0.04 | 0.05 | 0.07 |
| RUSSELL2000 | 0.11 | 0.05 | 0.10 | 0.12 | 0.04 | 0.05 | 0.07 | 0.09 |
Table 17.
Turnover of the proposed portfolio over six different evaluation periods when completely simulated data were considered.
Table 17.
Turnover of the proposed portfolio over six different evaluation periods when completely simulated data were considered.
| Case | Evaluation Period | Equally-Weighted | GMVP |
|---|
| W-R | W-S | N-R | N-S | W-R | W-S | N-R | N-S |
|---|
| 1–5000 | 0.05 | 0.05 | 0.09 | 0.11 | 0.05 | 0.04 | 0.03 | 0.03 |
| 1–1000 | 0.06 | 0.06 | 0.08 | 0.10 | 0.06 | 0.03 | 0.03 | 0.03 |
| 1001–2000 | 0.02 | 0.08 | 0.07 | 0.11 | 0.10 | 0.05 | 0.04 | 0.02 |
| 2001–3000 | 0.08 | 0.04 | 0.08 | 0.10 | 0.02 | 0.06 | 0.02 | 0.04 |
| 3001–4000 | 0.06 | 0.04 | 0.09 | 0.12 | 0.01 | 0.02 | 0.01 | 0.04 |
| 4001–5000 | 0.05 | 0.02 | 0.11 | 0.13 | 0.04 | 0.04 | 0.03 | 0.03 |
| 1–5000 | 0.05 | 0.06 | 0.10 | 0.08 | 0.04 | 0.03 | 0.02 | 0.03 |
| 1–1000 | 0.03 | 0.10 | 0.11 | 0.15 | 0.06 | 0.03 | 0.01 | 0.04 |
| 1001–2000 | 0.07 | 0.04 | 0.13 | 0.12 | 0.06 | 0.03 | 0.04 | 0.01 |
| 2001–3000 | 0.02 | 0.12 | 0.11 | 0.11 | 0.02 | 0.03 | 0.01 | 0.05 |
| 3001–4000 | 0.06 | 0.04 | 0.05 | 0.04 | 0.01 | 0.03 | 0.02 | 0.01 |
| 4001–5000 | 0.07 | 0.02 | 0.07 | 0.10 | 0.05 | 0.03 | 0.04 | 0.02 |
Table 18.
Standard deviations of the returns of the proposed portfolios and benchmark portfolios when 12 real datasets were used. The two benchmark portfolios, equally-weighted portfolio and GMVP, were considered when constructing the proposed portfolios, respectively. The differences of standard deviations between proposed portfolios and benchmark are also given in parenthesis. If the standard deviation of the proposed portfolio is significantly lower than that of the benchmark (p-value ), the corresponding values are marked in bold. “Bench” represents the benchmark, and “W-R” (“N-R”) and “W-S” (“N-S”) represent the west (north) portfolios using the mean return and Sharpe ratio as criterion functions in the cross validation, respectively.
Table 18.
Standard deviations of the returns of the proposed portfolios and benchmark portfolios when 12 real datasets were used. The two benchmark portfolios, equally-weighted portfolio and GMVP, were considered when constructing the proposed portfolios, respectively. The differences of standard deviations between proposed portfolios and benchmark are also given in parenthesis. If the standard deviation of the proposed portfolio is significantly lower than that of the benchmark (p-value ), the corresponding values are marked in bold. “Bench” represents the benchmark, and “W-R” (“N-R”) and “W-S” (“N-S”) represent the west (north) portfolios using the mean return and Sharpe ratio as criterion functions in the cross validation, respectively.
| Data | Equally-Weighted | GMVP |
|---|
| Bench | W-R | W-S | N-R | N-S | Bench | W-R | W-S | N-R | N-S |
|---|
| DOW30 | 0.617 | 0.516 | 0.529 | 0.564 | 0.578 | 0.355 | 0.359 | 0.353 | 0.381 | 0.379 |
| | | (−0.101) | (−0.088) | (−0.053) | (−0.039) | | (0.004) | (−0.002) | (0.026) | (0.024) |
| DAX30 | 0.802 | 0.720 | 0.713 | 0.760 | 0.759 | 0.489 | 0.480 | 0.480 | 0.504 | 0.528 |
| | | (−0.082) | (−0.089) | (−0.042) | (−0.043) | | (−0.009) | (−0.009) | (0.015) | (0.039) |
| FTSE100 | 0.643 | 0.535 | 0.554 | 0.662 | 0.664 | 0.298 | 0.314 | 0.309 | 0.349 | 0.352 |
| | | (−0.108) | (−0.089) | (0.019) | (0.021) | | (0.016) | (0.011) | (0.051) | (0.054) |
| SP100 | 0.706 | 0.668 | 0.678 | 0.632 | 0.611 | 0.300 | 0.314 | 0.316 | 0.320 | 0.320 |
| | | (−0.038) | (−0.028) | (−0.074) | (−0.095) | | (0.014) | (0.016) | (0.020) | (0.020) |
| FTSE250 | 0.670 | 0.642 | 0.639 | 0.634 | 0.613 | 0.242 | 0.275 | 0.262 | 0.301 | 0.275 |
| | | (−0.028) | (−0.031) | (−0.036) | (−0.057) | | (0.033) | (0.020) | (0.059) | (0.033) |
| SP500 | 0.733 | 0.680 | 0.693 | 0.666 | 0.655 | 0.082 | 0.114 | 0.103 | 0.169 | 0.121 |
| | | (−0.053) | (−0.040) | (−0.067) | (−0.078) | | (0.032) | (0.021) | (0.087) | (0.039) |
| Hang Seng | 0.843 | 0.723 | 0.699 | 0.886 | 0.882 | 0.362 | 0.353 | 0.352 | 0.402 | 0.390 |
| | | (−0.120) | (−0.144) | (0.043) | (0.039) | | (−0.009) | (−0.010) | (0.040) | (0.028) |
| FF49 | 0.634 | 0.552 | 0.546 | 0.560 | 0.556 | 1.467 | 1.472 | 1.514 | 1.542 | 1.508 |
| | | (−0.082) | (−0.088) | (−0.074) | (−0.078) | | (0.005) | (0.047) | (0.075) | (0.041) |
| NASDAQ100 | 0.679 | 0.629 | 0.600 | 0.685 | 0.716 | 0.389 | 0.430 | 0.393 | 0.440 | 0.423 |
| | | (−0.050) | (−0.079) | (0.006) | (0.037) | | (0.041) | (0.004) | (0.051) | (0.034) |
| Euro Stoxx50 | 0.641 | 0.570 | 0.577 | 0.682 | 0.678 | 0.397 | 0.398 | 0.399 | 0.420 | 0.417 |
| | | (−0.071) | (−0.064) | (0.041) | (0.037) | | (0.001) | (0.002) | (0.023) | (0.020) |
| NASDAQ3000 | 0.880 | 0.790 | 0.790 | 0.845 | 0.857 | 0.090 | 0.116 | 0.096 | 0.167 | 0.099 |
| | | (−0.090) | (−0.090) | (−0.035) | (−0.023) | | (0.026) | (0.006) | (0.077) | (0.009) |
| RUSSELL2000 | 0.961 | 0.821 | 0.800 | 0.953 | 0.890 | 0.084 | 0.105 | 0.083 | 0.133 | 0.091 |
| | | (−0.140) | (−0.161) | (−0.008) | (−0.071) | | (0.021) | (−0.001) | (0.049) | (0.007) |
Table 19.
Standard deviations of the returns of the proposed portfolios and benchmark when partially simulated data were considered.
Table 19.
Standard deviations of the returns of the proposed portfolios and benchmark when partially simulated data were considered.
| Data | Equally-Weighted | GMVP |
|---|
| Bench | W-R | W-S | N-R | N-S | Bench | W-R | W-S | N-R | N-S |
|---|
| DOW30 | 0.626 | 0.539 | 0.518 | 0.625 | 0.640 | 0.396 | 0.393 | 0.392 | 0.406 | 0.401 |
| | | (−0.087) | (−0.108) | (−0.001) | (0.014) | | (−0.003) | (−0.004) | (0.010) | (0.005) |
| DAX30 | 0.813 | 0.721 | 0.713 | 0.767 | 0.771 | 0.553 | 0.555 | 0.554 | 0.566 | 0.565 |
| | | (−0.092) | (−0.100) | (−0.046) | (−0.042) | | (0.002) | (0.001) | (0.013) | (0.012) |
| FTSE100 | 0.638 | 0.557 | 0.547 | 0.676 | 0.658 | 0.437 | 0.433 | 0.436 | 0.441 | 0.444 |
| | | (−0.081) | (−0.091) | (0.038) | (0.020) | | (−0.004) | (−0.001) | (0.004) | (0.003) |
| SP100 | 0.716 | 0.681 | 0.691 | 0.639 | 0.615 | 0.418 | 0.425 | 0.415 | 0.417 | 0.421 |
| | | (−0.035) | (−0.025) | (−0.077) | (−0.101) | | (0.007) | (−0.003) | (−0.001) | (0.003) |
| FTSE250 | 0.674 | 0.632 | 0.629 | 0.643 | 0.619 | 0.439 | 0.470 | 0.446 | 0.468 | 0.463 |
| | | (−0.042) | (−0.045) | (−0.031) | ( −0.055) | | (0.031) | (0.007) | (0.029) | (0.024) |
| SP500 | 0.716 | 0.681 | 0.691 | 0.639 | 0.615 | 0.418 | 0.425 | 0.415 | 0.417 | 0.421 |
| | | (−0.035) | (−0.025) | (−0.077) | (−0.101) | | (0.007) | (−0.003) | (−0.001) | (0.003) |
| Hang Seng | 0.847 | 0.720 | 0.713 | 0.891 | 0.886 | 0.434 | 0.443 | 0.444 | 0.450 | 0.425 |
| | | (−0.127) | (−0.134) | (0.044) | (0.039) | | (0.009) | (0.010) | (0.016) | (−0.009) |
| FF49 | 0.635 | 0.558 | 0.551 | 0.599 | 0.599 | 0.651 | 0.560 | 0.530 | 0.643 | 0.641 |
| | | (−0.077) | (−0.084) | (−0.036) | (−0.036) | | (−0.091) | (−0.121) | (−0.008) | (−0.010) |
| NASDAQ100 | 0.684 | 0.614 | 0.601 | 0.691 | 0.695 | 0.541 | 0.530 | 0.526 | 0.546 | 0.578 |
| | | (−0.070) | (−0.083) | (0.007) | (0.011) | | (−0.011) | (−0.015) | (0.005) | (0.037) |
| Euro Stoxx50 | 0.648 | 0.579 | 0.606 | 0.704 | 0.680 | 0.503 | 0.496 | 0.496 | 0.491 | 0.495 |
| | | (−0.069) | (−0.042) | (0.056) | (0.032) | | (−0.007) | (−0.007) | (−0.012) | (−0.008) |
| NASDAQ3000 | 0.678 | 0.600 | 0.593 | 0.739 | 0.729 | 0.433 | 0.424 | 0.427 | 0.470 | 0.443 |
| | | (−0.078) | (−0.085) | (0.061) | (0.051) | | (−0.009) | (−0.006) | (0.037) | (0.010) |
| RUSSELL2000 | 0.762 | 0.671 | 0.650 | 0.748 | 0.709 | 0.461 | 0.434 | 0.448 | 0.470 | 0.470 |
| | | (−0.091) | (−0.112) | (−0.014) | (−0.053) | | (−0.027) | (−0.013) | (0.009) | (0.009) |
Table 20.
Standard deviations of the returns of the proposed portfolios and benchmark over six different evaluation periods when completely simulated data were considered.
Table 20.
Standard deviations of the returns of the proposed portfolios and benchmark over six different evaluation periods when completely simulated data were considered.
| Case | Evaluation Period | Equally-Weighted | GMVP |
|---|
| Bench | W-R | W-S | N-R | N-S | Bench | W-R | W-S | N-R | N-S |
|---|
| 1–5000 | 4.0669 | 3.7180 | 3.3415 | 3.9032 | 3.9483 | 0.0193 | 0.1716 | 0.1202 | 0.1783 | 0.1437 |
| | | (−0.348) | (−0.725) | (−0.163) | (−0.118) | | (0.152) | (0.100) | (0.150) | (0.124) |
| 1–1000 | 4.0935 | 3.7686 | 3.5633 | 4.1073 | 4.0980 | 0.0167 | 0.1660 | 0.1411 | 0.1678 | 0.1448 |
| | | (−0.324) | (−0.530) | (0.013) | (0.005) | | (0.149) | (0.124) | (0.151) | (0.128) |
| 1001–2000 | 3.0568 | 2.4361 | 2.6038 | 2.3061 | 2.6315 | 0.0198 | 0.0914 | 0.1135 | 0.1330 | 0.1325 |
| | | (−0.620) | (−0.453) | (−0.750) | (−0.425) | | (0.071) | (0.093) | (0.113) | (0.113) |
| 2001–3000 | 4.3230 | 3.9553 | 3.3051 | 4.1044 | 4.1224 | 0.0185 | 0.1545 | 0.0789 | 0.1525 | 0.1105 |
| | | (−0.367) | (−1.017) | (−0.218) | (−0.201) | | (0.136) | (0.060) | (0.134) | (0.092) |
| 3001–4000 | 4.1685 | 4.0305 | 3.4752 | 4.1462 | 4.1147 | 0.0188 | 0.2085 | 0.1278 | 0.2093 | 0.1649 |
| | | | (−0.130) | (−0.693) | (−0.022) | (−0.054) | | (0.189) | (0.109) | (0.191) | (0.146) |
| | 4001–5000 | 4.3691 | 4.0321 | 3.5400 | 4.3510 | 4.3653 | 0.0210 | 0.2012 | 0.1287 | 0.2089 | 0.1593 |
| | | | (−0.330) | (−0.829) | (−0.018) | (−0.004) | | (0.180) | (0.107) | (0.187) | (0.138) |
| 1–5000 | 3.9109 | 3.5662 | 3.2815 | 3.7898 | 3.7519 | 0.0050 | 0.1647 | 0.0804 | 0.1647 | 0.1018 |
| | | (−0.344) | (−0.629) | (−0.121) | (−0.159) | | (0.159) | (0.075) | (0.159) | (0.097) |
| 1–1000 | 3.4069 | 2.8111 | 2.8602 | 3.1938 | 3.1182 | 0.0048 | 0.0948 | 0.0753 | 0.1021 | 0.1085 |
| | | (−0.595) | (−0.546) | (−0.213) | (−0.289) | | (0.090) | (0.070) | (0.097) | (0.104) |
| 1001–2000 | 3.5042 | 2.9347 | 2.7890 | 3.2132 | 3.2144 | 0.0044 | 0.1193 | 0.0493 | 0.1234 | 0.0619 |
| | | (−0.569) | (−0.715) | (−0.291) | (−0.289) | | (0.114) | (0.044) | (0.119) | (0.058) |
| 2001–3000 | 3.6790 | 3.6613 | 3.2299 | 3.6819 | 3.6405 | 0.0048 | 0.1735 | 0.0908 | 0.1764 | 0.1248 |
| | | (−0.017) | (−0.449) | (0.003) | (−0.038) | | (0.168) | (0.086) | (0.171) | (0.120) |
| 3001–4000 | 4.3018 | 4.1665 | 3.7725 | 4.3407 | 4.2974 | 0.0056 | 0.2115 | 0.1011 | 0.2098 | 0.1179 |
| | | | (−0.135) | (−0.529) | (0.039) | (−0.004) | | (0.205) | (0.095) | (0.204) | (0.112) |
| | 4001–5000 | 4.1815 | 3.7467 | 3.3789 | 3.9801 | 3.9520 | 0.0050 | 0.1804 | 0.0711 | 0.1733 | 0.0767 |
| | | | (−0.434) | (−0.802) | (−0.201) | (−0.229) | | (0.175) | (0.066) | (0.168) | (0.072) |
Table 21.
Sharpe ratio of the proposed portfolios and benchmark portfolios when 12 real datasets were used. The two benchmark portfolios, equally-weighted portfolio and GMVP, were considered when constructing the proposed portfolios, respectively. The differences of Sharpe ratios between proposed portfolios and benchmark are also given in parenthesis. If the Sharpe ratio of the proposed portfolio is significantly higher than that of the benchmark (p-value ), those values are marked in bold. “Bench" represents the benchmark, and “W-R" (“N-R") and “W-S" (“N-S") represent the west (north) portfolios using the mean return and Sharpe ratio as criterion functions in the cross validation, respectively.
Table 21.
Sharpe ratio of the proposed portfolios and benchmark portfolios when 12 real datasets were used. The two benchmark portfolios, equally-weighted portfolio and GMVP, were considered when constructing the proposed portfolios, respectively. The differences of Sharpe ratios between proposed portfolios and benchmark are also given in parenthesis. If the Sharpe ratio of the proposed portfolio is significantly higher than that of the benchmark (p-value ), those values are marked in bold. “Bench" represents the benchmark, and “W-R" (“N-R") and “W-S" (“N-S") represent the west (north) portfolios using the mean return and Sharpe ratio as criterion functions in the cross validation, respectively.
| Data | Equally-Weighted | GMVP |
|---|
| Bench | W-R | W-S | N-R | N-S | Bench | W-R | W-S | N-R | N-S |
|---|
| DOW30 | 0.208 | 0.221 | 0.207 | 0.265 | 0.239 | 0.300 | 0.284 | 0.296 | 0.281 | 0.297 |
| | | (0.013) | (−0.001) | (0.057) | (0.031) | | (−0.016) | (−0.004) | (−0.077) | (−0.087) |
| DAX30 | 0.146 | 0.173 | 0.173 | 0.163 | 0.160 | 0.206 | 0.199 | 0.194 | 0.223 | 0.213 |
| | | (0.027) | (0.027) | (0.017) | (0.014) | | (−0.007) | (−0.012) | (0.017) | (0.007) |
| FTSE100 | 0.211 | 0.250 | 0.223 | 0.241 | 0.242 | 0.419 | 0.425 | 0.426 | 0.411 | 0.425 |
| | | (0.039) | (0.012) | (0.030) | (0.031) | | (0.006) | (0.007) | (−0.008) | (0.006) |
| SP100 | 0.181 | 0.179 | 0.200 | 0.210 | 0.258 | 0.372 | 0.358 | 0.351 | 0.397 | 0.366 |
| | | (−0.002) | (0.019) | (0.029) | (0.077) | | (−0.014) | (−0.021) | (0.025) | (−0.006) |
| FTSE250 | 0.216 | 0.219 | 0.245 | 0.237 | 0.241 | 0.653 | 0.597 | 0.614 | 0.578 | 0.609 |
| | | (0.003) | (0.029) | (0.021) | (0.025) | | (−0.056) | (−0.039) | (−0.075) | (−0.044) |
| SP500 | 0.195 | 0.191 | 0.208 | 0.215 | 0.263 | 0.902 | 0.672 | 0.694 | 0.573 | 0.608 |
| | | (−0.004) | (0.013) | (0.020) | (0.068) | | (−0.230) | (−0.208) | (−0.329) | (−0.294) |
| Hang Seng | 0.045 | 0.030 | 0.031 | 0.067 | 0.065 | 0.166 | 0.171 | 0.172 | 0.219 | 0.169 |
| | | (−0.015) | (−0.014) | (0.022) | (0.015) | | (0.005) | (0.006) | (0.053) | (0.003) |
| FF49 | 0.187 | 0.226 | 0.237 | 0.234 | 0.235 | 0.374 | 0.366 | 0.359 | 0.343 | 0.360 |
| | | (0.039) | (0.050) | (0.047) | (0.048) | | (−0.008) | (−0.015) | (−0.031) | (−0.014) |
| NASDAQ100 | 0.251 | 0.240 | 0.265 | 0.286 | 0.28 | 0.291 | 0.299 | 0.277 | 0.310 | 0.301 |
| | | (−0.011) | (0.014) | (0.035) | (0.029) | | (0.008) | (−0.014) | (0.019) | (0.010) |
| Euro Stoxx50 | 0.145 | 0.172 | 0.183 | 0.152 | 0.158 | 0.255 | 0.278 | 0.247 | 0.238 | 0.255 |
| | | (0.027) | (0.038) | (0.007) | (0.013) | | (−0.058) | (−0.018) | (−0.017) | (0.000) |
| NASDAQ3000 | 0.169 | 0.161 | 0.168 | 0.191 | 0.184 | 0.853 | 0.764 | 0.832 | 0.562 | 0.822 |
| | | (−0.008) | (−0.001) | (0.022) | (0.015) | | (−0.089) | (−0.021) | (−0.291) | (−0.031) |
| RUSSELL2000 | 0.152 | 0.162 | 0.158 | 0.154 | 0.147 | 0.722 | 0.691 | 0.827 | 0.540 | 0.750 |
| | | (0.010) | (0.006) | (0.002) | (−0.005) | | (−0.031) | (0.105) | (−0.182) | (0.028) |
Table 22.
Sharpe ratio of the proposed portfolios and benchmark when partially simulated data were considered.
Table 22.
Sharpe ratio of the proposed portfolios and benchmark when partially simulated data were considered.
| Data | Equally-Weighted | GMVP |
|---|
| Bench | W-R | W-S | N-R | N-S | Bench | W-R | W-S | N-R | N-S |
|---|
| DOW30 | 0.202 | 0.198 | 0.214 | 0.252 | 0.248 | 0.257 | 0.255 | 0.253 | 0.271 | 0.259 |
| | | (−0.004) | (0.012) | (0.050) | (0.046) | | (−0.002) | (−0.004) | (0.014) | (0.002) |
| DAX30 | 0.139 | 0.136 | 0.138 | 0.126 | 0.131 | 0.170 | 0.155 | 0.155 | 0.180 | 0.169 |
| | | (−0.003) | (−0.001) | (−0.013) | (−0.008) | | (−0.015) | (−0.015) | (0.010) | (−0.001) |
| FTSE100 | 0.199 | 0.223 | 0.235 | 0.229 | 0.238 | 0.303 | 0.313 | 0.315 | 0.330 | 0.307 |
| | | (0.024) | (0.036) | (0.030) | (0.039) | | (0.010) | (0.012) | (0.027) | (0.004) |
| SP100 | 0.175 | 0.163 | 0.168 | 0.195 | 0.253 | 0.261 | 0.269 | 0.256 | 0.277 | 0.239 |
| | | (−0.012) | (−0.007) | (0.020) | (0.078) | | (0.008) | (−0.005) | (0.016) | (−0.022) |
| FTSE250 | 0.203 | 0.201 | 0.216 | 0.211 | 0.241 | 0.329 | 0.279 | 0.314 | 0.288 | 0.314 |
| | | (−0.002) | (0.013) | (0.008) | (0.038) | | (−0.050) | (−0.015) | (−0.041) | (−0.015) |
| SP500 | −0.175 | 0.155 | 0.162 | 0.195 | 0.252 | 0.261 | 0.269 | 0.256 | 0.277 | 0.239 |
| | | (0.330) | (0.337) | (0.370) | (0.427) | | (0.008) | (−0.005) | (0.016) | (−0.022) |
| Hang Seng | 0.031 | 0.020 | 0.037 | 0.057 | 0.058 | 0.176 | 0.147 | 0.145 | 0.216 | 0.181 |
| | | (−0.011) | (0.006) | (0.026) | (0.027) | | (−0.029) | (−0.031) | (0.040) | (0.005) |
| FF49 | 0.150 | 0.180 | 0.193 | 0.195 | 0.197 | 1.087 | 1.245 | 1.314 | 1.699 | 1.705 |
| | | (0.030) | (0.043) | (0.045) | (0.047) | | (0.158) | (0.227) | (0.612) | (0.618) |
| NASDAQ100 | 0.240 | 0.226 | 0.244 | 0.280 | 0.244 | 0.240 | 0.239 | 0.256 | 0.195 | 0.225 |
| | | (−0.014) | (0.004) | (0.040) | (0.004) | | (−0.001) | (0.016) | (−0.045) | (−0.015) |
| Euro Stoxx50 | 0.137 | 0.151 | 0.165 | 0.121 | 0.134 | 0.209 | 0.211 | 0.203 | 0.211 | 0.209 |
| | | (0.014) | (0.028) | (−0.016) | (−0.003) | | (0.002) | (−0.006) | (0.002) | (0.000) |
| NASDAQ3000 | 0.281 | 0.307 | 0.326 | 0.272 | 0.267 | 0.363 | 0.370 | 0.376 | 0.339 | 0.317 |
| | | (0.026) | (0.045) | (−0.009) | (−0.014) | | (0.007) | (0.013) | (−0.024) | (−0.046) |
| RUSSELL2000 | 0.228 | 0.209 | 0.219 | 0.181 | 0.225 | 0.345 | 0.353 | 0.362 | 0.301 | 0.302 |
| | | (−0.019) | (−0.009) | (−0.047) | (−0.003) | | (0.008) | (0.017) | (−0.044) | (−0.043) |
Table 23.
Sharpe ratio of the proposed portfolios and benchmark over six different evaluation periods when completely simulated data were considered.
Table 23.
Sharpe ratio of the proposed portfolios and benchmark over six different evaluation periods when completely simulated data were considered.
| Case | Evaluation Period | Equally-Weighted | GMVP |
|---|
| Bench | W-R | W-S | N-R | N-S | Bench | W-R | W-S | N-R | N-S |
|---|
| 1–5000 | 0.147 | 0.162 | 0.159 | 0.173 | 0.165 | 0.103 | 0.193 | 0.197 | 0.239 | 0.249 |
| | | (0.015) | (0.012) | (0.026) | (0.018) | | (0.090) | (0.094) | (0.136) | (0.146) |
| 1–1000 | 0.007 | 0.024 | 0.023 | 0.015 | 0.023 | −0.125 | −0.035 | 0.111 | 0.034 | 0.094 |
| | | (0.017) | (0.016) | (0.008) | (0.016) | | (0.090) | (0.236) | (0.159) | (0.219) |
| 1001–2000 | −0.166 | −0.118 | −0.138 | −0.105 | −0.150 | −0.120 | −0.059 | −0.028 | 0.066 | 0.127 |
| | | (0.048) | (0.028) | (0.061) | (0.016) | | (0.061) | (0.092) | (0.186) | (0.247) |
| 2001–3000 | 0.282 | 0.267 | 0.285 | 0.270 | 0.272 | 0.329 | 0.353 | 0.279 | 0.412 | 0.421 |
| | | (−0.015) | (0.003) | (−0.012) | (−0.010) | | (0.024) | (−0.050) | (0.083) | (0.092) |
| 3001–4000 | 0.355 | 0.344 | 0.362 | 0.348 | 0.352 | 0.360 | 0.344 | 0.356 | 0.363 | 0.341 |
| | | (−0.011) | (0.007) | (−0.007) | (−0.003) | | (−0.016) | (−0.004) | (0.003) | (−0.019) |
| 4001–5000 | 0.172 | 0.188 | 0.203 | 0.223 | 0.222 | 0.141 | 0.242 | 0.289 | 0.278 | 0.281 |
| | | (0.016) | (0.031) | (0.051) | (0.050) | | (0.101) | (0.148) | (0.137) | (0.140) |
| 1–5000 | 0.127 | 0.157 | 0.165 | 0.143 | 0.153 | 0.204 | 0.183 | 0.162 | 0.193 | 0.159 |
| | | (0.030) | (0.038) | (0.016) | (0.026) | | (−0.021) | (−0.042) | (−0.011) | (−0.045) |
| 1–1000 | −0.285 | −0.253 | −0.243 | −0.293 | −0.287 | −0.187 | −0.068 | −0.163 | −0.155 | −0.194 |
| | | (0.032) | (0.042) | (−0.008) | (−0.002) | | (0.119) | (0.024) | (0.032) | (−0.007) |
| 1001–2000 | 0.104 | 0.146 | 0.159 | 0.124 | 0.141 | 0.25 | −0.026 | 0.222 | 0.124 | 0.259 |
| | | (0.042) | (0.055) | (0.020) | (0.037) | | (−0.276) | (−0.028) | (−0.126) | (0.009) |
| 2001–3000 | 0.419 | 0.417 | 0.424 | 0.408 | 0.427 | 0.386 | 0.389 | 0.371 | 0.398 | 0.334 |
| | | (−0.002) | (0.005) | (−0.011) | (0.008) | | (0.003) | (−0.015) | (0.012) | (−0.052) |
| 3001–4000 | 0.330 | 0.323 | 0.325 | 0.352 | 0.351 | 0.423 | 0.395 | 0.286 | 0.386 | 0.254 |
| | | (−0.007) | (−0.005) | (0.022) | (0.021) | | (−0.028) | (−0.137) | (−0.037) | (−0.169) |
| 4001–5000 | 0.040 | 0.061 | 0.111 | 0.061 | 0.070 | 0.149 | 0.063 | 0.066 | 0.058 | 0.188 |
| | | (0.021) | (0.071) | (0.021) | (0.030) | | (−0.086) | (−0.083) | (−0.091) | (0.039) |
Table 24.
Information ratio of the proposed portfolio when 12 real datasets were considered. The two benchmark portfolios, equally-weighted portfolio and GMVP, were considered when constructing the proposed portfolios, respectively. “W-R” (“N-R”) and “W-S” (“N-S”) represent the west (north) portfolios using the mean return and Sharpe ratio as criterion functions in the cross validation, respectively.
Table 24.
Information ratio of the proposed portfolio when 12 real datasets were considered. The two benchmark portfolios, equally-weighted portfolio and GMVP, were considered when constructing the proposed portfolios, respectively. “W-R” (“N-R”) and “W-S” (“N-S”) represent the west (north) portfolios using the mean return and Sharpe ratio as criterion functions in the cross validation, respectively.
| Data | Equally-Weighted | GMVP |
|---|
| | W-R | W-S | N-R | N-S | W-R | W-S | N-R | N-S |
| DOW30 | −0.05 | −0.13 | 0.34 | 0.19 | −0.05 | −0.07 | 0.08 | 0.12 |
| DAX30 | −0.16 | −0.06 | 0.27 | 0.27 | 0.25 | 0.22 | 0.20 | 0.32 |
| FTSE100 | −0.01 | −0.04 | 0.35 | 0.44 | 0.36 | 0.40 | 0.38 | 0.60 |
| SP100 | −0.02 | 0.25 | 0.04 | 0.39 | 0.14 | −0.02 | 0.33 | 0.11 |
| FTSE250 | −0.05 | 0.02 | 0.16 | 0.21 | −0.10 | −0.03 | −0.03 | −0.01 |
| SP500 | −0.05 | 0.01 | 0.12 | 0.39 | 0.14 | −0.02 | 0.53 | −0.01 |
| Hang Seng | −0.01 | −0.08 | 0.34 | 0.26 | 0.01 | 0.02 | 0.50 | 0.09 |
| FF49 | 0.09 | 0.18 | 0.15 | 0.15 | −0.01 | −0.04 | 0.02 | 0.04 |
| NASDAQ100 | −0.05 | −0.04 | 0.45 | 0.11 | 0.31 | −0.03 | 0.45 | 0.31 |
| Euro Stoxx50 | −0.02 | −0.05 | −0.03 | 0.07 | 0.38 | −0.04 | 0.08 | 0.05 |
| NASDAQ3000 | −0.15 | −0.07 | 0.22 | 0.15 | 0.71 | 0.33 | 0.47 | 0.46 |
| RUSSELL2000 | −0.11 | −0.06 | 0.01 | −0.09 | 0.71 | 0.88 | 0.38 | 0.59 |
Table 25.
Information ratio of the proposed portfolio when partially simulated data were considered.
Table 25.
Information ratio of the proposed portfolio when partially simulated data were considered.
| Data | Equally-Weighted | GMVP |
|---|
| W-R | W-S | N-R | N-S | W-R | W-S | N-R | N-S |
|---|
| DOW30 | −0.10 | −0.09 | 0.59 | 0.67 | −0.04 | −0.06 | 0.19 | 0.03 |
| DAX30 | −0.08 | −0.10 | −0.04 | −0.03 | −0.11 | −0.11 | 0.18 | 0.03 |
| FTSE100 | −0.01 | 0.01 | 0.35 | 0.56 | 0.15 | 0.26 | 0.29 | 0.07 |
| SP100 | −0.12 | −0.07 | 0.01 | 0.39 | 0.31 | −0.09 | 0.11 | −0.07 |
| FTSE250 | −0.07 | −0.02 | −0.01 | 0.22 | −0.13 | −0.10 | −0.07 | 0.02 |
| SP500 | −0.17 | −0.12 | 0.00 | 0.38 | 0.31 | −0.09 | 0.11 | −0.07 |
| Hang Seng | −0.06 | 0.01 | 0.38 | 0.34 | −0.20 | −0.18 | 0.36 | 0.01 |
| FF49 | 0.33 | 0.83 | 0.19 | 0.24 | −0.06 | −0.01 | 1.45 | 1.32 |
| NASDAQ100 | −0.14 | −0.10 | 0.54 | 0.07 | −0.03 | 0.16 | −0.13 | 0.00 |
| Euro Stoxx50 | −0.01 | 0.25 | −0.02 | 0.02 | 0.01 | −0.06 | −0.01 | −0.02 |
| NASDAQ3000 | −0.04 | 0.02 | 0.13 | 0.03 | 0.00 | 0.25 | 0.01 | −0.10 |
| RUSSELL2000 | −0.12 | −0.12 | −0.15 | −0.06 | −0.08 | 0.17 | −0.09 | −0.11 |
Table 26.
Information ratio of the proposed portfolio over six different evaluation periods when completely simulated data were considered.
Table 26.
Information ratio of the proposed portfolio over six different evaluation periods when completely simulated data were considered.
| Case | Evaluation Period | Equally-Weighted | GMVP |
|---|
| W-R | W-S | N-R | N-S | W-R | W-S | N-R | N-S |
|---|
| 1–5000 | 0.01 | −0.02 | 0.09 | 0.08 | 0.20 | 0.20 | 0.25 | 0.26 |
| 1–1000 | 0.11 | 0.08 | 0.09 | 0.17 | −0.02 | 0.14 | 0.05 | 0.12 |
| 1001–2000 | 0.29 | 0.22 | 0.19 | 0.12 | −0.04 | −0.01 | 0.09 | 0.16 |
| 2001–3000 | −0.11 | −0.13 | −0.04 | −0.02 | 0.35 | 0.24 | 0.41 | 0.41 |
| 3001–4000 | −0.14 | −0.14 | −0.01 | −0.02 | 0.34 | 0.34 | 0.36 | 0.33 |
| 4001–5000 | 0.01 | −0.03 | 0.30 | 0.30 | 0.25 | 0.31 | 0.29 | 0.29 |
| 1–5000 | 0.10 | 0.05 | 0.07 | 0.12 | 0.18 | 0.16 | 0.19 | 0.15 |
| 1–1000 | 0.35 | 0.39 | 0.04 | 0.09 | −0.02 | −0.10 | −0.05 | −0.04 |
| 1001–2000 | 0.08 | 0.08 | 0.05 | 0.13 | −0.04 | 0.21 | 0.12 | 0.25 |
| 2001–3000 | −0.07 | −0.04 | −0.03 | 0.03 | 0.39 | 0.37 | 0.40 | 0.33 |
| 3001–4000 | −0.05 | −0.12 | 0.19 | 0.15 | 0.39 | 0.28 | 0.38 | 0.24 |
| 4001–5000 | 0.10 | 0.21 | 0.11 | 0.17 | 0.06 | 0.06 | 0.06 | 0.19 |