We will now start to analyze the ethical aspects of the TE by applying a number of well-established frameworks based on a common assumption of rationality, where we take a broad working definition of rationality here that considers a decision-maker’s choice as rational if the decision-maker knows of no alternative choice that gives her a strictly more-preferred prospect than the choice taken, in view of her knowledge, beliefs, and capabilities.
After that, we will refine the analysis by considering each generation a new decision-maker, so that humanity can no longer plan its own future choices, but rather a generation can only recommend and/or anticipate later generations’ choices. The natural framework for this kind of problem is the language of game theory. While most of economic theory applies game theory to selfish players, we will apply it instead to players with social preferences based on welfare measures since, in our TE, a generation’s welfare is deliberately assumed to be independent of their own choice between A and B.
3.1. Optimal Control Framework with Different Intergenerational Welfare Functions
3.1.1. Terminology
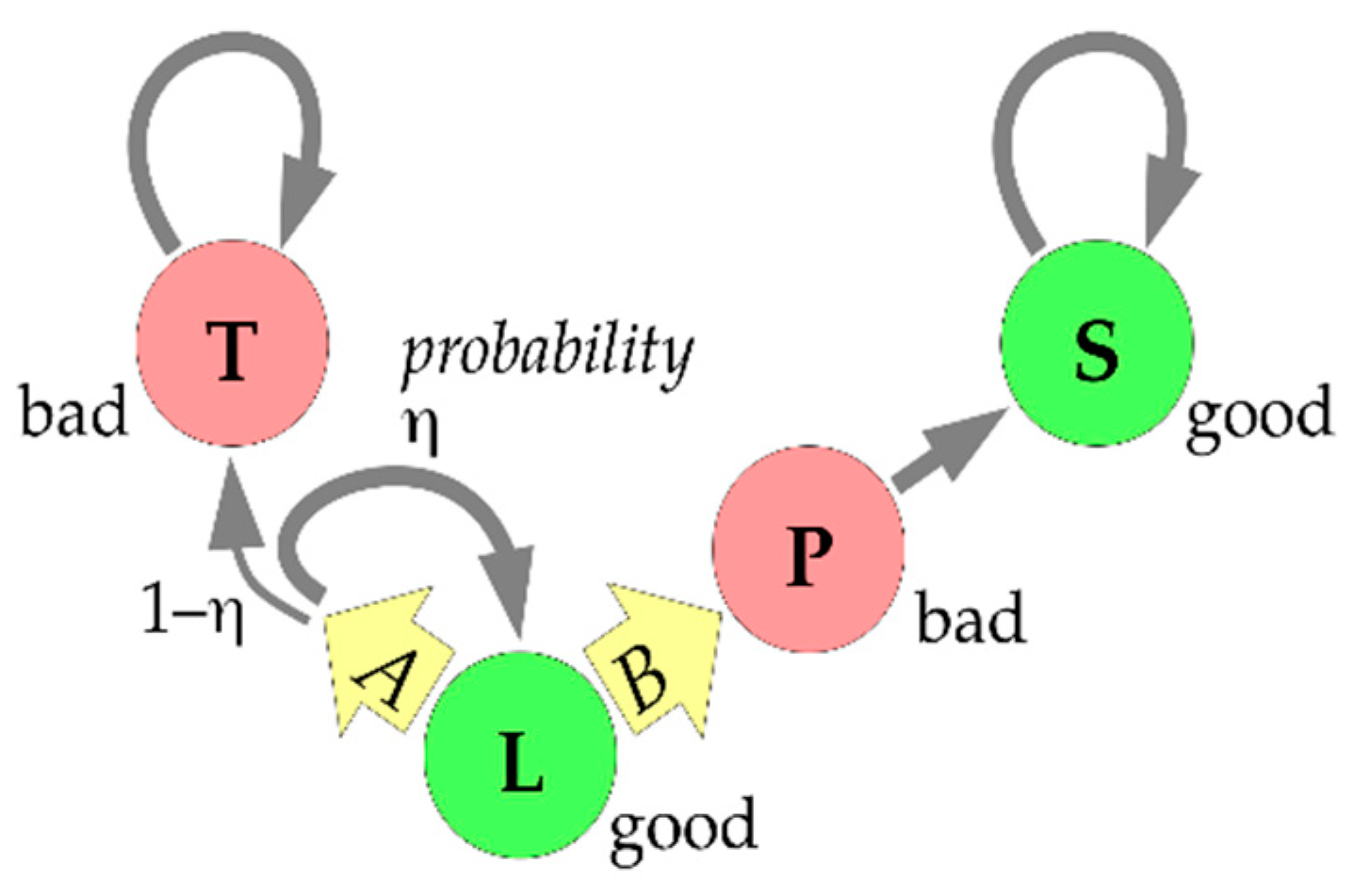
A trajectory, X, is a sequence of states X(0), X(1), … in the set {L, T, P, S}, where X(t) specifies the state generation t will be in. The only possible trajectories in our TE are
“XcLT” = (L, …, L, T, T, …), with c > 0 times L and then T forever (so that c is the time of “collapse”);
“XkLPS” = (L, …, L, P, S, S, …), with k > 0 times L, then once P, then S forever; and
“all-L” = (L, L, …), which is possible, but has a probability of zero.
A reward sequence (RS, sometimes also called a payoff stream), denoted r, is a sequence r(0), r(1), r(2), … in the set {0, 1}, where r(t) = 0 or 1 means generation t has low or high overall welfare, respectively. Each trajectory determines an RS via r(t) = 1 if X(t) in {L, S} and r(t) = 0 otherwise. The only possible RSs are, thus:
“rc10” = (1, …, 1, 0, 0, …) with c > 0 ones and then zeros forever;
“rk101” = (1, …, 1, 0, 1, 1, …) with k > 0 ones, then one zero, then ones forever; and
“all-1” = (1, 1, …), which is possible, but has a probability of zero.
A (randomized) policy (sometimes also called a strategy) from time 0 on, denoted as p, is just a sequence of numbers p(0), p(1), p(2), … in the interval [0, 1], where p(t) specifies the probability with which generation t will choose option A (staying in L) if they are in state L, i.e., if X(t) = L. In view of the possible trajectories, we may, without loss of generality, assume that if p(t) = 0 for some t, all later entries are irrelevant since state L will never occur after generation t. Thus, we consider only policies of the form:
infinite sequences (p(0), p(1), …) with all p(t) > 0,
finite sequences (p(0), p(1), …, p(k − 1), 0) with p(t) > 0 for all t < k.
The two most extreme (“polar”) policies are:
“all-A” = (1, 1, …),
“directly-B” = (0),
and another interesting set of policies is:
“Bk” = (1, 1, …, 1, 0) with k + 1 ones, where the case k = 0 is “directly-B” and k → ∞ is “all-A”,
all of which are deterministic. A policy p is time-consistent iff it is a Markov policy, i.e., if and only if all its entries p(t) are equal, so the only time-consistent policies are “all-A”, “directly-B”, and the policies:
“Ax” = (x, x, x, …) with 0 < x < 1, where the case x → 0 is “directly-B” and x → 1 is “all-A”.
Given a policy p, the possible trajectories and RSs have these probabilities:
P(XcLT|p) = P(rc10|p) = p(0) η p(1) η … p(c − 2) η p(c − 1) π
P(XkLPS|p) = P(rk101|p) = p(0) η p(1) η … p(k − 2) η (1 − p(k − 1))
P(all-L|p) = P(all-1|p) = 0
Thus, each policy p defines a probability distribution over RSs, called a reward sequence lottery (RSL) here, denoted as RSL(p).
The only missing part of our control problem specification is now a function that numerically evaluates RSLs, or some other information on what RSLs are preferred over which others, in a way that allows the derivation of optimal policies. Let us assume we have specified a binary social preference relation that decides for each pair of RSLs g, h which of the following four cases holds: (i) g is strictly better than h, denoted as g > h; (ii) the other way around, h > g; (iii) they are equally desirable, g ~ h; or (iv) they are incomparable, denoted as g|h. We use the abbreviation g ≥ h for g > h or g ~ h, and g ≤ h for g < h or g ~ h. For example, we might put g > h iff V(g) > V(h) and g ~ h iff V(g) = V(h) for some evaluation function V.
Let us assume the social preference relation has the “consistency” property that each non-empty set C of RSLs contains some g such that h > g for no h in C. Then for each non-empty set C of policies, we can call any policy p in C optimal under the constraint C (or C-optimal for short) iff RSL(q) > RSL(p) for no q in C. In particular, if the preference relation encodes ethical desirability, C contains all policies deemed ethically acceptable, and p is C-optimal, then generation 0 has a good ethical justification in choosing option A with probability p(0) and option B with probability 1 − p(0).
We will now discuss several such preference relations and the resulting optimal policies. A common way of assessing preferences over lotteries is by basing them on preferences over certain outcomes, hence, we first consider whether each of two certain RSs, r and s, is preferable. A minimal plausible preference relation is based only on the Pareto principle that r(t) ≥ s(t) for all t should imply r ≥ s, and r(t) ≥ s(t) for all t but r(t) > s(t) for some t should imply r > s. In our case, the only strict preferences would then be between the RSs “all-1”, “rk101”, “rc10”, and “rc’10” for c > c’, where we would have “all-1” > “rk101” > “rc10” > “rc’10”. However, this does not suffice to make policy decisions, e.g., when we just want to compare policies “directly-B” with “all-A”, we need to compare RS “rk101” for k = 1 with a lottery over RSs of the form “rc10” for all possible values of c.
One possible criterion for preferring r over s is their degree of “sustainability”. The literature contains several criteria by which the sustainability of an RS could be assessed (see [
20] for a detailed discussion). The
maximin criterion (also known as the Rawlsian rule) focuses on the lowest welfare level occurring in an RS, which in all our cases is 0, hence, this criterion does not help in distinguishing options A and B. The
satisfaction of basic needs criterion [
21] asks from what time on welfare stays above some minimal level; if we use 1 as that level, this criterion prefers RS (1, 0, 1, 1, …) to all other RS that can occur with positive probability in our TE, hence, it will recommend policy “directly-B”, since it makes sure that generation 2 on welfare stays high. The
overtaking and
long-run average criteria [
21] consider all RSs “rk101” equivalent and strictly more sustainable than all RSs “rc10”, hence, they also recommend “directly-B” since that is the only policy avoiding permanently low welfare for sure. Other sustainability criteria are based on the idea of aggregating welfare over time, which we will discuss next.
3.1.2. Aggregation of Welfare over Time
Let us now focus on the simple question whether the RS “rB” = (1, 0, 1, 1, …) that results from “directly-B” is preferable to the RS “rc10” = (1, 1, …, 1, 0, 0, …) with c ones, which may result from “all-A”? This may be answered quite differently. The easy way out is to deem them incomparable since, for some time points t, rB(t) > rc10(t), while for other t, rc10(t) > rB(t), but this does not help. A strong argument is that “rB” should be preferred since it has the larger number of generations with high welfare. Still, at least economists would object that real people’s evaluations of future prospects are typically subject to discounting, so that a late occurrence of low welfare would be considered less harmful than an early one. A very common approach in welfare economics is, therefore, to base the preference over RSs on some quantitative evaluation v(r), called an intergenerational welfare function, which in some way “aggregates” the welfare levels in r and can then also be used as a basis of an evaluation function V(g) of RSLs, which further aggregates the evaluations of all possible RSs in view of their probability. However, let us postpone the consideration of uncertainty for now and stick with the two deterministic RSs “rB” and “rc10”.
The most commonly used form of discounting (since it can lead to time-consistent choices) is
exponential discounting, which would make us evaluate any RS r as:
using powers of a discount factor 0 ≤ δ < 1 that encodes humanity’s “time preferences”. For the above “rB” and “rc10”, this gives v(rB) = (1 − δ + δ²)/(1 − δ) and v(rc10) = (1 − δ
c)/(1 − δ). Thus, with exponential discounting, “rB” > “rc10” iff 1 − δ + δ² > 1 − δ
c or, equivalently, δ
c−1 + δ > 1, i.e., the policy “directly-B” is preferable iff δ is large enough or c is small enough. Since 1/δ can be interpreted as a kind of (fuzzy) evaluation time horizon, this means that “directly-B” will be preferable iff the time horizon is large enough to “see” the expected ultimate transition to state T at time c under the alternative extreme policy “all-A”. At what δ exactly the switch occurs depends on how we take into account the uncertainty about the collapse time c, i.e., how we get from preferences over RSs to preferences over RSLs, which will be discussed later. A variant of the above evaluation v due to Chichilnisky [
21] adds to v(r) some multiple of the long-term limit, lim
t→∞ r(t), which is 1 for “rB” and 0 for all “rc10”, thus making “directly-B” preferable also for smaller δ, depending on the weight given to this limit.
Let us shortly consider the alternative policy “Bk” = (1, …, 1, 0) with k ones, where choosing B is delayed by k periods, and “B1” equals “directly-B”. If k < c, this results in RS r(k + 1)101, which is evaluated as (1 − δk+1 + δk+2)/(1 − δ), which grows strictly with growing k. Thus, if the collapse time c was known, the best policy among the “Bk” would be the one with k = c − 1, i.e., initiating the transition at the last possible moment right before the collapse, which is evaluated as (1 − δc + δc+1)/(1 − δ) > (1 − δc)/(1 − δ), hence, it would be preferred to “all-A”. However, c is, of course, not known, but a random variable, so we need to come back to this question when discussing uncertainty below.
An argument against exponential discounting is that even for values of δ close to 1, late generations’ welfare would be considered too unimportant. Under the most common alternative form of discounting,
hyperbolic discounting, one would instead have the evaluation:
with some positive constant κ. Hyperbolic discounting can easily be motivated by an intrinsic suspicion that, due to factors unaccounted for, the expected late rewards may not actually be realized, but that the probability of this happening is unknown and has to be modeled via a certain prior distribution [
22]. Under hyperbolic discounting, v(rB) is infinite while v(rc10) is finite independently of k, so the policy “directly-B” would always be preferable to “all-A” no matter how uncertainty about the actual c is accounted for.
A somewhat opposite alternative to hyperbolic discounting is what one could call “rectangular” discounting: simply average the welfare of only a finite number, say H many, of the generations:
where H is the evaluation horizon. With this, v(rB) = (H − 1)/H and v(rc10) = min(c, H)/H, so that v(rB) > v(rc10) iff H > c + 1. Thus, again, “directly-B” is preferable if the horizon is large enough.
3.1.3. Social Preferences over Uncertain Prospects: Expected Probability of Regret
Let us now consider evaluations of RSLs rather than RSs, which requires us to take into account the probabilities of all possible RSs that an RSL specifies.
If we already have a social preference relation “≥” on RSs, such as one of those discussed above, then a very simple idea is to consider an RSL g’’ strictly preferable to another RSL g’ iff the probability that a realization r’’(g’’) of the random process g’’ is strictly preferable to an independent realization r’(g’) of the random process g’ is strictly larger than ½:
The rationale for this is based in the idea of expected probability of regret. Assume policy p was chosen, resulting in some realization r(RSL(p)), and someone asks whether not policy q should have been taken instead and argues that this should be evaluated by asking how likely the realization r’(RSL(q)) under the alternative policy would have been strictly preferable to the actual realization r(RSL(p)). Then the probability of the latter, averaged over all possible realizations r(RSL(p)) of the policy actually taken, should be not too large. This expected probability of regret is just P(r’’(g’’) > r’(g’)) for g’ = RSL(p) and g’’ = RSL(q). Since for the special case where g’ = g’’, the value P(r’’(g’’) > r’(g’)) can be everything up to at most ½, the best we can hope for is that P(r’’(RSL(q)) > r’(RSL(p))) ≤ ½ for all q ≠ p if we want to call p optimal.
In our example, the polar policy “directly-B” results in an RSL “gB” which gives 100% probability to RS “rB”, the opposite polar policy “all-A” results in an RSL “gA” which gives a probability of ηc−1π to RS “rc10”, and other policies result in RSLs with more complicated probability distributions. e.g., with exponential discounting, rB > rc10 iff δc−1 + δ > 1, hence, “gB” > “gA” iff the sum of ηc−1π over all c with δc−1 + δ > 1 is larger than ½. If c(δ) is the largest such c, which can be any value between 1 (for δ → 0) and infinity (for δ → 1), that sum is 1 − ηc(δ), which can be any value between π (for δ → 0) and 1 (for δ → 1). Similarly, with rectangular discounting, “rB” > “rc10” iff H > c + 1, hence, “gB” > “gA” iff 1 − ηH−1 > ½. In both cases, if η < ½, “directly-B” is preferred to “all-A”, while for η > ½, it depends on δ or H, respectively. In contrast, under hyperbolic discounting, “directly-B” is always preferred to “all-A”.
What about the alternative policy “Bk” as compared to “all-A”? If c ≤ k, we get the same reward sequence as in “all-A”, evaluated as (1 − δc)/(1 − δ). If c > k, we get an evaluation of (1 − δk+1 + δk+2)/(1 − δ), which is larger than (1 − δc)/(1 − δ) iff δc−k−1 + δ > 1. Thus, RSL(Bk) > gA iff the sum of ηc−1π over all c > k with δc−k−1 + δ > 1 is larger than ½. Since the largest such c is c(δ) + k, that sum is ηk(1 − ηc(δ)), so whenever “Bk” is preferred to “all-A”, then so is “directly-B”. Let us also compare “Bk” to “directly-B”. In all cases, “directly-B” gets (1 − δ + δ2)/(1 − δ), while “Bk” gets the larger (1 − δk+1 + δk+2)/(1 − δ) if c > k, but only (1 − δc)/(1 − δ) if c ≤ k. The latter is < (1 − δ + δ2)/(1 − δ) iff c ≤ c(δ). Thus, “directly-B” is strictly preferred to “Bk” iff 1 − ηmin(c(δ),k) > ½, i.e., iff both c(δ) and k are larger than log(½)/log(η), which is at least fulfilled when η < ½. Conversely, “Bk” is strictly preferred to “directly-B” iff either c(δ) or k is smaller than log(½)/log(η). In particular, if social preferences were based on the expected probability of regret, delaying the choice for B by at least one generation would be strictly preferred to choosing B directly whenever η > ½, while at the same time, delaying it forever would be considered strictly worse at least if the time horizon is long enough. Basing decisions on this maxim would, thus, lead to time-inconsistent choices: in every generation, it would seem optimal to delay the choice B by the same positive number of generations, but not forever, so no generation would actually make that choice.
Before considering a less problematic way of accounting for uncertainty, let us shortly discuss a way of deriving preferences over RSs rather than RSLs that is formally similar to the above. In that case the rationale would not be in terms of regret but in terms of Rawls’
veil of ignorance. Given two RSs r’ and r’’, would one rather want to be born into a randomly selected generation in situation r’ or into a randomly selected generation in situation r’’? i.e., let us put:
where t’’, t’ are drawn independently from the same distribution, e.g., the uniform one on the first H generations or a geometric one with parameter δ. Then rB(t’’) > rc10(t’) iff rB(t’’) = 1 and rc10(t’) = 0, i.e., iff t’’ ≠ 1 and t’ > c. Under the uniform distribution over H generations, the latter has a probability of (H − 1)(H − c)/H² if H ≥ c, which can be any value between 0 (for H = c) and 1 (for very large H), hence, whether “rB” > “rc10” depends on H again. Similarly, rB(t’’) < rc10(t’) iff rB(t’’) = 0 and rc10(t’) = 1. This has probability min(c,H)/H², which is 1 for H = 1 and approaches 0 for very large H, hence, whether “rB” < “rc10” depends on H as well. However, this version of preferences over RS leaves a large possibility for undecidedness, “rB”|“rc10”, where neither “rB” > “rc10” nor “rc10” > “rB”. This is the case when both (H − 1)(H − c)/H² and min(c,H)/H² are at most ½, i.e., when max[(H − 1)(H − c), min(c,H)] ≤ H²/2, which is the case when H ≥ 2 and H² − 2(c + 1)H + 2c ≤ 0, i.e., when 2 ≤ H ≤ c + 1 + (c² + 1)½. A similar result holds for the geometric distribution with parameter δ. Thus, while the probability of regret idea can lead to time-inconsistent choices, the formally similar veil of ignorance idea may not be able to differentiate enough between choices. Another problematic property of our veil of ignorance-based preferences is that they can lead to preference cycles. e.g., assume H = 3 and compare the RSs r = (0, 1, 2), r’ = (2, 0, 1), and r’’ = (1, 2, 0). Then it would occur that r > r’ > r’’ > r, so there would be no optimal choice among the three.
3.1.4. Evaluation of Uncertain Prospects: Prospect Theory and Expected Utility Theory
We saw that the above preference relations based on regret and the veil of ignorance, while intuitively appealing, are, however, unsatisfactory from a theoretical point of view, since they can lead to time-inconsistent choices and preference cycles, i.e., they may fail to produce clear assessments of optimality. The far more common way of dealing with uncertainty is, therefore, based on numerical evaluations instead of binary preferences. A general idea, motivated by a similar theory regarding individual, rather than social, preferences, called
prospect theory [
23], is to evaluate an RSL g by a linear combination of some function of the evaluations of all possible RSs r with coefficients that depend on their probabilities:
In the simplest version, corresponding to the special case of
expected utility theory, both the probability weighting function w and the evaluation transformation function f are simply the identity, w(p) = p and f(v) = v, so that V(g) = ∑
r P(r|g) v(r) = E
g v(r), the expected evaluation of the RSs resulting from RSL g. If combined with a v(r) based on exponential discounting, this gives the following evaluations of our polar policies:
Hence, “directly-B” is preferred to “all-A” iff (1 − δ + δ²)(1 − ηδ) − 1 + δ > 0. Again, this is the case for δ > δcrit(η) with δcrit(0) = 0 and δcrit(1) = 1. The result for rectangular discounting is similar, while for hyperbolic discounting “directly-B” is always preferred to “all-A”, and all of this as expected from the considerations above.
In prospect theory, the transformation function f can be used to encode certain forms of risk attitudes. For example, we could incorporate a certain form of risk aversion against uncertain social welfare sequences by using a strictly concave function f, such as f(v) = v1−a with 0 < a < 1 (isoelastic case) or f(v) = −exp(−av) with a > 0 (constant absolute risk aversion) (welfare economists might be confused a little by our discussion of risk aversion since they are typically applying the concept in the context of consumption, income or wealth of individuals at certain points in time, in which context one can account for risk aversion already in the specification of individual consumers’ utility function, e.g., by making utility a concave function of individual consumption, income, or wealth. Here we are, however, interested in a different aspect of risk aversion, where we want to compare uncertain streams of societal welfare rather than uncertain consumption bundles of individuals. Thus, even if our assessment of the welfare of each specific generation in each specific realization of the uncertainty about the collapse time c already accounts for risk aversion in individual consumers in that generation, we still need to incorporate the possible additional risk aversion in the “ethical social planner”). This basically leads to a preference for small variance in v. One can see numerically that in both cases increasing the degree of risk aversion, a, lowers δcrit(η), not significantly so in the isoelastic case but significantly in the constant absolute risk aversion case, hence, risk aversion favors “directly-B”. In particular, the constant absolute risk aversion case with a → ∞ is equivalent to a “worst-case” analysis that always favors “directly-B”. Conversely, one can encode risk-seeking by using f(v) = v1+a with a > 0.
Under expected utility theory, the delayed policy “Bk” has:
which is either strictly decreasing or strictly increasing in k. Since “directly-B” and “all-A” corresponds to the limits k → 0 and k → ∞, “Bk” is never optimal but always worse than either “directly-B” or “all-A”. The same holds with risk-averse specifications of f. Under isoelastic risk-
seeking with f(v) = v
1+a, however, we have:
which may have a global maximum for a strictly positive and finite value of k, so that delaying may seem preferable. e.g., with δ = 0.8, η = 0.95, and a = ½, V(RSL(Bk)) is maximal for k = 6, i.e., one would want to choose six times A before choosing B, again a time-inconsistent recommendation.
As long as the probability weighting function w is simply the identity, there is always a deterministic optimal policy. While other choices for w could potentially lead to non-deterministic optimal policies, they can be used to encode certain forms of risk attitudes that cannot be encoded via f. e.g., one can introduce some degree of optimism or pessimism by over- or underweighing the probability of the unlikely cases where c is large. For example, if we put w(p) = p1−b with 0 ≤ b < 1, then increasing the degree of optimism b, one can move δcrit(η) arbitrarily close towards 1, which is not surprising. We will however not discuss this form of probability reweighting further but will use a different way of representing “caution” below. Since that form is motivated by its formal similarity to a certain form of inequality aversion, we will discuss the latter first now before returning to risk attitudes.
3.1.5. Inequality Aversion: A Gini-Sen Intergenerational Welfare Function
While discounting treats different generations’ welfare differently, it only does so based on time lags, and all the above evaluations still only depend on some form of (weighted) time-average welfare and are blind to welfare
inequality as long as these time-averages are the same. However, one may argue that an RS with less inequality between generations, such as (1, 1, 1, …), should be strictly preferable to one with the same average but more inequality, such as (2, 0, 2, 0, 2, 0, …). Welfare economics has come up with a number of different ways to make welfare functions sensitive to inequality, and although most of them were initially developed to deal with inequality between individuals of a society at a given point in time (which we might call “intragenerational” inequality here), we can use the same ideas to deal with inequality between welfare levels of different generations (“intergenerational” inequality). Since our basic welfare measure is not quantitative but qualitative since it only distinguishes “low” from “high” welfare, inequality metrics based on numerical transformations, such as the Atkinson-Theil-Foster family of indices, are not applicable in our context, but the Gini-Sen welfare function [
24], which only requires an ordinal welfare scale, is. The idea is that the value of a specific allocation of welfare to all generations is the expected value of the smaller of the two welfare values of two randomly-drawn generations. If the time horizon is finite, H > 0, this leads to the following evaluation of an RS r:
It is straightforward to generalize the idea from drawing two to drawing any integer number a > 0 of generations, leading to a sequence of welfare measures V
a(r) that get more and more inequality averse as a is increased from 1 (no inequality aversion, “utilitarian” case) to infinity (complete inequality aversion), where the limit for a → ∞ is the
egalitarian welfare function:
Note that I = 1 − V2(r)/V1(r) is the Gini index of inequality and the formula V2(r) = V1(r) (1 − I) is often used as the definition of the Gini-Sen welfare function.
Our RSs “rc10” then gets V
a(rc10) = min(c/H, 1)
a, while “rk101” gets V
a(rk101) = [(H − 1)/H]
a if k < H and V
a(rk101) = 1 if k ≥ H. Together with expected utility theory for evaluating the risk about c, this makes:
and V
a(directly-B) = [(H − 1)/H]
a. Numerical evaluation shows that even for large H, “all-A” may still be preferred due to the possibility that collapse will not happen before H and all generations will have the same welfare, but this is only the case for extremely large values of a. If we use exponential instead of rectangular discounting and compare the policies “directly-B”, “Bk”, and “all-A”, we may again get a time-inconsistent recommendation to choose B after a finite number of generations. e.g.,
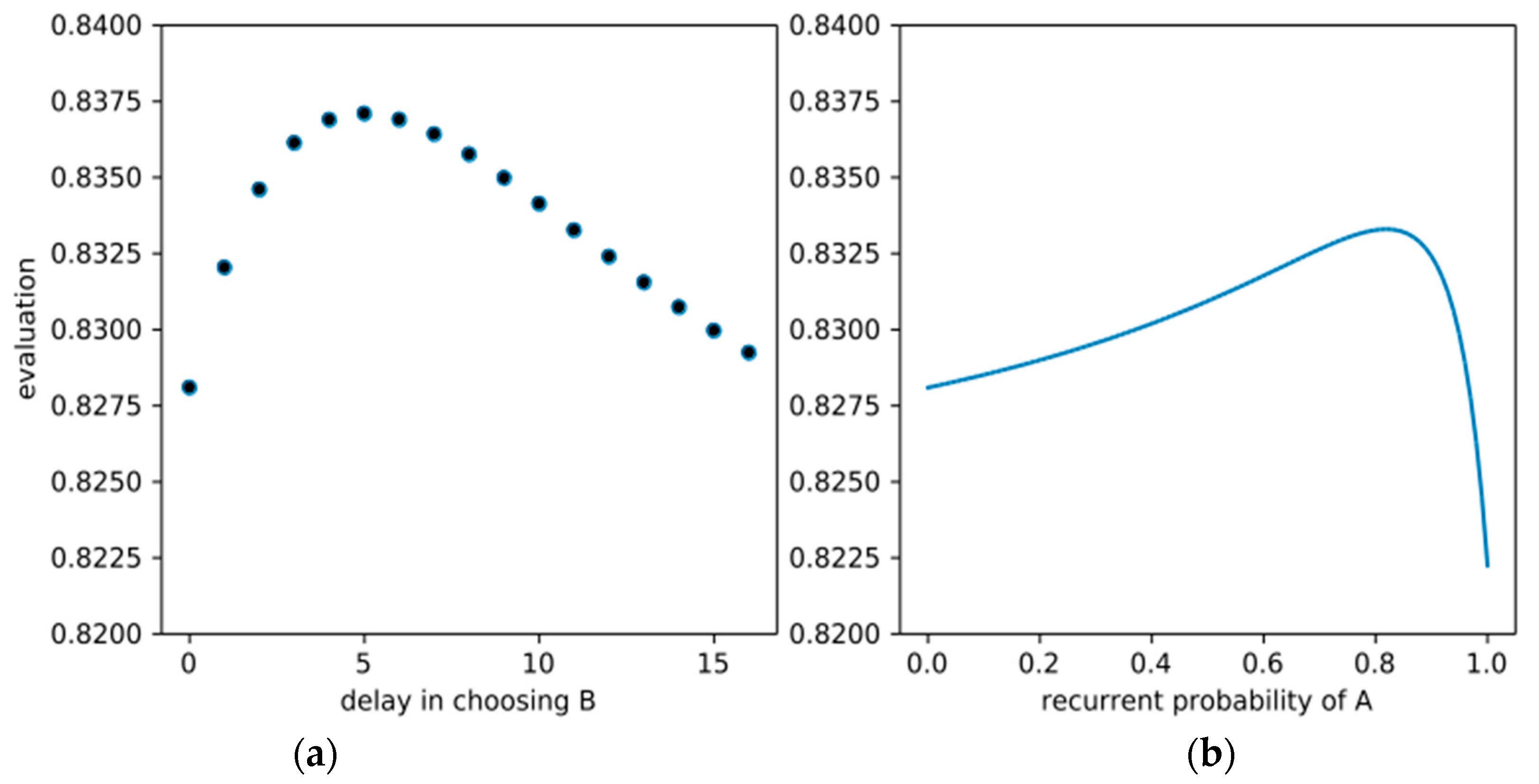
Figure 2a shows V(Bk) vs. k for the case η = 0.985, δ = 0.9, a = 2, where the optimal delay would appear to be five generations. If we restrict our optimization to the time-consistent policies “Ax”, the optimal x in that case would be ≈0.83, i.e., each generation would choose A with about 83% probability and B with about 17% probability, as shown in
Figure 2b. Still, note that the absolute evaluations vary only slightly in this example.
Let us see what effect a formally similar idea has in the context of risk aversion.
3.1.6. Caution: Gini-Sen Applied to Alternative Realizations
What happens if instead of drawing a ≥ 1 many generations t1, …, ta at random, we draw a ≥ 1 many realizations r1, …, ra of an RSL g at random and use the expected minimum of all the RS-evaluations V(ri) as a “cautious” evaluation of the RSL g?
For a = 1, this is just the expected utility evaluation of g, while for a → ∞, it gives a “worst-case” evaluation. For actual numerical evaluation, the following equivalent formula is more useful (assuming that all v(r) ≥ 0):
where P
g(v(r) ≥ x) is the probability that v(r) ≥ x if r is a realization of g. In that form, a can be any real number ≥ 1 and it turns out that the evaluation is a special case of
cumulative prospect theory [
23], with the cumulative probability weighting function w(p) = p
a. Focusing on “all-A” vs. “directly-B” again, we get V
a(all-A) = (1 − η
aH)/(1 − η
a)H and V
a(directly-B) = (H − 1)/H, hence, “all-A” is preferred iff (1 − η
aH)/(H − 1) > 1 − η
a, i.e., iff H and a are small enough and η is small enough. In particular, regardless of H and η, for a → ∞ we always get a preference for “directly-B” as in the constant absolute risk aversion. This is because with the Gini-Sen-inspired specification of caution, the degree of risk aversion effectively acts as an exponent to the survival probability η, i.e., increasing risk aversion has the same effect as increasing collapse probability, which is an intuitively appealing property.
3.1.7. Fairness as Inequality Aversion on Uncertain Prospects
Consider the RSs r1 = (1, 0, 1) and r2 = (1, 1, 0), and the RSL g that results in r1 or r2 with equal probability ½. If we apply inequality aversion on the RS level as above, say with a = 2, we get V(r1) = V(r2) = V(g) = 4/9. Still, g can be considered more
fair than both r1 and r2 since under g, the expected rewards are (1, ½, ½) rather than (1, 0, 1) or (1, 1, 0), so no generation is doomed to zero reward but all have a fair chance of getting a positive reward. It is, therefore, natural to consider applying “inequality aversion” on the RSL level to encode fairness, by putting:
where V(g, t) is some evaluation of the uncertain reward of generation t resulting from g, e.g., the expected reward or some form of risk-averse evaluation. The interpretation is that V
a(g) is the expected minimum of how two randomly drawn generations within the time horizon evaluate their uncertain rewards under g. Using exponential discounting instead, the formula becomes:
If we use the expected reward for V(g, t) and evaluate the time-consistent policies “Ax” with this V
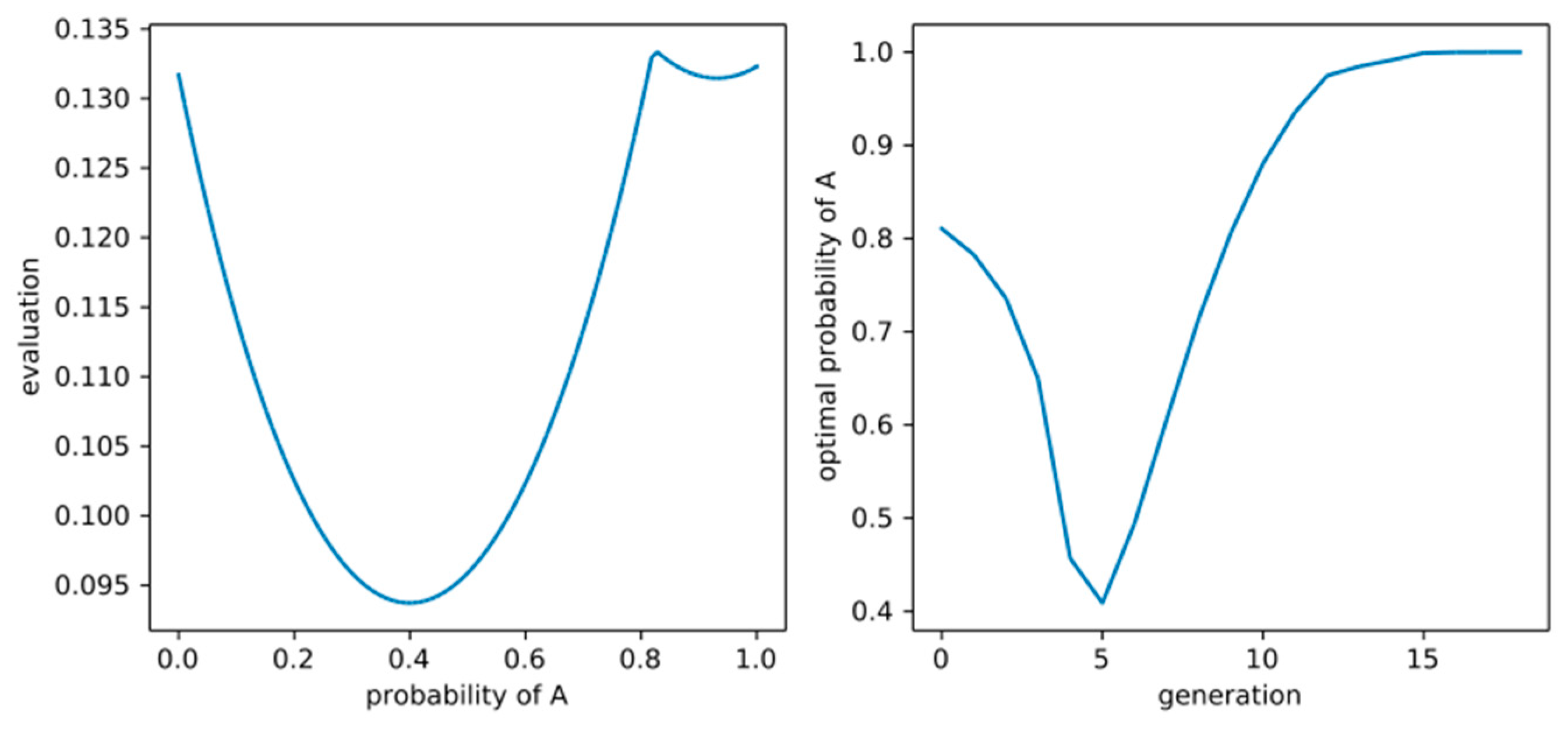
a(g), the result looks similar to
Figure 2b, i.e., the optimal time-consistent policy is again non-deterministic. A full optimization of V
a(g) over the space of all possible probabilistic policies shows that the overall optimal policy regarding V
a(g) is not much different from the time-consistent one, it prescribes choosing A with probabilities between 79% and 100% in different generations for the setting of
Figure 2.
3.1.8. Combining Inequality and Risk Aversion with Fairness
How could one consistently combine all the discussed aspects into one welfare function? Since a Gini-Sen-like technique of using minima can be used for each of them, it seems natural to base a combined welfare function on that technique as well. Let us assume we want to evaluate the four simple RSLs g
1, …, g
4 listed in
Table 1 in a way that makes V(g
1) > V(g
2) because the latter is more risky, V(g
2) > V(g
3) because the latter has more inequality, and V(g
3) > V(g
4) because the latter is less fair. Then we can achieve this by applying the Gini-Sen technique several times to define welfare functions V
0 … V
6 that represent more and more of our aspects as follows:
Simple averaging: V0(g) = Er Et r(t) where Er f(r) is the expectation of f(r) w.r.t. the lottery g and Et f(t) is the expectation of f(t) w.r.t. some chosen discounting weights;
Gini-Sen welfare of degree a = 3: V1(g) = Er Et1 Et2 Et3 min{r(t1), r(t2), r(t3)};
Overall risk-averse welfare: V2(g) = Er1 Er2 min{Et r1(t), Et r2(t)};
Fairness-seeking welfare of degree a = 3: V3(g) = Et1 Et2 Et3 min{Er r(t1), Er r(t2), Er r(t3)};
Inequality- and overall risk-averse welf.: V4(g) = Er1 Er2 min{v4(r1), v4(r2)} with v4(r) = Et1 Et2 Et3 min{r(t1), r(t2), r(t3)};
Inequality and overall risk index: I4(g) = 1 − V4(g)/V0(g);
Generational risk averse and fair welfare: V5(g) = Et1 Et2 Et3 min{V5(g, t1), V5(g, t2), V5(g, t3)} with V5(g, t) = Er1 Er2 min{r1(t), r2(t)};
Generational risk and fairness index: I5(g) = 1 − V5(g)/V0(g); and
All effects combined: V6(g) = V4(g)V5(g)/V0(g) = V0(g)[1 − I4(g)][1 − I5(g)]
The resulting evaluations for g
1 … g
4 can be seen in
Table 1. We chose a higher degree of inequality-aversion (a = 3) than the degree of risk-aversion (a = 2) so that V
6(g
2) > V
6(g
3) as desired. Applied to our thought experiment, V
6 can result in properly probabilistic and time-inconsistent policy recommendations, as shown in
Figure 3 for two example choices of η and discounting schemes. An alternative way of combining inequality and risk aversion into one welfare function would be to use the concept of
recursive utility [
25], which is, however, beyond the scope of this article.
Summarizing the results of our analysis in the optimal control framework that treats humanity as a single infinitely-lived decision-maker, we see that there is no clear recommendation to either choose A or B at time 0 since depending on the degrees and forms of time preferences/time horizon and risk/inequality/fairness attitudes, either one of the policies “all-A” or “directly-B” may appear optimal, or it may even appear optimal to deterministically delay the choice for B by a fixed number of generations or choose A by a time-varying probability, leading to time-inconsistent recommendations. At least we were able to formally confirm quite robustly the overall intuition that risk aversion and long time horizons are arguments in favor of B while risk seeking and short time horizons are arguments in favor of A. Only the effect of inequality aversion might be surprising, since it can lead to either recommending a time-inconsistent policy of delay (if we restrict ourselves to deterministic policies) or a probabilistic policy of choosing A or B with some probabilities (if we restrict ourselves to time-consistent policies). In the next subsection, we will see what difference it makes that no generation can be sure about the choices of future generations.
3.2. Game-Theoretical Framework
While the above analysis took the perspective of humanity as a single, infinitely lived “agent” that can plan ahead its long-term behavior, we now take the viewpoint of the single generations who care about intergenerational welfare, but cannot prescribe policies for future generations and have to treat them as separate “players” with potentially different preferences instead. For the analysis, we will employ game-theory as the standard tool for such multi-agent decision problems. Each generation, t, is treated as a player who, if they find themselves in state L, has to choose a potentially randomized strategy, p(t), which is, as before, the probability that they choose option A. Since each generation is still assumed to care about future welfare, the optimal choice of p(t) depends on what generation t believes future generations will do if in L. As usual in game theory, we encode these beliefs by subjective probabilities, denoting by q(t’, t) the believed probability by generation t’ that generation t > t’ will choose A when still in L.
Let us abbreviate generation t’ by G
t’ and the set of generations t > t’ by G
>t’ and focus on generation t’ = 0 at first. Let us assume that V = V
4, V
5, or V
6 with exponential discounting encodes their social preferences over RSLs. Given G
0′s beliefs about G
>0′s behavior, q(0, t) for all t > 0, we then need to find that x in [0, 1] which maximizes V(RSL(p
x,q)), where p
x,q is the resulting policy p
x,q = (x, q(0, 1), q(0, 2), …). If G
0 believes G
1 will choose B for sure (i.e., q = (0, …) = “directly-B”) and chooses strategy x, the resulting RSL(p
x,q) produces the reward sequence r
1 = (1, 0, 0, …) with probability xπ, r
2 = (1, 0, 1, 1, …) with probability 1 − x, and r
3 = (1, 1, 0, 1, 1, …) with probability xη. Hence:
Since the coefficient in front of x² is positive, V
4 is maximal for either x = 0, where it is (1 − δ + δ²)³, or for x = 1, where it is (δ³ − δ² + 1)³η² + (δ − 1)³(η² − 1), which is always smaller, so w.r.t. V
4, x = 0 (choosing B for sure) is optimal under the above beliefs. For V
5, we have V
5(RSL(p
x,q), t) = 1 for t = 0, (xη)² for t = 1, (1 − x)² for t = 2, and (1 − xπ)² for t > 2. If x < 1/(1 + η), we have (xη)² < (1 − x)² < (1 − xπ)² < 1, while for x > 1/(1 + η), we have (1 − x)² < (xη)² < (1 − xπ)² < 1. For x ≤ 1/(1 + η), V
5(RSL(p
x,q)) is again quadratic in x with a positive x² coefficient with value 1 + (1 − δ)³ − (1 − δ²)³ at x = 0 and, again, a smaller value at x = 1/(1 + η). Additionally, for x ≥ 1/(1 + η), V
5(RSL(p
x,q)) is quadratic in x with positive x² coefficient and a value of:
for x = 1, which is larger than the value for x = 0 if η is large enough and/or δ small enough. A similar thing holds for the combined welfare measure V
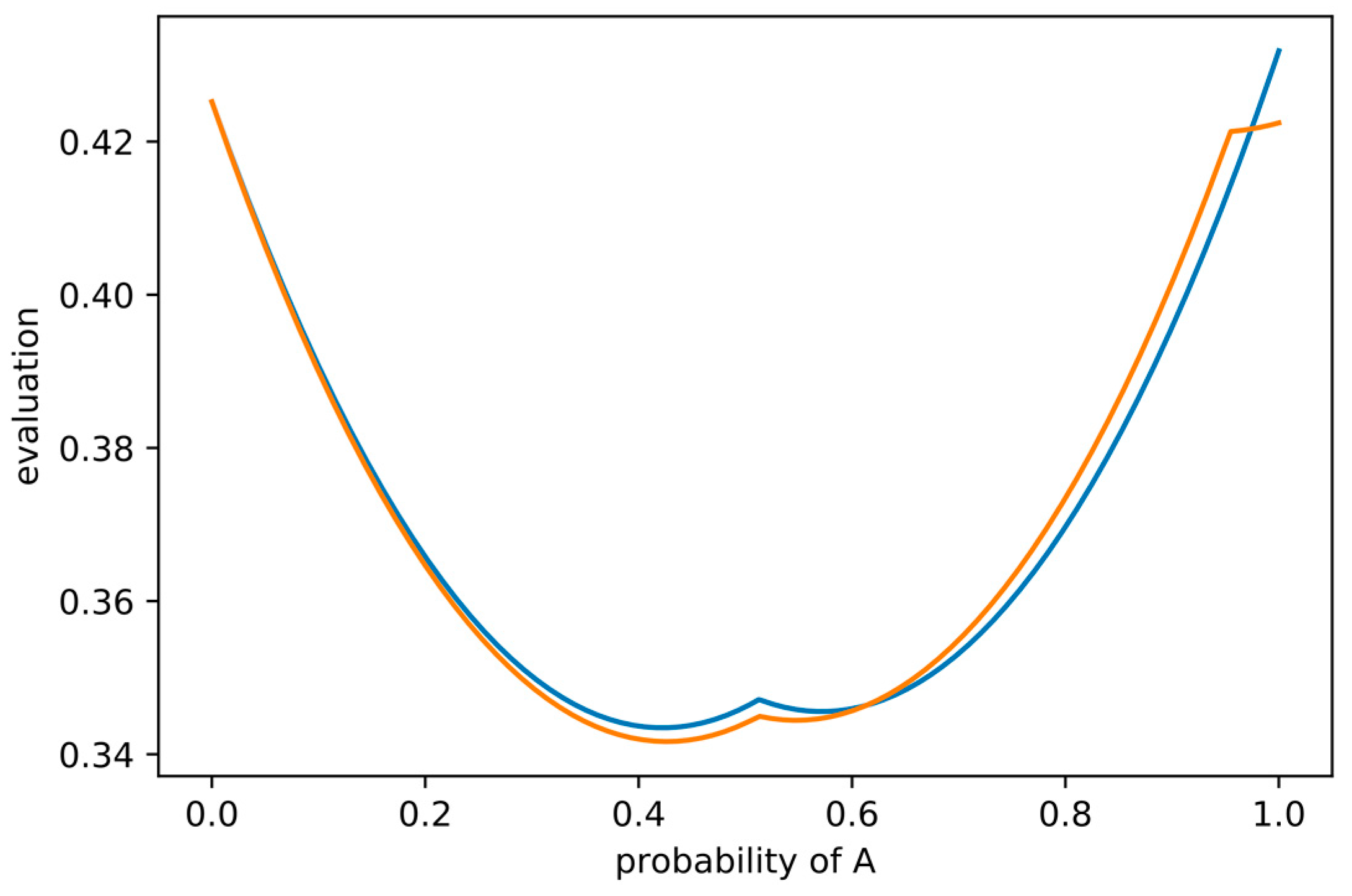
6, as shown in
Figure 4, blue line, for the case η = 0.95 and δ = 0.805, where G
0 will choose A if they believe G
1 will choose B, resulting in an evaluation V
6 ≈ 0.43. The orange line in the same plot shows V
6(RSL(p
x,q)) for the case in which G
0 believes that G
1 will choose A and G
2 will choose B if they are still in L, which corresponds to the beliefs q = (1, 0, …). Interestingly, in that case, it is optimal for G
0 to choose A, resulting in an evaluation V
6 ≈ 0.42. Since the dynamics and rewards do not explicitly depend on time, the same logic applies to all later generations, i.e., for that setting of η and δ and any t ≥ 0, it is optimal for G
t to choose A when they believe G
t+1 will choose B and optimal to choose B when they believe G
t+1 will choose A and G
t+2 will choose B.
Now assume that all generations have preferences encoded by welfare function V
6 and believe that all generations G
t with even t will choose A and all generations G
t with odd t will choose B. Then it is optimal for all generations to do just that. In other words, these assumed common beliefs form a
strategic equilibrium (more precisely, a subgame-perfect Nash equilibrium) for that setting of η and δ. However, under the very same set of parameters and preferences, the alternative common belief that all even generations will choose B and all odd ones A also forms such an equilibrium. Another equilibrium consists of believing that all generations choose A with probability ≈83.7% which all generations evaluate as only V
6 ≈ 0.40, which is less than in the other two equilibria. The existence of more than one strategic equilibrium is usually taken as an indication that the actual behavior is very difficult to predict even when assuming complete rationality. In our case, this means G
0 cannot plausibly defend any particular belief about G
>0′s policy on the grounds of G
>0′s rationality since G
>0 might follow at least either of the three identified equilibria (or still others). In other words, for many values of η and δ a game-theoretic analysis based on subgame-perfect Nash equilibrium might not help G
0 in deciding between A and B. A common way around this is to consider “stronger” forms of equilibrium to reduce the number of plausible beliefs, but this complex approach is beyond the scope of this article. An alternative and actually older approach [
26] is to use a different basic equilibrium concept than Nash equilibrium, not assuming players have beliefs about other players policies encoded as subjective probabilities, but rather assuming players apply a worst-case analysis. In that analysis, each player would maximize the minimum evaluation that could result from any policy of the others. For choosing B, this evaluation is simply v(1, 0, 1, 1, …), while, for choosing A, the evaluation can become quite complex. Instead of following this line here, we will use a similar idea when discussing the concept of responsibility in the next section, where we will discuss other criteria than rationality and social preferences.