Data-Driven Method to Estimate the Maximum Likelihood Space–Time Trajectory in an Urban Rail Transit System
Abstract
:1. Introduction
- A data-driven methodology to estimate a passenger’s detailed travel information is developed. Passengers’ detailed trajectories can be used for further study, such as analysis of path-choice behavior.
- A method to estimate walk parameters of subway stations using AFC data and train schedules is developed.
- At the aggregate level, we develop outputs of various kinds of statistical reports for operators, such as time-independent network passenger flow distribution and time-independent congestion of train vehicles and stations.
2. Conceptual Illustrations
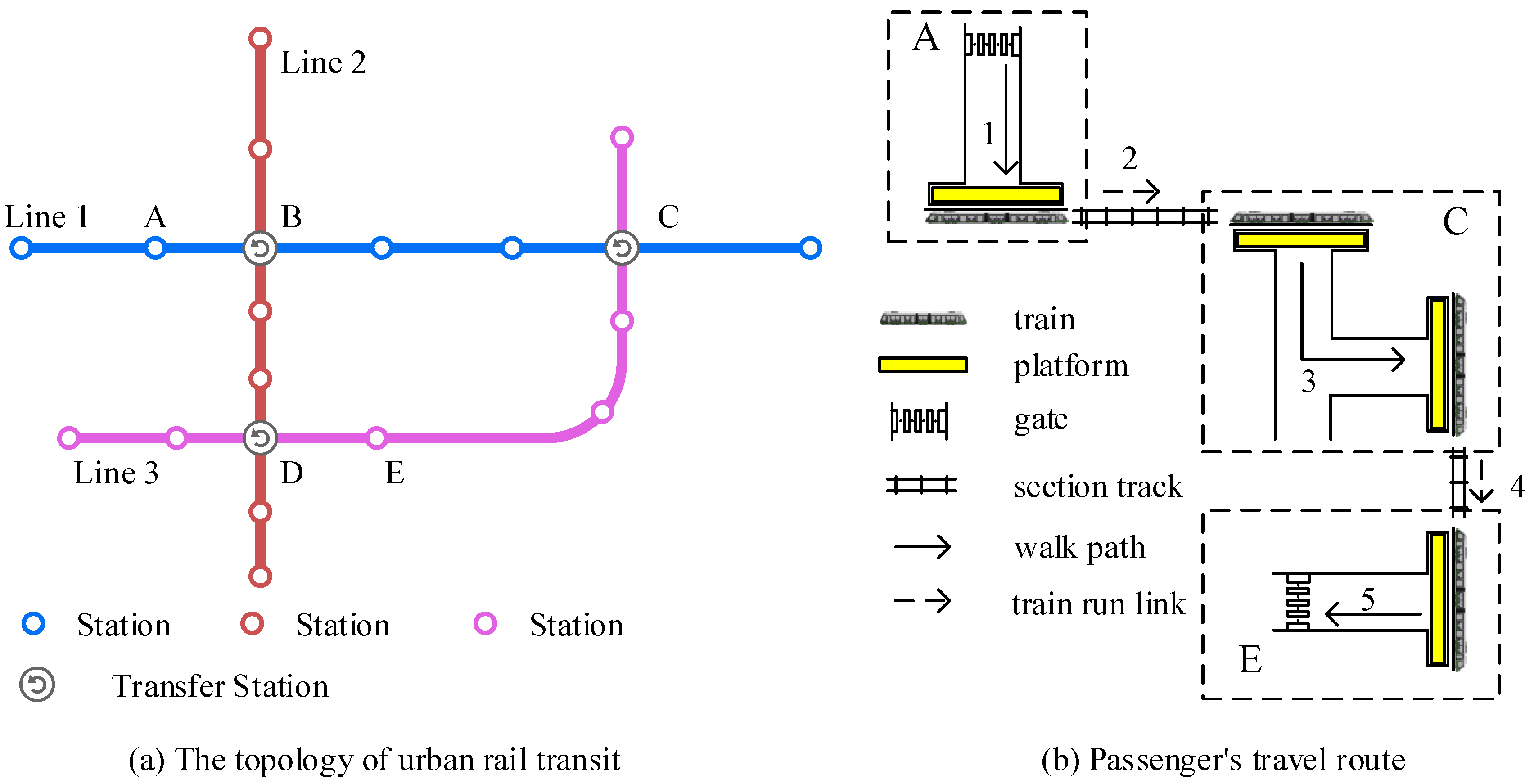
2.1. Passenger Travel Trajectory Components
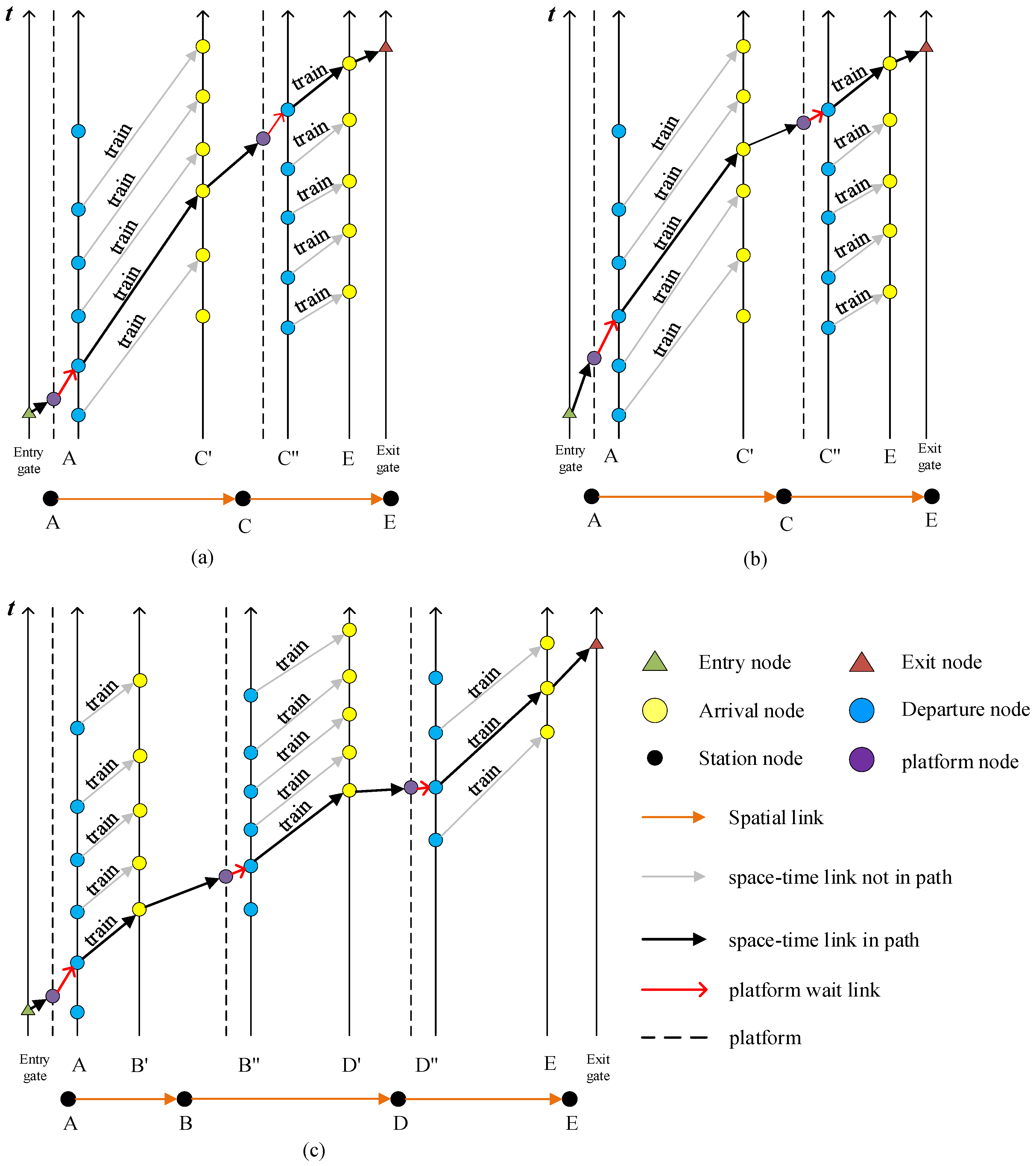
2.2. Passenger’s Space–Time Trajectory
3. Maximum Likelihood Space–Time Trajectory Estimation Models
3.1. Notations
3.2. Maximum Likelihood Space–Time Trajectory Estimation Model
4. Solution Algorithms
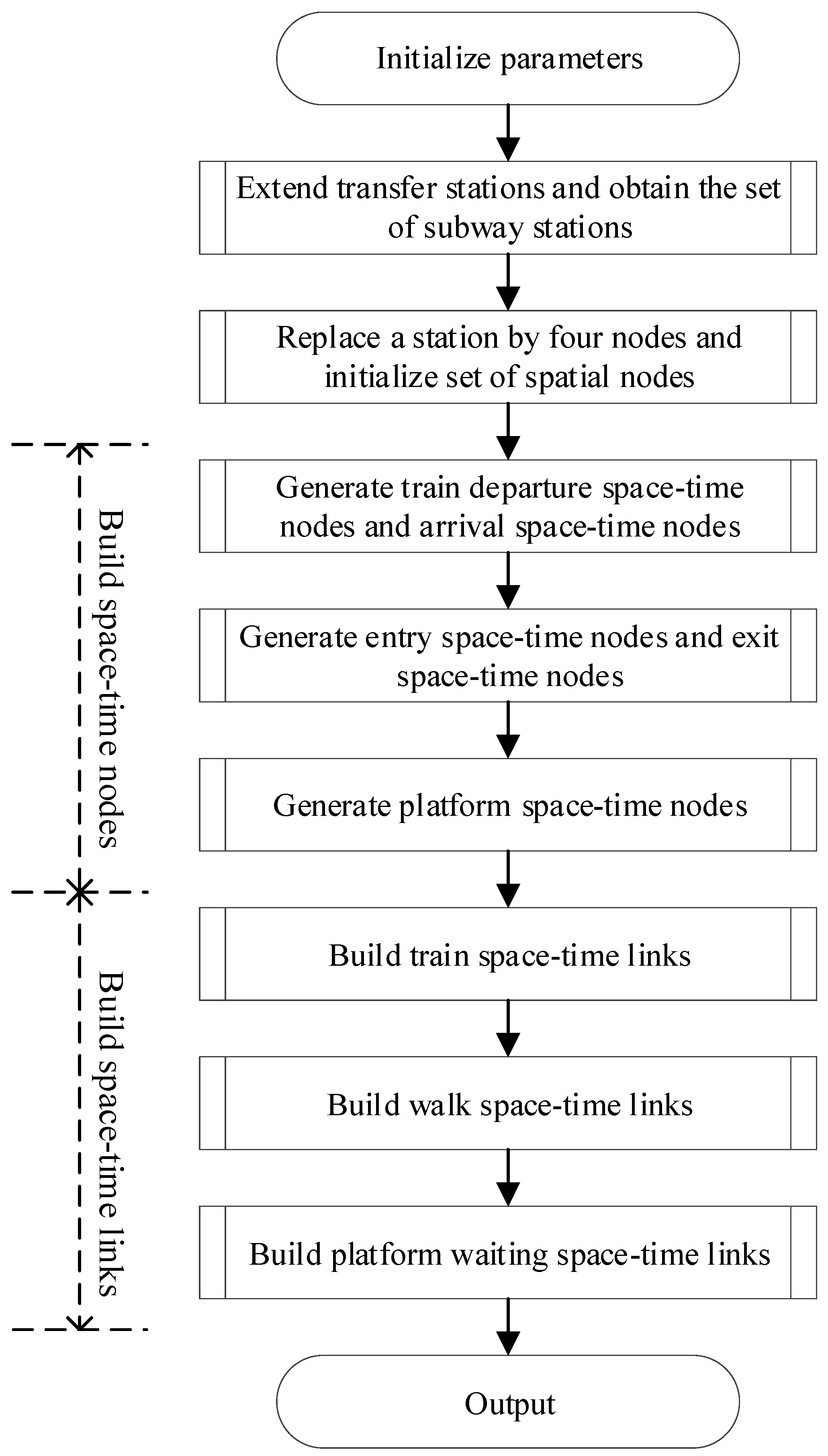
4.1. Feasible Trajectory Generation Algorithm
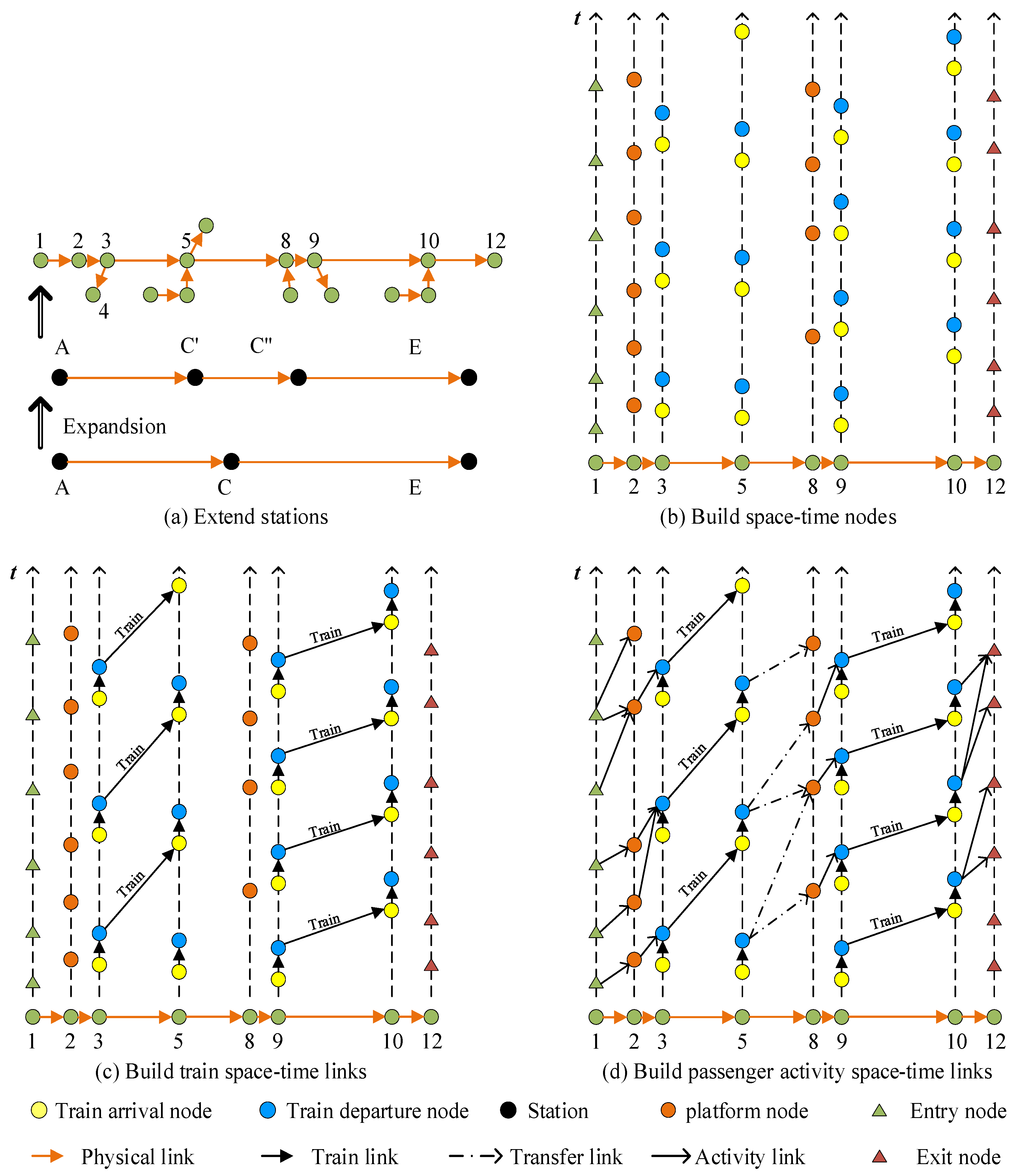
Algorithm. Building the space–time trajectory network
Input URT train timetable and AFC data, initialize parameters of the algorithm, and initialize variables and . Step 2. Extend subway stations. Step 2.1 Extend the transfer stations according to the count of accessing subway lines. The stations that represent the same transfer station have same station name. Add all stations to . Step 2.2 Replace a station by four spatial nodes that represent the entry gate, exit gate, platform and track of the station. These four nodes are either the start node or end node of passenger’s activity links. Add all spatial nodes to . Add all spatial nodes that represent platform to . Step 3. Build the space–time node set. Step 3.1 Generate train departure space–time nodes and arrival space–time nodes. Extend the track spatial nodes according to train arrival count and departure count. Add these space–time nodes to . Step 3.2 Generate passengers’ entry space–time nodes and exit space–time nodes. Extend the spatial nodes that represent entry gate or exit gate passengers’ entry information and exit records. Add these space–time nodes to . Step 3.3 Generate platform space–time nodes. Extend a platform spatial node according to the departure of a train accessing the platform. Add these space–time nodes to . Step 4. Build the space–time link set. Step 4.1 Build train space–time links. Connect the space–time departure node and arrival node of the same train according to the sequence of space–time nodes passing by train. Add these space–time links to . Step 4.2 Build walk space–time links. First, build the access walk space–time link between entry space–time nodes and platform space–time nodes with activity time cost constraint and the constraint that the platform arrival time should be less than the exit time. Assuming that passengers get off the train immediately while transferring at transfer station or arriving at their destination station, build the egress walk space–time links between platform space–time nodes and exit space–time nodes, and the transfer walk space–time links between platform space–time nodes. Add these space–time links to and . Step 4.3 Build platform waiting space–time links. Connect platform waiting space–time nodes and train departure space–time nodes with platform wait time constraint. Add these space–time links to . |
4.2. Weighted Assignment
5. Numerical Experiments
5.1. Input Data
5.2. Results and Discussion
5.2.1. Computational Efficiency
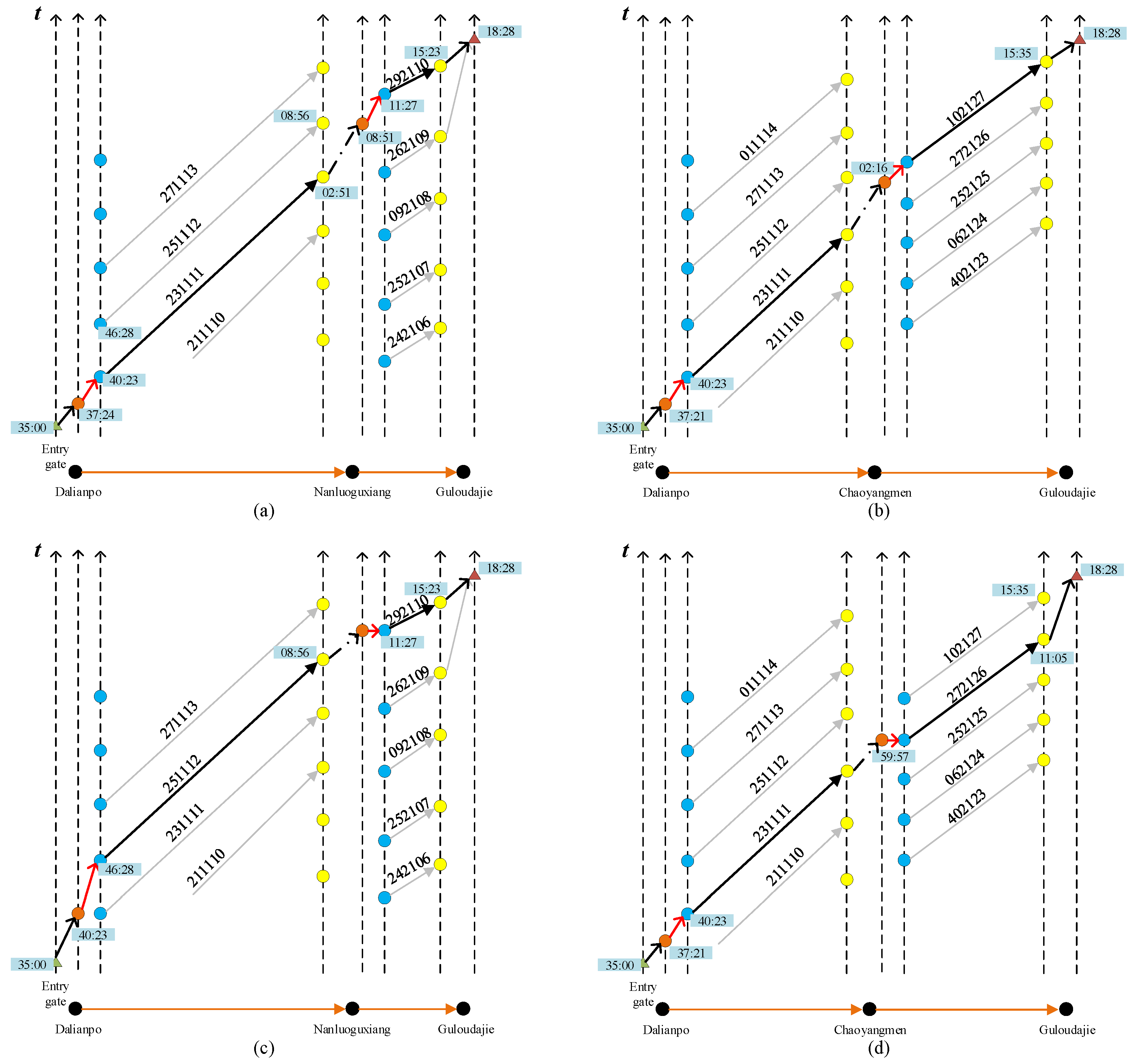
5.2.2. Detailed Space–Time Trajectory Information
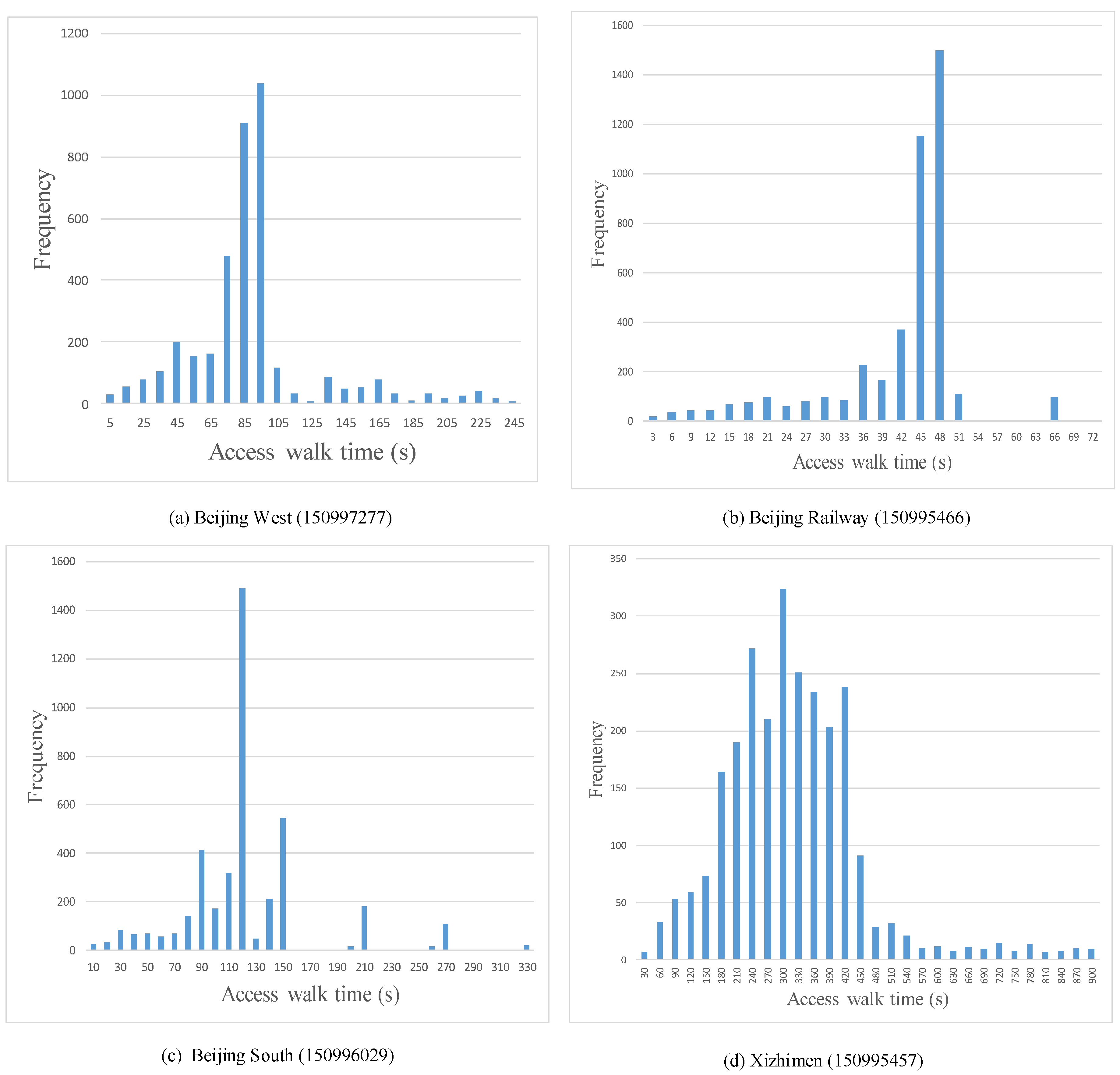
5.2.3. Estimation Result of Walk Time Parameters
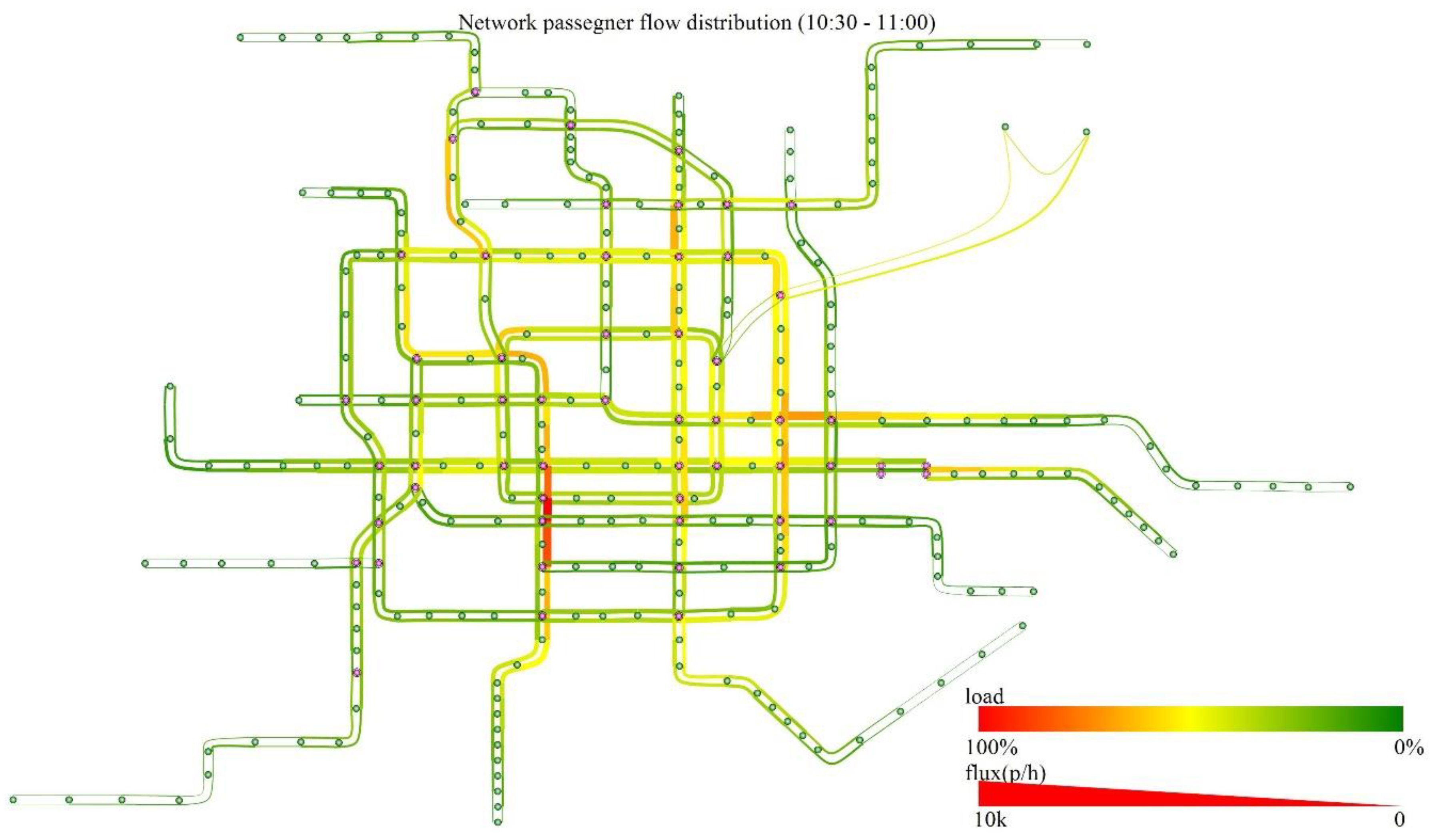
5.2.4. Distribution of the URT Network Passenger Flow
6. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Tong, C.O.; Wong, S.C. A stochastic transit assignment model using a dynamic schedule-based network. Transp. Res. Part B Methodol. 1999, 33, 107–121. [Google Scholar] [CrossRef]
- Tong, C.O.; Wong, S.C. A schedule-based time-dependent trip assignment model for transit networks. J. Adv. Transp. 1999, 33, 371–388. [Google Scholar] [CrossRef]
- Moller-Pedersen, J. Assignment model for timetable based systems (TPSCHEDULE). In Proceedings of the Seminar F, 27th European Transportation Forum, Cambridge, UK, 27–29 September 1999; pp. 159–168. [Google Scholar]
- Nielsen, O.A.; Jovicic, G. A large-scale stochastic timetable-based transit assignment model for route and submode choices. In Proceedings of the Seminar F, 27th European Transportation Forum, Cambridge, UK, 27–29 September 1999; pp. 169–184. [Google Scholar]
- Xu, R.; Luo, Q.; Gao, P. Passenger flow distribution model and algorithm for urban rail transit network based on multi-route choice. J. China Railway Soc. 2009, 31, 110–114. [Google Scholar]
- Poon, M.H.; Wong, S.C.; Tong, C.O. A dynamic schedule-based model for congested transit networks. Transp. Res. Part B Methodol. 2004, 38, 343–368. [Google Scholar] [CrossRef]
- Hamdouch, Y.; Lawphongpanich, S. Schedule-based transit assignment model with travel strategies and capacity constraints. Transp. Res. Part B Methodol. 2008, 42, 663–684. [Google Scholar] [CrossRef]
- Ben-Akiva, M.E.; Gao, S.; Wei, Z.; Wen, Y. A dynamic traffic assignment model for highly congested urban networks. Transp. Res. Part C Emerg. Technol. 2012, 24, 62–82. [Google Scholar]
- Cepeda, M.; Cominetti, R.; Florian, M. A frequency-based assignment model for congested transit networks with strict capacity constraints: Characterization and computation of equilibria. Transp. Res. Part B Methodol. 2006, 40, 437–459. [Google Scholar] [CrossRef]
- Richard, D.; Connors, A.S. A network equilibrium model with travellers’ perception of stochastic travel times. Transp. Res. Part B Methodol. 2009, 43, 614–624. [Google Scholar]
- Leurent, F.; Chandakas, E.; Poulhès, A. A passenger traffic assignment model with capacity constraints for transit networks. In Proceedings of the 15th Meeting of the EURO Working Group on Transportation, Paris, France, 10–13 September 2012. [Google Scholar]
- Schmocker, J.-D.; Bell, M.G.H.; Kurauchi, F. A quasi-dynamic capacity constrained frequency-based transit assignment model. Transp. Res. Part B Methodol. 2008, 42, 925–945. [Google Scholar] [CrossRef]
- Nuzzolo, A.; Crisalli, U.; Rosati, L. A schedule-based assignment model with explicit capacity constraints for congested transit networks. Transp. Res. Part C Emerg. Technol. 2012, 20, 16–33. [Google Scholar] [CrossRef]
- Leurent, F.; Chandakas, E.; Poulhes, A. A traffic assignment model for passenger transit on a capacitated network: Bi-layer framework, line sub-models and large-scale application. Transp. Res. Part C Emerg. Technol. 2014, 47, 3–27. [Google Scholar] [CrossRef]
- Lu, C.-C.; Liu, J.; Qu, Y.; Peeta, S.; Rouphail, N.M.; Zhou, X. Eco-system optimal time-dependent flow assignment in a congested network. Transp. Res. Part B Methodol. 2016, 94, 217–239. [Google Scholar] [CrossRef]
- Fu, Q.; Liu, R.; Hess, S. A review on transit assignment modelling approaches to congested networks: A new perspective. Soc. Behav. Sci. 2012, 54, 1145–1155. [Google Scholar] [CrossRef]
- Tong, C.O.; Wong, S.C. A predictive dynamic traffic assignment model in congested capacity-constrained road networks. Transp. Res. Part B Methodol. 2000, 34, 625–644. [Google Scholar] [CrossRef]
- Bekhor, S.; Chorus, C.; Toledo, T. Stochastic User Equilibrium for Route Choice Model Based on Random Regret Minimization. Transp. Res. Rec. 2012, 100–108. [Google Scholar] [CrossRef]
- Van Der Hurk, E.; Kroon, L.; Maróti, G.; Vervest, P. Deduction of Passengers’ Route Choices from Smart Card Data. IEEE Trans. Intell. Transp. Syst. 2015, 16, 430–440. [Google Scholar] [CrossRef]
- Shi, J.; Zhou, F.; Zhu, W.; Xu, R. Estimation method of passenger route choice proportion in urban rail transit based on AFC data. J. Southeast Univ. (Natl. Sci. Ed.) 2015, 1, 184–188. [Google Scholar]
- Kusakabe, T.; Iryo, T.; Asakura, Y. Estimation method for railway passengers’ train choice behavior with smart card transaction data. Transportation 2010, 37, 731–749. [Google Scholar] [CrossRef]
- Sun, Y.; Schonfeld, P.M. Schedule-Based Rail Transit Path-Choice Estimation using Automatic Fare Collection Data. J. Transp. Eng. 2016, 142, 04015037. [Google Scholar] [CrossRef]
- Zhou, F.; Xu, R. Model of passenger flow assignment for urban rail transit based on entry and exit time constraints. Transp. Res. Rec. 2012, 2284, 57–61. [Google Scholar] [CrossRef]
- Dai, X.; Tu, H.; Sun, L. A Multi-modal Evacuation Model for Metro Disruptions: Based on Automatic Fare Collection Data in Shanghai, China. In Proceedings of the 95th Annual Meeting of the Transportation Research Board, Washington, DC, USA, 10–14 January 2015. [Google Scholar]
- Ma, X.; Wu, Y.J.; Wang, Y.; Chen, F.; Liu, J. Mining smart card data for transit riders’ travel patterns. Transp. Res. Part C Emerg. Technol. 2013, 36, 1–12. [Google Scholar] [CrossRef]
- Zhu, W.; Hu, H.; Huang, Z. Calibrating Rail Transit Assignment Models with Genetic Algorithm and Automated Fare Collection Data. Comput.-Aided Civ. Infrastr. Eng. 2014, 29, 518–530. [Google Scholar] [CrossRef]
- Chen, X.; Zhou, L.; Tang, J.; Zhou, H. Estimating the most likely space-time path by mining automatic fare collection data. In Proceedings of the 98th Annual Meeting of the Transportation Research Board, Washington, DC, USA, 13–17 January 2018. [Google Scholar]
- Zhu, Y.; Koutsopoulos, H.N.; Wilson, N.H.M. A probabilistic Passenger-to-Train Assignment Model based on automated data. Transp. Res. Part B Methodol. 2017, 104, 522–542. [Google Scholar] [CrossRef]
- Zhu, Y. Passenger-to-Train Assignment Model Based on Automated Data. Master’s Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA. Available online: https://dspace.mit.edu/handle/1721.1/90075 (accessed on 27 May 2018).

| Publications | Objective Function | Solution Algorithm | Data | ||
|---|---|---|---|---|---|
| NT | TSD | AFCTD | |||
| Tong and Wong (1999a) [1] | Minimizing generalized cost | BBA | √ | √ | |
| Tong and Wong (1999b) [2] | Minimizing travel time consumed | TDNL | √ | √ | |
| Xu et al. (2009) [5] | Minimizing path impedance | MRA | √ | ||
| Poon et al. (2004) [6] | Equilibrating network flow | MSA | √ | √ | |
| Kusakabe et al. (2010) [21] | Minimizing the cost | DA | √ | √ | √ |
| Bekhor et al. (2012) [18] | Minimizing random regret | MSA | √ | ||
| Van der Hurk et al. (2015) [19] | Minimizing the deviation between path and conductor checks | BFA | √ | √ | √ |
| Chen et al. (2018) [27] | Maximizing the probability of a space–time | DA | √ | √ | √ |
| This paper | Minimizing the variances among the time cost of walk activities | SQP | √ | √ | √ |
| Symbol | Definition |
|---|---|
| Set of URT stations | |
| Set of URT connections, including sections and transfer links | |
| Set of spatial nodes | |
| Set of spatial nodes that represent the platform, | |
| Set of space–time nodes | |
| Set of space–time links | |
| Set of walk space–time links | |
| Set of passengers | |
| Set of activity times | |
| Set of URT lines | |
| Set of URT trains | |
| Index of stations, | |
| Index of passenger, | |
| Index of spatial nodes, | |
| Index of different time stamps, | |
| Index of space–time nodes, | |
| Index of URT connection, | |
| Index of space–time link indicating the actual movement at the entering time and leaving time on the spatial link , | |
| Name of station | |
| Index of station that spatial node belongs to, | |
| Index of origin node, destination node of passenger , , | |
| Time cost for passenger on link , | |
| Excepted value of the time cost of link , | |
| 0-1 binary variables: 1 if passengers must walk from node to node ; 0, otherwise, | |
| Interval time of train departure at station at , , | |
| Total time consume of passenger at station , , |
| Variable | Definition |
|---|---|
| Time at which passenger arrives at node , , | |
| 0–1 binary variables: 1 if passenger passes spatial link from time stamp at node to at node ; 0 otherwise. |
| Line Name | Train Num | Station | Arrival Time | Departure Time |
|---|---|---|---|---|
| 1 | 102116 | Dongdan | 09:51:07 | 09:51:52 |
| 1 | 102116 | Xidan | 09:42:59 | 09:43:33 |
| 1 | 102116 | Fuxingmen | 09:39:59 | 09:40:49 |
| … | … | … | … | … |
| 9 | 091070 | Beijing West Railway | 10:39:28 | 10:40:28 |
| 9 | 091070 | Liuliqiao | 10:44:58 | 10:45:58 |
| 9 | 091070 | Qilizhuang | 10:48:25 | 10:49:10 |
| Card ID | Origin | Entry Time | Destination | Exit Time |
|---|---|---|---|---|
| 15093451177 | Huilongguan | 10:14:00 | Fuchengmen | 10:56:24 |
| 15093451188 | Tiantongyuanbei | 11:03:00 | Beijing Railway | 11:53:00 |
| 15093452342 | Dalianpo | 11:35:00 | Guloudajie | 12:18:28 |
| 15093452355 | Chongwenmen | 11:49:00 | Guloudajie | 12:19:16 |
| 15093451636 | Jishuitan | 10:48:00 | Andingmen | 10:55:03 |
| 15093451646 | Huixi North | 11:16:00 | Beijing Railway | 11:50:04 |
| 15093451660 | Changchunjie | 11:44:00 | Fuchengmen | 11:54:04 |
| 15093450644 | Dalianpo | 10:08:00 | Fuchengmen | 10:56:02 |
| 15093451221 | Jishuitan | 11:42:00 | Xizhimen | 11:50:21 |
| 15093452373 | Jishuitan | 11:57:00 | Chongwenmen | 12:20:20 |
| 15093451672 | Wangfujing | 11:21:00 | Jishuitan | 11:53:21 |
| 15093450259 | Dajing | 10:55:00 | Yonghegong | 11:52:16 |
| Number of hours | 2 |
| Number of OD pairs | 117,992 |
| Number of trips | 320,228 |
| Number of trips for which no path was estimated | 8629 |
| Calculation time (min) | 4.2 |
| No. | Transfer Station | Board Train | Access Time | Transfer Time | Egress Time |
|---|---|---|---|---|---|
| 1 | Nanluoguxiang | 231111, 292110 | 144 s | 300 s | 185 s |
| 2 | Chaoyangmen | 231111, 102127 | 141 s | 336 s | 173 s |
| 3 | Nanluoguxiang | 251112, 292110 | 323 s | 151 s | 185 s |
| 4 | Chaoyangmen | 231111, 272126 | 141 s | 197 s | 443 s |
| Walk Time Parameter | Expected Value (s) |
|---|---|
| Access time of Dalianpo (150996535) | 120 |
| Transfer time of Nanluoguxiang (150996519) | 300 |
| Transfer time of Chaoyangmen (150996523) | 285 |
| Egress time of Guloudajie (150995473) | 46 |
| Egress time of Guloudajie (150997027) | 90 |
| Station | Survey (s) | Estimation (s) | Relative Deviation |
|---|---|---|---|
| Beijing West Railway station | 90 | 93 | 3.33% |
| Beijing Railway station | 39 | 41 | 5.13% |
| Beijing South Railway station | 123 | 116 | −5.69% |
| Xizhimen | 327 | 314 | −3.98% |
| Tiantongyuanbei | 47 | 49 | 4.26% |
| Dongzhimen | 222 | 233 | 4.96% |
| Section Name | TOCC | Estimate | Relative Deviation |
|---|---|---|---|
| Caishikou–Xuanwumen | 6369 | 6290 | −1.24% |
| Jintailu–Hujialou | 6055 | 5946 | −1.8% |
| Guomao–Yong’anli | 5789 | 5815 | 0.45% |
| Yong’anli–Jianguomen | 5708 | 5724 | 0.28% |
| Dawanglu–Guomao | 5468 | 5469 | 0.02% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Zhou, L.; Yue, Y.; Zhou, Y.; Liu, L. Data-Driven Method to Estimate the Maximum Likelihood Space–Time Trajectory in an Urban Rail Transit System. Sustainability 2018, 10, 1752. https://doi.org/10.3390/su10061752
Chen X, Zhou L, Yue Y, Zhou Y, Liu L. Data-Driven Method to Estimate the Maximum Likelihood Space–Time Trajectory in an Urban Rail Transit System. Sustainability. 2018; 10(6):1752. https://doi.org/10.3390/su10061752
Chicago/Turabian StyleChen, Xing, Leishan Zhou, Yixiang Yue, Yu Zhou, and Liwen Liu. 2018. "Data-Driven Method to Estimate the Maximum Likelihood Space–Time Trajectory in an Urban Rail Transit System" Sustainability 10, no. 6: 1752. https://doi.org/10.3390/su10061752
APA StyleChen, X., Zhou, L., Yue, Y., Zhou, Y., & Liu, L. (2018). Data-Driven Method to Estimate the Maximum Likelihood Space–Time Trajectory in an Urban Rail Transit System. Sustainability, 10(6), 1752. https://doi.org/10.3390/su10061752




