Environmental Fiscal Reform and the Double Dividend: Evidence from a Dynamic General Equilibrium Model

Abstract

An environmental fiscal reform (EFR) represents a transition of a taxation system toward one based in environmental taxation, rather than on taxation of capital, labor, or consumption. It differs from an environmental tax reform (ETR) in that an EFR also includes a reform of subsidies which counteract environmental policy. This research details different ways in which an EFR is not only possible but also a good option that provides economic and environmental benefits. We have developed a detailed dynamic CGE model examining 101 industries and commodities in Spain, with an energy and an environmental extension comprising 31 pollutant emissions, in order to simulate the economic and environmental effects of an EFR. The reform focuses on 39 industries related to the energy, water, transport and waste sectors. We simulate an increase in taxes and a reduction on subsidies for these industries and at the same time we use new revenues to reduce labor, capital and consumption taxes. All revenue recycling options provide both economic and environmental benefits, suggesting that the “double dividend” hypothesis can be achieved. After three to four years after implementing an EFR, GDP is higher than the base case, hydrocarbons consumption declines and all analyzed pollutants show a reduction.

1. Introduction

There is a growing consensus in the European Union that environmental taxes are a promising policy for reducing environmental impacts and also as a way to increase public revenues and reduce fiscal pressure [1]. Revenues from environmental taxes in Spain are the lowest in the EU-27, accounting for 1.57% of gross domestic product (GDP), far below the EU average, which was 2.40% in 2012. As is the case in most of the EU’s member states, environmental taxation in Spain is mostly focused on energy (1.3% of GDP) [2]. In the recent years, the European Commission has recommended that Spain increase its environmental taxes in order to converge with those of other Member States and to increase its public revenues [3]. The “Europe 2020” strategy calls for implementing policies that shift part of the tax base to environmentally damaging activities; this strategy is a vital part of an overall policy package that aims to tackle these multiple challenges [4].

The theoretical basis of environmental taxes has been well documented in early discussions of Baumol, Baumol and Oates [5,6]; such taxes create incentives to change behaviors toward sustainability targets in a Pigouvian sense [7]. The objective of an environmental tax is to reduce/internalize a negative externality such as pollution or natural resources exhaustion. The social benefits of a Pigouvian tax could outstrip its costs.

An environmental tax reform (ETR) consists in transitioning the national taxation system based on extant taxes on labor (personal income tax and social contributions), capital and consumption (VAT and other indirect taxes) to one based on consumption and production activities that generate environmental pressures, without affecting the overall government revenues coming from taxation. This shift could provide better signals to economic agents, leading to better functioning of markets. In a more general way, an environmental fiscal reform (EFR) also includes the elimination of environmentally harmful subsidies [1]. Some authors argue that this type of reform would reduce environmental impacts while at the same time improving the economy.

The “double dividend hypothesis” suggests that introducing environmental taxes and using the associated revenues to reduce other taxes not only reduces environmental problems but also has a positive impact on the economy, so long as the state maintains a constant level of total revenue and/or government expenditure [8,9,10,11]. However, the literature shows that there are uncertainties regarding the economic and environmental effects of such a reform in a specific region [12,13,14,15]. These studies also show that different schema for implementing an ETR or an EFR would lead to different results in terms of economic and environmental achievements.

Computable general equilibrium (CGE) models are the most comprehensive way to take into account the most relevant aspects of an economic system [16]. They allow researchers to assess the effect on different macroeconomic variables from external impacts or policies, such as changes to a taxation system. Some recent studies that have used CGE methods to model the effects of an ETR. Bye (2000), Ciaschini et al. (2012), Fernández et al. (2011), Holmlund and Kolm (2000), Jorgenson et al. (2013), Patuelli et al. (2005) and Wendner (2001) [17,18,19,20,21,22,23] all found that a carbon tax on the United States economy could achieve a double dividend by recycling revenues in capital taxes. A literature review on CGE modeling and the double dividend can be found in Freire-González [24] which draws two main conclusions: first, an environmental tax improves environmental conditions, which is the main objective of imposing such a tax; and second, the post-reform improvement of economic conditions remains uncertain. However, most simulations analyzed achieved a double dividend and literature shows that recycling government revenues to reduce other pre-existing taxes minimize costs. Bosquet [25] reviews the early literature on the use of simulations to analyze the double dividend hypothesis, finding some evidence of support in particular cases but also suggests potential improvements that this approach would benefit from. Also, Ekins and Speck [26] conducted a review of the subject, suggesting that in practice in the EU, many industries have circumvented the environmental taxes due to fears over competitiveness in the EU.

In the specific context of Spain, there are a number of extant studies that analyze the effects of environmental taxation and address their potential (e.g., [27,28,29,30]). Some studies use CGE models to assess the impact of environmental taxes, especially energy taxes, on the Spanish economy [31,32,33,34]. Few scholars have analyzed different forms of an ETR from a general equilibrium perspective [35,36,37].

In this research, we develop a dynamic CGE model that is highly disaggregated, encompassing 101 industries and commodities, to assess the economic and environmental effects of an EFR focused on the energy, water, transport and waste sectors in Spain. This is something that has never done before at this detail. We increase output taxes and reduce subsidies for 39 industries related to those sectors and use the government revenues generated to cut other pre-existing taxes, thus instituting a revenue-neutral reform. Specifically, we use these revenues to reduce value-added taxes along with taxes on capital and labor, testing the double dividend hypothesis for an EFR in Spain. Beyond the economic impacts of the reform, we also assess its effects on 31 different local and global pollutants and on the total use of coal, oil and gas. While a direct tax on pollutant emissions would create effective incentives, changing output taxes and subsidies is currently a common way to do an EFR in Spain and in Europe, even though there are many countries in the context of Europe, or the rest of the world that use pollutant or externality taxes (like a carbon tax). A description of the model follows in Section 2; Section 3 describes the data and the assumptions on exogenous variables; Section 4 describes the scenarios and the results of simulations and Section 5 lays out the main conclusions of the research.

2. The Energy-Environment-Economy Dynamic CGE Model

A dynamic CGE model for the Spanish economy is developed in this research. It is based on and has a structure similar to previous models developed by Dale Jorgenson and colleagues, previously used in Cao et al. (2009), Cao et al. (2013), Ho and Jorgenson (2007), Jorgenson et al. (2013) and Jorgenson and Wilcoxen (1993) [21,38,39,40,41], among others. A previous version of this model can be found in Freire-González and Ho [42]. The relevant features and adaptations are detailed in this section and in the technical Appendix A. The main characteristic of this model is that growth is driven by savings; thus, conceptually, it is a Solow growth based model. Savings come from three main sources: households, enterprises and the foreign sector. Households save a share of their income, enterprises retain part of their earnings and foreign sector invests through foreign investment. These savings finance the government deficit and are used for investment in domestic capital. Economic growth depends on population growth, capital accumulation and technical change or growth in total factor productivity.

As in many other CGE models, different agents are identified. They both receive and spend incomes and have other roles represented by the equations system shown in Appendix A. The four main agents represented in this system are:

• Households: Their main role is to supply labor, purchase goods and services and receive incomes from the labor they supply, from the capital and land they own, from the government and from the rest of the world. Households also pay taxes to government and save part of their total income.
• Government: Its main economic role is to collect and redistribute other agents’ incomes though taxes, subsidies and transfers. In our model, we categorize these taxes as tax on capital; tax on labor; property tax; tax on dividends; value-added tax (VAT) on products; special taxes on alcohol, tobacco, hydrocarbons, electricity and retail hydrocarbons; sales tax; other taxes on production; social security contributions; and import taxes (or tariffs). We also factor in other non-tax revenues from households and companies, along with production subsidies. The government also buys goods and services, invests and pays interests for government bonds. Government deficits are covered by domestic and foreign borrowing.
• Enterprises: Their role is mainly to produce commodities using intermediate and primary inputs purchased in the market; their revenue includes government output subsidies and other payments. They spend their earnings on dividends to households and taxes to government; they also save a share of their income by retaining part of the earnings. Regarding production, the model identifies 101 industries that produce 101 commodities, with high levels of detail in the electricity generation and waste treatment technology sectors.

The factors of production are capital, labor, land, energy and other intermediates. Production functions are specified as Cobb-Douglas technology functions with constant returns to scale, as output expands in proportion to inputs (There are no estimates of elasticities of substitution at this level of detail. Many models assume a fixed coefficient—Leontief—function for intermediate inputs, however, this is not consistent with data at the industry level; time series of input-output tables in many countries show substantial changes in most input coefficients.) Technical coefficients can change over time in two different ways: (1) there is technical progress, meaning that there is more output with the same inputs; and (2) there is biased technical change, i.e. changes in input demands unrelated to prices. The capital input for each industry is rented from a total capital stock that changes over time; it increases with new investments and decreases with depreciation. Labor is assumed to be mobile across sectors and the labor supply depends on the level of unemployment. The land factor has been designated for the agriculture, forestry and fishing industries and its supply is fixed exogenously.

• Rest of world: Its main role it to purchase exports, sell imports and provide foreign investment. It also receives and pays incomes from other agents. Imports and domestic output follow Armington’s assumption [43], to be combined through constant elasticity of substitution (CES) functions, producing a composite commodity supply.

The CGE model includes a submodel describing energy use and the emissions of 31 pollutants. Specifically, consumption of coal, oil, natural gas and electricity are identified. These energy coefficients (described in Appendix A) were estimated using data from the International Energy Agency (IEA) on total energy consumption and input-output tables for Spain; in this way, we were able to estimate total energy consumption over time and under the different policies simulated. As there is no available data at the industry level on the use of hydrocarbons for the 101 sectors considered, an average coefficient has been used. This allows for an estimation of overall energy use.

To obtain CO₂ emissions from energy use, we linked them using data from IEA (2016) [44] on CO₂ emissions from fuel combustion of coal, oil and natural gas. Along with CO₂, we have included 31 additional pollutants in the environmental module—some related to global warming, others more related to health risks. Coefficients for each pollutant and industry have been calculated from emissions data from Exiobase datasets for each industry.

3. Data

Implementing the model described above requires a massive amount of data. In this section, we describe the data we used to feed the model. A combination of economic and environmental data translated into the various parameters and variables needed to first calibrate the model and then to run simulations.

The main source of the economic data is a social accounting matrix (SAM) for the Spanish economy. This is a square matrix that provides information on the different flows of payments among the various elements of the economic system described: commodities, industries, capital, labor, land, households, enterprises, government, taxes and tariffs, investments, savings and the exterior sector. We have built a SAM that differentiates between commodities and industries, employing both supply and use tables. Supply and use tables have been developed using information from the National Statistics Institute of Spain (INE) and Exiobase [45,46]. Exiobase provides an input-output framework for 2007 that includes environmental information at a detailed industry level, disaggregated for 163 industries and 200 commodities. With the INE tables as a starting point, we developed new supply and use matrices by breaking down electricity and waste treatment industries using information from the Exiobase tables. In this way, we were able to complete the SAM while avoiding heterogeneity problems with other sources of information. The other information needed to complete the SAM comes from the INE and the Spanish government. After adjustments (Some industries have been aggregated to correspond with similar industries or commodities, thus reducing the number of very small or irrelevant industries from the analysis.), the resulting matrix encompasses 101 industries and 101 commodities, with high detail in the areas of electricity generation technologies (coal, gas, nuclear, hydro, wind, petroleum, biomass, solar, wave, geothermal and other) and waste treatment technologies (incineration, biogasification, composting and landfill). INE and Exiobase tables also provide other information needed to feed the SAM, such as final demand components, imports and data on taxes, compensation of employees, employment and operating surplus. The EU KLEMS project on growth and productivity provided data on the stock of capital and depreciation rates by industry [47]. The SAM also includes details on different forms of industry taxation, including VAT, sales taxes, other taxes on products, tariffs and VAT imports.

The matrix also includes economic information on income flows between agents. Figures for government accounts, including social security and tax accounts, have been obtained from the General Intervention Board of the State Administration (IGAE). Figures for foreign sector accounts have been obtained from the INE; they contain a detail on the balance of payments. Enterprise accounts have been obtained from the Bank of Spain and include details on the annual accounts of firms.

Besides the economic information, the model is fed with energy and environmental data. Figures for the consumption of coal, oil and natural gas and the resultant CO₂ emissions, have been obtained from the IEA [44]. The information on the emissions of the other pollutants modeled have been obtained from the Exiobase dataset.

A summary of the described SAM for the Spanish economy for 2007 is shown in

Table 1. Summary of the social accounting matrix of the Spanish economy, 2007, in millions of euros.

	Commodity	Industry	Labor	Capital	Land	Households	Enterprise	Government	Taxes Less Subs. on Products	Other Taxes on Products	Social Security	Tariff	VAT for Import	Capital a/c	Rest of World	Total
Commodity		1,126,644				604,429		193,474						326,422	283,331	2,534,300
Industry	2,151,706															2,151,706
Labor		510,296														510,296
Capital		414,982														414,982
Land		18,822														18,822
Households			373,879		18,822		299,539	155,808							–20,312	827,736
Enterprise				404,703												404,703
Government				10,279		84,363	89,388		80,238	724	136,417	145	28,330	–14,238		415,646
Taxes less subs. on products		80,238														80,238
Other taxes on products		724														724
Social Security			136,417													136,417
Tariff	145															145
VAT for import	28,330															28,330
Capital a/c						138,944	15,776	49,467							107,996	312,184
Rest of World	354,119							16,897								371,016
Total	2,534,300	2,151,706	510,296	414,982	18,822	827,736	404,703	415,646	80,238	724	136,417	145	28,330	312,184	371,016

Source: Own elaboration.

. We have four different agents represented in the SAM: households, government, enterprises and foreign sector. There are 15 big columns and rows, representing the different aspects we detail in our system. The detailed SAM contains a total of 119 columns and rows, including all industries, all commodities, a detail of different taxes, etc. Columns represent the payments and rows represent the receipts of incomes. In this way, all transactions between economic sectors and agents are represented as a square matrix. For instance, in the Households column we can see expenditures of €604,429 million in goods and services; the Government column shows total transfers of €155,808 million from public institutions to households. Cells should not be read literally, as in some cases we have considered net values, implying payments less charges. For instance, the Enterprise column considers payments to government (mainly from corporate income tax) minus transfers from the government to enterprises, yielding a net payment from enterprises to government of €89,388 million.

Some of the variables of the model are set exogenously. Most of them have been kept constant during the entire 30-year period assessed in this research, given the uncertainty regarding their evolution and the purpose of this research. However, different projections can be assumed depending on the expected evolution or the objective of the analysis. The variables that has been kept constant are government deficit share of GDP, interest paid by government, government payments to the rest of the world, net transfers from the rest of the world to households and dividend rate. The parameters of household consumption and investments have also kept constant. Savings rate and technical input-output coefficients are assumed to be unchanged during the period of analysis. Projections on population for the next years have been obtained from the INE. The sectoral labor force figure is based on working-age population data from Exiobase and has been assumed to increase at a same rate as the population. Growth of total factor productivity (TFP) is calibrated to produce an annual GDP growth rate of around 2% per year and the current account deficit is projected to decline.

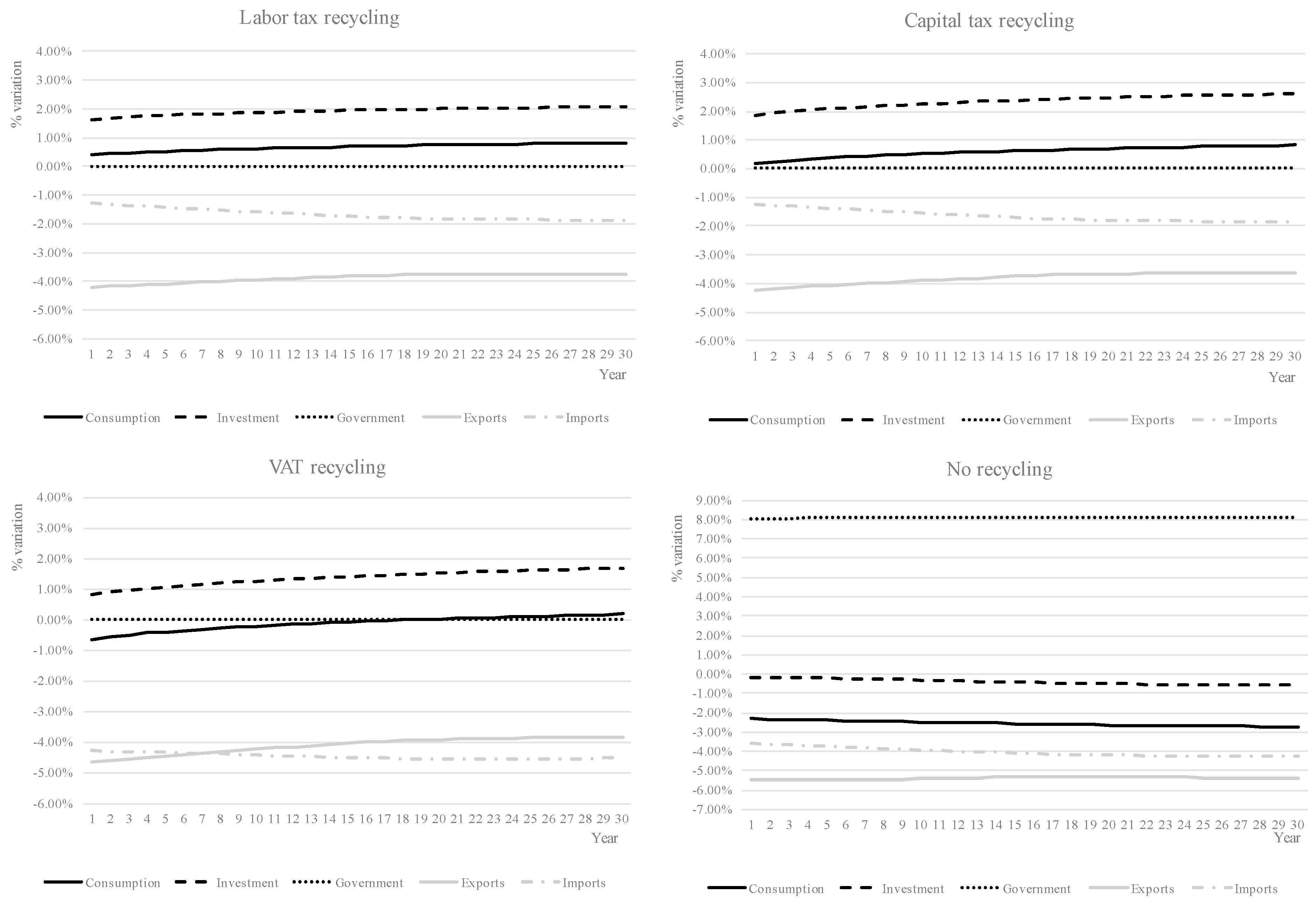
4. Scenarios and Results

This section describes the policy scenarios simulated with the model and the results obtained in terms of economic and environmental impacts. The literature discusses the best option for recycling the revenues generated by environmental taxes. Most studies suggest that recycling them through lowering distortionary taxes is more efficient than returning them via lump-sum transfers to households or other economic agents [14,21,48,49,50,51].

The EFR we simulate is predicated on adding/increasing a tax on 39 different industry outputs while reducing/eliminating subsidies in those same industries. Specifically, the new tax represents a 20% of total output; subsidies are correspondingly reduced by 20% of their total output (Total output is variable QI, detailed in Equation (A3) from the Appendix A.1). The new tax is equivalent to an ad valorem tax of 20%. Levied industries are related to energy sectors; water supply; sales of motor vehicles and water and air transport; and waste treatment activities:

• Energy industry reforms are expected to increase the price of energy, thus reducing overall demand and consequently the emission of several pollutants. Particularly, they are expected to have a specific impact on GHG emissions. In our model, there are 16 industries in this category: coal and lignite peat; extraction of crude petroleum and services related to crude oil extraction; extraction of natural gas and services related to natural gas extraction, excluding surveying and mining of uranium and thorium ores; coke, refinement of petroleum and nuclear fuel; electricity by coal; electricity by gas; electricity by nuclear; electricity by hydro; electricity by wind; electricity by petroleum and other oil derivatives, electricity by biomass and waste, electricity by solar photovoltaic; electricity by solar thermal; electricity (other); transmission services of electricity; distribution and trade services of electricity; and production and distribution of natural gas.
• Water supply industry fiscal reform is expected to increase the price of water and thereby reduce its consumption. This reduction is not reflected in air pollutants modeled in this research but is consistent with an EFR that aims to reduce environmental loads. Given the constraints of the model, we tax the overall sector; in practice, however, the reform should be implemented as a progressive tax. The specific industry affected is: “Collected and purified water, distribution services of water”.
• Fiscal reform of transport industries is expected to have an effect similar to that of taxation of water, increasing the price of levied transport and reducing its consumption. We have simulated affectation on three transport industries, with different types of effects, some related to the production of transport units and some to their use: (i) “Sale of motor vehicles” would reduce purchases of motor vehicles and thus the externalities associated with their production; (ii) “Retail trade services of motor fuel” would reduce the use of motor vehicles and therefore the externalities associated with their use; (iii) “Air transport services” would reduce the use of air transportation.
• Waste-treatment industry reform aims to increase the costs and market prices of waste treatment and thereby to reduce waste generation. Consequently, pollutants associated with waste treatment would drop. There are 19 industries in this category: food waste for treatment—incineration; paper waste for treatment—incineration; plastic waste for treatment—incineration; inert/metal waste for treatment—incineration; textiles waste for treatment—incineration; wood waste for treatment—incineration; oil/hazardous waste for treatment—incineration; food waste for treatment—biogasification and land application; paper waste for treatment—biogasification and land application; sewage sludge for treatment—biogasification and land application; food waste for treatment—composting and land application; food waste for treatment—wastewater treatment; other waste for treatment—wastewater treatment; food waste for treatment—landfill; paper for treatment—landfill; plastic waste for treatment—landfill; inert/metal/hazardous waste for treatment—landfill; textiles waste for treatment—landfill; and wood waste for treatment—landfill.

Additionally, we use the increase in government revenues (from the new environmental taxes) and the reduction in government spending (from reduced subsidies) from these fiscal changes to reduce other pre-existing taxes. We set four different scenarios related to revenue recycling: a reduction of taxes on capital; a reduction of taxes on labor; a reduction of value-added taxes; and a scenario where revenues are not recycled, so there is more government spending. If the government’s deficit is kept constant, government spending must be the same as in the base case. We introduce an additional endogenous variable ${\lambda }_t$ into the equations system, to scale the tax rates:

$$t_{jt}^{w;EFR}={\lambda }_t{t}_{j0}^w$$

(1)

where $t_{jt}^{w;ETR}$ is the tax rate for the tax $w$ (in our case, the tax on capital, the tax on labor, or the VAT) and industry $j$, under the EFR and the 0 subscript denotes base case values. We also incorporate an additional restriction into the model to keep government expenditures neutral:

$$G{G}_{EFR}\left(t\right)=G{G}_{base}\left(t\right)$$

(2)

where $GG$ is the quantity of aggregate government purchases (see Equation (A29) in the Appendix A.3). This variable is endogenous in the base case and exogenous in the policy scenario. In this policy scenario, the tax scale variable (${\lambda }_t$) and tax rates of modified pre-existing taxes become endogenous.

The first simulation conducted—the base case scenario—was performed using the initial information included in the SAM, using the actual tax rates to obtain a base-case growth path. Then, we ran the model with the EFR—adding or modifying taxes and subsidies on targeted industries in order to compare the obtained results with the base case. The main macroeconomic results for the described scenarios are presented in Figure 1 and Figure 2. Figure 1 shows the evolution of the percentage variation of GDP of an EFR under the different recycling scenarios described. Figure 2 shows the percentage variation of different components of GDP under the different scenarios—specifically, consumption, investment, public spending, exports and imports—projected for 30 years.

In all revenue-recycling scenarios, we observe a fall in GDP in the first few years of the EFR but higher investment eventually led to a higher GDP than in the base case. The scenario with no recycling of revenues, by contrast, shows a sustained decrease in GDP when compared to the base case. In pure efficiency terms, cutting capital taxes is the option that generates the highest economic benefit in the mid- and long-term. Different recycling scenarios lead to evolution of GDP components along different paths, as shown in Figure 2. Labor and capital tax recycling produce a greater increase in consumption than in other components, while capital tax recycling triggers the greatest improvement in investment. This shift towards investment comes from improved terms of trade that reduces exports in the 3 recycling scenarios. In the VAT cut case there is also a reduction in consumption in the first few years. We observe that in the scenario with no revenue recycling, only government purchases increase; the rest of the components decrease.

Analyzing industry-level results, we observe that as the new taxes rise, cost and prices increase and output falls; this is particularly pronounced in directly levied industries but also occurs in other related industries that buy inputs from them. This pattern is observed in all recycling scenarios, with small differences.

Regarding the energy consumption and the environmental consequences of an EFR, we observe an annual average reduction in coal consumption of 24.6%; an annual average reduction of 7% for oil consumption; and 36.9% for natural gas consumption. The differences among the scenarios are so small as to be insignificant, so a mean value is shown. Similarly,

Table 2. Average annual percentage variation in emissions of different pollutants for an EFR in relation to the base case in Spain.

Pollutant Emissions	% Variation	Pollutant Emissions	% Variation
CO2	−13.99%	HCB	−12.35%
CH4	−44.14%	NMVOC	−3.50%
N2O	−4.91%	TSP	−6.17%
HFC	−3.42%	PCBs	−10.44%
PM10	−11.89%	As	−6.61%
PM2.5	−6.25%	Cd	−6.28%
SO2	−24.47%	Cr	−5.07%
NOx	−16.30%	Cu	−6.25%
NH3	−1.76%	Hg	−6.57%
CO	−7.59%	Ni	−8.39%
Benzo(a)pyrene	−1.72%	Pb	−3.62%
Benzo(b)fluoranthene	−0.86%	Se	−22.39%
Benzo(k)fluoranthene	−3.97%	Zn	−7.30%
Indeno(1,2,3-cd)pyrene	−5.16%	SF6	−8.61%
PAH	−1.60%	PFC	−5.50%
PCDD_F	−5.18%

Source: Own elaboration.

shows the average annual percentage variation on emissions of 31 pollutants for the different projected scenarios.

All pollutants show a reduction in relation to the base case, as most of them are directly or indirectly related to the affected industries. Greenhouse gases or climate change related pollutants deserve special consideration here; they experience an important annual reduction with the EFR: CO₂ drops by 14%; CH4 reduces 44.14%; N₂O reduces 4.9% and HFC reduces 3.42%. There is also an important reduction in some pollutants that produce damaging health effects, such as SO₂, which sees a 24.47% reduction; NOx, with a 16.3% reduction; and Se, with a 22.39% reduction. Thus, the tested EFR triggers an important reduction of pollutant emissions related to both climate change and health risks.

5. Conclusions

This article investigates the potential of an EFR to tackle climate change and health risks without disrupting the economic system. We develop a dynamic CGE model with an energy and environmental extension that models 31 different pollutant emissions; using this model, we simulate an increase in output taxes of 20% and a reduction in subsidies of 20% for several industries related to energy, water supply, transport and waste treatment activities.

Our observations show that this reform reduces the annual consumption of coal, oil and gas and reduces all 31 different pollutant emissions assessed. Moreover, we obtain a long-term double dividend if a revenue-neutral EFR is implemented by reducing capital taxes, labor taxes, or VAT (or some combination). GDP increases within three to four years after implementation, so under some conditions, both an economic and an environmental benefit are possible at the same time if specific pre-existing taxes are reduced as taxation is imposed. In only one scenario, under which the revenues of the EFR were not used to reduce other taxes, did we observe a persistent reduction of GDP.

The EU is committed to reducing the 1990 level of emissions by 40% by the year 2030. We show that it is possible to meet the reduction objectives of CO₂ with limited costs, or even with benefits, in a big Member State like Spain, using taxation. Another important point is the collateral effects, that is, how an EFR like this would affect the emission of other pollutants. We show that this is possible in a framework like the one we have developed. Our modeling method assumes a somewhat flexible degree of substitution in production and consumption, a more inelastic framework could estimate smaller gains or even losses. We aim to investigate this in future research.

It is worth considering that we tested a general EFR, not focusing on pollutants but with focus on some particular industries. Other reforms could be more focused on the reduction of specific pollutants, as by levying those industries that directly and indirectly push their emissions; this would require a quite different approach to future research. Another important aspect for further investigation is the redistribution effects of a reform like this. This research is focused primarily on the efficiency of a fiscal reform effort and on its global costs; however, the implementation of such a reform could take different forms, each of which would have a different effect on income distribution. All aspects related to the design and implementation of any EFR and its implications for the population, need to be fully considered; these considerations fall outside the scope of this investigation. This research, however, shows how trade-offs between environment and economy can be overcome with well-designed fiscal systems.