Cost Forecasting of Substation Projects Based on Cuckoo Search Algorithm and Support Vector Machines
Abstract
:1. Introduction
2. Basic Theory
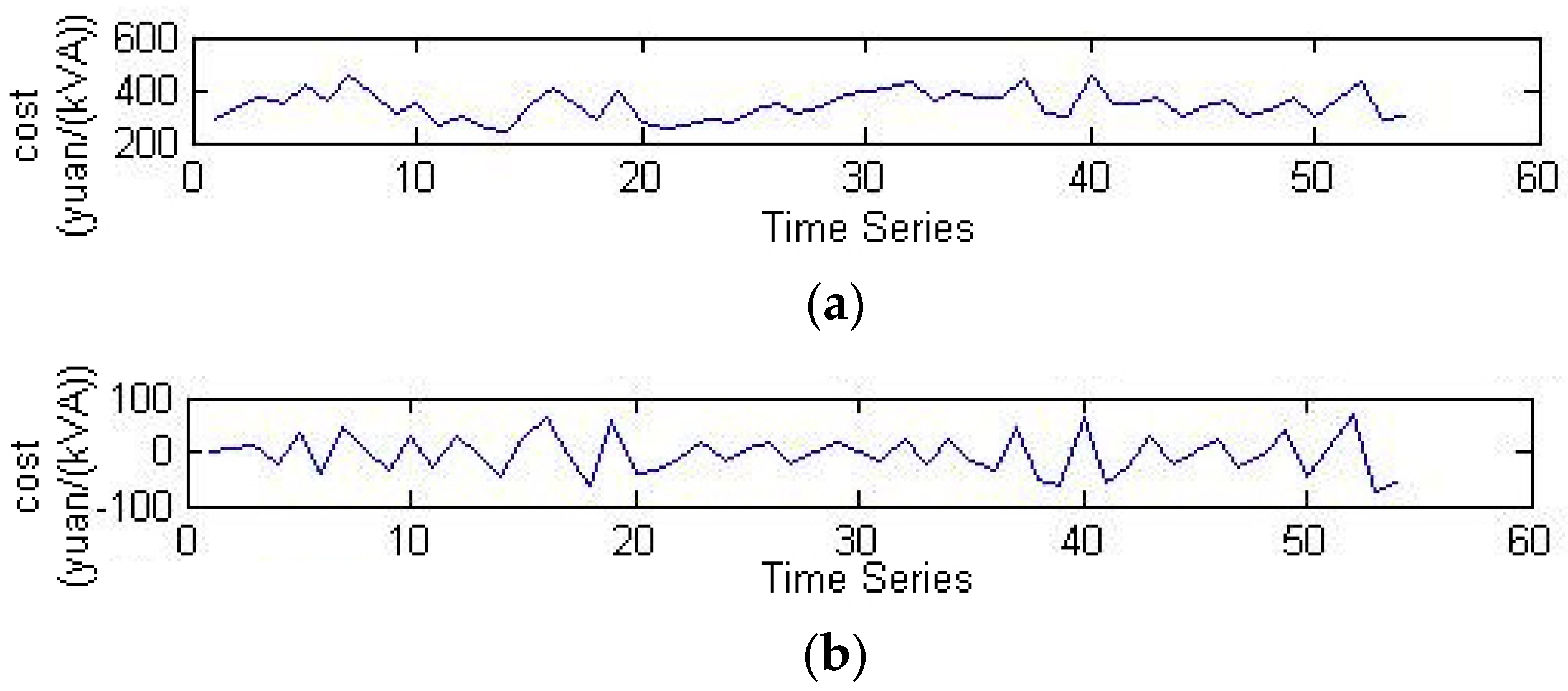
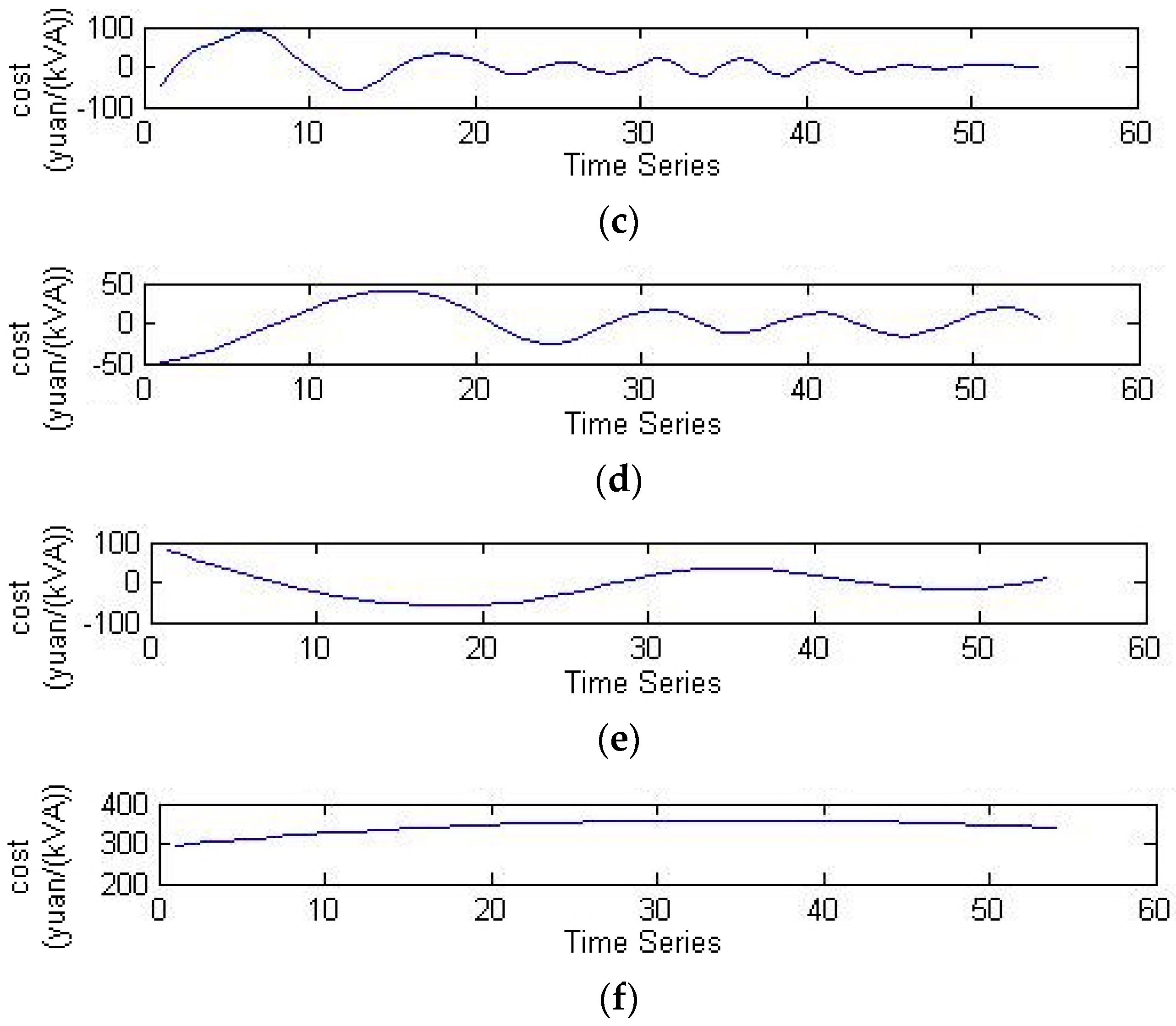
2.1. EEMD
- Determine the number of decomposed IMFs and the number of decompositions
- Add Gaussian white noise sequence to the input signals
- Normalize the signals after adding the white noise sequence
- Decompose the normalized signals to obtain multiple IMF components and one surplus variable:
2.2. SVM
2.3. Optimized CS Algorithm
- The number of eggs produced by a cuckoo per time is 1.
- The host bird’s nest where high-quality eggs are located is the optimal solution and will be retained for the next generation.
- The number of host nests is certain, and the probability that cuckoo eggs are found by nest owners is .
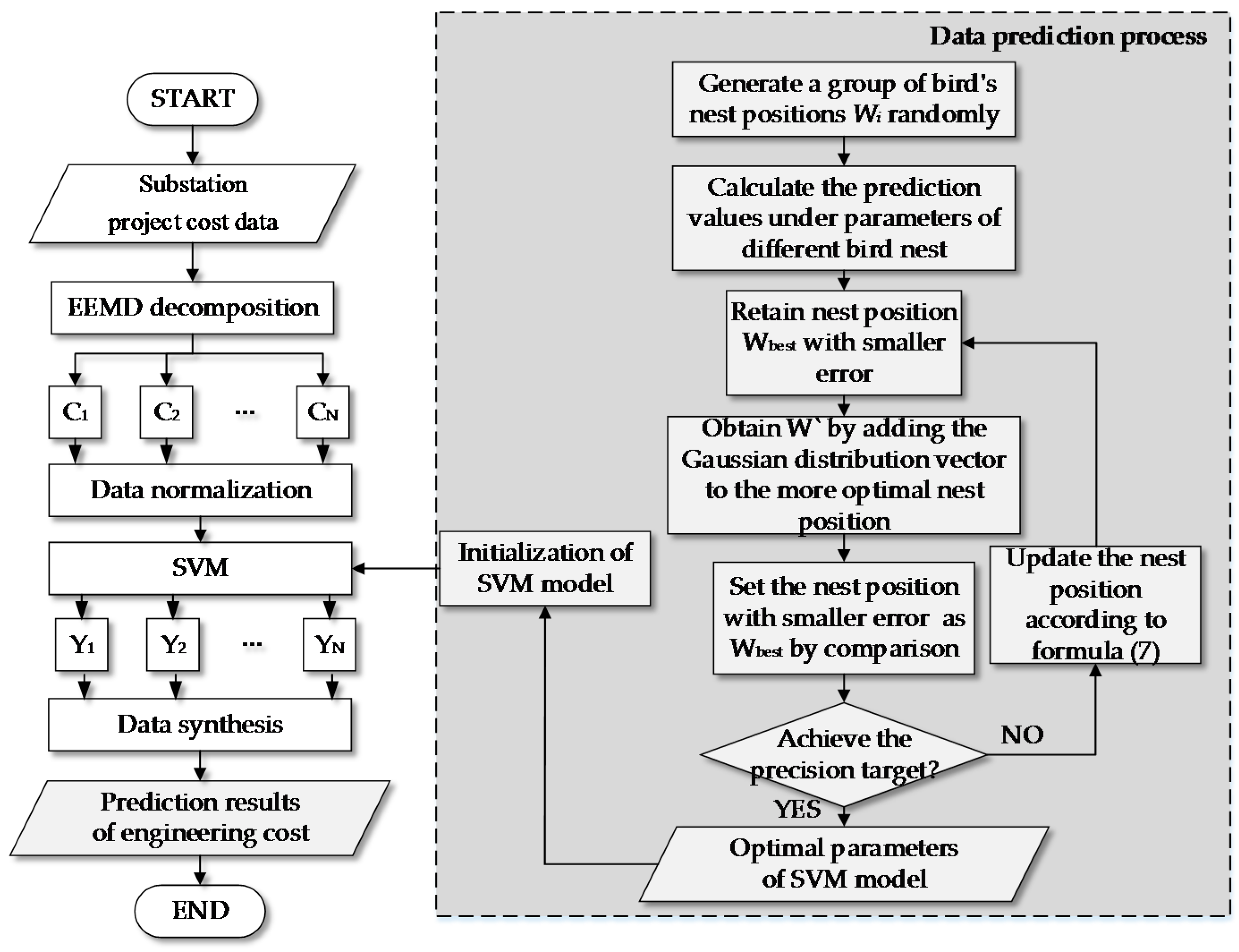
3. Substation Project Cost Prediction Model Based on EEMD-GCS-SVM
- Decompose the substation cost data to obtain the IMF components and surplus variables through the EEMD method, and normalize the data.
- Initialize the parameters and kernel functions of SVM model, input the normalized decomposed variables into SVM model, and find and determine the optimal parameters and kernel function of SVM model by using GCS algorithm. In order to search for the best parameters of the prediction model faster, the range of c, are set as [0.01, 100], [0.01, 100], respectively. Then, train the prediction model by plugging the historical data into the model and search the best parameter by using the GCS Algorithm. Firstly, set the Nnest (number of birds’ nest) as 20, while Pa (probability of bird’s eggs by bird’s nest owner) is 0.45, and N (number of iterations) is 200. After that, randomly generate Nnest bird nest location W = (W1, W2, ..., Nnest)T. Each bird nest Wi has s parameters (s = the number of weights between input layer and hidden layer + the number of weights between hidden layer and output layer + the number of translation factors + the number of expansion factors). The predicted values of each bird’s nest were calculated, and the nest which has the smallest error in the 20 nests is found, marked as Wbest. Then Wbest retain to the next generation.
- Train the SVM model by using the training set, and then input the test set data to obtain the predictive value of the cost data.
4. Example Analysis
4.1. Basic Data
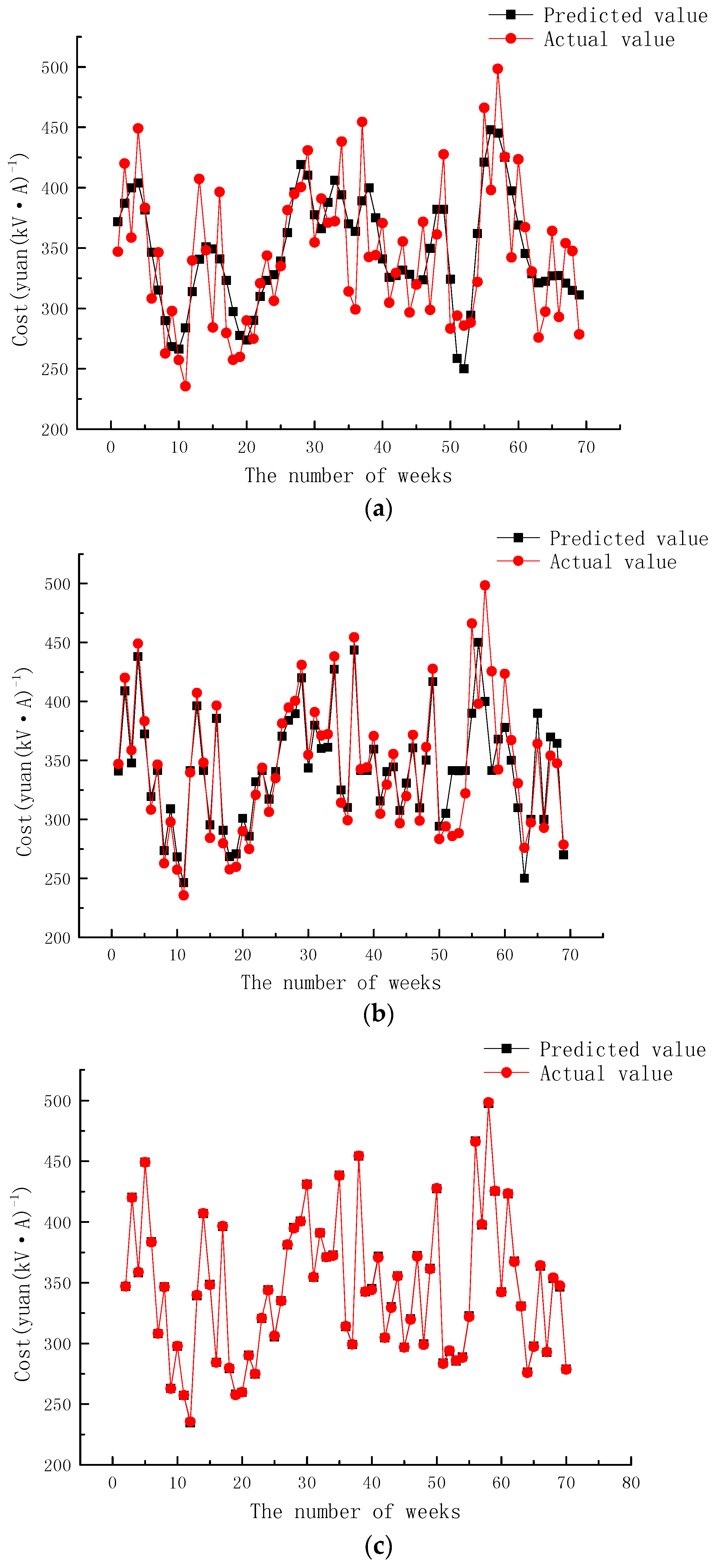
4.2. Results Analysis and Comparison
5. Conclusions
- (1)
- The EEMD-GCS-SVM model established in this paper can effectively improve the prediction accuracy of substation project cost with a MAPE value of only 0.13%, which is much better than that of the un-optimized and EEMD models.
- (2)
- EEMD method can decompose irregular and non-stationary sequence signals into multiple IMF components and surplus components. The decomposed signals show regularity and periodicity obviously, which improves the prediction accuracy of the model.
- (3)
- On the basis of CS optimized SVM parameters and kernel function, adding Gauss perturbation can effectively improve the search vitality and range of CS algorithm. The optimal SVM parameters are obtained, the calculation of kernel function is faster, and the computational efficiency and prediction accuracy is improved in the model.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Rao, R.; Zhang, X.; Shi, Z.; Luo, K.; Tan, Z.; Feng, Y. A Systematical Framework of Schedule Risk Management for Power Grid Engineering Projects’ Sustainable Development. Sustainability 2014, 6, 6872–6901. [Google Scholar] [CrossRef]
- Zhao, H.; Li, N. Risk Evaluation of a UHV Power Transmission Construction Project Based on a Cloud Model and FCE Method for Sustainability. Sustainability 2015, 7, 2885–2914. [Google Scholar] [CrossRef]
- Tao, Y.; Cui, S.; Ke, X. Forecasting Tendency of the Transmission Line Project Cost Index Using Markov Chain. Open Electr. Electron. Eng. J. 2014, 8, 56–63. [Google Scholar] [CrossRef]
- Zhu, J.; Yao, X.; Zhao, Z. Empirical Research on Cost Prediction Model of Technical Renovation for Electric Power Substation Project. Eng. Econ. 2017, 3, 5–9. [Google Scholar]
- Pei, Q.F.; Zhang, H.M.; Yang, Y.K. Study on the Management of Construction Cost in Substation Project. Adv. Mater. Res. 2014, 1030–1032, 2639–2642. [Google Scholar] [CrossRef]
- Jaleel, J.A.; Sadina, M.F. Reliability Evaluation of 220 kV Substation Using Fault Tree Method and Its Prediction Using Neural Networks. Environ. Manag. 2013, 54, 951–970. [Google Scholar]
- Ling, Y.; Yan, P.; Han, C.; Yang, C. Prediction model of transmission line engineering cost based on BP neural network. China Power 2012, 45, 95–99. [Google Scholar]
- Liu, W.; Shi, H.; Lu, Y.; Hua, F.; Qiu, J. Study on Grid Engineering Cost Index Forecasting Based on ARIMA-ES Hybrid Model. Manag. Rev. 2016, 28, 45–53. [Google Scholar]
- Niu, D.X.; Hua, F.Y. Research on Prediction of Transmission and Transformation Project Cost Index Based on ARIMA and Exponential Smoothing Models. In Proceedings of the 22nd International Conference on Industrial Engineering and Engineering Management 2015; Atlantis Press: Paris, France, 2016; pp. 771–779. [Google Scholar]
- Zhou, M.; Zhao, S.; Zhu, J. Index Evaluation System of Power Transmission Project Cost Based on Support Vector Machine Method. Electr. Power Constr. 2014, 35, 102–106. [Google Scholar]
- Huang, J. Substation project cost management and control measures. Sci. Res. 2016, 15, 00102–00103. [Google Scholar]
- Wang, N.N.; Wang, F.; Yin, Y.T.; Li, H.; Hou, Y. Research on Cost Predicting of Power Transformation Projects Based on SVM. Const. Econ. 2016, 37, 48–52. [Google Scholar]
- Song, Z.; Niu, D.; Xiao, X.; Zhu, L. Substation Engineering Cost Forecasting Method Based on Modified Firefly Algorithm and Support Vector Machine. Electr. Power 2017, 50, 168–173. [Google Scholar]
- Xu, J.W.; Moon, S. Stochastic Forecast of Construction Cost Index Using a Cointegrated Vector Autoregression Model. J. Manag. Eng. 2013, 29, 10–18. [Google Scholar] [CrossRef]
- Zhu, X.W.; Li, W.J. Prediction Model of Urban Real Estate Project Cost. Stats. Decis. 2010, 14, 47–49. [Google Scholar]
- Shahandashti, S.M.; Ashuri, B. Highway Construction Cost Forecasting Using Vector Error Correction Models. J. Manag. Eng. 2016, 32. [Google Scholar] [CrossRef]
- Qin, Z.F.; Lei, X.L.; Zhai, D.; Jin, L.Z. Forecasting the Costs of Residential Construction Based on Support Vector Machine and Least Squares-Support Vector Machine. J. Zhejiang Univ. Sci. A 2016, 43, 357–363. [Google Scholar]
- Zhou, J.Y.; Zhang, K.W. Cigarette Sales Forecasting Based on Hybrid Kernels Least Square Support Vector Machine Optimized by Modified Cuckoo Search Algorithm. Comput. Eng. Appl. 2015, 51, 250–254. [Google Scholar]
- Shao, Z.; Gao, F.; Yang, S.L.; Yu, B. A new semiparametric and EEMD based framework for mid-term electricity demand forecasting in China: Hidden characteristic extraction and probability density prediction. Renew. Sustain. Energy Rev. 2015, 52, 876–889. [Google Scholar] [CrossRef]
- Huang, Y.; Wu, D.; Zhang, Z.; Chen, H.; Chen, S. EMD-based pulsed TIG welding process porosity defect detection and defect diagnosis using GA-SVM. J. Mater. Process. Technol. 2017, 239, 92–102. [Google Scholar] [CrossRef]
- He, K.; Wang, H.; Du, J.; Zou, Y. Forecasting Electricity Market Risk Using Empirical Mode Decomposition (EMD)—Based Multiscale Methodology. Energies 2016, 9, 931. [Google Scholar] [CrossRef]
- Amjady, N.; Abedinia, O. Short Term Wind Power Prediction Based on Improved Kriging Interpolation, Empirical Mode Decomposition, and Closed-Loop Forecasting Engine. Sustainability 2017, 9, 2104. [Google Scholar] [CrossRef]
- Malik, H.; Sharma, R. EMD and ANN based intelligent fault diagnosis model for transmission line. J. Intell. Fuzzy Syst. 2017, 32, 3043–3050. [Google Scholar] [CrossRef]
- Acharya, U.R.; Fujita, H.; Sudarshan, V.K.; Oh, S.L.; Muhammad, A.; Koh, J.E.W.; Tan, J.H.; Chua, C.K.; Chua, K.P.; Tan, R.S. Application of empirical mode decomposition (EMD) for automated identification of congestive heart failure using heart rate signals. Neural Comput. Appl. 2016, 28, 3073–3094. [Google Scholar] [CrossRef]
- Helske, J.; Luukko, P. Ensemble Empirical Mode Decomposition (EEMD) and Its Complete Variant (CEEMDAN). Int. J. Public Health 2016, 60, 1–9. [Google Scholar]
- Lee, D.H.; Ahn, J.H.; Koh, B.H. Fault Detection of Bearing Systems through EEMD and Optimization Algorithm. Sensors 2017, 17, 2477. [Google Scholar] [CrossRef] [PubMed]
- Montalvo, C.; Gavilán-Moreno, C.J.; García-Berrocal, A. Cofrentes nuclear power plant instability analysis using ensemble empirical mode decomposition (EEMD). Ann. Nucl. Energy 2017, 101, 390–396. [Google Scholar] [CrossRef]
- Li, W.; Yang, X.; Li, H.; Su, L. Hybrid Forecasting Approach Based on GRNN Neural Network and SVR Machine for Electricity Demand Forecasting. Energies 2017, 10, 44. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Arabloo, M.; Ziaee, H.; Lee, M.; Bahadori, A. Prediction of the properties of brines using least squares support vector machine (LS-SVM) computational strategy. J. Taiwan Inst. Chem. Eng. 2015, 50, 123–130. [Google Scholar] [CrossRef]
- Fan, J.; Wu, J.; Kong, W.; Zhang, M.H. Predicting Bio-indicators of Aquatic Ecosystems Using the Support Vector Machine Model in the Taizi River, China. Sustainability 2017, 9, 892. [Google Scholar] [CrossRef]
- Liang, Y.; Niu, D.; Ye, M.; Hong, W.-C. Short-Term Load Forecasting Based on Wavelet Transform and Least Squares Support Vector Machine Optimized by Improved Cuckoo Search. Energies 2016, 9, 827. [Google Scholar] [CrossRef]
- Liu, J.-P.; Li, C.-L. The Short-Term Power Load Forecasting Based on Sperm Whale Algorithm and Wavelet Least Square Support Vector Machine with DWT-IR for Feature Selection. Sustainability 2017, 9, 1188. [Google Scholar] [CrossRef]
- Kachoosangi, F.T. How Reliable Are ANN, ANFIS, and SVM Techniques for Predicting Longitudinal Dispersion Coefficient in Natural Rivers? J. Hydraul. Eng. 2016, 142. [Google Scholar] [CrossRef]
- Giorgi, M.G.D.; Ficarella, A.; Lay-Ekuakille, A. Cavitation Regime Detection by LS-SVM and ANN with Wavelet Decomposition Based on Pressure Sensor Signals. IEEE Sens. 2015, 15, 5701–5708. [Google Scholar] [CrossRef]
- Tian, J.; Li, C.; Liu, J.; Yu, F.L.; Cheng, S.H.; Zhao, N.; Jaafar, W.Z.W. Groundwater Depth Prediction Using Data-Driven Models with the Assistance of Gamma Test. Sustainability 2016, 8, 1076. [Google Scholar] [CrossRef]
- Sun, W.; Sun, J. Daily PM2.5 concentration prediction based on principal component analysis and LSSVM optimized by cuckoo search algorithm. J. Environ. Manag. 2017, 188, 144–152. [Google Scholar] [CrossRef] [PubMed]
- Xiao, L.; Shao, W.; Yu, M.; Ma, J.; Jin, C. Research and application of a hybrid wavelet neural network model with the improved cuckoo search algorithm for electrical power system forecasting. Appl. Energy 2017, 198, 203–222. [Google Scholar] [CrossRef]
- Mellal, M.A.; Williams, E.J. Cuckoo optimization algorithm with penalty function for combined heat and power economic dispatch problem. Energy 2015, 93, 1711–1718. [Google Scholar] [CrossRef]
- Kaboli, S.H.A.; Selvaraj, J.; Rahim, N.A. Long-term electric energy consumption forecasting via artificial cooperative search algorithm. Energy 2016, 115, 857–871. [Google Scholar] [CrossRef]
- Makhloufi, S.; Mekhaldi, A.; Teguar, M. Three powerful nature-inspired algorithms to optimize power flow in Algeria’s Adrar power system. Energy 2016, 116, 1117–1130. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, C.; Wu, J. Wind Energy Potential Assessment and Forecasting Research Based on the Data Pre-Processing Technique and Swarm Intelligent Optimization Algorithms. Sustainability 2016, 8, 1191. [Google Scholar] [CrossRef]
- Cai, X.; Nan, X.; Gao, B. Application of SVM Optimized ICS in Fault Diagnosis of Analog Circuit. Bull. Sci. Technol. 2017, 33, 79–82. [Google Scholar]
- Zheng, H.; Zhou, Y. A novel Cuckoo Search optimization algorithm base on gauss distribution. J. Comput. Inf. Syst. 2012, 8, 4193–4200. [Google Scholar]
- Lai, J.; Liang, S.; Center, C. Application of GCS-SVM model in network traffic prediction. Comput. Eng. Appl. 2013, 49, 75–78. [Google Scholar]

| Serial Number | Cost (Yuan/kV·A) | Serial Number | Cost (Yuan/kV·A) | Serial Number | Cost (Yuan/kV·A) | Serial Number | Cost (Yuan/kV·A) |
|---|---|---|---|---|---|---|---|
| 1 | 284.22 | 19 | 396.62 | 37 | 438.26 | 55 | 285.86 |
| 2 | 337.44 | 20 | 279.78 | 38 | 314.15 | 56 | 288.38 |
| 3 | 369.32 | 21 | 257.53 | 39 | 299.14 | 57 | 321.98 |
| 4 | 347.03 | 22 | 259.8 | 40 | 454.53 | 58 | 466.19 |
| 5 | 419.99 | 23 | 290.07 | 41 | 342.54 | 59 | 398.09 |
| 6 | 358.64 | 24 | 275 | 42 | 344.12 | 60 | 498.41 |
| 7 | 449.02 | 25 | 320.91 | 43 | 370.65 | 61 | 425.52 |
| 8 | 383.35 | 26 | 343.77 | 44 | 304.73 | 62 | 342.21 |
| 9 | 308.3 | 27 | 306.23 | 45 | 329.5 | 63 | 423.47 |
| 10 | 346.53 | 28 | 335 | 46 | 355.37 | 64 | 367.21 |
| 11 | 262.64 | 29 | 381.5 | 47 | 296.73 | 65 | 330.49 |
| 12 | 297.97 | 30 | 394.85 | 48 | 319.74 | 66 | 275.96 |
| 13 | 257.35 | 31 | 400.6 | 49 | 371.6 | 67 | 297.36 |
| 14 | 235.51 | 32 | 430.9 | 50 | 298.83 | 68 | 364.17 |
| 15 | 339.83 | 33 | 354.63 | 51 | 361.29 | 69 | 292.85 |
| 16 | 407.24 | 34 | 390.91 | 52 | 427.77 | 70 | 354.06 |
| 17 | 348.25 | 35 | 371.08 | 53 | 283.38 | 71 | 347.54 |
| 18 | 284.35 | 36 | 372.2 | 54 | 294.15 | 72 | 278.54 |
| Model | BP | SVM | GCS-SVM | EEMD-CS-SVM | EEMD-GCS-SVM |
|---|---|---|---|---|---|
| RMSE (yuan/kV·A) | 78.47 | 53.45 | 24.76 | 36.02 | 0.51 |
| MAE (yuan/kV·A) | 57.85 | 42.10 | 16.71 | 31.38 | 0.43 |
| MAPE | 16.42% | 12.36% | 4.72% | 9.28% | 0.13% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niu, D.; Zhao, W.; Li, S.; Chen, R. Cost Forecasting of Substation Projects Based on Cuckoo Search Algorithm and Support Vector Machines. Sustainability 2018, 10, 118. https://doi.org/10.3390/su10010118
Niu D, Zhao W, Li S, Chen R. Cost Forecasting of Substation Projects Based on Cuckoo Search Algorithm and Support Vector Machines. Sustainability. 2018; 10(1):118. https://doi.org/10.3390/su10010118
Chicago/Turabian StyleNiu, Dongxiao, Weibo Zhao, Si Li, and Rongjun Chen. 2018. "Cost Forecasting of Substation Projects Based on Cuckoo Search Algorithm and Support Vector Machines" Sustainability 10, no. 1: 118. https://doi.org/10.3390/su10010118
APA StyleNiu, D., Zhao, W., Li, S., & Chen, R. (2018). Cost Forecasting of Substation Projects Based on Cuckoo Search Algorithm and Support Vector Machines. Sustainability, 10(1), 118. https://doi.org/10.3390/su10010118





