Path Tracking of Autonomous Vehicle Based on Optimal Control
Abstract
:1. Introduction
2. Vehicle Model
2.1. Mathematical Model of Vehicle
2.2. Optimal Control Object
2.3. Constraints
3. Adaptive Pseudospectral Method
3.1. Multiple Phase Adaptive Radau Pseudospectral Method
3.2. Adaptive Collocation Point Method
3.3. Calculation Process of Multi-Interval Radau Pseudospectral Method
- Step (1). Dividing the entire time into K subintervals, each subinterval being .
- Step (2). Transforming the optimal control problem into an NLP problem using LGR collocation points for solution.
- Step (3). Calculating for each subinterval using Equation (19). If , the available result is obtained; otherwise, proceeding to Step (4).
- Step (4). Using Equation (20) to increase the order of the polynomial within each sub-interval; using Equation (21) to update the number of collocation points and interval numbers within each subinterval.
- Step (5). Repeating step (2).
4. Result Analysis
4.1. Numerical Simulations
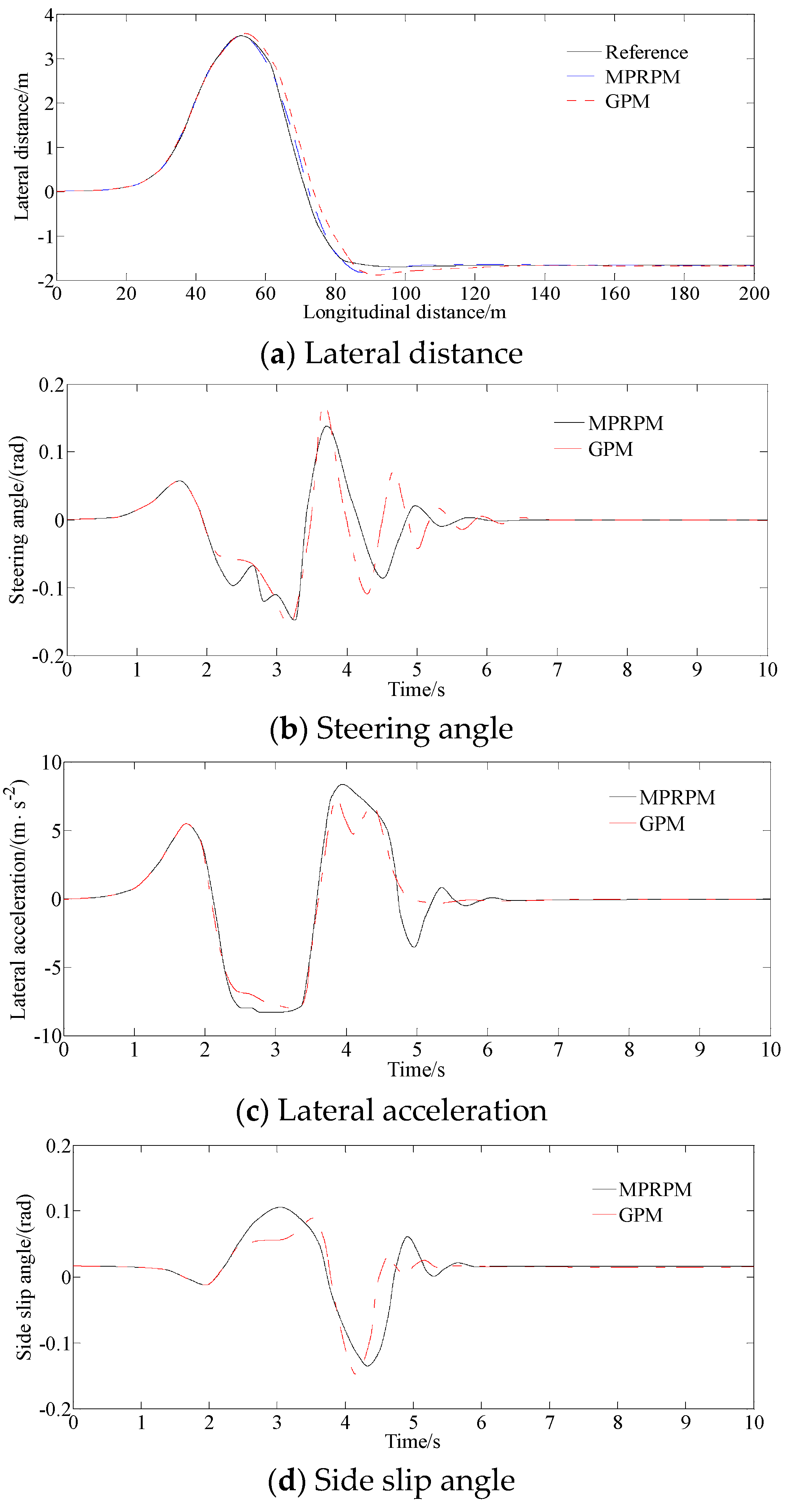
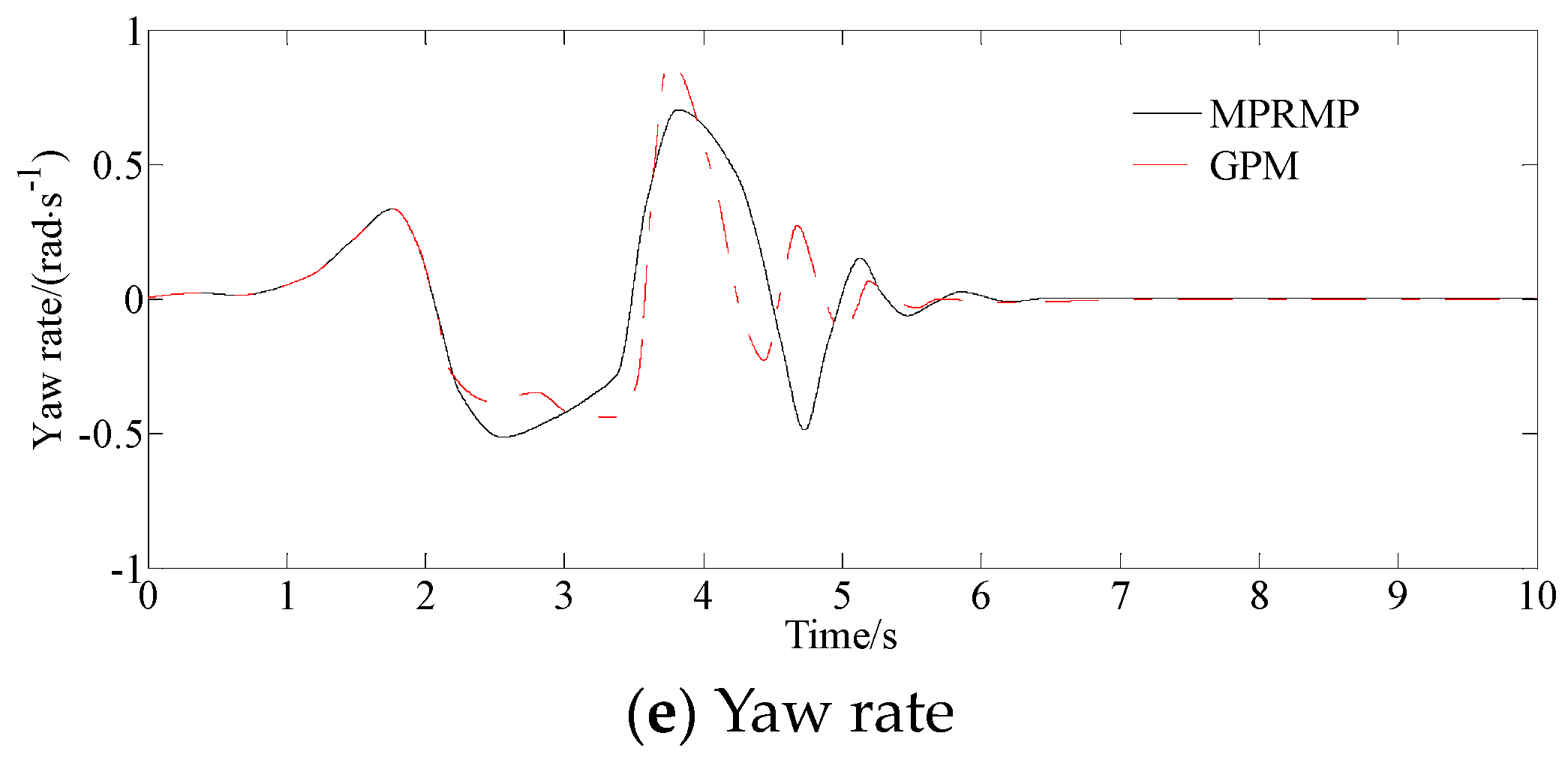
4.1.1. Double Lane Changing Road
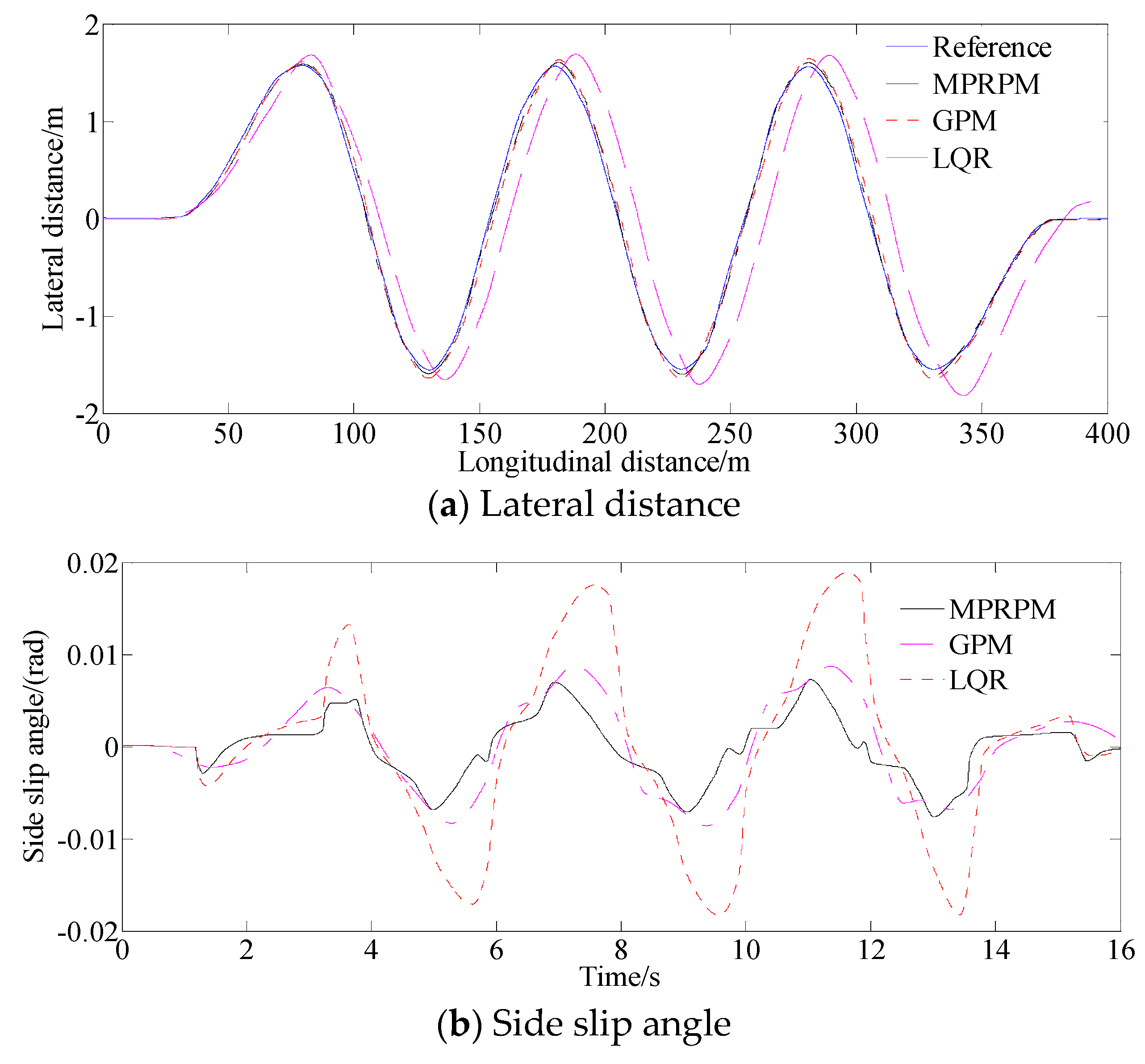
4.1.2. Serpentine Road
4.2. Analysis of Control Performance
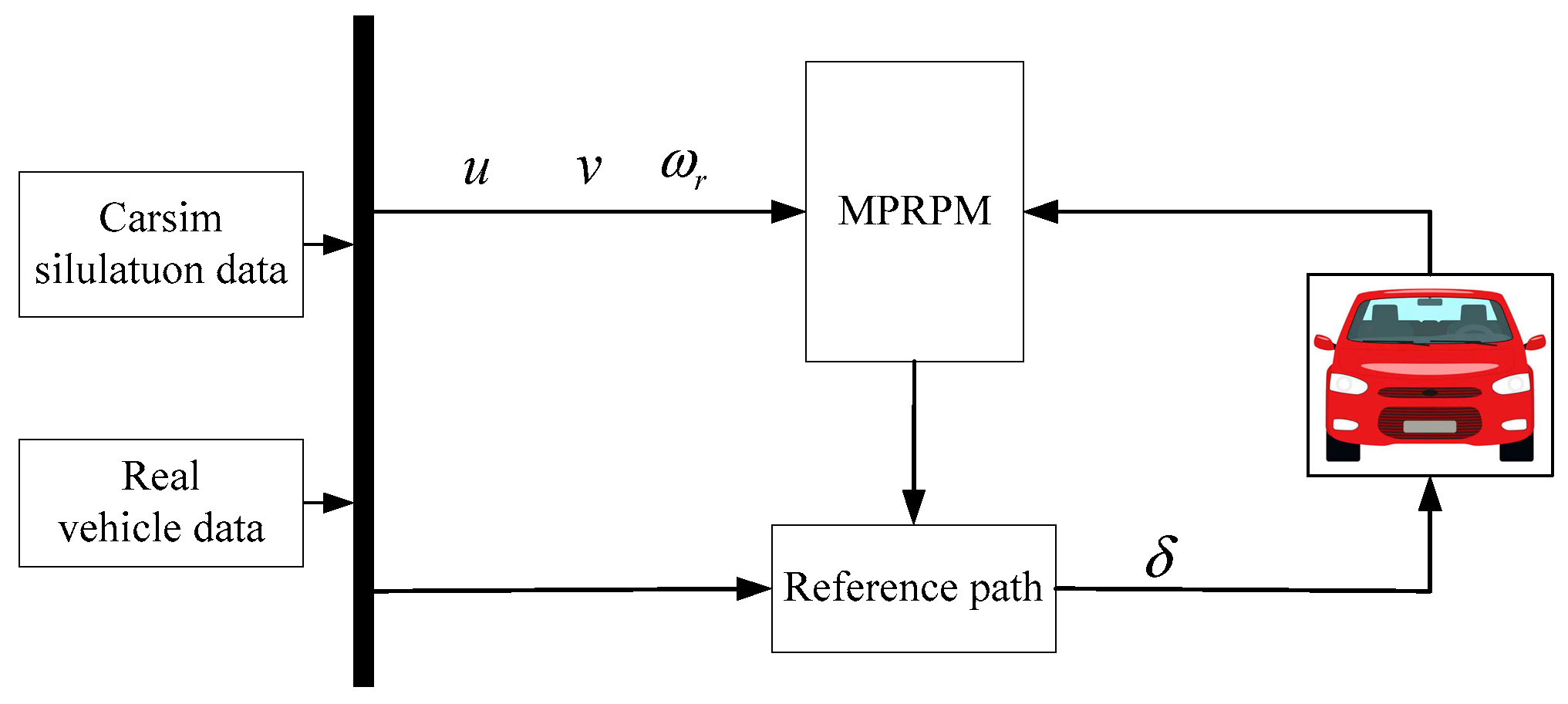
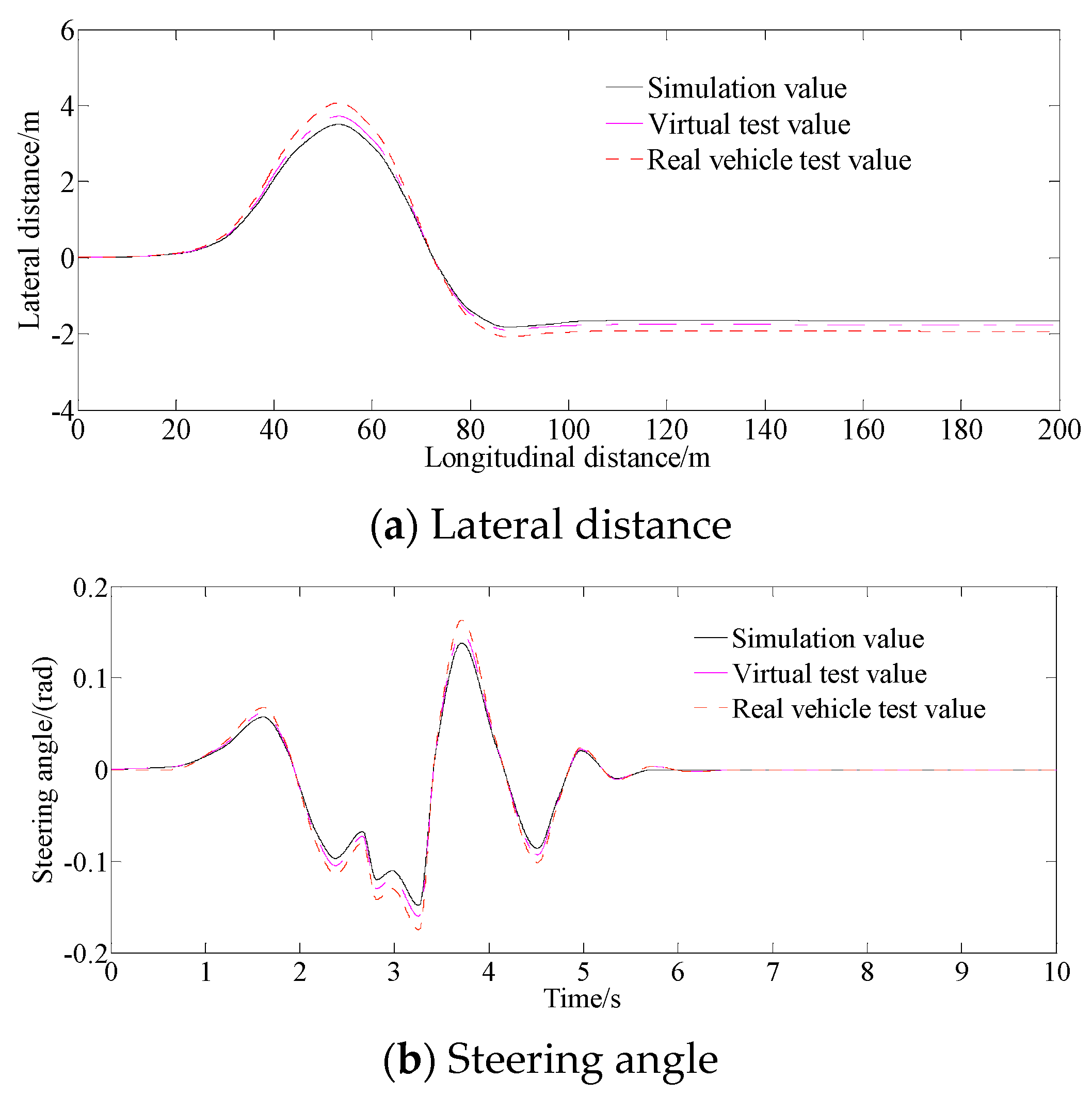
4.3. Experimental Verification
4.4. Summary of Different Path Tracking Methods
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| RPM | Radau pseudospectral method; |
| MPRPM | multiple phase Radau pseudospectral method; |
| GPM | Gaussian pseudospectral method; |
| LQR | linear quadratic regulator; |
| KKT | Karush Kuhn Tucker; |
| NLP | nonlinear programming; |
| LGR | Legendre–Gauss–Radau; |
| m (kg) | vehicle mass; |
| Iz (kg∙m2) | moment of inertia around the z axis; |
| a (m) | distances of front axle from the center of gravity; |
| b (m) | distances of rear axle from the center of gravity; |
| k1 (N∙rad−1) | synthesized stiffness of front tire; |
| k2 (N∙rad−1) | synthesized stiffness of rear tire; |
| i | transmission ratio of the steering system; |
| Iw (kg·m2) | moment of inertia of the steering system; |
| drag coefficient; | |
| synthesized cornering stiffness; | |
| front wheel aligning arm of force; | |
| hg (m) | height of the center gravity. |
References
- Liu, Y.J.; Cui, D.W.; Peng, W. Optimum Control for Path Tracking Problem of Vehicle Handling Inverse Dynamics. Sensors 2023, 23, 6673. [Google Scholar] [CrossRef]
- Liu, Y.J.; Cui, D.W. Estimation algorithm for vehicle state estimation using ant lion optimization algorithm. Adv. Mech. Eng. 2022, 14, 16878132221085839. [Google Scholar] [CrossRef]
- Liu, Y.J.; Cui, D.W.; Peng, W. Optimal Lane Changing Problem of Vehicle Handling Inverse Dynamics Based on Mesh Refinement Method. IEEE Access 2023, 11, 115617–115626. [Google Scholar] [CrossRef]
- Hwang, C.L.; Yang, C.C.; Hung, J.Y. Path tracking of an autonomous ground vehicle with different payloads by hierarchical improved fuzzy dynamic sliding-mode control. IEEE Trans. Fuzzy Syst. 2018, 26, 899–914. [Google Scholar] [CrossRef]
- Yu, R.; Ding, S.; Tian, H.; Chen, Y.H. A hierarchical constraint approach for dynamic modeling and trajectory tracking control of a mobile robot. J. Vib. Control. 2022, 28, 564–576. [Google Scholar] [CrossRef]
- Yin, H.; Chen, Y.H.; Huang, J.; Lü, H. Tackling mismatched uncertainty in robust constraint-following control of underactuated systems. Inf. Sci. 2020, 520, 337–352. [Google Scholar] [CrossRef]
- Wu, Y.; Wang, L.; Zhang, J.; Li, F. Path following control of autonomous ground vehicle based on nonsingular terminal sliding mode and active disturbance rejection control. IEEE Trans. Veh. Technol. 2019, 68, 6379–6390. [Google Scholar] [CrossRef]
- Imine, H.; Madani, T. Sliding-mode control for automated lane guidance of heavy vehicle. Int. J. Robust Nonlinear Control. 2013, 23, 67–76. [Google Scholar] [CrossRef]
- Han, Y.X.; Cheng, Y.; Xu, G.W. Trajectory tracking control of AGV based on sliding mode control with the improved reaching law. IEEE Access 2019, 7, 20748–20755. [Google Scholar] [CrossRef]
- Sabiha, A.D.; Kamel, M.A.; Said, E.; Hussein, W.M. ROS-based trajectory tracking control for autonomous tracked vehicle using optimized backstepping and sliding mode control. Robot. Auton. Syst. 2022, 152, 104058. [Google Scholar] [CrossRef]
- Zhang, S.W.; Ma, L.; Li, Q.; Wang, H. Observer-based adaptive path tracking control for autonomous ground vehicle with singularities and time-varying delays. J. Mech. Sci. Technol. 2025, 39, 1443–1456. [Google Scholar] [CrossRef]
- Dekhterman, S.R.; Norris, W.R.; Nottage, D.; Soylemezoglu, A. Hierarchical Rule-Base Reduction Fuzzy Control for Path Tracking Variable Linear Speed Differential Steer Vehicles. IEEE Trans. Fuzzy Syst. 2025, 33, 828–841. [Google Scholar] [CrossRef]
- Zhou, X.; Wang, H.; Li, Q.; Wu, L. Adaptive path tracking control for autonomous vehicles with sideslip effects and unknown input delays. Trans. Inst. Meas. Control. 2025, 47, 444–453. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, Y.; Li, G.; Wang, Y. Path tracking control of autonomous vehicles via prescribed performance approach. Neural Comput. Appl. 2025, 37, 3839–3856. [Google Scholar] [CrossRef]
- Xu, D.H.; Xu, G.J.; Ye, S.X.; Wu, X.F.; Tang, D.J. Nonlinear Closed-loop Optimal Ascent Guidance for Aerospace Vehicle Based on Pseudospectral Method. Tactical Missile Technol. 2017, 4, 57–65. [Google Scholar]
- Hu, S.Q.; Chen, Y. Analysis of pseudospectral methods applied to aircraft trajectory optimization. J. Rocket. Propuls. 2014, 40, 61–68. [Google Scholar]
- Liu, Y.J.; Cui, D.W. Optimal Control of Vehicle Path Tracking Problem. World Electr. Veh. J. 2024, 15, 429. [Google Scholar] [CrossRef]
- Chen, T.T.; Sun, C.Z. Flight Corridor Planning Method of RBCC Ascent. Ordnance Ind. Autom. 2019, 38, 50–53. [Google Scholar]
- Benson, D. A Gauss Pseudospectral Transcription for Optimal Control. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2004. [Google Scholar]
- Huntington, G.T.; Rao, A.V. Optimal reconfiguration of spacecraft formation using the Gauss pseudospectral method. AIAA J. Guid. Control. Dyn. 2008, 31, 689–698. [Google Scholar] [CrossRef]
- Garg, D.; William, W.H.; Rao, A.V. Gauss pseudospectral method for solving infinite-horizon optimal control problems. In Proceedings of the AIAA Guidance Navigation Control Conference, AIAA, Toronto, ON, Canada, 2–5 August 2010; pp. 1011–1020. [Google Scholar]
- Mei, J.; Ma, G.F.; Yang, B. Fuel-optimal control of satellite relative orbit transfer based on legendre pseudospectral method. J. Harbin Inst. Technol. 2010, 42, 352–357. [Google Scholar]
- Betts, J.T. Practical methods for optimal control and estimation using nonlinear programming. Appl. Mech. Rev. 2002, 55, 1–449. [Google Scholar] [CrossRef]
- Yan, C.X.; Tong, Y.A.; Song, J.H.; Lu, B.G.; Zhao, L.B. Optimization of Trajectory with Terminal Constraints Based on Multiple Phase Radau Pseudospectral Method. Tactical Missile Technol. 2021, 2, 94–100. [Google Scholar]
- Geoffrey, T.; Huntington; Rao, A.V. Optimal Configuration of Spacecraft Formations Via A Gauss Pseudospectral Method. Adv. Astronaut. Sci. 2005, 120, 33–50. [Google Scholar]
- Benson, D.A.; Huntington, G.T.; Thorvaldsen, T.P.; Rao, A.V. Direct Trajectory Optimization and Costate Estimation via an Orthogonal Collocation Method. J. Guid. Control. Dyn. 2006, 29, 1435–1440. [Google Scholar] [CrossRef]





| Parameter | Value |
|---|---|
| m (kg) | 1265 |
| Iz (kg·m2) | 1800 |
| a (m) | 1.170 |
| b (m) | 1.195 |
| k1 (N·rad−1) | 60,042 |
| k2 (N·rad−1) | 109,295 |
| i | 20 |
| Iw (kg·m2) | 16.38 |
| 140 | |
| 0 | |
| 0.021 | |
| hg (m) | 0.53 |
| Algorithms | Mean of Absolute Error of Path Tracking(m) | Advantages | Disadvantages |
|---|---|---|---|
| MPRPM | 0.075 | The MPRPM utilizes Gauss integration to configure differential algebraic equations at discrete points, resulting in higher computational efficiency. Meanwhile, the MPRPM exhibits good convergence. | For large-scale or multi- interval problems, the MPRPM may require significant computational resources and time, especially when performing high-precision calculations. |
| GPM | 0.029 | The GPM has the characteristics of high computational accuracy, good stability, and wide applicability. When dealing with complex constraint conditions, GPM remains efficient and can generate smooth and constraint compliant paths. | In some cases, GPM may be sensitive to initial conditions. And improper selection of initial conditions may lead to convergence problems or suboptimal solutions. |
| LQR | 0.05 | LQR can obtain the optimal control law of state linear feedback, which makes it easy to form closed-loop optimal control, thereby achieving system stability and performance optimization. | The performance of LQR is highly sensitive to the selection of weight matrices Q and R, and improper parameter selection may lead to system performance degradation or instability. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, B.; Liu, Y.; Wang, Q. Path Tracking of Autonomous Vehicle Based on Optimal Control. World Electr. Veh. J. 2025, 16, 340. https://doi.org/10.3390/wevj16070340
Wu B, Liu Y, Wang Q. Path Tracking of Autonomous Vehicle Based on Optimal Control. World Electric Vehicle Journal. 2025; 16(7):340. https://doi.org/10.3390/wevj16070340
Chicago/Turabian StyleWu, Bingshuai, Yingjie Liu, and Qianqian Wang. 2025. "Path Tracking of Autonomous Vehicle Based on Optimal Control" World Electric Vehicle Journal 16, no. 7: 340. https://doi.org/10.3390/wevj16070340
APA StyleWu, B., Liu, Y., & Wang, Q. (2025). Path Tracking of Autonomous Vehicle Based on Optimal Control. World Electric Vehicle Journal, 16(7), 340. https://doi.org/10.3390/wevj16070340





