PMSM Position Sensorless Control Based on Improved Second-Order SOIFO

Abstract

Due to detection errors, motor parameter deviations, and other uncertainties, traditional motor flux estimation models suffer from the complications of DC bias and high-order harmonics. To address these issues, two flux observers, the second-order generalized integrator flux observer (SOIFO) and the second-order SOIFO, are designed for position sensorless control of permanent magnet synchronous motors (PMSMs). The position sensorless control of PMSMs based on an improved second-order SOIFO is proposed in this paper. The proposed method enhances the frequency-locked loop (FLL) in the observer by introducing a double-axis frequency-locked loop (DFLL), which improves the dynamic performance and disturbance rejection capability of the flux observer. By replacing FLL with DFLL for angular frequency estimation, the method effectively eliminates second-harmonic interference while reducing estimation delays, leading to faster and more accurate rotor position estimation in the second-order SOIFO. Additionally, the improved observer demonstrates enhanced robustness against disturbances, ensuring more stable position sensorless control. The effectiveness of the proposed approach is validated through both simulations and experimental comparisons.

1. Introduction

Permanent magnet synchronous motors (PMSMs) are widely used in electrical vehicles (EVs), industrial applications, and rail transit because of their high reliability, high efficiency and high power density [1]. Accurate speed control typically requires a position sensor mounted on the motor shaft to obtain position information. However, in practical industrial applications, position sensors increase both cost and mechanical complexity. To address these challenges and enhance motor control performance, position sensorless control technology has gained significant attention for its ability to operate without a position sensor.

Sensorless control methods can be broadly classified into the model-based control method and the signal injection control method [2], which are suitable for medium-to-high-speed ranges and low-speed ranges, respectively. In model-based methods, back electromotive force (back EMF) [3], extended back EMF [4,5,6,7], and rotor flux [8,9,10,11] are commonly used as estimation variables. Rotor flux estimation has the advantage of being independent of speed, giving it a theoretically broader operating range compared to back EMF or extended back EMF estimation. Rotor flux estimation methods are typically divided into observer-based approaches, where flux is estimated using an observer, and integration-based approaches, where flux is obtained by integrating the back EMF. The integration method is simple and practical, and has been widely studied in recent years. However, pure integration has limitations, due to the presence of the integral initial value and initial phase drift. In [12,13], various low-pass filters are used instead of pure integrators. In these low-pass filters, DC bias can decay exponentially with time, but it will cause fundamental phase delay and amplitude attenuation [14]. The second-order generalized integrator (SOIFO) proposed in [15] has no phase delay and amplitude attenuation, and can also suppress high-order harmonics. However, the DC bias is inversely proportional to the speed and cannot be completely eliminated. In recent years, compared with the traditional flux observer, the second-order SOIFO proposed in [16] can completely eliminate the negative effects caused by DC bias and it demonstrates excellent performance in eliminating high-order harmonics existing in the back EMF.

In the conventional second-order SOIFO, the frequency-locked loop (FLL) is used to track the estimated angular frequency. However, it introduces a second harmonic component, causing estimation delays and reducing the observer’s resistance to disturbances. To address this issue, a double-axis frequency-locked loop (DFLL) is introduced to eliminate the second harmonic influence. By using DFLL instead of FLL, the system achieves faster frequency and angle estimation, improving response speed and overall performance. In addition, to ensure practical implementation in a digital system, the transfer function is discretized using the bilinear transform and applied in experiments. Finally, both simulations and experimental results confirm the effectiveness of the proposed method.

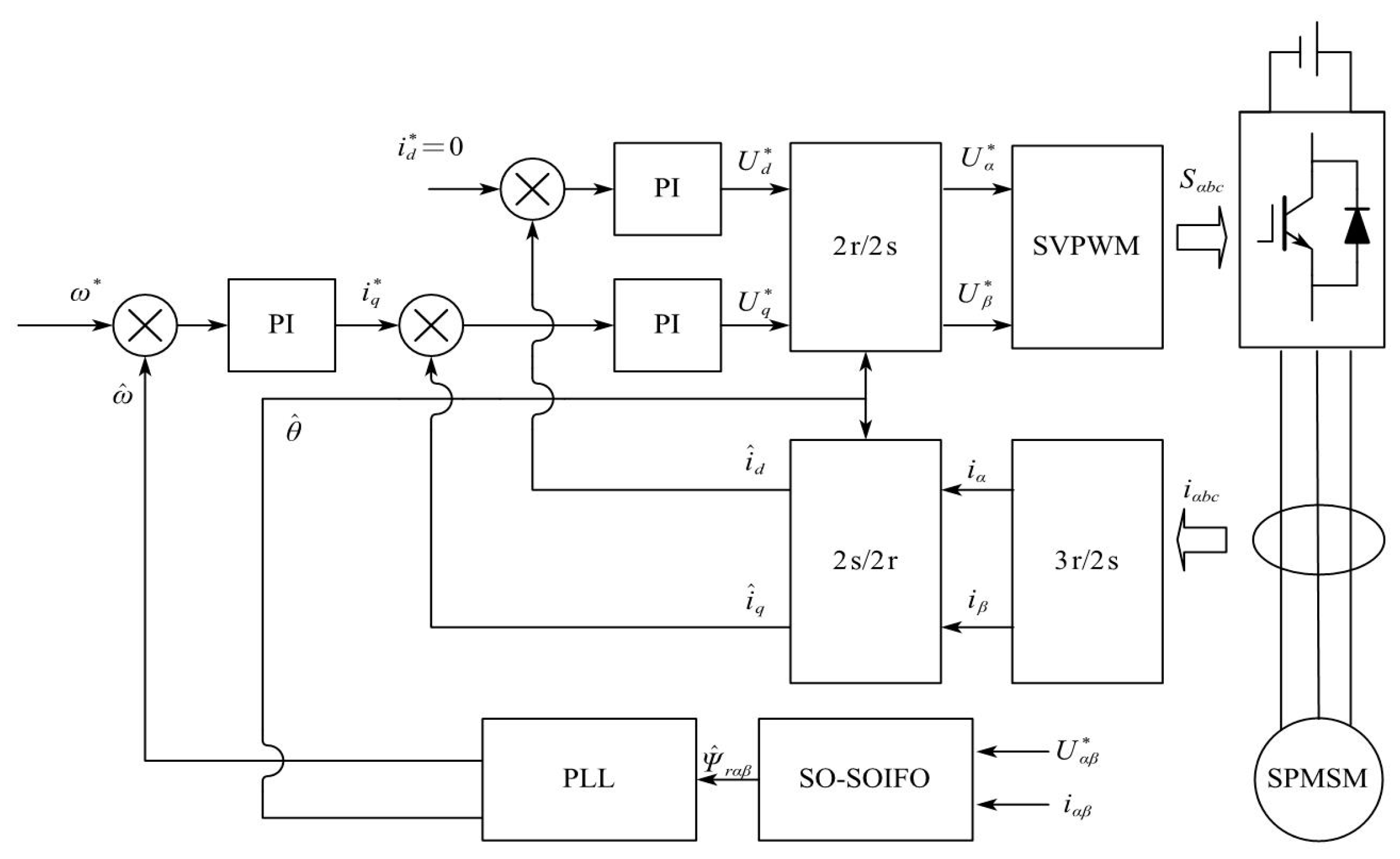
2. Analysis of Proposed Sensorless PMSM Control

2.1. PMSM Mathematical Model

The mathematical expression of surface-mounted PMSMs (SPMSMs) in the $\alpha$ − $\beta$ axis is as follows:

$$\left[\begin{array}{l}{u}_{\alpha }\\ u_{\beta }\end{array}\right]=\left[\begin{array}{cc}{R}_s+pL& 0\\ 0& R_s+pL\end{array}\right]\left[\begin{array}{l}{i}_{\alpha }\\ i_{\beta }\end{array}\right]+p\left[\begin{array}{l}{\psi }_{r\alpha }\\ {\psi }_{r\beta }\end{array}\right]$$

(1)

$$\left[\begin{array}{l}{\psi }_{r\alpha }\\ {\psi }_{r\beta }\end{array}\right]={\psi }_f\left[\begin{array}{l}\cos \left({\theta }_e\right)\\ \sin \left({\theta }_e\right)\end{array}\right]$$

(2)

$$p{\theta }_e={\omega }_e$$

(3)

where $u_{\alpha },u_{\beta }{,i}_{\alpha },i_{\beta },R_s,L$ are the stator voltage in the $\alpha$ – $\beta$ axis, the stator current in the $\alpha$ − $\beta$ axis, the stator resistance, and the stator inductance, respectively, ${\psi }_{r\alpha },{\psi }_{r\beta }$ are the stator flux, ${\psi }_f$ is the flux linkage, $p$ is the differential operator, and ${\omega }_e,{\theta }_e$ are the rotor electrical angular velocity and the rotor electrical position.

As shown in (1), the rotor flux is the integration of back EMF, which can be given as

$$\left[\begin{array}{l}{\psi }_{r\alpha }\\ {\psi }_{r\beta }\end{array}\right]={\displaystyle \int \left(\left[\begin{array}{l}{u}_{\alpha }\\ u_{\beta }\end{array}\right]-\left[\begin{array}{cc}{R}_s+pL& 0\\ 0& R_s+pL\end{array}\right]\left[\begin{array}{l}{i}_{\alpha }\\ i_{\beta }\end{array}\right]\right)}dt={\displaystyle \int \left(\left[\begin{array}{l}{E}_{r\alpha }\\ E_{r\beta }\end{array}\right]\right)}dt$$

(4)

$$\left[\begin{array}{l}{E}_{r\alpha }\\ E_{r\beta }\end{array}\right]={\omega }_e{\psi }_f\left[\begin{array}{l}-\sin \left({\theta }_e\right)\\ \cos \left({\theta }_e\right)\end{array}\right]$$

(5)

where $E_{r\alpha },E_{r\beta }$ are the back EMF of the motor in the $\alpha$ – $\beta$ axis.

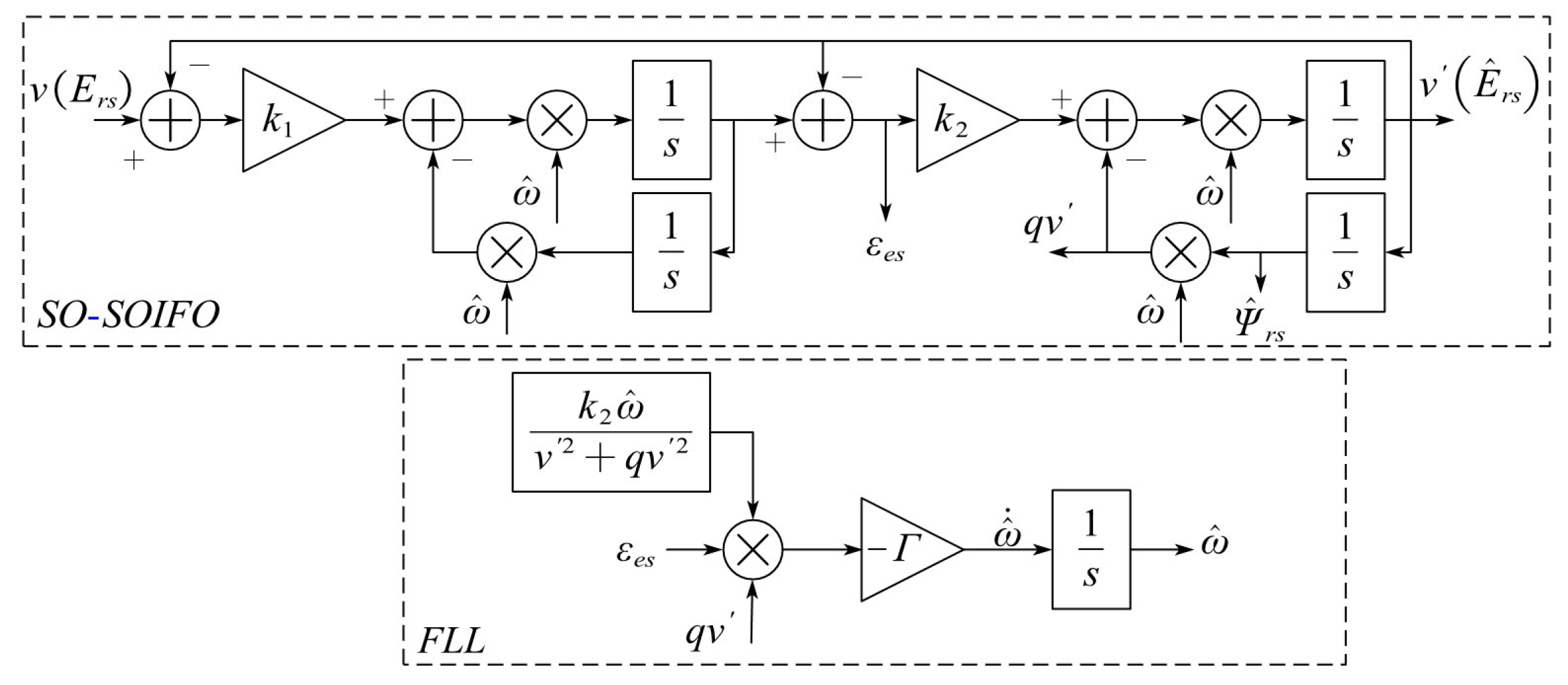
2.2. Second-Order SOIFO

Although the rotor flux can be obtained from (4), the pure integrator introduces DC bias, causing the rotor flux to drift. In addition, the nonlinear characteristics of the inverter, sampling error of the current and voltage, zero drift of the sensor, temperature change, and other problems will make the flux estimation more inaccurate. To better analyze these issues, the actual back EMF can be expressed as follows:

$$E_{rs}=(u_s+\Delta u_s)-((R_{s0}+\Delta R_s)+p(L_0+\Delta L))(i_s+\Delta i_s)+E_{rs0}+{\delta }_s$$

(6)

where “s” represents $\alpha$ or $\beta$, $\Delta u_s,\Delta i_s$ are the stator voltage error and the stator current error, respectively. $\Delta L,\Delta R_s$ is the error of the motor’s parameter. $E_{rs0}$ is the initial back EMF. ${\delta }_s$ are the other disturbances. In the form of DC bias, fundamental and harmonic components (6) can be described as

$$E_{rs}(t)=A_0+A_1\sin ({\omega }_{1}t+{\theta }_1)+{\displaystyle \sum _{h=2}^{\infty }{A}_h\sin }({\omega }_{h}t+{\theta }_h)$$

(7)

where ${\omega }_1,{\omega }_h$ are the fundamental angular frequency and the harmonic angular frequency, respectively. $A_0,A_1,A_h$ are the amplitude of the DC component, the amplitude of the fundamental wave, and the amplitude of the high-order harmonic wave, respectively. ${\theta }_1,{\theta }_h$ are the initial phase angle of the fundamental wave and the initial phase angle of the high-order harmonic wave, respectively.

The Laplace transformation of (7) can be expressed as

$$E_{rs}(s)={\displaystyle \frac{A_0}{s}}+A_1{\displaystyle \frac{s\sin {\theta }_1+{\omega }_1\cos {\theta }_1}{s^2+{\omega }_1^2}}+{\displaystyle \sum _{i=2}^{\infty }{A}_h\frac{s\sin {\theta }_h+{\omega }_h\cos {\theta }_h}{s^2+{\omega }_h^2}}$$

(8)

where $E_{rs}(s)$ is the Laplace transform of $E_{rs}(t)$.

If the back EMF is directly integrated, the estimated rotor flux $E_{rs}(s)·1/s$ is given as

$$\begin{array}{cc}\hfill {\psi }_{rs\_I}(t)& =L^{-1}\left\{\left.{\displaystyle \frac{E_{rs}(s)}{s}}\right\}\right.\hfill \\ & =A_{0}t+A_1{\displaystyle \frac{\cos {\theta }_1}{{\omega }_1}}+{\displaystyle \sum _{h=2}^{\infty }{A}_h}{\displaystyle \frac{\cos {\theta }_h}{{\omega }_h}}+{\displaystyle \frac{A_1}{{\omega }_1}}\sin ({\omega }_{1}t+{\theta }_1-{\displaystyle \frac{\pi }{2}})+{\displaystyle \sum _{h=2}^{\infty }\frac{A_h}{{\omega }_h}\sin ({\omega }_{1}t+{\theta }_h-\frac{\pi }{2})}\hfill \end{array}$$

(9)

In (9), due to the presence of the integral initial value $A_{0}t$, the rotor flux will increase with time and eventually saturate, making it difficult for position sensorless control to accurately estimate the motor’s electrical angle and speed. Moreover, under low-speed conditions, the harmonic amplitude ${\displaystyle \frac{A_h}{{\omega }_h}}$ will also increase, leading to inaccurate position estimation.

To eliminate DC bias and high-order harmonics in the back EMF of PMSM, the second-order SOIFO is proposed in [16]. The basic structure of the second-order SOIFO is shown in Figure 1, which consists of two parts: the second-order SOIFO and FLL. $v$ is the input signal, but also the actual back EMF, $v^{\prime }$ is the estimation of the input signal, but also the estimated back EMF, ${\epsilon }_{es}$ is the synchronous error, $q{v}^{\prime }$ is the orthogonal quantity of $v^{\prime }$, $\widehat{\omega }$ is the synchronous estimation of the angular frequency, but also the center frequency of the observer, ${\widehat{\psi }}_{rs}$ is the estimation of the rotor flux linkage, $k_1,k_2$ are the gain coefficient of second-order SOIFO, and $\Gamma$ is the gain coefficient of FLL.

In order to analyze the influence of FLL and facilitate its application in discrete systems, this paper gives the transfer functions of the estimation of input signal and input signal, the orthogonal quantity of input signal and input signal, and synchronization error and input signal as follows

$$D(s)={\displaystyle \frac{v^{\prime }(s)}{v(s)}}={\displaystyle \frac{k_1{k}_2{\widehat{\omega }}^2{s}^2}{s^4+k_2\widehat{\omega }{s}^3+(2+k_1{k}_2){\widehat{\omega }}^2{s}^2+k_2{\widehat{\omega }}^{3}s+{\widehat{\omega }}^4}}$$

(10)

$$Q(s)={\displaystyle \frac{q{v}^{\prime }(s)}{v(s)}}={\displaystyle \frac{k_1{k}_2{\widehat{\omega }}^{3}s}{s^4+k_2\widehat{\omega }{s}^3+(2+k_1{k}_2){\widehat{\omega }}^2{s}^2+k_2{\widehat{\omega }}^{3}s+{\widehat{\omega }}^4}}$$

(11)

$$E(s)={\displaystyle \frac{{\epsilon }_{es}(s)}{v(s)}}={\displaystyle \frac{k_1\widehat{\omega }s(s^2+{\widehat{\omega }}^2)}{s^4+k_2\widehat{\omega }{s}^3+(2+k_1{k}_2){\widehat{\omega }}^2{s}^2+k_2{\widehat{\omega }}^{3}s+{\widehat{\omega }}^4}}$$

(12)

In the steady state, it is defined that $s=j\widehat{\omega }$, ${\widehat{\psi }}_{\mathrm{rs}}={\displaystyle \frac{q{v}^{\prime }}{\widehat{\omega }}}$, $v=E_{rs}$; thus, (11) can be expressed as

$${\widehat{\psi }}_{\mathrm{rs}}={\displaystyle \frac{1}{s}}{E}_{rs}$$

(13)

In the steady state, the estimated flux linkage is the integral of back EMF, which is the real flux linkage, so the flux linkage observation can be realized. In order to ensure that the center frequency is synchronized with the fundamental frequency of back EMF, FLL is introduced to estimate the frequency.

2.3. Improved Second-Order SOIFO

2.3.1. Analysis of FLL

In (5), the input signal $v(s)$ can be expressed as

$$v\left(t\right)=A\cos (\omega t+\phi )=A\cos (\theta )$$

(14)

where $A,\omega ,\phi ,\theta$ are the amplitude, angular frequency, initial phase angle, and phase angle of the input signal, respectively. Thus, the output signal $v^{\prime }$ and $q{v}^{\prime }$ can be described as

$$\left\{\begin{array}{l}{v}^{\prime }=\widehat{A}\cos \left(\widehat{\theta }\right)\\ q{v}^{\prime }=\widehat{A}\sin \left(\widehat{\theta }\right)\end{array}\right.$$

(15)

where $\widehat{A},\widehat{\theta }$ are the estimated amplitude and phase angle. Thus, (5) can be expressed as

$$\left\{\begin{array}{l}{v}_{\alpha }^{\prime }={\widehat{E}}_{r\alpha }=-\widehat{A}\sin \left(\widehat{\theta }\right)\\ q{v}_{\alpha }^{\prime }=\widehat{A}\cos \left(\widehat{\theta }\right)\\ v_{\beta }^{\prime }={\widehat{E}}_{r\beta }=\widehat{A}\cos \left(\widehat{\theta }\right)\\ q{v}_{\beta }^{\prime }=\widehat{A}\sin \left(\widehat{\theta }\right)\end{array}\right.$$

(16)

By dividing (11) and (12), it is given as

$${\displaystyle \frac{{\epsilon }_{es}}{q{v}^{\prime }}}={\displaystyle \frac{s^2+{\widehat{\omega }}^2}{k_2{\widehat{\omega }}^2}}$$

(17)

In the steady state, it is defined as $s=j\omega$, (17) can be described as

$${\epsilon }_{es}=qv\prime {\displaystyle \frac{{\widehat{\omega }}^2-{\omega }^2}{k_2{\widehat{\omega }}^2}}$$

(18)

From Figure 1, it is given as

$$\dot{\widehat{\omega }}=-\Gamma ·{\epsilon }_{es}·q{v}^{\prime }·{\displaystyle \frac{k_2\widehat{\omega }}{v^2+q{v}^{\prime 2}}}$$

(19)

By introducing (18) and (15) into (19), it is given as

$$\dot{\widehat{\omega }}=-\Gamma ·{\displaystyle \frac{{\widehat{\omega }}^2-{\omega }^2}{\widehat{\omega }}}·{\displaystyle \frac{\left(1+\cos \left(2\widehat{\theta }\right)\right)}{2}}$$

(20)

In the steady state, it is defined $\omega \approx \widehat{\omega }$, thus (20) can be described as

$$\dot{\widehat{\omega }}=-\Gamma (\widehat{\omega }-\omega )(1+\cos \left(2\widehat{\theta }\right))$$

(21)

Because the second harmonic component is included in (21), the estimated frequency fluctuates more violently when back EMF changes, and the frequency change in back EMF is related to the speed of the PMSM. Therefore, when the speed of the PMSM changes, this second harmonic component will change the value of angular frequency estimated by FLL. The angular frequency estimated by FLL interferes with the flux linkage estimated by the second-order SOIFO, ultimately leading to disturbances in the entire system.

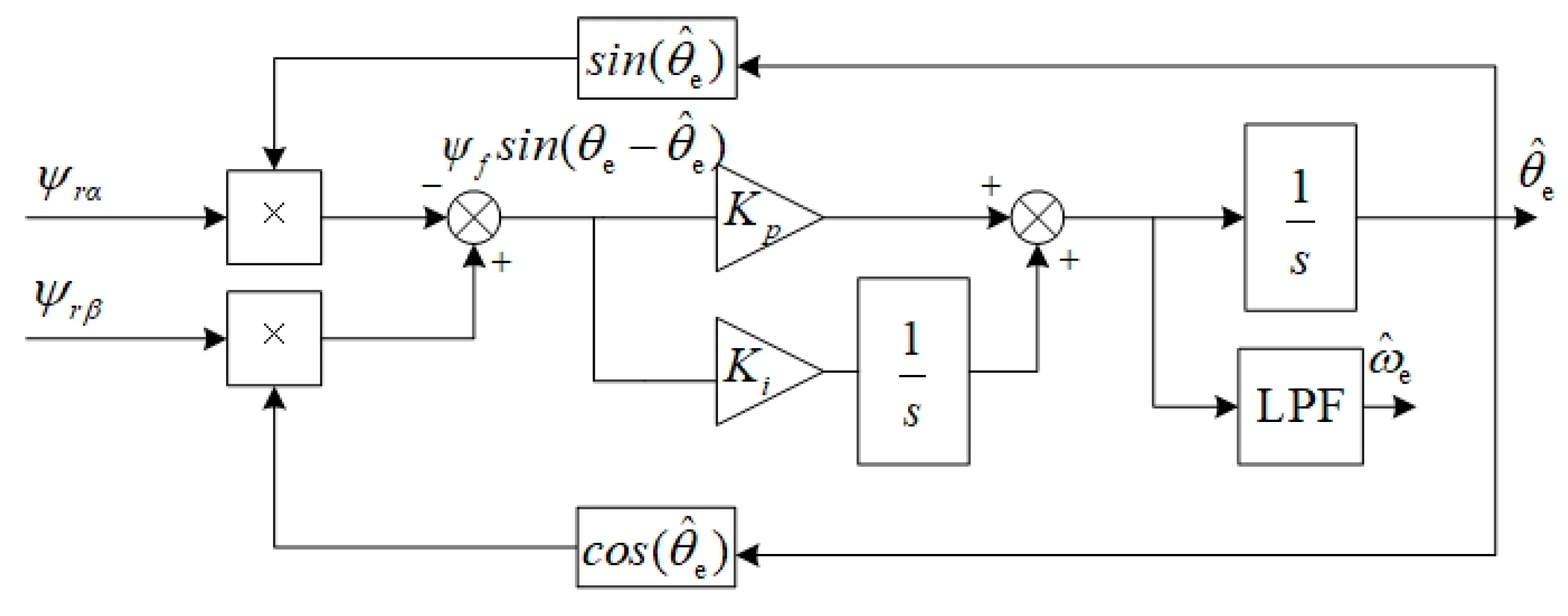
2.3.2. Analysis of DFLL

Figure 2 shows the diagram of FLL/DFLL. In Figure 2a, there is a squared trigonometric function on either the $\alpha$ axis or the $\beta$ axis. After the trigonometric transformation, the fundamental angular frequency is doubled, resulting in a second-harmonic component in the estimated motor angular frequency. Therefore, a DFLL method is used to solve this issue, and the structure of DFLL is shown in Figure 2b. As shown in Figure 2, using $\cos \left({\widehat{\theta }}^2\right)+\sin \left({\widehat{\theta }}^2\right)=1$, the second-harmonic component from FLL can be estimated.

Using DFLL, (19) can be rewritten as

$$\dot{\widehat{\omega }}=-{\displaystyle \frac{\Gamma }{2}}·{\displaystyle \frac{{\widehat{\omega }}^2-{\omega }^2}{k_2{\widehat{\omega }}^2}}·\left(q{v}_{\alpha }^{\prime 2}+q{v}_{\beta }^{\prime 2}\right)·{\displaystyle \frac{2k_2\widehat{\omega }}{v_{\alpha }^{\prime 2}+q{v}_{\alpha }^{\prime 2}+v_{\beta }^{\prime 2}+q{v}_{\beta }^{\prime 2}}}=-\Gamma ·{\displaystyle \frac{{\widehat{\omega }}^2-{\omega }^2}{2\widehat{\omega }}}$$

(22)

In the steady state, it is defined as $\omega \approx \widehat{\omega }$, (22) can be rewritten as

$$\dot{\widehat{\omega }}=-\Gamma ·\left(\widehat{\omega }-\omega \right)$$

(23)

Compared with (21) and (23), it can be seen that the frequency response of the DFLL does not fluctuate twice as much as the frequency, which effectively improves the accuracy and speed of synchronous angular frequency estimation. However, in reality, the observer’s estimated value still contains noise and high-frequency oscillation. In addition, using the arctangent function to estimate the phase angle introduces high-frequency oscillations into the estimated value, leading to greater angle estimation errors. Therefore, this paper uses a phase-locked loop (PLL) to process the estimated values of angle and speed. The PLL is shown in Figure 3.

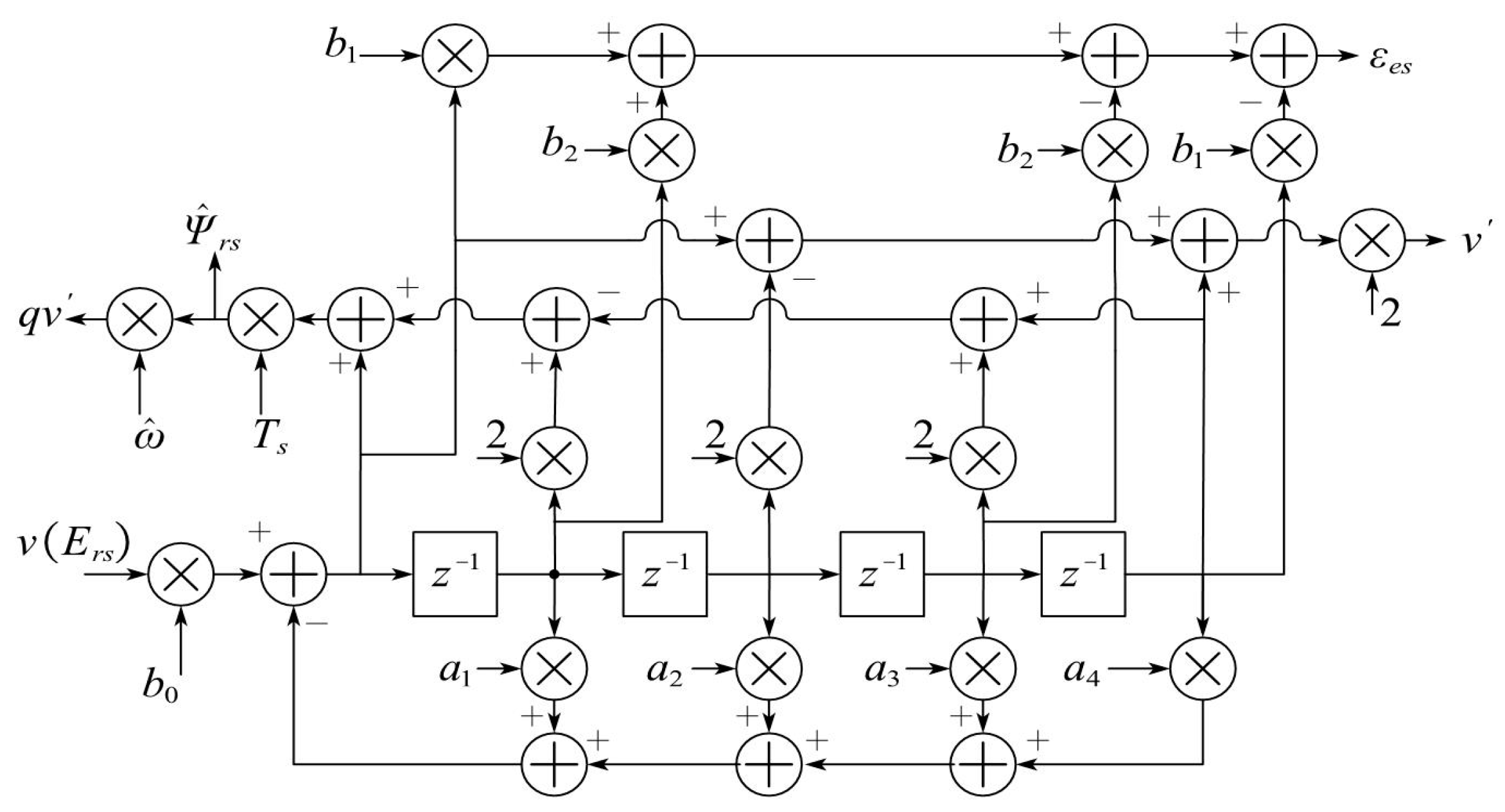
2.4. Discretization Method

In reference [17], a method for the discretization of second-order generalized integrators is proposed, and it is widely used in many papers and engineering applications. Therefore, this paper also adopts the method of bilinear transformation to discretize ($s={\displaystyle \frac{2}{T_s}}{\displaystyle \frac{1-z^{-1}}{1+z^{-1}}}$). The discrete forms of (10)–(12) are given as

$$D(z)={\displaystyle \frac{2b_0(1-2z^{-2}+z^{-4})}{1+a_1{z}^{-1}+a_2{z}^{-2}+a_3{z}^{-3}+a_4{z}^{-4}}}$$

(24)

$$Q(z)={\displaystyle \frac{b_0\widehat{\omega }{T}_s(1+2z^{-1}-2z^{-3}-z^{-4})}{1+a_1{z}^{-1}+a_2{z}^{-2}+a_3{z}^{-3}+a_4{z}^{-4}}}$$

(25)

$$E(z)={\displaystyle \frac{b_1+b_2{z}^{-1}-b_2{z}^{-3}-b_1{z}^{-4}}{1+a_1{z}^{-1}+a_2{z}^{-2}+a_3{z}^{-3}+a_4{z}^{-4}}}$$

(26)

where $u=2k_1{k}_2{\widehat{\omega }}^2{T}_s^2$, $v=8k_2\widehat{\omega }{T}_s$, $w=4(2+k_1{k}_2){\widehat{\omega }}^2{T}_s^2$, $x=2k_2{\widehat{\omega }}^3{T}_s^3$, $y={\widehat{\omega }}^4{T}_s^4$, $a_1={\displaystyle \frac{-64-2v+2x+4y}{16+v+w+x+y}}$, $a_2={\displaystyle \frac{96-2w+6y}{16+v+w+x+y}}$, $a_3={\displaystyle \frac{-64+2v-2x+4y}{16+v+w+x+y}}$, $a_4={\displaystyle \frac{16-v+w-x+y}{16+v+w+x+y}}$, $b_0={\displaystyle \frac{u}{16+v+w+x+y}}$, $b_1={\displaystyle \frac{k_1}{k_2}}{\displaystyle \frac{x+v}{16+v+w+x+y}}$, $b_2={\displaystyle \frac{2k_1}{k_2}}{\displaystyle \frac{x-v}{16+v+w+x+y}}$.

The bilinear discrete implementation structure of the improved second-order SOIFO is shown in Figure 4.

3. Simulation Analysis

3.1. Simulation Parameters

In order to verify the rationality and effectiveness of the method, this paper uses Matlab R2021a/Simulink for simulation. The structural block diagram of simulation and experiment is shown in Figure 5, and the parameters of simulation and motor platform are shown in

Table 1. The parameters of the PMSM.

Parameters	Value
Rated voltage	48 V
Rated speed	3000 r/min
Rated current	11 A
Rated torque	1.27 N·m
Rotational inertia	5.8 × 10−5 kg·m2
Stator resistance	0.48 Ω
Stator inductance	0.56 mH
Pole-pair number	5
Flux linkage of permanent magnet	0.0142 Wb

. In order to ensure the scientific comparison experiment, the PI controller parameters of the speed loop and current loop are kept consistent in the simulation. In order to make the simulation effect close to reality, it is set so that the simulation adopts a fixed step 1 × 10⁻⁵ and SVPWM modulation, and the parameters of the second-order SOIFO are $k_1=1.56$, $k_2=3.11$, and $\Gamma =100$. In this article, the position error refers to the actual motor angle obtained from the encoder minus the estimated motor angle from the position sensorless control algorithm.

3.2. Simulation Result

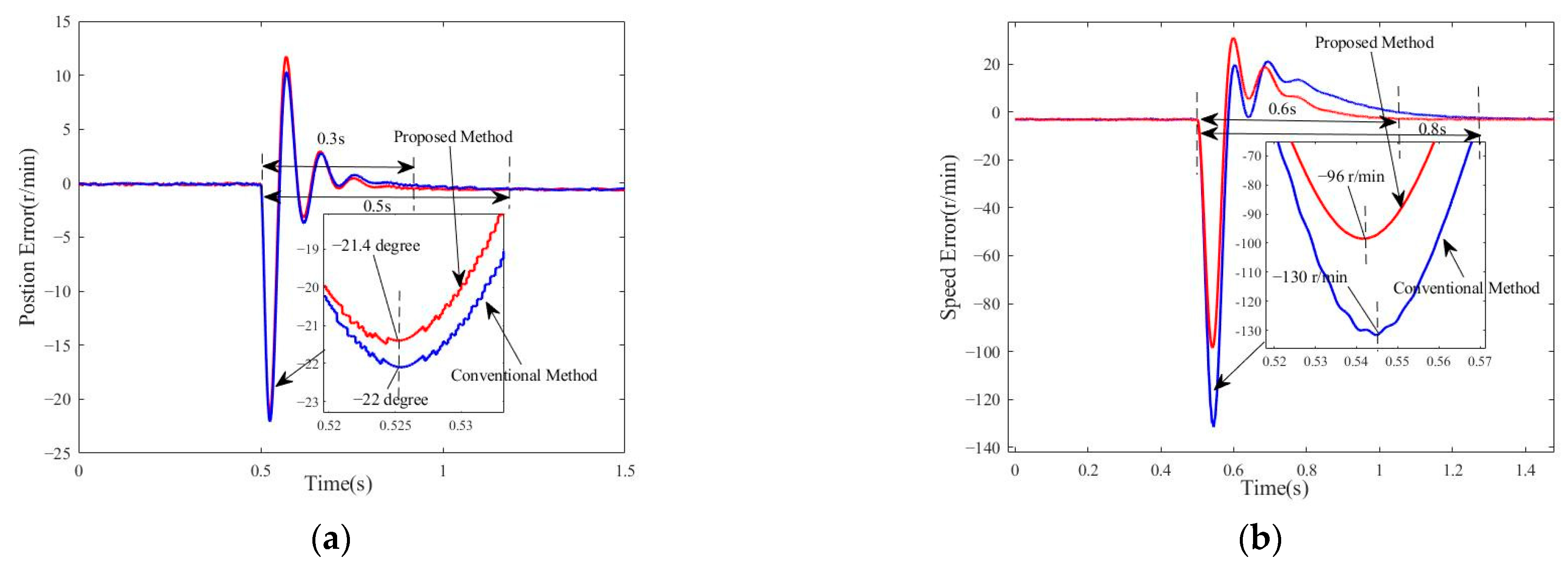
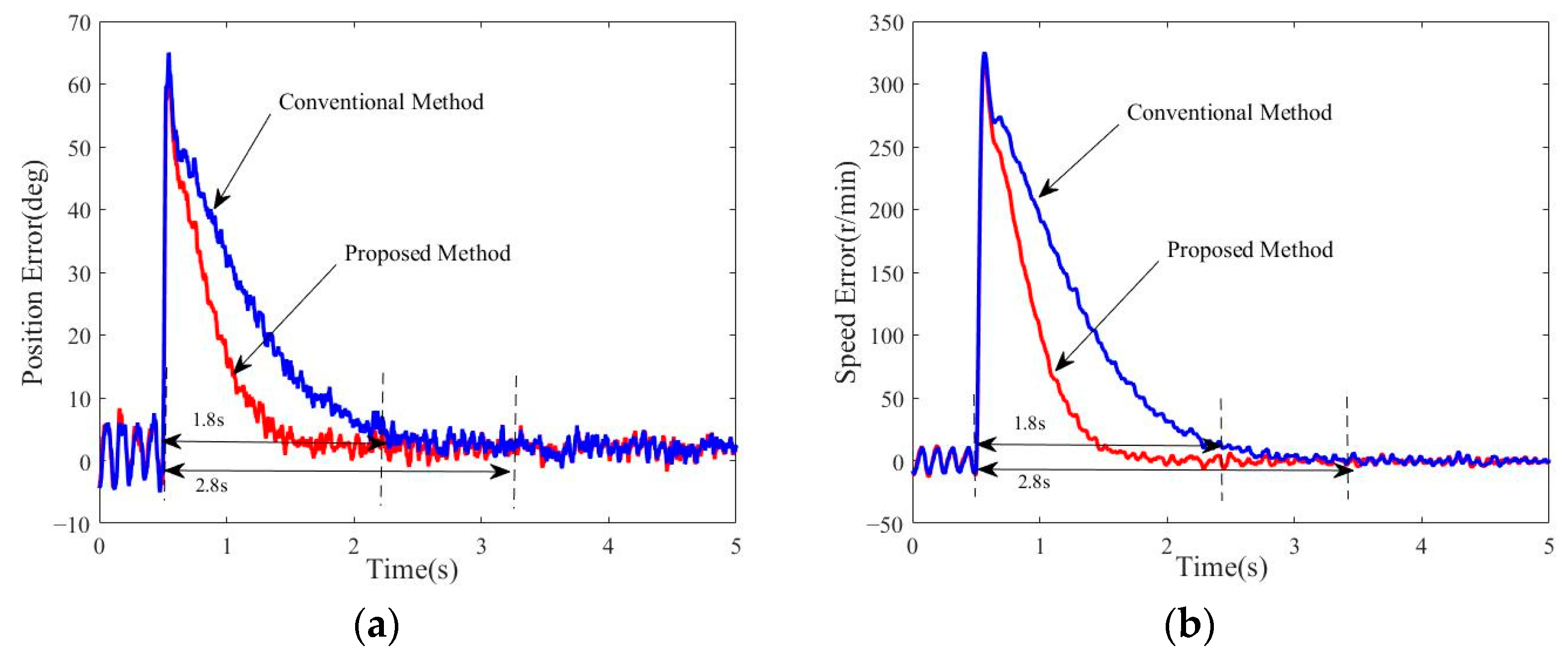
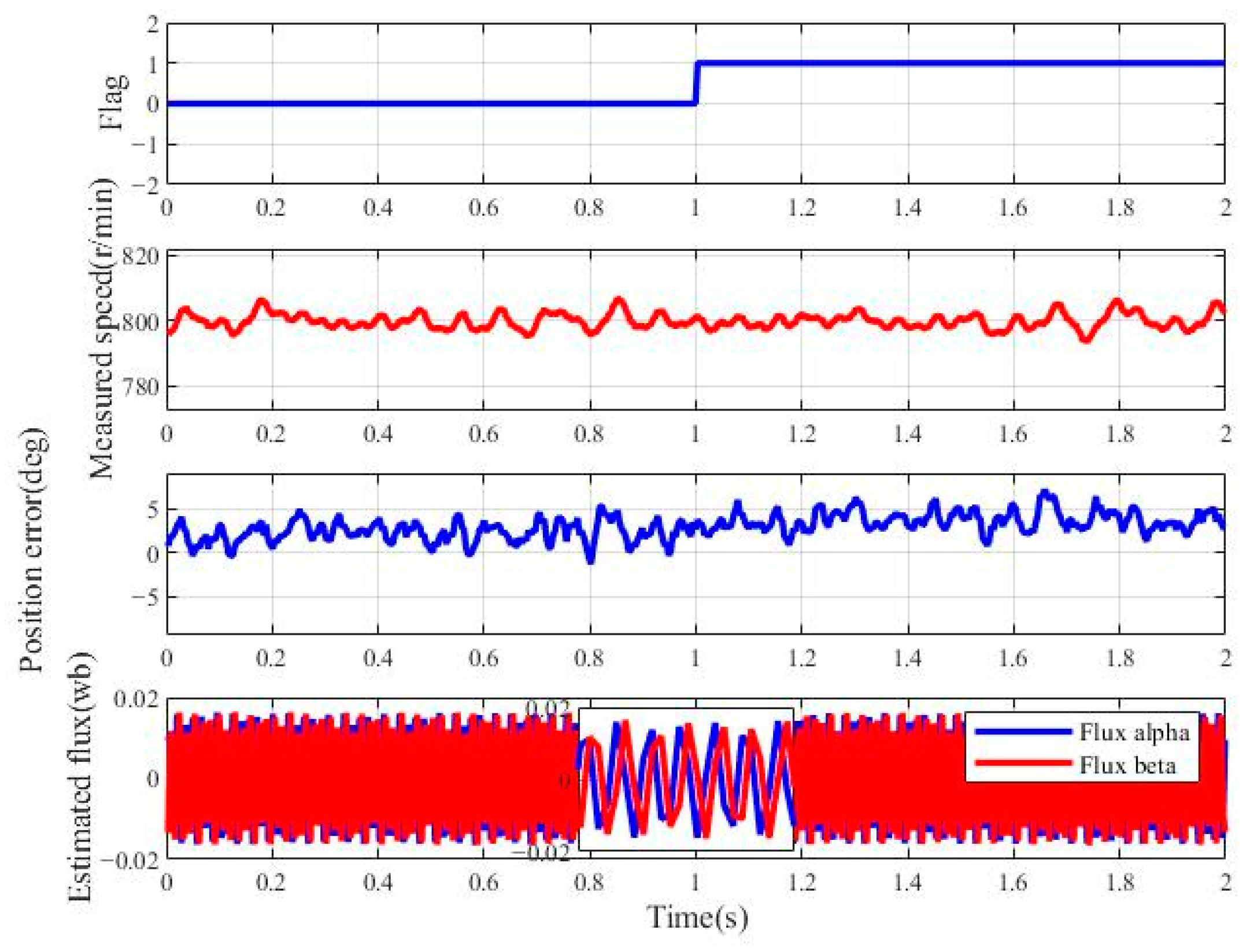
3.2.1. Simulation of Motor Operation Under Sudden Speed Variations

To compare the dynamic performance of the proposed strategy under a sudden speed change, the SPMSM is operated at 500 r/min, and suddenly increased to 800 r/min at 1 s. Figure 6 shows the simulation results of the position sensorless control strategies under speed variations. In Figure 6, the “traditional method” refers to the position sensorless control based on second-order SOIFO, while the “proposed method” refers to the position sensorless control based on improved second-order SOIFO. In Figure 6b, the speed error is defined as the actual speed obtained by the encoder minus the speed obtained by the FLL/DFLL. As shown in Figure 6, the settling time of angle error in the traditional method is about 3.1 s, while that in the proposed method is about 5.5 s, which is about 44% shorter than that in the traditional method, thus verifying that the proposed method in this paper can effectively enhance the observer’s response speed under sudden speed variations.

3.2.2. Simulation of Motor Operation Under Load Variations

To evaluate the dynamic performance of the proposed strategy under a sudden load change, the SPMSM is operated at 1500 r/min, and a 5% rated load is added at 0.5 s. Figure 7 presents the simulation results of the position sensorless control strategies under load variations. In Figure 7, the “traditional method” refers to the position sensorless control based on second-order SOIFO, while the “proposed method” refers to the position sensorless control based on improved second-order SOIFO. In Figure 7b, the speed error is defined as the actual speed obtained by the encoder minus the speed obtained by the FLL/DFLL. As shown in Figure 7, under the control of the traditional method when the motor is subjected to a load change, the angle error is disturbed by external disturbance, resulting in a maximum drop of 22°, while the speed error results in a maximum drop of 130 r/min. However, under the control of proposed method, the angle error is disturbed by external disturbance, resulting in a drop of 21.4°, while the speed error results in a maximum drop of 96 r/min. Compared to the conventional method, the proposed method reduces the angular error drop by 4.5% and the velocity error drop by 26.1%. Furthermore, Figure 7b shows that the settling time of the speed error using the conventional method is shorter than that using the proposed method, which shows that the proposed strategy has better anti-disturbance performance and dynamic performance.

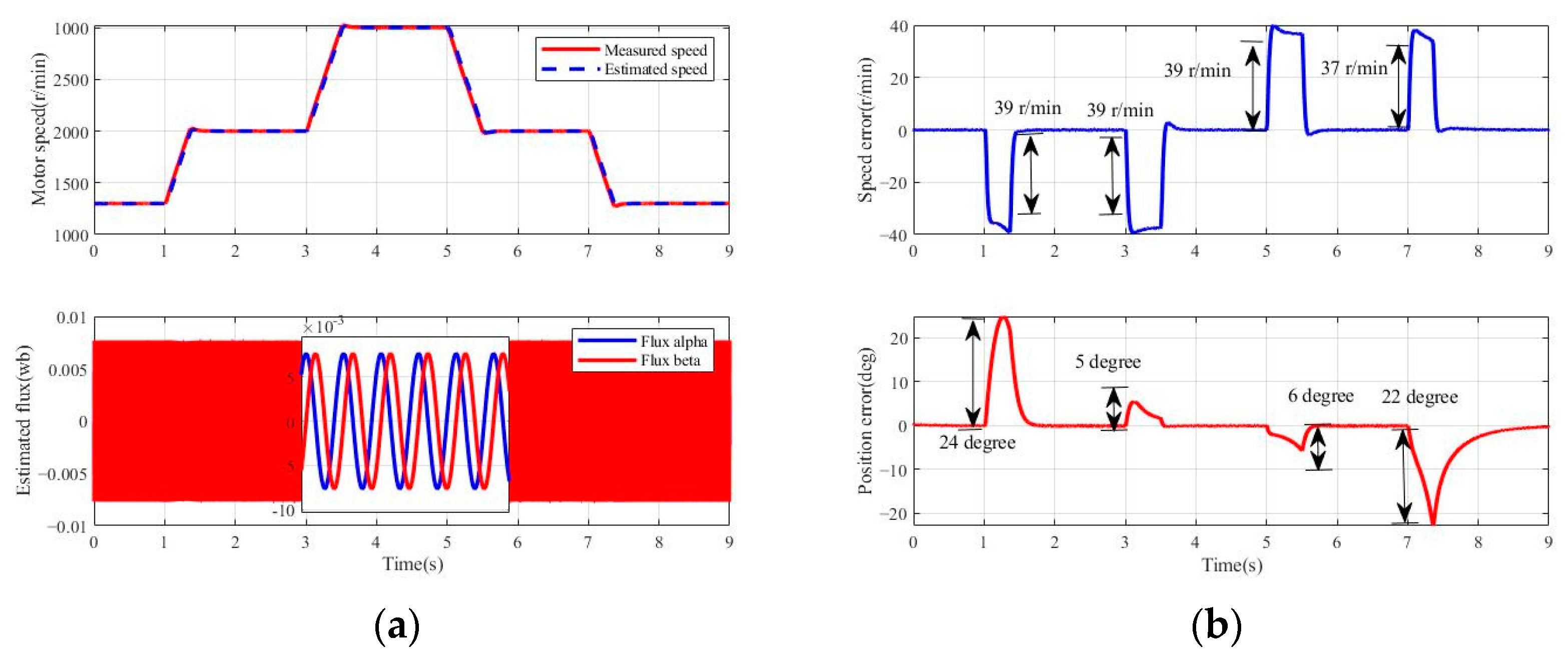
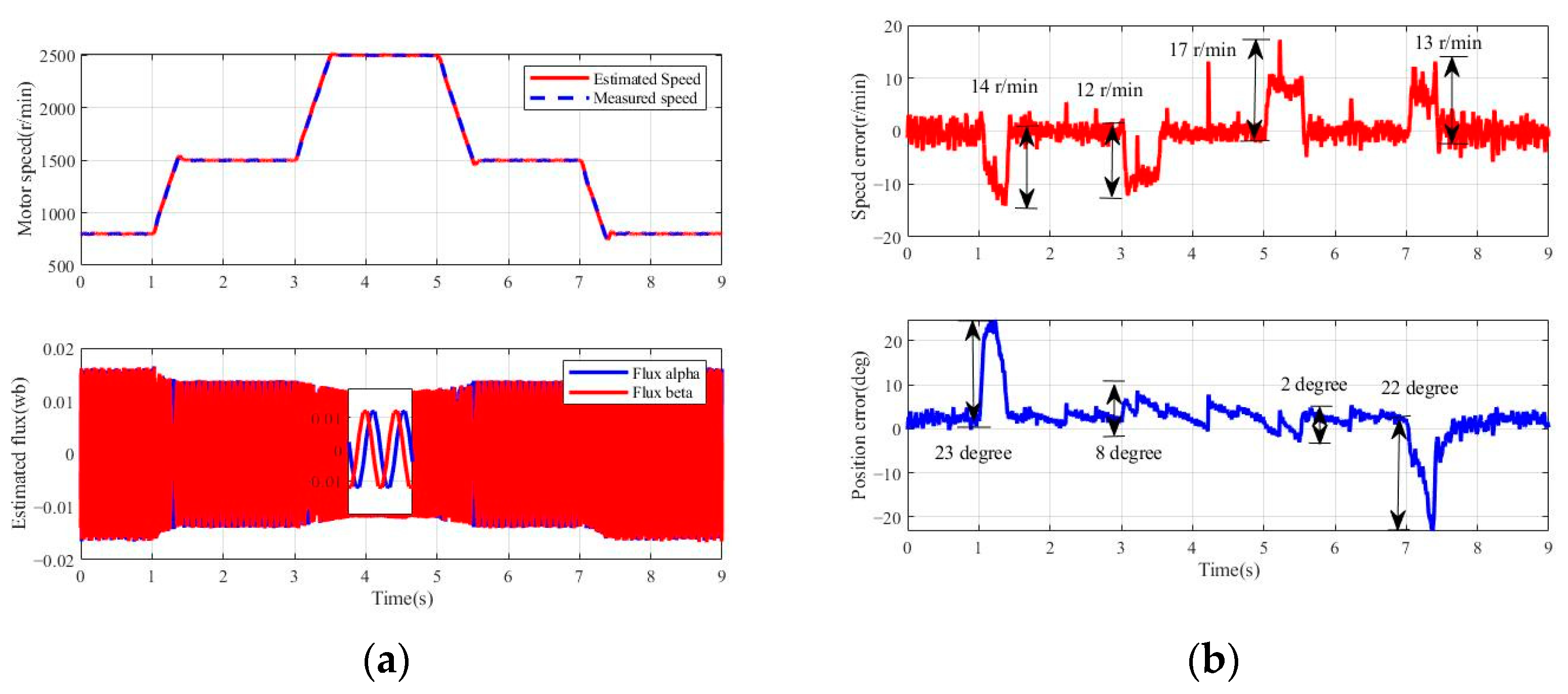
3.2.3. Simulation of Motor Operation over a Wide Speed Range

To verify the speed and position estimation performance of the position sensorless control strategy based on the improved second-order SOIFO over a wide speed range, the setting speed changes as 800–1500–2500–1500–800 r/min with no load, and the acceleration rate is 2000 r/min, and the deceleration rate is 2000 r/min.

Figure 8a displays the simulation waveforms of the estimated speed, actual speed, and estimated flux linkage using the position sensorless control based on the improved second-order SOIFO. Figure 8b illustrates the simulation waveforms of speed error and position error. In Figure 8, the speed error refers to the actual motor speed obtained from the encoder minus the estimated motor speed from the improved second-order SOIFO. As shown in Figure 8b, when the speed increases from 800 r/min to 1500 r/min, the maximum speed estimation error is approximately 39 r/min, and the maximum angle estimation error is about 24°. When the speed increases from 800 r/min to 1500 r/min, the maximum speed estimation error remains around 39 r/min, while the maximum angle estimation error is about 5°. These results indicate that the proposed scheme demonstrates excellent speed and position estimation capabilities over a wide speed range.

3.2.4. Simulation of the Motor Operation with Parameter Deviation or DC Bias

To evaluate the speed and position estimation performance of the position sensorless control algorithm based on the improved second-order SOIFO under the conditions of motor parameter deviation and DC bias, the following simulation is conducted.

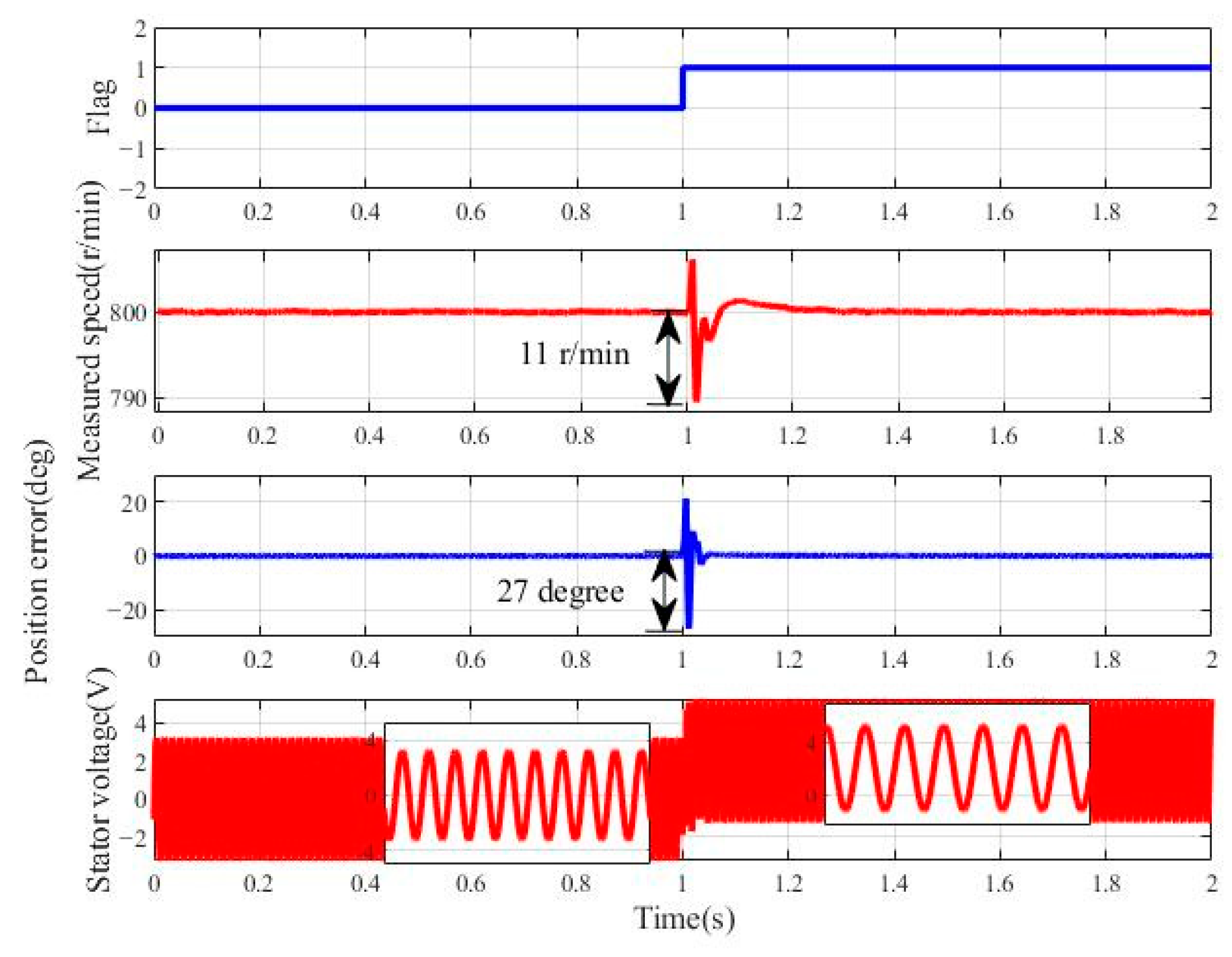
• Simulation of the motor operation with a voltage DC bias
  Under actual experimental conditions, the acquired voltage signals may contain a DC bias. To evaluate the robustness of the proposed method, the speed command is set to 800 r/min with no load and a 2 V DC offset is imposed on the stator voltage at 1 s. In the Figure 9, $Flag=0$ represents $\Delta u_{\alpha }=$ 0 V, and $Flag=1$ represents $\Delta u_{\alpha }=$ +2 V. As shown in Figure 9, after the stator voltage $u_{\alpha }$ increases, the maximum speed drop is approximately 11 r/min, and the maximum position error reaches around 27°. The system then quickly recovers to a steady state, demonstrating that the proposed scheme has excellent performance in suppressing DC voltage bias.
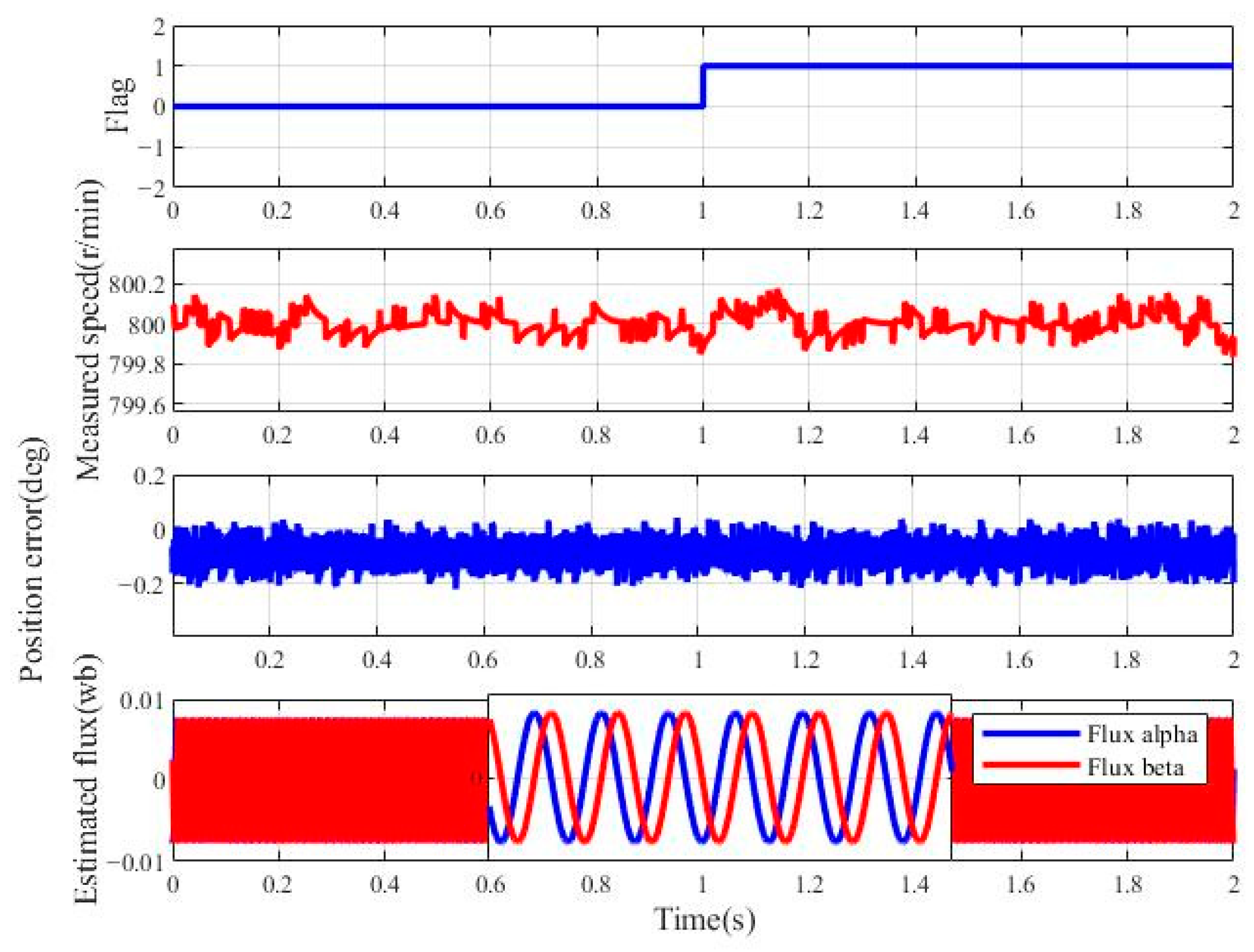
• Simulation of the motor operation with a current DC bias
  Under actual experimental conditions, the acquired current signals may contain a DC bias. To assess the robustness of the proposed method, the speed command is set to 800 r/min with no load and a 1.5 A DC bias is imposed on the stator current at 1 s. In Figure 10, $Flag=0$ represents $\Delta i_{\alpha }=$ 0 A, and $Flag=1$ represents $\Delta i_{\alpha }=$ +1.5 A. As shown in Figure 10, after imposing the DC bias on the stator current $i_{\alpha }$, the maximum measured speed drop is approximately 3 r/min, and the maximum position error is around 6°. The system then quickly recovers to a steady state, demonstrating that the proposed scheme has excellent performance in suppressing current DC bias.
• Simulation of the motor operation with stator resistance deviation
  Under actual experimental conditions, the resistance value used in the control algorithm may have measurement errors. To evaluate the robustness of the proposed method, the speed command is set to 800 r/min with no load and the stator resistance is increased to 1.5 times its original value at 1 s. In Figure 11, $Flag=0$ represents $\Delta R_s=0$, and $Flag=1$ represents $\Delta R_s=0.5R_s$. As shown in Figure 11, after the stator resistance is increased by 50%, the estimated rotor flux linkage remains almost unchanged, the actual motor speed remains unaffected, and the position error remains stable. Therefore, the proposed scheme has excellent performance in suppressing the resistance deviation.
• Simulation of the motor operation with stator inductance deviation
  Under actual experimental conditions, the stator inductance used in the control algorithm may have measurement errors. To evaluate the robustness of the proposed method, the speed command is set to 800 r/min with no load, and the stator inductance is increased to 1.5 times its original value at 1 s. In Figure 12, $Flag=0$ represents $\Delta L_s=0$, and $Flag=1$ represents $\Delta L_s=0.5L_s$. As shown in Figure 12, after the stator inductance is increased by 50%, the estimated flux linkage remains almost unchanged, the actual motor speed is not affected, and the position error remains the same. Therefore, the proposed scheme has excellent performance in suppressing inductance measurement errors.

4. Experimental Analysis

4.1. Experiment Parameters

As shown in Figure 13, the experimental platform is a permanent magnet synchronous motor drag system, which consists of a controlled motor and a load motor. Among them, the controlled motor is an SPMSM, which is controlled by an inverter platform driven by the main control chip TMS320F28335. The load motor is a servo motor, which communicates with the PC through Ethercat to provide load torque. To accurately measure the real angle and real speed, a 2500-line magnetic encoder is installed at the end of the SPMSM. This experiment utilizes a MATLAB R2021a embedded code support package provided by TI company, which generates and writes code to the control chip. The motor is then controlled via a PC and the experimental data are recorded for further analysis. The parameters of the SPMSM experimental platform are consistent with Table 1.

4.2. Experimental Results

4.2.1. Experimental Verification of Motor Operation Under Sudden Speed Variations

To compare the dynamic performance of the proposed method under a sudden speed change, the command speed of the SPMSM is increased from 500 r/min to 800 r/min at 0.5 s. Figure 14 shows the experimental results of the position sensorless control strategies under speed changes. In Figure 14, the “traditional method” refers to the position sensorless control based on a second-order SOIFO, and the “proposed method” refers to the position sensorless control based on an improved second-order SOIFO. In Figure 14b, the speed error refers to the actual speed obtained by the encoder minus the speed obtained by the FLL/DFLL. Figure 14 shows that the adjustment time of angle error in the traditional method is about 2.8 s, while that in the proposed method is about 1.8 s. Comparatively, the adjustment time of the proposed method is 55% shorter than that of the traditional method, which is consistent with the conclusion of simulation analysis.

4.2.2. Experimental Verification of Motor Operation Under Load Variations

To compare the dynamic performance of the proposed strategy under a sudden load change, the SPMSM is operated at 1500 r/min, and the load torque is changed from 0% rated load to 5% rated load at 0.69 s. Figure 15 shows the experimental results of the position sensorless control strategies under load changes. In Figure 15, the “traditional method” refers to the position sensorless control based on a second-order SOIFO, and the “proposed method” refers to the position sensorless control based on an improved second-order SOIFO. In Figure 15b, the speed error is defined as the actual speed obtained by the encoder minus the speed obtained by the FLL/DFLL. As shown in Figure 15, under the control of the traditional method, when the SPMSM is loaded, the position error is disturbed by external disturbance, resulting in a drop of 8.1°, while the speed error results in a drop of 94 r/min. However, under the control of the proposed method, the angle error caused by external disturbance dropped by 9.3°, while the speed error results in a drop of 49 r/min. Compared to the traditional method, the proposed method reduces the angular error drop by 12.3% and the velocity error drop by 47.9%. Furthermore, in Figure 15b, the settling time of the speed error under proposed control is shorter than that under conventional control, which is consistent with the simulation analysis conclusion.

4.2.3. Experimental Verification of Motor Operation over a Wide Speed Range

To verify the speed and position estimation performance of the proposed improved second-order SOIFO over a wide speed range from 800 to 2500 r/min, the same procedure as in the simulation is followed under no-load conditions: the setting speed changes as 800–1500–2500–1500–800 r/min, and the acceleration rate is 2000 r/min, and the deceleration rate is 2000 r/min.

Figure 16a presents the simulation waveforms of the estimated speed, actual speed, and estimated flux linkage using the position sensorless control scheme based on the improved second-order SOIFO. Figure 16b illustrates the experimental results of speed error and position error. In Figure 16b, the speed error refers to the actual speed obtained by the encoder minus the speed obtained by the position sensorless control scheme based on the improved second-order SOIFO. As shown in Figure 16, when the speed increases from 800 r/min to 1500 r/min, the maximum speed estimation error is approximately 14 r/min, and the maximum angle estimation error is about 23°. When the speed increases from 1500 r/min to 2500 r/min, the maximum speed estimation error is about 12 r/min, and the maximum angle estimation error is around 8°. When the speed decreases from 2500 r/min to 1500 r/min, the maximum speed estimation error is approximately 17 r/min, and the maximum angle estimation error is about 2°. When the speed decreases from 1500 r/min to 800 r/min, the maximum speed estimation error is about 13 r/min, and the maximum angle estimation error is around 22°. These results demonstrate that the proposed scheme has excellent speed and position estimation capabilities over a wide speed range.

4.2.4. Experiment of the Motor Operation with Parameter Deviation

To verify the speed and position estimation performance of the proposed improved second-order SOIFO with parameter deviation, the following experiments are conducted.

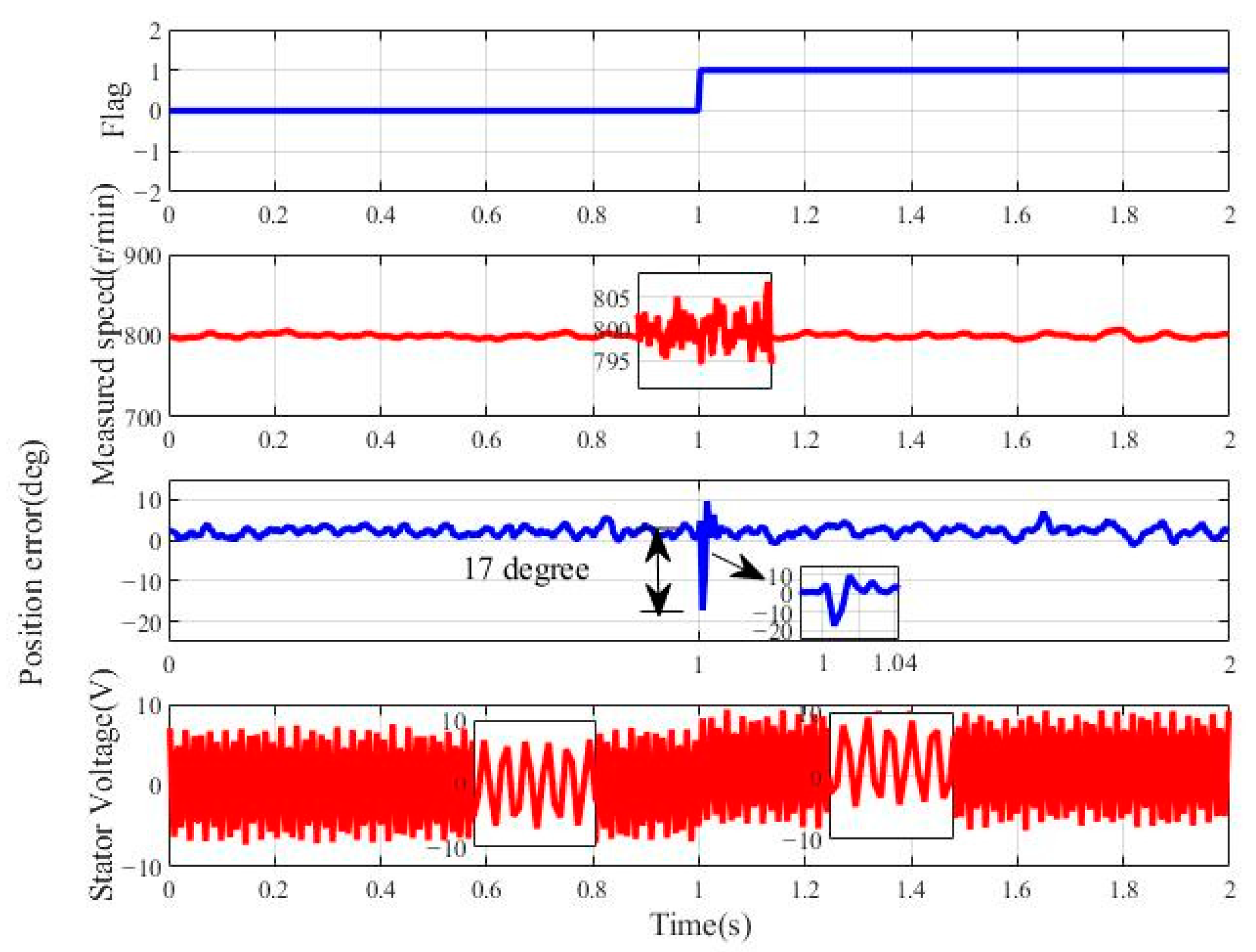
• Experiment of the motor operation with a voltage DC bias
  Under actual experimental conditions, the acquired voltage signals may contain a DC bias. Therefore, the speed command is set to 800 r/min with no load and a 2 V DC offset is imposed on the stator voltage at 1s. In Figure 17, $Flag=0$ represents $\Delta u_{\alpha }=$ 0 V, and $Flag=1$ represents $\Delta u_{\alpha }=$ +2 V. As shown in Figure 17, after the stator voltage $u_{\alpha }$ increases, the actual motor speed is not affected, and the maximum position error is around 17°. The system then quickly recovers to a steady state, demonstrating that the proposed scheme has excellent performance in suppressing DC voltage bias.
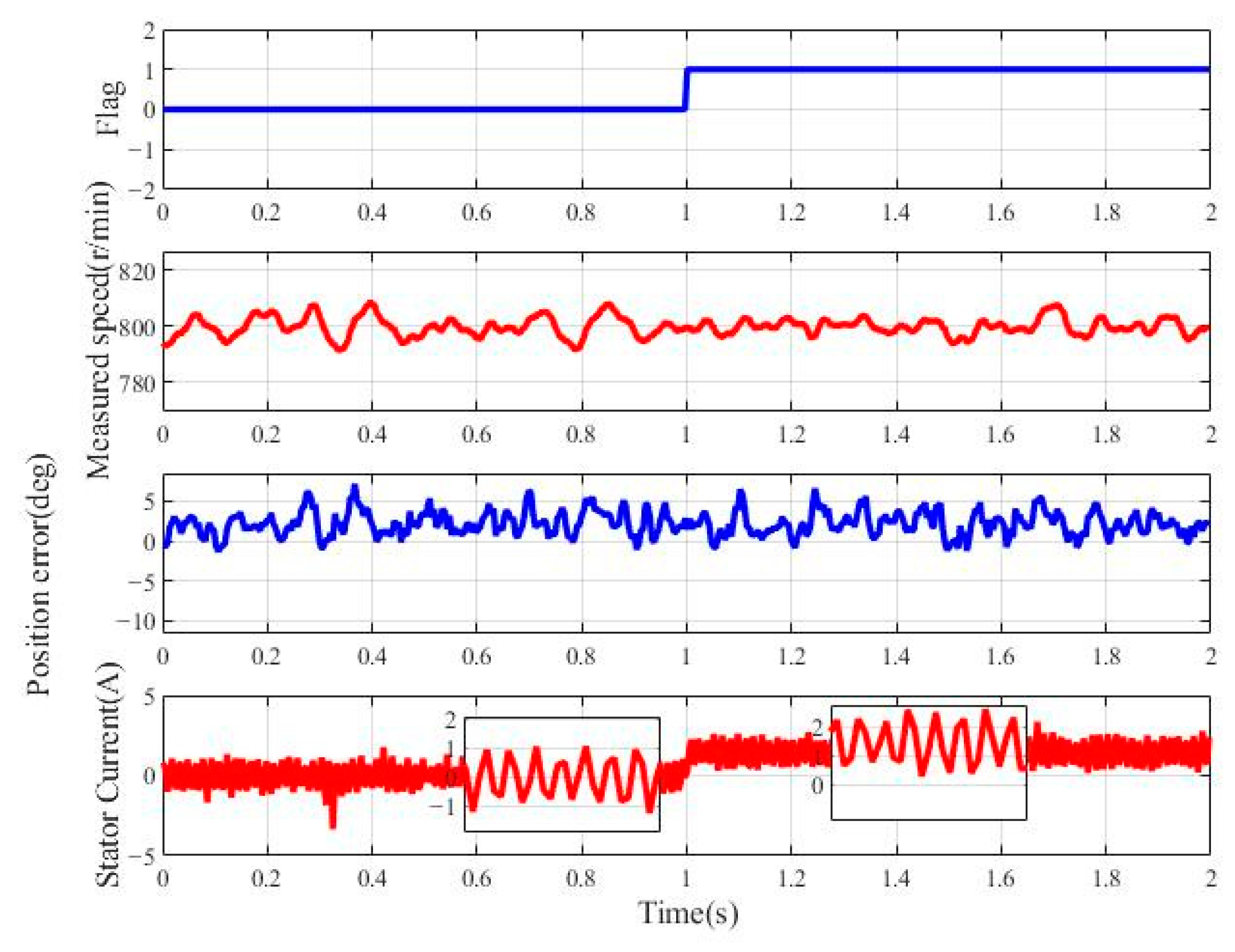
• Experiment of the motor operation with a current DC bias
  Under actual experimental conditions, the acquired current signals may contain a DC bias. Therefore, the speed command is set to 800 r/min with no load and a 1.5 A DC bias is imposed on the stator current at 1s. In Figure 18, $Flag=0$ represents $\Delta i_{\alpha }=$ 0 A and $Flag=1$ represents $\Delta i_{\alpha }=$ +1.5 A. As shown in Figure 18, after imposing the DC bias on the stator current $i_{\alpha }$, the actual motor speed is not affected, and the position error remains the same. Therefore, the proposed scheme has excellent performance in suppressing the current DC bias.
• Experiment of the motor operation with stator resistance deviation
  Under actual experimental conditions, the resistance value used in the control algorithm may have measurement errors. Therefore, the speed command is set to 800 r/min with no load and the stator resistance is increased to 1.5 times its original value at 1 s. In Figure 19, $Flag=0$ represents $\Delta R_s=0$, and $Flag=1$ represents $\Delta R_s=0.5R_s$. As shown in Figure 19, after the stator resistance is increased by 50%, the estimated rotor flux linkage remains almost unchanged, the actual motor speed is not affected, and the position error remains the same. Therefore, the proposed scheme has excellent performance in suppressing the resistance deviation.
• Experiment of the motor operation with stator inductance deviation
  Under actual experimental conditions, the stator inductance used in the control algorithm may have measurement errors. Therefore, the speed command is set to 800 r/min with no load, and the stator inductance is increased to 1.5 times its original value at 1 s. In Figure 20, $Flag=0$ represents $\Delta L_s=0$, and $Flag=1$ represents $\Delta L_s=0.5L_s$. As shown in Figure 20, after the stator inductance is increased by 50%, the estimated flux linkage remains almost unchanged, the actual motor speed is not affected, and the position error remains the same. Therefore, the proposed scheme has excellent performance in suppressing inductance measurement errors.

5. Conclusions

In this study, an improved second-order SOIFO is proposed for estimating the flux of PMSMs. The estimated flux is further processed through a phase-locked loop (PLL) to obtain the motor speed and rotor position. Section 2 presents the mathematical modeling of the PMSM, introduces the fundamental principles and transfer function of the second-order SOIFO, and analyzes the FLL to explain the origin of second-harmonic components. To address this issue, a DFLL is employed to suppress the second-harmonic disturbance. In Section 3, MATLAB-based simulations are conducted to validate the proposed position sensorless control method. The results demonstrate that the proposed method achieves a faster response time compared to traditional approaches and exhibits robustness against parameter variations and DC bias. In Section 4, experimental validation is conducted using a motor control platform based on the DSP TMS320F28335.

On one hand, this study provides a comprehensive theoretical analysis of the second-harmonic components generated by the FLL, highlighting the necessity for improvement. Compared to conventional methods, the proposed position sensorless control approach based on the improved second-order SOIFO significantly enhances system performance. Specifically, when the motor undergoes a sudden speed change, the settling time of the estimated rotor position error (actual motor angle measured by an encoder minus the estimated angle from position sensorless control) is reduced by nearly 50%. When the motor is subjected to a sudden load change, the peak deviation of the rotor position error decreases by 19%, and the peak deviation of the speed error (actual speed minus the estimated speed from FLL/DFLL) is reduced by 47.9%. These results confirm that the proposed method exhibits superior robustness in handling speed and load disturbances compared to conventional approaches. On the other hand, both simulation and experimental results verify that the proposed method operates effectively over a wide speed range while demonstrating resistance to parameter variations and DC bias. Furthermore, the introduced discretization approach facilitates seamless implementation in MATLAB/Simulink and can be conveniently deployed on embedded platforms via a MATLAB embedded code support package provided by TI company.

In summary, the proposed method outperforms traditional position sensorless control techniques in handling sudden speed and load changes, provides a wider operational speed range, and effectively mitigates parameter deviations such as motor parameter variations and DC bias. Future research could focus on optimizing parameter tuning strategies to further improve adaptability to complex operating conditions. Additionally, the proposed position sensorless control can contribute to the development of high-performance, energy-efficient, and intelligent EV systems.