Estimation of Vehicle Mass and Road Slope for Commercial Vehicles Utilizing an Interacting Multiple-Model Filter Method Under Complex Road Conditions
Abstract
1. Introduction
2. Commercial Vehicle Model
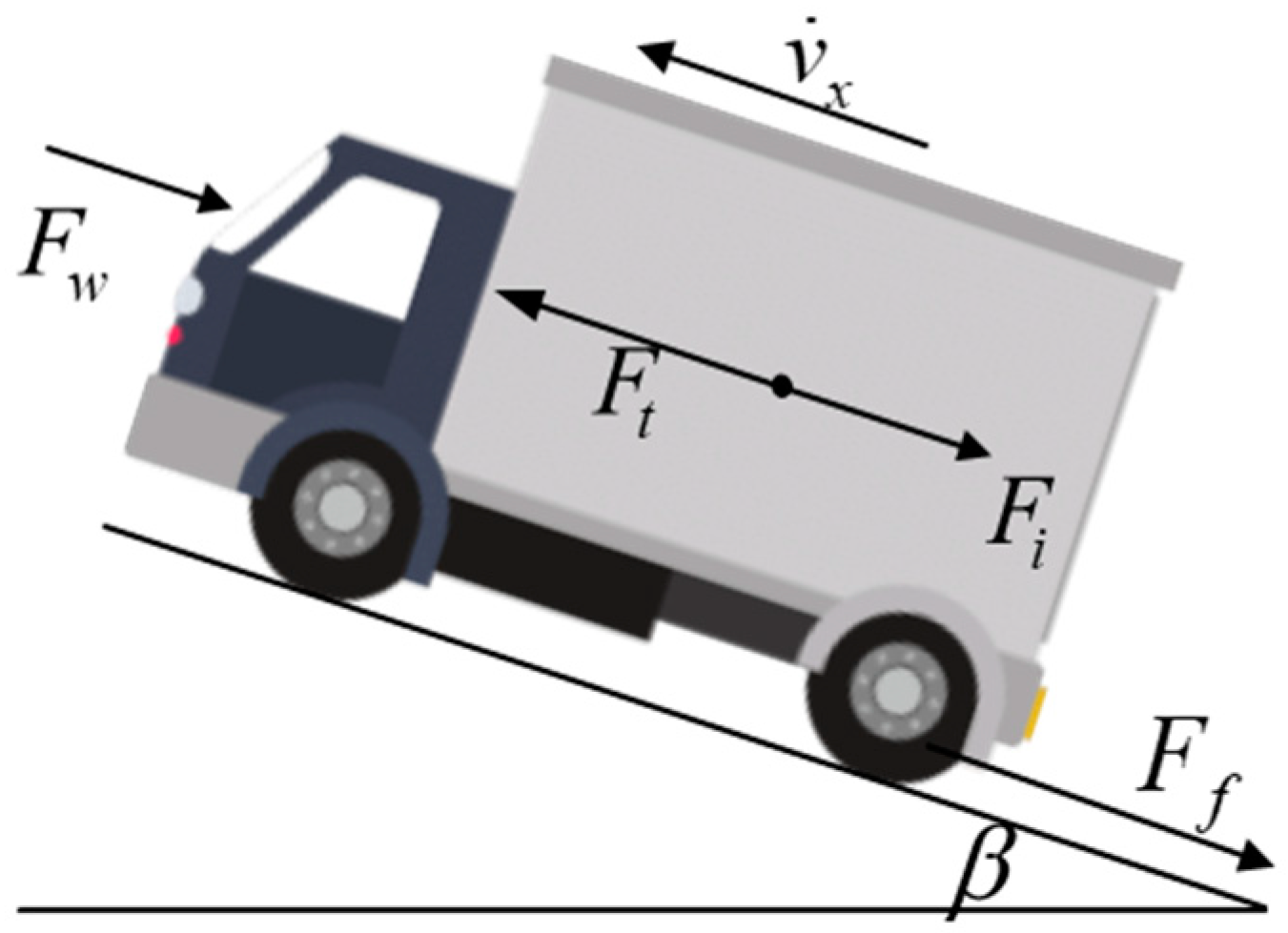
2.1. Vehicle Longitudinal Dynamics Model
2.2. Kinematic Model Based on Acceleration Sensor
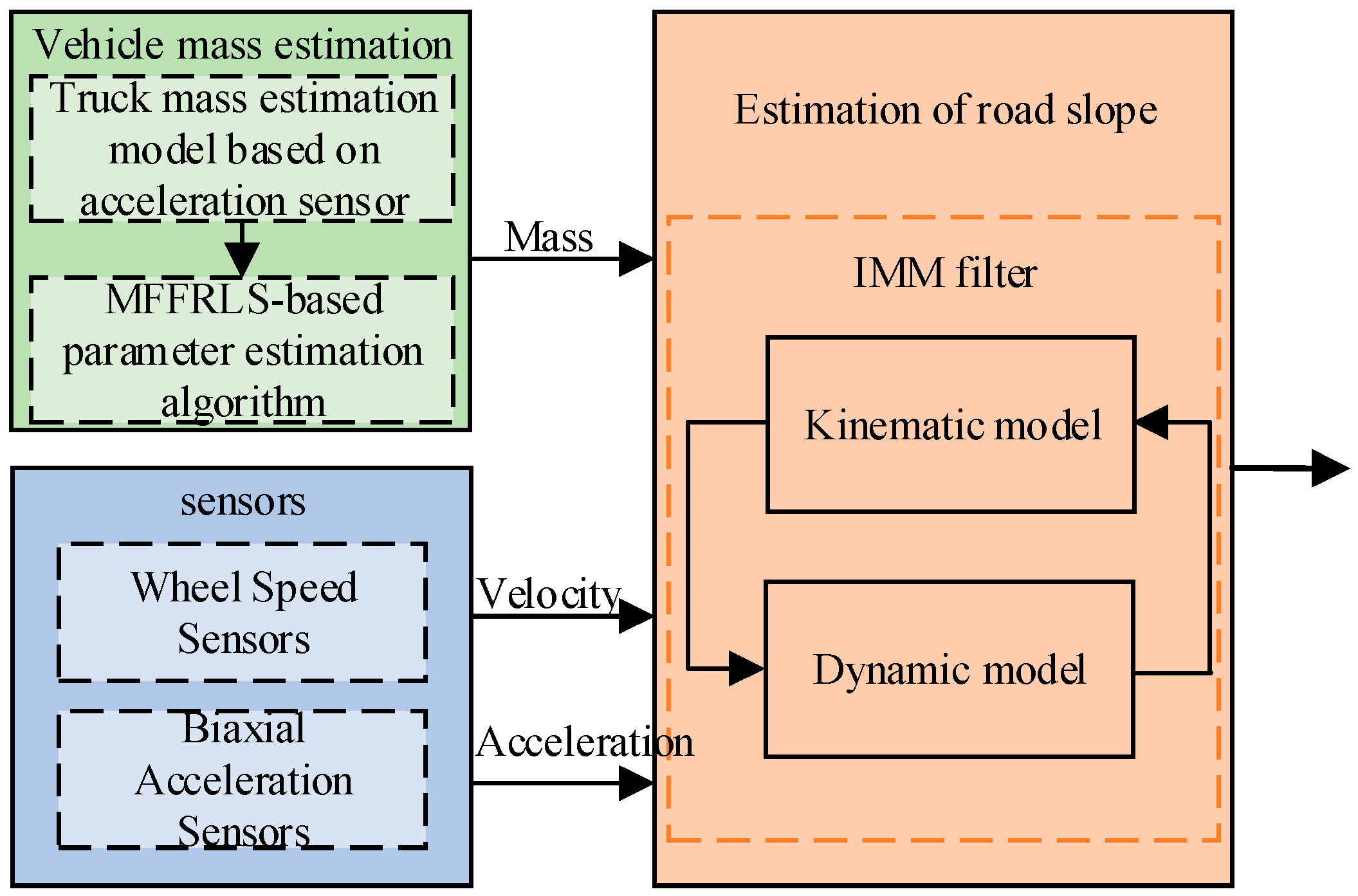
3. Estimation of Commercial Vehicle Mass
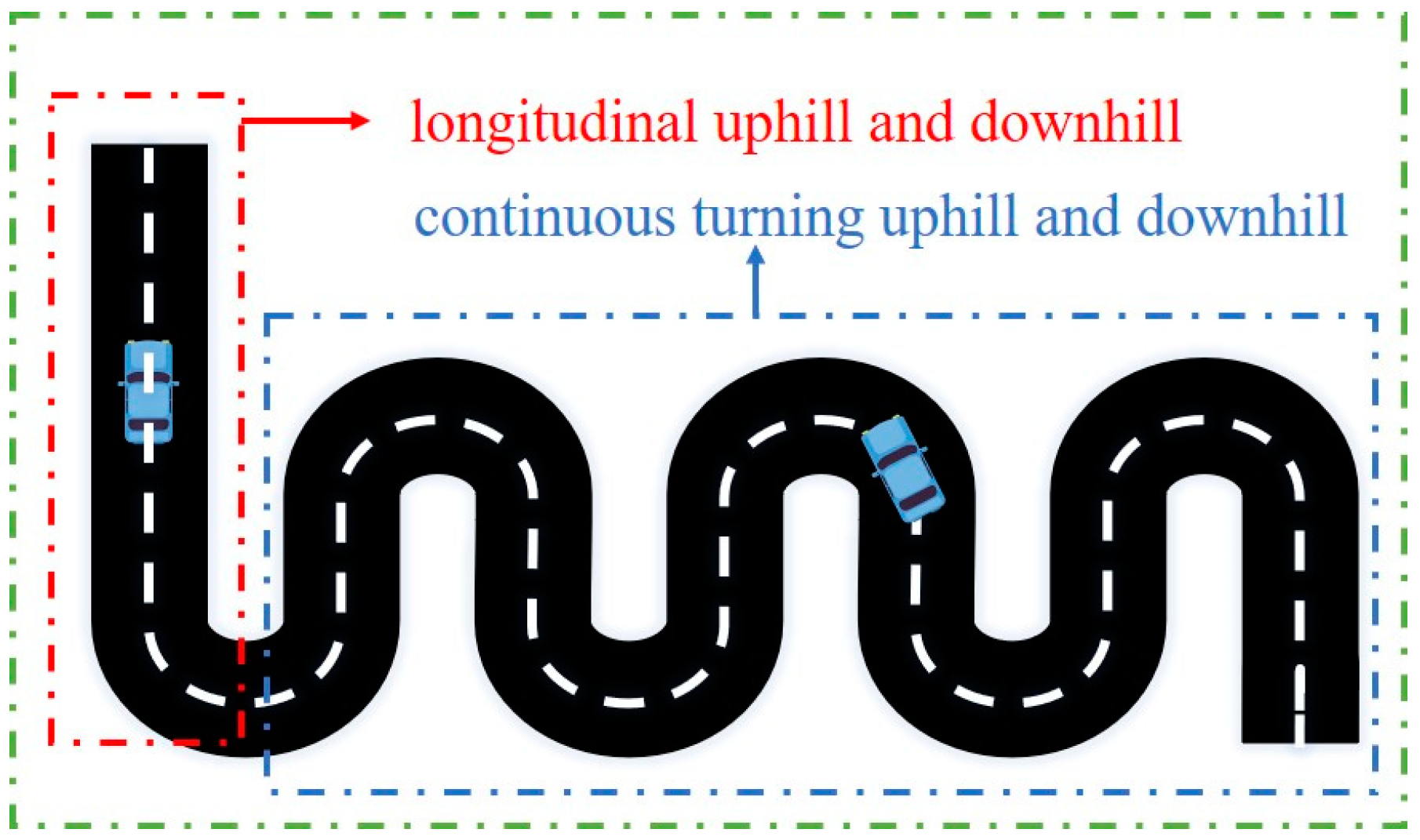
4. Slope Estimation Under Complex Conditions
4.1. Design of State Equations and Observation Equations Under Complex Road Conditions
4.2. Error Compensator Design
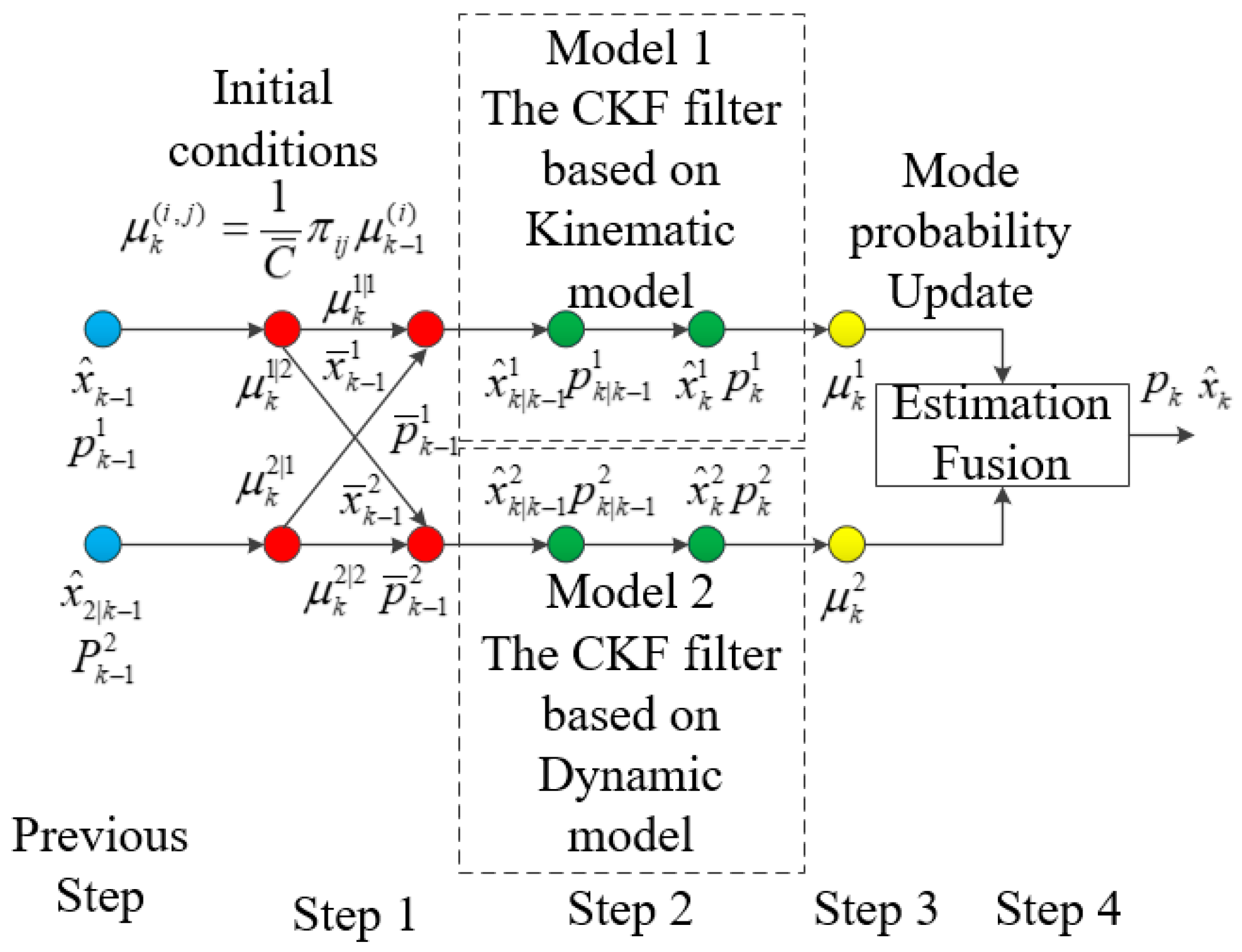
4.3. Interacting Multiple-Model Road Slope Estimation Algorithm
- Step 1: Interacting
- Step 2: Model-matched filtering
- (i).
- Time update:
- (ii).
- Measurement update:
- Step 3: Model probability update
- Step 4: Estimation Fusion
5. Simulation and Analysis
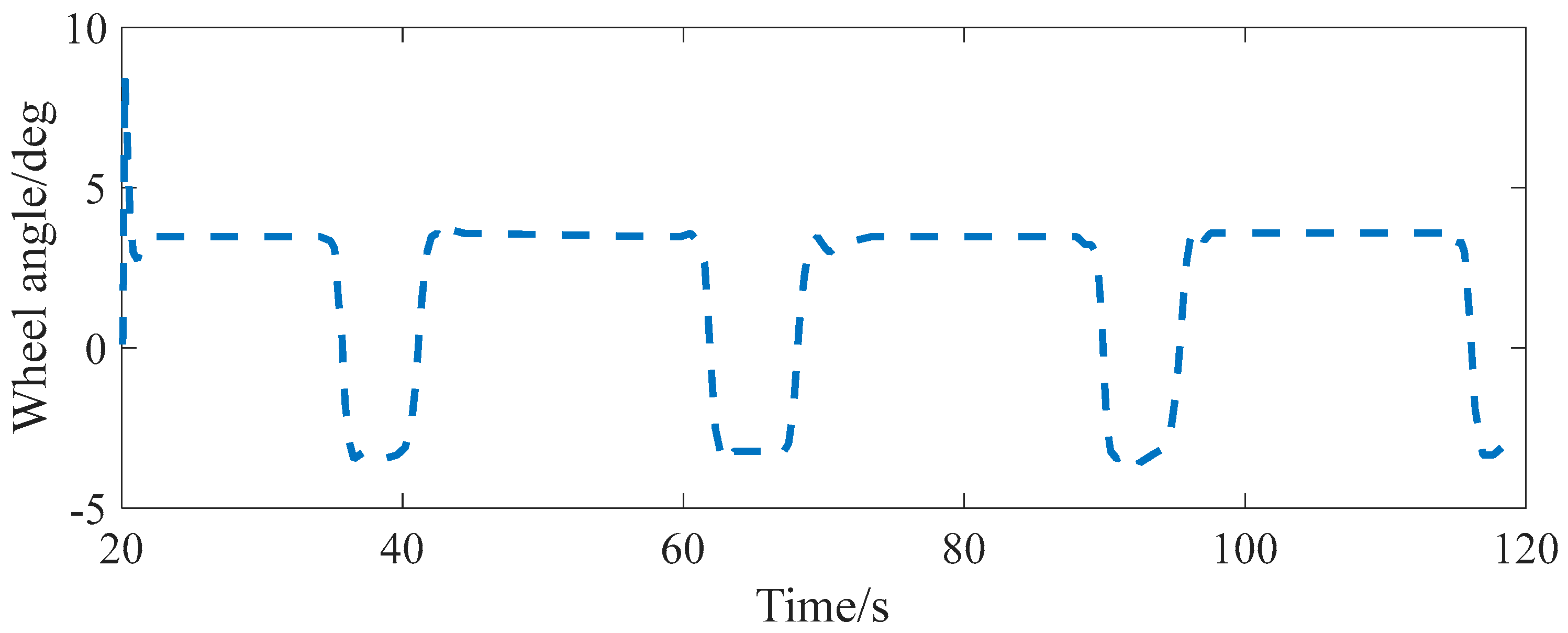
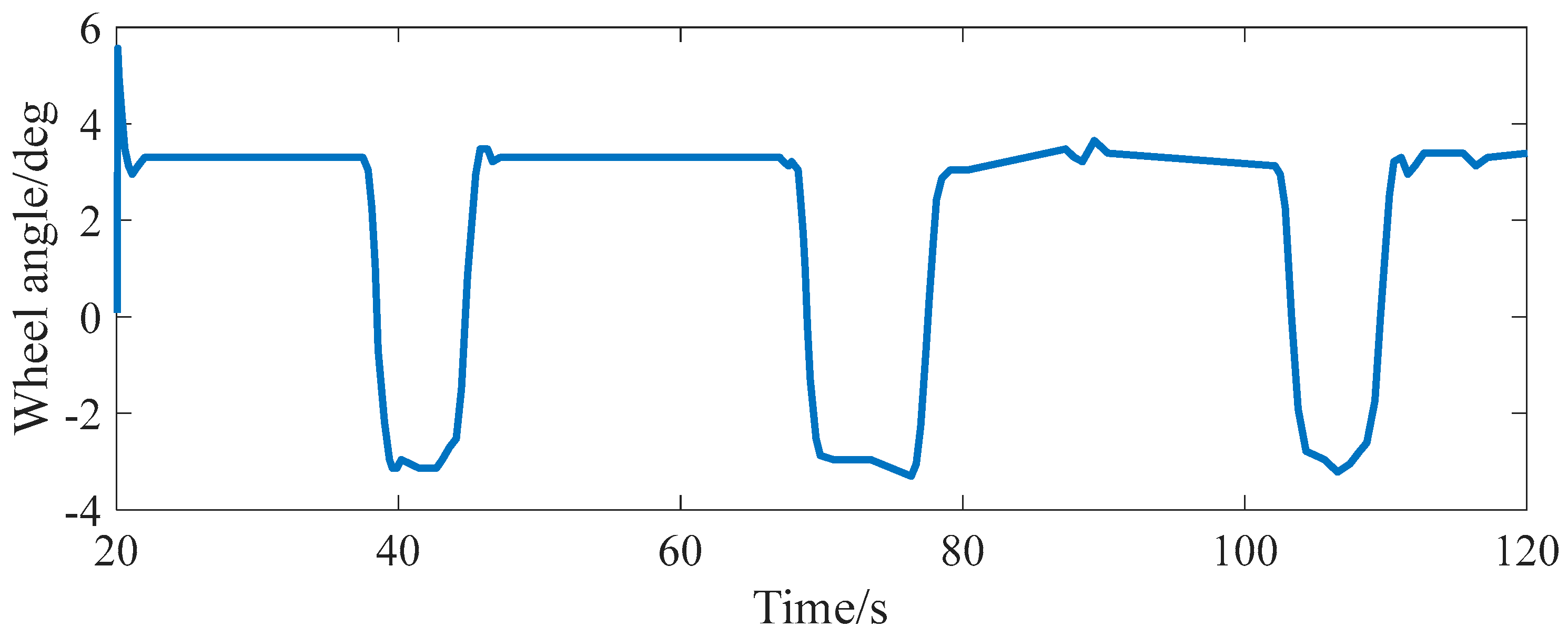
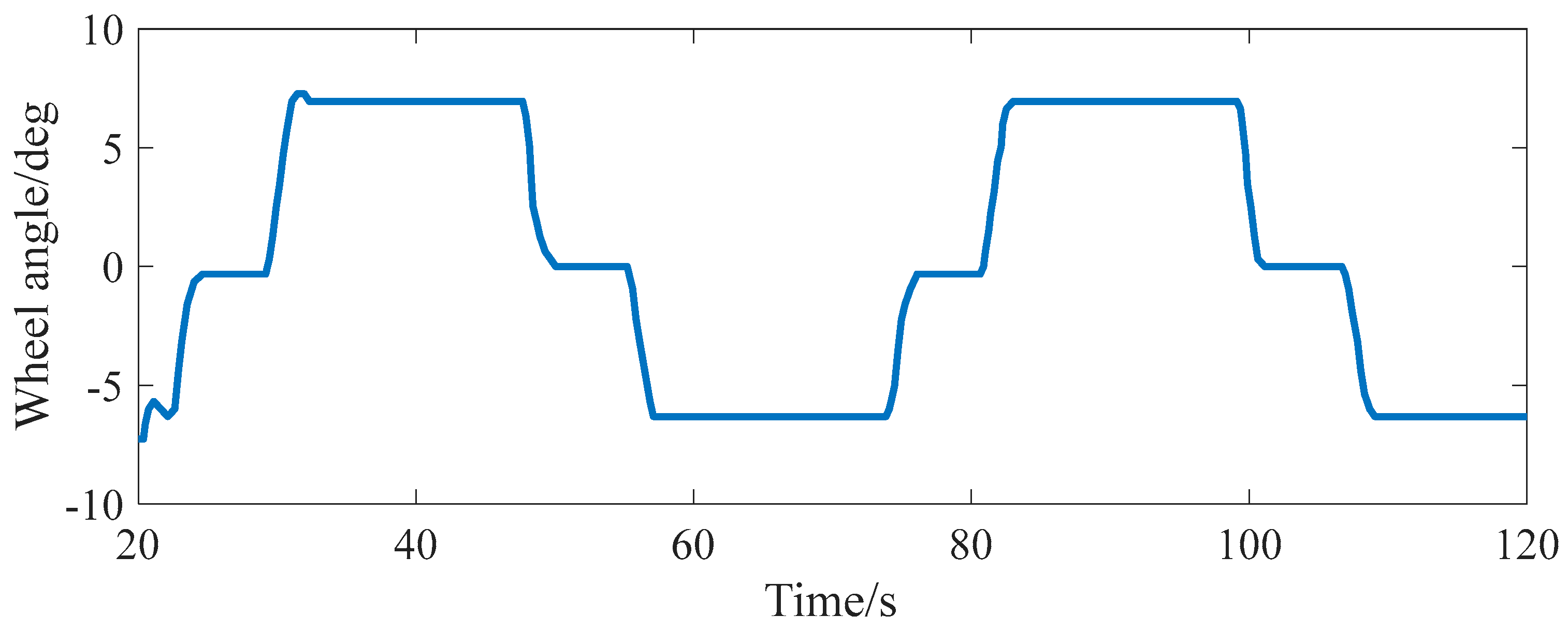
5.1. Introduction of Test Conditions and Initial Value Setting
5.2. Analysis of Simulation Results
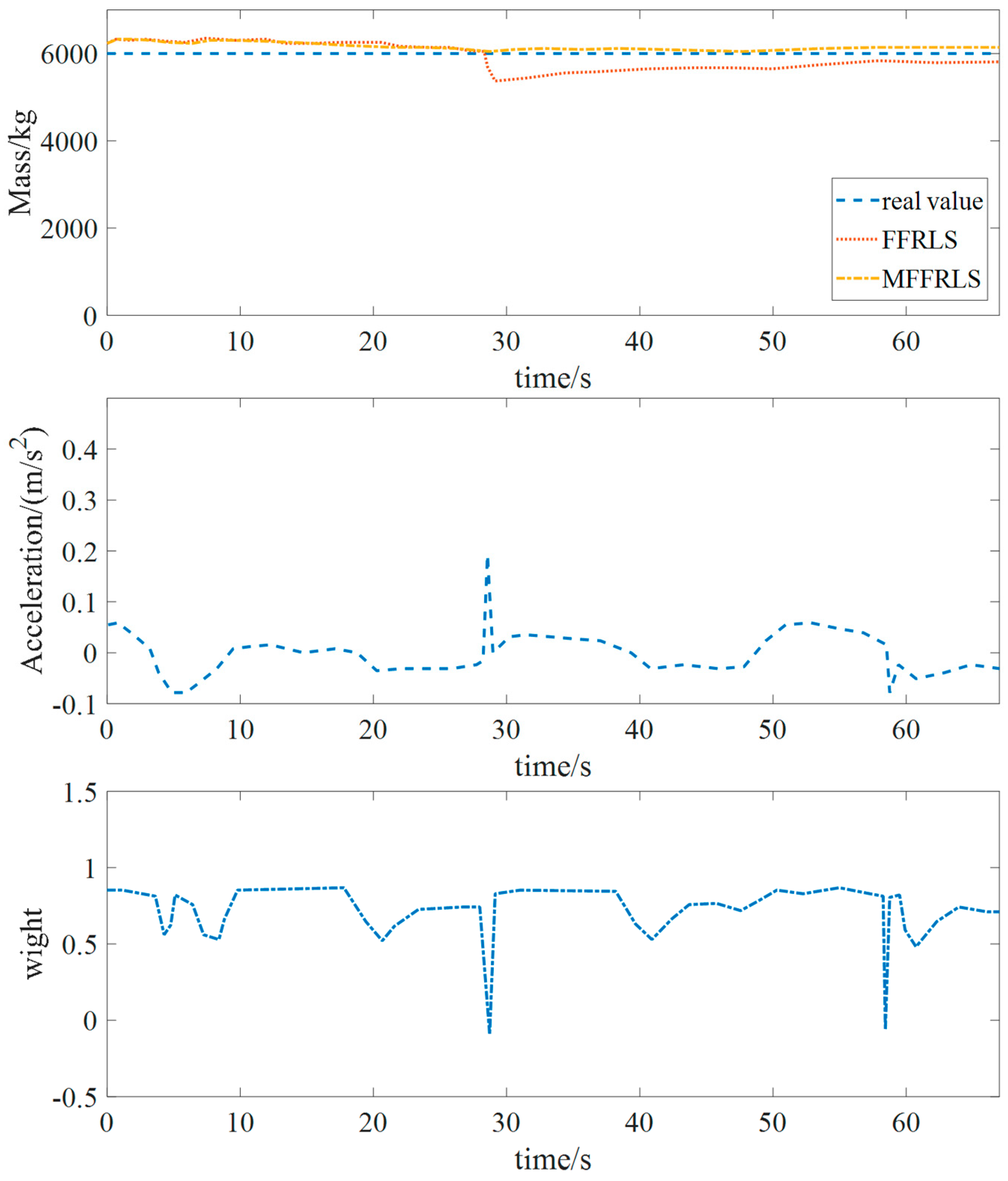
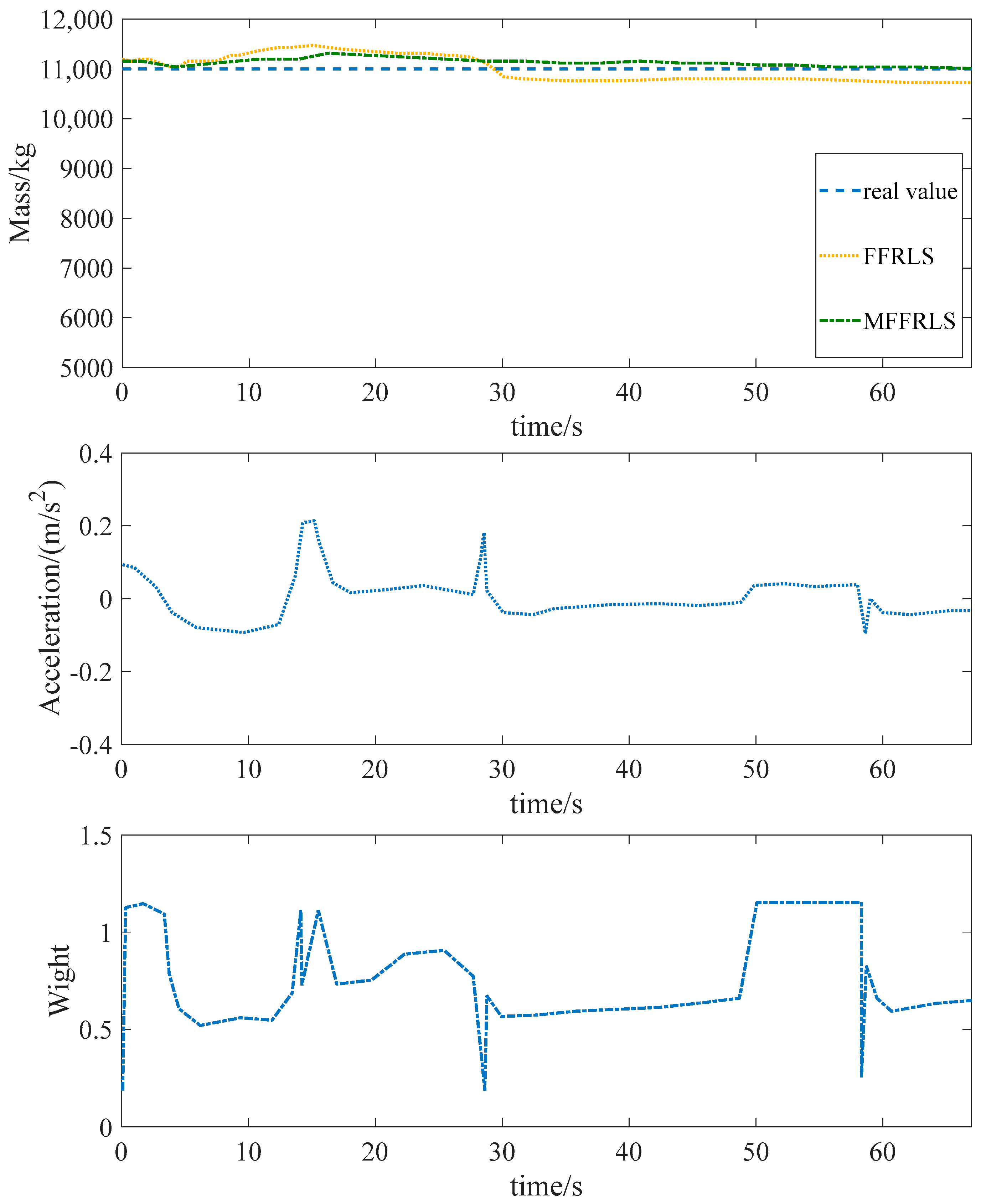
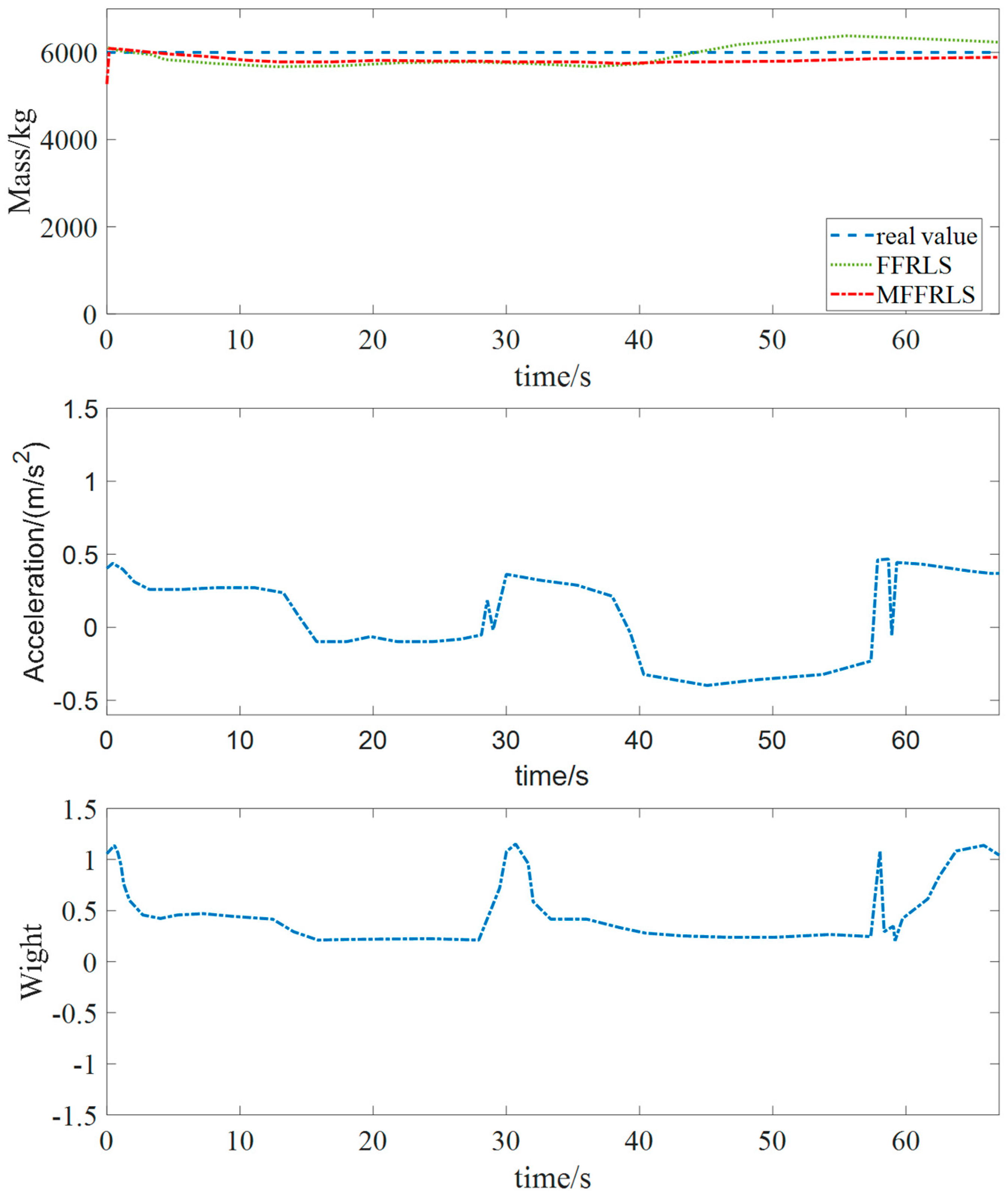
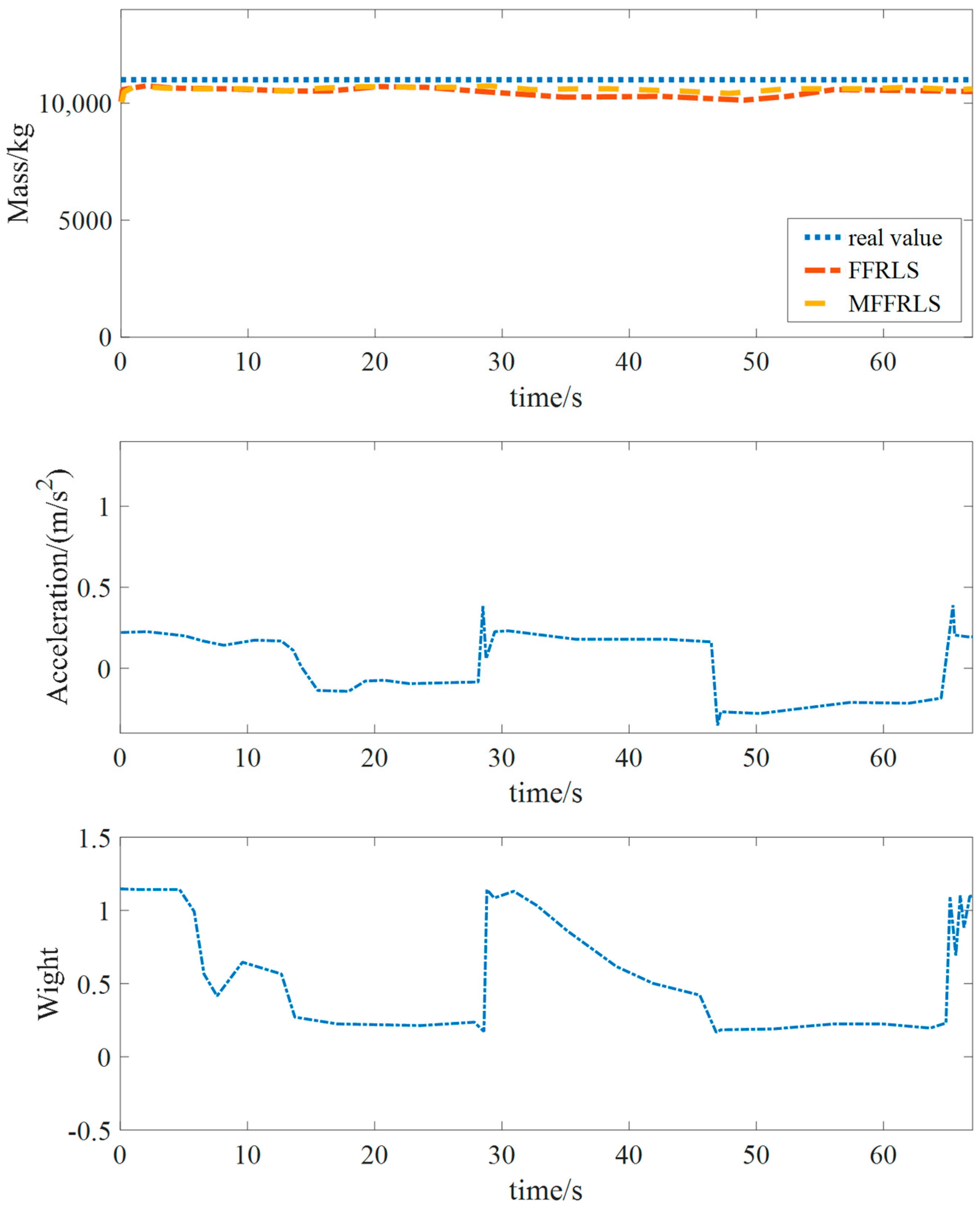
5.2.1. Simulation Test of Mass Estimation Under Different Accelerations
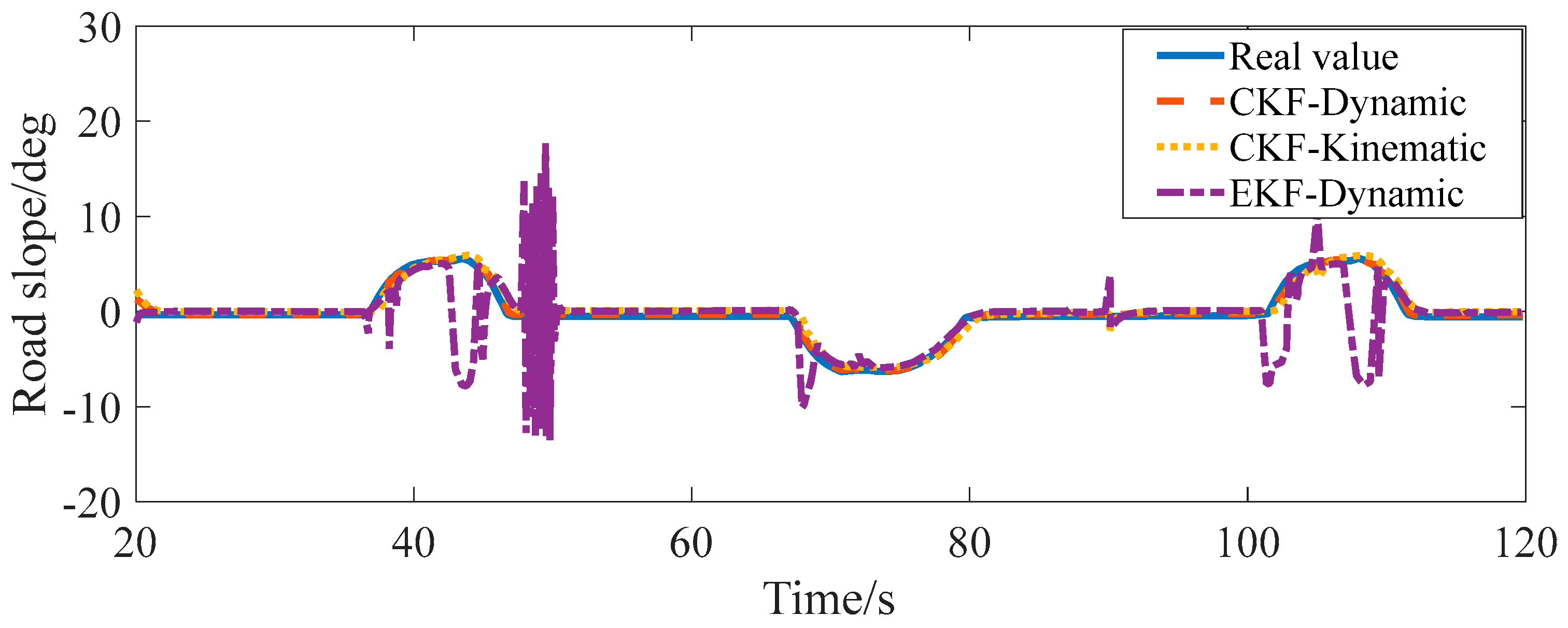
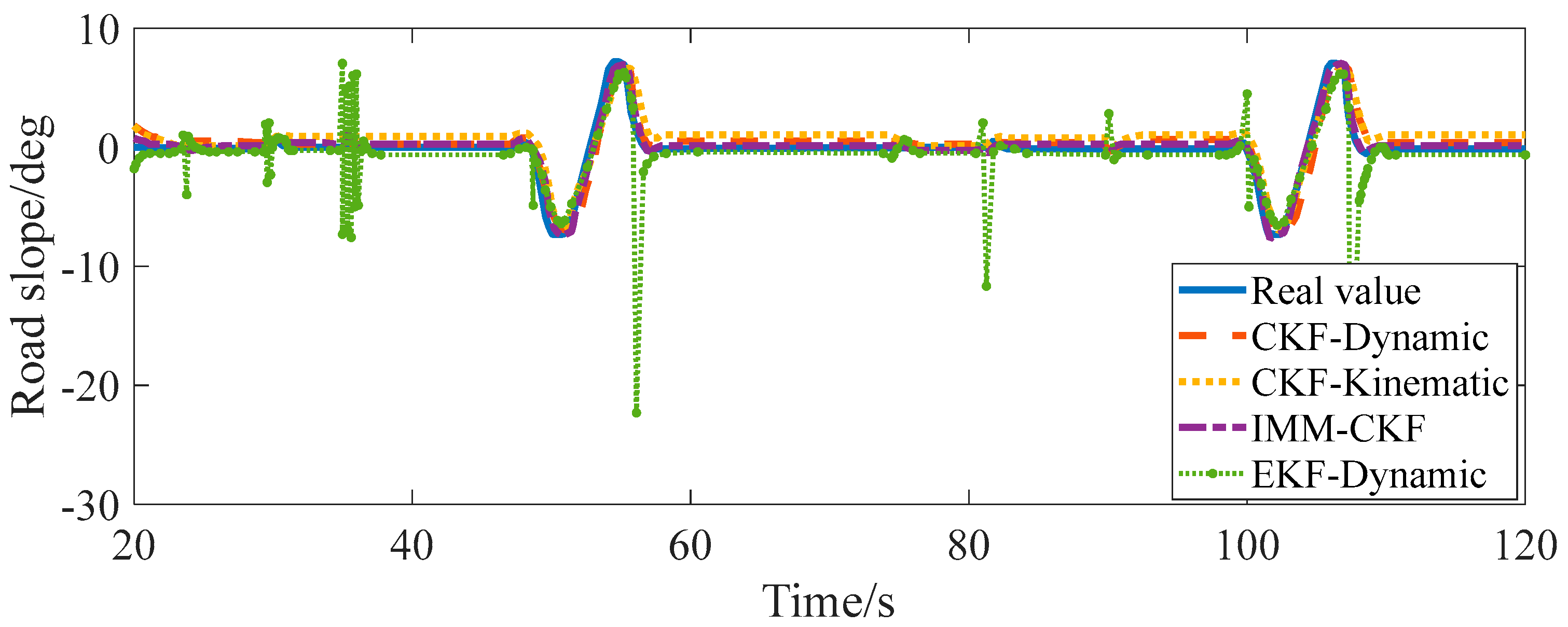
5.2.2. Simulation Experiment of Slope Estimation Under Complex Coupled Road Conditions
5.3. Analysis of Error Results
6. Conclusions
- (1)
- By combining the M-estimation method with the recursive least squares method with a forgetting factor, the mass estimation of trucks is realized. Under both the micro-acceleration and normal acceleration working conditions, the estimation accuracy of the MFFRLS (M-estimation-based Forgetting Factor Recursive Least Squares) is superior to that of the FFRLS (Forgetting Factor Recursive Least Squares) algorithm, and it has strong anti-interference characteristics.
- (2)
- Aiming at the complex situation that combines the working conditions of straight uphill and downhill and continuous turning uphill and downhill, a road slope estimation algorithm based on the IMM-CKF is proposed. Under different load conditions, compared with the estimation algorithm based on a single model, the accuracy of the estimation results of the proposed algorithm is improved by 3%, and it has good robustness.
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| road slope angle (deg) | |
| longitudinal acceleration of the vehicle (m/s2) | |
| total mass of commercial vehicles (kg) | |
| driving torque of the vehicle (N·m) | |
| transmission ratio of commercial vehicle transmissions | |
| final transmission ratio of the entire transmission system | |
| transmission efficiency (%) | |
| rolling radius of the wheel (m) | |
| wind resistance coefficient | |
| windward area of the vehicle (m2) | |
| air density (kg/m3) | |
| gravitational acceleration (m/s2) | |
| rolling resistance coefficient of the vehicle | |
| wheel radius (m) | |
| longitudinal acceleration value measured by the acceleration sensor (m/s2) | |
| lateral speed of the vehicle (m/s) | |
| yaw rate (rad/s) | |
| longitudinal force of the tire (N) | |
| lateral force of the tire (N) | |
| front wheel angle (deg) |
References
- Shi, J.; Lu, T.; Li, X.; Zhang, J. Self-adaptive slope gearshift strategy for automatic transmission vehicles. Trans. Chin. Soc. Agric. Mach. 2011, 42, 1–7. [Google Scholar]
- Yin, Z.; Dai, Q.; Guo, H.; Chen, H.; Chao, L. Estimation road slope and longitudinal velocity for four-wheel drive vehicle. IFAC-PapersOnLine 2018, 51, 72–577. [Google Scholar] [CrossRef]
- Xu, S.; Li, S.E.; Cheng, B.; Li, K. Instantaneous feedback control for a fuel-prioritized vehicle cruising system on highways with a varying slope. IEEE Trans. Intell. Transp. Syst. 2016, 18, 1210–1220. [Google Scholar] [CrossRef]
- Li, S.E.; Guo, Q.; Xu, S.; Duan, J.; Li, S.; Li, C.; Su, K. Performance enhanced predictive control for adaptive cruise control system considering road elevation information. IEEE Trans. Intell. Veh. 2017, 2, 150–160. [Google Scholar] [CrossRef]
- Jin, M.; Zhao, J.; Jin, J.; Yu, G.; Li, W. The adaptive Kalman filter based on fuzzy logic for inertial motion capture system. Measurement 2014, 49, 196–204. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, L.; Li, J.; Ouyang, M. Real-time estimation of vehicle mass and road grade based on multi-sensor data fusion. In Proceedings of the 2013 IEEE Vehicle Power and Propulsion Conference (VPPC), Beijing, China, 15–18 October 2013. [Google Scholar]
- Apriliani, E.; Nurhadi, H. Ensemble and Fuzzy Kalman Filter for position estimation of an autonomous underwater vehicle based on dynamical system of AUV motion. Expert Syst. Appl. 2017, 68, 29–35. [Google Scholar]
- Johansson, K. Road Slope Estimation with Standard Truck Sensors; KTH: Stockholm, Sweden, 2005. [Google Scholar]
- Hao, S.; Luo, P.; Xi, J. Estimation of vehicle mass and road slope based on steady-state Kalman filter. In Proceedings of the 2017 IEEE International Conference on Unmanned Systems (ICUS), Beijing, China, 27–29 October 2017. [Google Scholar]
- Massel, T.; Ding, E.; Arndt, M. Investigation of different techniques for determining the road uphill gradient and the pitch angle of vehicles. In Proceedings of the 2004 American Control Conference, Boston, MA, USA, 30 June–2 July 2004; Volume 3. [Google Scholar]
- McIntyre, M.L.; Ghotikar, T.J.; Vahidi, A.; Song, X.; Dawson, D.M. A two-stage Lyapunov-based estimator for estimation of vehicle mass and road grade. IEEE Trans. Veh. Technol. 2009, 58, 3177–3185. [Google Scholar] [CrossRef]
- Lei, Y.; Fu, Y.; Liu, K.; Zeng, H.; Zhang, Y. Vehicle Mass and Road Grade Estimation Based on Extended Kalman Filter. Trans. Chin. Soc. Agric. Mach. 2014, 45, 9–14. [Google Scholar]
- Lingman, P.; Schmidtbauer, B. Road slope and vehicle mass estimation using Kalman filtering. Veh. Syst. Dyn. 2002, 37 (Suppl. 1), 12–23. [Google Scholar] [CrossRef]
- Bar-Shalom, Y.; Li, X.R.; Kirubarajan, T. Estimation with Applications to Tracking and Navigation: Theory Algorithms and Software; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Tsunashima, H.; Murakami, M.; Miyataa, J. Vehicle and road state estimation using interacting multiple model approach. Veh. Syst. Dyn. 2006, 44 (Suppl. 1), 750–758. [Google Scholar] [CrossRef]
- Blom, H.; Bar-Shalom, Y. The interacting multiple model algorithm for systems with Markovian switching coefficients. IEEE Trans. Autom. Control. 1988, 33, 780–783. [Google Scholar] [CrossRef]
- Barrios, C.; Himberg, H.; Motai, Y.; Sadek, A. Multiple model framework of adaptive extended Kalman filtering for predicting vehicle location. In Proceedings of the 2006 IEEE Intelligent Transportation Systems Conference, Toronto, ON, Canada, 17–20 September 2006. [Google Scholar]
- Ndjeng, A.N.; Glaser, S.; Gruyer, D. A multiple model localization system for outdoor vehicles. In Proceedings of the 2007 IEEE Intelligent Vehicles Symposium, Istanbul, Turkey, 13–15 June 2007. [Google Scholar]
- Dawood, M.; Cappelle, C.; El Najjar, M.E.; Khalil, M.; Pomorski, D. Vehicle geo-localization based on IMM-UKF data fusion using a GPS receiver, a video camera and a 3D city model. In Proceedings of the 2011 IEEE Intelligent Vehicles Symposium (IV), Baden, Germany, 5–9 June 2011. [Google Scholar]
- Zhang, Z.; Zheng, L.; Li, Y.; Yu, Y. Research on intelligent vehicle target state tracking based on robust adaptive sckf. J. Mech. Eng. 2021, 57, 181–193. [Google Scholar]
- He, Y.; Yan, X.; Chu, D.; Lu, X.-Y.; Wu, C. A probabilistic prediction model for the safety assessment of HDVs under complex driving environments. IEEE Trans. Intell. Transp. Syst. 2016, 18, 858–868. [Google Scholar] [CrossRef]
- Li, E.; He, W.; Yu, H.; Xi, J. Model-based embedded road grade estimation using quaternion unscented kalman filter. IEEE Trans. Veh. Technol. 2022, 71, 3704–3714. [Google Scholar] [CrossRef]
- Liu, W.; He, H.; Sun, F. Vehicle state estimation based on minimum model error criterion combining with extended Kalman filter. J. Frankl. Inst. 2016, 353, 834–856. [Google Scholar] [CrossRef]
- Pacejka, H.B.; Bakker, E. The magic formula tyre model. Veh. Syst. Dyn. 1992, 21, 1–18. [Google Scholar] [CrossRef]
- Guo, K.; Lu, D.; Chen, S.-K.; Lin, W.C.; Lu, X.-P. The UniTire model: A nonlinear and non-steady-state tyre model for vehicle dynamics simulation. Veh. Syst. Dyn. 2005, 43, 341–358. [Google Scholar] [CrossRef]
- Jo, K.; Chu, K.; Sunwoo, M. Interacting multiple model filter-based sensor fusion of GPS with in-vehicle sensors for real-time vehicle positioning. IEEE Trans. Intell. Transp. Syst. 2011, 13, 329–343. [Google Scholar] [CrossRef]
- Toledo-Moreo, R.; Zamora-Izquierdo, M.A.; Ubeda-Minarro, B.; Gómez-Skarmeta, A.F. High-integrity IMM-EKF-based road vehicle navigation with low-cost GPS/SBAS/INS. IEEE Trans. Intell. Transp. Syst. 2007, 8, 491–511. [Google Scholar] [CrossRef]



| Parameter Name | Value |
|---|---|
| Vehicle mass | 6000 kg |
| Effective rolling radius of the tire | 0.6 m |
| Transmission efficiency | 0.92 |
| Air density | 1.206 kg/m3 |
| Windward area A | 0.8 m2 |
| Drag coefficient | 7 |
| Test Conditions | Load Mass |
|---|---|
| Micro-acceleration | 0 kg |
| Micro-acceleration | 5000 kg |
| Normal acceleration | 0 kg |
| Normal acceleration | 5000 kg |
| Parameter | Load Mass (kg) | FFRLS | MFFRLS |
|---|---|---|---|
| Vehicle mass | 0 | 269.72 | 167.34 |
| 3000 | 222.12 | 175.37 | |
| 5000 | 259.16 | 169.75 |
| Parameter | Load Mass (kg) | FFRLS | MFFRLS |
|---|---|---|---|
| Vehicle mass | 0 | 269.72 | 159.28 |
| 3000 | 390.11 | 311.78 | |
| 5000 | 406.57 | 345.67 |
| Parameter | Load Mass | Dynamic Model | Kinematic Model | IMM_CKF |
|---|---|---|---|---|
| Slope | 0 | 0.331 | 2.547 | 0.328 |
| 3000 | 0.348 | 2.387 | 0.331 | |
| 5000 | 0.309 | 2.648 | 0.301 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, G. Estimation of Vehicle Mass and Road Slope for Commercial Vehicles Utilizing an Interacting Multiple-Model Filter Method Under Complex Road Conditions. World Electr. Veh. J. 2025, 16, 172. https://doi.org/10.3390/wevj16030172
Liu G. Estimation of Vehicle Mass and Road Slope for Commercial Vehicles Utilizing an Interacting Multiple-Model Filter Method Under Complex Road Conditions. World Electric Vehicle Journal. 2025; 16(3):172. https://doi.org/10.3390/wevj16030172
Chicago/Turabian StyleLiu, Gang. 2025. "Estimation of Vehicle Mass and Road Slope for Commercial Vehicles Utilizing an Interacting Multiple-Model Filter Method Under Complex Road Conditions" World Electric Vehicle Journal 16, no. 3: 172. https://doi.org/10.3390/wevj16030172
APA StyleLiu, G. (2025). Estimation of Vehicle Mass and Road Slope for Commercial Vehicles Utilizing an Interacting Multiple-Model Filter Method Under Complex Road Conditions. World Electric Vehicle Journal, 16(3), 172. https://doi.org/10.3390/wevj16030172





