Multi-UAV Delivery Path Optimization Based on Fuzzy C-Means Clustering Algorithm Based on Annealing Genetic Algorithm and Improved Hopfield Neural Network
Abstract
1. Introduction
- Multi-algorithm fusion: by combining the advantages of an SA, GA, and FCM and an improved HNN, a dynamic balance between the global search and local optimization is achieved.
- Fuzzy clustering guidance: the FCM is used to fuzzy divide the problem space, and the algorithm is guided to search in key areas to reduce the computational complexity.
- Dynamic collaboration mechanism: through the dynamic collaboration mechanism, the SA-GA-FCM and improved HNN can give full play to their respective advantages at different stages and significantly improve the solution efficiency.
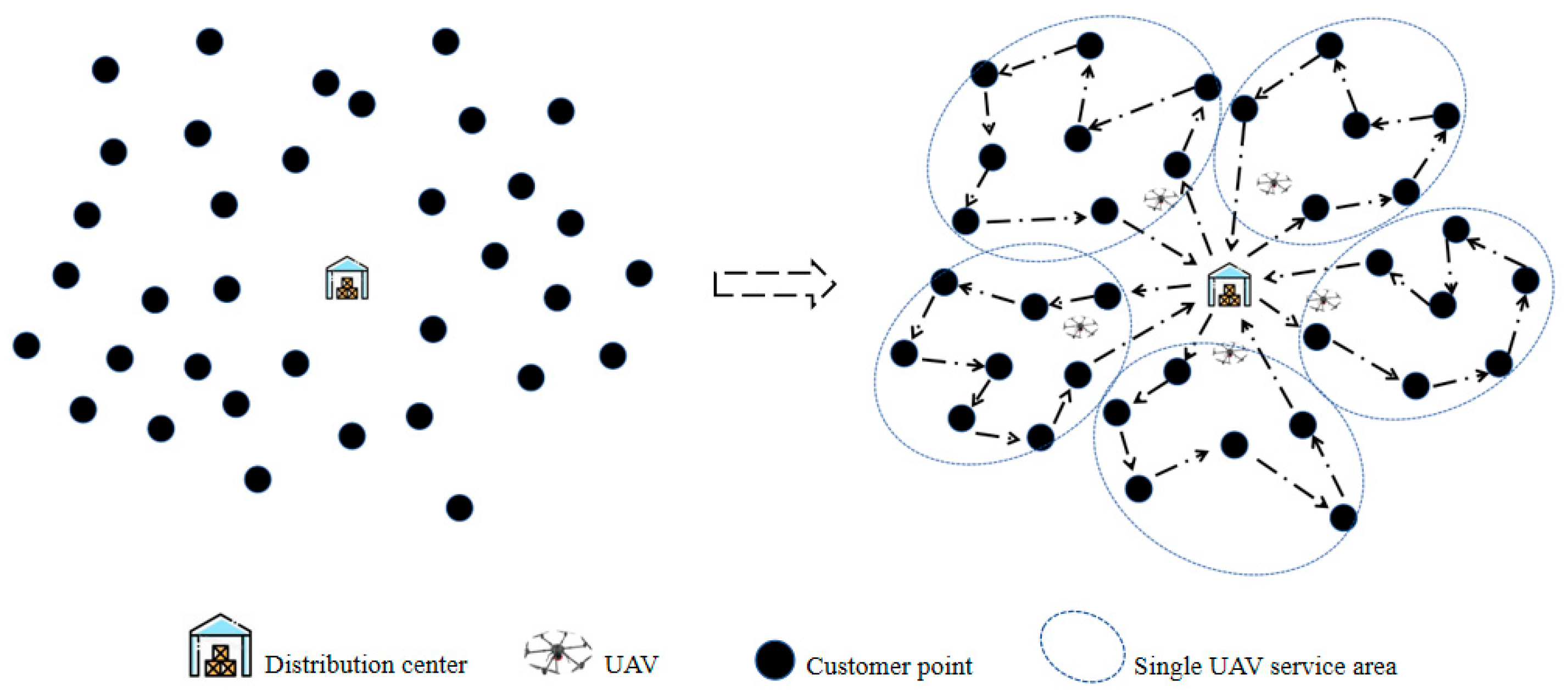
2. Modeling the MTSP of Multi-UAV Collaborative Distribution
2.1. Problem Description
- (1)
- The demand and coordinates of each customer are known;
- (2)
- The speed of each UAV is the same and constant, regardless of the influence of weather on the UAV;
- (3)
- There is only one distribution center in an area;
- (4)
- Each customer can be served once and only by one UAV;
- (5)
- The take-off and landing time of UAVs and the time to serve customers are not considered.
2.2. Mathematical Model
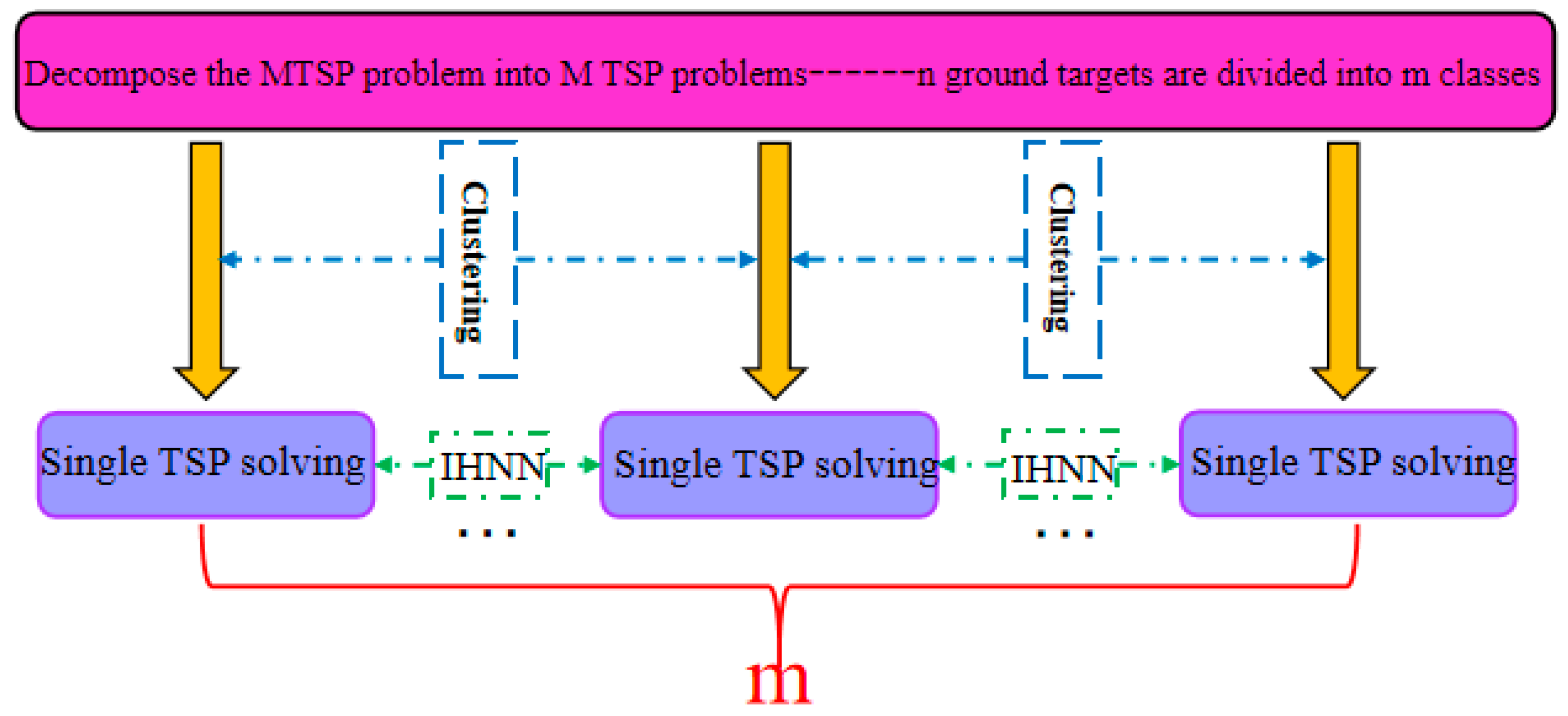
3. Hybrid Optimization Algorithm for Solving MTSP
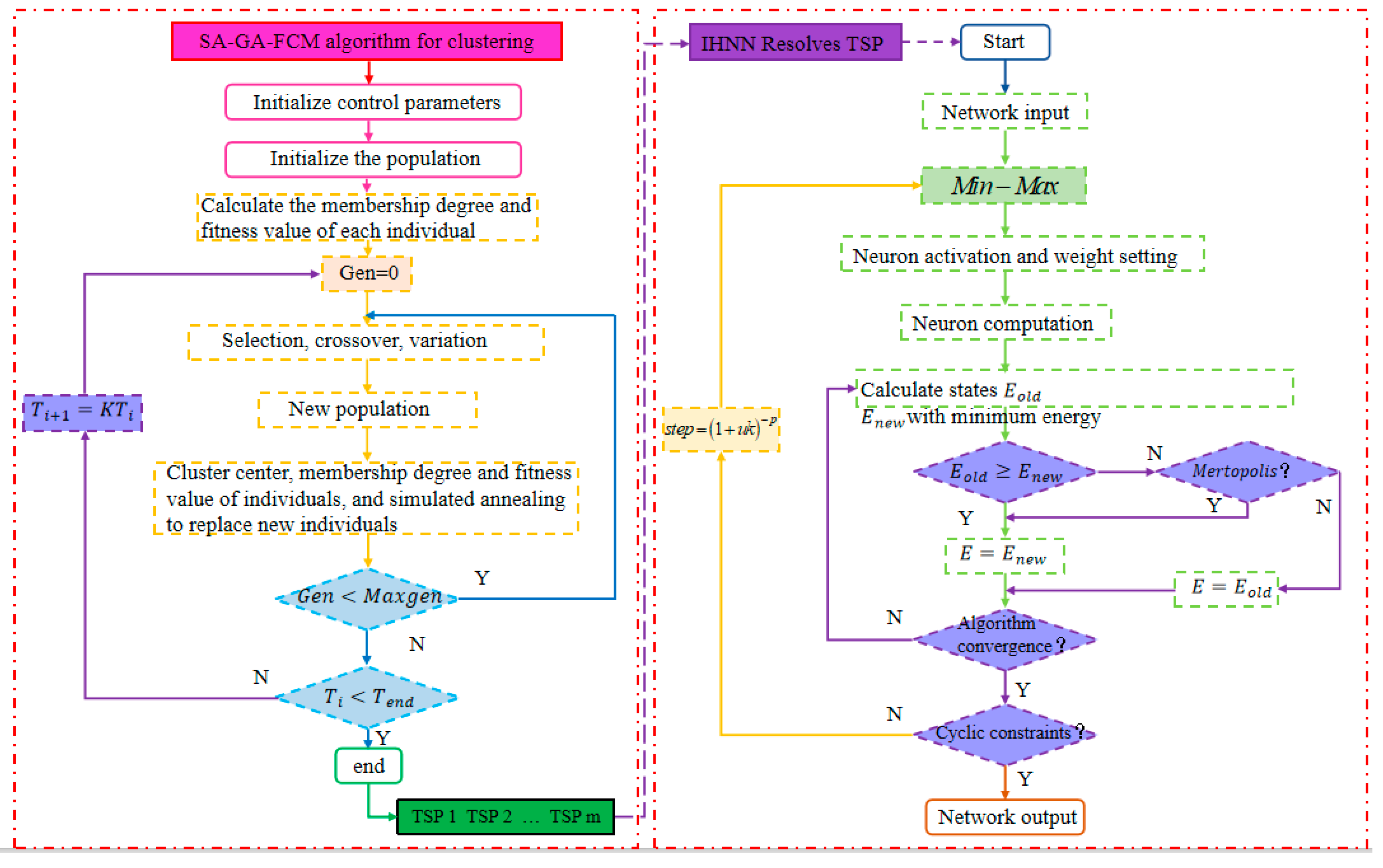
3.1. Fuzzy C-Means Clustering Algorithm Based on Annealing Genetic Algorithm (SA-GA-FCM)
- Denote as the individual size of the population; as the maximum number of evolution; and , represent the probability of crossover and mutation, respectively. and represent the initial temperature and the termination temperature when the annealing operation is performed, respectively, and represents the cooling coefficient of the temperature.
- Randomly calculate the number of clustering centers c; at this time, an initial population is generated, denoted as C. Using Formulas (15) and (16), the membership degree of each sample in the cluster center and the fitness value of each individual in the population are calculated.
- Set the loop parameters so that GEN = 0.
- Perform a genetic operation on population C, that is, selection, crossover, and mutation, and new individuals will be generated at this time. In the same step ②, calculate the clustering center of the new individuals, the membership degree of the samples at this time, and the fitness value of each individual in the new population. If , the old individual is abandoned and the newly generated individual is accepted; otherwise, the probability is calculated to accept the new individual with a probability of .
- If Gen < M, let Gen = Gen + 1, and return to step 4 to continue the cycle; otherwise, proceed directly to step ⑥.
- If , it means that the algorithm ended successfully, and the global optimal solution is output at this time; otherwise, the cooling operation is performed according to the annealing algorithm , and return to step ③ to continue the cycle.
3.2. Improved Hopfield Neural Network Algorithm (IHNN)
3.2.1. Data Normalization
3.2.2. The Introduction of Dynamic Step Size
3.2.3. Application of Simulated Annealing Algorithm
3.3. Algorithm Flow
4. Simulation Analysis
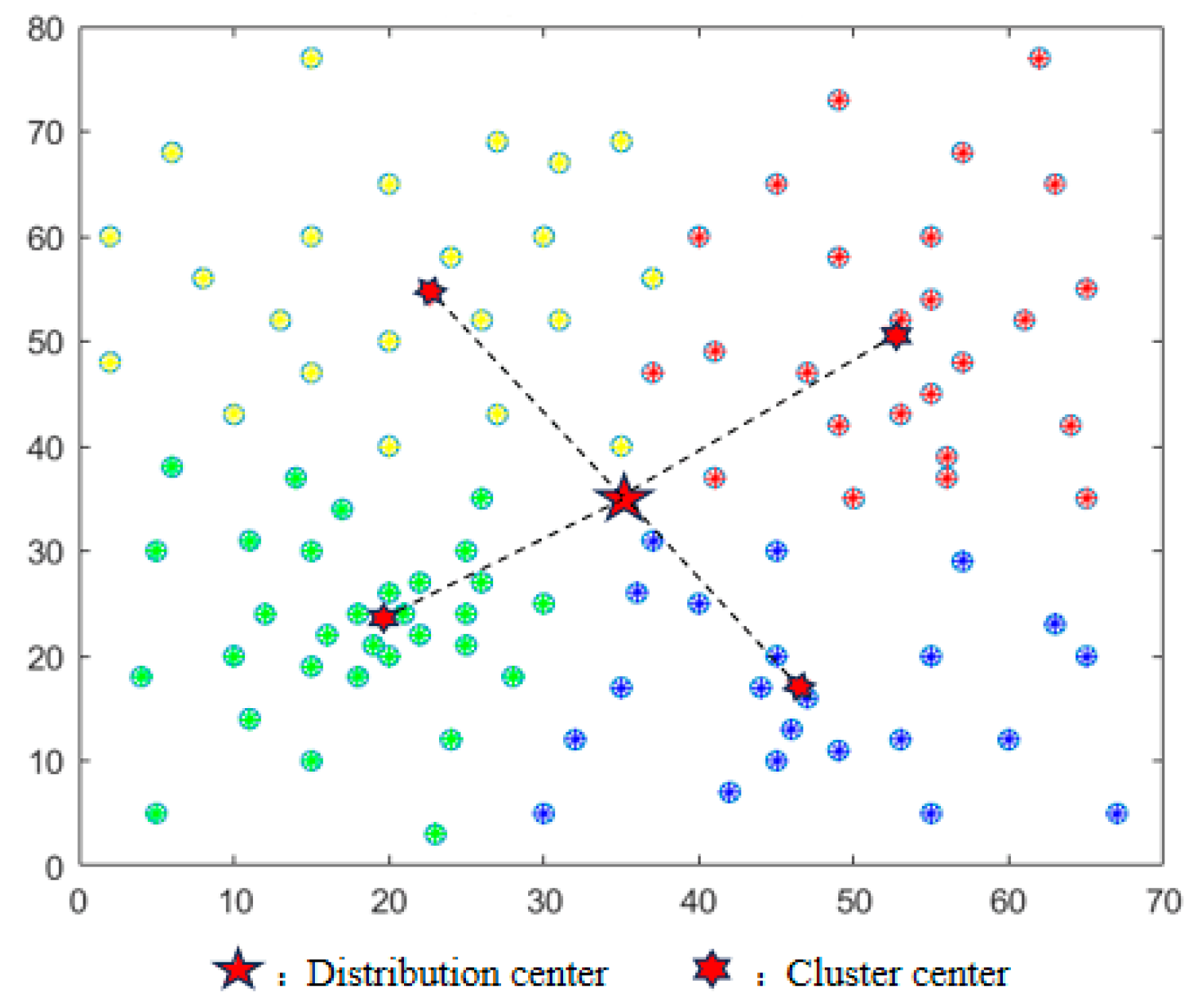
4.1. Simulation of Clustering Problem
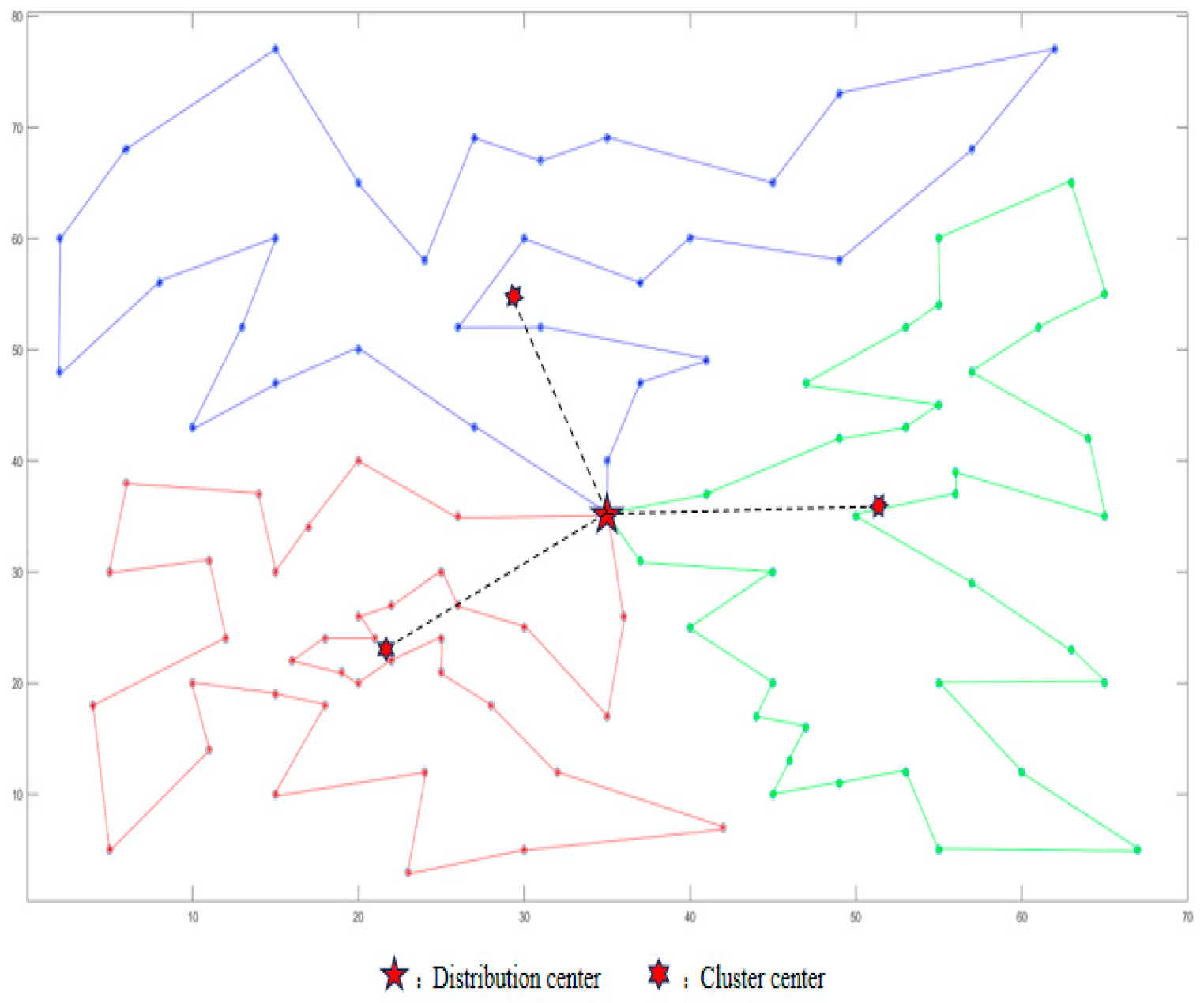
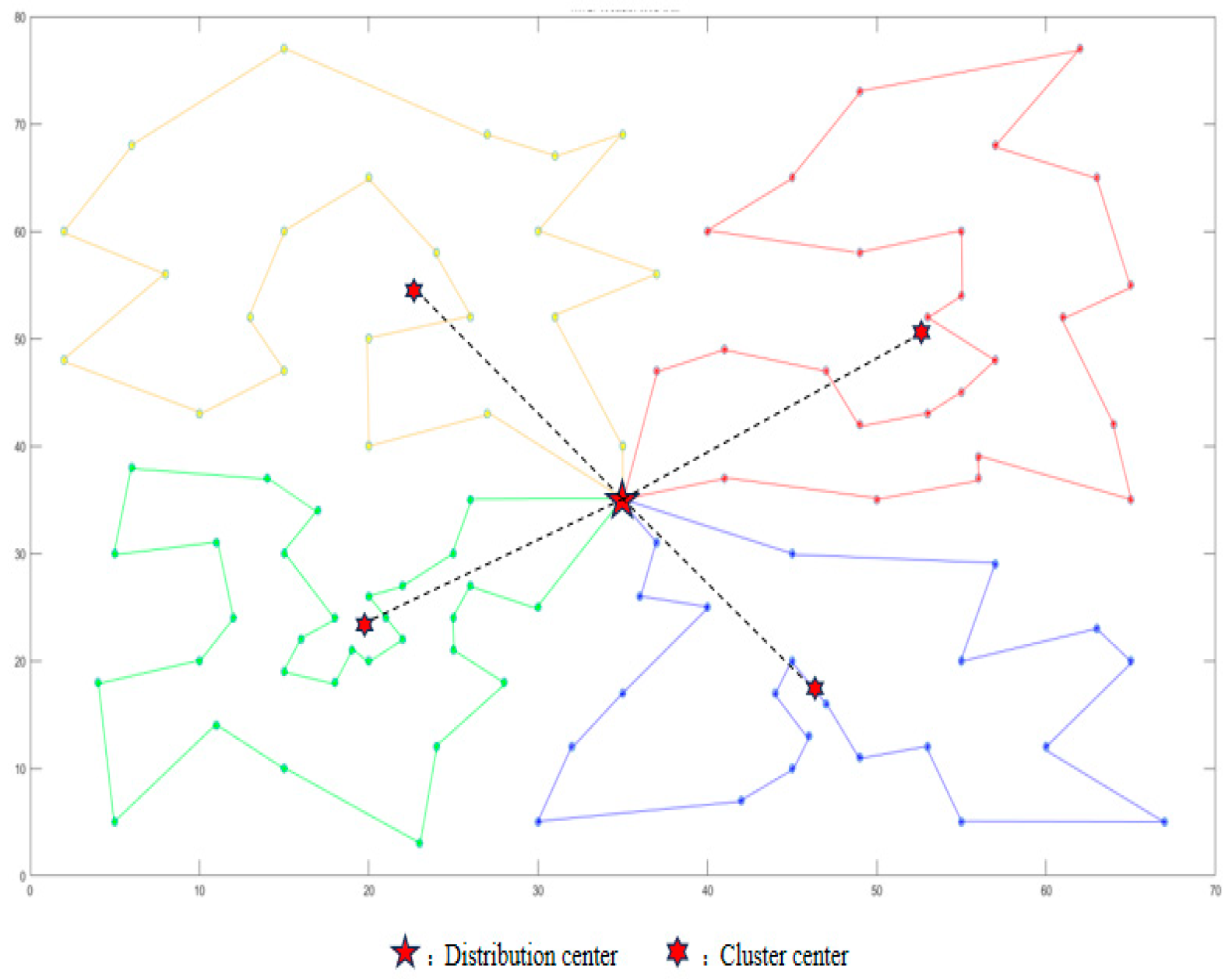
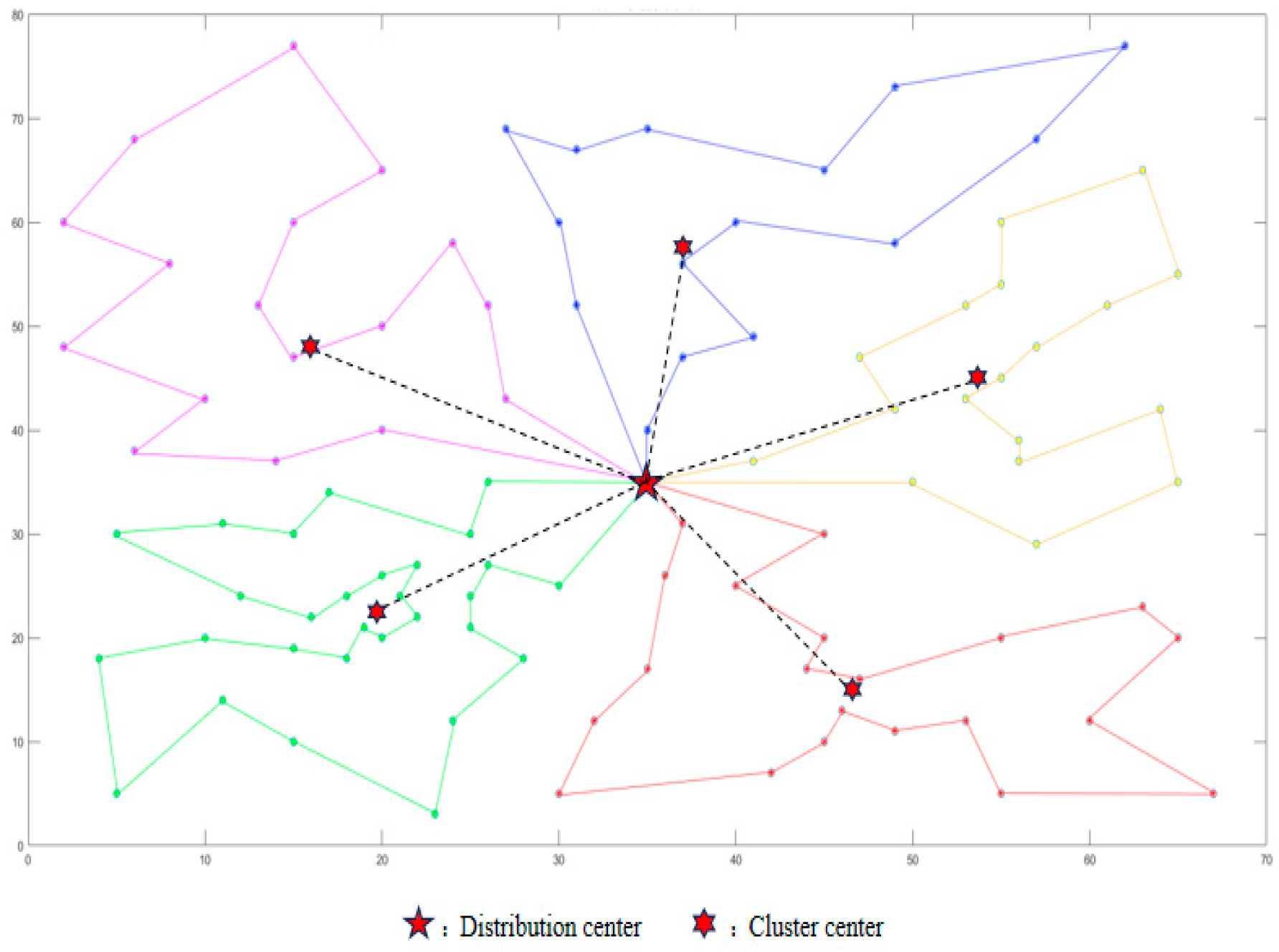
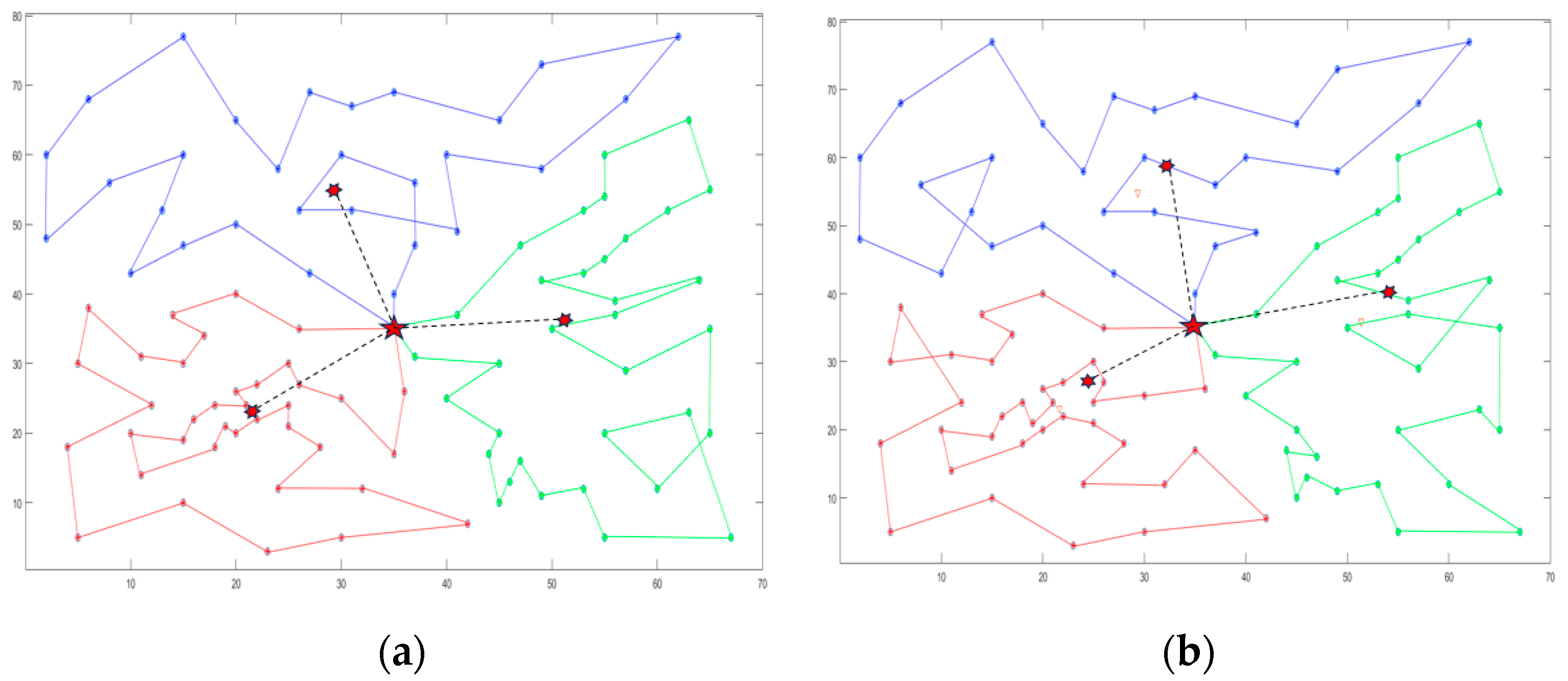
4.1.1. Clustering Results Analysis
4.1.2. Comparison of Clustering Algorithms
4.2. Simulation of Path Problem
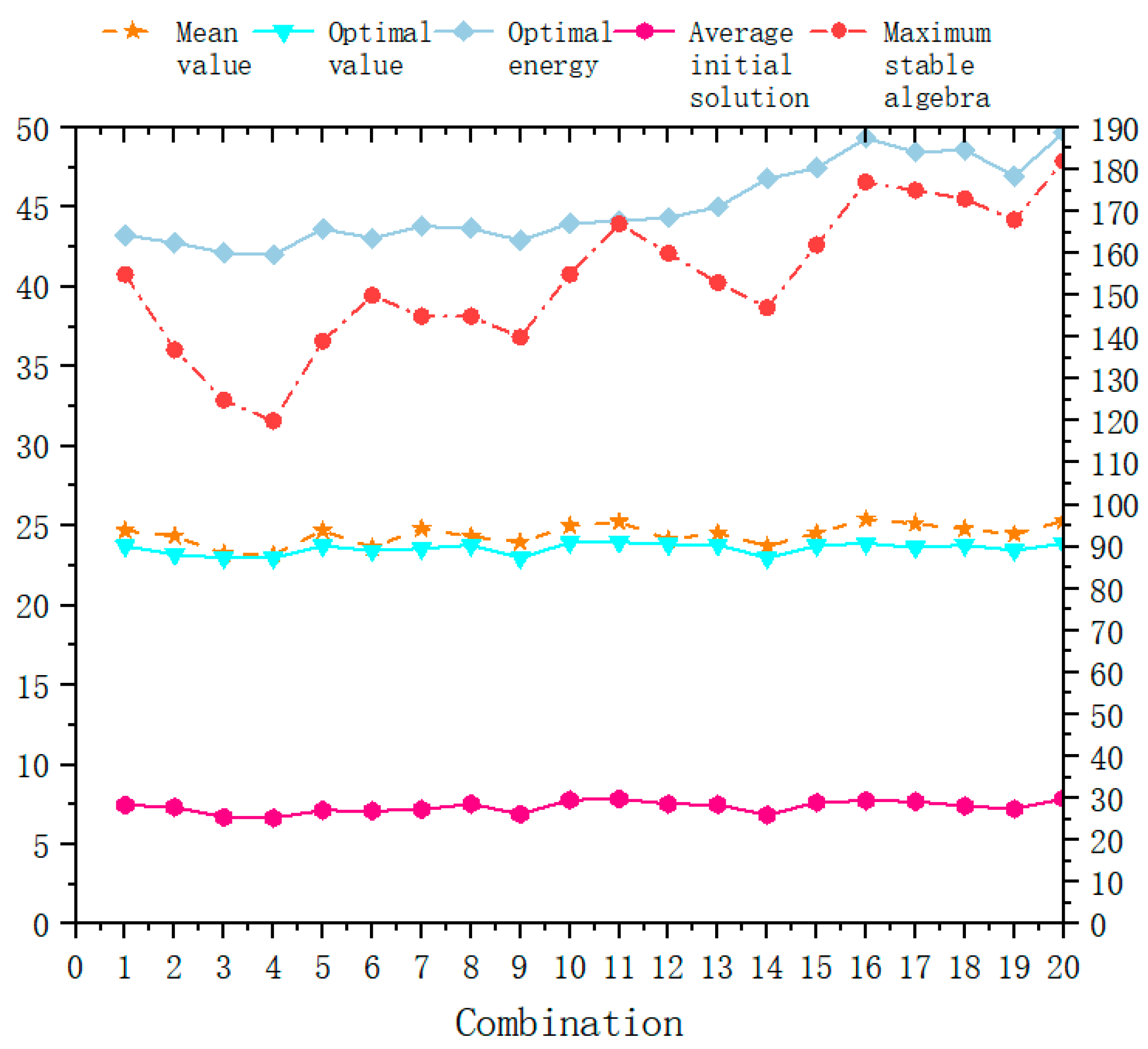
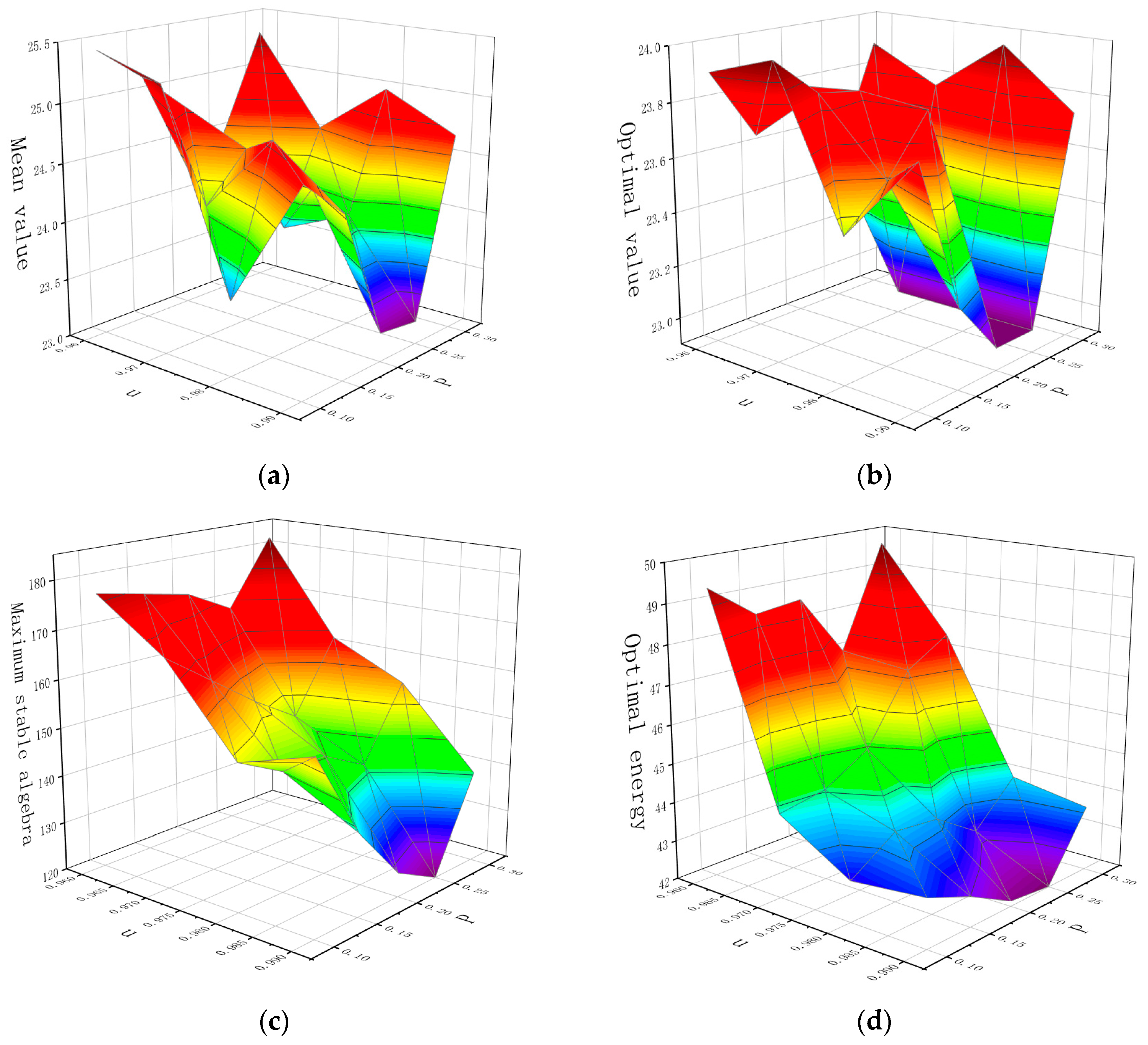
4.2.1. Parameter Sensitivity Analysis
4.2.2. Path Simulation Analysis
4.2.3. Comparison of Optimization Algorithms
5. Conclusions
- (1)
- A clustering algorithm is used to cluster the large-scale customer points, and the UAVs are delivered to the areas that need service. A stable clustering value is obtained each time, and the clustering effect is good.
- (2)
- In terms of path optimization, the IHNN algorithm designed in this paper has an improved computation efficiency, convergence, and results, and the shortest path and iteration times are reduced to different degrees compared with the genetic algorithm and ant colony algorithm.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, Z.; Li, X. Optimization model of cold chain logistics delivery path based on genetic algorithm. Int. J. Ind. Eng. Theory Appl. Pract. 2024, 31, 152. [Google Scholar]
- Chen, C.; Luo, Z.; Du, S. Optimization of electric vehicle-UAV collaborative distribution path under partial charging strategy. J. Chang. Univ. Sci. Technol. 2025, 1–11. [Google Scholar] [CrossRef]
- Wang, J.Q.; Gao, X.G.; Shi, J.G.; Li, B. Unmanned Aerial Vehicle’s Path Planning for Scout. Fire Control Command. Control 2008, 33, 16–18. [Google Scholar]
- Fu, Z.T.; Hu, Z.H.; Fei, H.P. Hazardous container yard patrol optimization research with UAVS. J. Railw. Sci. Eng. 2017, 14, 2467–2471. [Google Scholar] [CrossRef]
- Liu, W.B.; Wang, Y.D. Path planning of Multi-UAV cooperative search for multiple targets. Electron. Opt. Control 2019, 26, 35–38, 73. [Google Scholar]
- Cao, Z.K. UAV-Based Land Surveying Route Planning and Scheduling. J. Geomat. 2021, 46, 64–67. [Google Scholar]
- Mao, H.T.; Shi, J.M.; Zhou, Y.Z.; Liu, Z. Small UAV routing planning for reconnaissance missions with recharging. J. Command. Control 2022, 8, 206–213. [Google Scholar]
- Wang, S.; Lv, X.; Li, Y.; Jing, L.; Fang, X.; Peng, G.; Zhou, Y.; Sun, W. A novel hybrid improved dingo algorithm for unmanned aerial vehicle path planning. J. Braz. Soc. Mech. Sci. Eng. 2025, 47, 10. [Google Scholar] [CrossRef]
- Hu, K.; Mo, Y. A novel unmanned aerial vehicle path planning approach: Sand cat optimization algorithm incorporating learned behaviour. Meas. Sci. Technol. 2024, 35, 046203. [Google Scholar] [CrossRef]
- Wang, Z.; Sun, G.; Zhou, K.; Zhu, L. A parallel particle swarm optimization and enhanced sparrow search algorithm for unmanned aerial vehicle path planning. Heliyon 2023, 9, e14784. [Google Scholar] [CrossRef]
- Ait-Saadi, A.; Meraihi, Y.; Soukane, A.; Yahia, S.; Ramdane-Cherif, A.; Gabis, A.B. An enhanced African vulture optimization algorithm for solving the unmanned aerial vehicles path planning problem. Comput. Electr. Eng. 2023, 110, 108802. [Google Scholar] [CrossRef]
- Van Nguyen, L.; Kwok, N.M.; Ha, Q.P. Fermat-Weber location particle swarm optimization for cooperative path planning of unmanned aerial vehicles. Appl. Soft Comput. 2024, 167, 112269. [Google Scholar] [CrossRef]
- Hopfield, J.J.; Tank, D.W. Neural computation of decisions in optimization problems. Biol. Cybern. 1985, 52, 141–152. [Google Scholar] [CrossRef]
- Chen, X.; Ruan, C. An improvement of Hopfield network to solve TSP algorithm. J. Beijing Univ. Posts Telecommun. 1996, 99–102. [Google Scholar]
- Dang, J.; Jin, F. Research on the application of neural network in solving MTSP. J. China Railw. Soc. 1997, 64–70. [Google Scholar]
- Wang, C.; Xuan, G. A new method of artificial neural network to solve TSP problem. Comput. Appl. Softw. 2001, 59–65. [Google Scholar] [CrossRef]
- Yan, C.; Wang, Z. Research on TSP problem based on improved energy function and transient chaotic neural network. J. Syst. Simul. 2006, 1402–1405. [Google Scholar]
- Jolai, F.; Ghanbari, A. Integrating data transformation techniques with Hopfield neural networks for solving travelling salesman problem. Expert Syst. Appl. 2010, 37, 5331–5335. [Google Scholar] [CrossRef]
- An, J.L.; Gao, J.; Lei, J.H.; Gao, G.H. An improved algorithm for TSP problem solving with Hopfield neural networks. Adv. Mater. Res. 2011, 143, 538–542. [Google Scholar] [CrossRef]
- Lin, N.; Liu, H. Dynamic route guidance algorithm based on improved hopfield neural network and genetic algorithm. Int. J. Innov. Comput. Inf. Control 2014, 10, 811–822. [Google Scholar]
- Guo, Z.; Jin, L.; Zheng, C. Research on improved algorithm of artificial neural network for solving TSP problem. Comput. Simul. 2014, 31, 355–358. [Google Scholar]
- Tarkov, M.S. Solving the traveling salesman problem using a recurrent neural network. Numer. Anal. Appl. 2015, 8, 275–283. [Google Scholar] [CrossRef]
- Kai, C. An ad-hoc network routing algorithm based on improved neural network under the influence of COVID-19. J. Intell. Fuzzy Syst. 2020, 39, 8767–8774. [Google Scholar] [CrossRef]
- Hu, Y.; Duan, Q. Solving the TSP by the AALHNN algorithm. Math. Biosci. Eng. 2022, 19, 3427–3448. [Google Scholar] [CrossRef]
- Dutta, G. Solving The Travelling Salesmen Problem using HNN and HNN-SA algorithms. arXiv 2022, arXiv:2202.13746. [Google Scholar]
- Comert, S.E.; Yazgan, H.R.; Turk, G. Hopfield neural network based on clustering algorithms for solving green vehicle routing problem. Int. J. Ind. Eng. Comput. 2022, 13, 573–586. [Google Scholar] [CrossRef]
- Almuhanna, H.; Alenezi, M.; Abualhasan, M.; Alfadhli, R.; Alajmi, S.; Aldashti, Z.; Salman, M. A Novel Hybrid Solution for Traveling Salesman Problem. In International Conference on Advanced Engineering, Technology and Applications; Springer Nature: Cham, Switzerland, 2024. [Google Scholar]
- Li, X.; Yang, X.; Ju, X. A novel fractional-order memristive Hopfield neural network for traveling salesman problem and its FPGA implementation. Neural Netw. 2024, 179, 106548. [Google Scholar] [CrossRef]
- Che, H.; Chen, K.; Wang, Y.; Liu, X. Fuzzy C-means clustering algorithm with deep neighborhood information. J. Huazhong Univ. Sci. Tech. (Nat. Sci. Ed.) 2022, 50, 135–141. [Google Scholar]
- Bai, L.; Hu, S.; Liu, S. A Fuzzy Clustering Algorithm Based on Simulated Annealing and Genetic Algorithm. Comput. Eng. Appl. 2005, 41, 55–59. [Google Scholar]
- Xue, J.; Chang, X. Mobile beacon path planning of UWSNs based on Hopfield neural network. Transducer Microsyst. Technol. 2020, 39, 35–42. [Google Scholar]
- Zhang, X.; Wang, Y.G.; Chen, H.Y.; Hang, W.; Cao, L.; Deng, H.; Yuan, J. Optimization of Fixed-abrasive Tool Development Parameters Based on BP Neural Network and Genetic Algorithm. Surf. Technol. 2022, 51, 358–366. [Google Scholar]
- Yu, Z.M. Hopfield neural network based on genetic simulated annealing strategy to solve TSP problem. China Water Transp. 2019, 19, 89–91. [Google Scholar]
- Liu, S.; Chen, S.-J.; Han, Z.-H. Study for Flexible Flow Shop Scheduling Problem with Advanced HNN Algorithm. Control Eng. China 2019, 26, 1667–1674. [Google Scholar]
- Lv, C.; Xu, J. Multi-compartment vehicle selection and delivery strategy with time windows under multi-objective optimization. Alex. Eng. J. 2023, 85. [Google Scholar] [CrossRef]






| Author | Year | Literature | Improved Energy Function | Improvement Step Size | Other Improvements |
|---|---|---|---|---|---|
| Chen Xiao | 1996 | Literature [14] | - | - | Adopt a fixed travel starting point and reduce the number of neurons. |
| Dang Jianwu | 1997 | Literature [15] | - | - | Change progress and column constraints. |
| Wang Chao | 2001 | Literature [16] | Optimization constraints | - | - |
| Yan Chen | 2006 | Literature [17] | Aiyer improved energy function is adopted | - | - |
| Jolai | 2010 | Literature [18] | - | - | Data Transformation Technology (DTT). |
| An | 2011 | Literature [19] | Optimize energy term | - | - |
| Lin | 2014 | Literature [20] | - | Dynamic step size | Combined with genetic algorithm. |
| Guo Zhonghua | 2014 | Literature [21] | The energy function "row" and "column" items are strictly constrained | - | Improvement of neuron dynamic equation using soft-limiting function. |
| Tarkov | 2015 | Literature [22] | - | - | Deep learning (WTA) and 2 opt optimization methods. |
| Kai | 2020 | Literature [23] | Optimize energy term | - | Adopt a fixed travel starting point and reduce the number of neurons. |
| Hu | 2022 | Literature [24] | - | - | Constraints are multiplied by a Lagrange multiplier and an augmented Lagrange multiplier, respectively. |
| Dutta | 2022 | Literature [25] | - | - | Combined with SA algorithm. |
| Comert | 2022 | Literature [26] | - | - | Hybrid algorithm of K-Means and K-Medoids algorithms and HNN. |
| Almuhanna | 2024 | Literature [27] | - | - | Combined with genetic algorithm. |
| Li | 2024 | Literature [28] | Combining fractional calculus and memristors | Piecewise dynamic step size | - |
| Name | Symbols | Definition |
|---|---|---|
| Parameter | , | Customer nodes on path, |
| Arc segment, | ||
| The distance between customer i and customer j | ||
| Quantity demanded by customer i | ||
| The total number of customers, i, served when the UAV arrives at customer i | ||
| UAV serial number, | ||
| UAV u flight distance | ||
| The maximum flight distance of the UAV | ||
| T | The time when the UAV serves the last customer | |
| Maximum load capacity of UAV | ||
| Flight speed of UAVs | ||
| Flight time of UAV u | ||
| Decision variables | Equal to 1 when UAV u passes i and j, otherwise 0 | |
| When the UAV passes through the arc segment (i, j) is 1, otherwise 0 |
| Number of Clustering Centers | Frequency | Jb Value of FCM (×103) | FCM Mean Jb Value (×103) | Jb Value of SA-GA-FCM (×103) |
|---|---|---|---|---|
| 3 | 1 | 6.9033 | 6.8410 | 6.7913 |
| 2 | 6.8316 | |||
| 3 | 6.8142 | |||
| 4 | 6.8119 | |||
| 5 | 6.8442 | |||
| 4 | 1 | 3.8362 | 3.6810 | 3.5142 |
| 2 | 3.6927 | |||
| 3 | 3.5145 | |||
| 4 | 3.7761 | |||
| 5 | 3.5852 | |||
| 5 | 1 | 2.2211 | 2.2312 | 2.2198 |
| 2 | 2.2374 | |||
| 3 | 2.2450 | |||
| 4 | 2.2221 | |||
| 5 | 2.2306 |
| Combination | u | p | Mean Value | Average Initial Solution | Optimal Value | Maximum Stable Algebra | Optimal Energy |
|---|---|---|---|---|---|---|---|
| 1 | 0.99 | 0.10 | 24.693 | 28.374 | 23.738 | 155 | 43.246 |
| 2 | 0.99 | 0.15 | 24.358 | 27.891 | 23.196 | 137 | 42.765 |
| 3 | 0.99 | 0.20 | 23.245 | 25.456 | 22.984 | 125 | 42.135 |
| 4 | 0.99 | 0.25 | 23.197 | 25.298 | 22.984 | 120 | 42.012 |
| 5 | 0.99 | 0.30 | 24.693 | 27.123 | 23.746 | 139 | 43.657 |
| 6 | 0.98 | 0.10 | 23.629 | 26.987 | 23.432 | 150 | 43.042 |
| 7 | 0.98 | 0.15 | 24.817 | 27.345 | 23.575 | 145 | 43.802 |
| 8 | 0.98 | 0.20 | 24.319 | 28.648 | 23.786 | 145 | 43.680 |
| 9 | 0.98 | 0.25 | 23.975 | 26.235 | 22.984 | 140 | 42.913 |
| 10 | 0.98 | 0.30 | 24.988 | 29.583 | 23.957 | 155 | 43.978 |
| 11 | 0.97 | 0.10 | 25.244 | 29.875 | 23.981 | 167 | 44.146 |
| 12 | 0.97 | 0.15 | 24.143 | 28.634 | 23.836 | 160 | 44.346 |
| 13 | 0.97 | 0.20 | 24.536 | 28.458 | 23.810 | 153 | 45.024 |
| 14 | 0.97 | 0.25 | 23.718 | 25.985 | 22.984 | 147 | 46.791 |
| 15 | 0.97 | 0.30 | 24.543 | 28.996 | 23.765 | 162 | 47.468 |
| 16 | 0.96 | 0.10 | 25.421 | 29.432 | 23.901 | 177 | 49.340 |
| 17 | 0.96 | 0.15 | 25.129 | 29.198 | 23.636 | 175 | 48.458 |
| 18 | 0.96 | 0.20 | 24.798 | 28.134 | 23.789 | 173 | 48.596 |
| 19 | 0.96 | 0.25 | 24.469 | 27.457 | 23.467 | 168 | 46.967 |
| 20 | 0.96 | 0.30 | 25.325 | 29.928 | 23.894 | 182 | 49.685 |
| Situation | UAV | Cluster Center | Number of Customers | Path Length (km) | Total Length of Air Route (km) | Delivery Time (min) | Algorithm Runtime (×10−3 s) |
|---|---|---|---|---|---|---|---|
| One | 1 | (51.35, 35.86) | 34 | 22.984 | 70.133 | 27.58 | 54.899 |
| 2 | (21.62, 23.07) | 37 | 22.553 | 27.06 | 58.827 | ||
| 3 | (29.35, 54.88) | 29 | 24.596 | 29.52 | 47.280 | ||
| Two | 1 | (22.67, 54.54) | 22 | 19.165 | 71.383 | 23.00 | 46.039 |
| 2 | (46.38, 17.11) | 22 | 16.063 | 19.28 | 45.277 | ||
| 3 | (19.59, 23.56) | 31 | 17.957 | 21.55 | 49.346 | ||
| 4 | (52.60, 50.66) | 25 | 18.198 | 21.84 | 47.165 | ||
| Three | 1 | (46.60, 15.53) | 21 | 16.096 | 75.118 | 19.32 | 40.447 |
| 2 | (19.74, 22.48) | 29 | 16.819 | 20.18 | 47.198 | ||
| 3 | (15.98, 47.93) | 17 | 13.941 | 16.73 | 35.578 | ||
| 4 | (53.83, 44.98) | 18 | 13.223 | 15.87 | 35.771 | ||
| 5 | (37.10, 57.36) | 15 | 15.039 | 18.05 | 32.342 |
| UAV | Algorithm | Number of Iterations | Path Length | Delivery Time (min) | Algorithm Running Time (×10−3 s) |
|---|---|---|---|---|---|
| 1 | IHNN | 120 | 22.984 | 27.58 | 54.899 |
| ACA | 270 | 23.503 | 28.20 | 95.818 | |
| GA | 210 | 23.834 | 28.60 | 84.544 | |
| 2 | IHNN | 110 | 22.553 | 27.06 | 58.827 |
| ACA | 250 | 23.249 | 27.90 | 98.567 | |
| GA | 230 | 23.468 | 28.16 | 88.402 | |
| 3 | IHNN | 150 | 24.596 | 29.52 | 47.280 |
| ACA | 280 | 24.775 | 29.73 | 88.256 | |
| GA | 260 | 24.816 | 29.78 | 81.952 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Liu, D.; Le, M. Multi-UAV Delivery Path Optimization Based on Fuzzy C-Means Clustering Algorithm Based on Annealing Genetic Algorithm and Improved Hopfield Neural Network. World Electr. Veh. J. 2025, 16, 157. https://doi.org/10.3390/wevj16030157
Liu S, Liu D, Le M. Multi-UAV Delivery Path Optimization Based on Fuzzy C-Means Clustering Algorithm Based on Annealing Genetic Algorithm and Improved Hopfield Neural Network. World Electric Vehicle Journal. 2025; 16(3):157. https://doi.org/10.3390/wevj16030157
Chicago/Turabian StyleLiu, Song, Di Liu, and Meilong Le. 2025. "Multi-UAV Delivery Path Optimization Based on Fuzzy C-Means Clustering Algorithm Based on Annealing Genetic Algorithm and Improved Hopfield Neural Network" World Electric Vehicle Journal 16, no. 3: 157. https://doi.org/10.3390/wevj16030157
APA StyleLiu, S., Liu, D., & Le, M. (2025). Multi-UAV Delivery Path Optimization Based on Fuzzy C-Means Clustering Algorithm Based on Annealing Genetic Algorithm and Improved Hopfield Neural Network. World Electric Vehicle Journal, 16(3), 157. https://doi.org/10.3390/wevj16030157






