Anti-Lock Braking System Performance Optimization Based on Fitted-Curve Road-Surface Recognition and Sliding-Mode Variable-Structure Control
Abstract
1. Introduction
2. Methodology
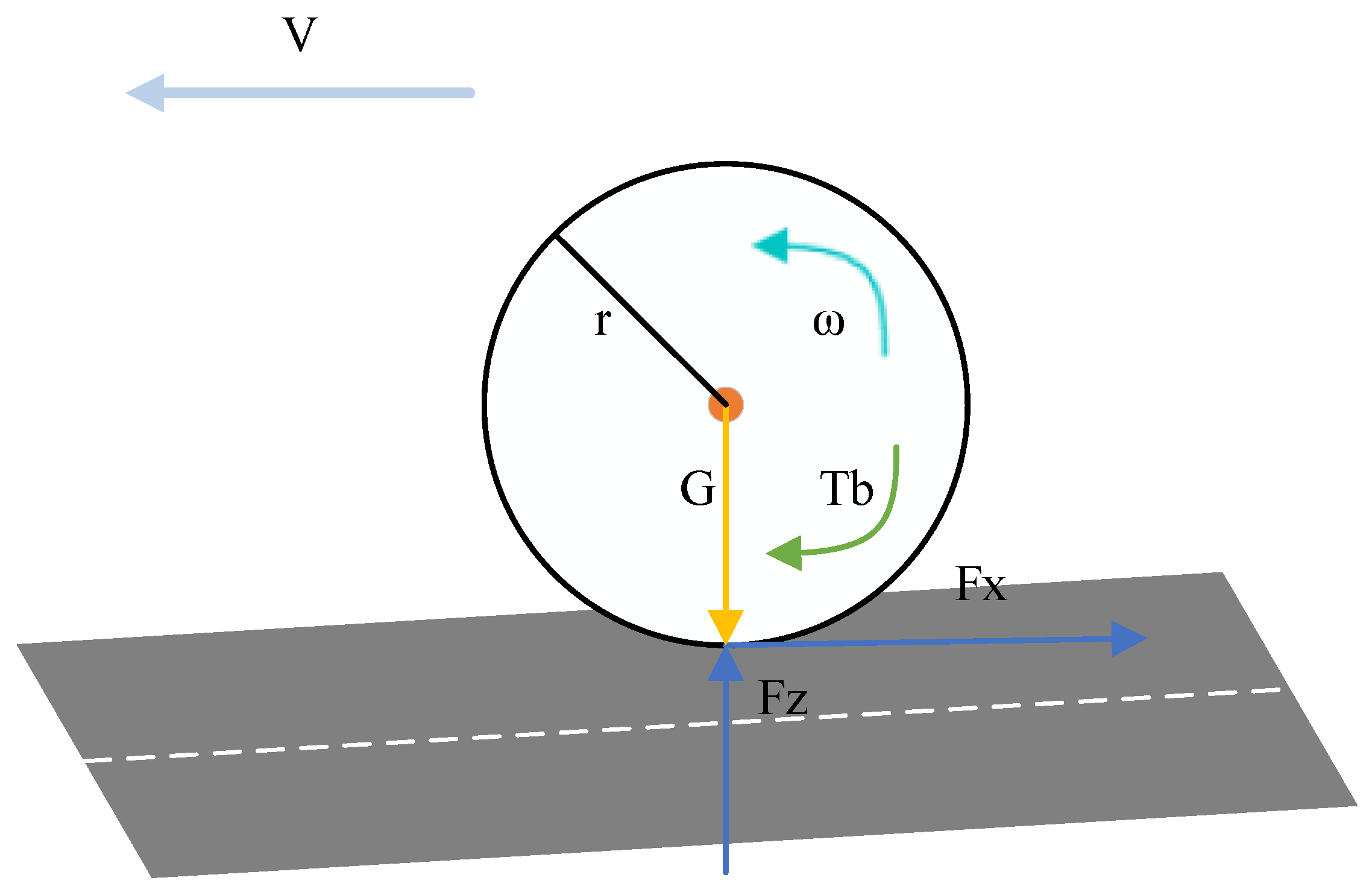
2.1. Single-Wheel Braking Model
2.2. Slip-Rate Model
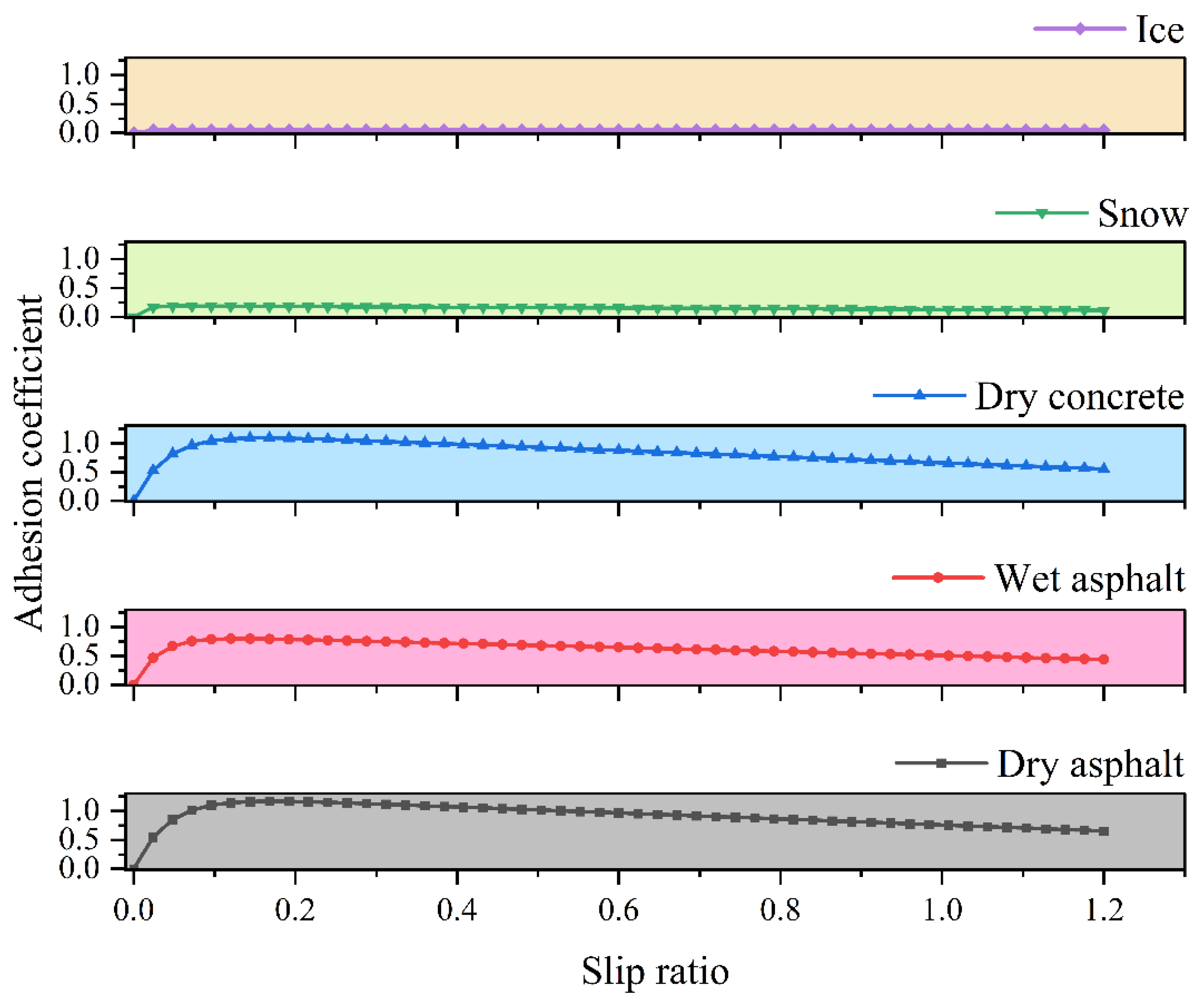
2.3. Burckhardt Tire Model
2.4. Calculation of Wheel Utilization Adhesion Coefficient
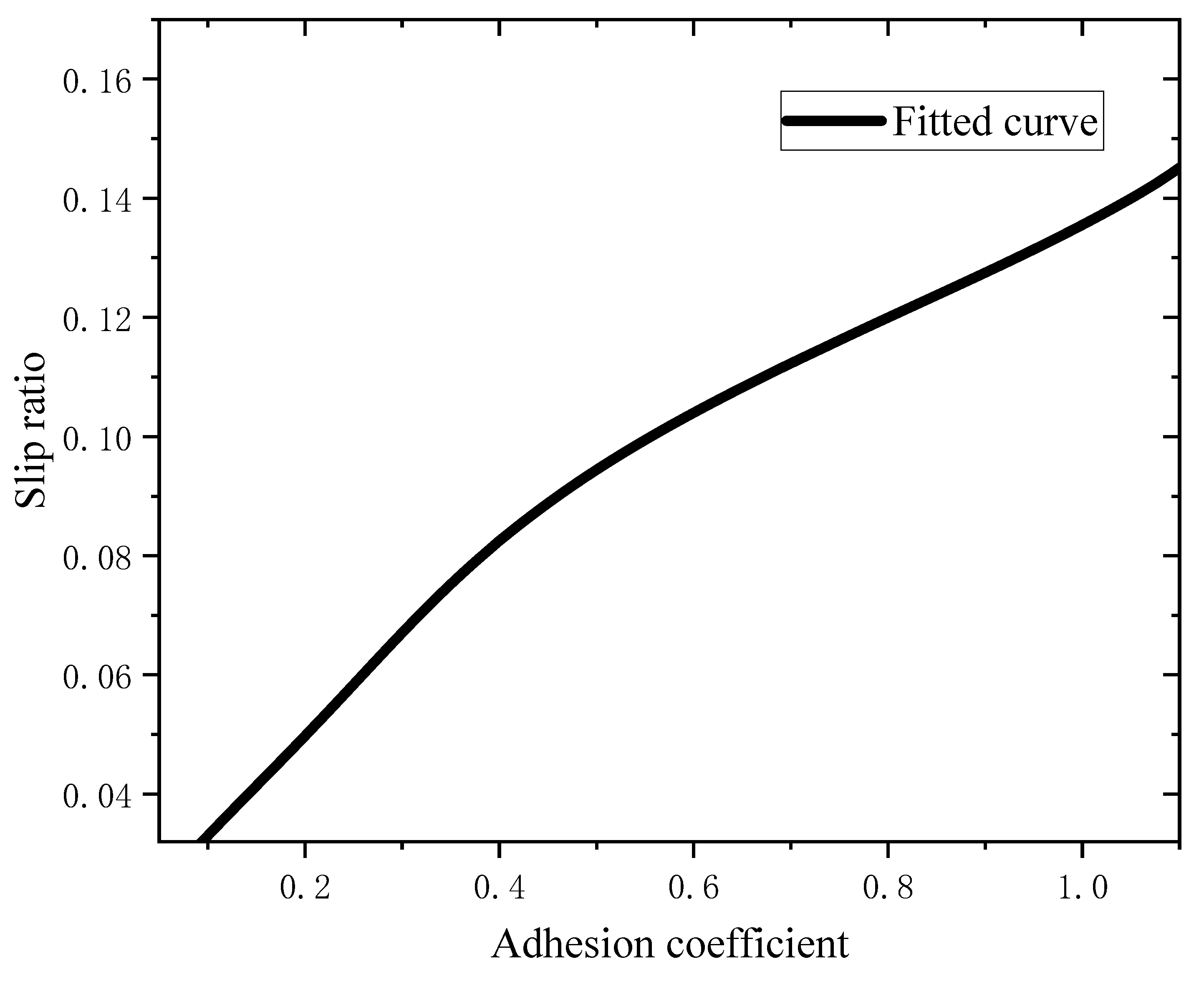
2.5. Road-Surface Recognition Algorithm Design
2.6. Slip-Rate Control Based on Sliding-Mode Control
3. Results and Discussion
3.1. Simulation Model and Parameter Settings
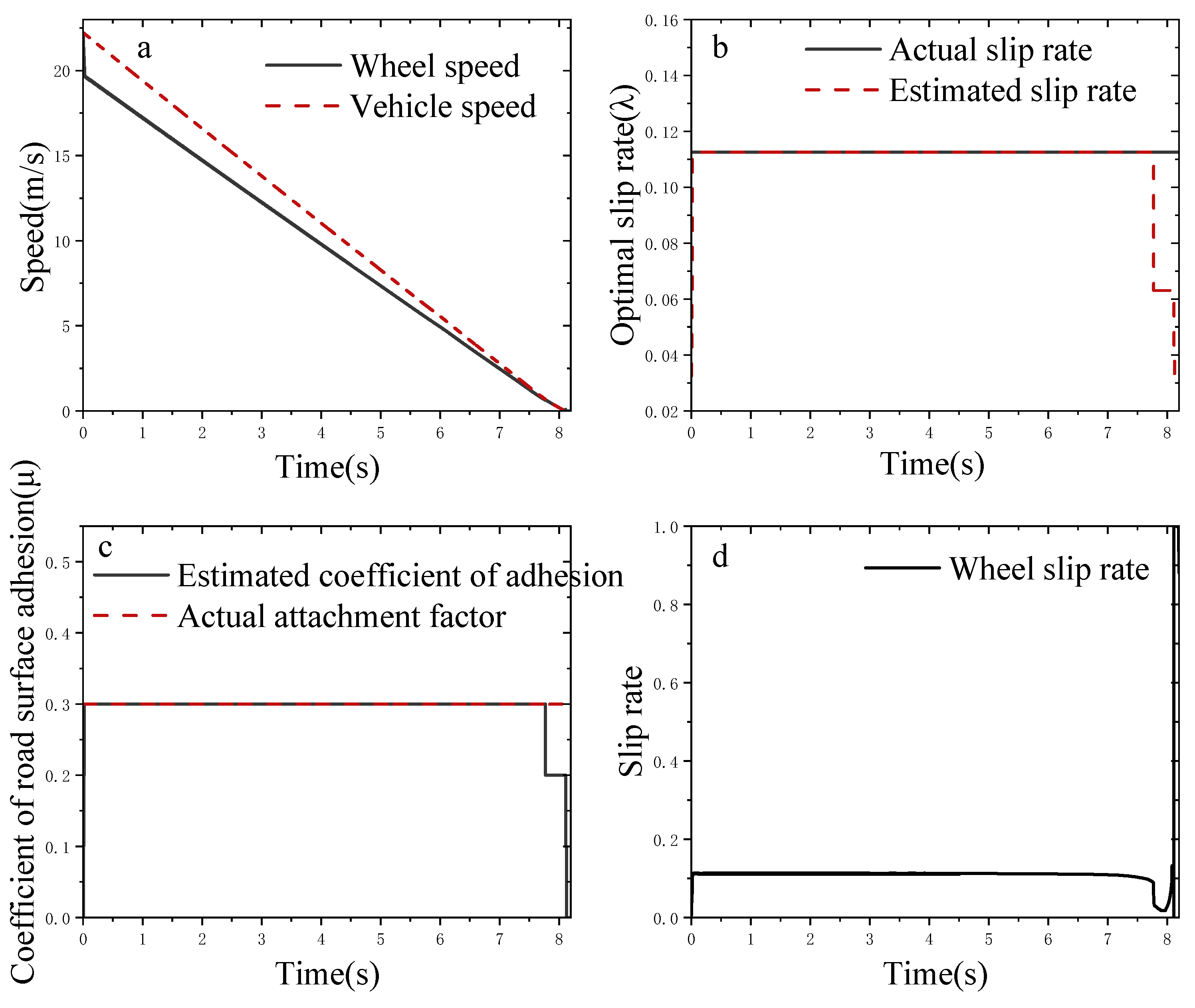
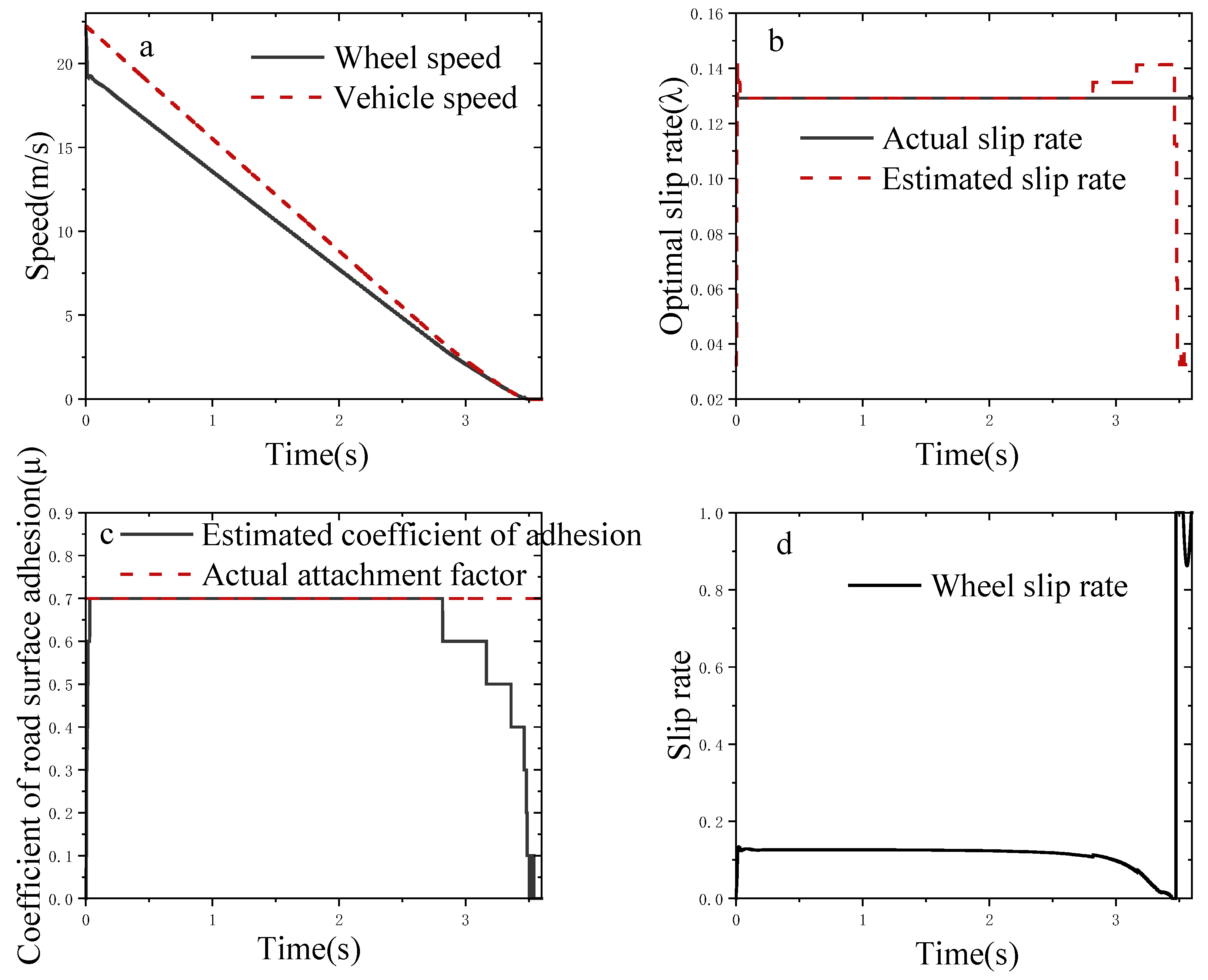
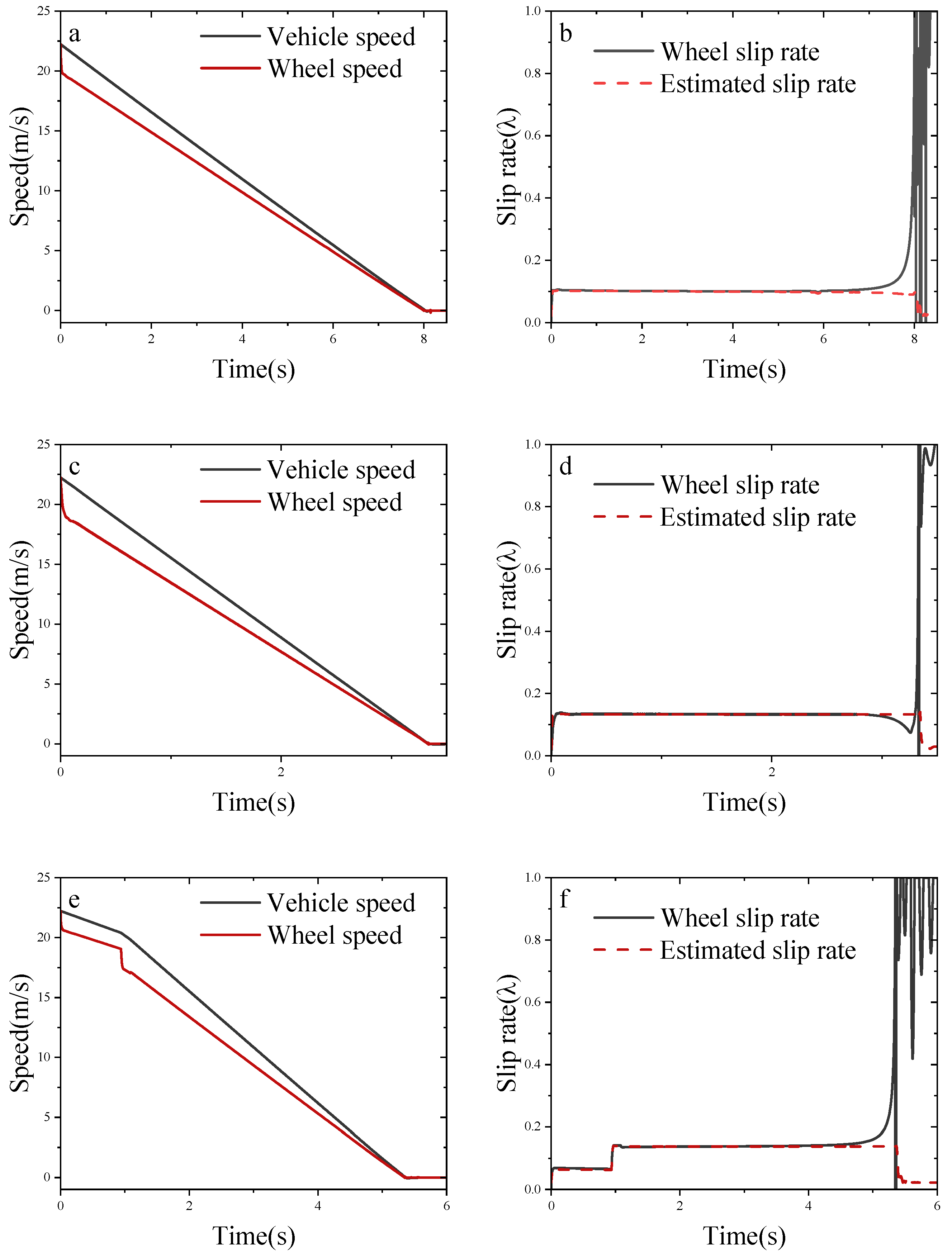
3.2. Simulation Analysis on a Single Road Surface
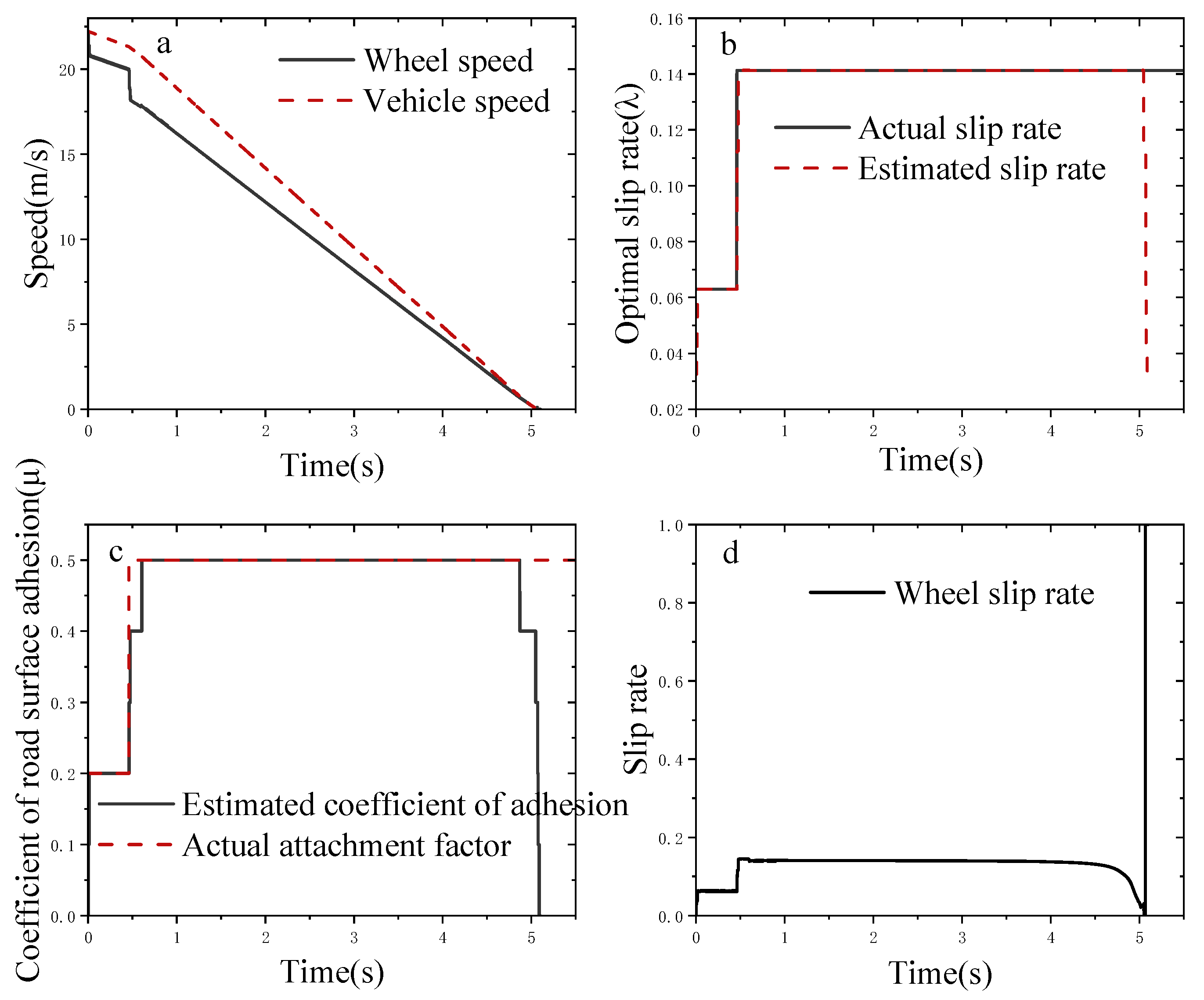
3.3. Simulation Analysis on Changing Adhesion Coefficient Road Surface
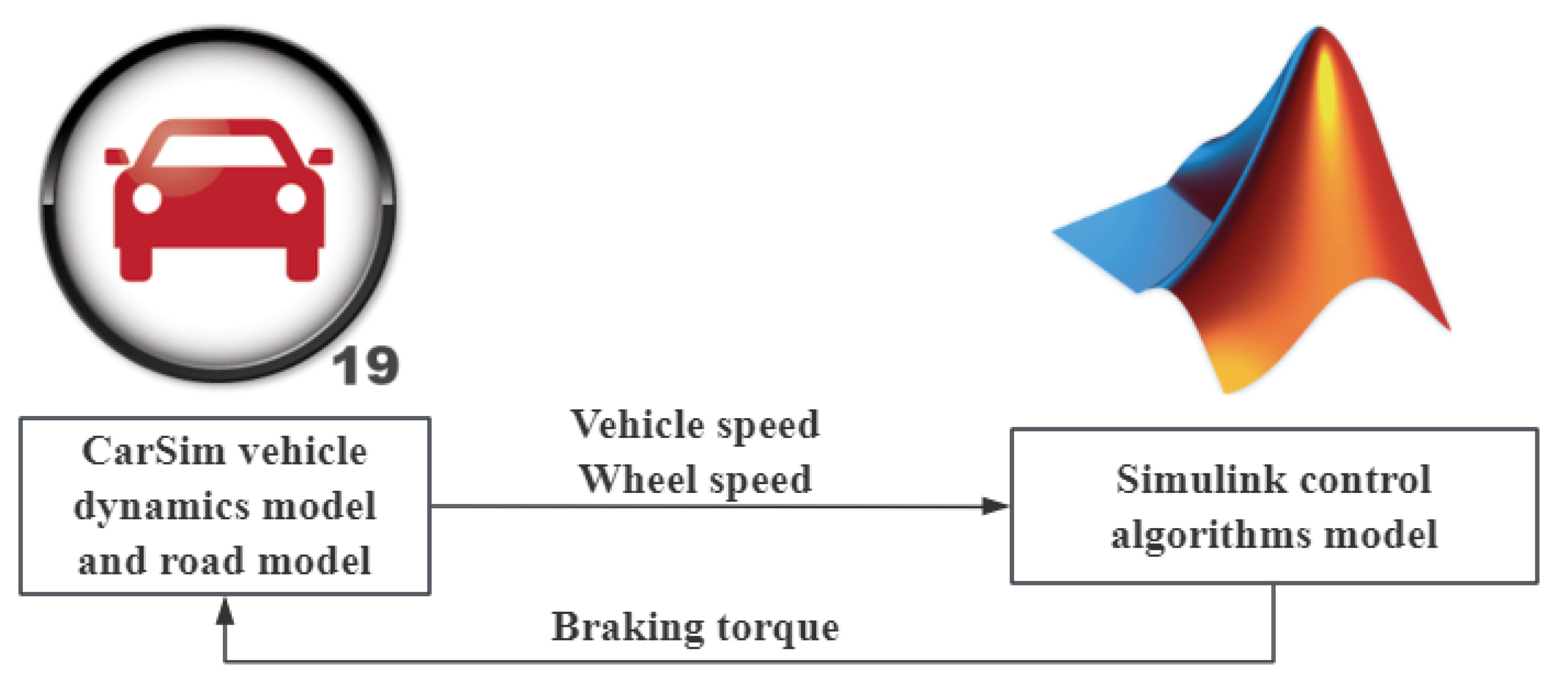
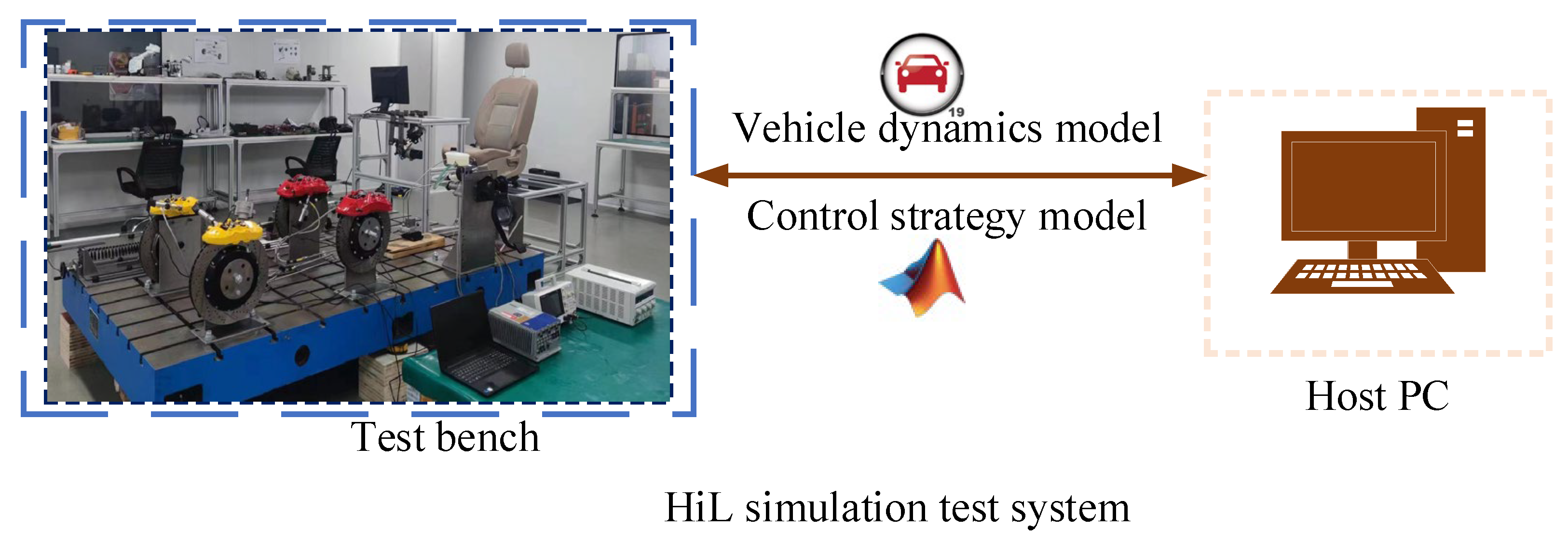
3.4. HiL Simulation Test Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhao, X.; Xiong, L.; Zhuo, G.; Tian, W.; Li, J.; Shu, Q.; Zhao, X.; Xu, G. A Review of One-Box Electro-Hydraulic Braking System: Architecture, Control, and Application. Sustainability 2024, 16, 1049. [Google Scholar] [CrossRef]
- Li, M.; Wang, H.; Chen, Y. Advanced braking systems in modern vehicles: A comprehensive review. IEEE Trans. Veh. Technol. 2019, 68, 4074–4093. [Google Scholar]
- Kim, S.; Lee, J.; Yi, K. Development of an electronic hydraulic brake system for improved braking performance. SAE Int. J. Passeng. Cars Mech. Syst. 2018, 11, 241–253. [Google Scholar]
- Robert Bosch GmbH. Automotive Handbook, 10th ed.; Wiley: Hoboken, NJ, USA, 2018. [Google Scholar]
- Rajamani, R. Vehicle Dynamics and Control, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Mauer, G.F. A fuzzy logic controller for an ABS braking system. IEEE Trans. Fuzzy Syst. 1995, 3, 381–388. [Google Scholar] [CrossRef]
- Wang, J.; Song, J.; Che, H. A review of ABS control algorithms: From logic threshold to intelligent control. Veh. Syst. Dyn. 2018, 56, 1129–1151. [Google Scholar]
- Unsal, C.; Kachroo, P. Sliding mode measurement feedback control for antilock braking systems. IEEE Trans. Control Syst. Technol. 1999, 7, 271–281. [Google Scholar] [CrossRef]
- Siddique, M.A.A.; Kim, W.-S.; Kim, Y.-S.; Kim, T.-J.; Choi, C.-H.; Lee, H.-J.; Chung, S.-O.; Kim, Y.-J. Effects of temperatures and viscosity of the hydraulic oils on the proportional valve for a Rice transplanter based on PID control algorithm. Agriculture 2020, 10, 73. [Google Scholar] [CrossRef]
- Xu, F.; Liang, X.; Chen, M.; Liu, W. Robust self-learning PID control of an aircraft anti-skid braking system. Mathematics 2022, 10, 1290. [Google Scholar] [CrossRef]
- Chen, J.; Wang, G.; Zhao, C.; Song, J. A PID control strategy research of vehicle ABS braking based on slip. In Proceedings of the 5th International Conference on Traffic Engineering and Transportation System (ICTETS 2021), Chongqing, China, 24–26 September 2021; p. 39. [Google Scholar]
- Quan, V.H.; Long, L.T.; Ngoc, N.A.; Tien, N.M. A comparison of the performance of anti-lock braking system (ABS) using fuzzy and PID controllers. In Proceedings of the 6th International Conference on Green Technology and Sustainable Development (GTSD), Nha Trang City, Vietnam, 29–30 July 2022; pp. 243–248. [Google Scholar]
- Chen, S.; Zhang, X.; Wang, J. Sliding mode control of vehicle equipped with brake-by-wire system considering braking comfort. Shock Vib. 2020, 2020, 5602917. [Google Scholar] [CrossRef]
- Jeong, Y. Path tracking control for four-wheel-steering autonomous vehicles based on adaptive sliding mode control with control allocation. In Proceedings of the 21st International Conference on Control, Automation and Systems (ICCAS), Jeju, Republic of Korea, 12–15 October 2021; pp. 1741–1746. [Google Scholar]
- Hongbo, W.; Boyang, Z.; Jinfang, H.; Jiahao, X.; Linfeng, Z.; Xianjun, Y. Road surface recognition based slip rate and stability control of distributed drive electric vehicles under different conditions. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2023, 237, 2511–2526. [Google Scholar] [CrossRef]
- Ho, C.C.; Ulfitria, R.U.S. Automatic anti-lock brake system for anti-rollover control of autonomous heavy-duty truck. In Proceedings of the 2022 IEEE International Conference on Consumer Electronics, Taipei, Taiwan, 6 July 2022; pp. 181–182. [Google Scholar]
- El-Fatah, S.A.; Sharkawy, A.-N.; Ghazaly, N.; Moaaz, A. A comparative study of different control methods for anti-lock braking system (ABS). SVU-Int. J. Eng. Sci. Appl. 2021, 2, 27–34. [Google Scholar] [CrossRef]
- Han, K.; Lee, B.; Choi, S.B. Development of an antilock brake system for electric vehicles without wheel slip and road friction information. IEEE Trans. Veh. Technol. 2019, 68, 5506–5517. [Google Scholar] [CrossRef]
- Kang, Y.; Cheng, S.; Guo, L.; Zheng, C.; Zhao, J. An Adaptive Multi-Layer Anti-Lock Braking Control Method Based on Fuzzy Logic. IEEE Access 2024, 12, 149468–149480. [Google Scholar] [CrossRef]
- Guo, H.; Zhao, X.; Liu, J.; Dai, Q.; Liu, H.; Chen, H. A fusion estimation of the peak tire–road friction coefficient based on road images and dynamic information. Mech. Syst. Signal Process. 2023, 189, 110029. [Google Scholar] [CrossRef]
- Yan, J.; Kong, H.; Man, Z. Recurrent neural network-based nonlinear optimization for braking control of electric vehicles. Energies 2022, 15, 9486. [Google Scholar] [CrossRef]
- Hamou, A.A.; Khaled, M.; Cylia, A.; Billel, N. Comparative study of the intelligent techniques (fuzzy logic and neural network) of the ABS system. In Proceedings of the 19th International Multi-Conference on Systems, Signals & Devices (SSD), Sétif, Algeria, 6–10 May 2022; pp. 1497–1503. [Google Scholar]
- Li, M.; Li, S.; Ahn, C.K.; Xiang, Z. Adaptive fuzzy event-triggered command-filtered control for nonlinear time-delay systems. IEEE Trans. Fuzzy Syst. 2022, 30, 1025–1035. [Google Scholar] [CrossRef]
- Liu, Y.; Sun, J.; Li, L. A review on development of electronic hydraulic brake system. Automot. Eng. 2019, 41, 881–893. [Google Scholar]
- Cao, W. Modeling and simulation of the anti-lock braking system based on MATLAB/Simulink. J. Phys. Conf. Ser. 2021, 1941, 012075. [Google Scholar] [CrossRef]
- Zhang, W. Automotive Theory; Machinery Industry Press: Beijing, China, 2005. [Google Scholar]
- Unguritu, M.G.; Nichitelea, T.C. Design and Assessment of an Anti-lock Braking System Controller. Rom. J. Inf. Sci. Technol. 2023, 26, 21–32. [Google Scholar] [CrossRef]
- Kiencke, U.; Nielsen, L. Automotive Control Systems; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Liu, Y.; Pei, X.; Guo, X. Redundancy Control of Anti-lock Braking System Based on Electro-hydraulic Braking System. SAE Int. J. Veh. Dyn. Stab. NVH 2023, 7, 53–67. [Google Scholar] [CrossRef]
- Yang, F.; Chen, X.; Guo, D.; Hu, M.; Liao, Z.; Fu, Z.; Gong, Q. Electric-hydraulic Compound Control Anti-lock Braking System. Int. J. Automot. Technol. 2022, 23, 1593–1608. [Google Scholar] [CrossRef]
- Jennan, N.; Mellouli, E.M. Anti-Lock Braking System Control using Backstepping Method Based Fuzzy Logic. Sens. Transducers 2023, 261, 10–14. [Google Scholar]

| Road Type | |||
|---|---|---|---|
| Dry Asphalt | 1.2801 | 23.99 | 0.52 |
| Wet Asphalt | 0.857 | 33.822 | 0.347 |
| Dry Concrete | 1.1973 | 25.168 | 0.5373 |
| Snow | 0.1946 | 94.129 | 0.0646 |
| Ice | 0.05 | 306.39 | 0 |
| Road Surfaces | Dry Asphalt | Dry Concrete | Wet Asphalt | Snow | Ice | |
|---|---|---|---|---|---|---|
| Parameter | ||||||
| 1.171 | 1.089 | 0.800 | 0.190 | 0.050 | ||
| 0.170 | 0.160 | 0.131 | 0.060 | 0.032 | ||
| Parameter Name | Value |
|---|---|
| Vehicle weight/kg | 1412 |
| Sprung mass/kg | 1270 |
| Wheel rotational inertia/kg·m2 | 0.9 |
| Height of sprung mass center of gravity/m | 0.54 |
| Front and rear tire mass/kg | 71 |
| Distance from center of gravity to front axle/m | 1.015 |
| Distance from center of gravity to rear axle/m | 1.895 |
| Distance between front and rear axles/m | 2.91 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, H.; Liu, W.; Wang, R.; Ding, R.; Guo, Z.; Ye, Q.; Meng, X.; Sun, D.; Liu, W. Anti-Lock Braking System Performance Optimization Based on Fitted-Curve Road-Surface Recognition and Sliding-Mode Variable-Structure Control. World Electr. Veh. J. 2025, 16, 156. https://doi.org/10.3390/wevj16030156
Zhou H, Liu W, Wang R, Ding R, Guo Z, Ye Q, Meng X, Sun D, Liu W. Anti-Lock Braking System Performance Optimization Based on Fitted-Curve Road-Surface Recognition and Sliding-Mode Variable-Structure Control. World Electric Vehicle Journal. 2025; 16(3):156. https://doi.org/10.3390/wevj16030156
Chicago/Turabian StyleZhou, Haiqing, Wenguang Liu, Ruochen Wang, Renkai Ding, Zhongyang Guo, Qing Ye, Xiangpeng Meng, Dong Sun, and Wei Liu. 2025. "Anti-Lock Braking System Performance Optimization Based on Fitted-Curve Road-Surface Recognition and Sliding-Mode Variable-Structure Control" World Electric Vehicle Journal 16, no. 3: 156. https://doi.org/10.3390/wevj16030156
APA StyleZhou, H., Liu, W., Wang, R., Ding, R., Guo, Z., Ye, Q., Meng, X., Sun, D., & Liu, W. (2025). Anti-Lock Braking System Performance Optimization Based on Fitted-Curve Road-Surface Recognition and Sliding-Mode Variable-Structure Control. World Electric Vehicle Journal, 16(3), 156. https://doi.org/10.3390/wevj16030156







