Intelligent Vehicle Trajectory Tracking Based on Horizontal and Vertical Integrated Control
Abstract
1. Introduction
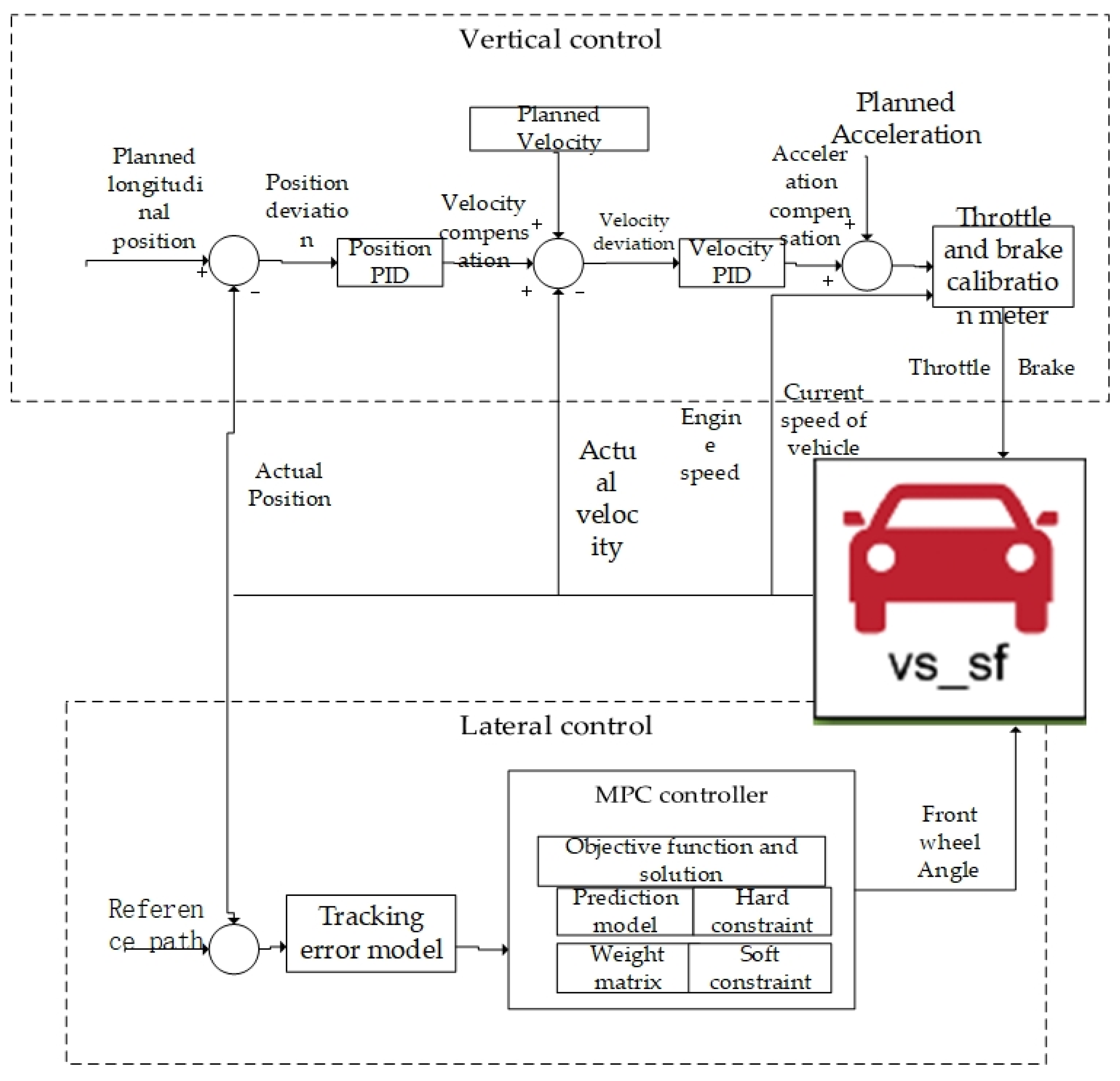
2. Overall Design of Control System
2.1. Establishment of Vehicle Dynamics Model
- (1)
- Suspension system effects are disregarded, assuming front-wheel steering configuration.
- (2)
- The vehicle’s movement is constrained to the horizontal plane, omitting vertical dynamics.
- (3)
- Vehicle speed remains nearly constant throughout the analysis.
- (4)
- Aerodynamic influences on the vehicle are excluded from consideration.
- (5)
- Each tire is assumed to possess identical mechanical characteristics, with no additional lateral forces or restoring moments factored in.
- (6)
- The vehicle maintains constant rotational inertia, and there is no lateral displacement of the center of mass, ensuring minimal lateral load variation.
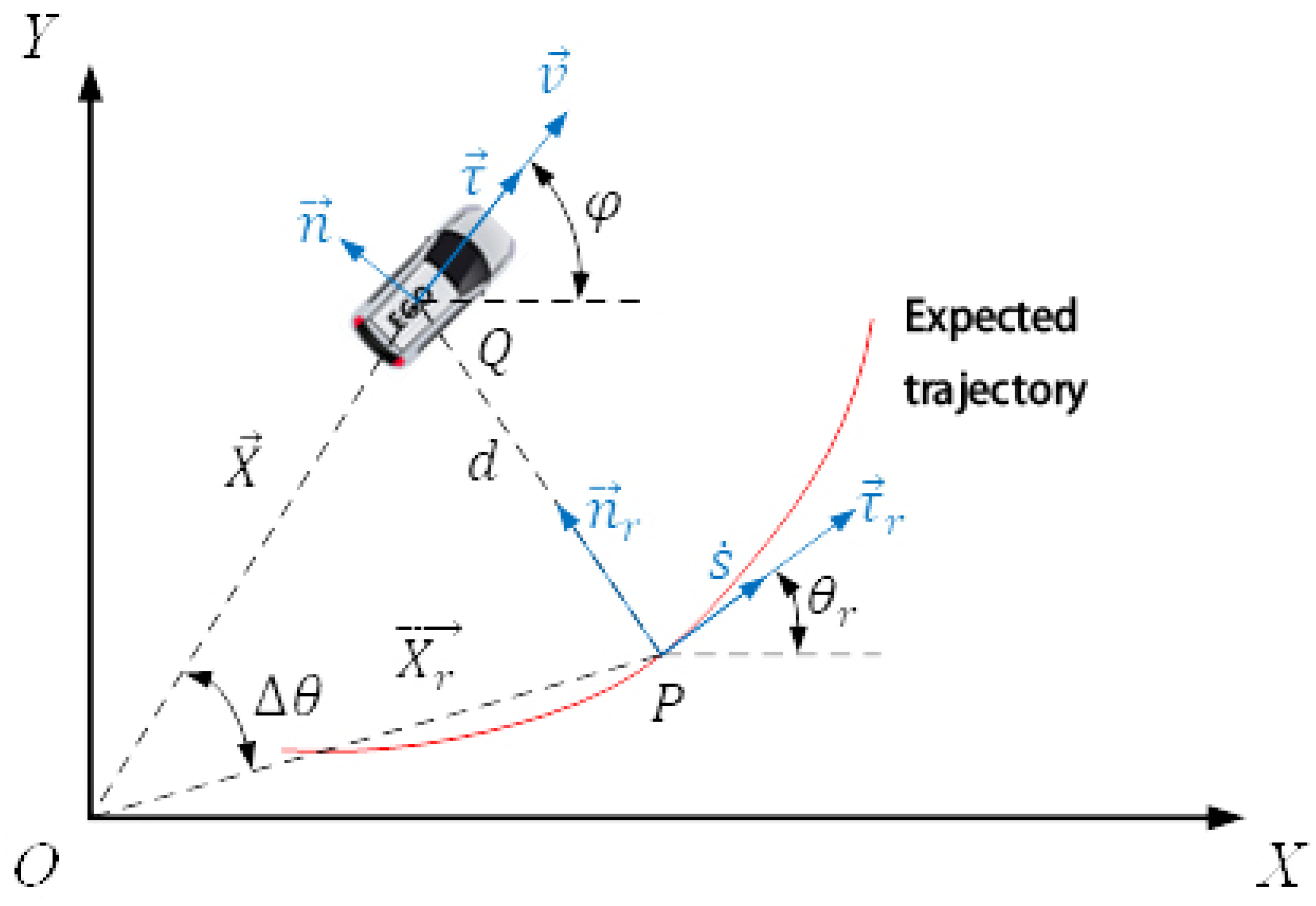
2.2. Establishment of the Tracking Error Model
3. Design of Cross- and Longitudinal Tracking Controllers
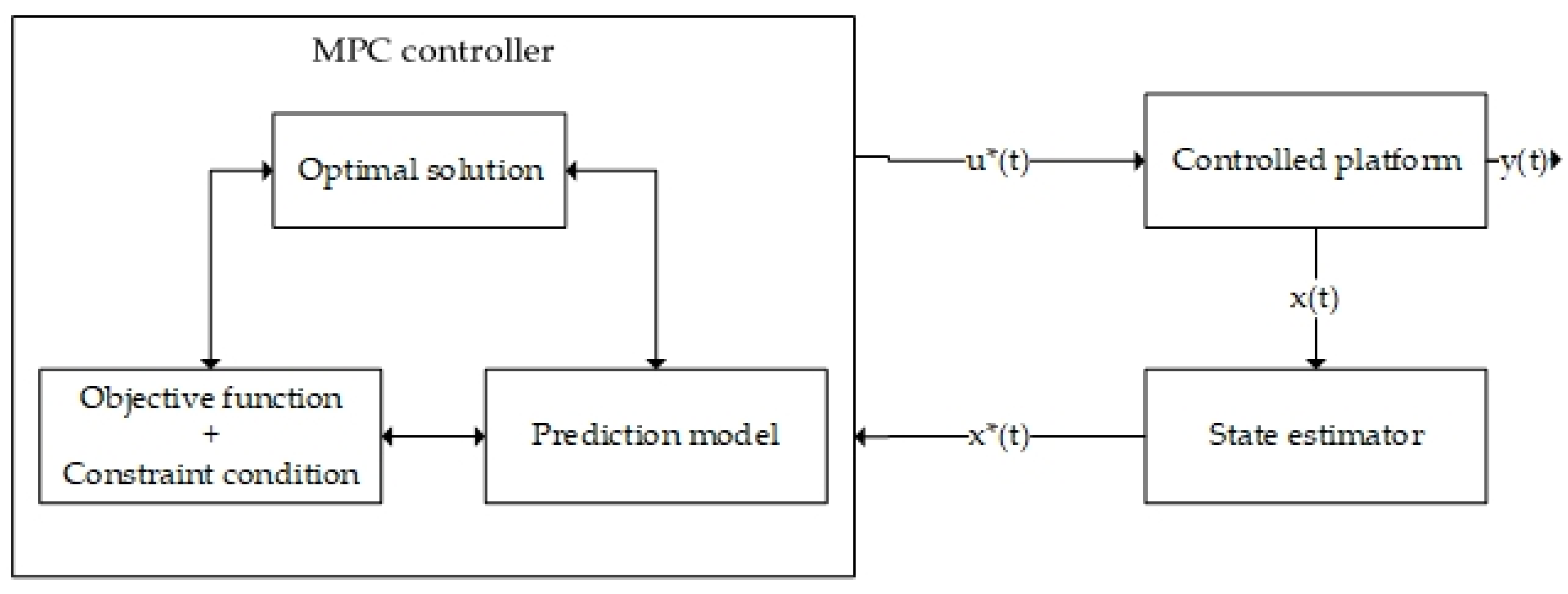
3.1. Design of Lateral Model Predictive Controller
3.1.1. Linearization and Discretization of Nonlinear Systems
3.1.2. Reformulate It as a Quadratic Programming Problem for Resolution
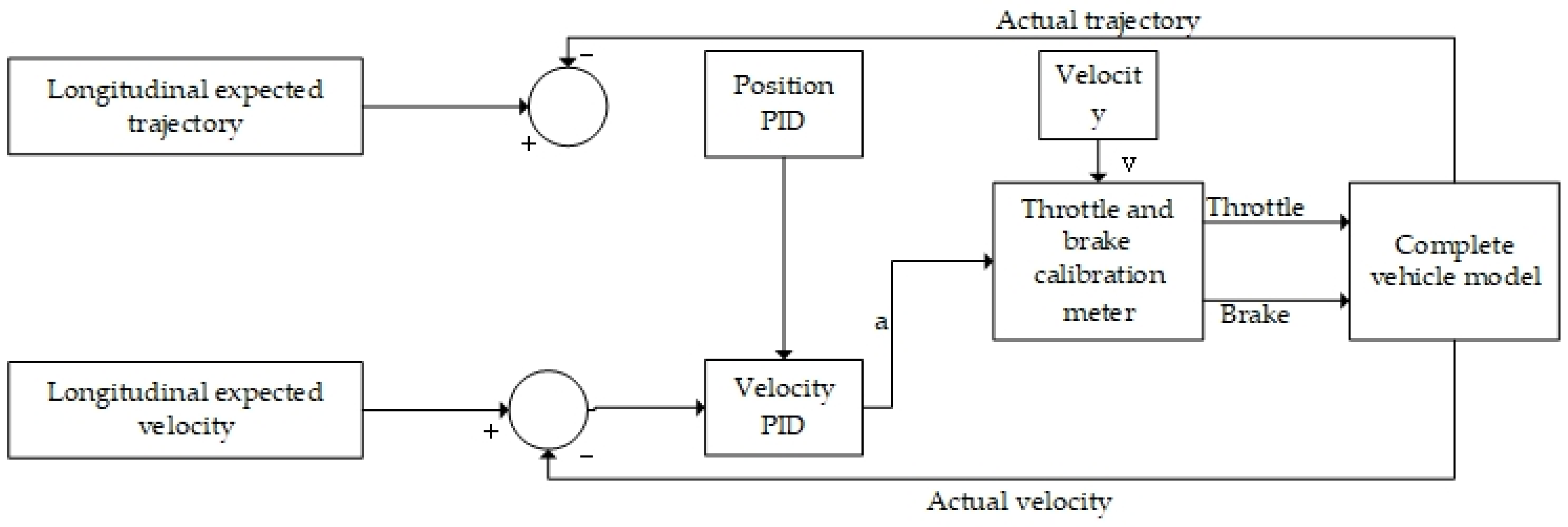
3.2. Design of Vertical Controller
3.3. Analysis of Stability of Cross and Longitudinal Control Systems
3.3.1. Stability Analysis of Lateral MPC Control System
3.3.2. Stability Analysis of Longitudinal PID Control System
3.3.3. Stability Analysis of Horizontal and Vertical Integrated Control System
4. Tracking Simulation and Result Analysis
4.1. Vehicle Parameters and Road Model
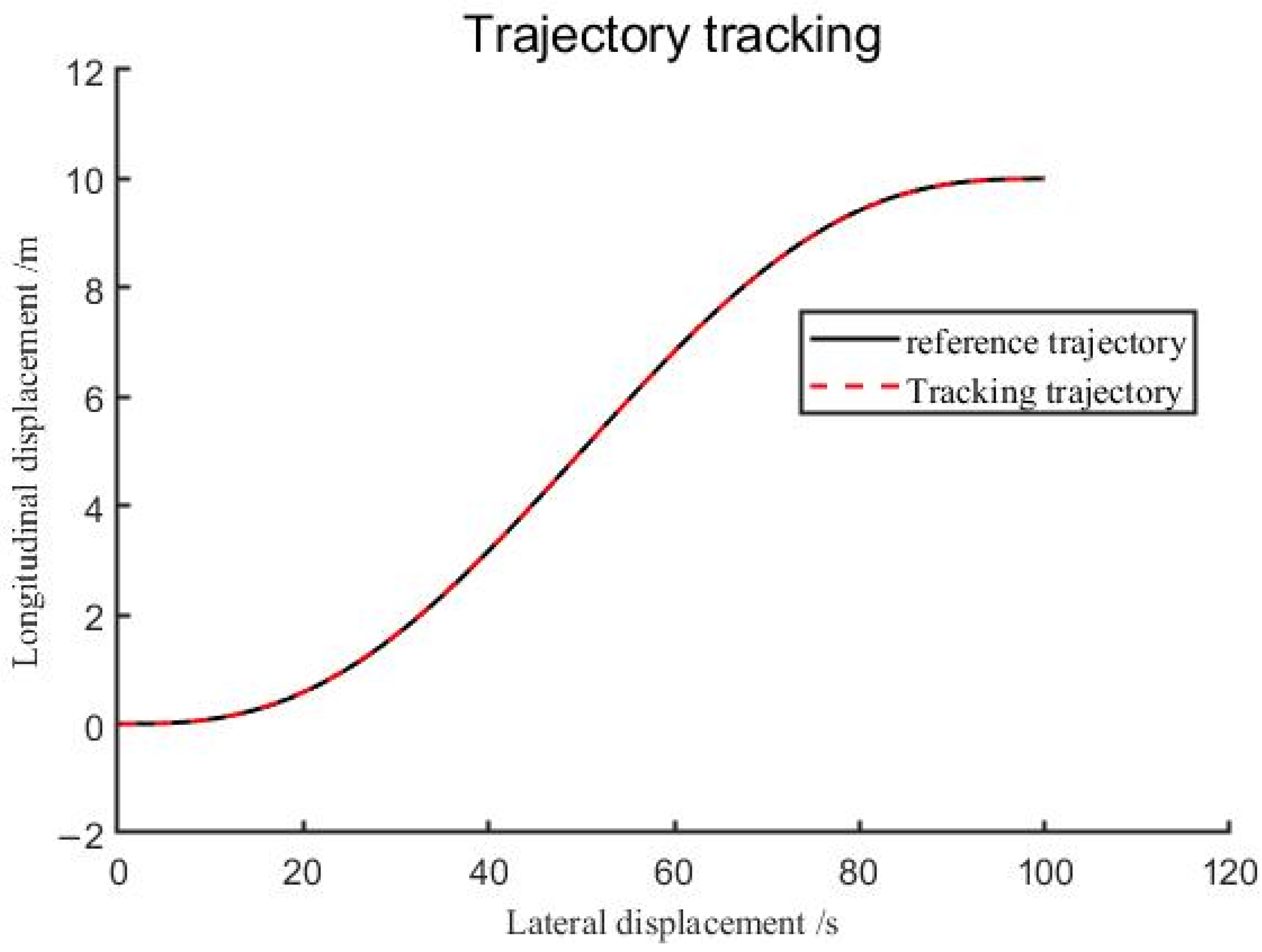
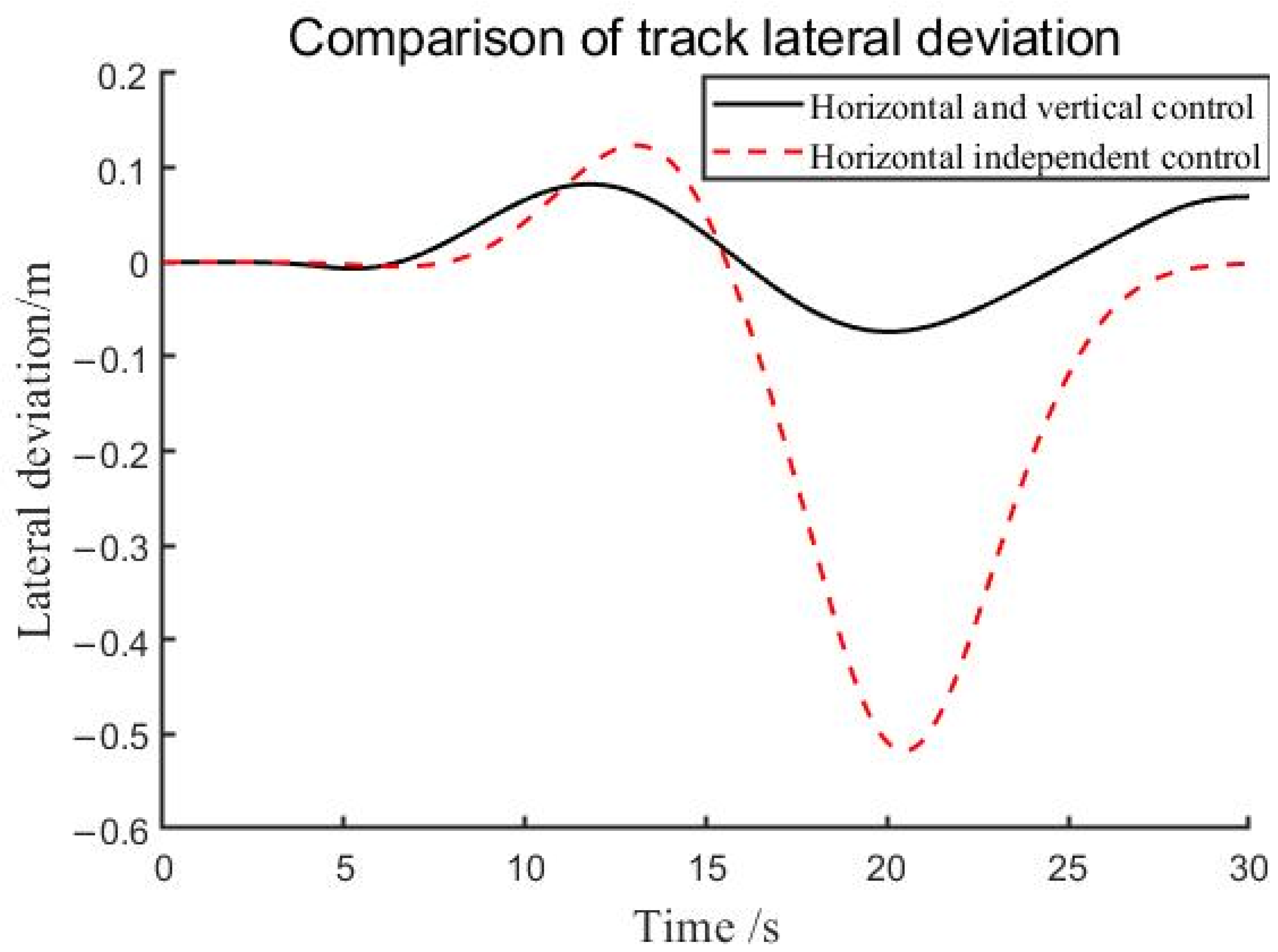
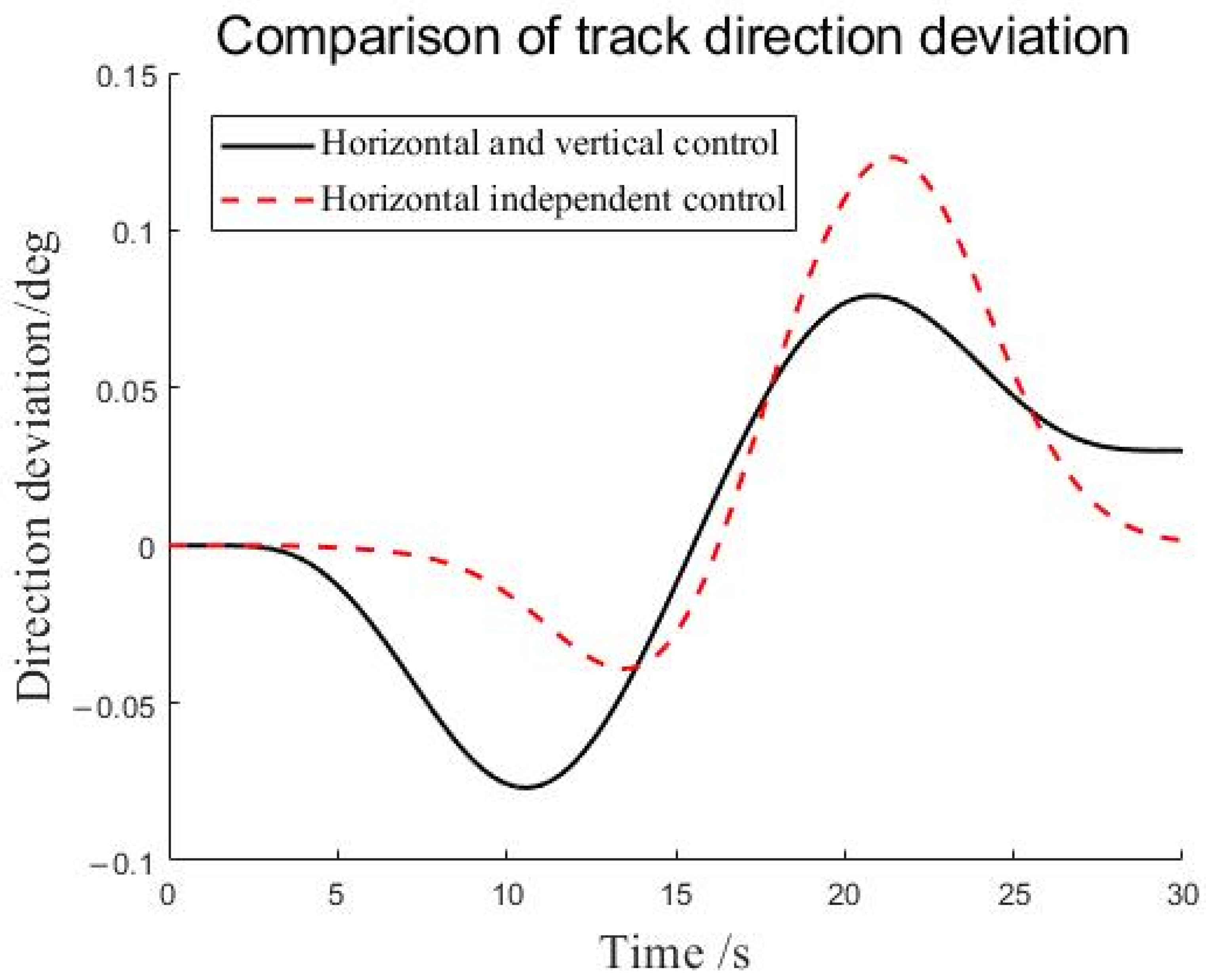
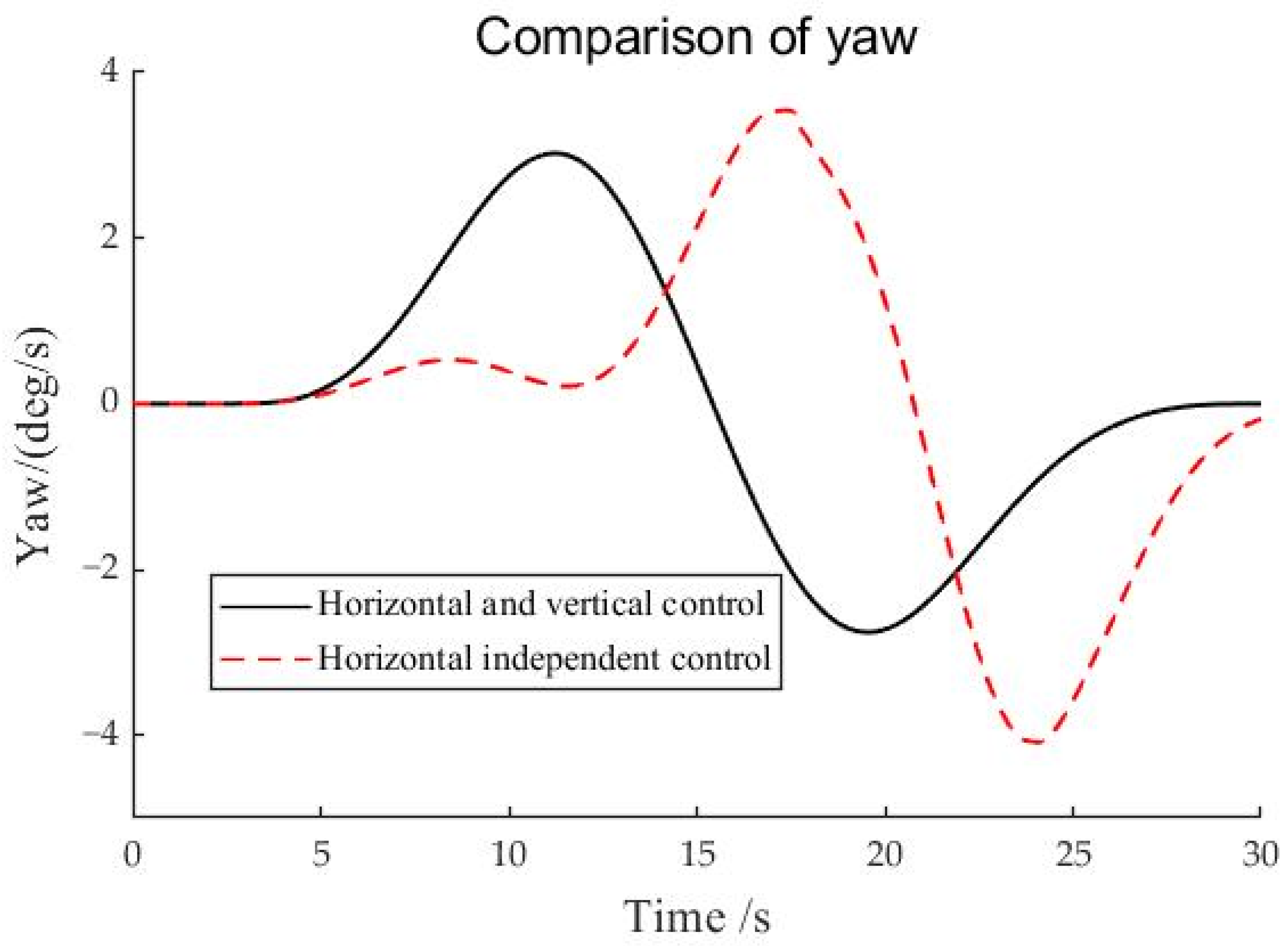
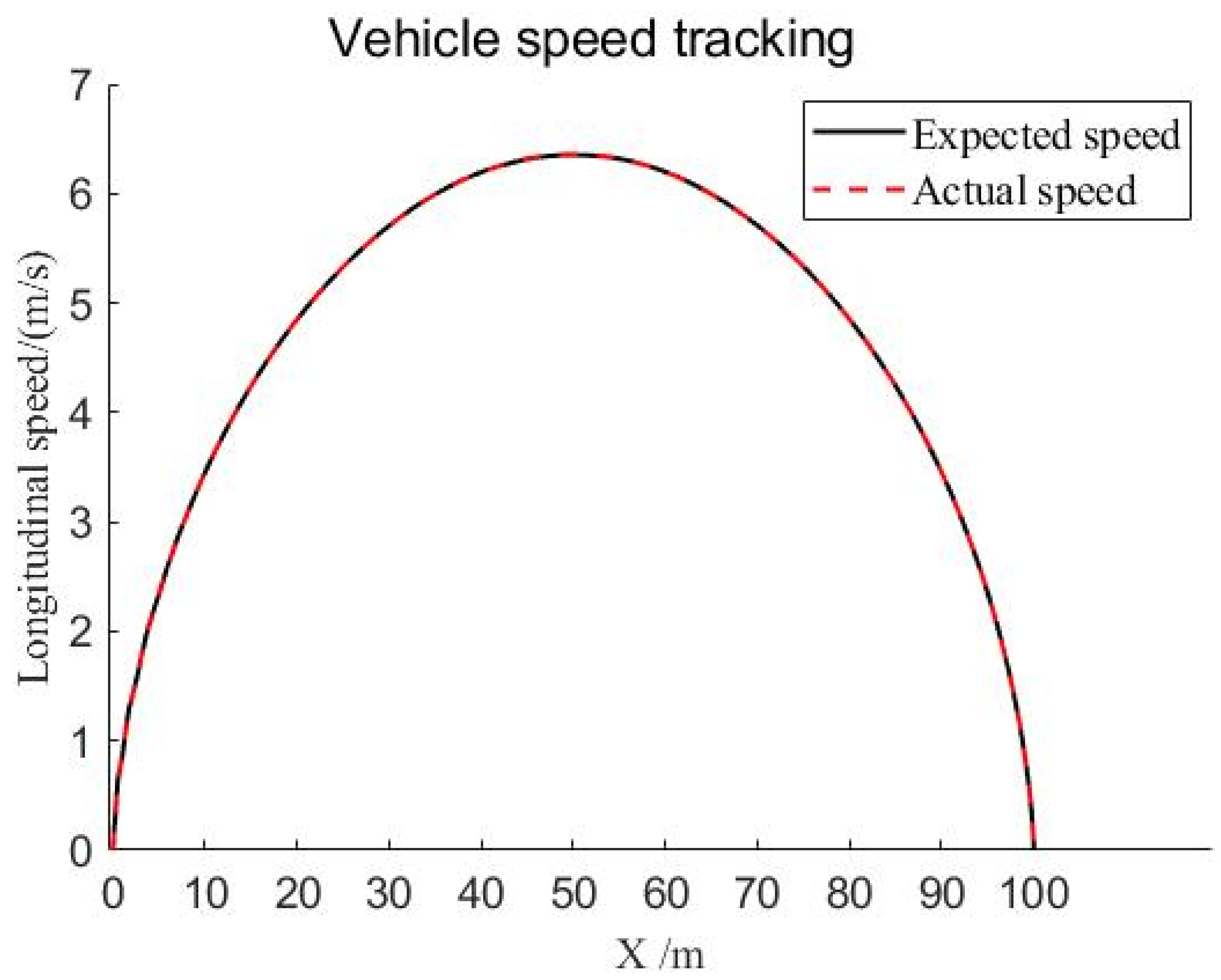
4.2. Simulation Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhao, B.; Wang, H.; Li, Q.; Li, J.; Zhao, Y. PID trajectory tracking control of autonomous ground vehicle based on genetic algorithm. In Proceedings of the 2019 Chinese Control And Decision Conference (CCDC), Nanchang, China, 3–5 June 2019; pp. 3677–3682. [Google Scholar]
- Zhou, W. Adaptive preview based control system for unmanned vehicle path tracking. Int. J. Veh. Struct. Syst. 2021, 13, 398–404. [Google Scholar] [CrossRef]
- Marino, R.; Scalzi, S.; Netto, M. Nseted PID steering control for lane keeping in autonomous vehicles. Control. Eng. Pract. 2011, 19, 1459–1467. [Google Scholar] [CrossRef]
- Pan, S.; Li, J.; Li, H.; Lou, J.; Xu, Y. Path Following Method of Intelligent Vehicles Based on Feedback Pure Tracking Method. Automot. Eng. 2019, 41, 1021–1027. [Google Scholar]
- Li, S. Overview of Algorithm Research on Trajectory Tracking and Control for Intelligent Vehicles. Automot. Dig. 2023, 9, 19–27. [Google Scholar]
- Zhou, W.; Zhao, Y.; Liu, Q.; Chen, L. Lateral control strategy of vehicle path tracking based on improved LQR. J. Huazhong Univ. Sci. Technol. (Nat. Sci. Ed.) 2024, 52, 135–141. [Google Scholar]
- Zeng, Y.; Tang, X.; Lu, X. Redundant control of Automatic driving trajectory Tracking for Complex Road Scenarios. Automot. Pract. Technol. 2024, 49, 11–17+48. [Google Scholar]
- Vu, T.M.; Moezzi, R.; Cyrus, J.; Hlava, J. Model predictive control for autonomous driving vehicles. Electronics 2021, 10, 2593. [Google Scholar] [CrossRef]
- Xie, X.; Jin, L.; Du, J. MPC-based trajectory tracking control for autonomous vehicles. J. Mach. Des. 2024, 41, 20–26. [Google Scholar]
- Zhang, K.; Sun, Q.; Shi, Y. Trajectory tracking control of autonomous ground vehicles using adaptive learning MPC. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 5554–5564. [Google Scholar] [CrossRef] [PubMed]
- Hu, L. Intelligent electric Vehicle trajectory Tracking Control based on MPC-PID. Intell. Comput. Appl. 2019, 14, 155–164. [Google Scholar] [CrossRef]
- Zhou, Y.; Yang, W. Path Tracking Control of Unmanned Vehicles Based on MPC and PID. Agric. Equip. Veh. Eng. 2019, 61, 78–81+116. [Google Scholar]
- Chung, S. Research on Tracking Control Method of Autonomous Vehicle Based on Model Predictive Control; South China University of Technology: Guangzhou, China, 2020. [Google Scholar]
- Zhang, B.; Zhou, B.; Xia, Q. Research on trajectory tracking Control Algorithm of unmanned mining transport Vehicle. J. Automot. Eng. 2024, 14, 168–180. [Google Scholar]
- Chen, T.; Xu, X.; Cai, Y.; Chen, L.; Sun, X. Coordinated Control of front wheel Angle and yaw stability of unmanned vehicle based on State estimation. J. Beijing Inst. Technol. 2021, 41, 1050–1057. [Google Scholar]
- Wu, X.; Wei, C.; Zhai, J. Research on Trajectory Tracking Control Optimization of unmanned vehicle considering yaw Stability. Chin. J. Mech. Eng. 2022, 58, 130–142. [Google Scholar]
- Gong, J.; Jiang, Y.; Xu, W. Autonomous Vehicle Model Predictive Control; Beijing Institute of Technology Press: Beijing, China, 2014. [Google Scholar]
- Sun, Y. Research on Trajectory Tracking Control Algorithm of Unmanned Vehicle Based on Model Predictive Control; Beijing Institute of Technology: Beijing, China, 2015. [Google Scholar]

| Related Parameters | Numerical Value |
|---|---|
| Vehicle mass/kg | 1270 |
| Distance from center of mass to front axis/m | 1.015 |
| Distance from center of mass to rear axis/m | 1.895 |
| Moment of inertia of the vehicle/(kg·m2) | 1536.7 |
| Front wheel side stiffness/(N/rad) | −67,656 |
| Rear wheel side stiffness/(N/rad) | −65,000 |
| Related Parameters | Numerical Value |
|---|---|
| Position Proportion | 2 |
| Position Integration | 0.5 |
| Position Differentiation | 0.1 |
| Speed Proportion | 1.8 |
| Speed Integration | 0.8 |
| Speed Differentiation | 0.1 |
| Prediction time domain | 20 |
| Control time domain | 20 |
| Sampling period | 0.05 |
| 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Published by MDPI on behalf of the World Electric Vehicle Association. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, J.; Zhao, J.; Zheng, J.; Liu, H. Intelligent Vehicle Trajectory Tracking Based on Horizontal and Vertical Integrated Control. World Electr. Veh. J. 2024, 15, 513. https://doi.org/10.3390/wevj15110513
Xu J, Zhao J, Zheng J, Liu H. Intelligent Vehicle Trajectory Tracking Based on Horizontal and Vertical Integrated Control. World Electric Vehicle Journal. 2024; 15(11):513. https://doi.org/10.3390/wevj15110513
Chicago/Turabian StyleXu, Jingbo, Jingbo Zhao, Jianfeng Zheng, and Haimei Liu. 2024. "Intelligent Vehicle Trajectory Tracking Based on Horizontal and Vertical Integrated Control" World Electric Vehicle Journal 15, no. 11: 513. https://doi.org/10.3390/wevj15110513
APA StyleXu, J., Zhao, J., Zheng, J., & Liu, H. (2024). Intelligent Vehicle Trajectory Tracking Based on Horizontal and Vertical Integrated Control. World Electric Vehicle Journal, 15(11), 513. https://doi.org/10.3390/wevj15110513






