1. Introduction
India represents the largest two-wheeler market with the majority having an internal combustion engine; However, electric two-wheelers (E2Ws) are quickly catching up due to several advantages and government support [
1,
2]. E2Ws only use 30% of the total energy required by traditional passenger vehicles and also contribute significantly less air pollution than conventional internal combustion engines [
3]. From 2018, over 0.8 million E2Ws have been sold in the Indian market, accounting for a 4% market share which is expected to exponentially grow [
4] in the near future. The E2W has been popular in India due to the country’s diverse transportation demands, habits, and preferences, which differ from other nations’ needs, policies, and business models. With a previously high import content, India is gradually moving towards emerging India-specific research and development [
5,
6].
Currently, with the exception of a few manufacturers, the majority of electric two-wheeler (E2W) manufacturers rely on heavily imports for critical components such as powertrains, batteries, and controllers. Unfortunately, there is a noticeable lack of design consideration and validation tailored to suit the specific climatic and environmental conditions in India. This oversight has led to significant performance issues and failures in E2W products. Sales of new vehicles, mostly motorized two- and three-wheelers, have increased significantly in recent years as a result of India’s rapid economic expansion and urbanization [
7]. With the depletion of fossil fuel stock, a high import burden, increasing fuel costs, and the government’s obligation to reduce greenhouse gas emissions, the shift towards electric vehicles (mostly two- and three-wheeler) has become noticeable. This is also fueled by government support and the depleted cost of key components such as the battery and brushless direct-current (BLDC) motors [
8].
At present, electric vehicles (EVs) represent less than 1% of the total Indian automotive vehicles (293 million), of which, 95% are two-wheelers [
9]. However, due to the high import dependency on fossil fuels, the number of electric two- and three-wheel will rise in the near future [
10]. The total trade balance of the nation would improve if the Indian vehicle industry were to become independent of oil and natural gas [
11]. To create an indigenized, sustainable, cleaner, and more economical transportation ecosystem, higher-efficiency vehicles with significantly lower energy consumption and fast-tracking transportation electrification are needed [
12]. The creation of effective and computationally efficient engineering tools, design development, and validation efforts for diverse sub-systems, scaling operations, etc., may all lead to advancement. Apart from buying preferences and governmental initiatives, at present, E2Ws are not fully satisfactory for Indian consumers compared to fossil-fuel-based vehicles due to several reasons [
13], such as economic reasons, driving range, unique features, and the ease of licensing. The industry is at a crossroads and is undoubtedly preparing for a total transition as a result of the recent disruptions brought on by environmental requirements [
14], conscientiousness, and economic viability [
15].
Assessing the electric two-wheeler ecosystem using the Pareto optimality and Technique for Order Preference by Similarity to Ideal Solution (TOPSIS) methods helps to identify an ideal design solution based on multiple criteria. The Pareto-optimality concept is based on the idea that an optimal solution should not be dominated by any other feasible solution in terms of multiple criteria. In the context of the electric two-wheeler ecosystem, this means identifying design solutions that provide the best trade-off among various criteria. It is important to note that the success of these methods relies on the accurate definition of criteria, the appropriate weight of criteria, and the availability of reliable data or expert input for evaluating design solutions.
Pareto optimality needs to define the criteria that are relevant to the electric two-wheeler ecosystem. These criteria include factors such as energy efficiency, range, charging infrastructure availability, battery life, manufacturing cost, user affordability, environmental impact, and safety. Each criterion should be quantifiable and measurable. Next, a set of design solutions is generated, each representing a combination of different features, technologies, and specifications for the electric two-wheeler. The solutions were evaluated against the defined criteria and the Pareto-optimality principle was applied to identify solutions that are not dominated by any other solution across all criteria.
The TOPSIS method is a decision-making technique used to rank alternatives based on their proximity to the ideal solution. It involves determining the similarity of each alternative to the ideal solution and the worst solution for each criterion. In the TOPSIS implementation criteria, definition and their relative weights are assigned against each criterion. The criteria should align with the relevant aspects of the electric two- and three-wheeler ecosystem. To assess each design solution against the criteria, scores are assigned to indicate the performance and suitability of each solution for each criterion. The TOPSIS method then calculates the similarity of each alternative to the ideal solution by comparing its performance to the best and worst solutions for each criterion. A comprehensive similarity score is computed for each alternative, and they are ranked based on their proximity to the ideal solution.
This study was based on multi-objective optimization, multi-attribute decision-making, and TOPSIS analysis on the techno-commercial aspects of present adaptability strategies in order to make the modification more practical and reasonable in the future. This study sought to find optimal design choices and proposes a novel two-stage hybrid methodology: in the first stage to generate an approximate Pareto-optimal front of non-dominated solutions, and in the second stage, using the TOPSIS method, devoted to ranking the potential solutions to be proposed to the decision-maker.
This study covers the technical assessments of two- and three-wheeler electric vehicle design and its implementation process with significant key attributes. The study highlights major technical challenges that hamper the wide adaptation of electric vehicles in India, despite the government’s prudent initiatives. It also demonstrates the futuristic development of electric vehicles, which can lead to economic prosperity, environmentally sustainable development, and technological advancement. This paper includes five sections:
Section 2 covers the concept of multi-objective optimization (MOO) and the multi-attribute decision-making method (MADM); it also covers the Pareto-optimality (PO) front for the heterogeneous MOO and TOPSIS approaches for multi-attribute decision-making; Then, the proposed methodology is discussed, covering two stages of TOPSIS analysis for the identification of ranking in terms of order of preference. The Results and Discussion sections cover the survey results on electric two-wheelers regarding comfort, security, reliability, styling, navigation and control, ease of charging infrastructure, and driving range. Finally, conclusions and proposed future work are presented.
2. Multi-Objective Optimization (MOO) and the Multi-Attribute Decision-Making Method (MADM)
In the current human lifestyle, vehicles are not only seen as a necessity but they are also expected to provide a sophisticated experience, including features such as connection to the Internet of Things, infotainment, a speed sensor, etc. Recent developments in E2Ws include: the availability of E2Ws with longer ranges [
2], allowing riders to travel further without needing to recharge; improvements in battery technology [
6], leading to faster charging times for electric two-wheelers, making them more convenient for everyday use; smart connectivity features [
10], such as a Global Positioning System (GPS) tracking, remote diagnostics, and smartphone integration [
12,
13]; improved performance, with faster acceleration and higher top speeds [
16]; and more affordable prices as a result of advances in technology and increasing competition, making E2Ws a more accessible option for consumers. Overall, E2Ws are becoming more practical, convenient, and cost-effective, making them an increasingly popular choice for urban transportation. The transition from carbon-based-fuel-fed internal combustion engines to battery-powered motor-driven vehicles [
16] has changed the landscape of vehicle manufacturing, and several small-scale assemblers with little to no research in this field have entered the market. India lacks the key resources necessary for E2W: batteries (lithium-ion) due to poor natural resource availability, battery management systems due to environmental issues with semiconductor development, and EV-grade permanent magnet motors [
17]. Also, due to the high cost of molds for body parts, it is cheaper to import them. In totality, a significant proportion of E2W parts are imported, which are neither manufactured nor engineered for Indian needs and suitability. This has resulted in several failures and even accidents that have happened in the recent past, forcing the government to impose strict regulation and testing protocols [
18]. Also, the lack of standardization has resulted in a mushrooming of different foam-factored thermal- and electrical-monitoring-type lithium ion batteries—with different electrochemistry—which are yet to be fully validated in typical Indian environmental and operating conditions [
19,
20].
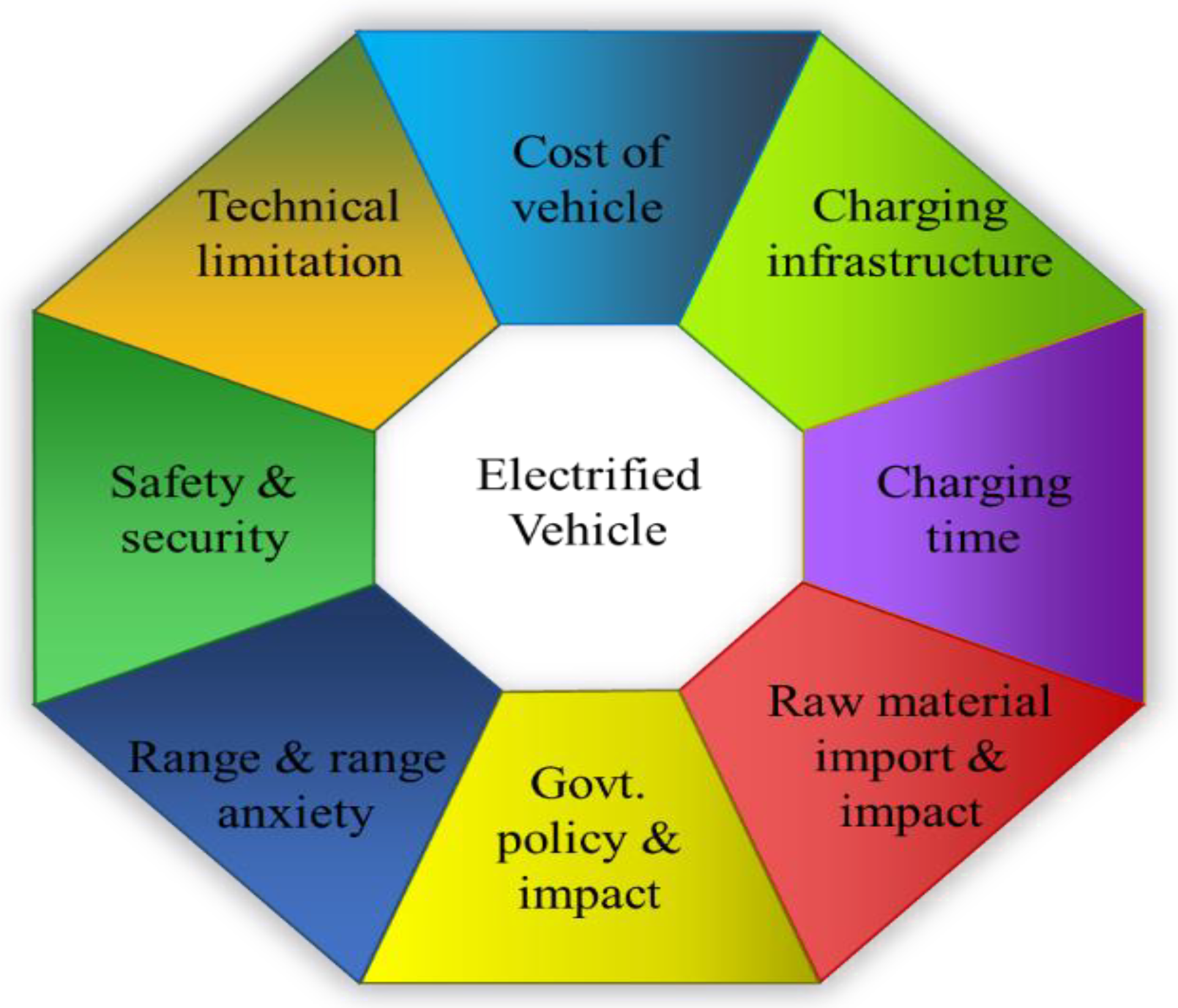
Figure 1 illustrates the key attribute of electric two-wheelers (E2Ws) and electric three-wheelers (E3Ws) with selection parameters, along with major components.
Selecting the right components, like batteries or an electric motor, to fit a particular E2W is not always straightforward. Several variables need to be addressed as these crucial components can affect the efficiency, performance, cost, weight, reliability, and output power. There are several selection criteria, including vehicular characteristics [
9,
10], driving cycles [
6], vehicle configuration [
12], maximal output (speed, torque, power) [
16], battery characteristics (electrochemistry, voltage, and capacity) [
12,
13], powertrain architecture (direct drive or geared drive) [
9,
17], cost [
19,
20], etc.
The optimal design and control in developing the E2W ecosystem involve several attributes, as well as alternatives that impact decisions and involve multiple objectives. The goals are not quantifiable in terms of less is better or more is better; rather, each goal has an ideal target value, and the goal has to be as near as possible to the target value. One posterior preference approach that commonly generates sets of solutions is the visualization of the Pareto front, which enables the calculation of an approximate Pareto front [
17,
21]. The design of an automobile involves a series of compromises on different parameters to fit into optimal solutions under a variety of different operating and environmental states. Each situation or task has its optimum vehicle design, which will maximize performance for that particular state [
22].
MOO is a fundamental part of real-world optimization activities, that is ideally suited to be modeled using multiple conflicting objectives and is an indispensable assignment in engineering to ensure maximization. In the past 10 years, metaheuristic algorithms have attracted a lot of interest for their use in solving challenging MOO issues [
10]. Metaheuristic hybridization is a fascinating and productive topic of research since it enhances the functionality of the current algorithms. PO-TOPSIS hybrid methodologies are selectively used in engineering design [
23], inventory control [
24], supply chain planning [
25], automobile wireless sensor networks [
26,
27], etc.
3. Pareto-Optimality Front for Heterogeneous MOO
The strength of the Pareto evolutionary algorithm [
19,
23] in this context is that it is a multi-objective optimization algorithm used to find Pareto-optimal solutions for ideal design solutions in electric two- and three-wheelers [
24]. It is a non-dominated sorting algorithm approach [
25] that uses a fitness assignment technique to generate a set of Pareto-optimal solutions [
26]. The Pareto evolutionary algorithm for ideal design solutions in electric two- and three-wheelers works as follows:
- (a)
Initialize a population of ideal design solutions randomly.
- (b)
Evaluate the fitness of each solution in the population based on its non-domination level and its density.
- (c)
Select the non-dominated solutions from the population.
- (d)
If the number of non-dominated solutions is greater than the desired population size, use a truncation operator to select the best solutions.
- (e)
If the number of non-dominated solutions is less than the desired population size, use a reproduction operator to generate new solutions.
- (f)
Apply inherent operators such as crossover and mutation to the selected solutions.
- (g)
Repeat steps (b) to (f) until a stopping criterion is met, such as a maximum number of iterations or a minimum level of convergence.
Vilfredo Pareto is best known for his work on the distribution of income and wealth, which led to the development of the Pareto principle (also known as the 80-20 rule) and the concept of Pareto optimality [
24]. His ideas continue to play an important role in the development of technology, economic theory, and policy, and his contributions have had a lasting impact on the field of economics and its practitioners [
26]. It employs quick methods to locate a non-dominated collection of options, also known as the Pareto-optimal front, which is of greater importance than making decisions, since each aim is stated as being equally excellent. One may evaluate how constructed systems can best satisfy various requirements using Pareto optimality. When several competing objectives need to be taken into account during an optimization process, Pareto optimality serves as a gauge of efficiency. It is used to rank the order in which problems should be solved to identify the one that will have the most impact on the process [
28].
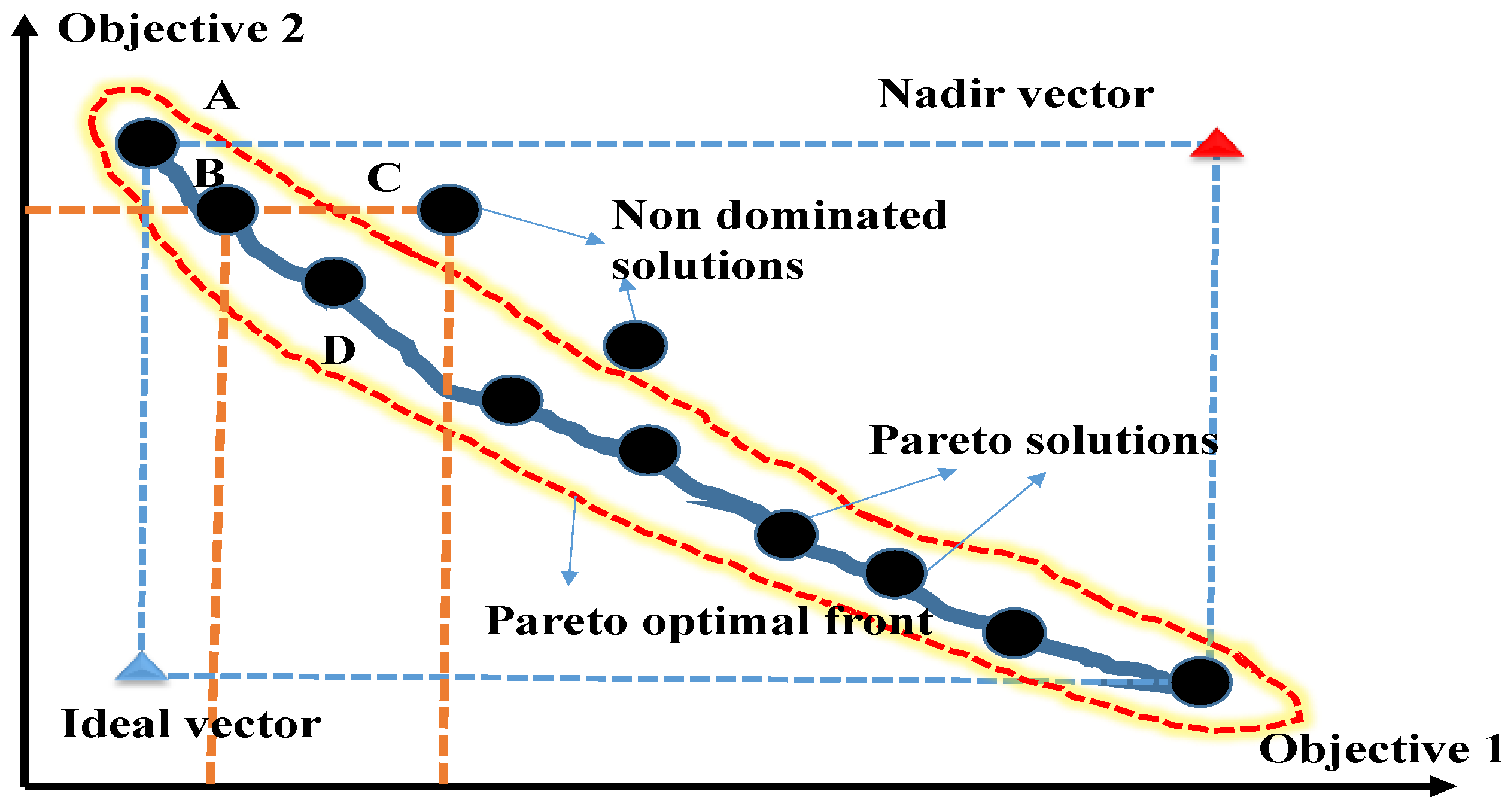
If no other design exists that may increase the value of any one of a design’s objective criteria without degrading at least one other criterion, the design is said to be Pareto optimum. This resulted in an optimization problem formulation without objective function aggregation and normalization. A point k* in the feasible design space ‘S’ is Pareto optimal if, and only if, another point ‘k’ in the set ‘S’ does not exist, such that Y(k) ≤ Y(k*) with at least one Y1(k) > Y1(k*). Unless otherwise indicated, the term “Pareto optimum” is considered to refer to the complete decision of variable space. The inequalities between vectors components applied to each attribute are represented as Y(k) ≤ Y(k*), which implies Y1 ≤ Y1*, Y2 ≤ Y2*, and so on. The Pareto-optimum set, which can refer to points in the design space or points in the criteria space, is the collection of all Pareto-optimal points. According to the criteria above, there must be no other point in the feasible design space ‘S’ that improves at least one objective function while leaving others intact for ‘k*’ to be referred to be the Pareto-optimum point. In
Figure 2, the idea of Pareto optimality is shown; it is using multi-objective optimization techniques for an optimal solution on the Pareto front. The ideal solution covers multiple objective optimizations with non-dominated solutions on the Pareto-optimal front.
Pareto optimality is regularly implemented in various electric vehicle design applications ranging from vehicle suspension [
29,
30], braking systems [
31], permanent magnet motors [
32], control system design, cell design [
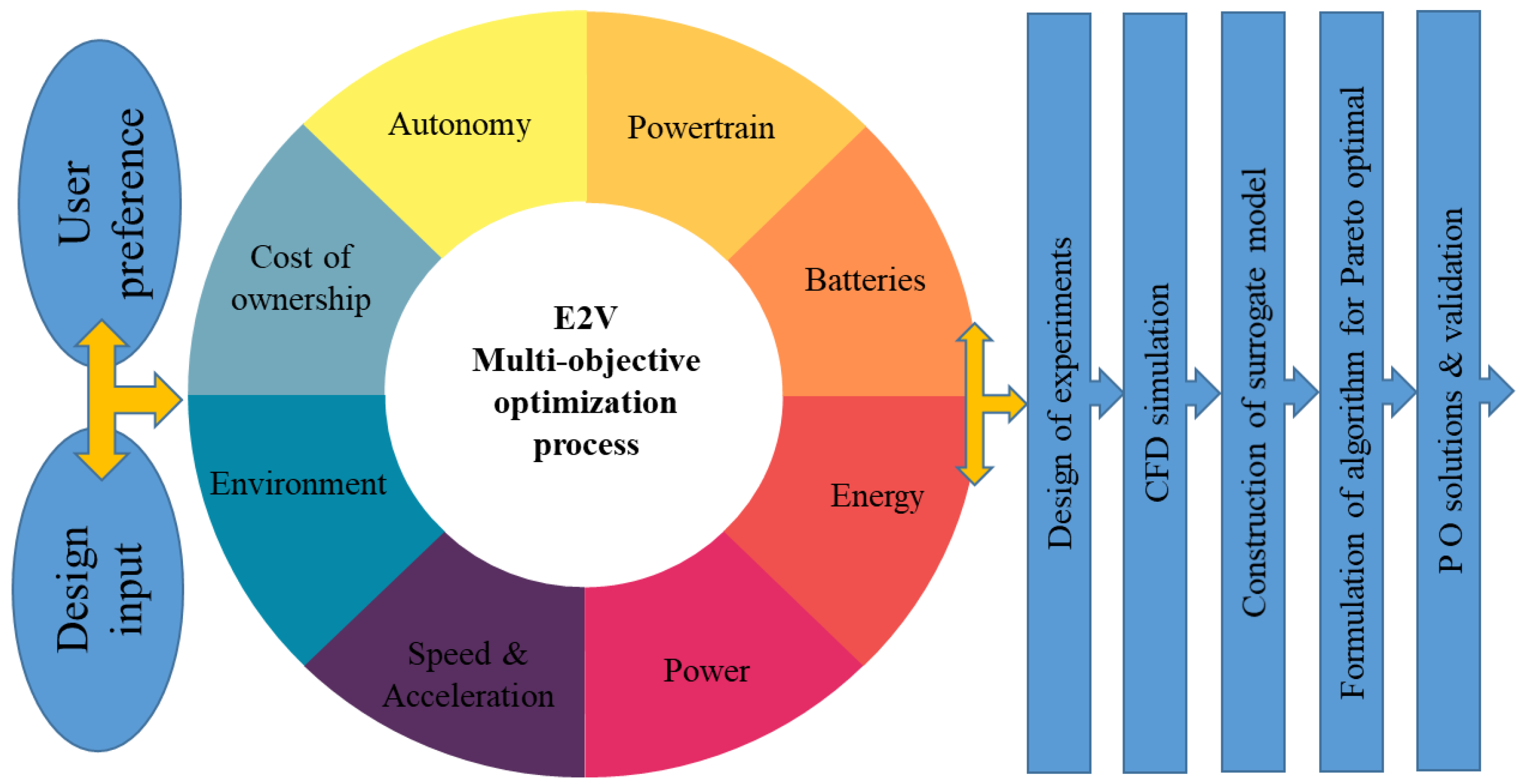
33], etc. The components of the objectives are not combined into a single fitness function; instead, they are kept distinct at all times during the optimization process. They can resolve all competing design requirements independently and concurrently. The solutions on a Pareto front consequently have the optimal objective functions, given their constraints, and are not dominated by any other locations in the design space. The system block diagram of electric two- and three-wheelers with a multi-objective optimization process is shown in
Figure 3. It covers autonomy, the powertrain, batteries, the management system, environmental conditions, and power.
4. TOPSIS Approach for Multi-Attribute Decision-Making
The TOPSIS developed by Ching-Lai Hwang and Yoon in 1981 [
25] uses the basic mathematical approach to find the optimal alternative. It covers the analytical multi-attribute decision-making method and works on the main idea of seeking the preferred alternative to the closest to the positive ideal solution. The same approach is used for the calculation and analysis of a negative ideal solution. By adding the Euclidean distance to determine the relative proximity geometrically, the TOPSIS rule states that the selected option must be the closest to the positive ideal solution and the farthest from the negative ideal solution.
The TOPSIS approach is a multi-criteria decision-making method used to determine the best alternative among a set of options. It aims to find the alternative that has the shortest distance to the ideal solution and the farthest distance to the negative ideal solution. The TOPSIS approach provides a systematic and quantitative way of evaluating alternatives based on multiple criteria. It helps decision-makers consider various factors and their relative importance when making choices. The step-by-step implementation details of the TOPSIS approach are as follows:
Create a decision matrix, where each row represents an alternative and each column represents a criterion. The values in the decision matrix represent the performance of each alternative on each criterion.
Normalize the decision matrix to ensure that all criteria are on the same scale. This can be carried out by dividing each value in the matrix by the sum of the squared values in the column or by using normalization techniques.
Determine the weighted normalized decision matrix and assign weights to each criterion based on their relative importance. The weights reflect the significance of each criterion in the decision-making process. Multiply each normalized value in the decision matrix by its corresponding weight to obtain the weighted normalized decision matrix.
Determine the ideal and negative ideal solutions for each criterion, and identify the best (ideal) and worst (negative ideal) possible values. The ideal solution represents the highest or most desirable value for each criterion, while the negative ideal solution represents the lowest or least desirable value. The ideal and negative ideal solutions are determined by either finding the maximum and minimum values for each criterion in the decision matrix or by incorporating additional information or expert opinions.
Calculate the Euclidean distance between each alternative and the ideal solution, as well as the distance between each alternative and the negative ideal solution. The Euclidean distance measures the straight-line distance between two points in a multi-dimensional space.
Calculate the relative closeness of each alternative to the ideal solution by dividing the distance to the negative ideal solution by the sum of the distances to both the ideal and negative ideal solutions.
Rank the alternatives based on their relative closeness values. The alternative with the highest relative closeness value is considered the best solution.
The fundamental idea behind TOPSIS is to standardize the index values in the original multi-attribute decision matrix, and choose the best index value to create a positive ideal solution and the worst index value to create a negative ideal solution.
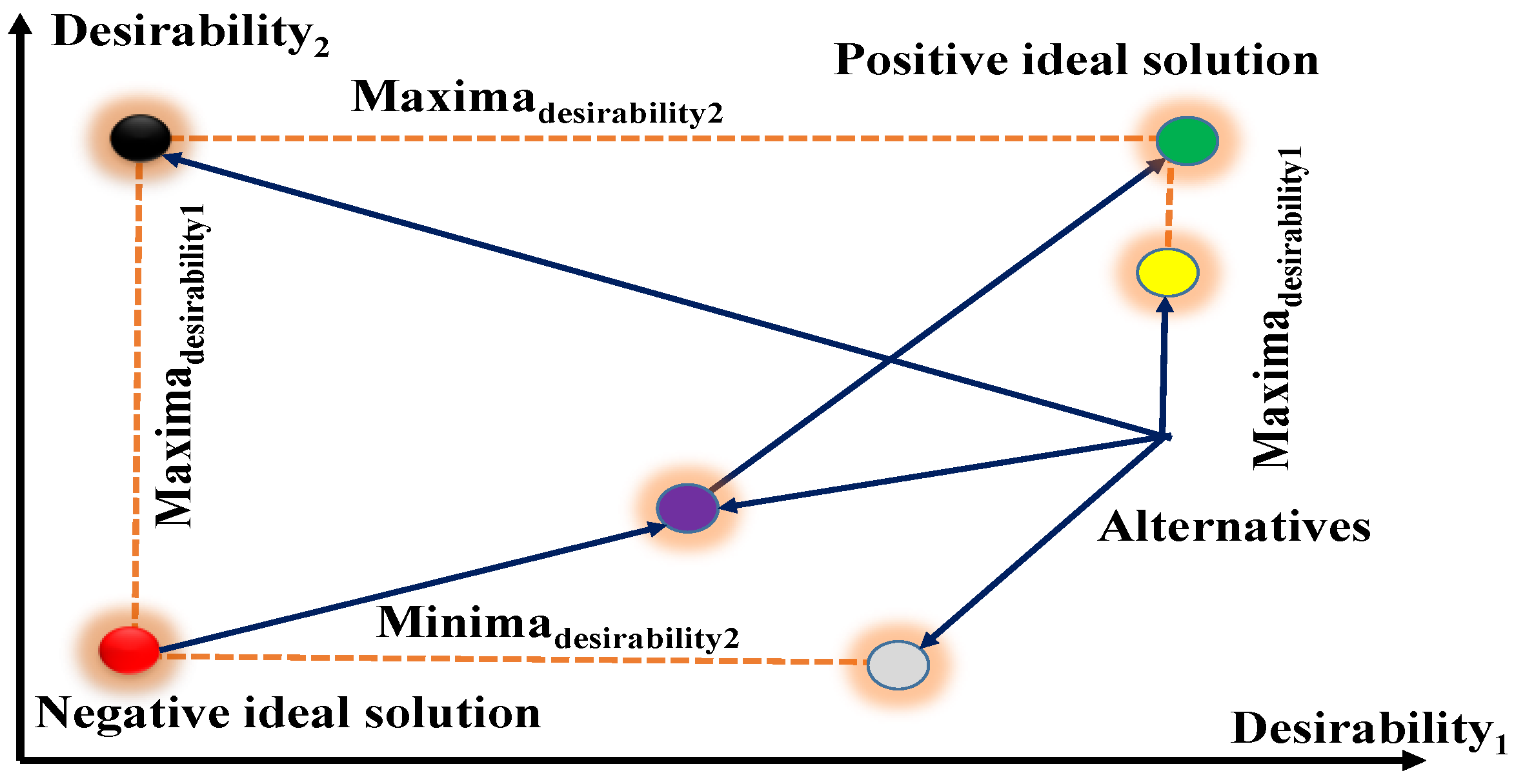
Figure 4 provides a graphical illustration of TOPSIS with two attributes and four alternatives based on the order of the indicators, measuring how close each scheme is to the positive and negative ideal solutions to determine how close it is to the ideal value, and then ranking the schemes according to how close they are.
Compensatory aggregation is a method used in multi-criteria decision analysis to combine multiple attributes into a single decision-making score [
24]. It allows for the consideration of trade-offs between different criteria and aims to find the best overall solution by compensating the weaknesses in one criterion with strengths in another [
33]. Multi-objective optimization with different attributes is developed using Matlab software. In the solver option “gamultiobj”, Pareto set fraction is selected under the algorithm setting with “ParetoOptimalTracing”. The finite element expectations, arrangement, and settlements follow the “Sigmund” function, and all of the parameters are summarized in
Figure 5. This compensatory aggregation method compares a set of alternatives by normalizing scores for each criterion, setting weights for each criterion, calculating the geometric distance between each alternative and the ideal alternative, and providing the best alternative with the best score for each criterion [
34,
35]. By determining weights for each criterion, normalizing scores for each criterion, and calculating the geometric distance between each alternative and the ideal alternative, which is the alternative with the best score for each criterion, this compensatory aggregation method compares a set of alternatives. The main idea of this technique is to identify the preferred alternative with the closest ideal solution.
Decision-makers can use a system that uses TOPSIS methodologies to evaluate the performance of alternatives based on several competing yet specified criteria or objectives.
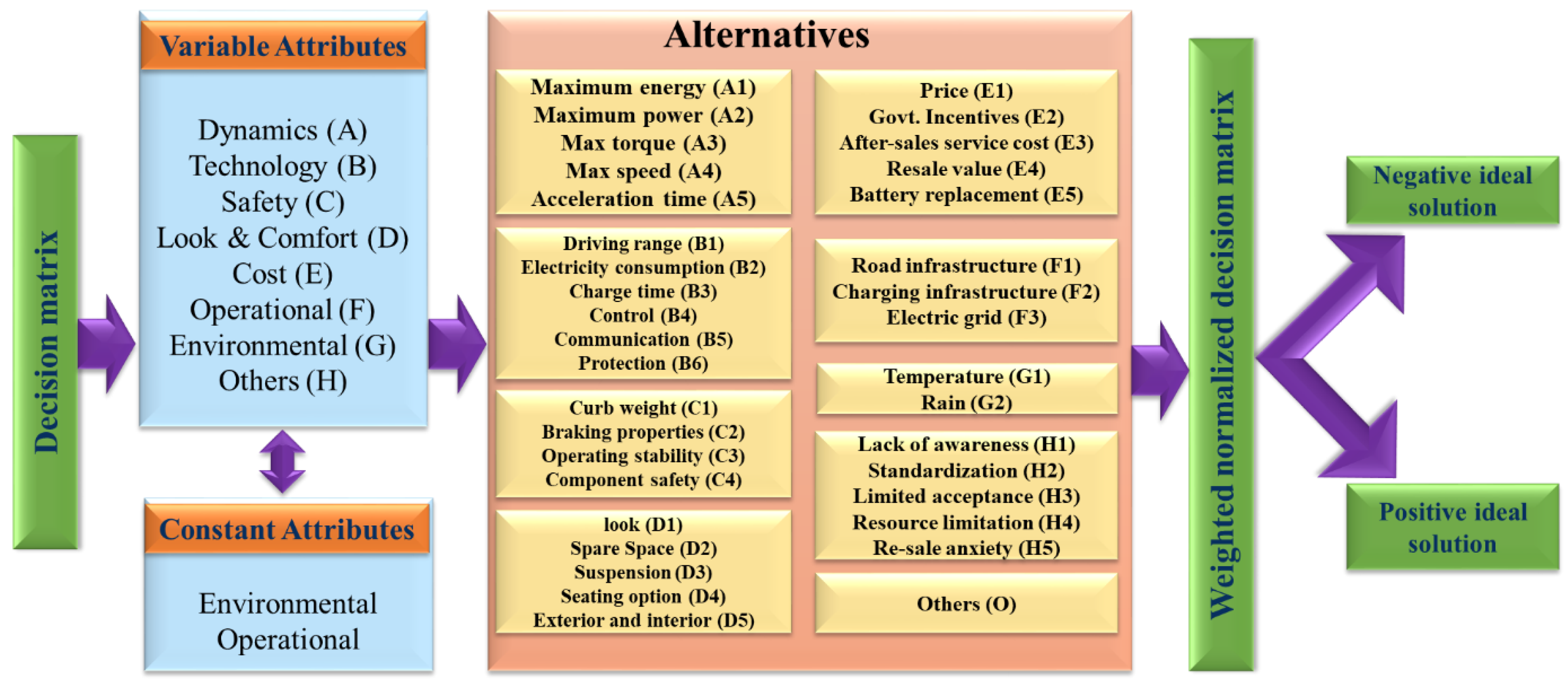
Figure 5 explains the TOPSIS analysis with different attributes for E2W and E3W selection and decision matrix solutions covering vehicle dynamics, technology, and operational and maintenance costs. It also provides details of maximum energy, power, torque, speed, acceleration time, curb weight, communication techniques, etc. The matrix has multiple attributes that cover different alternatives and the weighted normalized decision matrix provides an ideal solution. The process transforms different attribute dimensions into nondimensional attributes that perform comparison across different criteria. A weighted decision matrix is used specifically to identify a decision regarding the selection of attributes and an ideal solution.
5. Methods
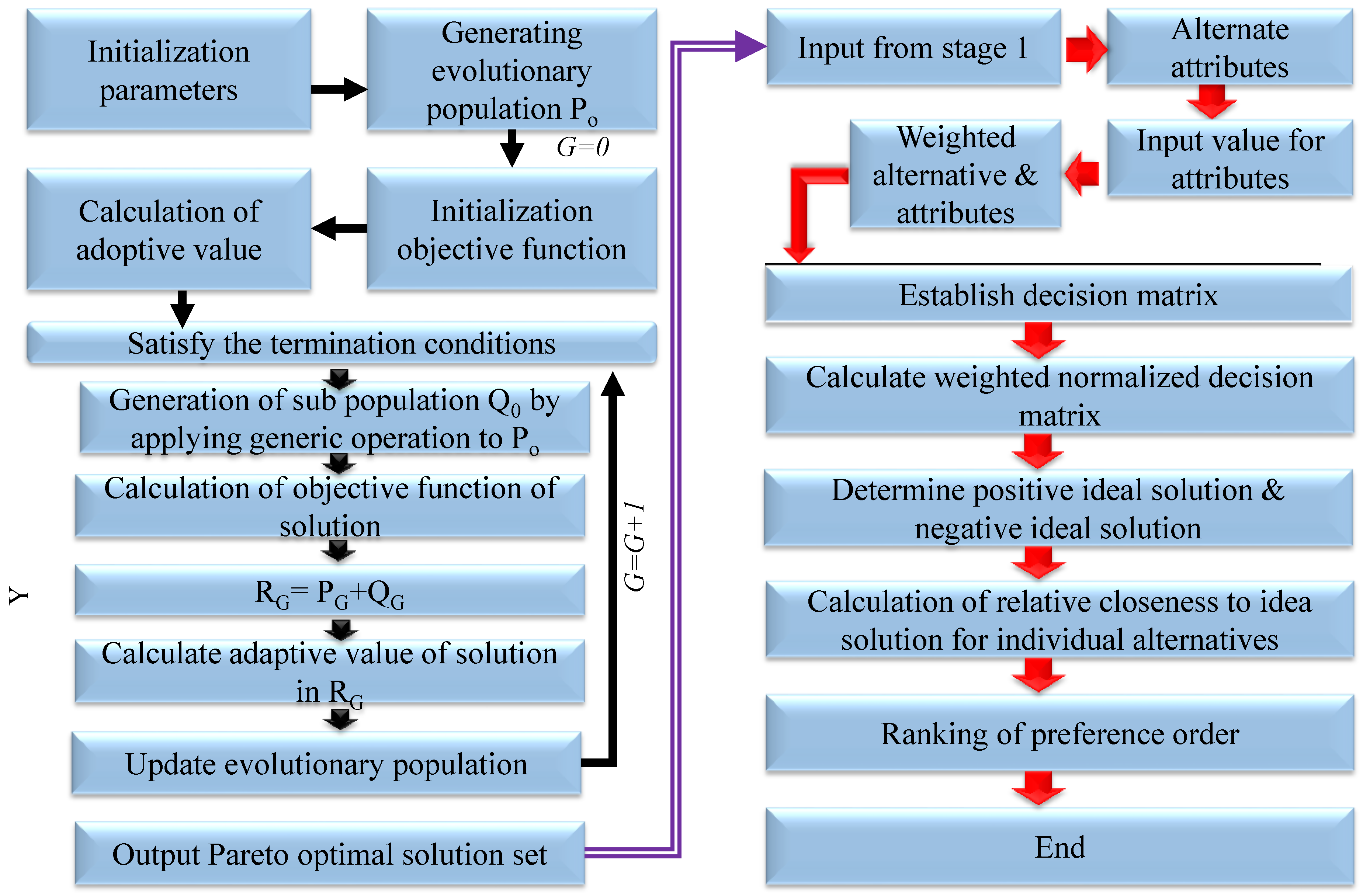
The literature suggests that a novel TOPSIS methodology is an ideal design solution for E2W with different attributes and conditions. The TOPSIS method deals with parameter selection, initialization of objective function, satisfying termination conditions with adaptive value, calculation of objective function, and generating a PO solution set. The proposed method explains the two independent technical stages of the TOPSIS analysis shown in
Figure 6. Stage 1 covers the initialization of different parameters, calculation of adaptive values, calculation of objective functions, and generation of the optimal solution set, whereas stage 2 deals with the identification of weighted attributes, establishing the decision matrix, determination of positive, and negative ideal solutions, and identification of ranking with preference order. The TOPSIS method calculates the distance between different alternatives for each row from the ideal worst to the ideal best values and vice versa. In comparison to non-compensatory techniques, this method offers a realistic approach for alternate methods based on a strict cutoff. Data regarding the adoption of E2Ws in India were collected using a standard questionnaire, and the survey includes details on important attributes and their constituent parts. The procedure for framing a standard questionnaire typically involves defining the objective of the questionnaire, identifying the target audience, determining the type of questions to be included, and reviewing or refining the questions to meet the objective and achieve the desired results.
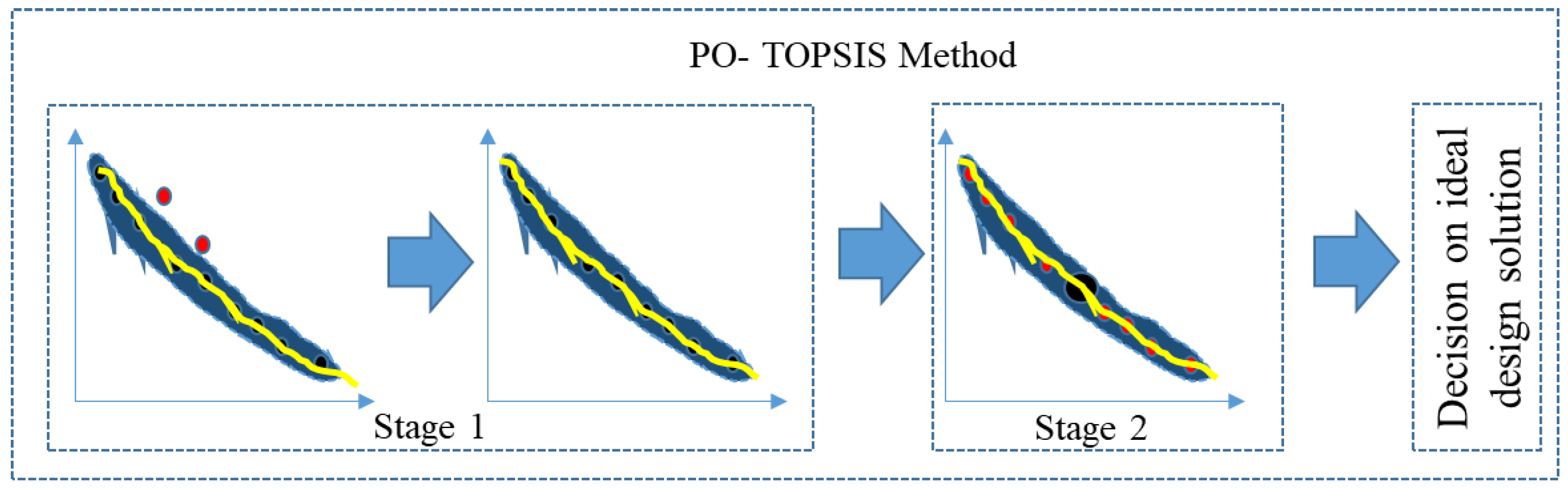
A useful method for analyzing customer acceptance or rejection is external preference mapping. The findings of preference maps will be improved by combining TOPSIS analysis with PO design. In the PO-TOPSIS method, allocating ranks is based on the impact and weights of the variable attributes and their alternatives. Weights indicate how much a certain component should be taken into account; for all factors, the default weight is 1 and the highest weight is 3. Impact denotes whether a particular variable’s features and alternative factors have a favorable or unfavorable effect. The preferred option should be the one with the least geometric distance from the perfect solution, and the one with the largest geometric distance from the ideal solution, according to the multi-criteria decision analysis technique known as the technique for order of preference by similarity to the ideal solution. The distinctive feature of this technique is its ability to assess a synthetic criterion’s values that takes into account the separation of an evaluated item from both a positive ideal solution and a negative ideal solution, as shown in
Figure 7. In the PO-TOPSIS method, attribute values must be numeric, monotonically non-increasing, or non-decreasing, have commensurable units, and be used to calculate a synthetic index based on a set of diagnostic variables. TOPSIS aids in rating the alternatives and determining the most advantageous design solution based on the supplied criteria by evaluating alternatives based on their resemblance to the positive ideal solution and dissimilarity to the negative ideal solution.
6. Results and Discussion
Electric vehicles are responsible for a big buzz in India, and E2W and E3W are extensively available in the market. However, social acceptance is poor because of comfort, range anxiety, battery technology, resale value, performance, and charging infrastructure [
1,
4]. Future buyers and users of electric two-wheelers and electric three-wheelers will be more familiar with vehicle features and variable attributes with multiple alternatives. The main criteria and sub-criteria are the main attributes for E2W and E3W selection and decision matrix solutions covering vehicle dynamics, technology, and operational and maintenance costs. It also provides details of maximum energy, power, torque, speed, acceleration time, curb weight, communication techniques, etc. The matrix has multiple attributes that cover different alternatives and the weighted normalized decision matrix provides an ideal solution. With a standardized questionnaire, data were gathered on the adaption of electric two-wheelers in India. Information regarding the construction of key attributes and their components [
16,
19] was included in the survey. The questionnaire was divided into two sections; the first section concentrated on information on the respondents’ demographic characteristics such as age, gender, annual income, demographic location, and nature of the house. Different two-wheel electric vehicle attributes were measured in the questionnaire’s second section such as available charging infrastructure, range anxiety, convenience, battery life, vehicle performance, and safety.
There is no established formula for structured equation modeling to choose the proper sample size. In this survey, a sample size of 134 was taken into consideration and covered all the demographic parts of India such as cities in the north, south, east, and west. A total of 134 valid answers to this article cover new users, existing owners, and technocrats’ chosen respondents. They were locals of Dehradun, New Delhi, Hyderabad, Bangalore, and Pune. More than 300 people were approached for the survey and 134 responded. The replies were accurate, and there were no missing data. In the survey, 14% of respondents were aged 18–25 years, 34% were aged 26–35 years, and 52% were aged 36 years and above. In terms of gender, 74% of respondents were male and 26% were female. Of the respondents, 49% resided in a flat, 48% stayed in their independent house, and 3% did not want to answer. Furthermore, 48% of the respondents were from metro cities, whereas 48% were from non-metro cities, and 4% were from rural areas. The annual income of the respondents was: 7–10 lakhs, 23%; and 3–7 lakhs, 26%; however, 51% of respondents did not want to answer this question.
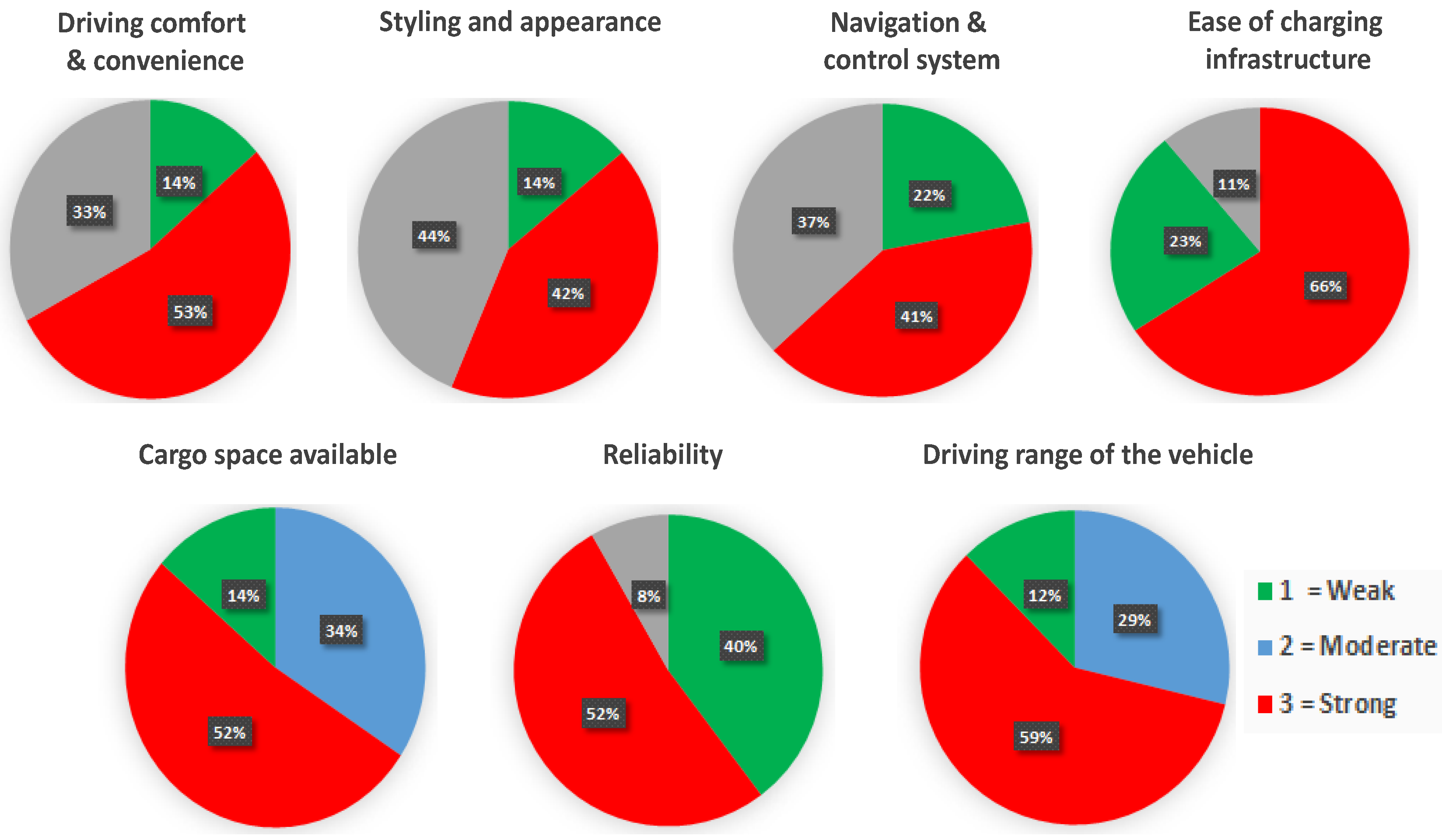
Figure 8 illustrates the survey results regarding E2Ws on comfort, security, reliability, styling, navigation and control, ease of charging infrastructure, and driving range, with a rating of 1 being weak, 2 representing moderate agreement, and 3 representing strong agreement. It covers how crucial the key elements are in promoting more widespread EV adoption through government subsidies, improved charging infrastructure, longer driving range, lower prices for electric vehicles, public education, and awareness.
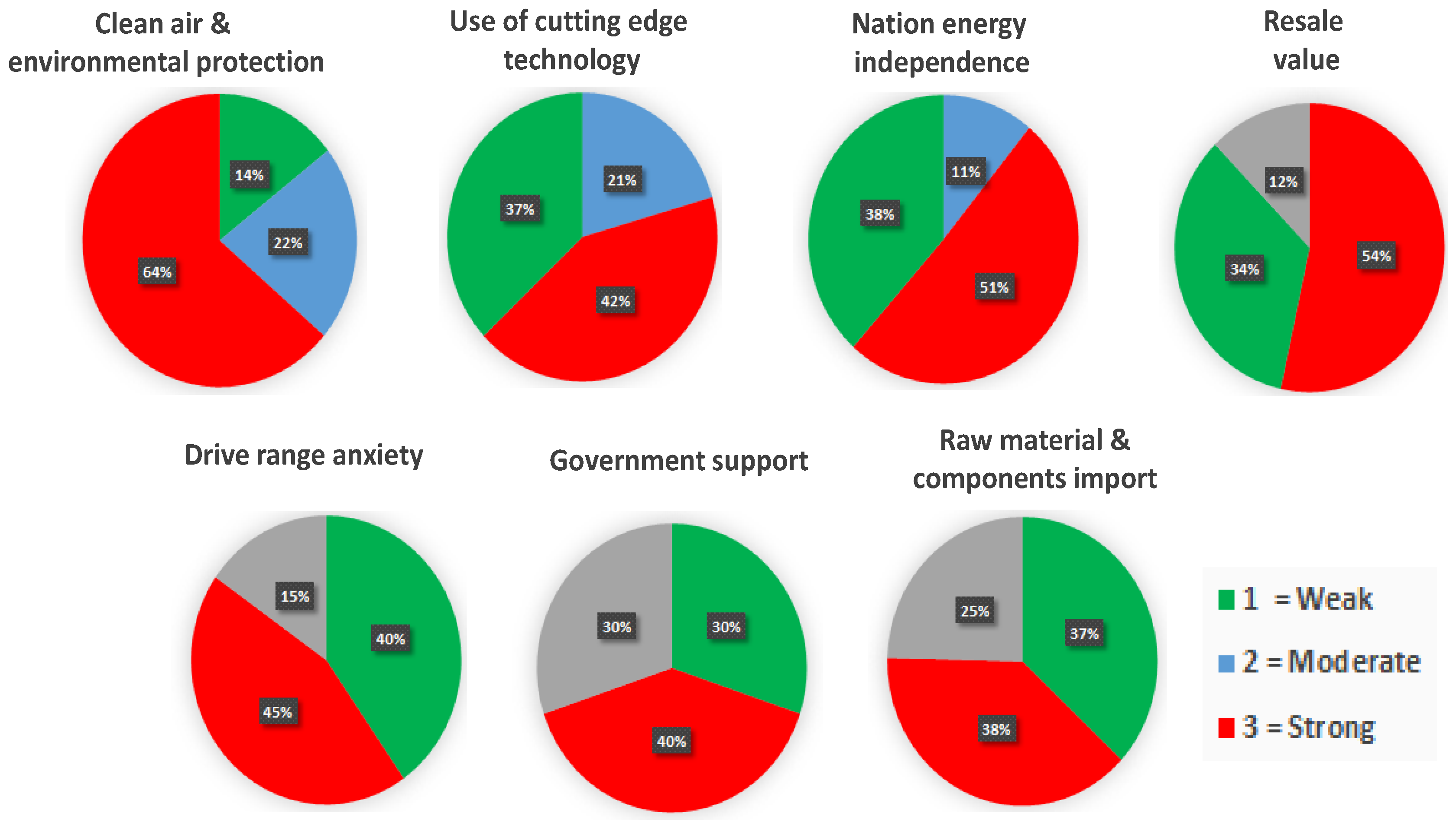
Figure 9 illustrates the survey results regarding E2Ws on clean air and environmental protection, innovative technology, national energy independence, resale value, driving range anxiety, government support, and raw material and component export. A rating of 1 = weakly agree, 2 = moderately agree, and 3 = strongly agree.
The application covers the parameter selection option among different categories. Pareto and TOPSIS analyses were applied to evaluate performance based on multiple criteria such as cost, timeline, resource requirements, environmental impact, and stakeholder satisfaction. The methods help to identify the best trade-off among main or sub-criteria and rank them according to their similarity to the ideal solution.
Table 1 lists out key attributes for electric two- and three-wheel vehicles covering the battery rating in kWh, traction motor rating in kW, driving range in km/charge, kerb weight in kg, torque generated by the traction motor in Nm, cost of the vehicle in ₹, and company infrastructure for sales, services, and charging infrastructure.
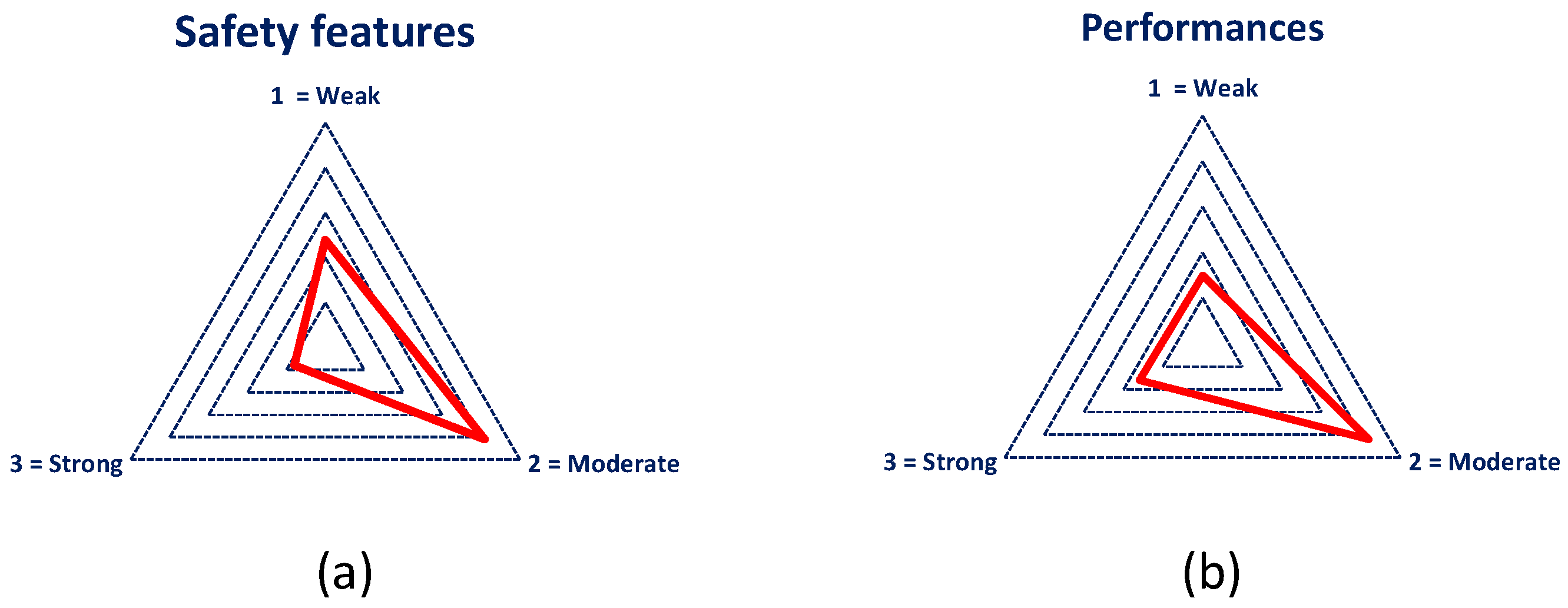
Figure 10a,b illustrates the Pareto-optimality performance characteristics for different electric two- and three-wheeler key attributes.
Figure 10a covers the safety feature attributes, with 1–3 being the Pareto-optimal solution set representing a positive to negative ideal solution, whereas
Figure 10b illustrates the vehicle performance attributes.
7. Conclusions
A unique assessment methodology for the electric two-wheeler ecosystem was offered in this study to find the best design option that satisfies many criteria, and is in line with customer desires and sustainability principles. To efficiently assess and rank design solutions, the suggested framework integrated the significant ideas of Pareto optimality and TOPSIS methodologies. The study ensured a thorough investigation of the design space by producing a comprehensive set of design options and exposing them to rigorous examination against several criteria. The non-dominated solutions, which outperform others on all criteria, were identified with great importance using the Pareto-optimality method, providing a solid foundation for further investigation. When objective measurements and subjective preferences were taken into consideration, the TOPSIS approach integration made it easier to identify the design option that was most similar to the ideal state. As a result, the selection process might be more carefully tailored, resulting in a solution that perfectly balances trade-offs between features, technologies, and standards.
The case study showed how the framework is used in practice and highlighted how well it could help manufacturers and policymakers make decisions. The outcomes underlined how crucial it is to take a variety of factors into account when building electric two-wheelers, including energy efficiency, manufacturing viability, and market viability. This study supports broader initiatives for environmental sustainability and urban mobility by promoting the adoption of eco-friendly transportation choices. The optimal design option discovered using this framework can be used as a guide for creating electric two-wheelers that not only adhere to legal requirements, but also take user preferences and demands into account. Overall, this study represents a substantial advancement in the approaches to ecosystem assessment and the development of electric two-wheeler technology. The results of this study have the potential to influence a more sustainable and environmentally friendly future, benefiting both urban settings and the global fight against climate change, as electric transportation grows in popularity around the world. The indigenous E2W ecosystem along with TOPSIS and PO strategies will help to achieve the Government of India’s new electric mission plans to penetrate 30% of private cars, 40% of buses, 70% of commercial cars, and 100% of two- and three-wheelers by 2030.