Research on a Multimode Adaptive Cruise Control Strategy with Emergency Lane-Changing Function
Abstract
1. Introduction
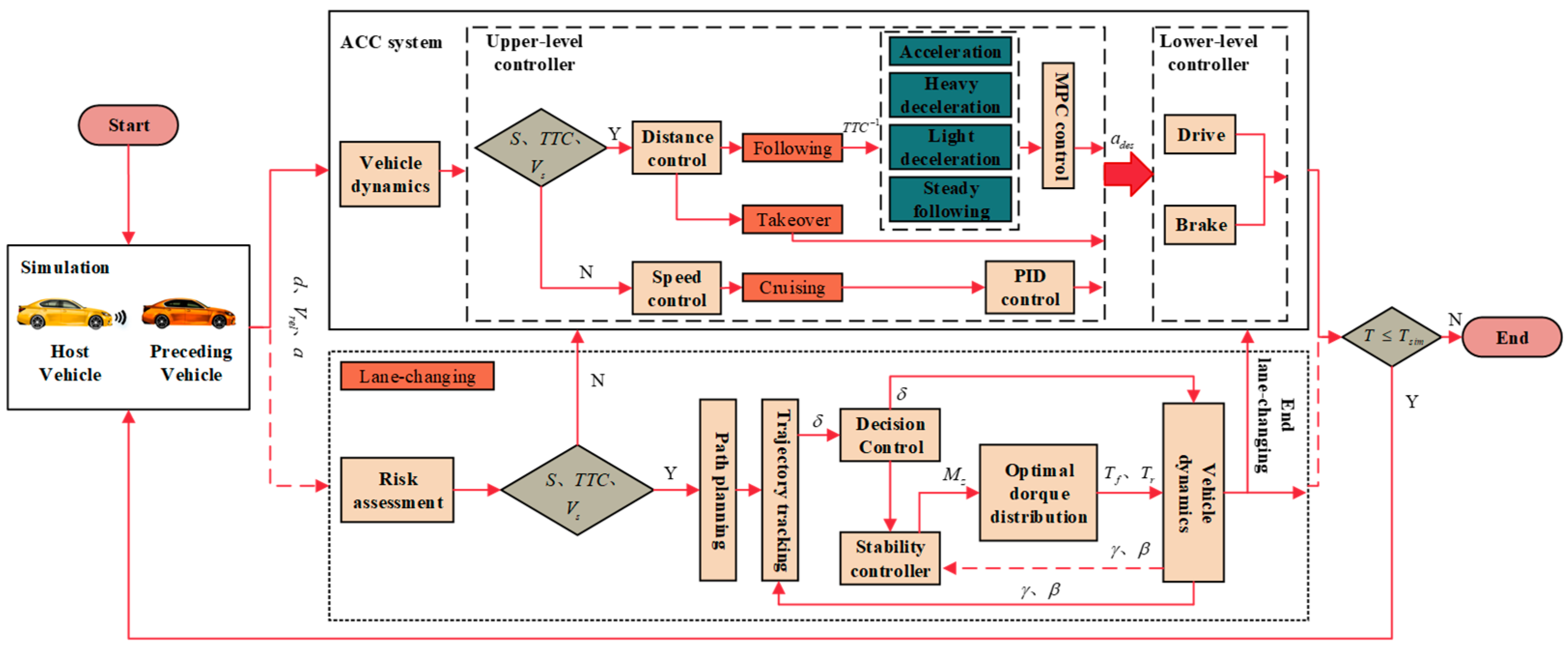
2. ACC Framework Definition
3. Design of Mode Switching Strategy
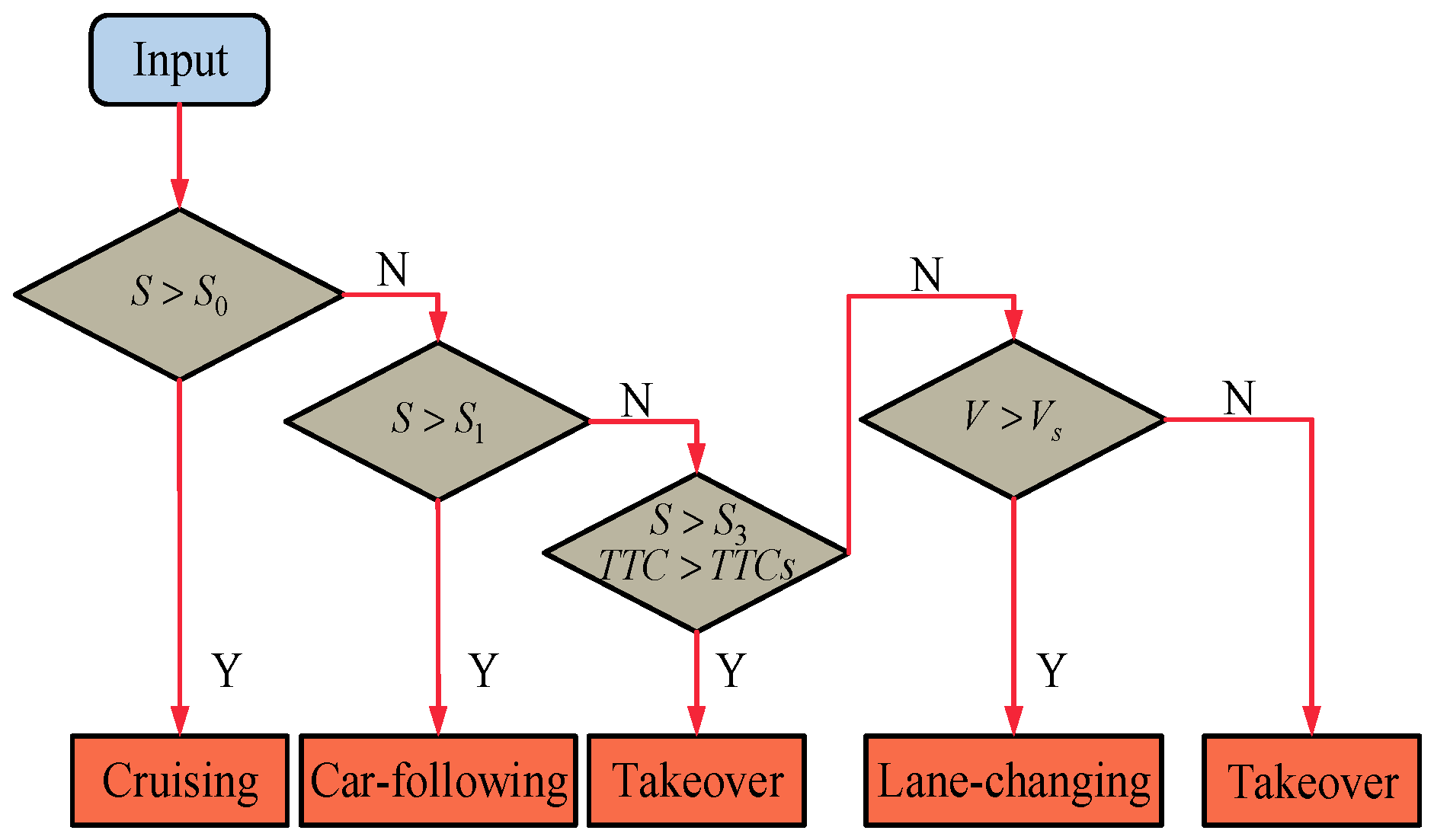
3.1. Four Main Modes of Division
- (1)
- Cruising distance
- (2)
- Takeover distance
- (3)
- Car-following distance
- (4)
- Emergency lane change criteria
3.2. Four Sub-Mode Division
- When [35], the vehicle is in steady following condition, and its acceleration range is −0.6–0.6 m/s2;
- When , the vehicle is in weak deceleration condition, and its maximum deceleration constraint is −2 m/s2;
- When , the vehicle is in strong deceleration condition, and its maximum deceleration constraint is −5 m/s2;
- When , the vehicle is in the acceleration condition, and its acceleration constraint range is 0.6–3.5 m/s2.
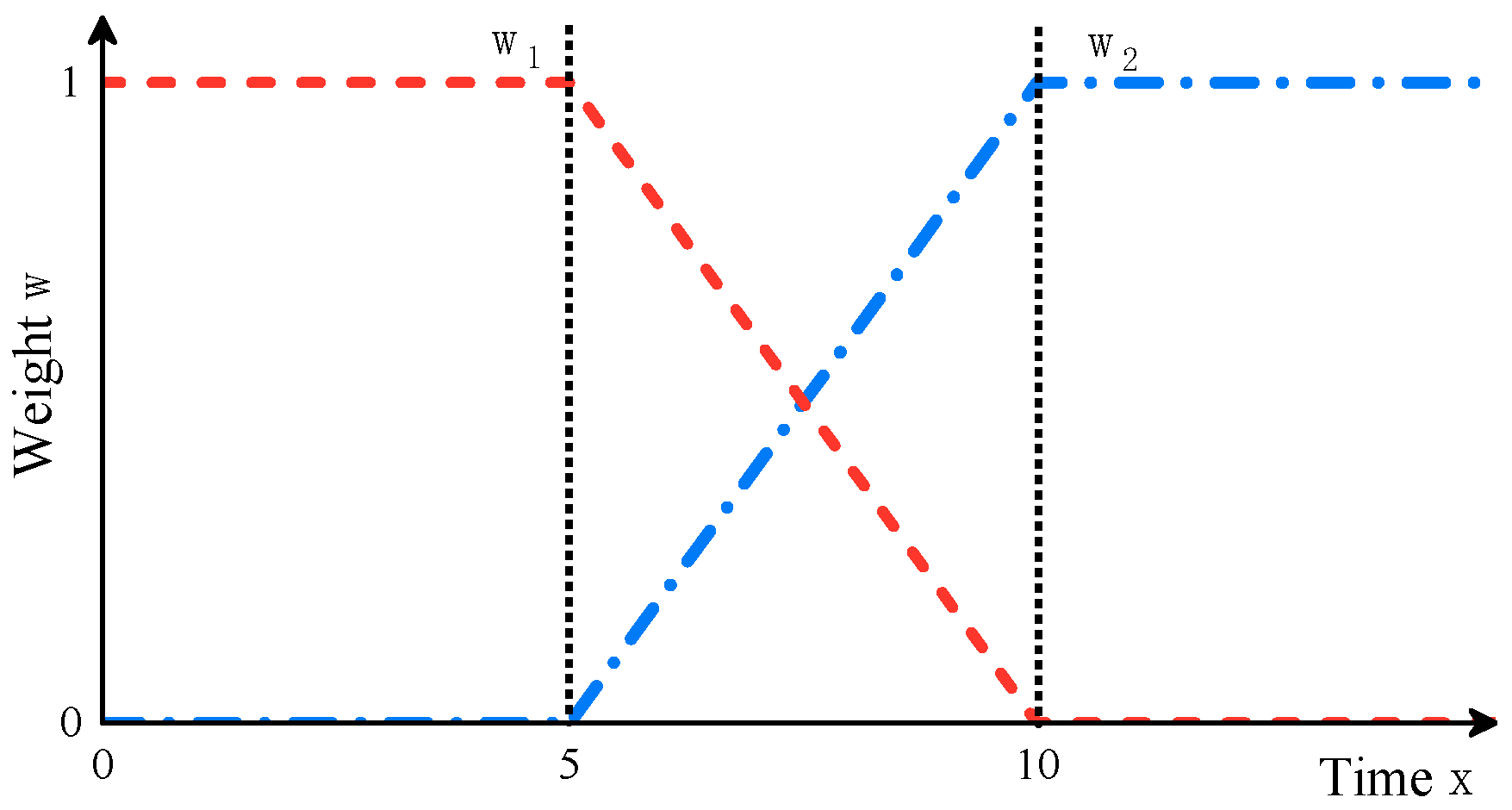
3.3. Overall Mode Switching Strategy
4. Design of Hierarchical Control Strategy for the ACC Mode
4.1. Upper-Level Controller Design
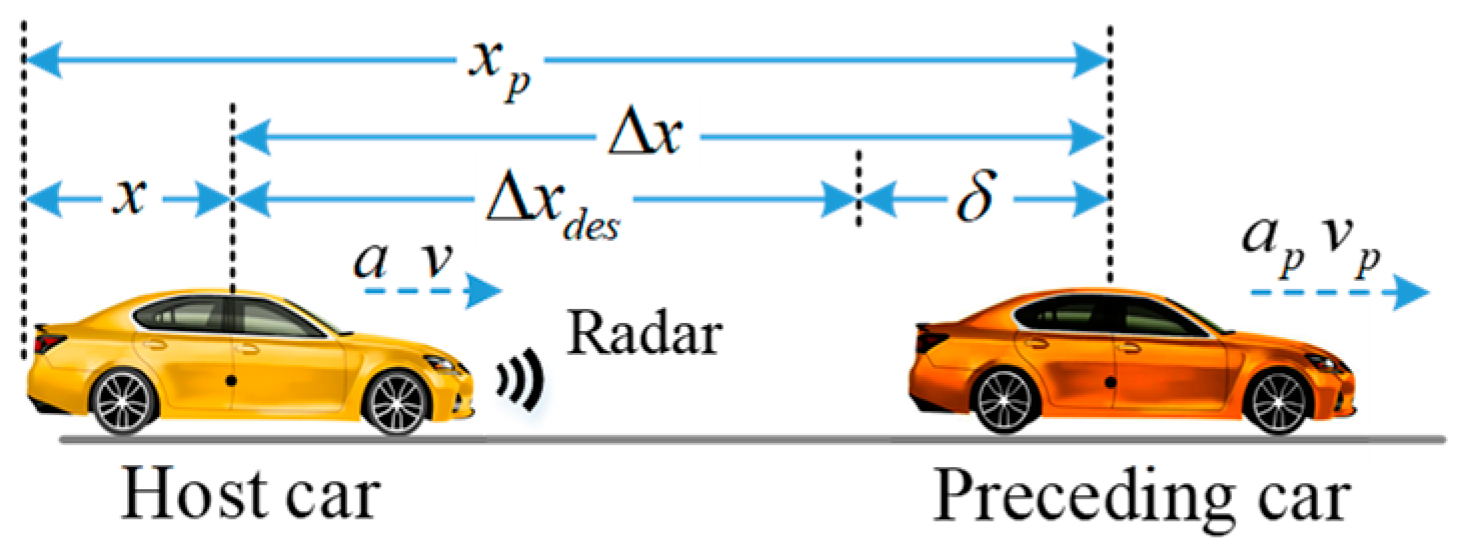
4.1.1. Cruising Mode Design
4.1.2. Car-Following Mode Design
- (1)
- Longitudinal dynamic model design
- (2)
- Control purpose and constraint analysis
- (3)
- MPC-based acc control algorithm design
4.1.3. Takeover Mode Design
4.1.4. Emergency Lane-Change Mode Design
- (1)
- Path planning
- (2)
- Path tracking controller design
- (3)
- Yaw moment calculation
- (4)
- Torque distribution strategy
4.2. Lower-Level Controller Design
- (1)
- Vehicle driving model
- (2)
- Vehicle braking model
- (3)
- Driving/Braking switching strategy and control method
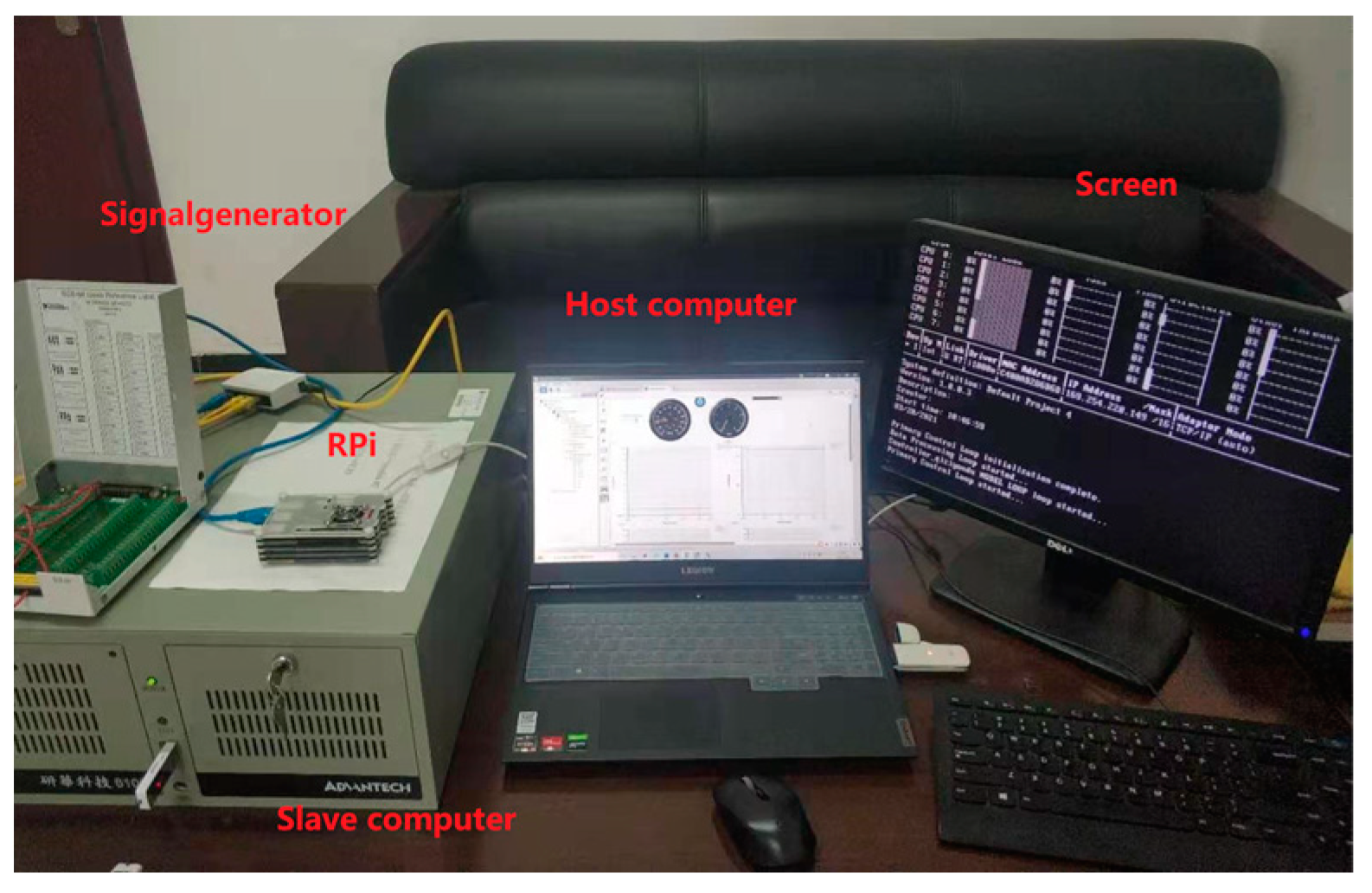
5. Simulation and Results
5.1. Simulation Setup
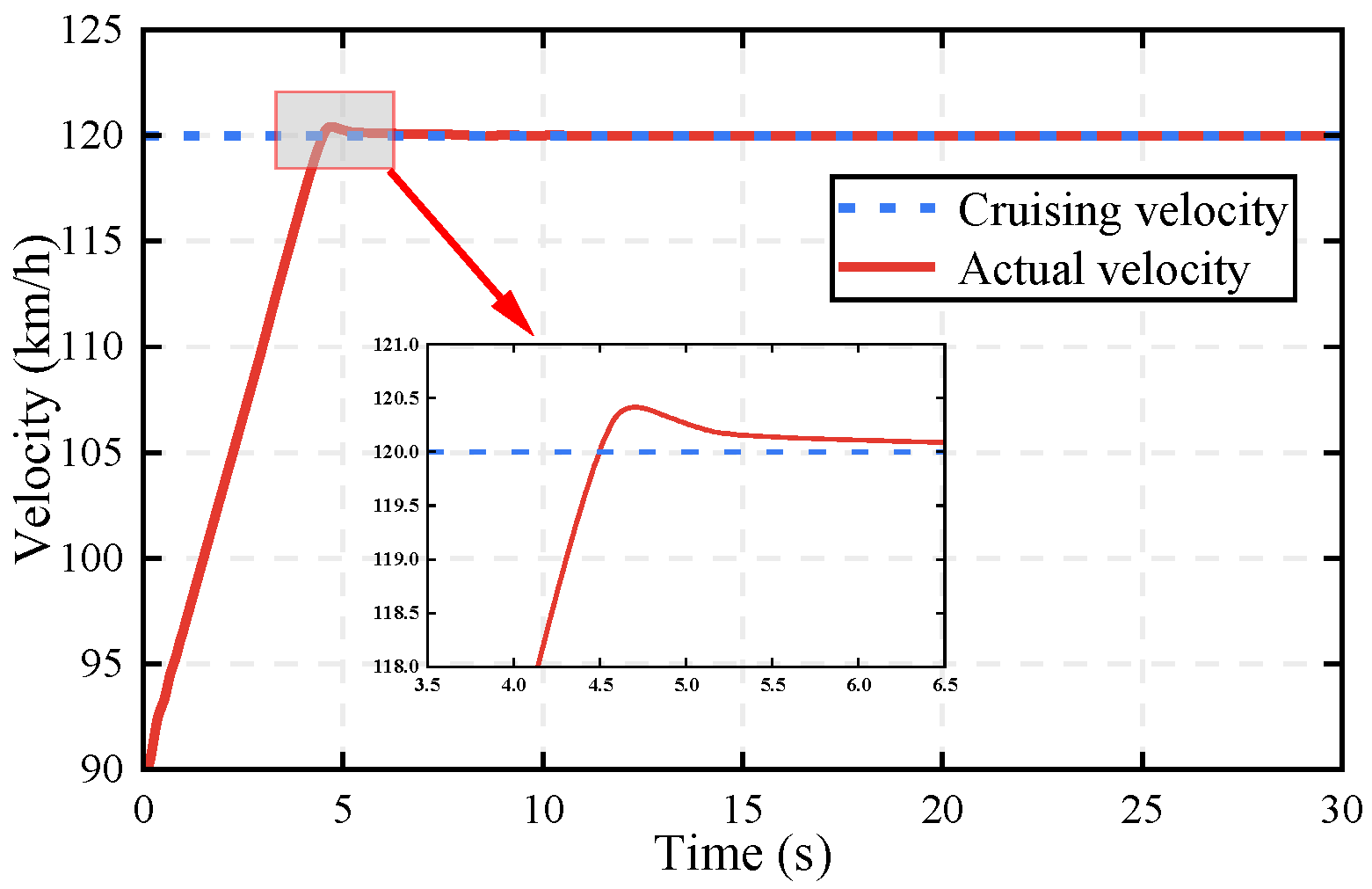
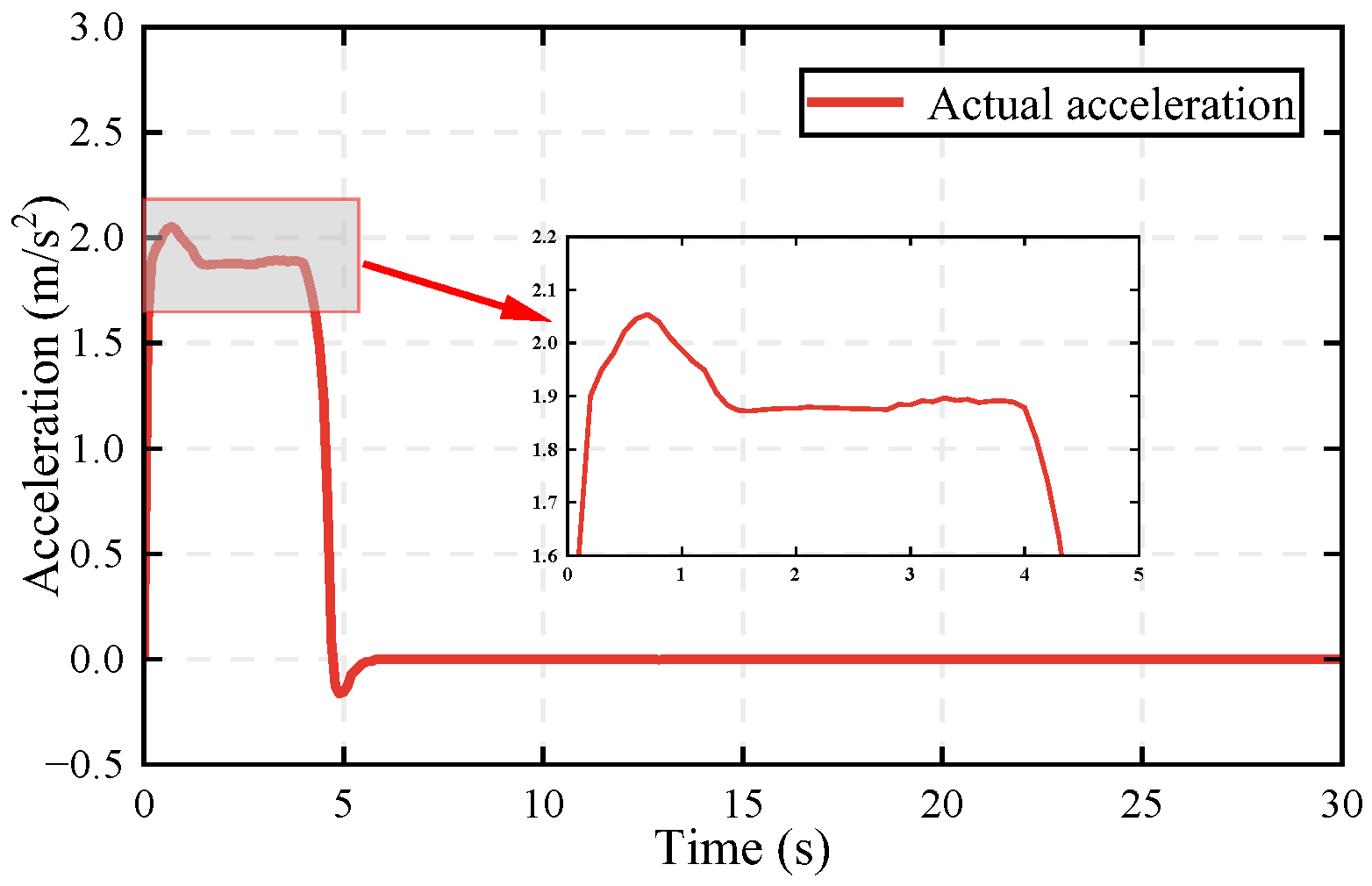
- Cruise control scenario: The vehicle’s initial velocity is 90 km/h, the cruise velocity is 120 km/h; there is no vehicle ahead of the host vehicle.
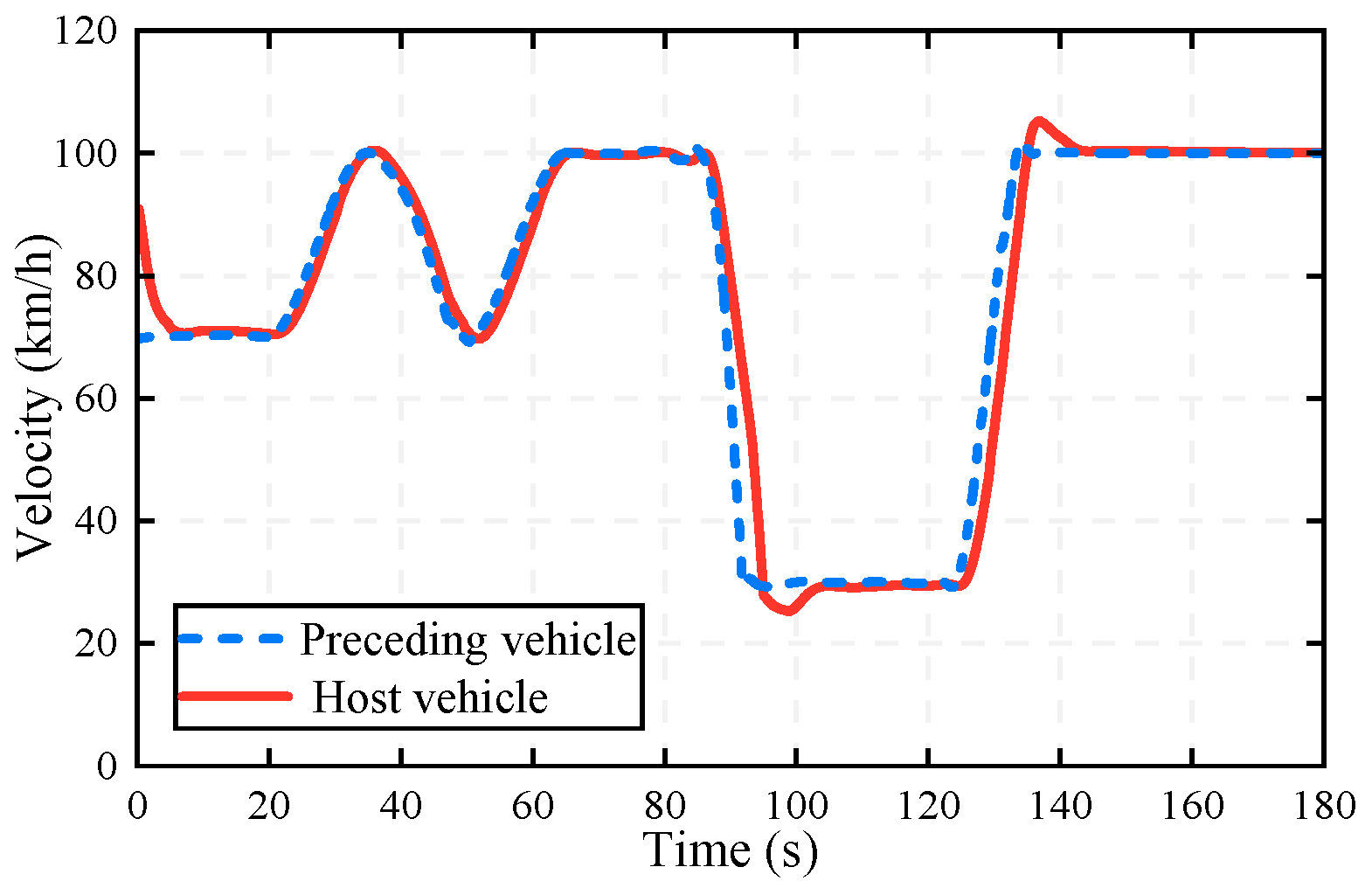
- Car-following scenario: The preceding vehicle performs acceleration, weak deceleration, strong deceleration, and steady-state following actions between 0 and 180 s.
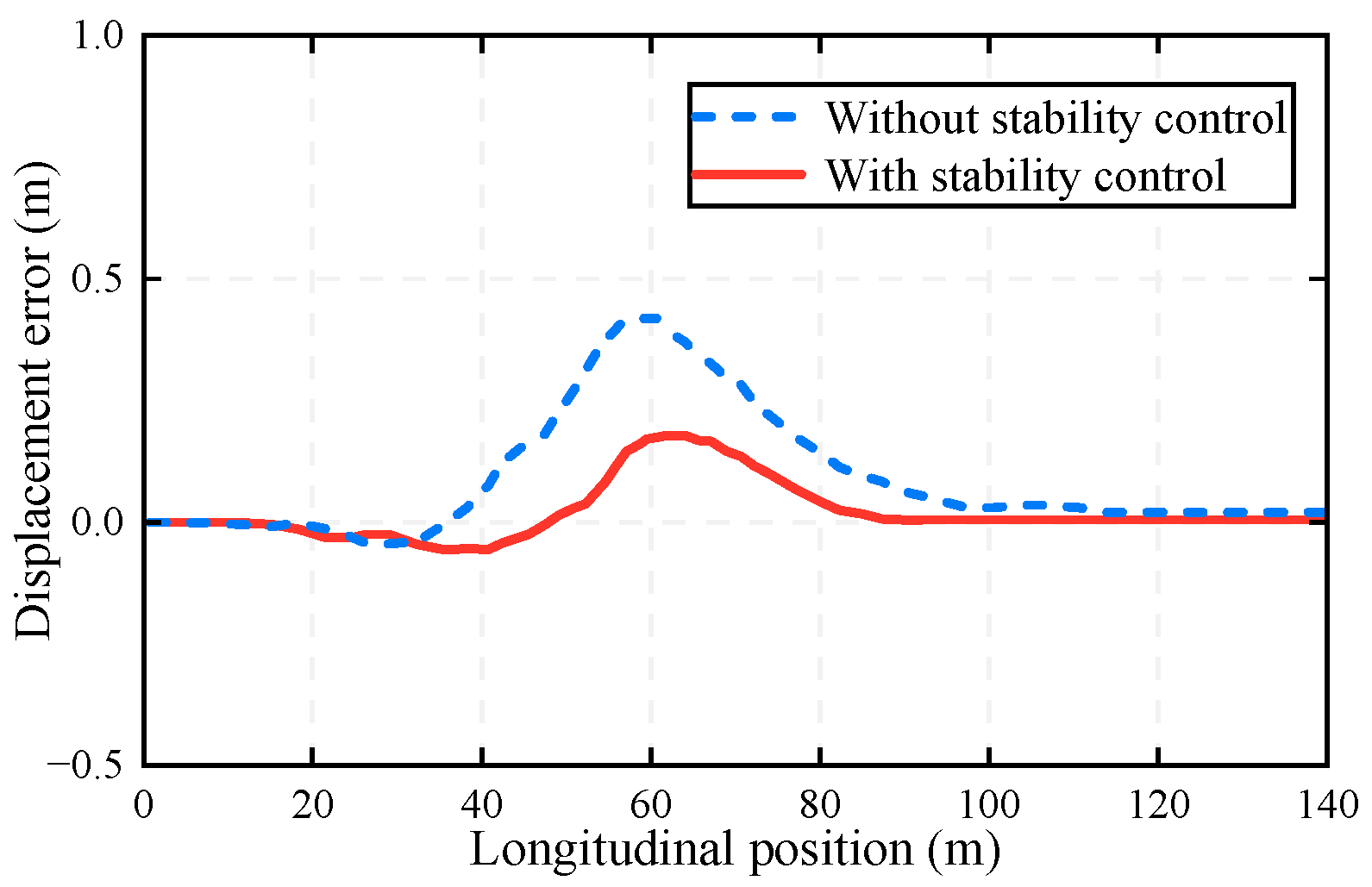
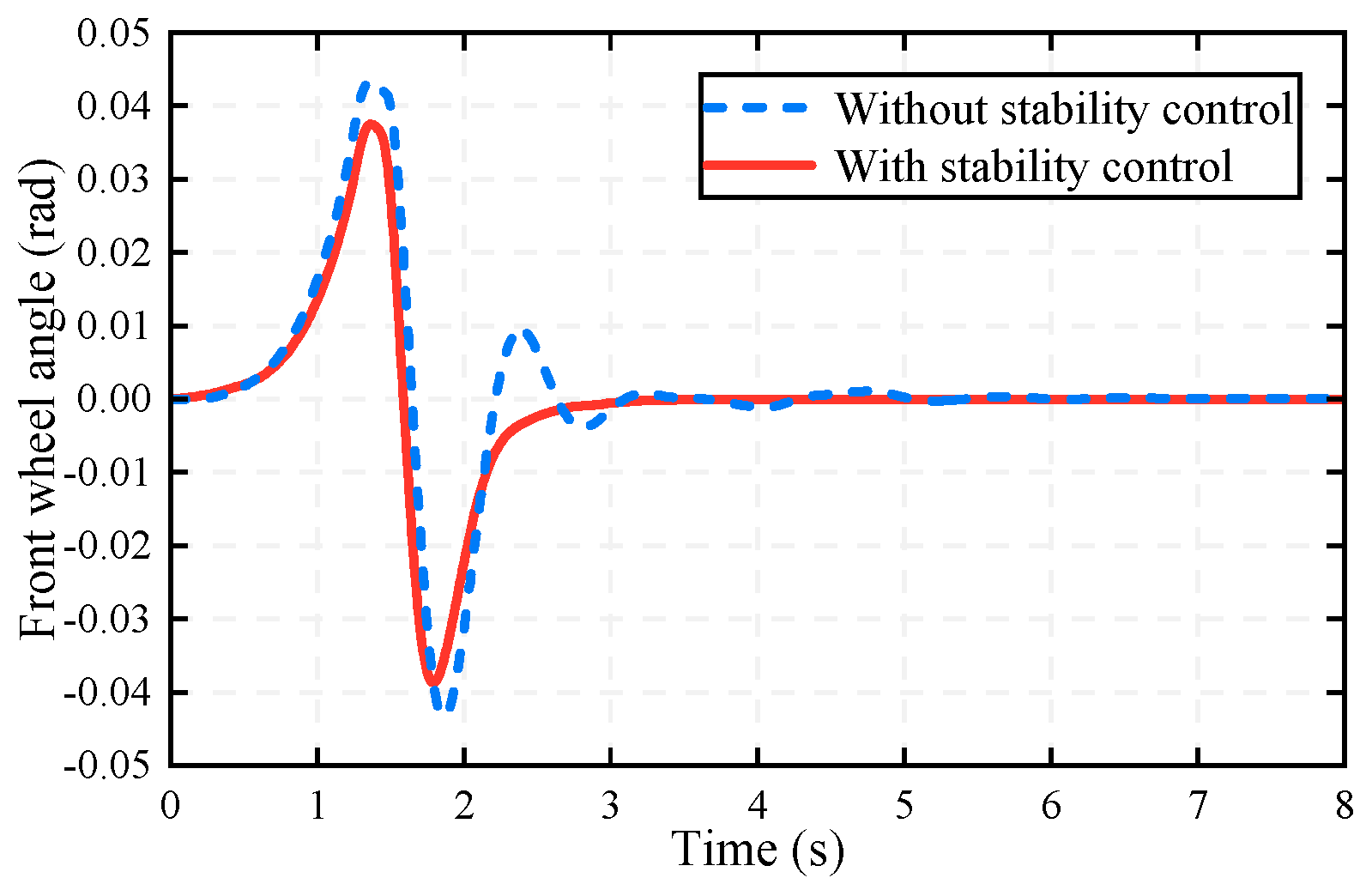
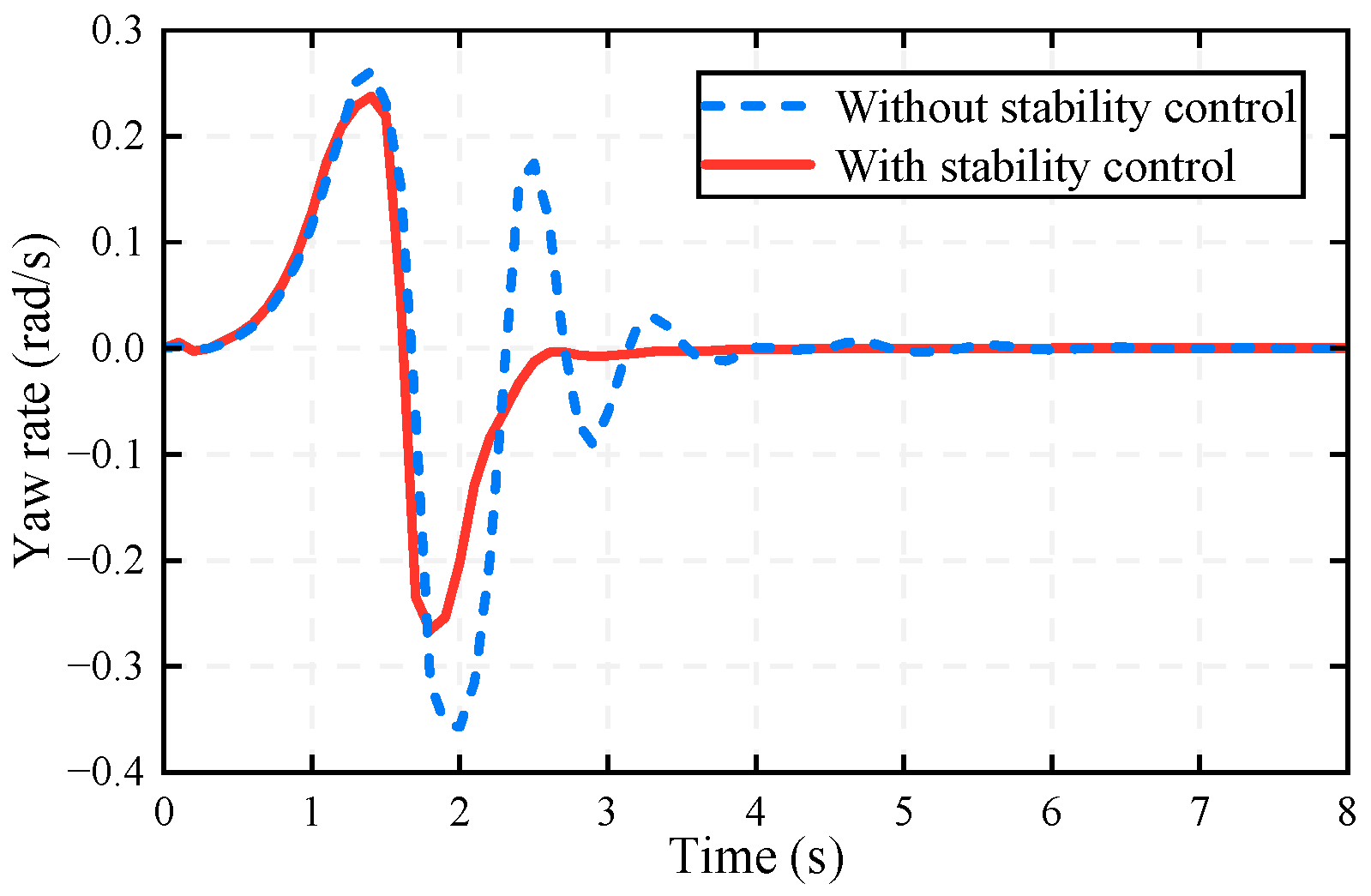
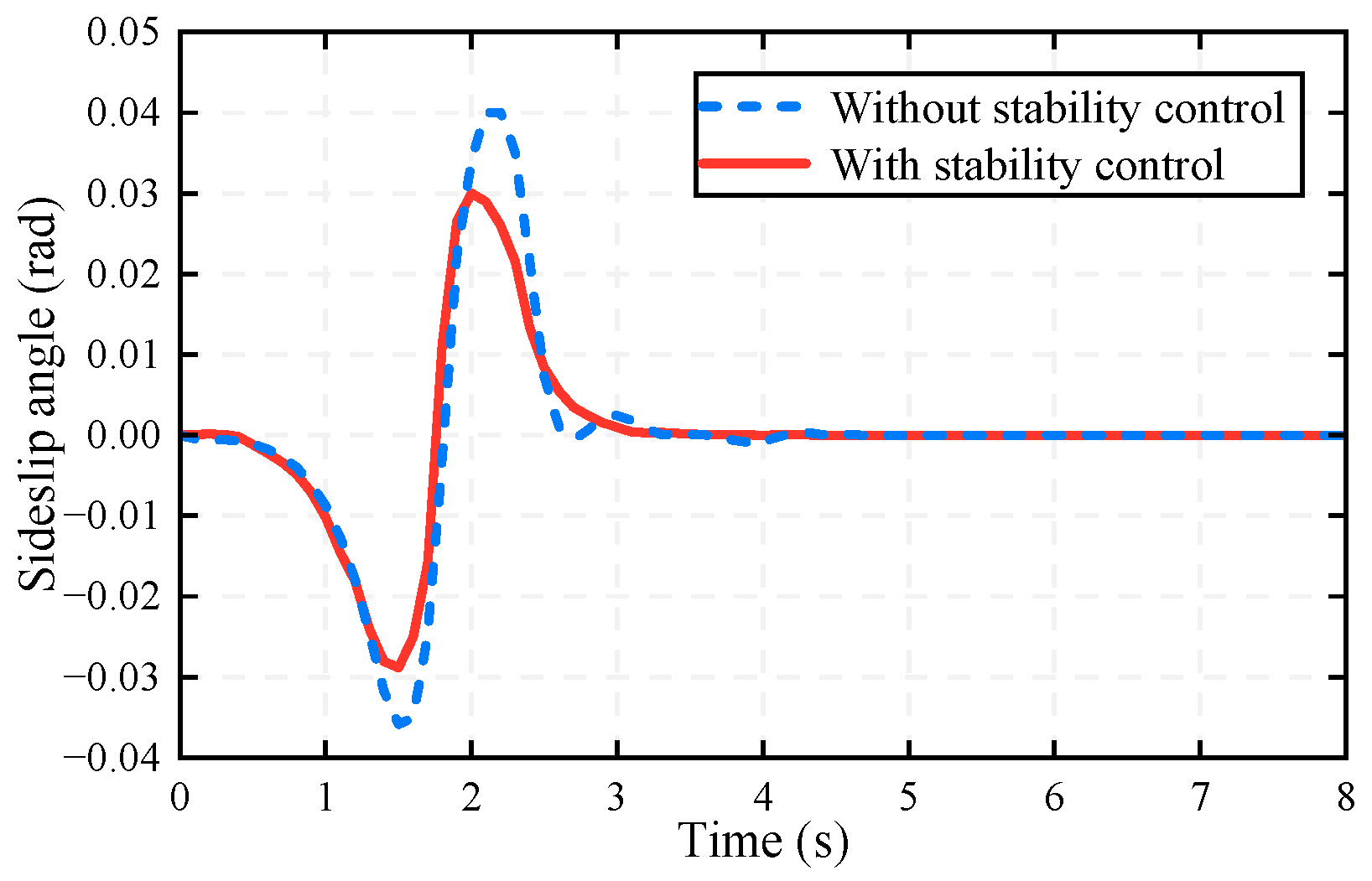
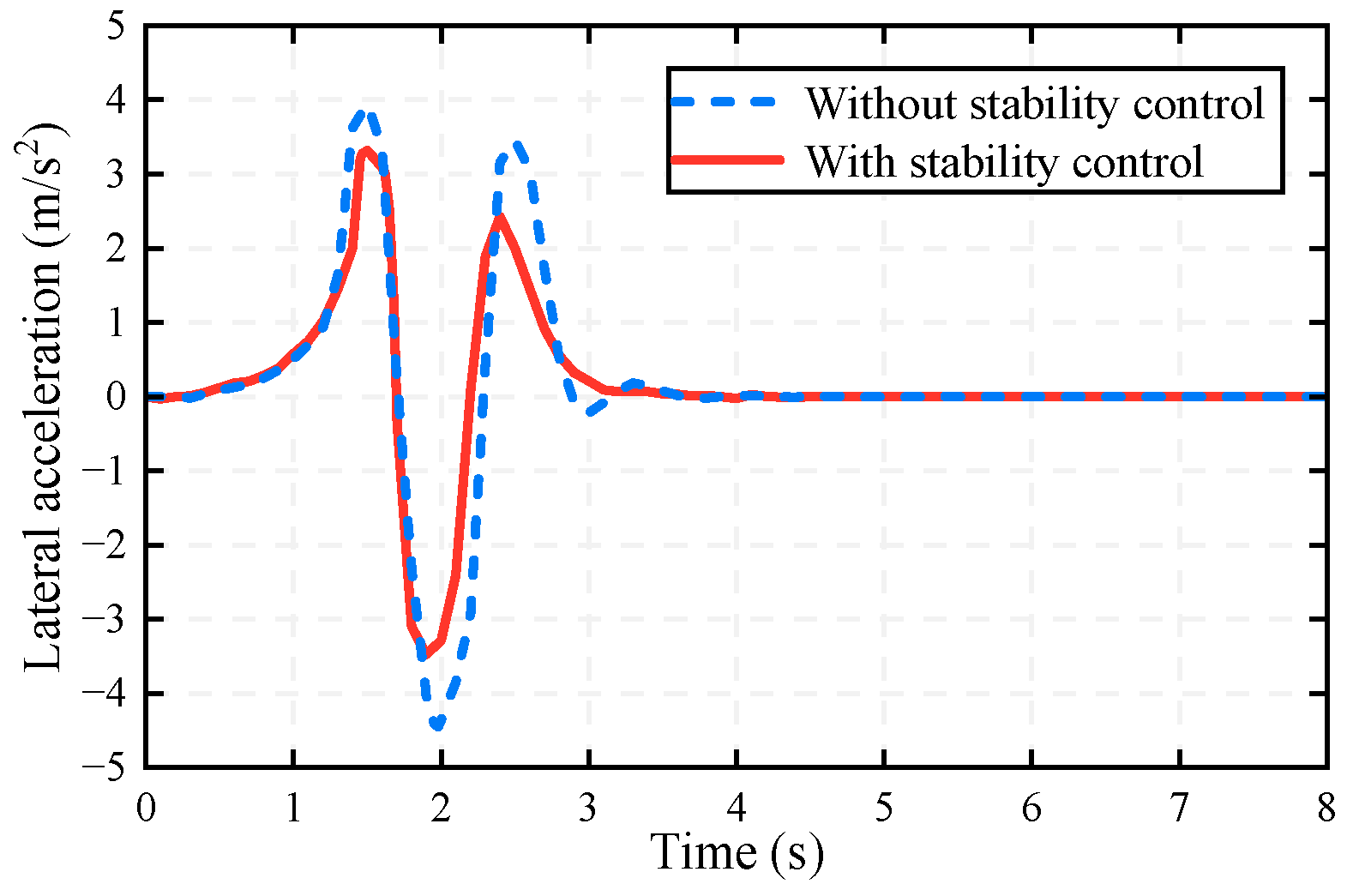
- Emergency lane-changing scenario: A stationary obstacle is placed and the host vehicle’s initial velocity is 120 km/h in CarSim. Two types of controllers are used to verify the control effect, without stability and with stability.
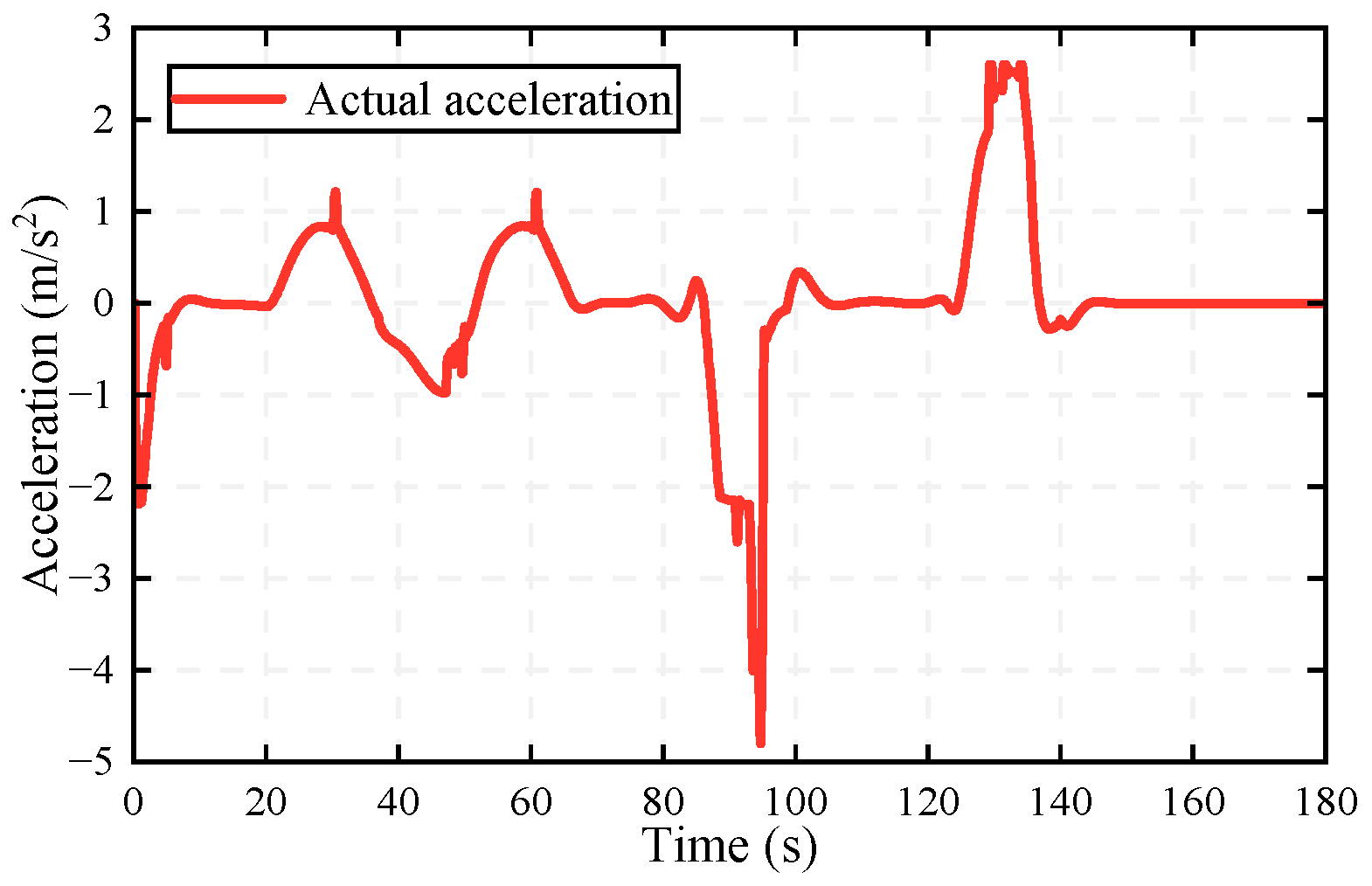
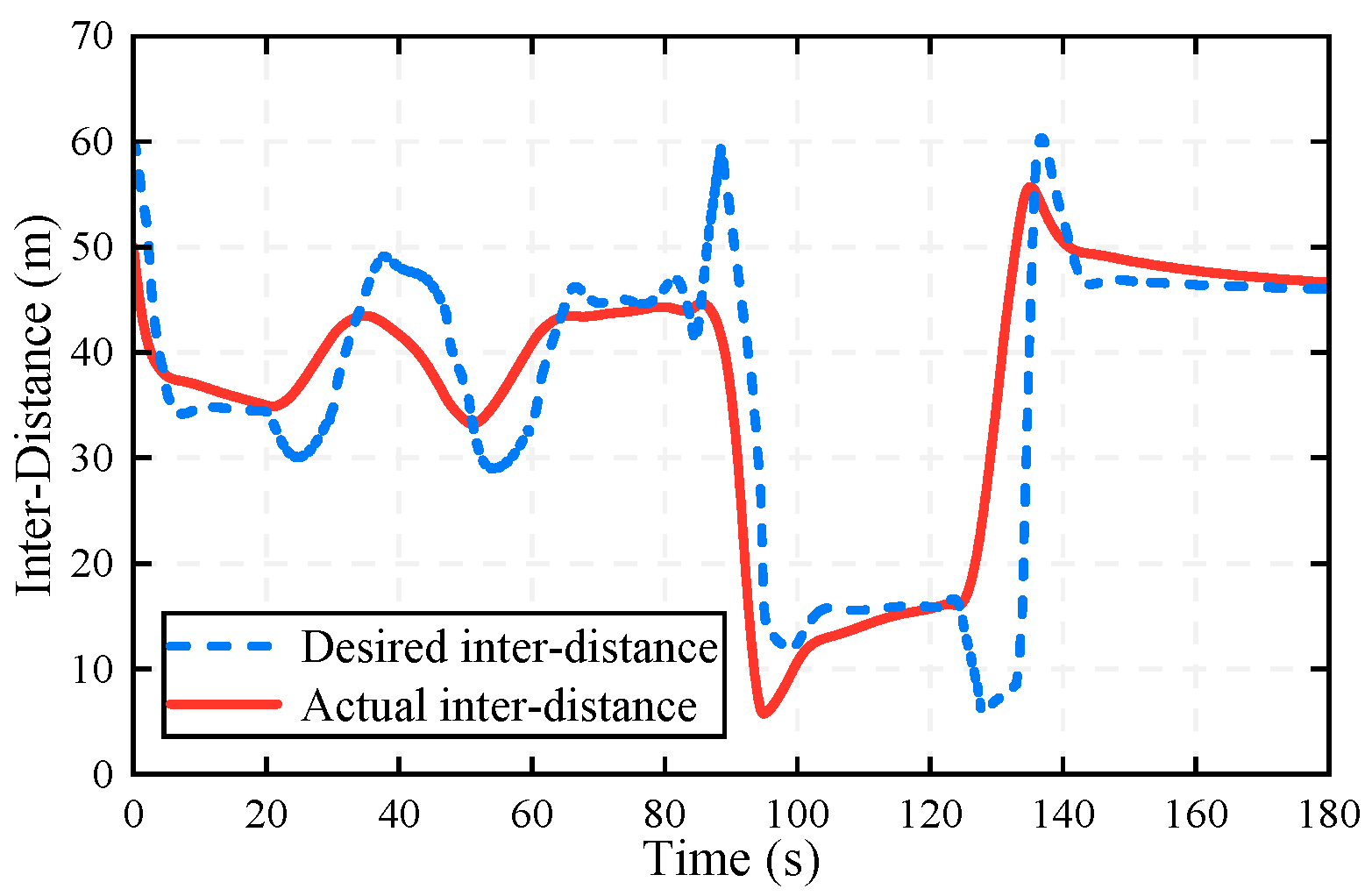
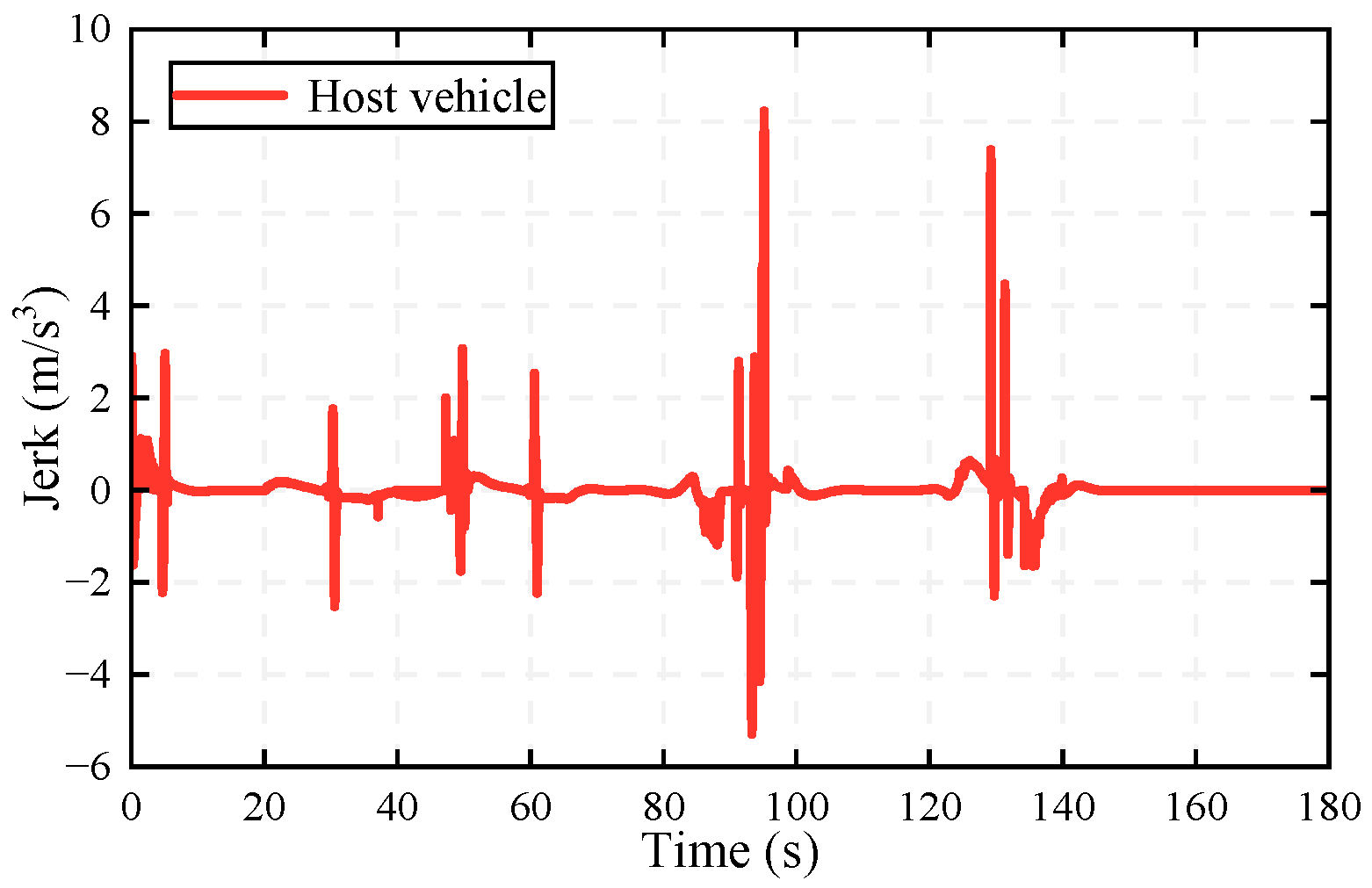
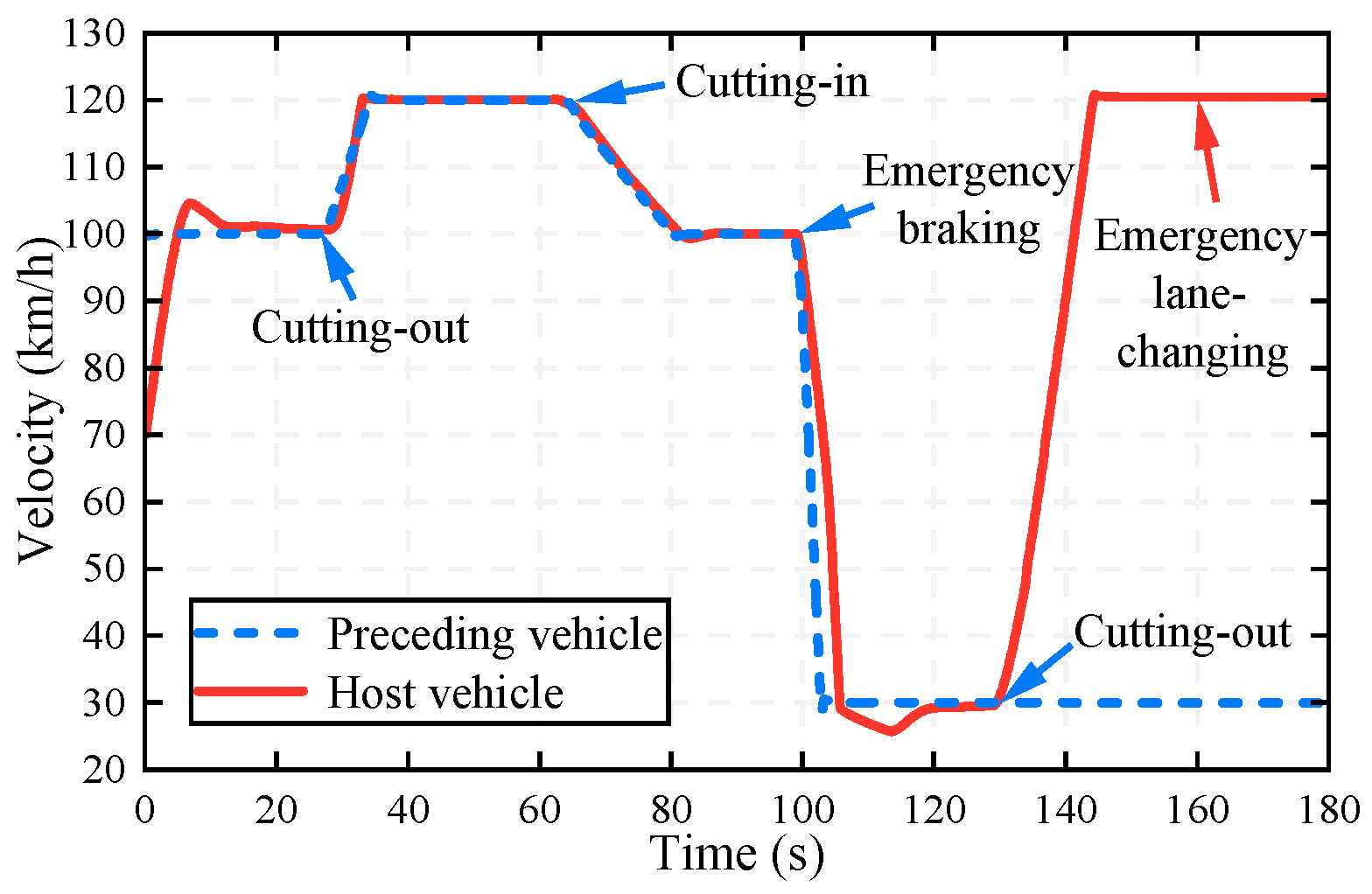
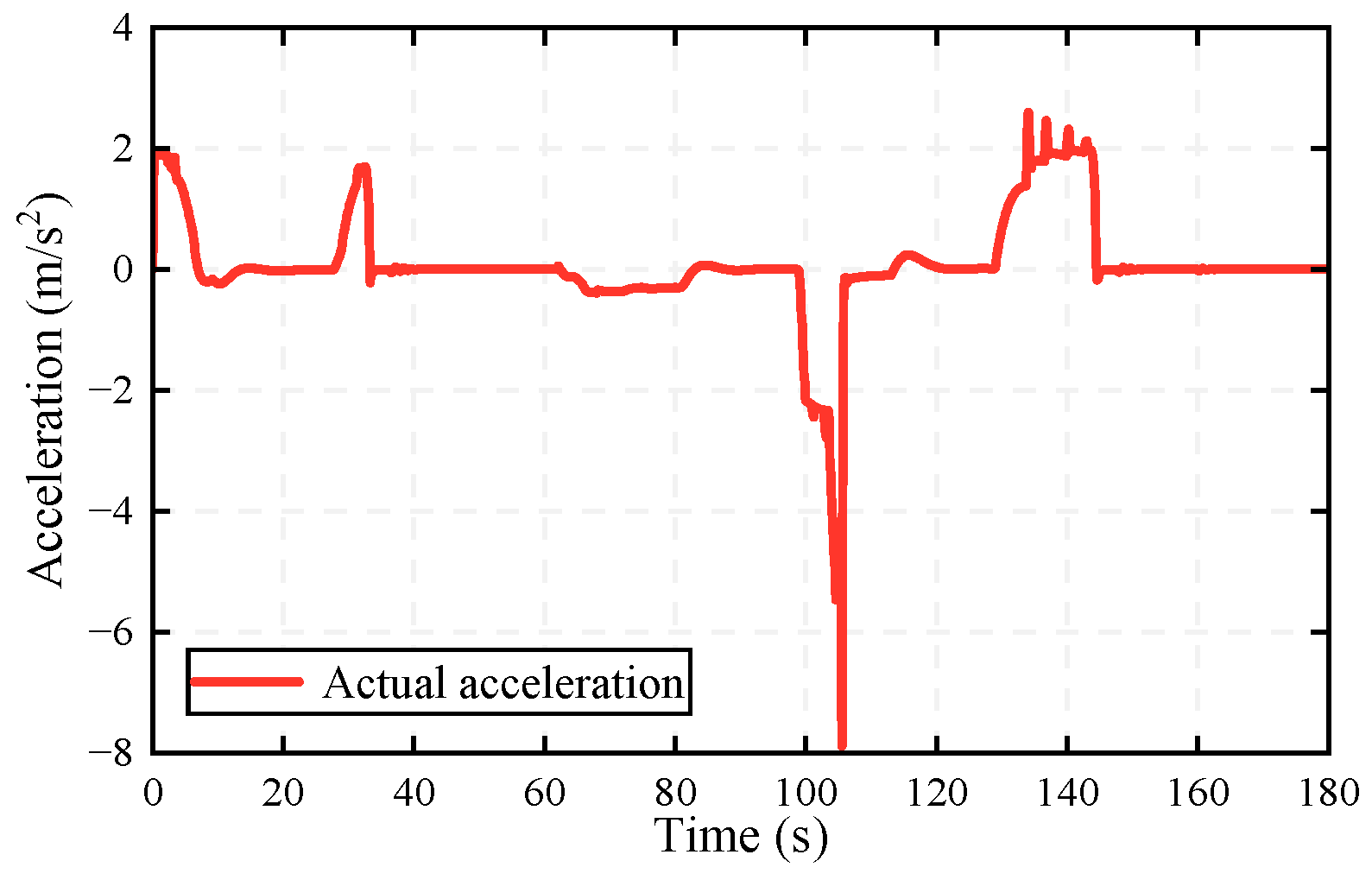
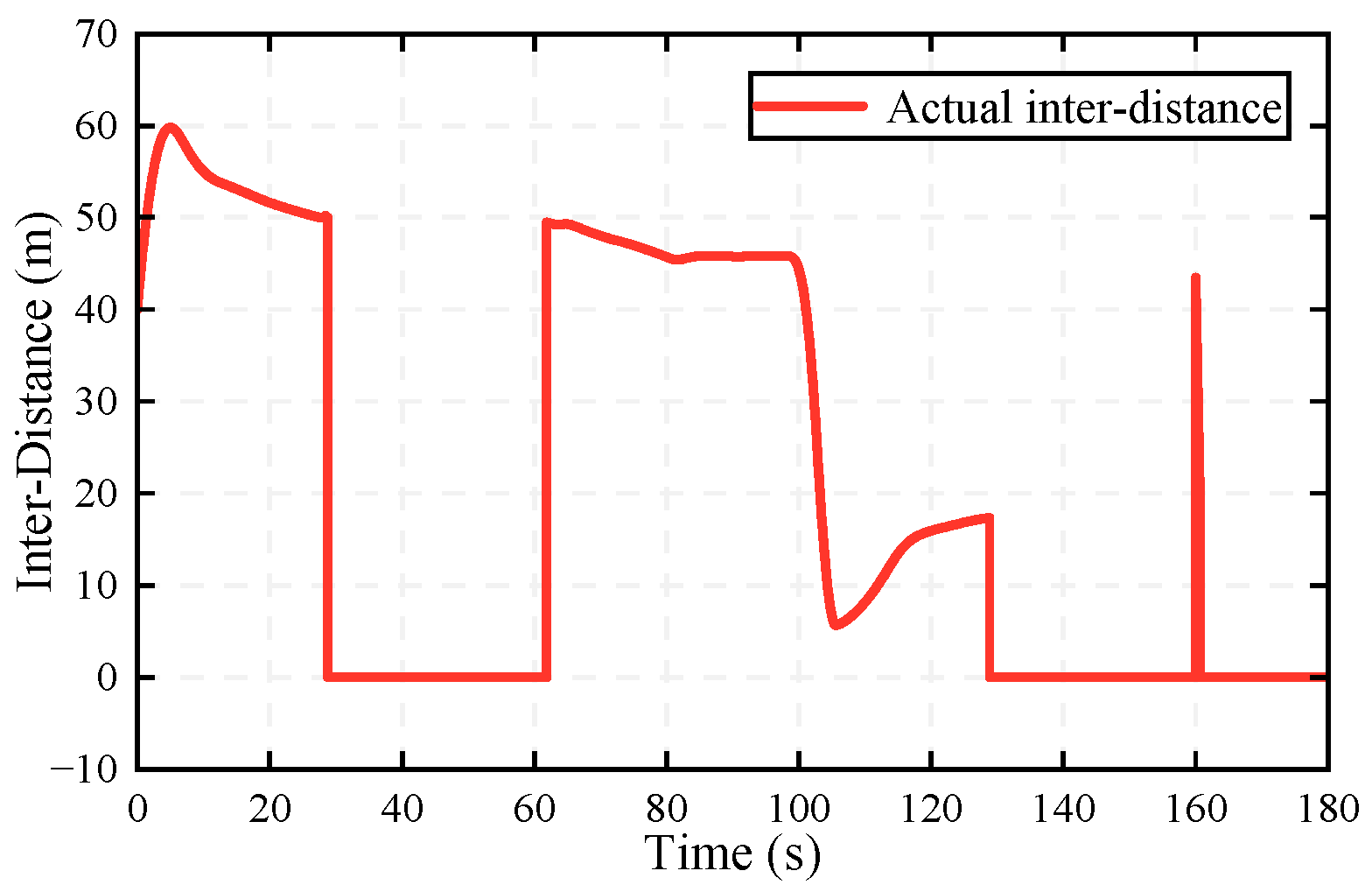
- Mixed switching scenario: The preceding vehicle performs acceleration, weak deceleration, strong deceleration, and steady following actions between 0 and 180 s. Notice that its cruise velocity is 120 km/h and a stationary obstacle abruptly appears at 160 s.
5.2. Results
- (1)
- (2)
- (3)
- (4)
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Azim, E. Handbook of Intelligent Vehicles; China Machine Press: Beijing, China, 2017. [Google Scholar]
- Bian, Y.; Li, S.E.; Xu, B.; Qin, X.; Li, S.; Xu, Q. Behavioral harmonization of a cyclic vehicular platoon in a closed road network. IEEE TIV. 2021, 6, 559–570. [Google Scholar] [CrossRef]
- Pan, C.; Huang, A.; Wang, J.; Chen, L.; Liang, J.; Zhou, W.; Yang, J. Energy-optimal adaptive cruise control strategy for electric vehicles based on model predictive control. Energy 2022, 241, 122793. [Google Scholar] [CrossRef]
- Li, S.E.; Zheng, Y.; Li, K.Q.; Wang, L.Y.; Zhang, H.W. Platoon control of connected vehicles from a networked control perspective: Literature review, component modeling, and controller synthesis. IEEE Trans. Veh. Technol. 2017, 1. [Google Scholar] [CrossRef]
- Li, S.E.; Qin, X.; Zheng, Y.; Wang, J.; Li, K.; Zhang, H. Distributed platoon control under topologies with complex eigenvalues: Stability analysis and controller synthesis. IEEE Trans. Control. Syst. Technol. 2017, 27, 206–220. [Google Scholar] [CrossRef]
- Jing, Y.J. Research on Vehicular Multi-objective Adaptive Cruise Control System Based on MPC Algorithm. Master’s Thesis, Chang’an University, Chang’an, China, 2019. [Google Scholar]
- Al-Gabalawy, M.; Hosny, N.S.; Aborisha, A.H.S. Model predictive control for a basic adaptive cruise control. Int. J. Dynam. Control. 2021, 9, 1132–1143. [Google Scholar] [CrossRef]
- Muslim, H. Design and evaluation of lane-change collision avoidance systems in semi-automated driving. IEEE Trans. Veh. Technol. 2023, 72, 7082–7094. [Google Scholar] [CrossRef]
- Chu, L.; Li, H.; Xu, Y.; Zhao, D.; Sun, C. Research on longitudinal control algorithm of adaptive cruise control system for pure electric vehicles. World Electr. Veh. J. 2023, 14, 32. [Google Scholar] [CrossRef]
- Kabasakal, B.; Üçüncü, M. The design and simulation of adaptive cruise control system. Int. J. Auto. Sci. Tech. 2022, 6, 242–256. [Google Scholar] [CrossRef]
- Abdurohman, A.; Kang, H.X.; Hidayat, T. Vehicle acc control based on fuzzy pid. Int. J. Electron. Comm. 2022, 1, 36–55. [Google Scholar] [CrossRef]
- Maruyama, N.; Mouri, H. A proposal for adaptive cruise control balancing followability and comfortability through reinforcement learning. Robomech J. 2022, 9, 22. [Google Scholar] [CrossRef]
- Cao, W.; Liu, S.; Li, J.; Zhang, Z.; He, H. Analysis and design of adaptive cruise control for smart electric vehicle with domain-based poly-service loop delay. IEEE Trans. Ind. Electron. 2022, 70, 866–877. [Google Scholar] [CrossRef]
- Yu, L.; Wang, R. Researches on adaptive cruise control system: A state of the art review. Proc. Inst. Mech. Eng. Part D 2022, 236, 211–240. [Google Scholar] [CrossRef]
- Zhai, C.; Chen, C.; Zheng, X.; Han, Z.; Gao, Y.; Yan, C.; Xu, J. Ecological cooperative adaptive cruise control for heterogenous vehicle platoons subject to time delays and input saturations. IEEE Trans. Intell. Transp. 2022, 24, 2862–2873. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, Z.; Zhang, Y.; Shang, Z.; Wang, P.; Zou, Q.; Hu, J. Human-lead-platooning cooperative adaptive cruise control. IEEE Trans. Intell. Transp. 2022, 23, 18253–18272. [Google Scholar] [CrossRef]
- Chen, C.; Guo, J.; Guo, C.; Chen, C.; Zhang, Y.; Wang, J. Adaptive Cruise Control for Cut-In Scenarios Based on Model Predictive Control Algorithm. Appl. Sci. 2021, 11, 5293. [Google Scholar] [CrossRef]
- Hu, J.; Zhang, Y.; Rakheja, S. Adaptive lane change trajectory planning scheme for autonomous vehicles under various road frictions and vehicle speeds. IEEE Trans. Intell. Transp. Veh. 2022, 8, 1252–1265. [Google Scholar] [CrossRef]
- Liu, Y. Research on Autonomous Lane Changing Strategy of In-Wheel Motor Drive Electric Vehicles. Master’s Thesis, Jilin University, Jilin, China, 2020. [Google Scholar]
- Yu, Y.; Luo, X.; Su, Q.; Peng, W. A dynamic lane-changing decision and trajectory planning model of autonomous vehicles under mixed autonomous vehicle and human-driven vehicle environment. Phys. A: Stat. Mech. Its Appl. 2023, 609, 128361. [Google Scholar] [CrossRef]
- He, W.R. Research on Vehicle Path Planning Algorithm Based on Ga Algorithm. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2020. [Google Scholar]
- Chen, T.; Cai, Y.; Chen, L.; Xu, X. Trajectory and velocity planning method of emergency rescue vehicle based on segmented three-dimensional quartic bezier curve. IEEE Trans. Intell. Transp. 2022, 24, 3461–3475. [Google Scholar] [CrossRef]
- Wu, X.; Zhou, B.; Wu, T.; Pan, Q. Research on intervention criterion and stability coordinated control of AFS and DYC. Int. J. Veh. Des. 2022, 90, 116–141. [Google Scholar] [CrossRef]
- Wang, Z.; Ding, X.; Zhang, L. Chassis coordinated control for full x-by-wire four-wheel-independent-drive electric vehicles. IEEE Trans. Veh. Technol. 2022, 72, 4394–4410. [Google Scholar] [CrossRef]
- Wang, H.; Zhou, J.; Hu, C.; Chen, W. Vehicle lateral stability control based on stability category recognition with improved brain emotional learning network. IEEE Trans. Veh. Technol. 2022, 71, 5930–5943. [Google Scholar] [CrossRef]
- Chang, X.H.; Liu, Y. Quantized output feedback control of AFS for electric vehicles with transmission delay and data dropouts. IEEE Trans. Intell. Transp. 2022, 23, 16026–16037. [Google Scholar] [CrossRef]
- Widmann, G.R.; Daniels, M.K.; Hamilton, L.; Humm, L.; Riley, B.; Schiffmann, J.K.; Wishon, W.H. Comparison of lidar-based and radar-based adaptive cruise control systems. SAE Trans. 2000, 109, 126–139. [Google Scholar]
- Prestl, W.; Sauer, T.; Steinle, J.; Tschernoster, O. The BMW active cruise control ACC. SAE Tech. Pap. 2000, 109, 119–125. [Google Scholar]
- Xu, L.W. Study on Multi-mode Switching of Adaptive Cruise Control and Active Lane change of Vehicle. Master’s Thesis, Hefei University of Technology, Hefei, China, 2019. [Google Scholar]
- Yan, W. Study on Adaptive Cruise Control Algorithms Imitating Car-following Behaviors of Drivers. Ph.D. Thesis, Jilin University, Jilin, China, 2016. [Google Scholar]
- Bareket, Z.; Fancher, P.S.; Peng, H.; Lee, K.; Assaf, C.A. Methodology for assessing adaptive cruise control behavior. IEEE Trans. Intell. Transp. 2003, 4, 123–131. [Google Scholar] [CrossRef]
- Pei, X.F.; Liu, Z.D.; Ma, G.C.; Qi, Z.Q. Multi-mode switching controller for vehicle adaptive cruise control system. Chin. J. Mech. Eng. 2012, 48, 96–102. [Google Scholar] [CrossRef]
- Piao, C.; Gao, J.; Yang, Q.; Shi, J. Adaptive cruise control method based on hierarchical control and multi-objective optimization. Trans. Inst. Meas. Control. 2023, 45, 1298–1312. [Google Scholar] [CrossRef]
- Zou, D.B. Research on Multi-mode Switching Control of Automotive Adaptive Cruise Control System. Master’s Thesis, Hunan University, Hunan, China, 2018. [Google Scholar]
- Pei, X.F.; Liu, Z.D.; Ma, G.C.; Qi, Z.Q. An adaptive cruise control system based on throttle/brakes combined control. Automot. Eng. 2013, 35, 375–380. [Google Scholar]
- Li, L.; Zhu, X.C.; Chen, H.L. Drivers’ collision avoidance limit by braking and steering. J. Tongji. Univ. (Nat. Sci.) 2016, 44, 1743–1748. [Google Scholar]
- Li, F. Research on Active Collision Avoidance Control Strategy of In-Wheel-Motored Electric Vehicle. Master’s Thesis, Chongqing University of Technology, Chongqing, China, 2021. [Google Scholar]
- Yue, C.Y. Research on Longitudinal MPC Control Method for Intelligent Vehicle Full Speed ACC. Master’s Thesis, Chongqing University, Chongqing, China, 2019. [Google Scholar]
- Zhang, M.Z. Research on Adaptive Cruise Control Strategy for Electric Vehicle Based on MPC. Master’s Thesis, Jilin University, Jilin, China, 2020. [Google Scholar]


| (Mpa) | (m·s−2) | ||
|---|---|---|---|
| 80 km/h | 100 km/h | 120 km/h | |
| 3.85 | 5.88 | 5.97 | 6 |
| 4 | 6.1 | 6.17 | 6.25 |
| 5 | 7.5 | 7.64 | 7.7 |
| 6 | 7.6 | 7.9 | 7.98 |
| 7 | 8 | 8.1 | 8.18 |
| 8 | 8.23 | 8.28 | 8.33 |
| Para/Unit | Value | Para/Unit | Value | Para/Unit | Value |
|---|---|---|---|---|---|
| /kg | 1280 | /m | 5 | /(m) | 7 |
| /m | 540 | /(m/s) | 0 | /(m/s) | 40 |
| /m | 302 | /(m/s2) | −5.5 | /(m/s2) | 3.5 |
| /(m/s) | 120 | /(m/s2) | −5.5 | (m/s2) | 3.5 |
| /(N·m) | 200 | /(m/s3) | −3 | (m/s3) | 3 |
| 0.3 | /(s) | 0.5 | 0.96 | ||
| /m2 | 2.2 | 16 | 5 | ||
| 1.09 | 26 | 3 | |||
| 4.1 | /(s) | 0.2 | 1000 | ||
| 0.92 | (ACC) | Diag (40, 150, 2, 2) | (ACC) | 10 | |
| /m | 1880 | (Lane Change) | Diag (1000, 50) | (Lane Change) | 5 × 105 |
| /° | 0 | (DYC) | [1, 0; 0, 100] | (DYC) | [1, 0; 0, 1] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, D.; Ou, J.; Yang, E.; Lin, J.; Zhang, Y. Research on a Multimode Adaptive Cruise Control Strategy with Emergency Lane-Changing Function. World Electr. Veh. J. 2023, 14, 189. https://doi.org/10.3390/wevj14070189
Huang D, Ou J, Yang E, Lin J, Zhang Y. Research on a Multimode Adaptive Cruise Control Strategy with Emergency Lane-Changing Function. World Electric Vehicle Journal. 2023; 14(7):189. https://doi.org/10.3390/wevj14070189
Chicago/Turabian StyleHuang, Dong, Jian Ou, Echuan Yang, Jiayu Lin, and Yong Zhang. 2023. "Research on a Multimode Adaptive Cruise Control Strategy with Emergency Lane-Changing Function" World Electric Vehicle Journal 14, no. 7: 189. https://doi.org/10.3390/wevj14070189
APA StyleHuang, D., Ou, J., Yang, E., Lin, J., & Zhang, Y. (2023). Research on a Multimode Adaptive Cruise Control Strategy with Emergency Lane-Changing Function. World Electric Vehicle Journal, 14(7), 189. https://doi.org/10.3390/wevj14070189






