Research on Longitudinal Control Algorithm of Adaptive Cruise Control System for Pure Electric Vehicles
Abstract
1. Introduction
2. Materials and Methods
2.1. Vehicle Platform and Control Framework
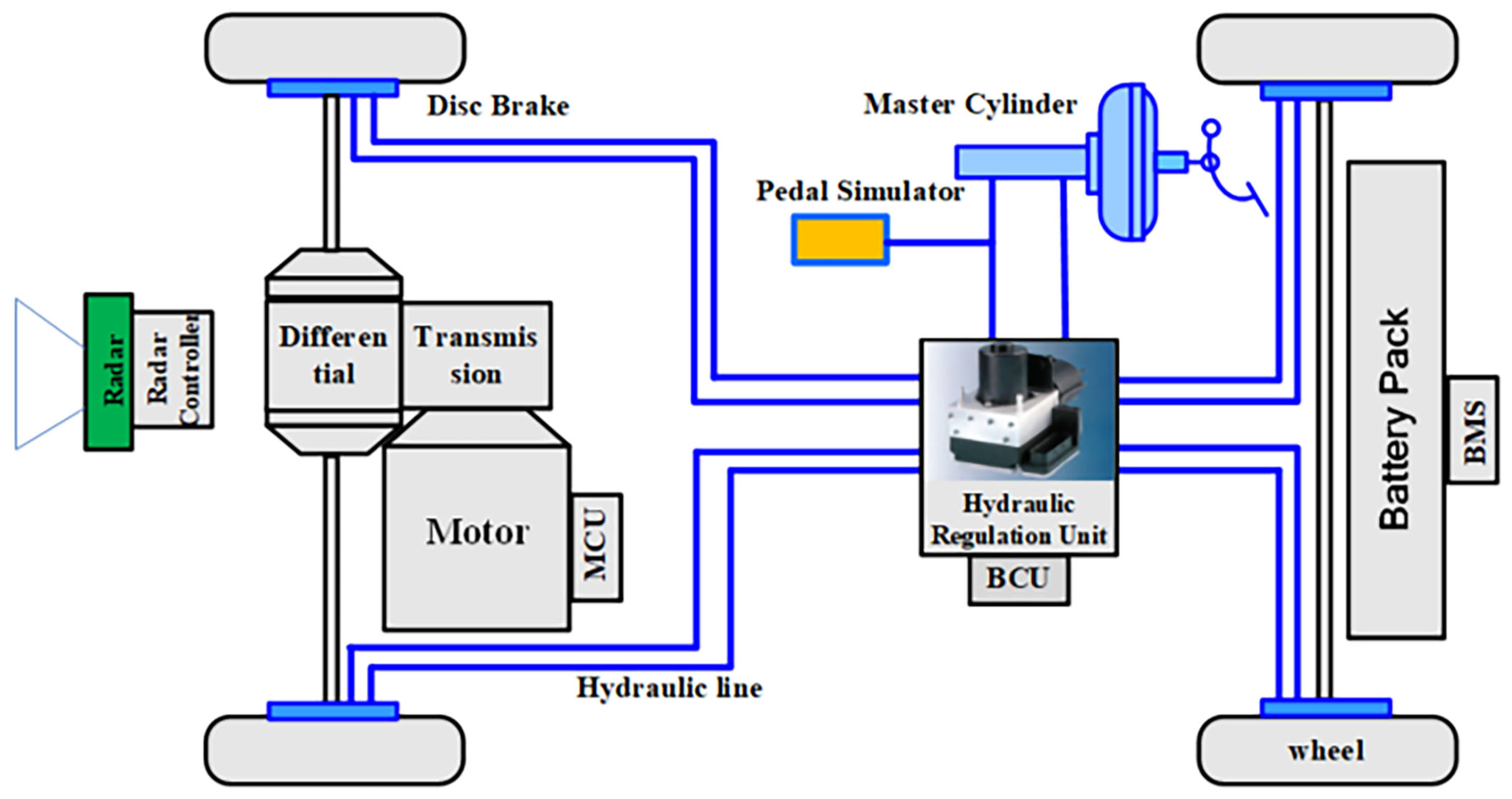
2.1.1. Vehicle Platform
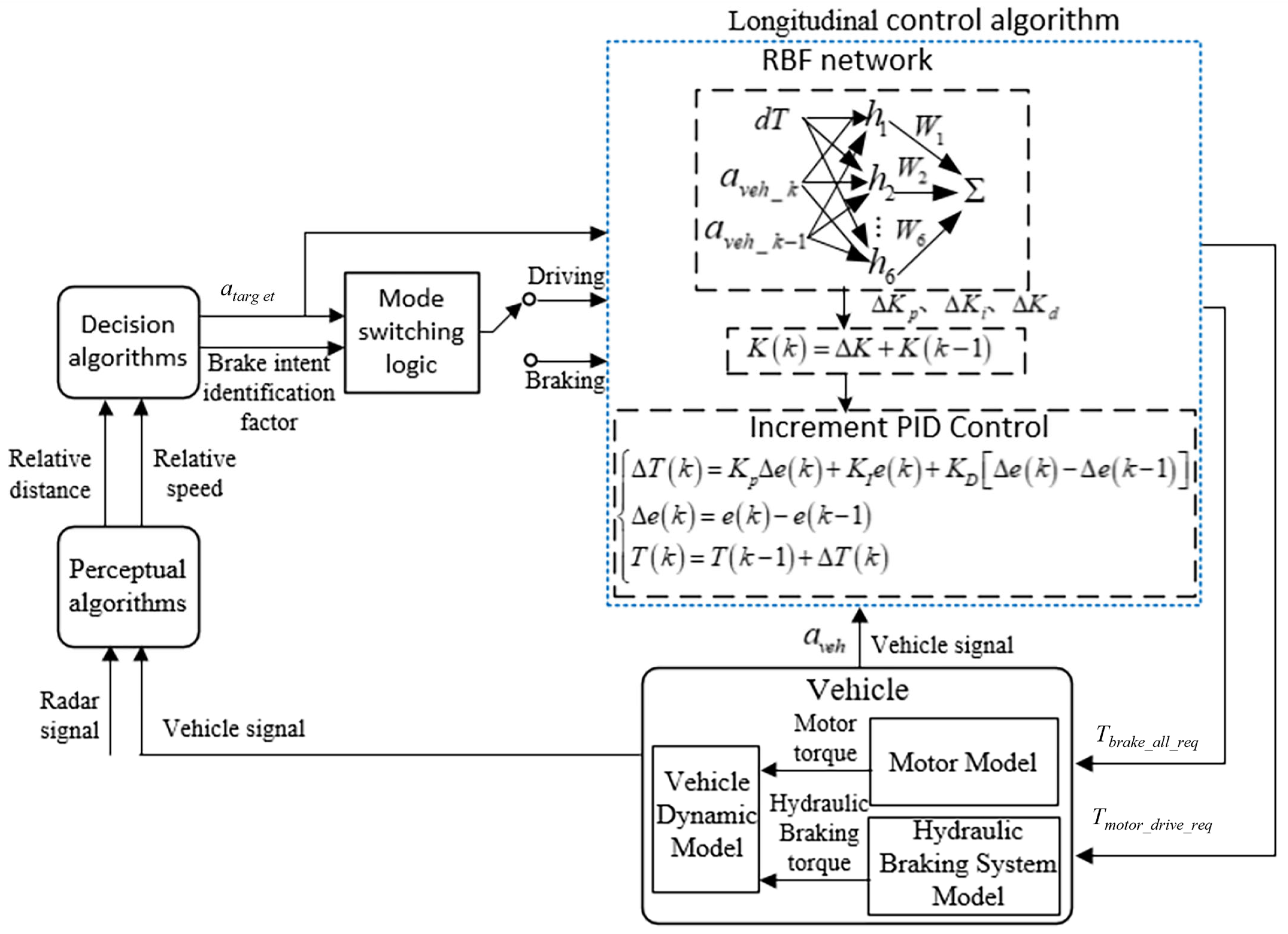
2.1.2. Control Framework
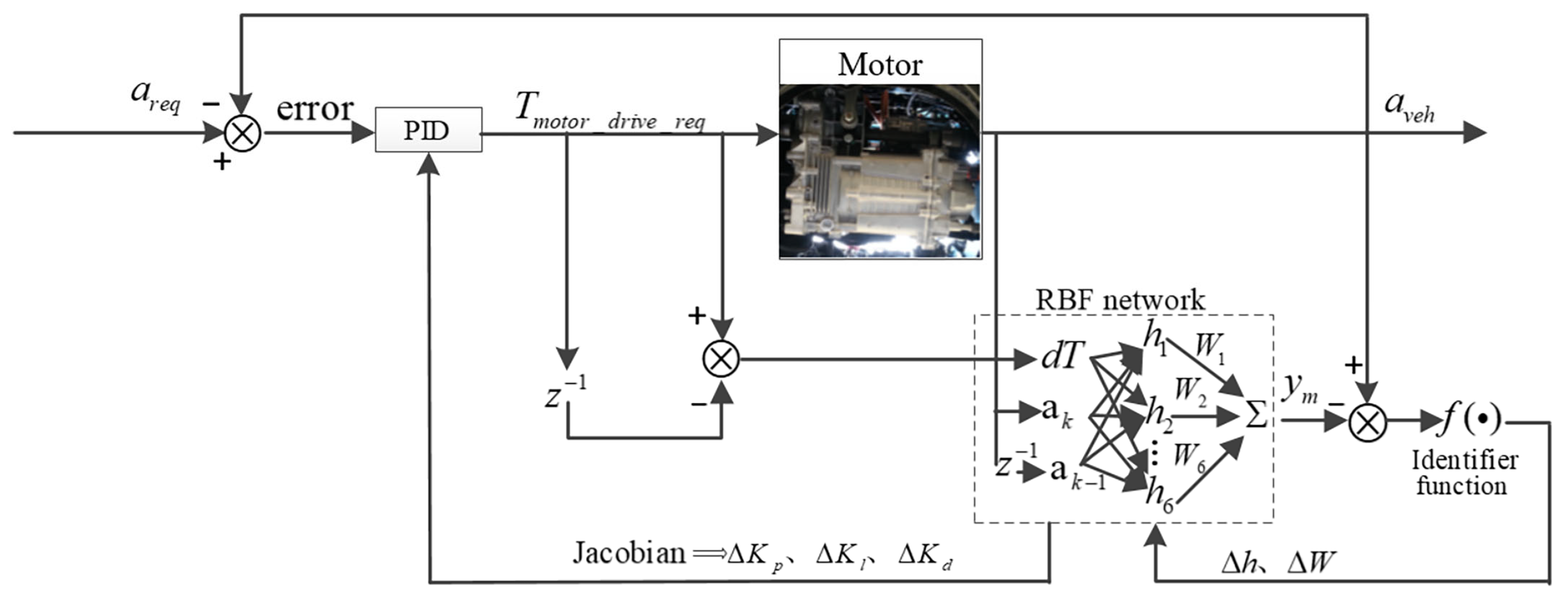
2.2. RBFNN-PID-Based Longitudinal Control Algorithm
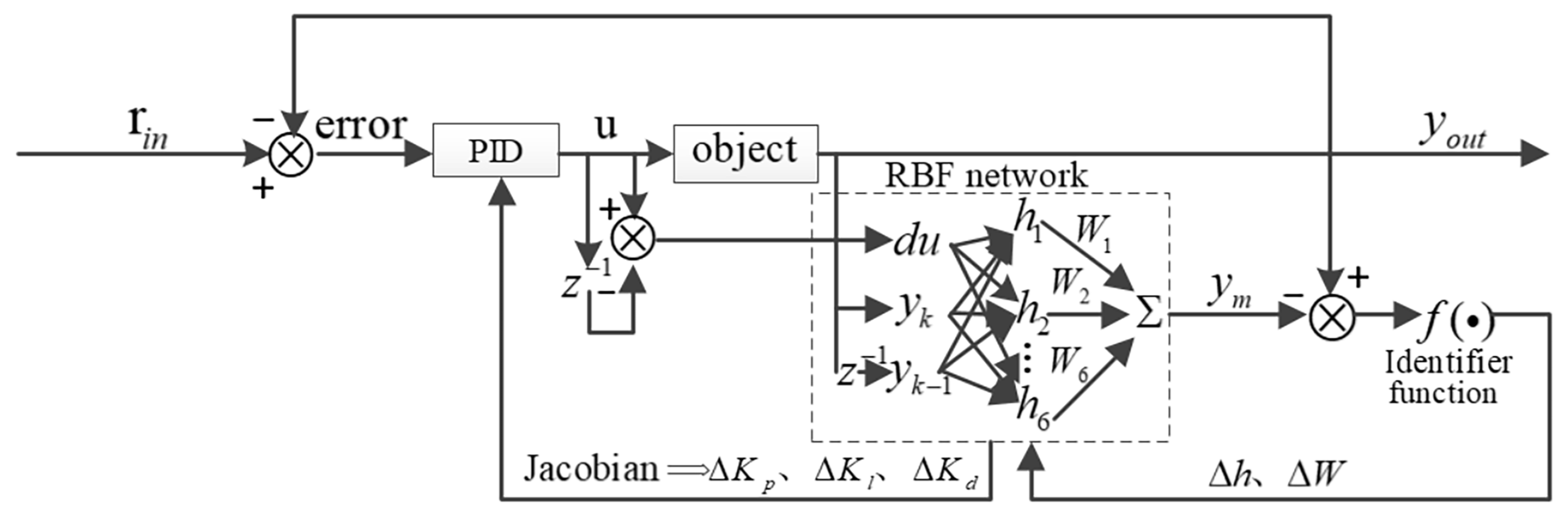
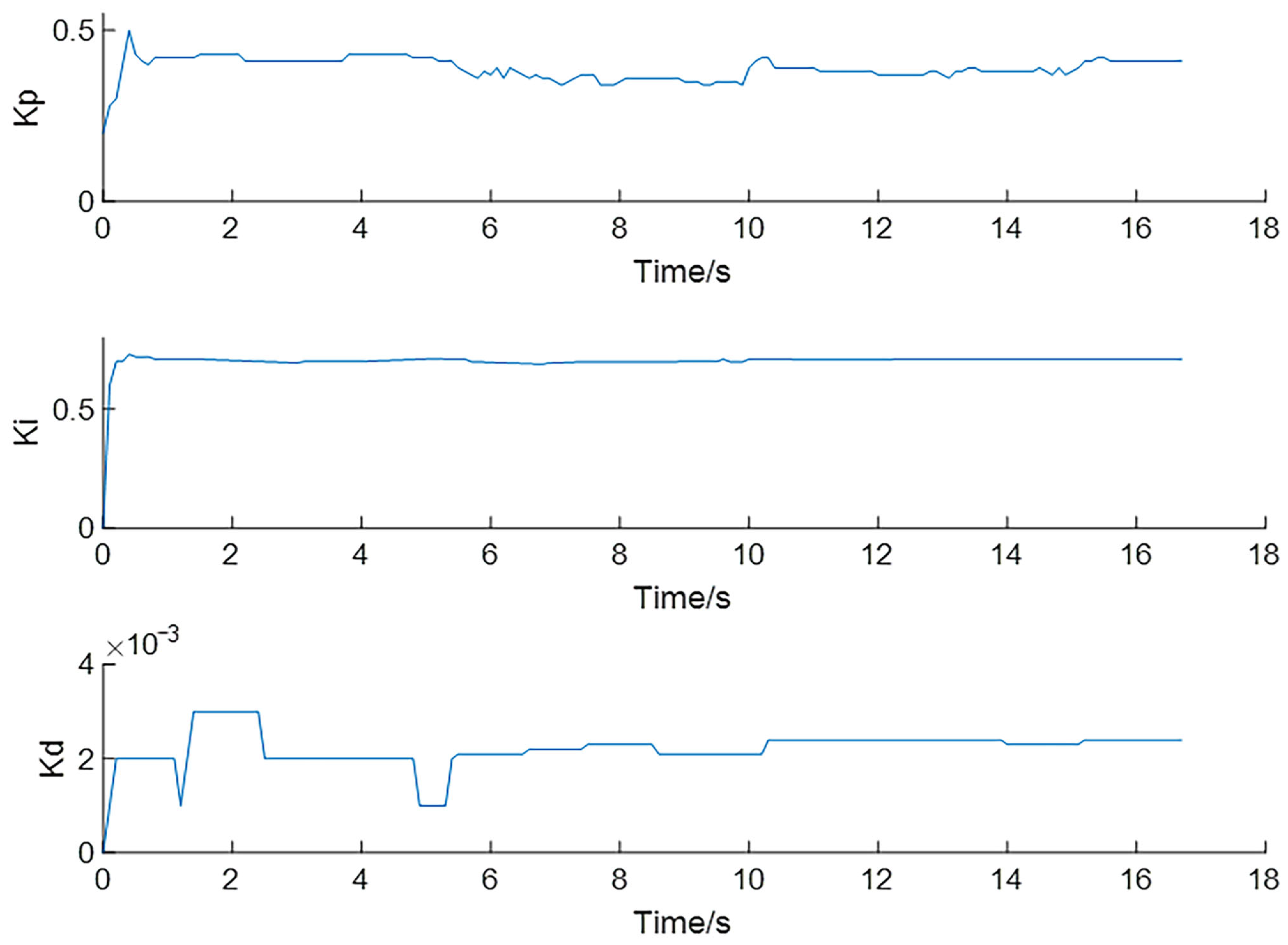
2.2.1. Parameter Tuning of RBFNN-Based PID
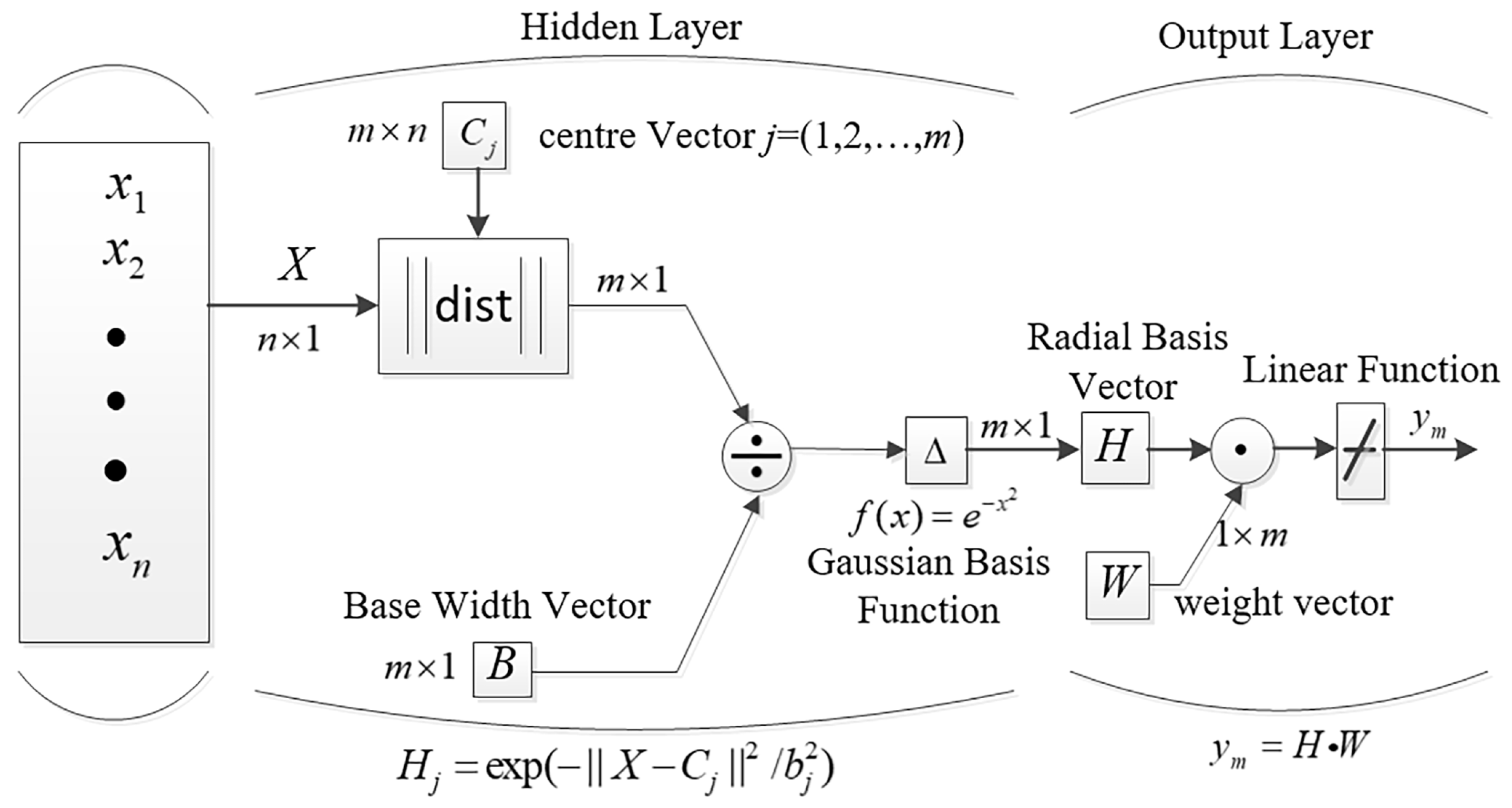
2.2.2. Jacobian Information Recognition Based on RBFNN
2.2.3. Longitudinal Control Algorithm
3. Results and Discussion
3.1. Results and Discussion of the Driving Process
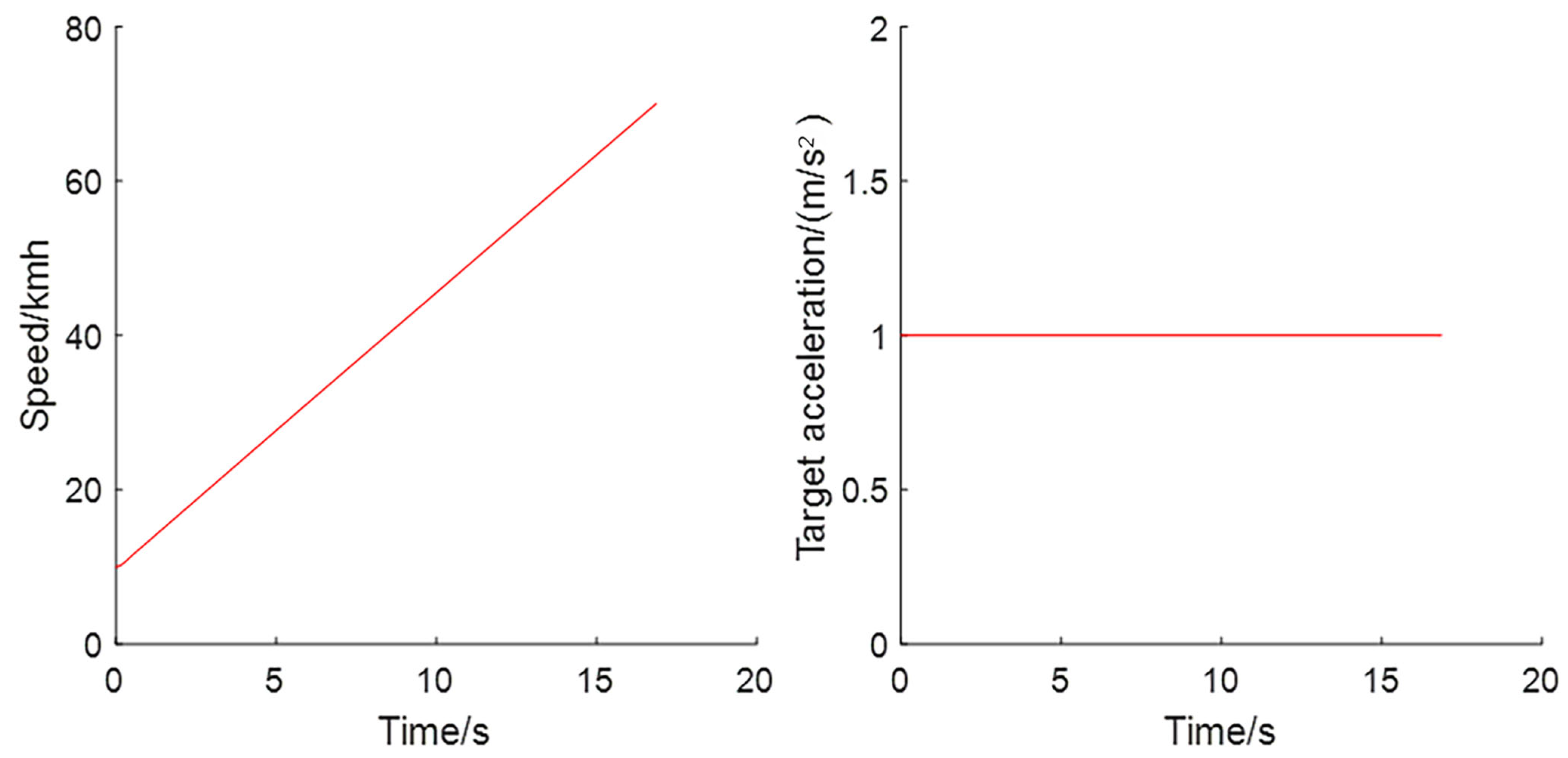
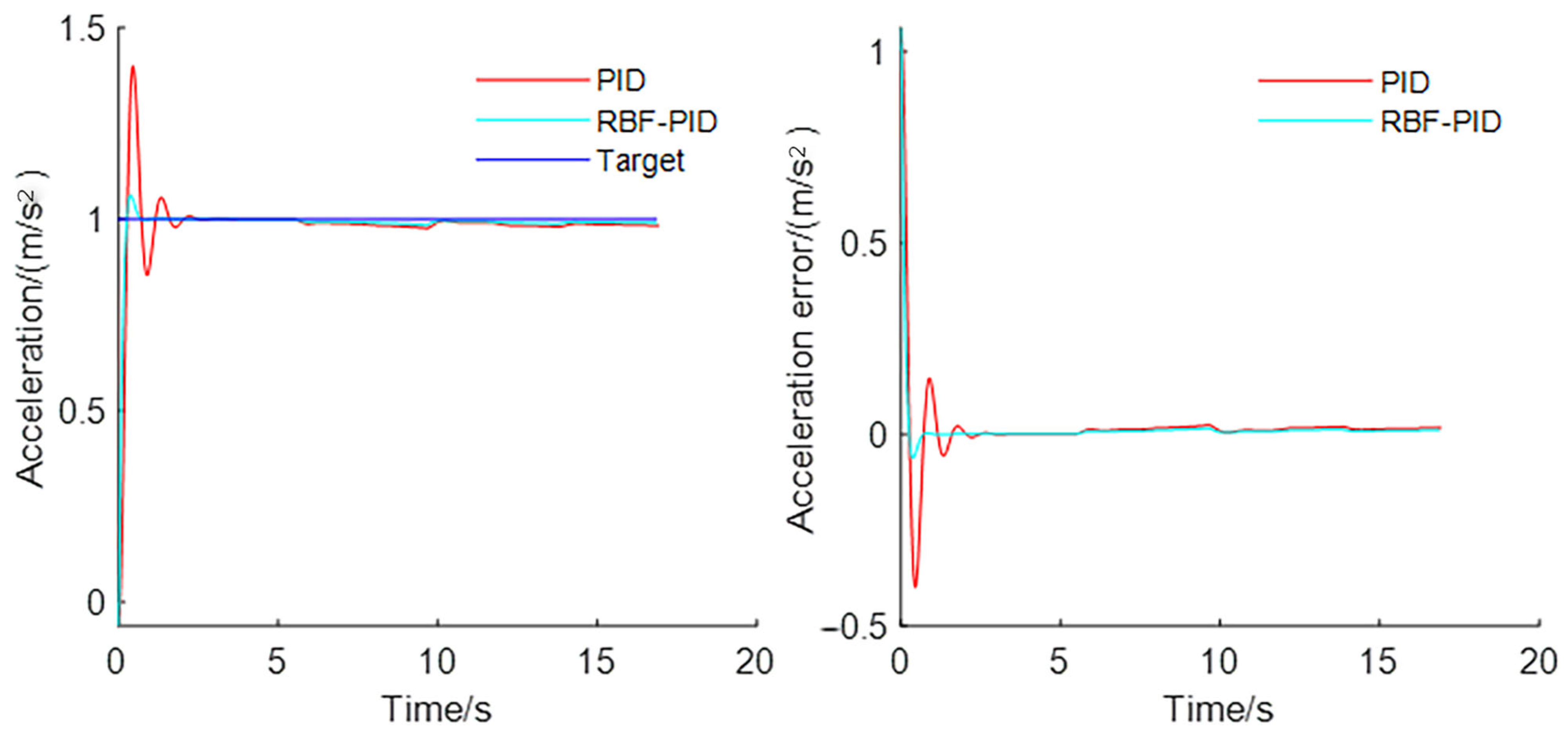
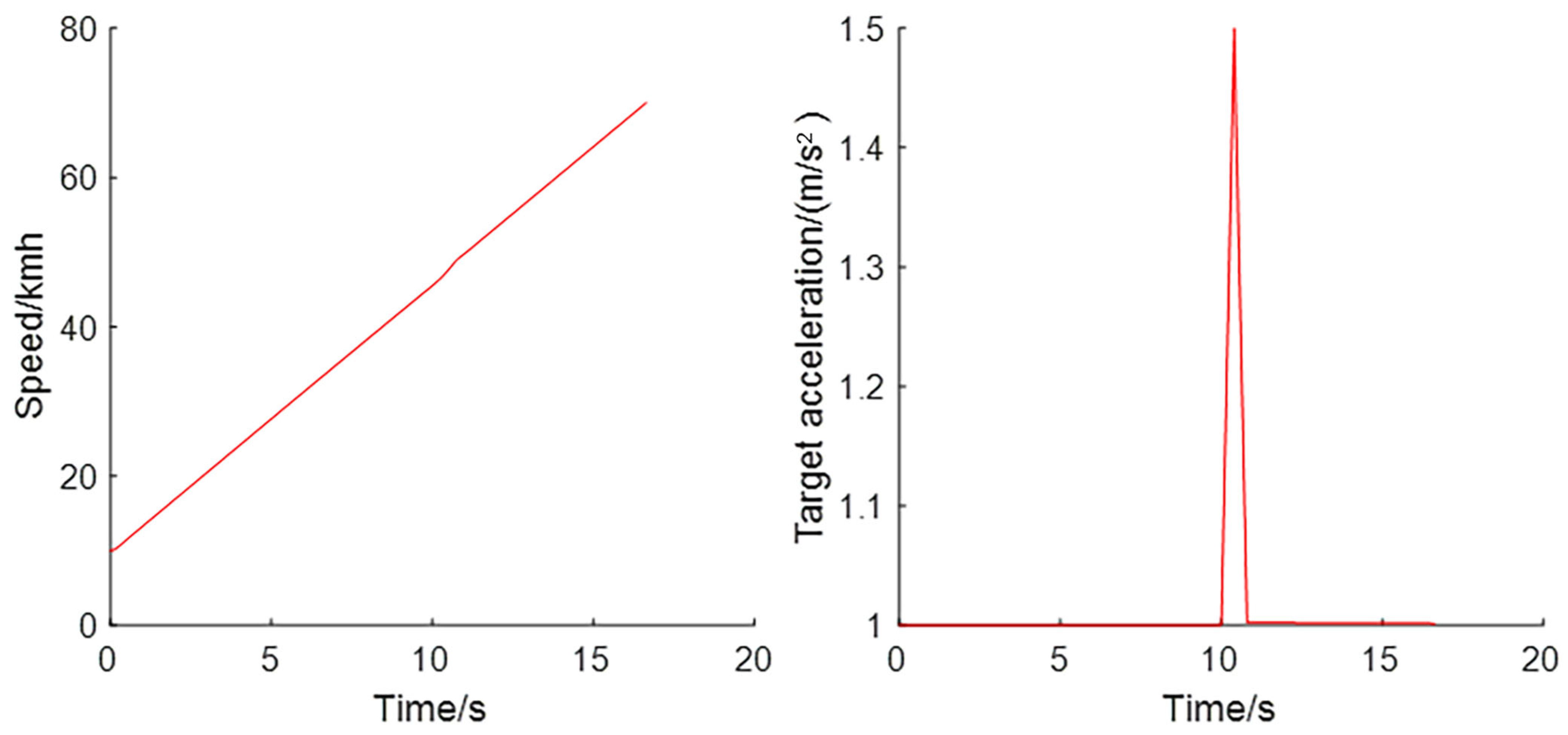
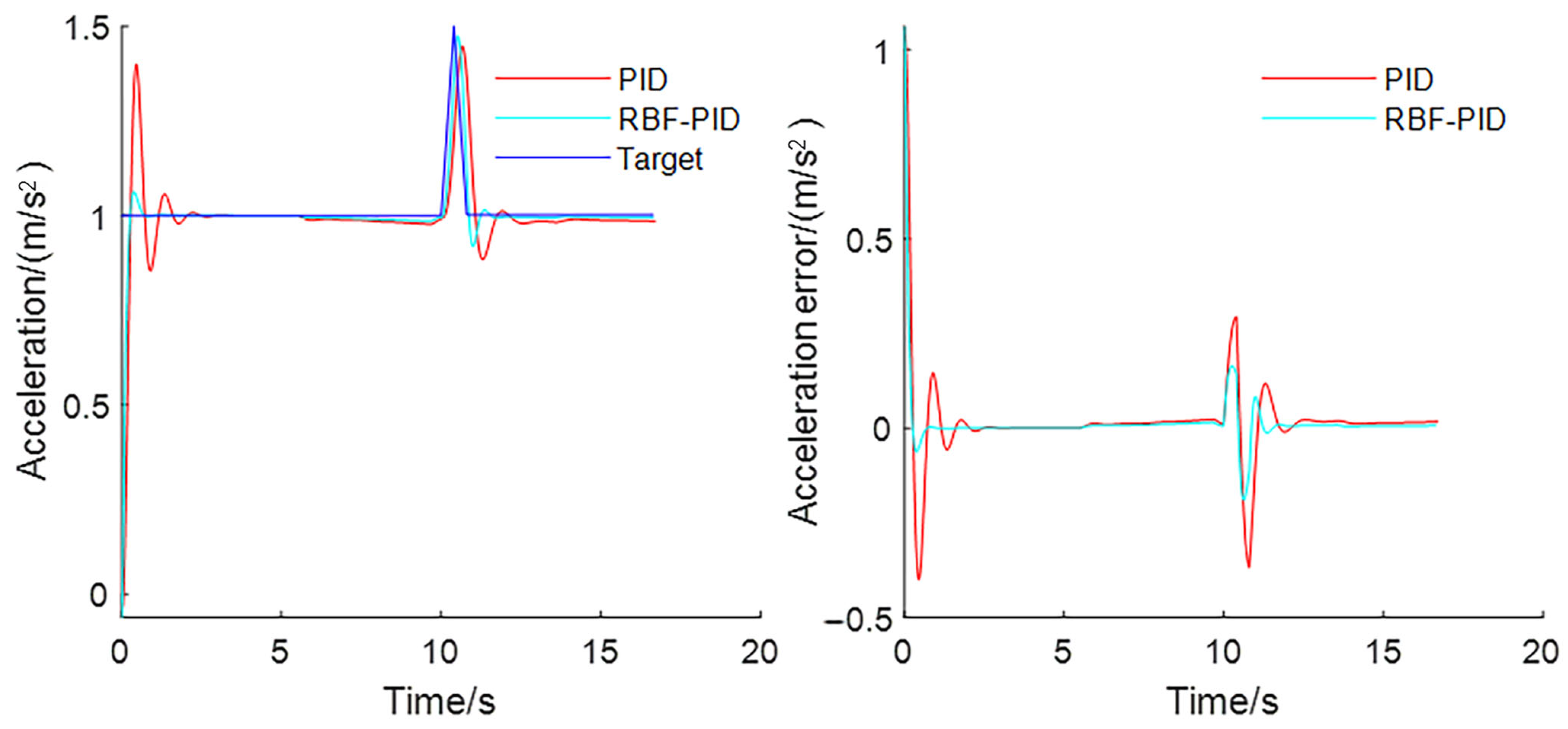
3.1.1. Step Response of the Driving Process
3.1.2. Response under Perturbation of the Driving Process
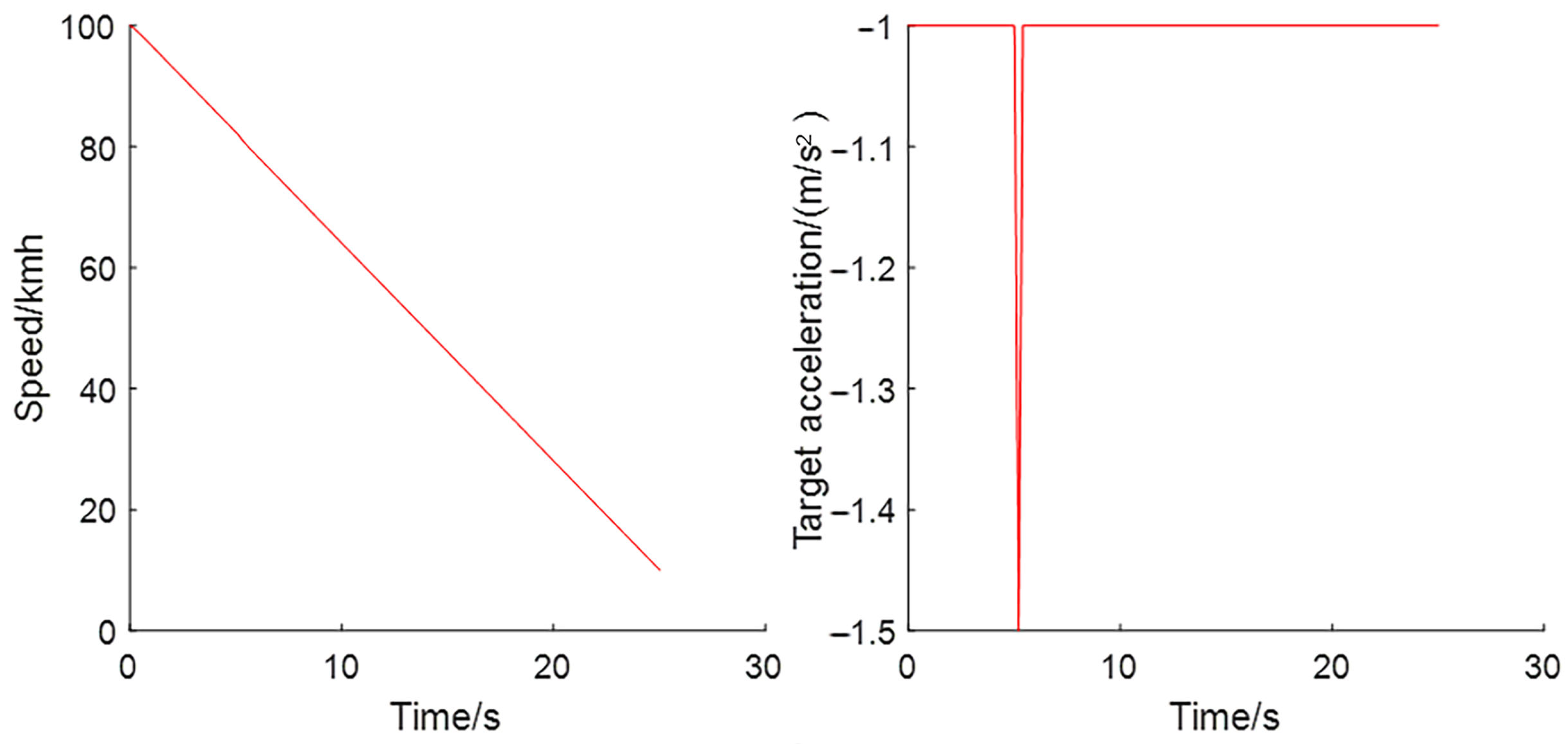
3.2. Results and Discussion of the Braking Process
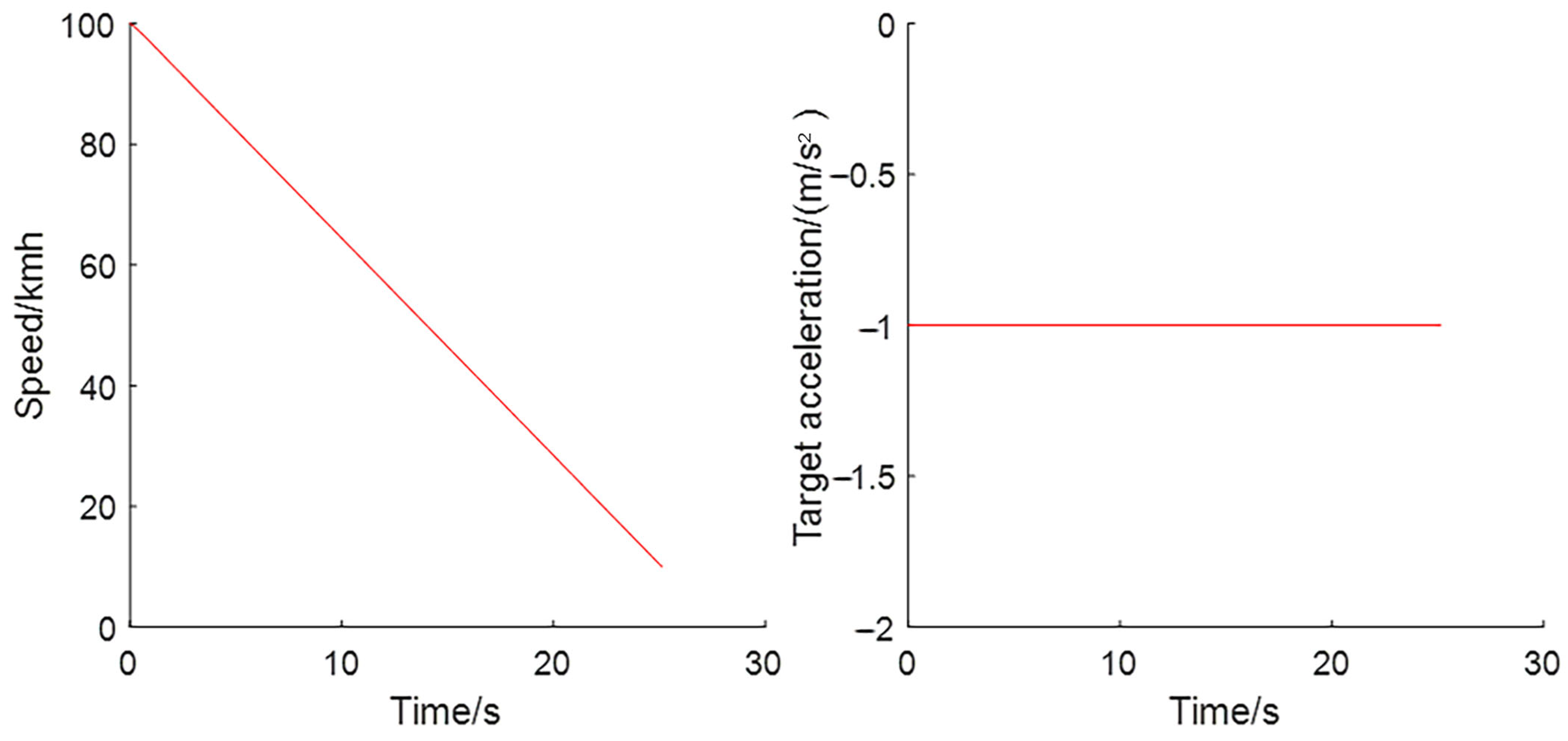
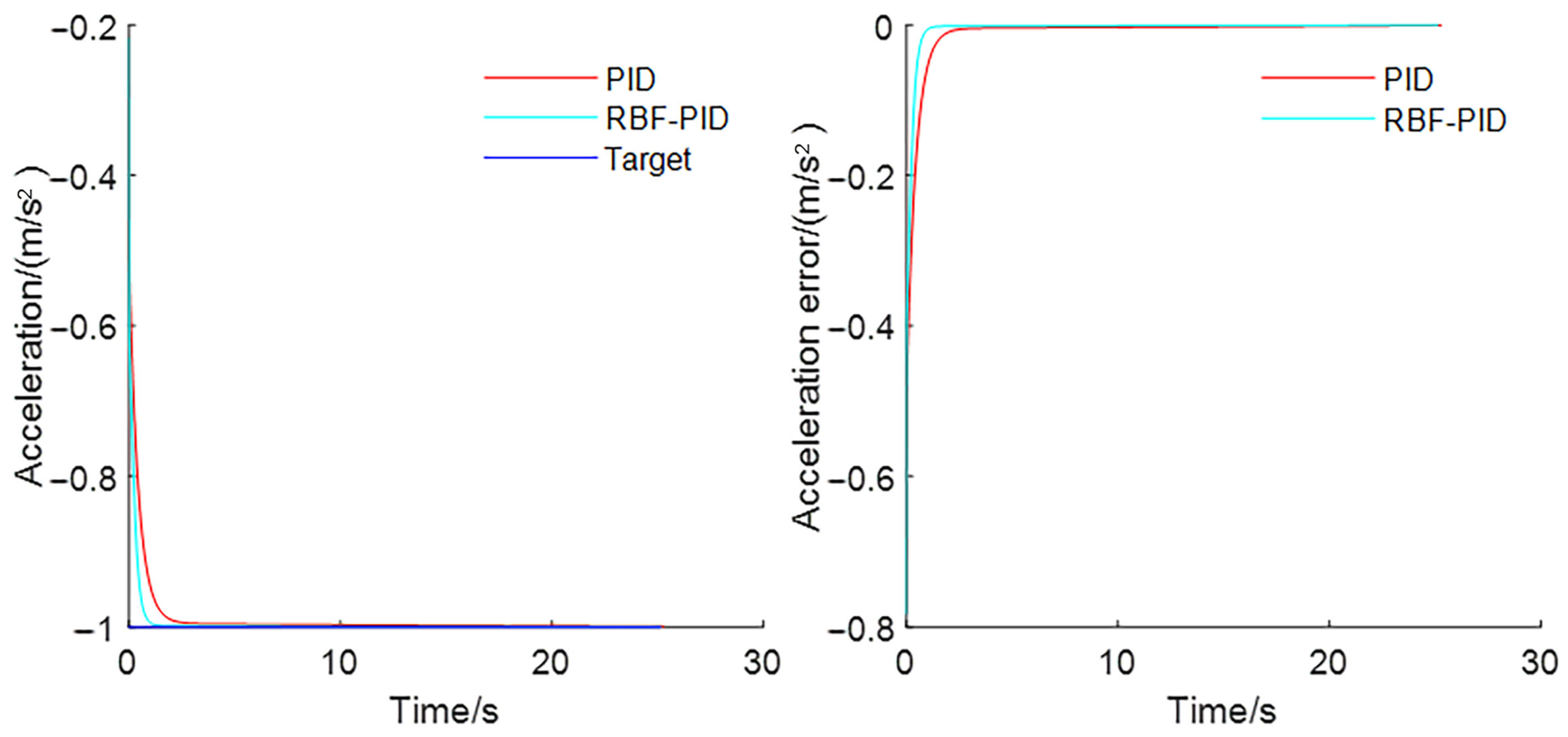
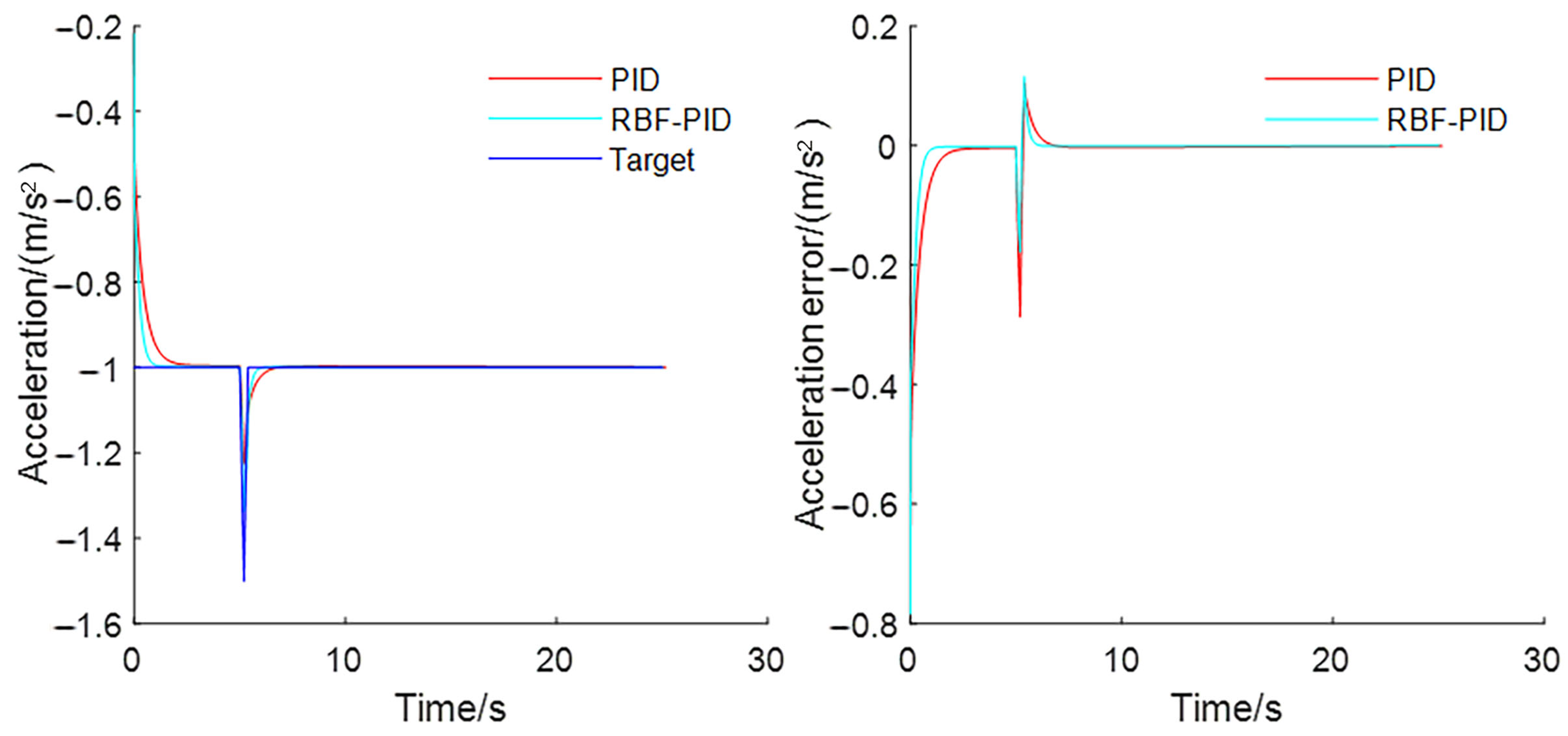
3.2.1. Step Response of the Braking Process
3.2.2. Response under Perturbation of the Braking Process
4. Conclusions
- (1)
- In response to the step signal in the driving case, the control method in this paper reaches the steady state with no static difference faster than the traditional PID control in the steady state condition, and the time required is reduced by about two-thirds. In addition, the maximum overshoot of this control algorithm is smaller, only about one-seventh of the traditional PID control, so the system response process is smoother. When adding disturbances, the control method used in this paper takes about three-tenths of the time to restore the steady state than the traditional PID control, showing a better anti-jamming ability;
- (2)
- In response to the step signal during the braking process, the response speed of this control algorithm is doubled compared with the traditional PID control. Similarly, when adding disturbances, this control algorithm takes less time to restore the steady state, which is about three-tenths less than the traditional PID control. The control algorithm has a better anti-jamming ability.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gao, J.; Chen, H.; Li, Y.; Chen, J.; Zhang, Y.; Dave, K.; Huang, Y. Fuel consumption and exhaust emissions of diesel vehicles in worldwide harmonized light vehicles test cycles and their sensitivities to eco-driving factors. Energy Convers. Manag. 2019, 196, 605–613. [Google Scholar] [CrossRef]
- Li, Q.; Tian, S.; Wang, W. Environmental and Social Problems and Countermeasures in Transportation System under Resource Constraints. Complexity 2020, 2020, 6629119. [Google Scholar] [CrossRef]
- Liu, Z.; Feng, K.; Davis, S.J.; Guan, D.; Chen, B.; Hubacek, K.; Yan, J. Understanding the energy consumption and greenhouse gas emissions and the implication for achieving climate change mitigation targets. Appl. Energy 2016, 184, 737–741. [Google Scholar] [CrossRef]
- Ziebinski, A.; Cupek, R.; Grzechca, D.; Chruszczyk, L. Review of advanced driver assistance systems (ADAS). AIP Conf. Proc. 2017, 1906, 120002. [Google Scholar]
- Izquierdo-Reyes, J.; Ramirez-Mendoza, R.A.; Bustamante-Bello, M.R. A study of the effects of advanced driver assistance systems alerts on driver performance. Int. J. Interact. Des. Manuf. IJIDeM 2017, 12, 263–272. [Google Scholar] [CrossRef]
- Marina Martinez, C.; Heucke, M.; Wang, F.-Y.; Gao, B.; Cao, D. Driving Style Recognition for Intelligent Vehicle Control and Advanced Driver Assistance: A Survey. IEEE Trans. Intell. Transp. Syst. 2018, 19, 666–676. [Google Scholar] [CrossRef]
- Divakarla, K.P.; Emadi, A.; Razavi, S. A Cognitive Advanced Driver Assistance Systems Architecture for Autonomous-Capable Electrified Vehicles. IEEE Trans. Transp. Electrif. 2019, 5, 48–58. [Google Scholar] [CrossRef]
- Arnaout, G.M.; Arnaout, J.-P. Exploring the effects of cooperative adaptive cruise control on highway traffic flow using microscopic traffic simulation. Transp. Plan. Technol. 2014, 37, 186–199. [Google Scholar] [CrossRef]
- Akhegaonkar, S.; Nouveliere, L.; Glaser, S.; Holzmann, F. Smart and Green ACC: Energy and Safety Optimization Strategies for EVs. IEEE Trans. Syst. Man Cybern. Syst. 2018, 48, 142–153. [Google Scholar] [CrossRef]
- Li, S.; Li, K.; Rajamani, R.; Wang, J. Model Predictive Multi-Objective Vehicular Adaptive Cruise Control. IEEE Trans. Control Syst. Technol. 2011, 19, 556–566. [Google Scholar] [CrossRef]
- Fritz, A.; Schiehlen, W. Automatic Cruise Control of a Mechatronically Steered Vehicle Convoy. Veh. Syst. Dyn. 1999, 32, 331–344. [Google Scholar] [CrossRef]
- Schiehlen, W.; Fritz, A. Nonlinear Cruise Control Concepts for Vehicles in Convoy. Veh. Syst. Dyn. 2019, 33, 256–269. [Google Scholar] [CrossRef]
- Batra, M.; McPhee, J.; Azad, N.L. Parameter identification for a longitudinal dynamics model based on road tests of an electric vehicle. In Proceedings of the ASME 2016 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Charlotte, NC, USA, 21–24 August 2016; p. V003T001A026. [Google Scholar]
- Shakouri, P.; Ordys, A.; Laila, D.S.; Askari, M. Adaptive Cruise Control System: Comparing Gain-Scheduling PI and LQ Controllers. IFAC Proc. Vol. 2011, 44, 12964–12969. [Google Scholar] [CrossRef]
- Feng, D.N.; Liu, Z.D.; Pei, X. Precise electric throttle openness control for vehicle adaptive cruise control system. Trans. Beijing Inst. Technol. 2011, 31, 528–532. [Google Scholar]
- Pei, X.F.; Liu, Z.D.; Ma, G.C.; Qi, Z.Q. An adaptive cruise control system based on throttle/brakes combined control. Automot. Eng. 2013, 35, 375–380. [Google Scholar]
- Zhao, J.; El Kamel, A. Coordinated throttle and brake fuzzy controller design for vehicle following. In Proceedings of the 13th International IEEE Conference on Intelligent Transportation Systems, ITSC 2010, Funchal, Portugal, 19–22 September 2010; pp. 659–664. [Google Scholar]
- Tsai, C.-C.; Hsieh, S.-M.; Chen, C.-T. Fuzzy Longitudinal Controller Design and Experimentation for Adaptive Cruise Control and Stop&Go. J. Intell. Robot. Syst. 2010, 59, 167–189. [Google Scholar] [CrossRef]
- Khooban, M.H.; Vafamand, N.; Niknam, T. T-S fuzzy model predictive speed control of electrical vehicles. ISA Trans. 2016, 64, 231–240. [Google Scholar] [CrossRef]
- Kumar, V.; Rana, K.P.S.; Mishra, P. Robust speed control of hybrid electric vehicle using fractional order fuzzy PD and PI controllers in cascade control loop. J. Frankl. Inst. 2016, 353, 1713–1741. [Google Scholar] [CrossRef]
- Zhan, J.; Zhang, T.; Shi, J.; Guan, X.; Nan, Z.; Zheng, N. A Dual Closed-loop Longitudinal Speed Controller Using Smooth Feedforward and Fuzzy Logic for Autonomous Driving Vehicles. In Proceedings of the 2021 IEEE International Intelligent Transportation Systems Conference (ITSC), Indianapolis, IN, USA, 19–22 September 2021; pp. 545–552. [Google Scholar]
- Sun, C.; Chu, L.; Guo, J.; Shi, D.; Li, T.; Jiang, Y. Research on adaptive cruise control strategy of pure electric vehicle with braking energy recovery. Adv. Mech. Eng. 2017, 9, 1687814017734994. [Google Scholar] [CrossRef]
- Chu, L.; Li, T.; Sun, C. A Research on Adaptive Cruise Longitudinal Control Scheme for Battery Electric Vehicles. Qiche Gongcheng/Automot. Eng. 2018, 40, 277–282 and 296. [Google Scholar]
- Gheisarnejad, M.; Mirzavand, G.; Ardeshiri, R.R.; Andresen, B.; Khooban, M.H. Adaptive Speed Control of Electric Vehicles Based on Multi-Agent Fuzzy Q-Learning. IEEE Trans. Emerg. Top. Comput. Intell. 2022, in press. [Google Scholar] [CrossRef]
- Li, Y.; Wu, G.; Wu, L.; Chen, S. Electric power steering nonlinear problem based on proportional–integral–derivative parameter self-tuning of back propagation neural network. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2020, 234, 4725–4736. [Google Scholar] [CrossRef]
- Fan, X.; Meng, F.; Fu, C.; Luo, Z.; Wu, S. Research of Brushless DC Motor Simulation System Based on RBF-PID Algorithm. In Proceedings of the 2009 Second International Symposium on Knowledge Acquisition and Modeling, Wuhan, China, 30 November–1 December 2009; pp. 277–280. [Google Scholar]
- Xu, Y.; Chu, L.; Zhao, D.; Chang, C. A Novel Adaptive Cruise Control Strategy for Electric Vehicles Based on a Hierarchical Framework. Machines 2021, 9, 263. [Google Scholar] [CrossRef]
- Chopra, V.; Singla, S.K.; Dewan, L. Comparative Analysis of Tuning a PID Controller using Intelligent Methods. Acta Polytech. Hung. 2014, 11, 235–249. [Google Scholar]
- Luo, Z.; Wei, L. Tracking of Mobile Robot Expert PID Controller Design and Simulation. In Proceedings of the International Symposium on Computer, Consumer and Control, Taichung, Taiwan, 10–12 June 2014. [Google Scholar]
- Liu, B.; Yao, G.; Xiao, X.; Yin, X. The Research on Self-adaptive Fuzzy PID Controller. In Proceedings of the 2013 International Conference on Mechatronics, Robotics and Automation (ICMRA 2013), Guangzhou, China, 13–14 June 2013; pp. 1462–1465. [Google Scholar]
- Niu, X.-j. The optimization for PID controller parameters based on Genetic Algorithm. In Proceedings of the 2014 International Conference on Advances in Materials Science and Information Technologies in Industry, Xi’an, China, 11–12 January 2014; pp. 4102–4105. [Google Scholar]
- Xiong, J.J.; Liu, J.Y. Neural Network PID Controller Auto-tuning Design and Application. In Proceedings of the 2013 25th Chinese Control and Decision Conference (CCDC), Guiyang, China, 25–27 May 2013; pp. 1370–1375. [Google Scholar]
- Chng, E.S.; Yang, H.H.; Bos, S. Orthogonal least-squares learning algorithm with local adaptation process for the radial basis function networks. IEEE Signal Process. Lett. 1996, 3, 253–255. [Google Scholar] [CrossRef]

| Para. | Value | Units |
|---|---|---|
| Vehicle weight | 1450 | kg |
| Rolling resistance coefficient | 0.015 | |
| Gravity acceleration | 9.8 | m/s2 |
| Aerodynamic drag coefficient | 0.3 | |
| Mass density of air | 1.29 | kg/m3 |
| Vehicle frontal area | 1.2258 | m2 |
| Vehicle transmission ratio | 8.28 | |
| Transmission efficiency | 0.9 | |
| Wheel radius. | 0.334 | m |
| Height of mass center | 530 | mm |
| Wheelbase | 2800 | mm |
| Tread | 1500 | mm |
| 0.2, 0.0005, 0 | ||
| 3 | ||
| 6 | ||
| 0.25 | ||
| 0.05 | ||
| in driving process | 0.4, 0.7, 0 | |
| in braking process | 2.2, 1.5, 0 | |
| Sampling time | 0.001 | s |
| Para. | Value | Units |
|---|---|---|
| Settling time of PID in driving process | 1.14 | s |
| Settling time of RBF-PID in driving process | 0.459 | s |
| Maximum overshoot of PID in driving process | 39.9 | % |
| Maximum overshoot of RBF-PID in driving process | 6 | % |
| Time to steady of PID under disturbance in driving process | 1.56 | s |
| Time to steady of RBF-PID under disturbance in driving process | 1.13 | s |
| Settling time of the PID in braking process | 1.051 | s |
| Settling time of the RBF-PID in braking process | 0.521 | s |
| Maximum overshoot of the PID in braking process | 0 | % |
| Maximum overshoot of the RBF-PID in braking process | 0 | % |
| Time to steady of PID under disturbance in braking process | 0.67 | s |
| Time to steady of RBF-PID under disturbance in braking process | 0.5 | s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chu, L.; Li, H.; Xu, Y.; Zhao, D.; Sun, C. Research on Longitudinal Control Algorithm of Adaptive Cruise Control System for Pure Electric Vehicles. World Electr. Veh. J. 2023, 14, 32. https://doi.org/10.3390/wevj14020032
Chu L, Li H, Xu Y, Zhao D, Sun C. Research on Longitudinal Control Algorithm of Adaptive Cruise Control System for Pure Electric Vehicles. World Electric Vehicle Journal. 2023; 14(2):32. https://doi.org/10.3390/wevj14020032
Chicago/Turabian StyleChu, Liang, Huichao Li, Yanwu Xu, Di Zhao, and Chengwei Sun. 2023. "Research on Longitudinal Control Algorithm of Adaptive Cruise Control System for Pure Electric Vehicles" World Electric Vehicle Journal 14, no. 2: 32. https://doi.org/10.3390/wevj14020032
APA StyleChu, L., Li, H., Xu, Y., Zhao, D., & Sun, C. (2023). Research on Longitudinal Control Algorithm of Adaptive Cruise Control System for Pure Electric Vehicles. World Electric Vehicle Journal, 14(2), 32. https://doi.org/10.3390/wevj14020032





