Abstract
Vehicle dynamics play an important role in determining a vehicle’s stability. It is necessary to identify and obtain models related to vehicle dynamics to evaluate the performance of electric vehicles, as well as how to control them. This paper presents fundamentals of vehicle dynamics, proposing a three-degree-of-freedom nonlinear observer and controller to control lateral velocity and tire torque in comparison to a PID control, while also utilizing a Lyapunov function to determine the stability of the controlled state feedback system concerning the observer, which estimates state errors. This work demonstrates the mathematical development of estimations that will be fed into the algorithms of two active nonlinear controls (state feedback and PID), utilizing the results from Matlab-Simulink simulations of tire torque, lateral and angular velocities based on longitudinal velocity measurements, and employing dynamic gains, such as response to a steering maneuver by the driver following the international standards ISO 7401/2011 and ISO 3888-2. It is concluded that the observer is robust and exhibits energy-saving efficiency in tire torque, even under conditions of variable tire-ground friction.
1. Introduction
Active control in a vehicle can provide driver assistance during car maneuvers, enhancing maneuverability in a safer manner, particularly in critical situations. Active control includes yaw stability [1,2], braking systems [3,4], suspension [5,6], tire-road grip [7,8], and integrated vehicle control [9,10].
Various control approaches have been investigated for these active systems. In [11], the tire-road adhesion coefficient is considered through robust anti-lock braking system (ABS) control assisted by an active suspension system (ASS). Analysis of the braking system’s parts and components has also been conducted to prevent severity and criticality in device failures, aiming to reduce maintenance costs [12]. Other research has focused on energy recovery systems with predictive and neuro-fuzzy controls, relating braking and suspension [13].
Significant research is being conducted on vehicle suspension to improve comfort and stability during vibrations. Various control approaches have been explored, including model-based control, feedback signals, and optimal control techniques. Electronically controlled hydraulic suspensions combined with an air system can be finely tuned using controllers like fuzzy control. This advancement allows them to outperform passive suspension systems in terms of vehicle maneuverability and ride comfort [14]. Recent research proposes double-integrated controller systems that activate two hydraulic actuators within the suspension system [15], while ref. [16] employs a controller to enhance pitch and roll movements in nonlinear systems with vibration attenuation, with the controller using fuzzy proportional-derivative (PD) control to compute four actuator forces.
Based on these considerations, both suspension and braking systems need to be simultaneously contemplated to ensure stability in understeer and oversteer conditions. In [17], a modular control system is specifically developed for electric vehicles (EVs) to improve stability in both longitudinal and lateral vehicle dynamics. Studies [18,19] have addressed slip angles in oversteer scenarios within single-input single-output (SISO) systems. However, in the case of electric vehicles equipped with independently driven wheel motors, both the longitudinal and lateral motion can be effectively controlled. This is achieved by utilizing drive distribution and regenerative braking torque within a multi-input multi-output (MIMO) system. This approach becomes particularly effective when tackling challenges related to actuators, such as managing four independent wheel motors while considering tire slip angles [20].
Due to the complexity involved in controlling multiple motors and distributed propulsion systems at the wheels, various control strategies have been implemented to achieve the desired stability. In [21], fuzzy logic control and state feedback are employed to rear-wheel active steering on an electric vehicle (EV). On the other hand, ref. [22] implements continuous torque control applied to individual wheels using sliding modes. Meanwhile, ref. [23] presents an integrated multi-objective controller for electric vehicles (EVs) that can consider slip control for traction and braking, lateral stability control, maneuverability, and roll prevention, unifying these maneuvers with a model predictive control framework similar to the one presented in [24,25]. The integrated control of active torque vectoring and electronic stability control has also been considered [26]. Direct yaw moment control utilizes the concept of energy efficiency in motor torque [27]. Rear torque vectoring is enabled for independent electric motors on the rear axle, controlling the nonlinear lateral dynamics of the vehicle [28] or for active front-steering maneuverability [29].
Solutions to studying the motor torque of EV or the wheel motors of electric vehicles are simulated for the validation of controls and observers on commercial platforms such as Matlab-Simulink [30,31], CarSim [32], or other self-designed hardware-in-the-loop (HiL) platforms [33]. For instance, ref. [34] introduces observer design-based fuzzy modeling to estimate the vehicle steering angle and sideslip angle without directly measuring them, but wind disturbances were not contemplated. Reference [35] proposes an observer based on a high-order sliding mode differentiator to estimate the lateral tire-road friction coefficient using as a reference the and , without considering the reference or wind disturbance. The authors in [36] propose the use of a permanent magnet synchronous motor as a powertrain to control longitudinal traction and generate yaw torque by varying the slips on the rear wheels, but they did not estimate the rear torque. The rear axle torque was not estimated, and the reference system did not include measurements of or . Additionally, there was no control input for the rear tires of the vehicle. The controller described in [37] incorporates robust observers designed to estimate vehicle states and parameters that cannot be directly measured. These include factors such as vehicle mass and road grade, where the torque is calculated from the brake control system. In [38], a collaborative control system was introduced to improve control precision in distributed-drive electric vehicles by coordinating all four wheels. This system utilized nonsingular terminal sliding mode control, along with a sliding mode observer, to enhance response speed and strengthen the robustness of the single motor controller. It is worth noting that this approach does not address the issue of wind disturbances.
Based on the aforementioned, this article introduces an active control methodology for electric vehicles, complemented by an observer. This approach factors in variables like variable coefficients of friction on asphalt and aerodynamic wind effects. It establishes a unified reference framework for both PID and state feedback controls, employing a mathematical model not previously utilized for regulating inputs to the rear axle electric motor (Mz) and power steering (). Furthermore, it presents a pioneering method for estimating rear tire torque based on the Mz control input in active state feedback control, a novelty not found in previous literature. This estimate is then compared to the rear tire torque achieved through PID control. By harnessing both PID and state feedback approaches, this methodology enables the computation of power () in the rear axle motor. This calculation, when applied to trajectory analysis, yields valuable insights into power in watts and vehicle energy. This innovative proposal holds promise for application in research concerning autonomy, efficiency, and greenhouse gas emissions, thus making a significant contribution to the current body of knowledge.
2. Mathematical Model of the Vehicle
2.1. Definition of the Mathematical Model of the Vehicle
The mathematical model of a vehicle is typically represented as a rigid body moving within a three-dimensional space, connected to the ground through its tires. This arrangement gives rise to a nonlinear behavioral model, as illustrated in Figure 1. The actuators employed in this application are active front steer (AFS) or steer by wire (SBW) for active front steering, and active brakes. The complexity of these nonlinear systems can be reduced by considering the following:
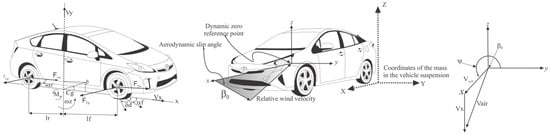
Figure 1.
Nonlinear model of the vehicle and aerodynamic reference point of the car.
- -
- When studying stability and maneuverability, the analysis focuses on the dynamics of lateral velocity and yaw angular velocity.
- -
- The active brake actuator, denoted Mz, is responsible for creating differential braking forces, generating a moment around the z-axis, which further impacts the dynamics of lateral velocity.
- -
- The dynamics of the pitch angle are not considered. Since the system is a rigid body, Figure 1 can be utilized to depict the nonlinear dynamics of the system.
- -
- is the angular velocity of turn (rad/s), which is in synchrony with [39].
- -
- R > 0 is a constant gain that is chosen so that the angular velocity of the turn is not saturated. It relates the input voltage on the actuator with the angular velocity obtained from [40].
- -
- , are the tire angle components imposed by the driver and controller (rad), is the angular velocity response of the actuator on the power steering wheel (rad/s), where is the input voltage to actuator (V), is an estimated back electromotive force constant (V/(rad/s)), is the resistance of the actuator (Ω), and I is the current (A), considering the simplified mathematical model of the cc motor where its values are obtained experimentally [41].
A theoretical verification of the mathematical model of the research article is carried out as an interesting proposal. The proposed mathematical model is analyzed using the following equations:
where:
- ➢
- m is the mass of the car (kg).
- ➢
- J expresses the moment of inertia of the vehicle (kg·m2).
- ➢
- h is the height of the center of gravity (C.G) with respect to the ground (m).
- ➢
- β denotes the chassis side-slip angle (rad).
- ➢
- lf, lr, are the lengths from the center of the vehicle to the front and rear tires (m).
- ➢
- r indicates the rolling radius of the tire (m).
- ➢
- vx signifies the longitudinal velocity (m/s).
- ➢
- vy represents the lateral velocity (m/s).
- ➢
- ωz is the angular rate of turn (rad).
- ➢
- x = [vx, vy, ωz] is the compact vector of the vehicle state.
- ➢
- αfy = αfyl = αfyr, αry = αryl = αryr denote the front and rear side-slip angles of the left and right tires (rad).
- ➢
- αf,0 = αrx0 are the uncontrolled front lateral and rear longitudinal slip angles respectively (rad).
- ➢
- αfx = αfxl = αfxr, αrx = αrxl = αrxr signify the front and rear longitudinal slip angles of the left and right wheels (rad).
- ➢
- Mz means the turning moment resulting from the active brakes (N·m).
- ➢
- μ is the coefficient of friction between the tire and the ground.
- ➢
- Fdx, Fdy are the longitudinal and lateral aerodynamic forces (N).
- ➢
- Mdz is the external aerodynamic yaw disturbance (N·m).
- ➢
- Ff,x, Fr,x are the front and rear longitudinal forces on the wheels (N).
- ➢
- Ff,y, Fr,y the front and rear lateral forces (N) as a function of the angle imposed on the front tires (δ = δd + δce).
Moreover, the lateral slip angles of the tires are defined as follows:
Similarly, the longitudinal slip angles are considered in the following manner:
The angular accelerations of the rear left and right tires are defined, suggesting:
Considering ωfxl, ωfxr as the angular velocities of the front left and right controlled tires (rad) and ωrx0l, ωrx0r as the uncontrolled rear left and right wheel revolution speeds (rad), Tn represents the applied torque for driving and braking at the tire Tn = Mzr/T (Nm), Jn being the moment of inertia of the tire (kgm2), T is the tire tread width (m), with Frxl Frxr denoting the rear left and right longitudinal forces, respectively. (Frxl + Frxr = Fr,x) and Frozl, Frozr represent the friction forces for the tires in the z-axis (N) [42]:
The normal force is calculated as Froz = m·g·cos (), where 0 to consider the EV on a flat road. However, the influence of gravity (g = 9.81 m/s2) and the coefficient are suggested to represent the average asphalt conditions. Additionally, = is used as the coefficient to account for the velocity effect on each rear tire.
2.2. Aerodynamics
The wind disturbances affecting the vehicle’s stability during movement include longitudinal forces (Ff,x = Ffxl + Ffxr, Fr,x), comprising the longitudinal air disturbance force Fdx, acting in the opposite direction, and lateral forces (Ff,y, Fr,y), as well as a counteracting lateral air disturbance force, Fdy. Depending on the disturbance caused by the wind, an aerodynamic turning disturbance denoted Mdz is created on the automobile chassis. Analyzing the wind impacts, it is essential to establish a coordinate system parallel to the coordinates of the automobile’s suspension mass, with the lateral displacement shown in Figure 1.
External disturbances can be represented by:
where As is the surface area of the vehicle (m2), ρ indicates the air mass density (kg/m3), means the constant aerodynamic coefficient, and vw signifies the air velocity (m/s). Therefore, the air disturbances are obtained as [43]:
The frontal and lateral surface areas of the vehicle are denoted As,f, and As,l, along with the longitudinal and lateral aerodynamic coefficients ca,x, ca,y, respectively, influenced by the wind velocity components along the x and y axes (va,w,x, va,w,y in m/s), acting on the vehicle’s suspension mass.
Additionally, in the Matlab-Simulink platform, these air disturbance parameters are used to set up conditions such as wind velocity (Vwind = vw,0) with a global wind yaw angle (Yaw wind = ), based on an aerodynamic slip angle (Beta air = β0) and relative wind velocity (Vair). The specific parameter values used are as follows and are obtained from [37]: vw, 0 = 28 m/s, β0 = −22.5°, As,f = 2.59 m2, As,l = 5.10 m2, ca,x = 0.3, ca,y = 0.6, ρ = 1.206 kg/m3, va,w,z = 0, = 225°, Vair = 185 km/h.
2.3. State Feedback Controller Design
Considering Equations (1)–(3) in a state-space form of the mathematical model for the EV as part of a control proposal:
Lateral acceleration can be expressed using Newton’s second law relating to the lateral forces on the tires:
Similarly, the longitudinal acceleration is established as:
The lateral and longitudinal forces can be defined using the formula:
For j = f,r, i = x,y, the constants Bj,i, Cj,i, Dj,i in Equations (1)–(3) are determined experimentally (see the end of subtopic 2). The control inputs will be considered as the result of the active brake torque moment Mz, the torque Tn applied to the rear tires, and the difference in lateral and longitudinal forces between the front and rear tires of the EV:
Furthermore, the control input for the power steering in the front tires will be ce, which can be determined by Equation (22):
The main objective of the control is to ensure that the system output (vx, vy, z) asymptotically follows a reference system characterized by having bounded derivatives. The significance of the reference system is established under ideal conditions, which assume a new vehicle, new tires, and new mechanical and electrical components with parameters, as exemplified in [34], is defined by:
x,ref (vx,ref, vy,ref, z,ref) is the compact reference vector of the vehicle state. J,ref = J, ,ref = are appropriate parameters, and Ffy,ref, Fry,ref, Ffx,ref, Frx,ref are ideal curves depending on:
For the design of state feedback linearization control, which will impose the desired behavior for lateral and yaw rate dynamics, this will be achieved by the reference signal from Equations (28)–(30) through the implementation of the inputs Fr,x, Ff,y and Mz, using the following control law:
where kii > 0, ii = 1, 2, 3. Therefore, the control inputs will be:
where CVE is defined as:
In Equation (38) 1, 2 and 3 are:
One of the considerations is the inverse of the matrix CVE, where the first column depends on the parameter μ, which will be invertible if 0:
2.4. Design of the State Feedback Observer
In certain cases, the measurement of lateral velocity may not be available. Therefore, it becomes necessary to design an observer to estimate this variable. The estimation of the moment is given by:
the estimation of the variation of the lateral forces:
and the torque:
considering:
establishing that:
Continuing with the assumption that ax, ay, ωz, vx, ωfxl, ωfxr are measured, which is a reasonable assumption in modern vehicles typically equipped with the necessary sensors, and measurements can also be taken using instruments such as the Autel Otofix Scanner and Hantek Oscilloscope-Multimeter to observe variables and dynamics. The proposal for the nonlinear observer for lateral velocity is performed as a copy of the plant in Equations (1) and (2):
where ko1, ko2 are the observer gains determined by Equations (1) and (2). Since the angular turn rate is approximated as , which is assumed to be measured, the variable is implicit in the estimation of the variable , thus facilitating the estimation of longitudinal velocity.
In Equations (52) and (53), there is a need to obtain the estimated errors:
and dynamic errors:
Equations (56) and (57) are linear and time-varying with the parameter ωz. To ensure exponential convergence of the error estimation, it is assumed that the yaw angular velocity ωz , considering z,max, with a maximum value (ωz,max), at all time t 0. These physical considerations are reasonable because the vehicle possesses finite energy, thereby bounding the maximum yaw angular velocity. In summary, during driver steering input maneuvers, ωz may pass through zero but cannot be zero within a finite time interval, and neither can the lateral forces of the vehicle’s tires.
The variables gain ko1, ko2 are obtained using the following candidate Lyapunov function:
with γ1 > > 0, 0, and sign (·) the signum function:
Based on the previous considerations, the derivative of the candidate Lyapunov function in Equation (58) is determined, considering the dynamic errors from Equations (56) and (57):
where the derivate:
Dirac distribution at D (ωz), for > 0, is considered zero (D (ωz) = 0), yielding to:
Equation (61) is solved using Cramer’s method to determine the gains of the observer:
By substituting the gains in Equations (62) and (63) into the derivative of the candidate function in Equation (61):
Therefore, the following values for Equation (64) are proposed:
By bounding Equation (64) with the conditions in Equations (65) and (66), the derivative of the Lyapunov function will be stable:
Next, a comparison will be made between the actively controlled feedback state designs in Equations (35)–(37) and a PID control under similar conditions.
2.5. Design of the Active PID Controller
For this PID controller, the control law is established in Equations (68)–(70), using the errors of longitudinal velocity in Equation (71), lateral velocity in Equation (72) and yaw angular velocity with Equation (73):
with errors:
The plant to be controlled is the mathematical model in Equations (17)–(19), with only its subscripts updated for the PID controller (Equations (74)–(76)) and other control inputs in Equations (77)–(79). Additionally, the reference system is given by Equations (28)–(30):
where is the compact vector of the vehicle state and the lateral acceleration can be expressed, relating to the lateral forces on the tires:
Similarly, the longitudinal acceleration is established as:
The lateral and longitudinal forces can be defined using the formula:
Moreover, the lateral slip angles of the tires are defined as follows:
Similarly, the longitudinal slip angles are considered in the following manner:
The angular accelerations of the rear left and right tires are defined, suggesting:
Considering ωfxlpid, ωfxrpid as the angular velocities of the front left and right controlled tires (rad) and ωrx0lpid, ωrx0rpid as the uncontrolled rear left and right wheel revolution speeds (rad), Tnpid represents the applied torque for driving and braking at the tire (N·m), with Frxlpid, Frxrpid denoting the rear left and right longitudinal forces, respectively (N). (Frxlpid + Frxrpid = Fr,xpid) and Frozlpid, Frozrpid represent the friction forces for the tires in the z-axis (N):
The normal force is calculated as Frozpid = m·g·cos (α). The values for kp, Ti, Td (established experimentally) are considered in the following parameters: m = 1550 kg, J = 3352 kgm2, lr = 1.53 m, lf = 1.38 m, Jn = 62 kgm2, r = 0.20 m, T = 0.16 m, = 0.9, h = 0.5 m, Bf,x = 6.9, Cf,x = 1.3, Df,x = 7500 N, Br,x = 7.1, Cr,x = 1.6, Dr,x = 7500 N, Br,y = 10, Cr,y = 1.32, Dr,y = 7834 N, Bf,y = 6.9, Cf,y = 1.78, Df,y = 7240 N, Kp = 100.475, Td = 0.00073, Ti = 45.84383, Bf,x,ref = 6.9, Cf,x,ref = 1.3, Df,x,ref = 10,000 N, Br,x,ref = 7.1, Cr,x,ref = 1.6, Dr,x,ref = 10,000 N, Br,y,ref = 10, Cr,y,ref = 1.32, Dr,y,ref = 10,000 N, Bf,y,ref = 6.9, Cf,y,ref = 1.78, Df,y,ref = 10,000 N. Moreover, the analysis includes Ff,ypid, Fr,ypid in Equation (22), but with the dynamics of the PID controller, along with Tnpid = Mzpid·r/T. These parameters are obtained from [37].
3. Experimental Results and Discussion
3.1. Maneuver ISO 7401
The ISO 7401 standard [44] (includes various test maneuvers. To evaluate the control proposal, Figure 2A shows a maneuver designed to assess performance, considering a tire-road friction coefficient of μ = 0.9 (dry surface, from 0 s (0 ms) to 3.5 s (3500 ms)). At 3.5 s, the vehicle transitions to a wet surface from μ = 0.9 to μ = 0.5, as illustrated in Figure 2B.
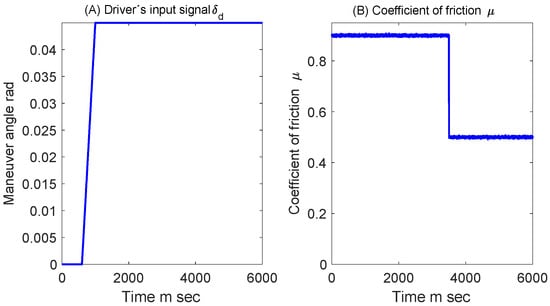
Figure 2.
δd and μ signals.
Figure 3A,B displays the values of lateral velocity and yaw rate, with the controllers from Equations (18) to (19) and Equations (75) to (76), compared to the reference system from Equations (29) to (30), and of the observer in Equations (52) and (53). Figure 3A exhibits a similarity to Figure 2A in terms of input signal tracking, but it displays an opposite sign relationship due to the nature of the lateral velocity variable. Notably, it is important to observe that the PID controller introduces a significant deviation from the reference system, leading to fluctuations in the PID lateral speed signal. This deviation results in inadequate control, particularly around the 4 s mark, attributed to the variable friction coefficient signal (Figure 2B), rendering the controller unreliable.
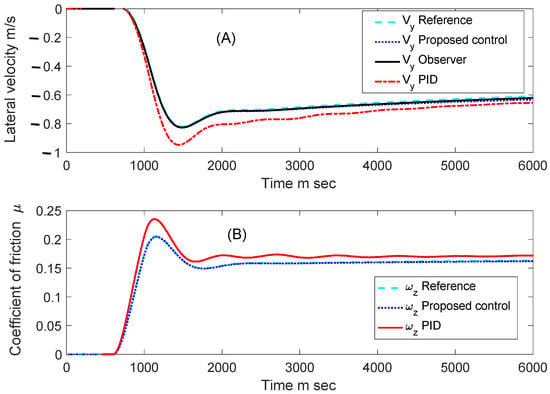
Figure 3.
Lateral vy and angular ωz velocities.
In contrast, the state feedback controller aligns closely with the reference system, presenting a signal that closely resembles the input maneuver (ISO 7401) [44]. Additionally, the observer proposed in this research article should be considered where the estimated signal of lateral velocity aligns closely with the reference signal. This demonstrates the robustness of the proposed estimator.
In the observer, we have the parameters k1 = 100, k2 = 100, k3 = 100 for Equations (35)–(37). For ko1, ko2 in Equations (62) and (63) is considered = 0.023, = 0.15, = 1, which are carried out experimentally in simulations. The results for the longitudinal velocity also start with vx = 28 m/s. Additionally, the values obtained with the PID controller deviate from the reference value, in contrast to the state feedback control, which is accurately estimated by the proposed state feedback observer. As a result, an estimated torque is achieved (Figure 4) for the rear tires of the electric vehicle with significant energy-saving efficiency, even under different tire-ground friction coefficient conditions. The state feedback control consistently shows positive power and torque values during the simulation, as it remains unaffected by changes in the tire-to-ground friction coefficient. In contrast, the PID control exhibits both positive and negative values due to the coefficient’s variability.
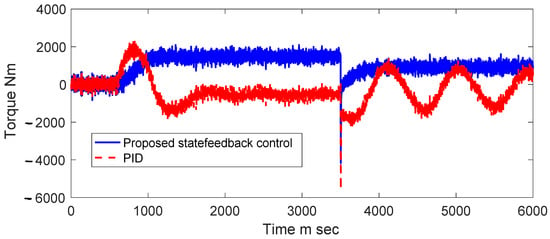
Figure 4.
Rear tire torque (N·m vs. s).
In addition to establishing the energy-saving efficiency of torque for the dynamics of each PID or state feedback controller, considering the rear axle of the vehicle, with Ttotal = Tfront + Trear, where the input torques can be defined as Tiii = (Fj,iiis·r)·kT·4 = Ttotal, j = f,r, iii = x, s = left, right, kT 15, with an adjustment gain (Figure 4), the system efficiency can be calculated as nsystem = /Ttotal, or nsystem = /Ttotal, for the state feedback controller and the PID controller, respectively. The motor power, Pmot = nsystem, iiii = corresponds to the vehicle’s wheels, as shown in Figure 5.
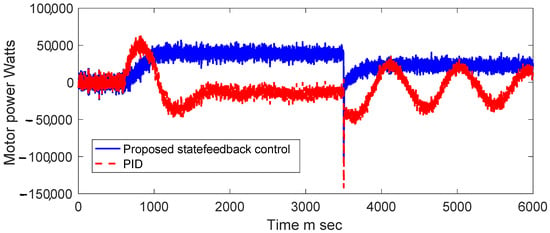
Figure 5.
Motor power Pmot in watts.
In the results of Figure 5 the power of the two PID controls and state feedback can be established with an analysis study as shown in the bibliographic reference [45], where the energy used for each controller can be calculated using the formula: .
3.2. Maneuver ISO 3888-2
This maneuver, known as “3888-2”, [46], is defined by the Driveability Testing Alliance and is extensively detailed in Figure 6. In this test, a variable friction coefficient is simulated, similar to the one depicted in Figure 2B. Its objective is to evaluate the vehicle’s stability when implementing the two control approaches proposed in this research article: the PID control and state feedback control.
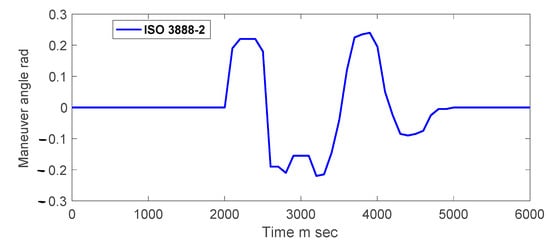
Figure 6.
Input signal maneuver δd.
In Figure 7, a significant proximity is observed between the reference lateral velocity and the velocity of the state feedback controller. Furthermore, it can be inferred that the observer’s estimation of lateral velocity closely tracks the reference lateral velocity. In contrast, for the PID controller, a considerable variation is noticeable concerning the reference signal.
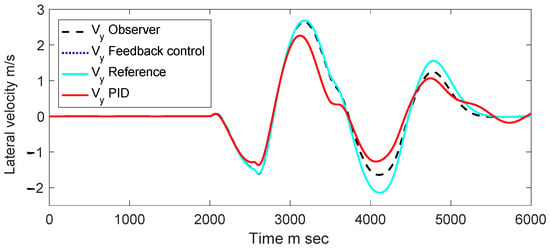
Figure 7.
Lateral velocity vy.
Regarding Figure 8, the reference yaw rate exhibits a close agreement with the of the state feedback controller, surpassing the tracking capability of the PID controller’s yaw rate.
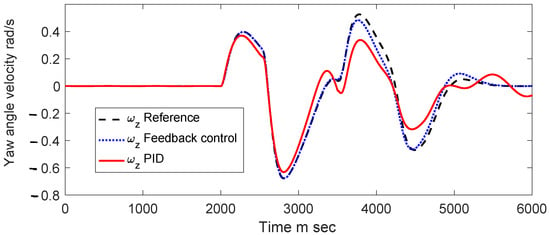
Figure 8.
Angular velocity ωz.
This observation suggests that the state feedback controller demonstrates superior reference tracking compared to the PID controller, as illustrated in Figure 7 and Figure 8.
When assessing the torque generated by both controllers, the PID and the state feedback controller, during the ISO 3888-2 [46] maneuver, we observe noteworthy differences in their performance. The PID controller demonstrates excessive oscillations in the signal, which could potentially have a detrimental impact on the rear axle motor of the electric vehicle over time. In contrast, when utilizing the signal from the controller in conjunction with the proposed observer, we notice a significant reduction in torque variation, as depicted in Figure 9.
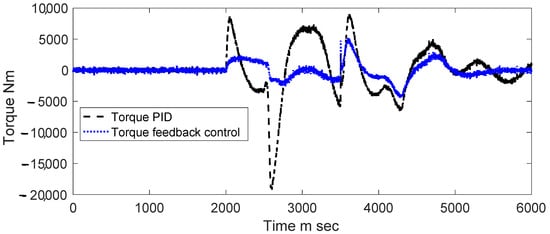
Figure 9.
Rear tire torque (N·m vs. s).
It is worth emphasizing that the PID controller demands substantial power peaks at specific instances, reaching approximately 200 kW, as depicted in Figure 10. Conversely, the state feedback controller requires less power and exhibits a more stable response (Figure 10).
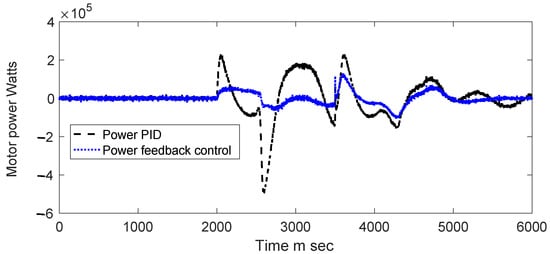
Figure 10.
Motor power Pmot in watts.
4. Conclusions
This research proposes an observer for lateral velocity using state feedback theory, based on the bicycle model, which is used for both different controllers (PID and state feedback) respectively, as an original idea, by also implementing a single reference system, thereby obtaining control input algorithms for the electric vehicle that will generate the controller signal (δce, δcpid) for the automotive power steering system. Therefore, it can be concluded that with ISO 7401 [44] and the ISO 3888-2 [46] standard, the PID controller encounters some issues in controlling the variables and dynamics of the vehicle in Section 3. Finally, it is established that the recommended control modes for obtaining a control observer for automotive power steering, studied in this research article, can be the state feedback approach, as a proposal for certain vehicle maneuvering situations. Furthermore, future work includes comparing the Matlab-Simulink platform with others, such as the National Instrument HiL, Carsim or dSpace MicroAutoBox.
Author Contributions
S.S.P., investigation planning, methodology, and validation; J.M.G.-L., formal analysis, methodology, software simulations, and writing—original draft; R.O.J.B., conceptualization, visualization, and writing—review and editing; G.B., resources. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhang, H.; Liang, J.; Jiang, H.; Cai, Y.; Xu, X. Stability Research of Distributed Drive Electric Vehicle by Adaptive Direct Yaw Moment Control. IEEE Access 2019, 7, 106225–106237. [Google Scholar] [CrossRef]
- De Bernardis, M.; Rini, G.; Bottiglione, F.; Hartavi, A.E.; Sorniotti, A. On nonlinear model predictive direct yaw moment control for trailer sway mitigation. Veh. Syst. Dyn. 2022, 61, 445–471. [Google Scholar] [CrossRef]
- Lin, C.-L.; Hung, H.-C.; Li, J.-C. Active Control of Regenerative Brake for Electric Vehicles. Actuators 2018, 7, 84. [Google Scholar] [CrossRef]
- Chen, L.; Li, Z.; Yang, J.; Song, Y. Lateral Stability Control of Four-Wheel-Drive Electric Vehicle Based on Coordinated Control of Torque Distribution and ESP Differential Braking. Actuators 2021, 10, 135. [Google Scholar] [CrossRef]
- Soliman, A.; Kaldas, M. Semi-active suspension systems from research to mass-market—A review. J. Low Freq. Noise Vib. Act. Control 2019, 40, 1005–1023. [Google Scholar] [CrossRef]
- Piñón, A.; Favela-Contreras, A.; Félix-Herrán, L.C.; Beltran-Carbajal, F.; Lozoya, C. An ARX Model-Based Predictive Control of a Semi-Active Vehicle Suspension to Improve Passenger Comfort and Road-Holding. Actuators 2021, 10, 47. [Google Scholar] [CrossRef]
- Huang, B.; Fu, X.; Wu, S.; Huang, S. Calculation Algorithm of Tire-Road Friction Coefficient Based on Limited-Memory Adaptive Extended Kalman Filter. Math. Probl. Eng. 2019, 2019, 1056269. [Google Scholar] [CrossRef]
- Jiang, B.; Sharma, N.; Liu, Y.; Li, C. Acceleration-based wheel slip control realized with decentralised electric drivetrain systems. IET Electr. Syst. Transp. 2022, 12, 143–152. [Google Scholar] [CrossRef]
- Leng, B.; Jiang, Y.; Yu, Y.; Xiong, L.; Yu, Z. Distributed drive electric autonomous vehicle steering angle control based on active disturbance rejection control. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2020, 235, 128–142. [Google Scholar] [CrossRef]
- Li, Y.; Zhai, D.; Fan, J.; Dong, G. Study on Lane-Change Replanning and Trajectory Tracking for Intelligent Vehicles Based on Model Predictive Control. World Electr. Veh. J. 2023, 14, 234. [Google Scholar] [CrossRef]
- Zhang, J.; Sun, W.; Jing, H. Nonlinear Robust Control of Antilock Braking Systems Assisted by Active Suspensions for Automobile. IEEE Trans. Control Syst. Technol. 2019, 27, 1352–1359. [Google Scholar] [CrossRef]
- Gong, J.; Luo, Y.; Qiu, Z.; Wang, X. Determination of key components in automobile braking systems based on ABC classification and FMECA. J. Traffic Transp. Eng. 2022, 9, 69–77. [Google Scholar] [CrossRef]
- Zhang, J.; Yang, Y.; Hu, M.; Yang, Z.; Fu, C. Longitudinal-vertical comprehensive control for four-wheel drive pure electric vehicle considering energy recovery and ride comfort. Energy 2021, 236, 121417. [Google Scholar] [CrossRef]
- Li, P.; Lam, J.; Cheung, K.C. Motion-based active disturbance rejection control for a non-linear full-car suspension system. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2017, 232, 616–631. [Google Scholar] [CrossRef]
- Qi, H.; Chen, Y.; Zhang, N.; Zhang, B.; Wang, D.; Tan, B. Improvement of both handling stability and ride comfort of a vehicle via coupled hydraulically interconnected suspension and electronic controlled air spring. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2019, 234, 552–571. [Google Scholar] [CrossRef]
- Nguyen, T.A. Improving the Comfort of the Vehicle Based on Using the Active Suspension System Controlled by the Double-Integrated Controller. Shock. Vib. 2021, 2021, 1426003. [Google Scholar] [CrossRef]
- Nahidi, A.; Kasaiezadeh, A.; Khosravani, S.; Khajepour, A.; Chen, S.-K.; Litkouhi, B. Modular integrated longitudinal and lateral vehicle stability control for electric vehicles. Mechatronics 2017, 44, 60–70. [Google Scholar] [CrossRef]
- Lenzo, B.; Sorniotti, A.; Gruber, P.; Sannen, K. On the experimental analysis of single input single output control of yaw rate and sideslip angle. Int. J. Automot. Technol. 2017, 18, 799–811. [Google Scholar] [CrossRef]
- Lenzo, B.; Zanchetta, M.; Sorniotti, A.; Gruber, P.; De Nijs, W. Yaw Rate and Sideslip Angle Control Through Single Input Single Output Direct Yaw Moment Control. IEEE Trans. Control Syst. Technol. 2021, 29, 124–139. [Google Scholar] [CrossRef]
- Zhou, H.; Jia, F.; Jing, H.; Liu, Z.; Guvenc, L. Coordinated Longitudinal and Lateral Motion Control for Four Wheel Independent Motor-Drive Electric Vehicle. IEEE Trans. Veh. Technol. 2018, 67, 3782–3790. [Google Scholar] [CrossRef]
- Xie, X.; Jin, L.; Jiang, Y.; Guo, B. Integrated Dynamics Control System With ESC and RAS for a Distributed Electric Vehicle. IEEE Access 2018, 6, 18694–18704. [Google Scholar] [CrossRef]
- Tota, A.; Lenzo, B.; Lu, Q.; Sorniotti, A.; Gruber, P.; Fallah, S.; Velardocchia, M.; Galvagno, E.; De Smet, J. On the Experimental Analysis of Integral Sliding Modes for Yaw Rate and Sideslip Control of an Electric Vehicle with Multiple Motors. Int. J. Automot. Technol. 2018, 19, 811–823. [Google Scholar] [CrossRef]
- Ataei, M.; Khajepour, A.; Jeon, S. Model Predictive Control for integrated lateral stability, traction/braking control, and rollover prevention of electric vehicles. Veh. Syst. Dyn. 2020, 58, 49–73. [Google Scholar] [CrossRef]
- Yin, D.; Sun, N.; Hu, J.-S. A Wheel Slip Control Approach Integrated With Electronic Stability Control for Decentralized Drive Electric Vehicles. IEEE Trans. Ind. Informatics 2019, 15, 2244–2252. [Google Scholar] [CrossRef]
- Asiabar, A.N.; Kazemi, R. A direct yaw moment controller for a four in-wheel motor drive electric vehicle using adaptive sliding mode control. J. Multi-Body Dyn. 2019, 233, 549–567. [Google Scholar] [CrossRef]
- Tahouni, A.; Mirzaei, M.; Najjari, B. Novel Constrained Nonlinear Control of Vehicle Dynamics Using Integrated Active Torque Vectoring and Electronic Stability Control. IEEE Trans. Veh. Technol. 2019, 68, 9564–9572. [Google Scholar] [CrossRef]
- Sun, P.; Trigell, A.S.; Drugge, L.; Jerrelind, J. Energy efficiency and stability of electric vehicles utilising direct yaw moment control. Veh. Syst. Dyn. 2022, 60, 930–950. [Google Scholar] [CrossRef]
- Vignati, M.; Sabbioni, E. A cooperative control strategy for yaw rate and sideslip angle control combining torque vectoring with rear wheel steering. Veh. Syst. Dyn. 2022, 60, 1668–1701. [Google Scholar] [CrossRef]
- Ahmadian, N.; Khosravi, A.; Sarhadi, P. Driver assistant yaw stability control via integration of AFS and DYC. Veh. Syst. Dyn. 2022, 60, 1742–1762. [Google Scholar] [CrossRef]
- Hu, J.; Tao, J.; Xiao, F.; Niu, X.; Fu, C. An Optimal Torque Distribution Control Strategy for Four-Wheel Independent Drive Electric Vehicles Considering Energy Economy. IEEE Access 2019, 7, 141826–141837. [Google Scholar] [CrossRef]
- Al-Fiky, H.T.; Asfoor, M.S.; Yacoub, M.I.; Sharaf, A.M. Electronic Differential Optimization for Electric Vehicle Full Model for In-Wheel Permanent Magnet Brushless DC Motors. In Proceedings of the 2019 7th International Conference on Control, Mechatronics and Automation (ICCMA), Delft, The Netherlands, 6–8 November 2019; pp. 15–20. [Google Scholar] [CrossRef]
- Guo, L.; Xu, H.; Zou, J. Acceleration slip regulation control strategy for four-wheel independent drive electric vehicles. IEEJ Trans. Electr. Electron. Eng. 2019, 14, 630–639. [Google Scholar] [CrossRef]
- Parra, A.; Zubizarreta, A.; Pérez, J. An energy efficient intelligent torque vectoring approach based on fuzzy logic controller and neural network tire forces estimator. Neural Comput. Appl. 2021, 33, 9171–9184. [Google Scholar] [CrossRef]
- Etienne, L.; Lúa, C.A.; Di Gennaro, S.; Barbot, J.-P. A Super-twisting Controller for Active Control of Ground Vehicles with Lateral Tire-road Friction Estimation and CarSim Validation. Int. J. Control Autom. Syst. 2021, 18, 1177–1189. [Google Scholar] [CrossRef]
- Heydrich, M.; Ricciardi, V.; Ivanov, V.; Mazzoni, M.; Rossi, A.; Buh, J.; Augsburg, K. Integrated Braking Control for Electric Vehicles with In-Wheel Propulsion and Fully Decoupled Brake-by-Wire System. Vehicles 2021, 3, 145–161. [Google Scholar] [CrossRef]
- Huang, H.; Tu, Q.; Jiang, C.; Pan, M.; Zhu, C. An Electronic Line-Shafting Control Strategy Based on Sliding Mode Observer for Distributed Driving Electric Vehicles. IEEE Access 2021, 9, 38221–38235. [Google Scholar] [CrossRef]
- Lúa, C.A.; Castillo-Toledo, B.; Di Gennaro, S. Integrated Active Control of Electric Vehicles. IFAC-PapersOnLine 2020, 53, 13781–13788. [Google Scholar] [CrossRef]
- Zhang, B.; Du, H.; Lam, J.; Zhang, N.; Li, W. A Novel Observer Design for Simultaneous Estimation of Vehicle Steering Angle and Sideslip Angle. IEEE Trans. Ind. Electron. 2016, 63, 4357–4366. [Google Scholar] [CrossRef]
- Borri, A.; Bianchi, D.; Benedetto, D.; Di Gennaro, S. Optimal workload actuator balancing and dynamic reference generation in active vehicle control. J. Frankl. Inst. 2017, 354, 1722–1740. [Google Scholar] [CrossRef]
- Coballes-Pantoja, J.; Gómez-Fuentes, R.; Noriega, J.R.; García-Delgado, L.A. Parallel Loop Control for Torque and Angular Velocity of BLDC Motors with DTC Commutation. Electronics 2020, 9, 279. [Google Scholar] [CrossRef]
- Pérez, S.S.; López, J.M.G.; Betancourt, R.O.J.; Laureano, E.V.; Solís, J.E.M.; Cervantes, M.G.S.; Guzmán, V.J.O. A Low-Cost Platform for Modeling and Controlling the Yaw Dynamics of an Agricultural Tractor to Gain Autonomy. Electronics 2020, 9, 1826. [Google Scholar] [CrossRef]
- Cheng, S.; Mei, M.-M.; Ran, X.; Li, L.; Zhao, L. Adaptive Unified Monitoring System Design for Tire-Road Information. J. Dyn. Syst. Meas. Control 2019, 141, 071006. [Google Scholar] [CrossRef]
- Daneshjo, N.; Mares, A.; Malega, P.; Francova, Z. CAD Model of Rear-View Mirror and Simulation of Its Aerodynamics and Noise. Int. J. Simul. Model. 2022, 21, 226–236. [Google Scholar] [CrossRef]
- ISO 7401/2011; Road Vehicles—Lateral Transient Response Test Methods—Open-Loop Test Methods. International Organization for Standardization: Geneva, Switzerland, 2011. Available online: www.conforward.cn/ueditor/php/upload/file/20150901/1441081386459881.pdf (accessed on 3 October 2023).
- Galindo-Muro, A.B.; Cespi, R.; Vallarta-Serrano, S.I. Applications of Electric Vehicles in Instant Deliveries. Energies 2023, 16, 1967. [Google Scholar] [CrossRef]
- ISO 3888-2; Passenger Cars—Test Track for a Severe Lane-Change Manoeuvre—Part 2: Obstacle Avoidance. International Organization for Standardization: Geneva, Switzerland, 2011. Available online: https://cdn.standards.iteh.ai/samples/57253/5e8cdcc7c2fe4c0c8fe6f1de8beb5dba/ISO-3888-2-2011.pdf (accessed on 3 October 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).