Multistage and Dynamic Layout Optimization for Electric Vehicle Charging Stations Based on the Behavior Analysis of Travelers
Abstract
:1. Introduction
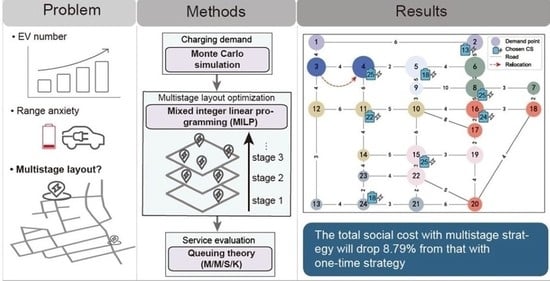
- First, multistage CS layout optimization is studied comprehensively with the dynamic EV charging demands of one day. The proposed method cannot only optimize the layout of CSs considering the numbers of EVs at different stages but also ensure the service quality by satisfying the charging demand at different time intervals in a day.
- Second, we designed a two-layer model to avoid the non-linear characteristics caused by the queuing phenomenon, which can improve the computational speed and consider the important queuing phenomenon during EV charging in a large road network.
2. Charging Demand Distribution
2.1. Problem Description
2.2. Travel Behavior Analysis
2.3. Charging Behavior Analysis
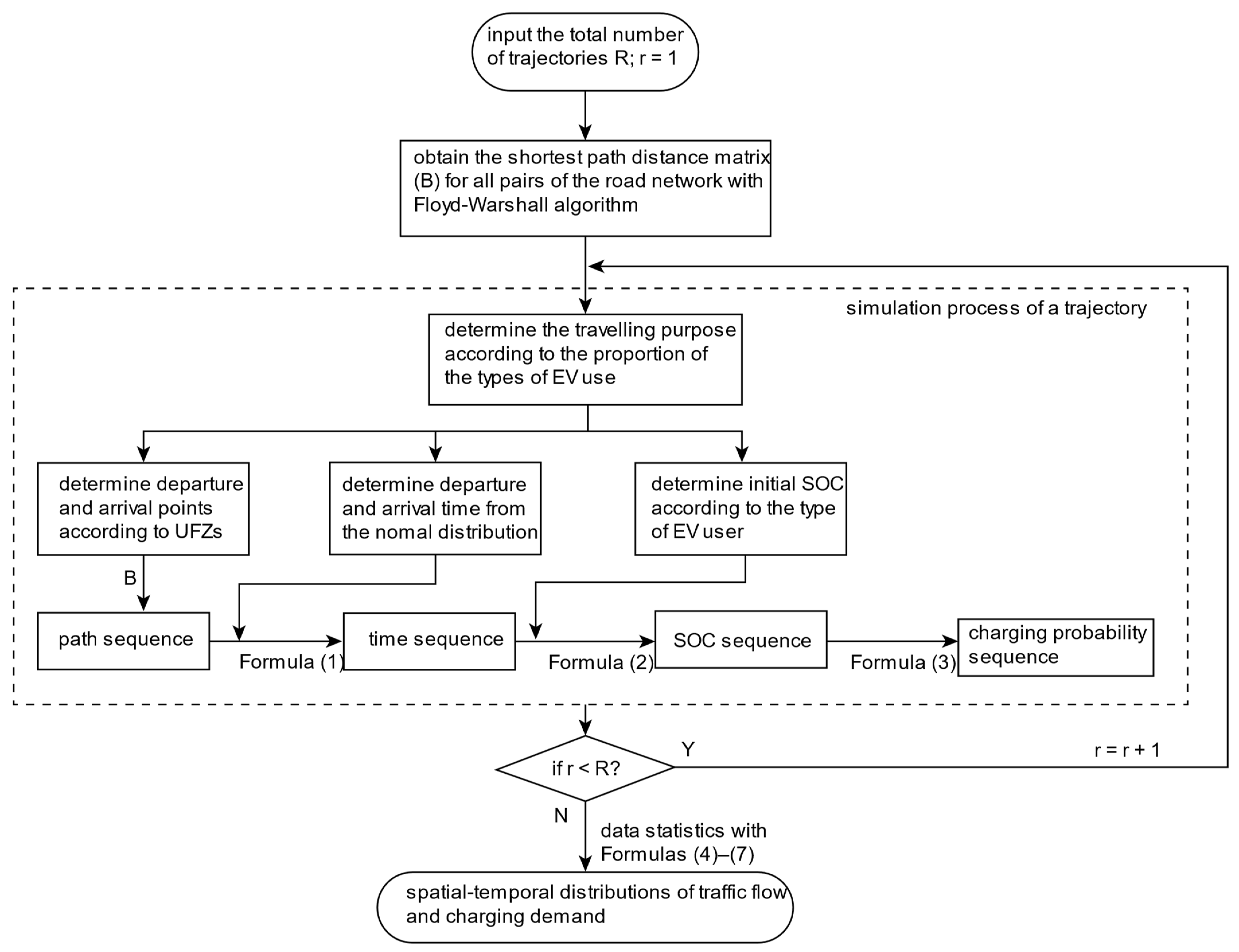
2.4. Monte Carlo Method
3. Mathematical Modeling
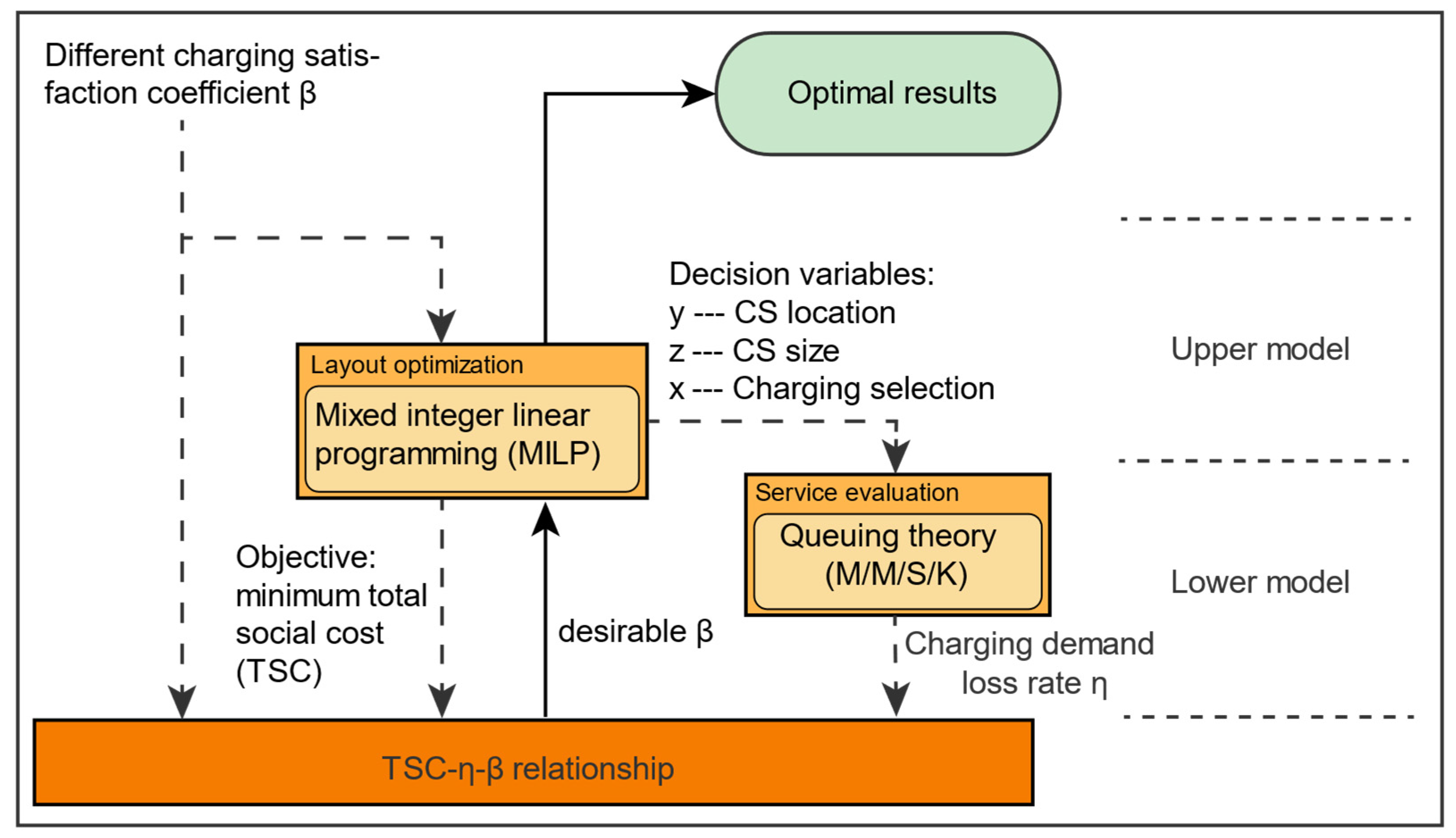
3.1. Mixed Integer Linear Programming (MILP) Model
3.1.1. Total Social Cost
3.1.2. Location Constraints
3.1.3. Capacity Constraints
3.1.4. Other Constraints
3.2. M/M/S/K Model of Queuing Theory
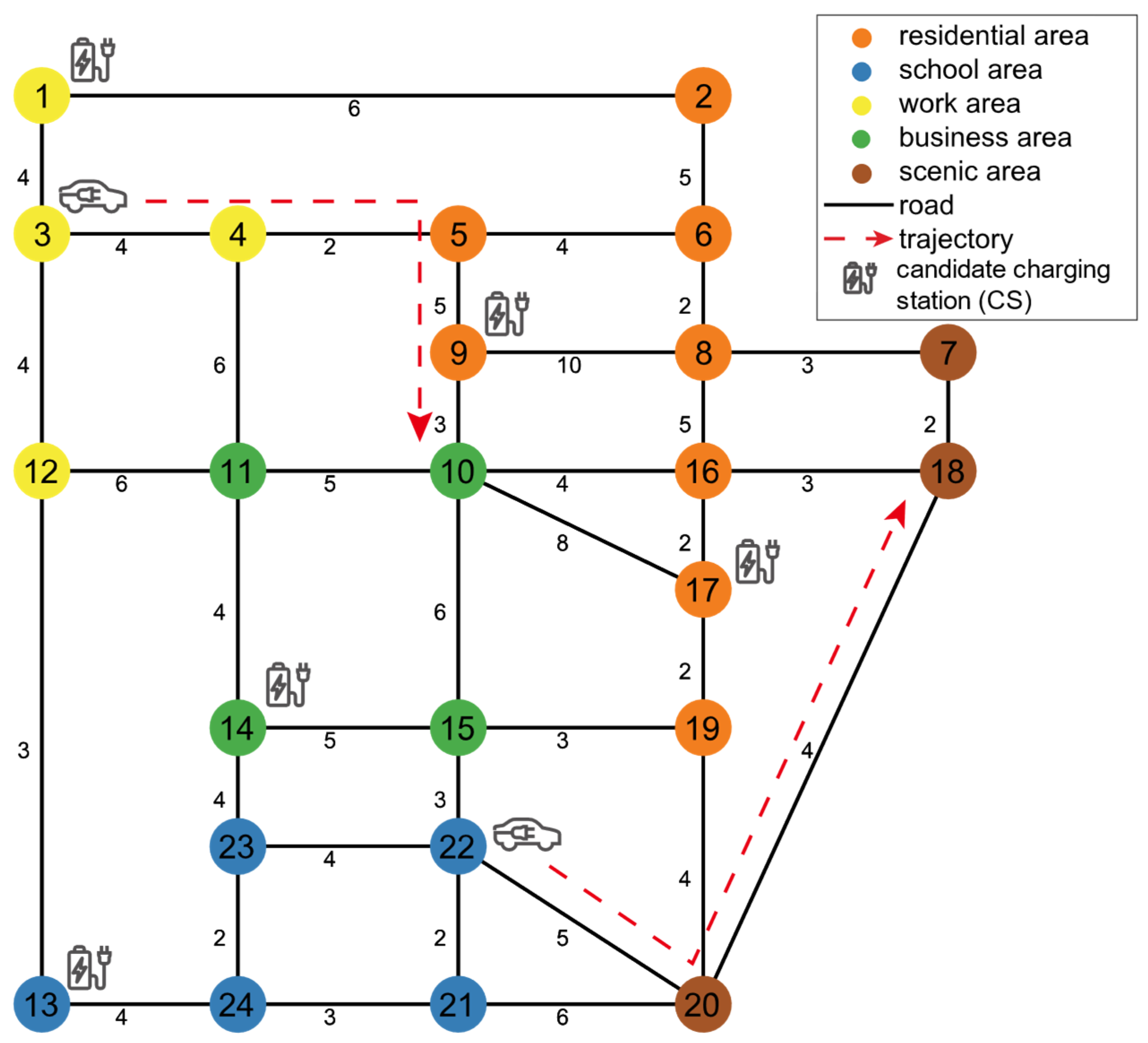
4. Case Study
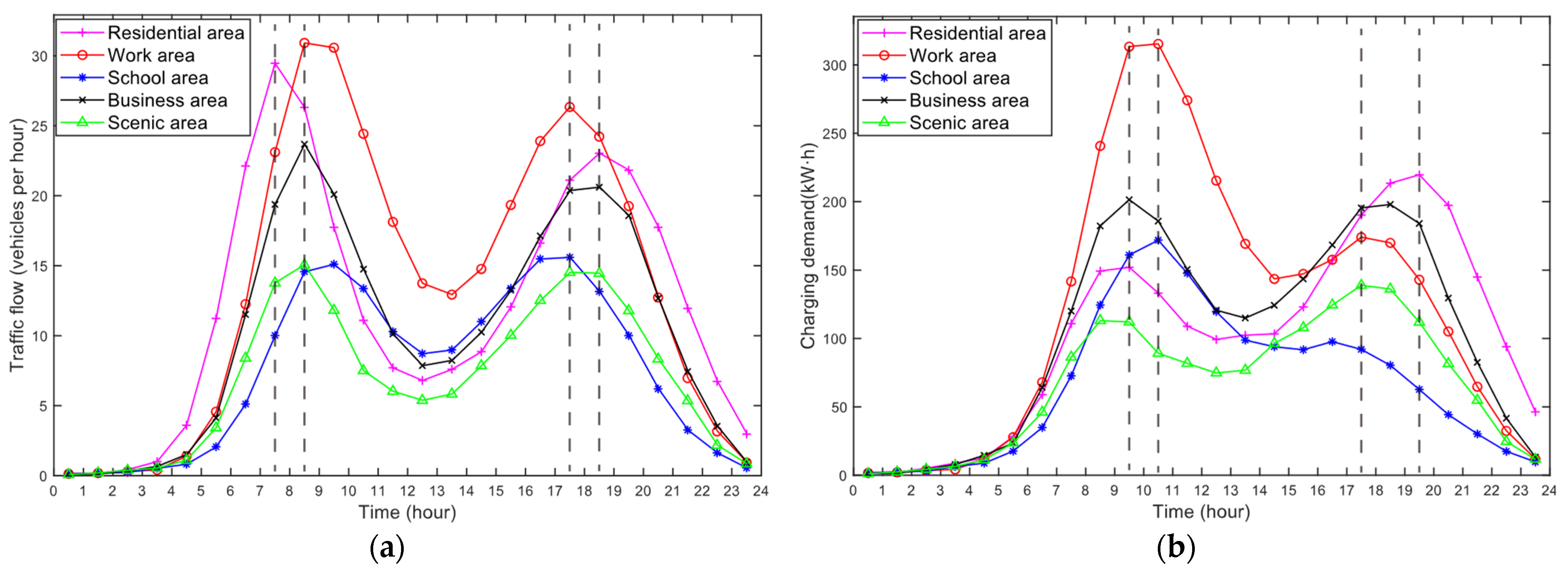
4.1. Simulation Results of Charging Demand Distribution
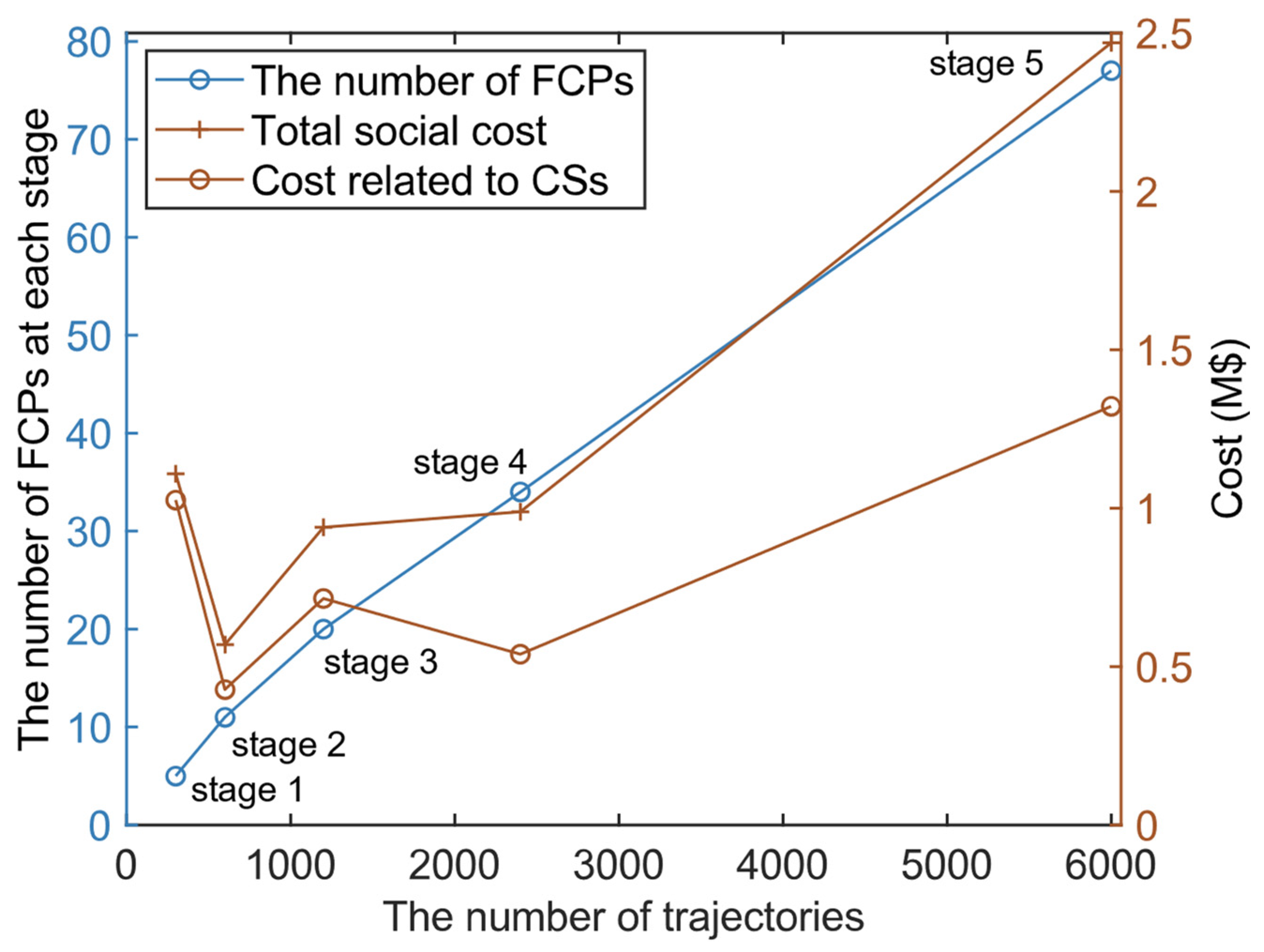
4.2. Layout Optimization Results
4.2.1. Location Optimization Results
4.2.2. Capacity Optimization Results
4.2.3. One-Time Strategy vs. Multistage Strategy
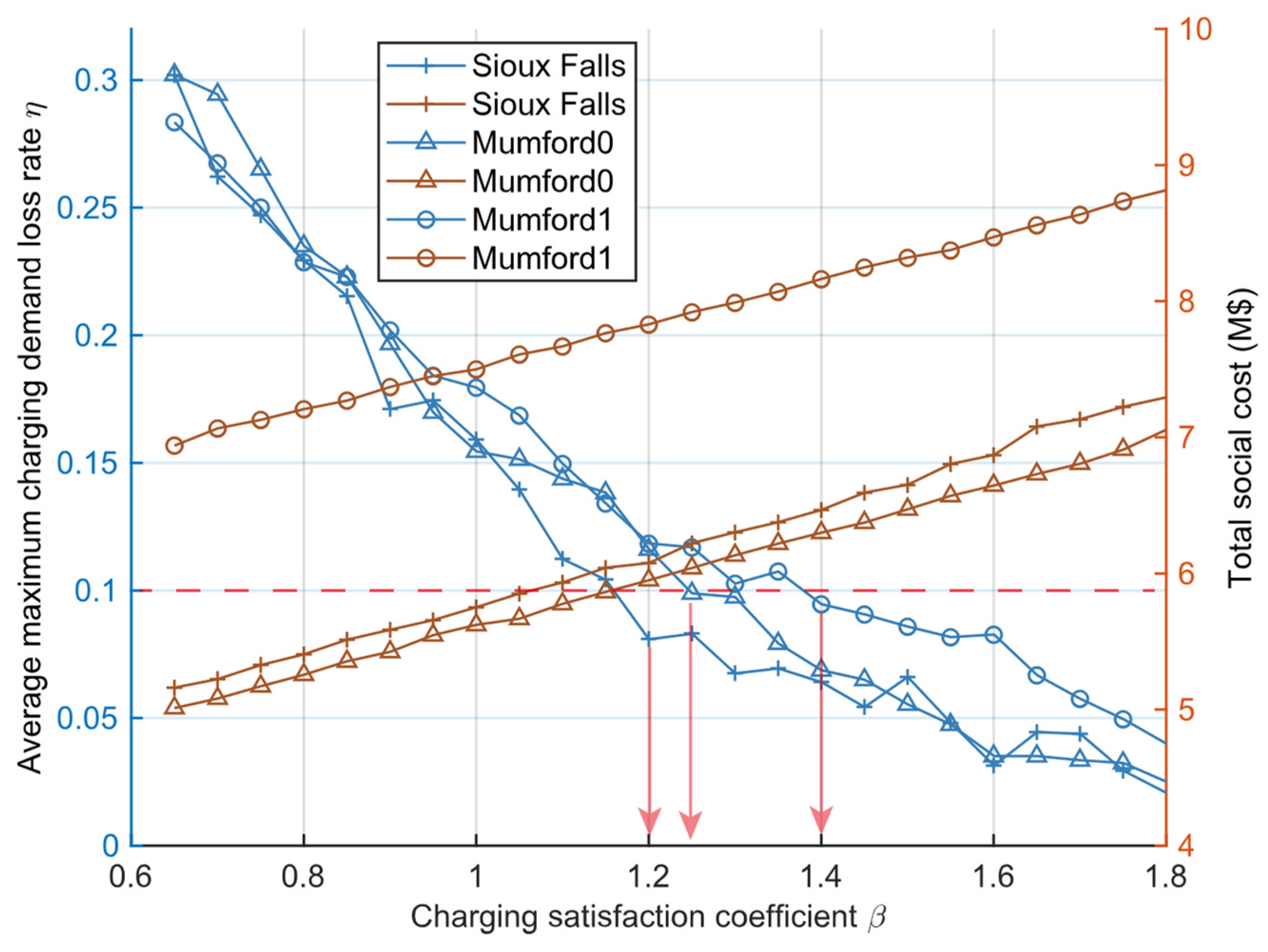
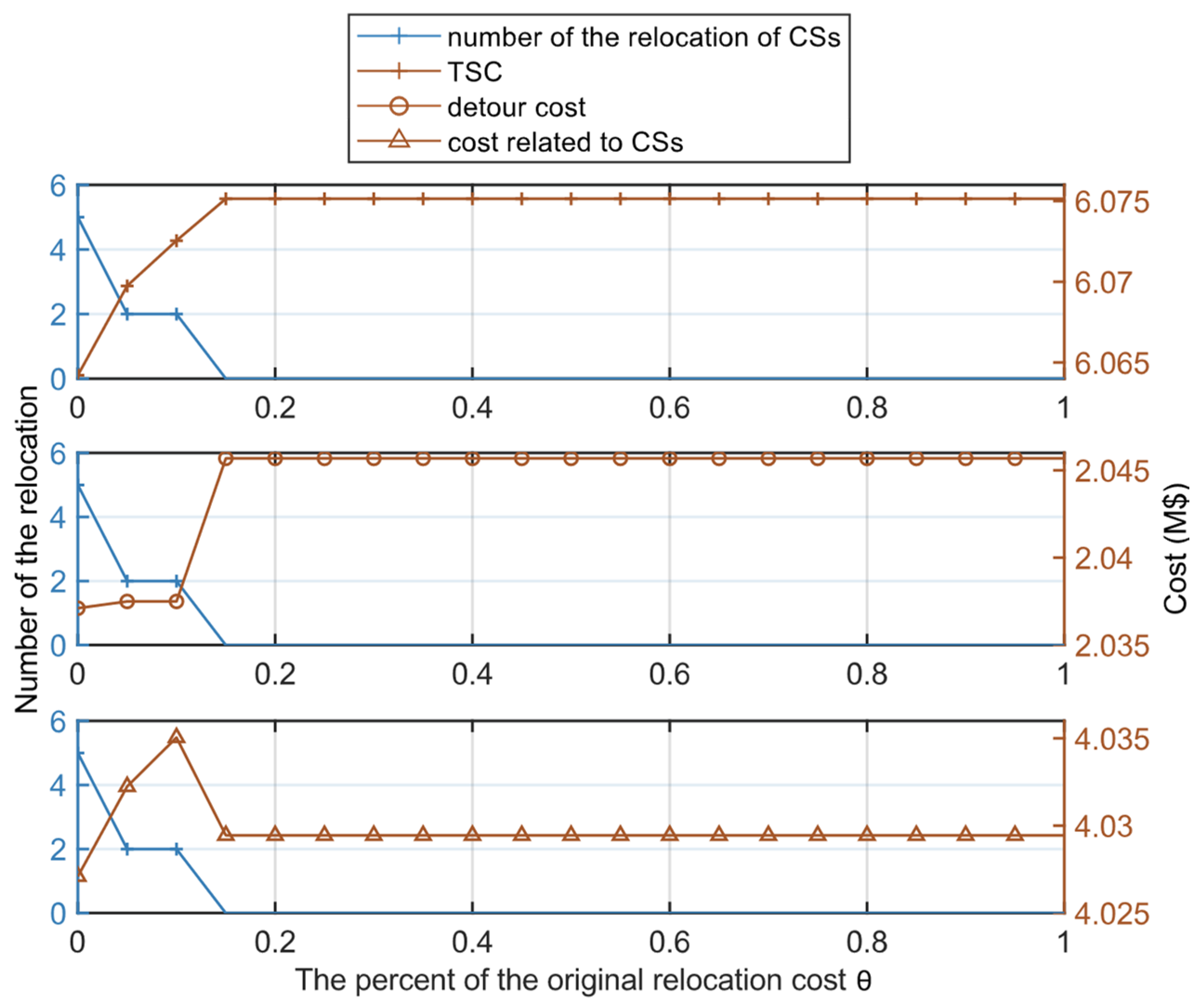
4.3. Sensitivity Analysis
4.3.1. Sensitivity Analysis and the Selection of
4.3.2. Sensitivity Analysis of the Relocation Cost
4.3.3. Sensitivity Analysis of Road Network Scales
5. Conclusions and Future Work
- The final stage with a relatively large number of EV trajectories has a great influence on the optimization results with both multistage strategy and one-time strategy. TSC with multistage optimization strategy can drop 8.79% from that with one-time optimization strategy in the case study, which can provide some meaningful suggestions for the long-term planning of EV CSs.
- Charging service quality, relocation cost, and road network scales have a significant impact on the optimization results. Surplus supply of charging demand for the charging peak is necessary to decrease the charging demand loss caused by uneven EV arrivals.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Abbreviations | |
| CCSs | candidate charging stations |
| CSs | charging stations |
| EV | electric vehicles |
| FCPs | fast charging piles |
| MILP | mixed integer linear programming |
| PWL | piecewise linear method |
| SOC | state of charge |
| TSC | total social cost |
| UFZ | urban functional zone |
| Indices | |
| trajectory from 1 to | |
| point on the trajectory from 1 to | |
| demand point from 1 to | |
| time interval from 1 to | |
| candidate charging station from 1 to | |
| planning stage from 1 to | |
| Parameters | |
| total number of trajectories | |
| total number of points on trajectory | |
| total number of demand points | |
| total number of time intervals | |
| total number of candidate charging stations | |
| total number of planning stages | |
| location of point on trajectory | |
| time of point on trajectory | |
| of point on trajectory | |
| charging probability of point on trajectory | |
| shortest path distance from point to the departure point on trajectory | |
| auxiliary probability of charging probability | |
| average EV speed | |
| driving range per kilowatt-hour | |
| rated capacity of EV battery | |
| upper/lower limit of charging | |
| control coefficient between the detour cost and cost related to CSs | |
| charging satisfaction coefficient | |
| monetary cost from to in time interval for an EV | |
| average hourly wage | |
| shortest path distance from to | |
| EV speed from to in time interval | |
| detour cost of EV users at stage | |
| cost related to CSs at stage | |
| construction and relocation cost of CS at stage | |
| installation and relocation cost of FCPs in CS at stage | |
| operating cost of CS /maintenance cost of FCPs in CS | |
| construction/operating/relocation cost of a CS | |
| installation/maintenance/relocation cost of a FCP | |
| charging rated power of FCPs | |
| a time interval | |
| upper limit of the number of FCPs caused by the land and the distribution grid | |
| Variables | |
| =1 represents the point on trajectory is at demand point in time interval ; 0, otherwise | |
| traffic flow at demand point in time interval | |
| charging demand at demand point in time interval | |
| =1 represents EVs at demand point choose CCS for charging; 0, otherwise | |
| =1 represents CCS is open at stage ; 0, otherwise | |
| number of FCPs installed in CCS at stage | |
Appendix A
References
- Global EV Outlook 2020. Available online: https://www.iea.org/reports/global-ev-outlook-2020 (accessed on 12 November 2021).
- Palomino, A.; Parvania, M. Advanced charging infrastructure for enabling electrified transportation. Electr. J. 2019, 32, 21–26. [Google Scholar] [CrossRef]
- Pure Electric Vehicles Feel Charging Pinch on Highways during National Day Holidays. Available online: https://www.globaltimes.cn/page/202110/1235651.shtml (accessed on 10 October 2021).
- Zhang, L.; Brown, T.; Samuelsen, S. Evaluation of charging infrastructure requirements and operating costs for plug-in electric vehicles. J. Power Sources 2013, 240, 515–524. [Google Scholar] [CrossRef]
- Tian, Z.; Hou, W.; Gu, X.; Gu, F.; Yao, B. The location optimization of electric vehicle charging stations considering charging behavior. Simulation 2018, 94, 625–636. [Google Scholar] [CrossRef] [Green Version]
- Xiang, Y.; Jiang, Z.; Gu, C.; Teng, F.; Wei, X.; Wang, Y. Electric vehicle charging in smart grid: A spatial-temporal simulation method. Energy 2019, 189, 116221. [Google Scholar] [CrossRef]
- Xie, F.; Liu, C.; Li, S.; Lin, Z.; Huang, Y. Long-term strategic planning of inter-city fast charging infrastructure for battery electric vehicles. Transp. Res. Part E Logist. Transp. Rev. 2018, 109, 261–276. [Google Scholar] [CrossRef]
- Lin, Y.; Zhang, K.; Shen, Z.-J.M.; Ye, B.; Miao, L. Multistage large-scale charging station planning for electric buses considering transportation network and power grid. Transp. Res. Part C Emerg. Technol. 2019, 107, 423–443. [Google Scholar] [CrossRef]
- Li, S.; Huang, Y.; Mason, S.J. A multi-period optimization model for the deployment of public electric vehicle charging stations on network. Transp. Res. Part C Emerg. Technol. 2016, 65, 128–143. [Google Scholar] [CrossRef]
- Han, B.; Lu, S.; Xue, F.; Jiang, L.; Xu, X. Three-stage electric vehicle scheduling considering stakeholders economic inconsistency and battery degradation. IET Cyber-Phys. Syst. 2017, 2, 102–110. [Google Scholar] [CrossRef]
- Zhang, H.; Moura, S.J.; Hu, Z.; Song, Y. PEV Fast-Charging Station Siting and Sizing on Coupled Transportation and Power Networks. IEEE Trans. Smart Grid 2018, 9, 2595–2605. [Google Scholar] [CrossRef]
- He, S.Y.; Kuo, Y.-H.; Wu, D. Incorporating institutional and spatial factors in the selection of the optimal locations of public electric vehicle charging facilities: A case study of Beijing, China. Transp. Res. Part C Emerg. Technol. 2016, 67, 131–148. [Google Scholar] [CrossRef]
- Ji, Z.; Huang, X. Plug-in electric vehicle charging infrastructure deployment of China towards 2020: Policies, methodologies, and challenges. Renew. Sustain. Energy Rev. 2018, 90, 710–727. [Google Scholar] [CrossRef]
- Vazifeh, M.M.; Zhang, H.; Santi, P.; Ratti, C. Optimizing the deployment of electric vehicle charging stations using pervasive mobility data. Transp. Res. Part A Policy Pract. 2019, 121, 75–91. [Google Scholar] [CrossRef] [Green Version]
- Guo, F.; Yang, J.; Lu, J. The battery charging station location problem: Impact of users’ range anxiety and distance convenience. Transp. Res. Part E Logist. Transp. Rev. 2018, 114, 1–18. [Google Scholar] [CrossRef]
- Ghamami, M.; Zockaie, A.; Wang, J.; Miller, S.; Kavianipour, M.; Shojaie, M.; Fakhrmoosavi, F.; Hohnstadt, L.; Singh, L. Electric Vehicle Charger Placement Optimization in Michigan: Phase I-Highways; Technical Report; 2019. Available online: https://www.researchgate.net/publication/331963177_Electric_Vehicle_Charger_Placement_Optimization_in_Michigan_Phase_I_-Highways (accessed on 1 September 2021).
- Transportation Networks for Research Core Team. Transportation Networks for Research. Available online: https://github.com/bstabler/TransportationNetworks (accessed on 18 September 2021).
- Mu, Y.; Wu, J.; Jenkins, N.; Jia, H.; Wang, C. A Spatial–Temporal model for grid impact analysis of plug-in electric vehicles. Appl. Energy 2014, 114, 456–465. [Google Scholar] [CrossRef] [Green Version]
- Sun, S.; Yang, Q.; Yan, W. A Novel Markov-Based Temporal-SoC Analysis for Characterizing PEV Charging Demand. IEEE Trans. Ind. Inf. 2018, 14, 156–166. [Google Scholar] [CrossRef]
- Lu, S.; Han, B.; Xue, F.; Jiang, L.; Feng, X. Stochastic bidding strategy of electric vehicles and energy storage systems in uncertain reserve market. IET Renew. Power Gener. 2020. [Google Scholar] [CrossRef]
- Lyu, M.; Han, B.; Lu, S. Electric Vehicle Operation Scheduling Optimization Considering Electrochemical Characteristics of Li-Ion Batteries. In Proceedings of the 2020 35th Youth Academic Annual Conference of Chinese Association of Automation (YAC), Zhanjiang, China, 16–18 October 2020; 2020. [Google Scholar]
- Cormen, T.H.; Leiserson, C.E.; Rivest, R.L. Introduction to Algorithms; MIT Press: Cambridge, MA, USA, 2007. [Google Scholar]
- Lin, M.-H.; Carlsson, J.G.; Ge, D.; Shi, J.; Tsai, J.-F. A Review of Piecewise Linearization Methods. Math. Probl. Eng. 2013, 2013, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Overcoming Barriers to Electric-Vehicle Deployment: Interim Report; National Academies Press: Washington, DC, USA, 2013; p. 18320. [CrossRef]
- Das, H.S.; Rahman, M.M.; Li, S.; Tan, C.W. Electric vehicles standards, charging infrastructure, and impact on grid integration: A technological review. Renew. Sustain. Energy Rev. 2020, 120, 109618. [Google Scholar] [CrossRef]
- Zhang, H.; Hu, Z.; Xu, Z.; Song, Y. An Integrated Planning Framework for Different Types of PEV Charging Facilities in Urban Area. IEEE Trans. Smart Grid 2016, 7, 2273–2284. [Google Scholar] [CrossRef]
- Public Transit Networks for Research. Transit Network Design Instances for Research. Available online: https://github.com/RenatoArbex/TransitNetworkDesign (accessed on 18 September 2021).
- Wei, W.; Wu, D.; Wu, Q.; Shafie-Khah, M.; Catalão, J.P.S. Interdependence between transportation system and power distribution system: A comprehensive review on models and applications. J. Mod. Power Syst. Clean Energy 2019, 7, 433–448. [Google Scholar] [CrossRef] [Green Version]
- Xiao, D.; An, S.; Cai, H.; Wang, J.; Cai, H. An optimization model for electric vehicle charging infrastructure planning considering queuing behavior with finite queue length. J. Energy Storage 2020, 29, 101317. [Google Scholar] [CrossRef]


| Parameters | Symbols | Value |
|---|---|---|
| Construction cost of a new CS | USD 163,000 | |
| Installation cost of a FCP | USD 23,500 | |
| Relocation cost of a CS 1 | USD 26,000 | |
| Relocation cost of a FCP | USD 500 | |
| Average hourly wage | USD 8.2 | |
| EV battery capacity 2 | 40 kW·h | |
| Driving range per kilowatt-hour 2 | 6.075 km/kW·h | |
| Rated charging power of FPCs 2 | 80 kW | |
| Upper/lower limit of charging | 0.80, 0.20 |
| Strategy | Total Number of CSs | Total Number of FCPs | Detour Cost (M$) | Cost Related to CSs (M$) | Total Social Cost (M$) | η |
|---|---|---|---|---|---|---|
| One-time | 8 | 77 | 1.9899 | 4.6703 | 6.6602 | 8.097% |
| Multistage | 8 | 77 | 2.0456 | 4.0295 | 6.0751 | 0.012% |
| Variation | 0 | 0 | +2.80% | −13.72% | −8.79% | +8.085% |
| Name | Number of Nodes | Number of Lines | Average Road Length (km) | Total Social Cost (M$) | Optimization Time (s) | Gap |
|---|---|---|---|---|---|---|
| Sioux Falls 1 | 24 | 38 | 4.13 | 6.0751 | 1.20 | 0 |
| Mumford 0 2 | 30 | 90 | 4.47 | 5.8642 | 1.44 | 0 |
| Mumford 1 2 | 70 | 210 | 4.58 | 7.7376 | 34.22 | 0 |
| Mumford 2 2 | 110 | 385 | 4.70 | 8.5771 | 164.01 | 0 |
| Mumford 3 2 | 127 | 425 | 4.62 | 8.8478 | 128.29 | 0 |
| Berlin Friedrichshain 1 | 224 | 523 | 4.60 | 11.217 | 138.28 | <0.5% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, F.; Feng, M.; Han, B.; Lu, S. Multistage and Dynamic Layout Optimization for Electric Vehicle Charging Stations Based on the Behavior Analysis of Travelers. World Electr. Veh. J. 2021, 12, 243. https://doi.org/10.3390/wevj12040243
Chen F, Feng M, Han B, Lu S. Multistage and Dynamic Layout Optimization for Electric Vehicle Charging Stations Based on the Behavior Analysis of Travelers. World Electric Vehicle Journal. 2021; 12(4):243. https://doi.org/10.3390/wevj12040243
Chicago/Turabian StyleChen, Feng, Minling Feng, Bing Han, and Shaofeng Lu. 2021. "Multistage and Dynamic Layout Optimization for Electric Vehicle Charging Stations Based on the Behavior Analysis of Travelers" World Electric Vehicle Journal 12, no. 4: 243. https://doi.org/10.3390/wevj12040243
APA StyleChen, F., Feng, M., Han, B., & Lu, S. (2021). Multistage and Dynamic Layout Optimization for Electric Vehicle Charging Stations Based on the Behavior Analysis of Travelers. World Electric Vehicle Journal, 12(4), 243. https://doi.org/10.3390/wevj12040243