Research on High Power Factor Single Tube Variable Structure Wireless Power Transmission
Abstract
:1. Introduction
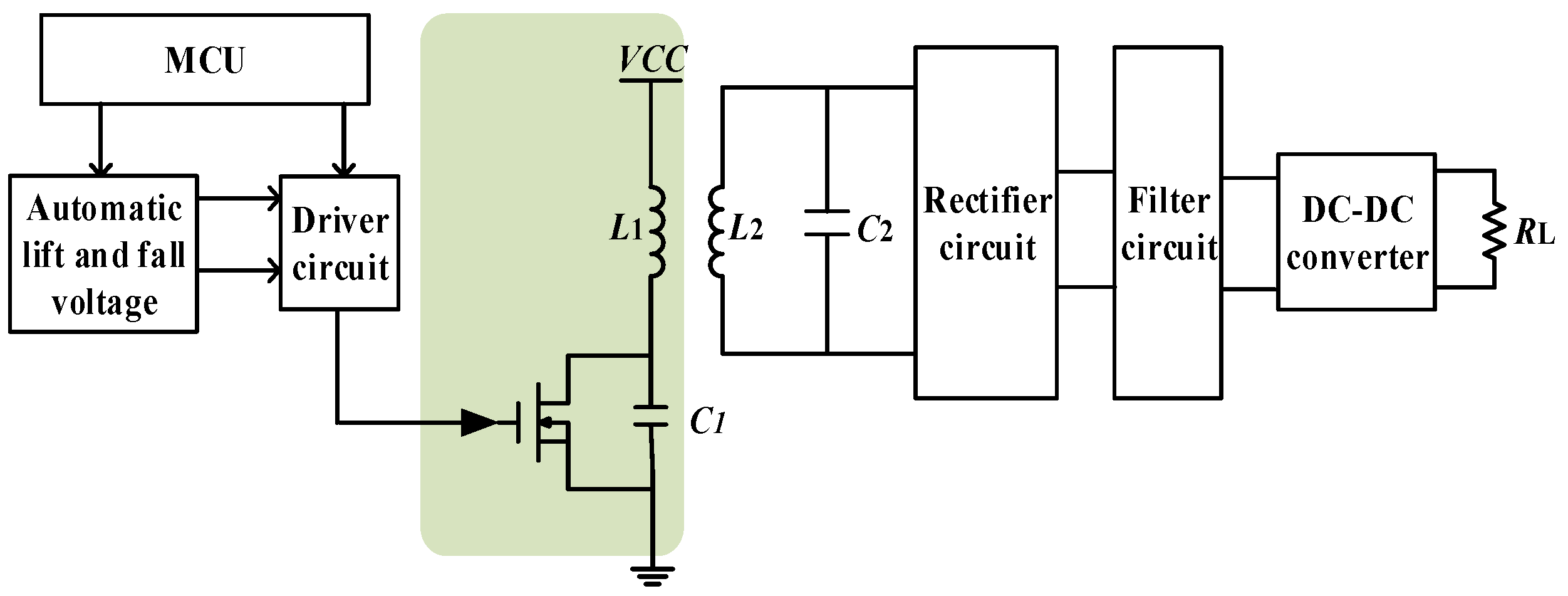
2. System Structure and Operation Process
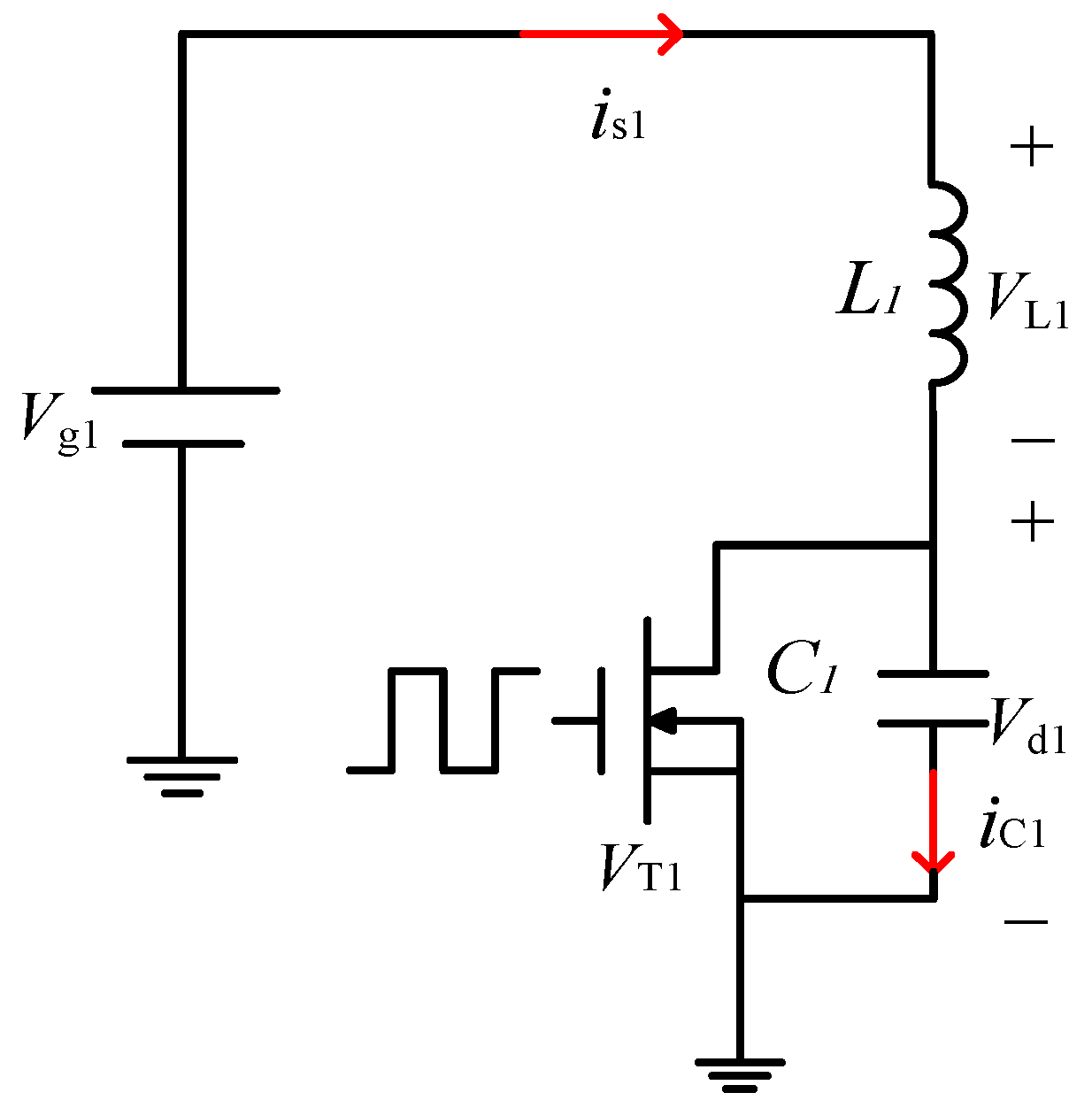
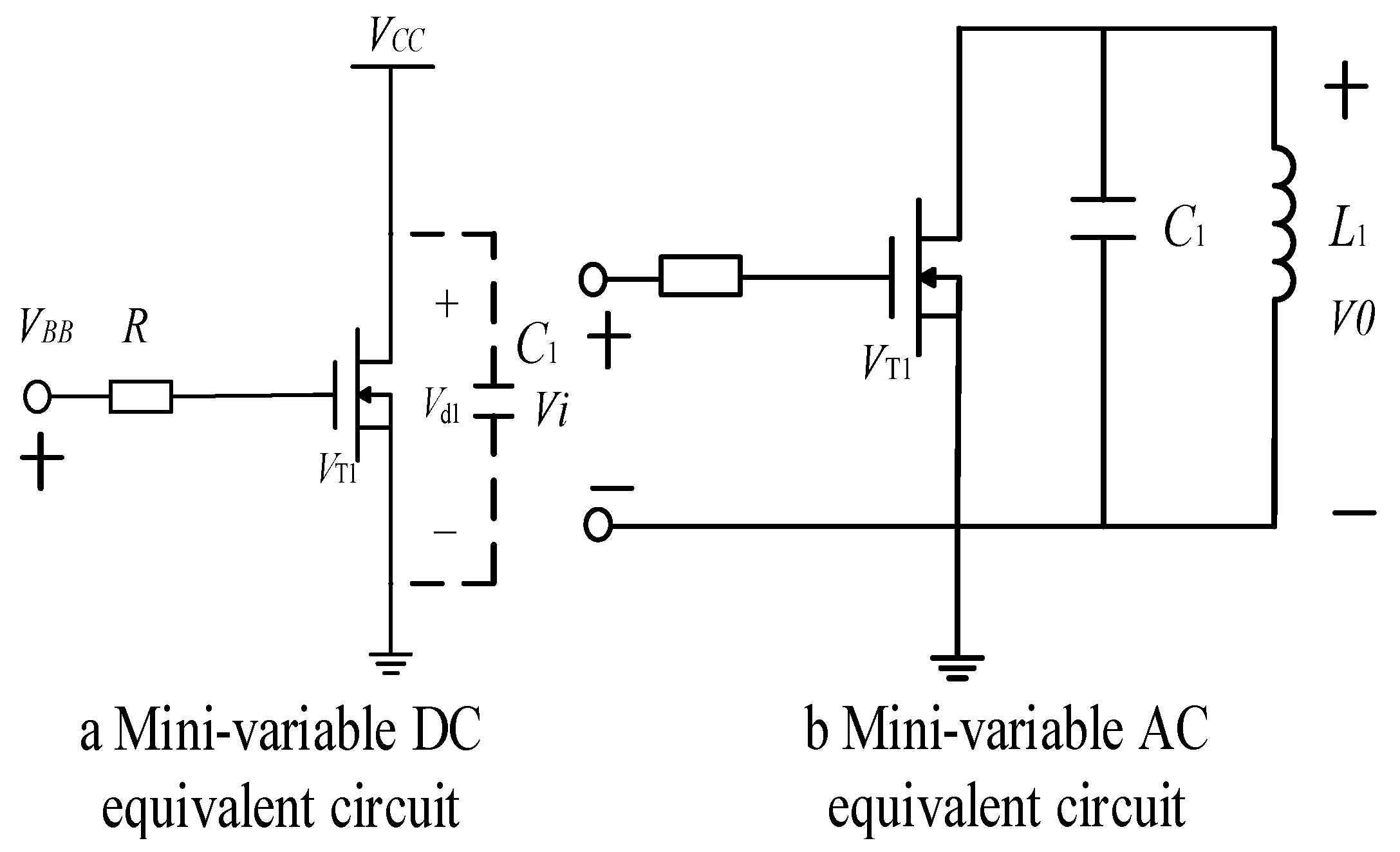
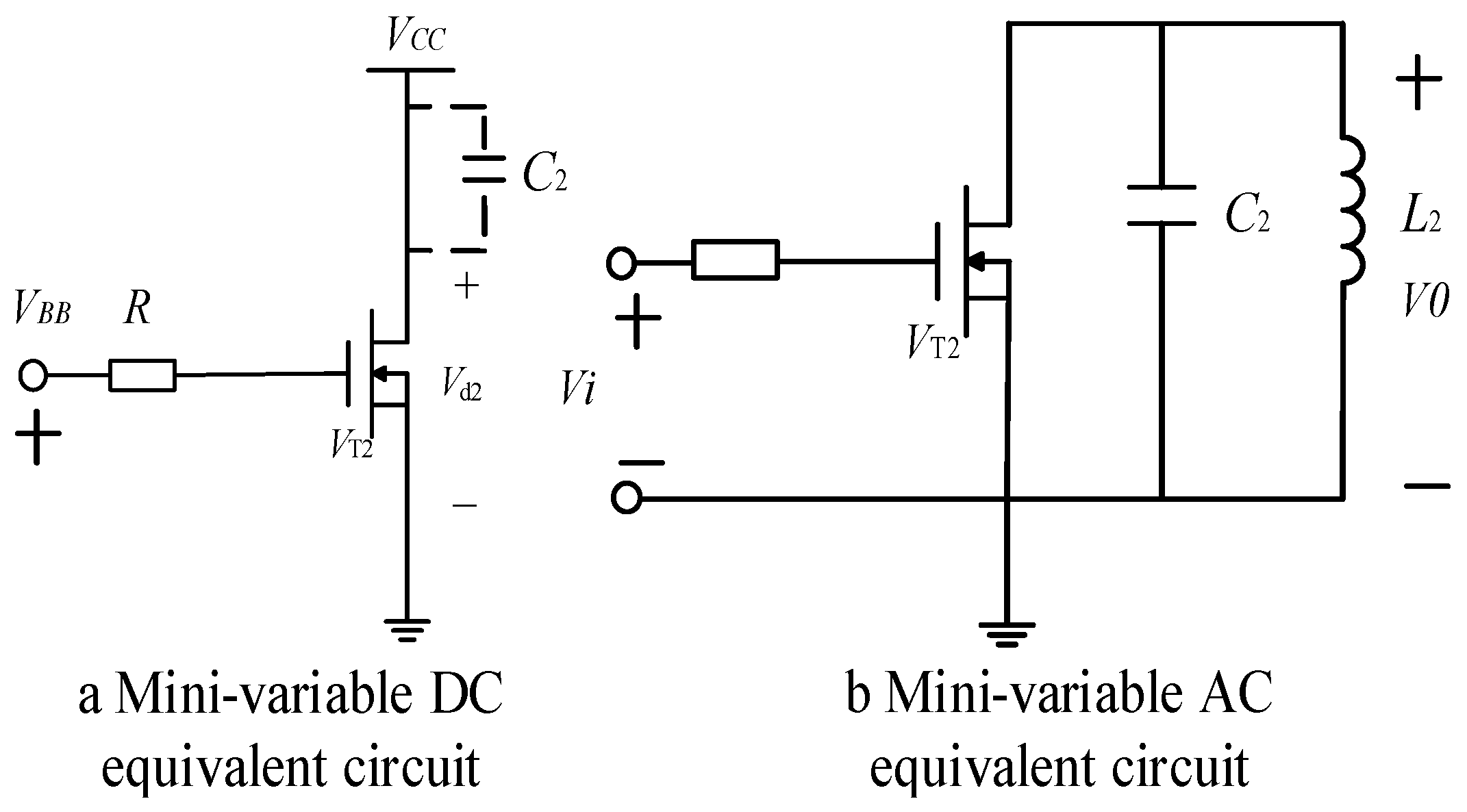
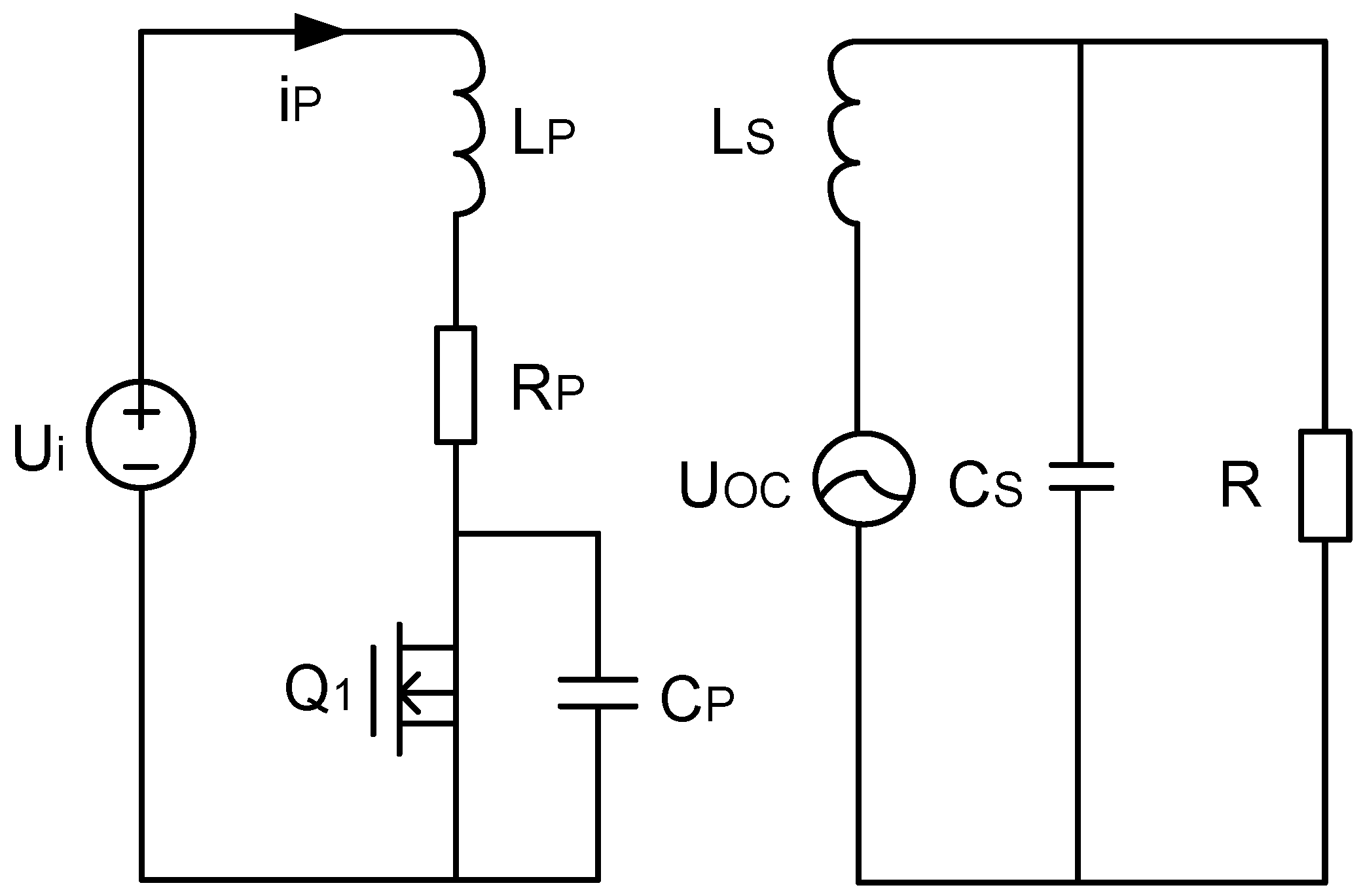
3. Circuit Model Analysis
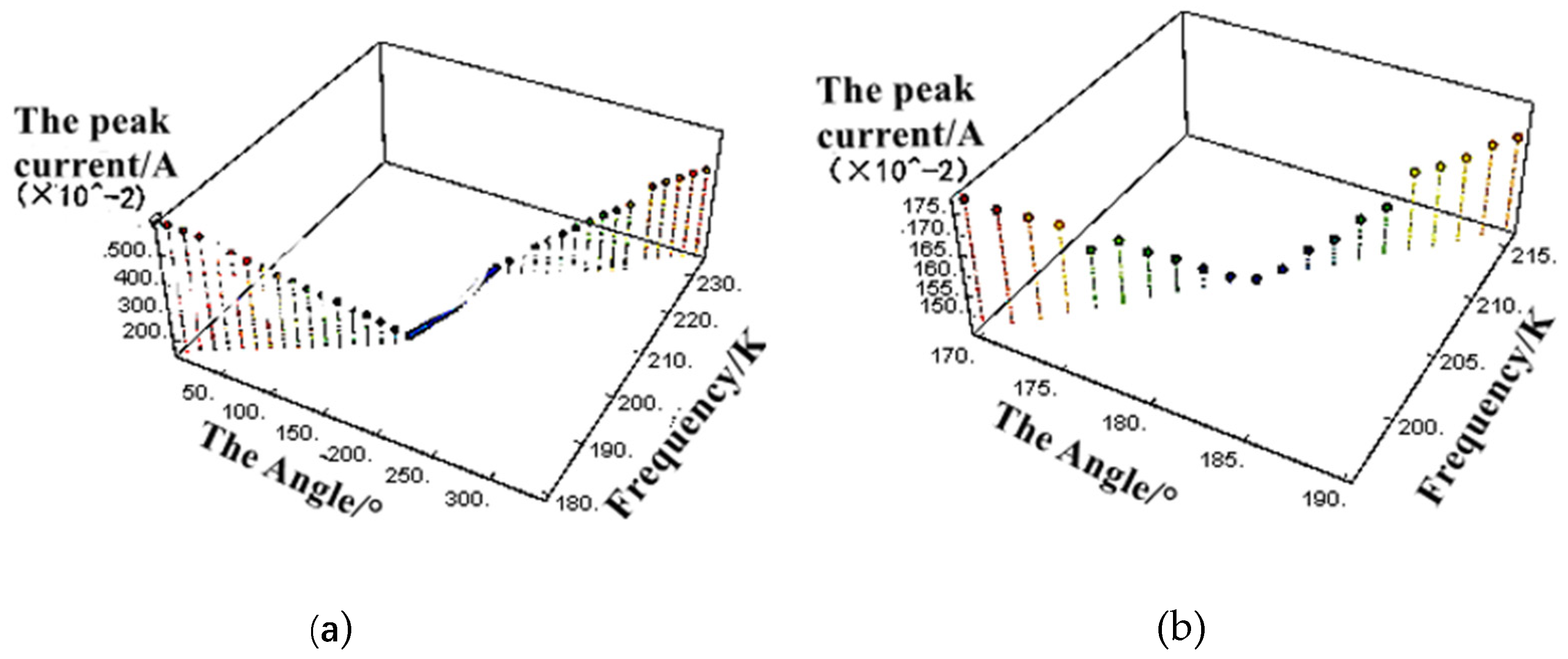
4. The Simulation Analysis
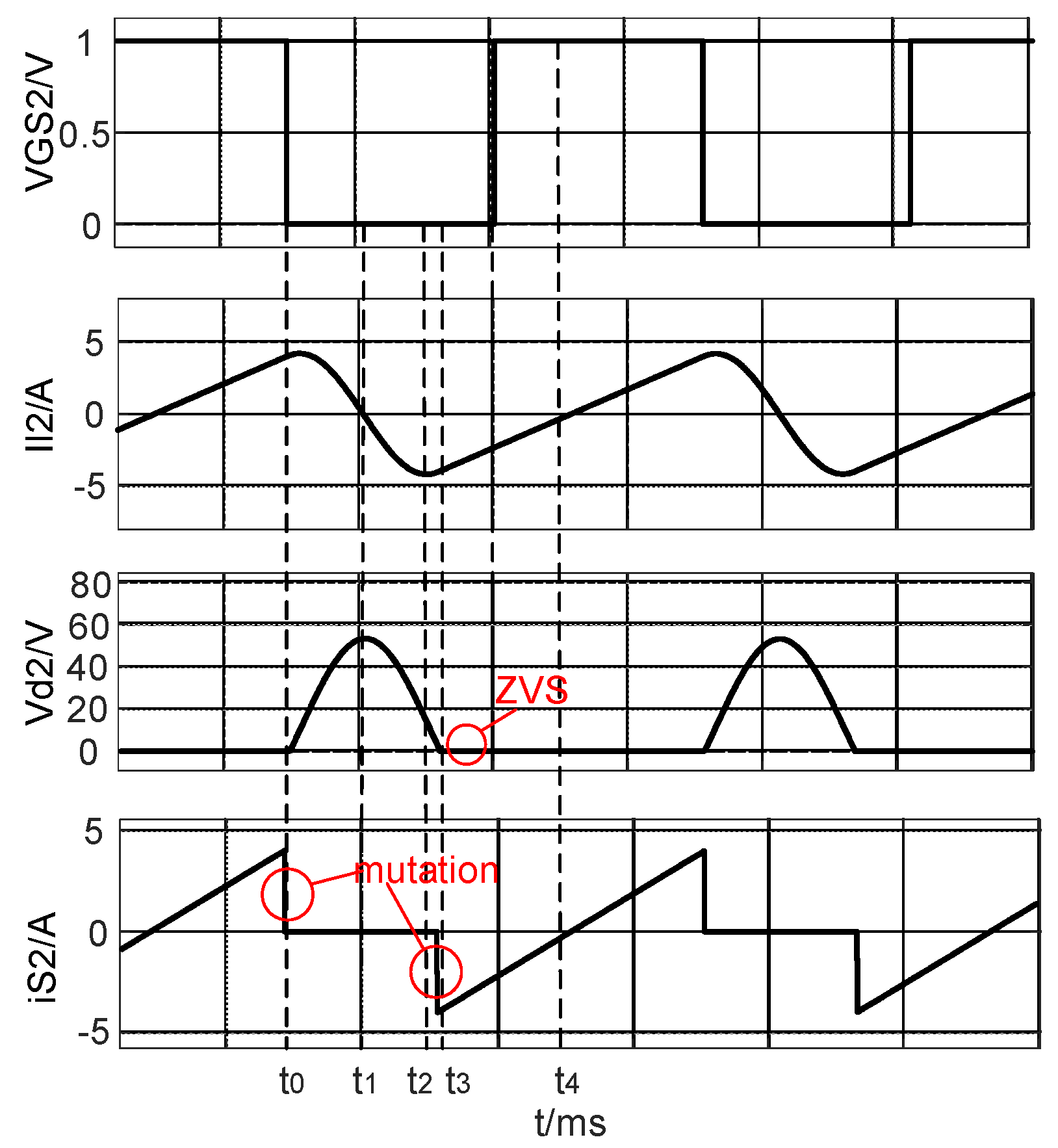
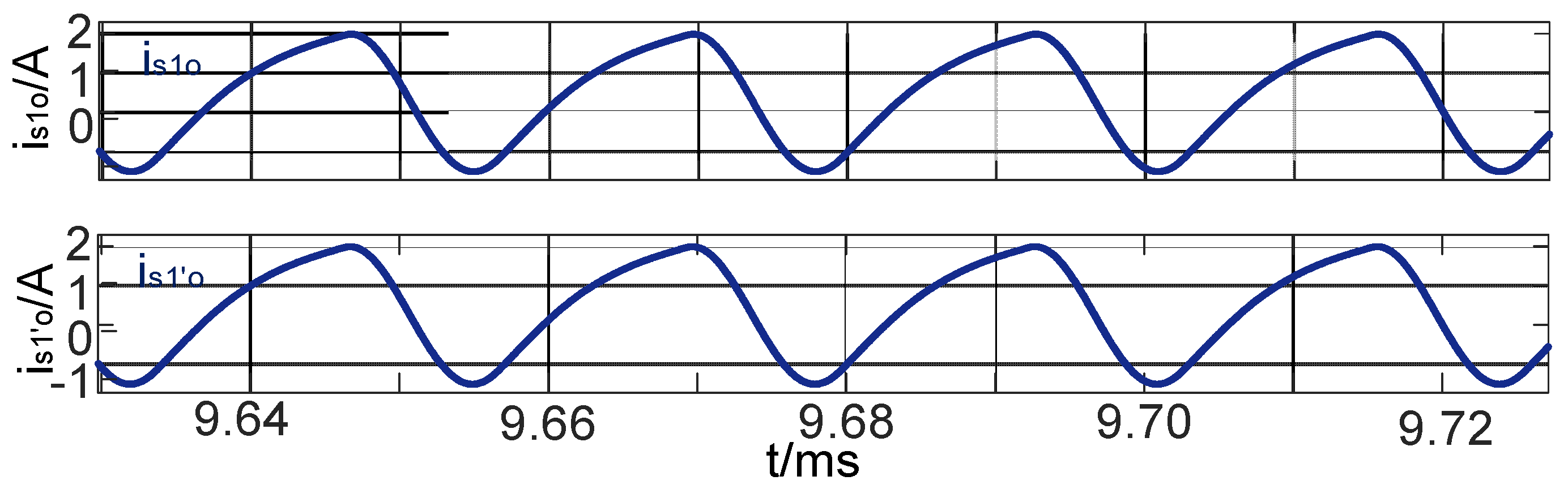
4.1. Simulation Analysis of Input Current
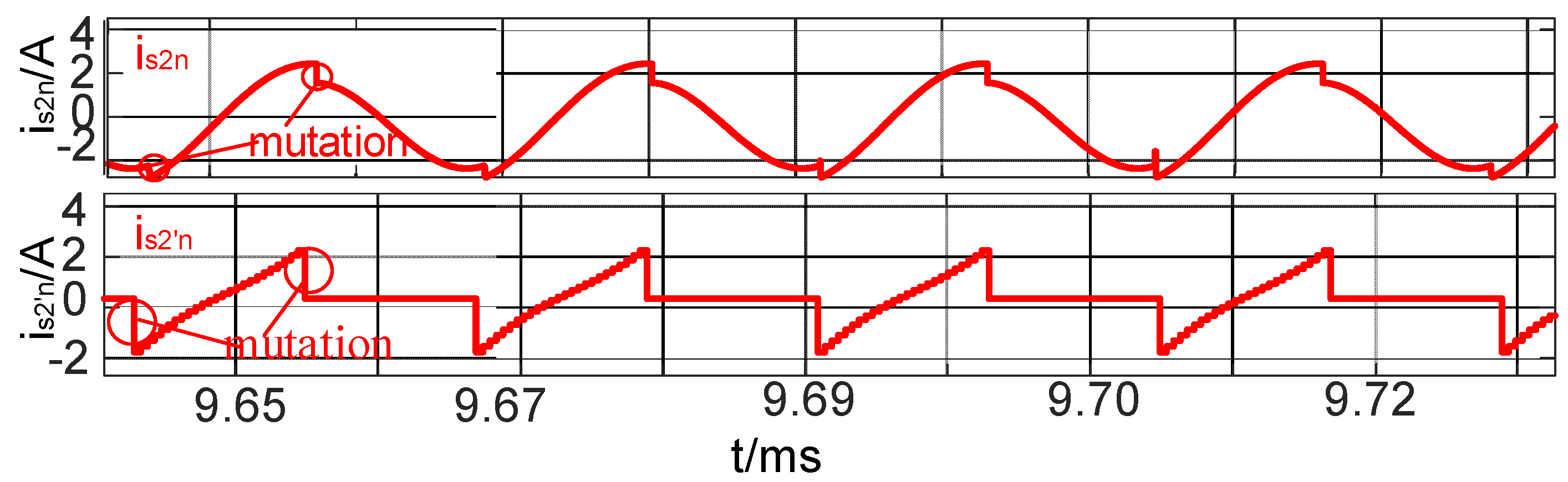
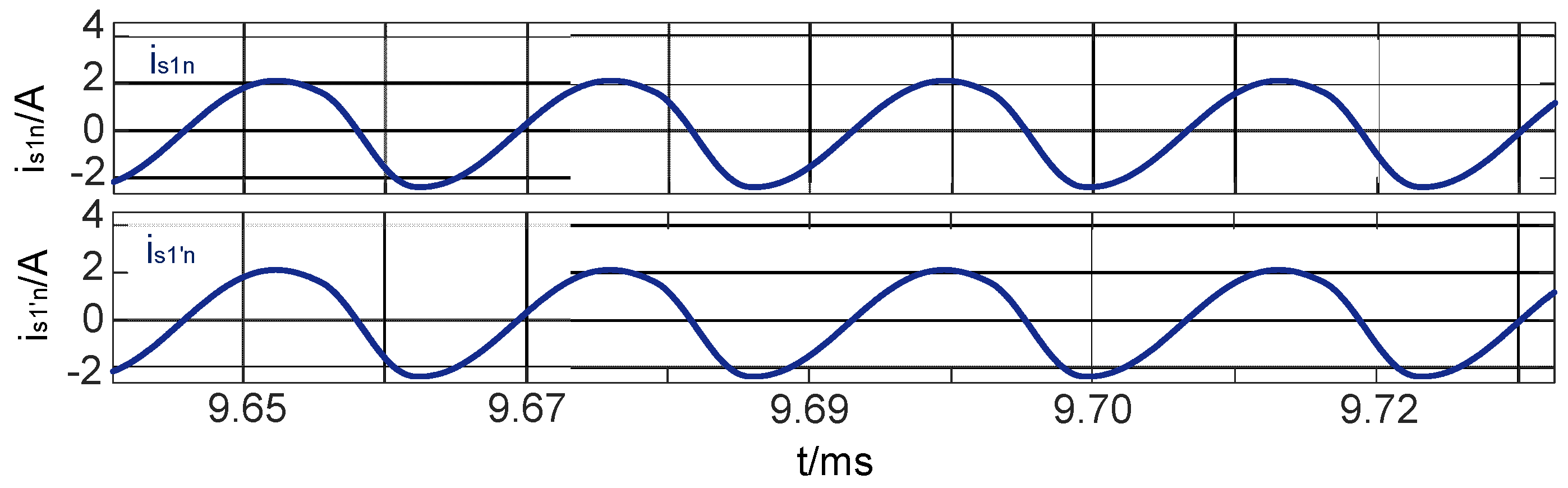
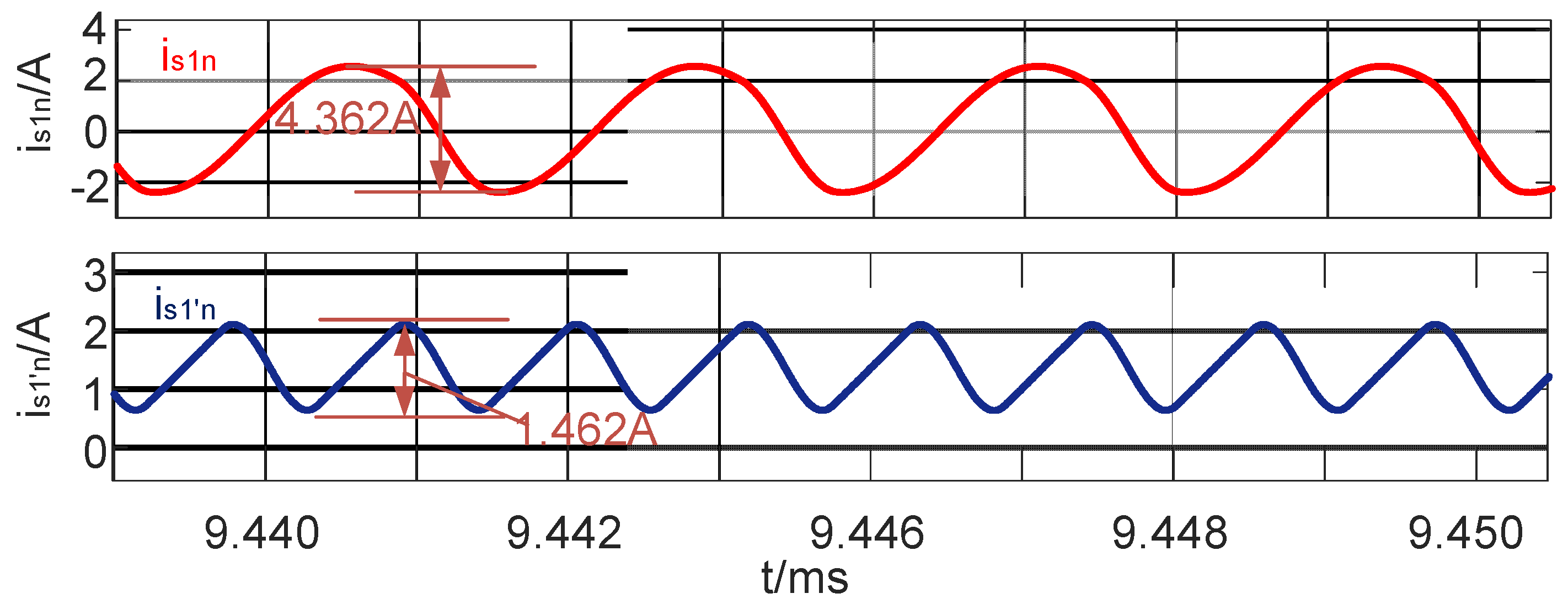
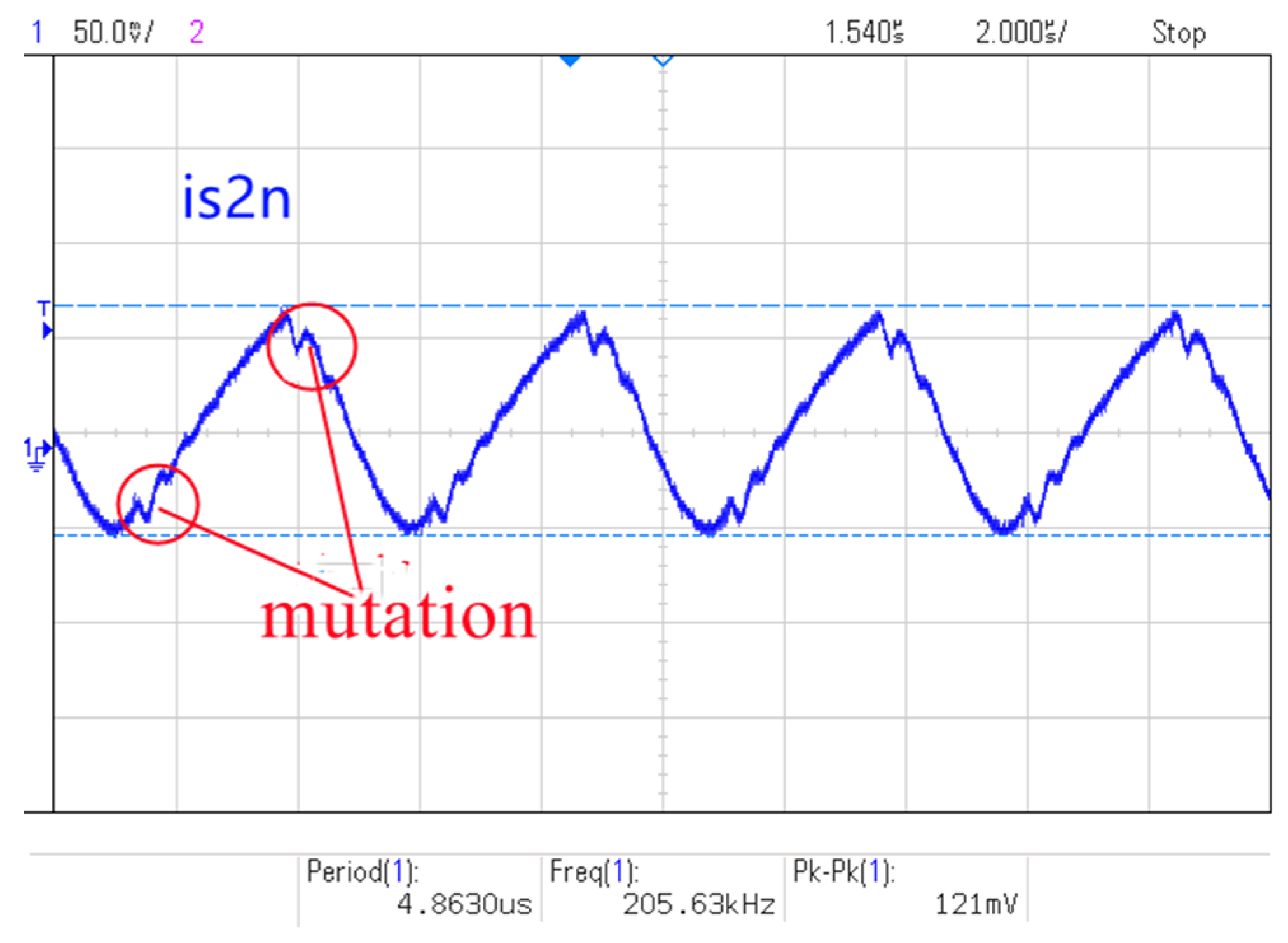
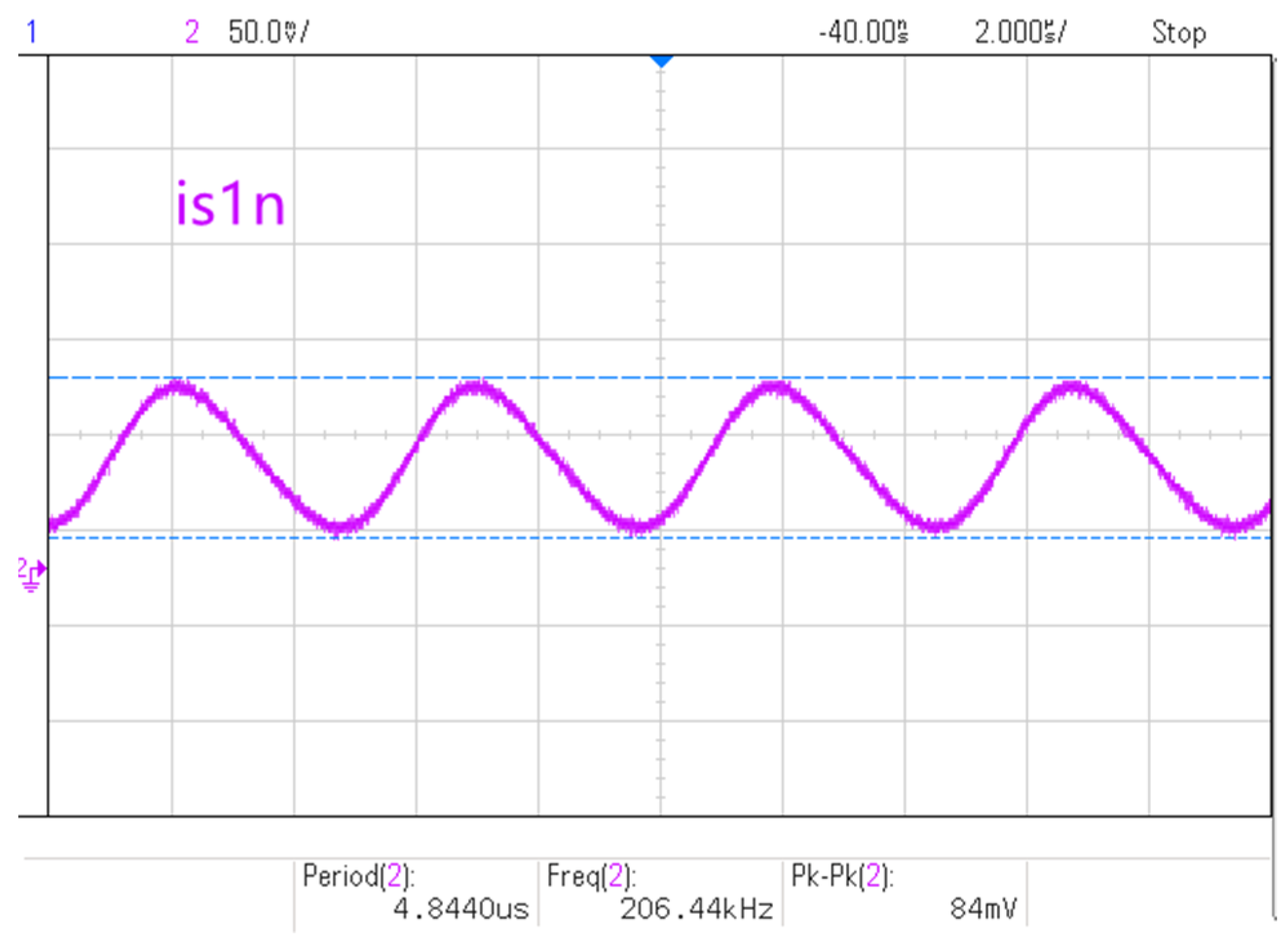
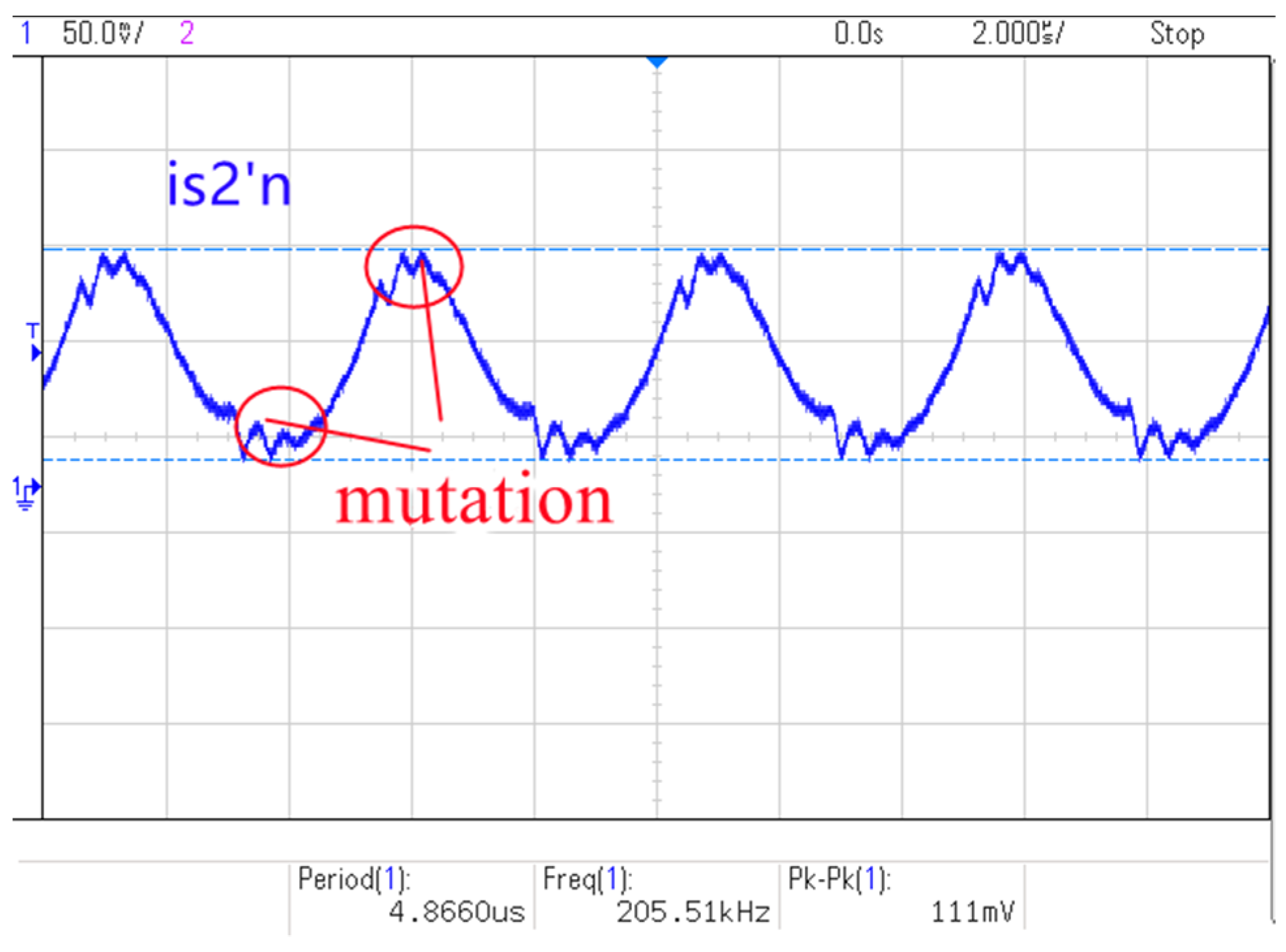
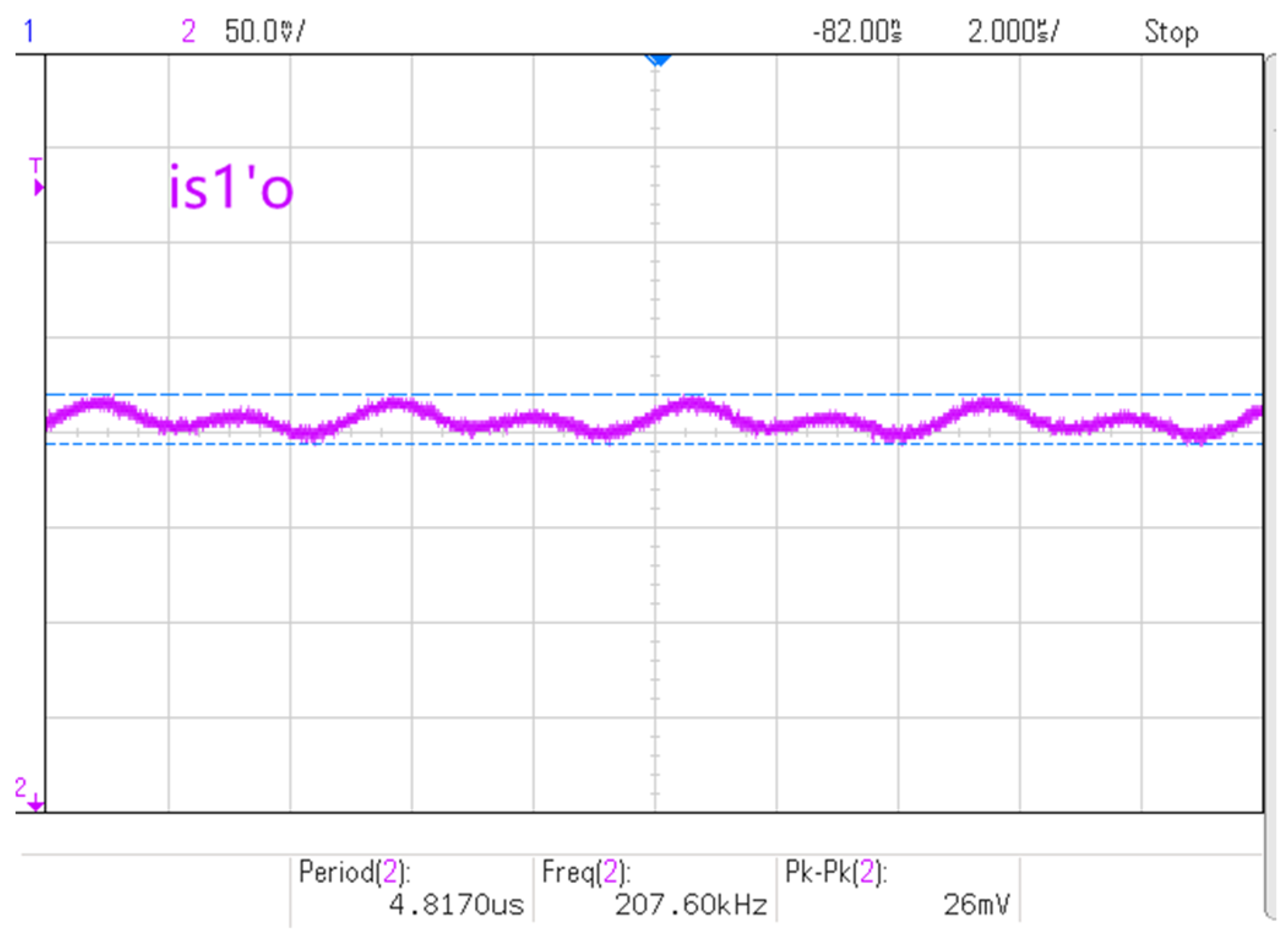
4.2. Simulation Analysis of Ripple Suppression
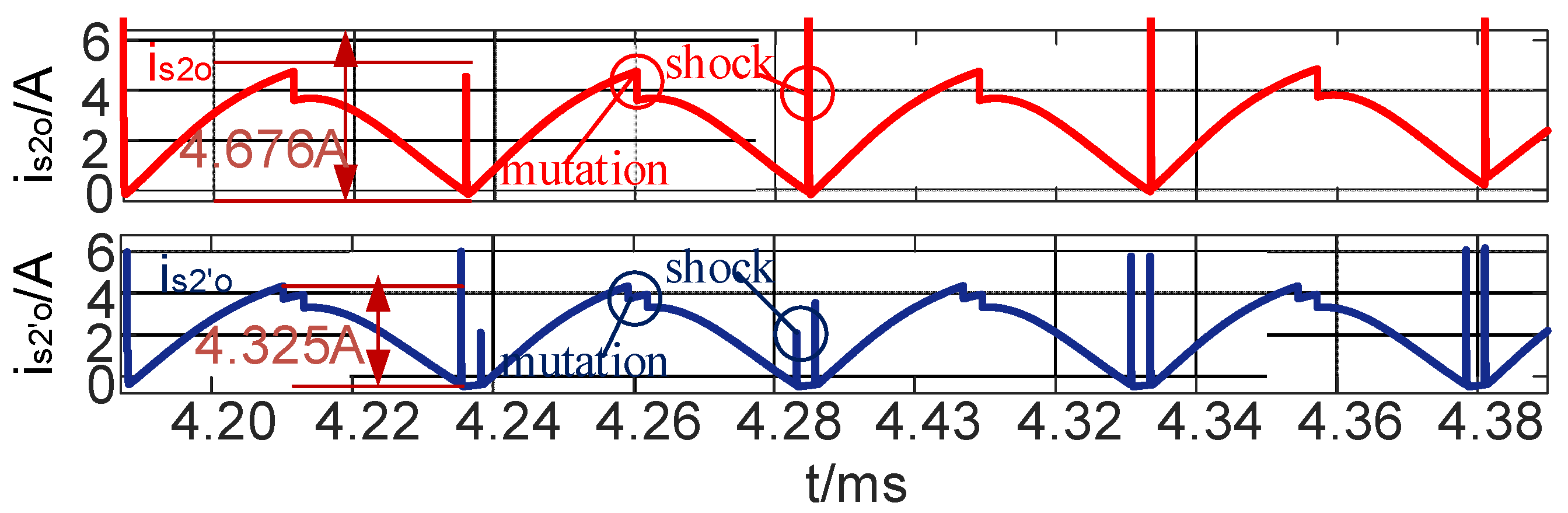
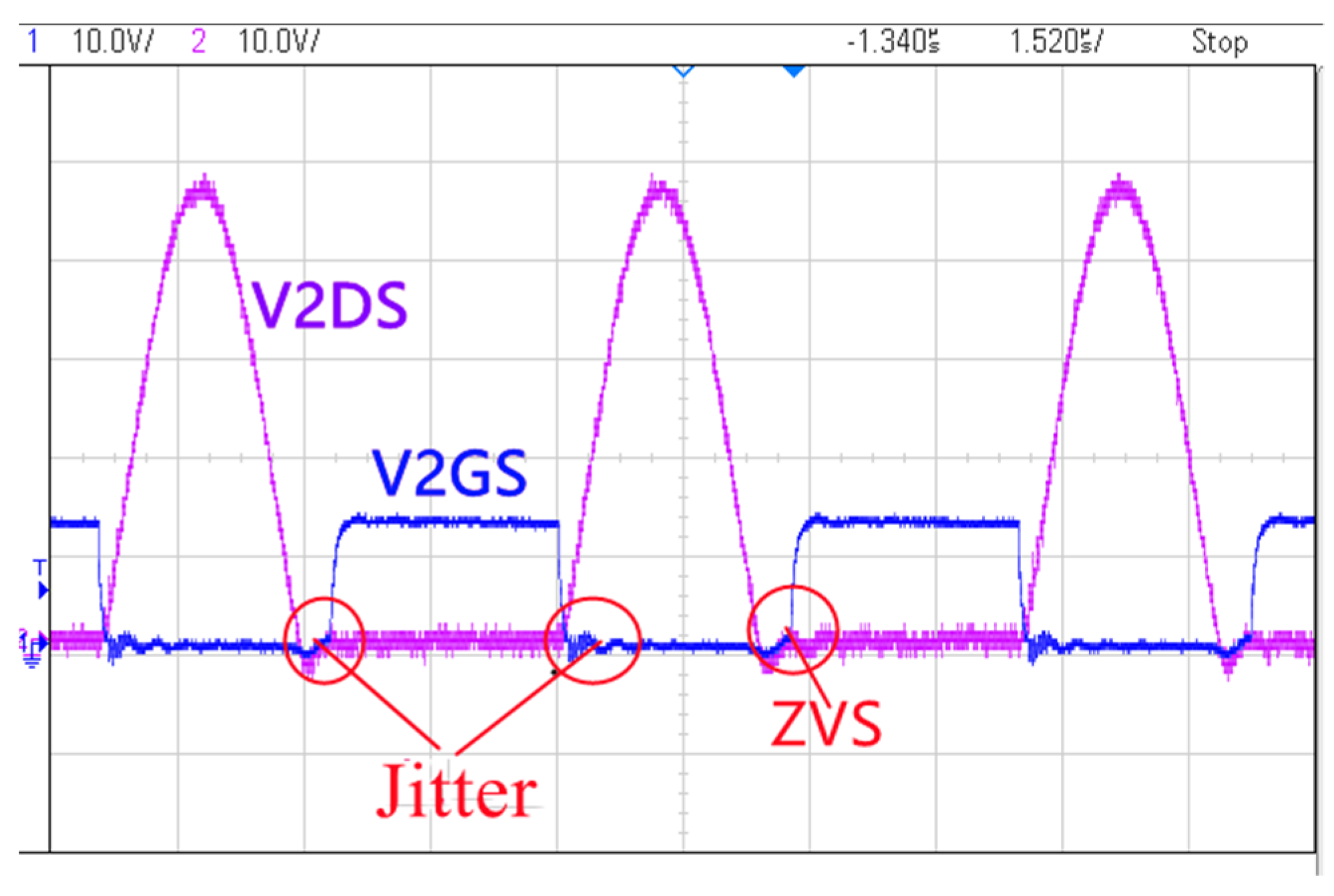
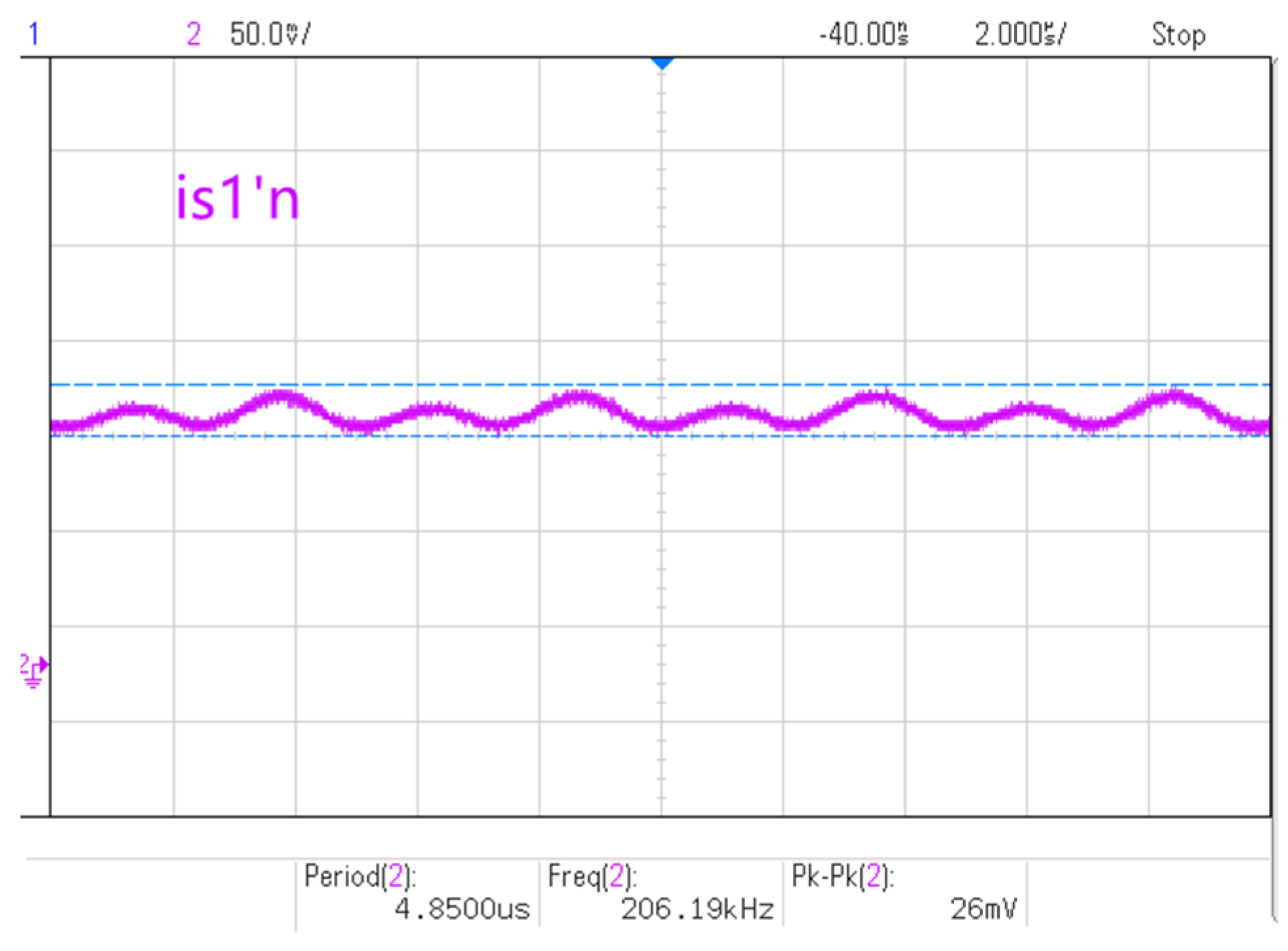
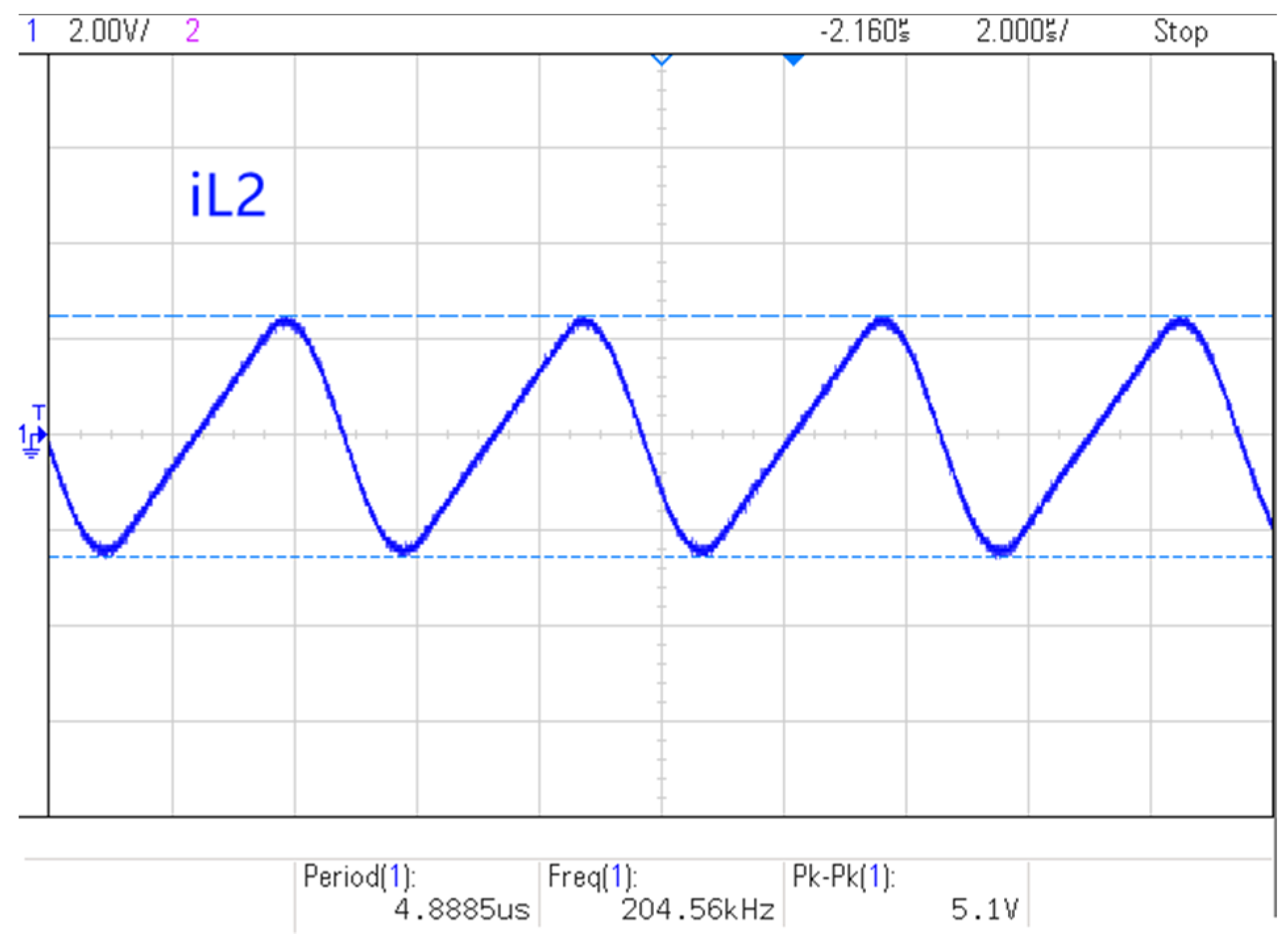
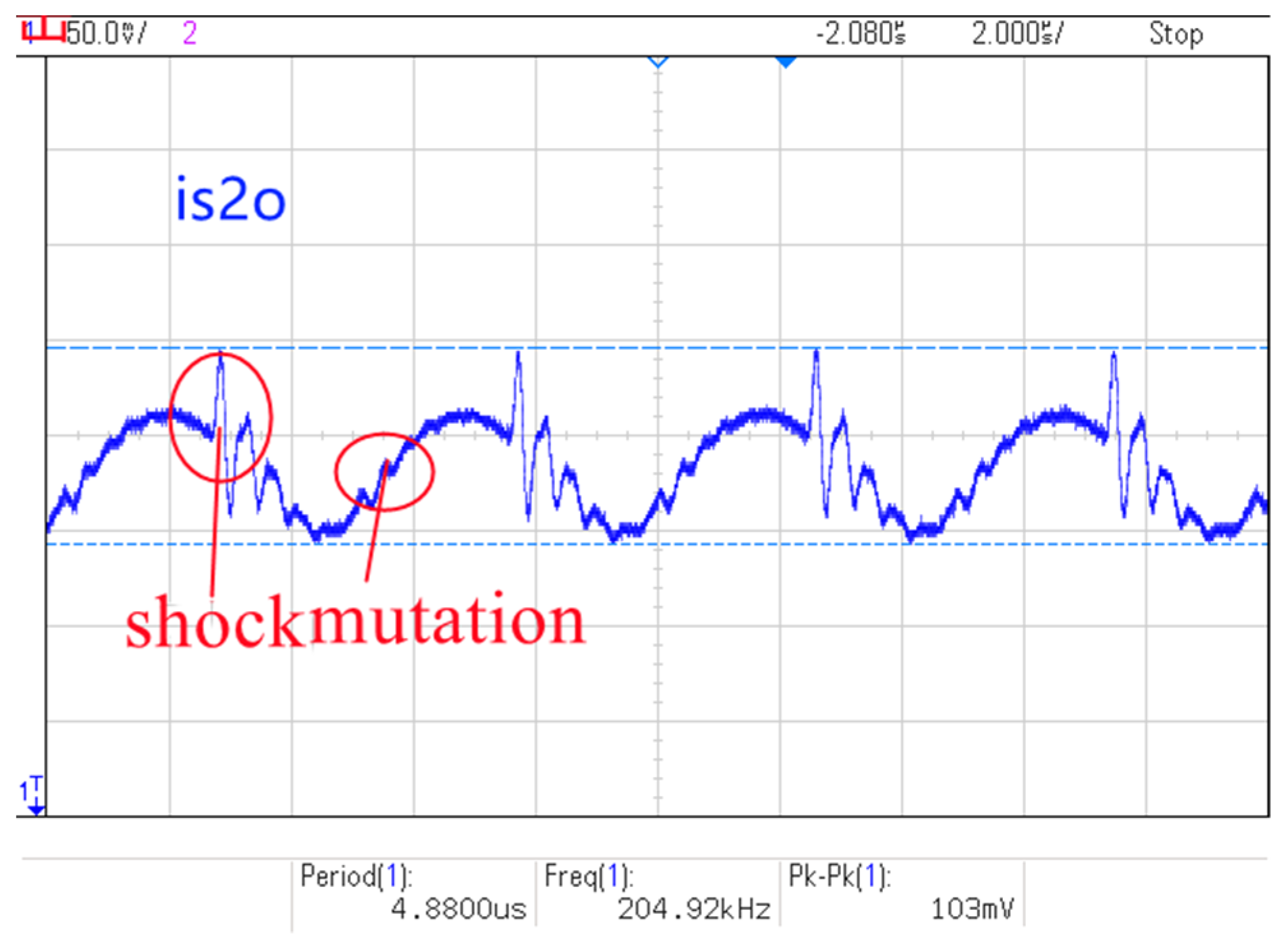
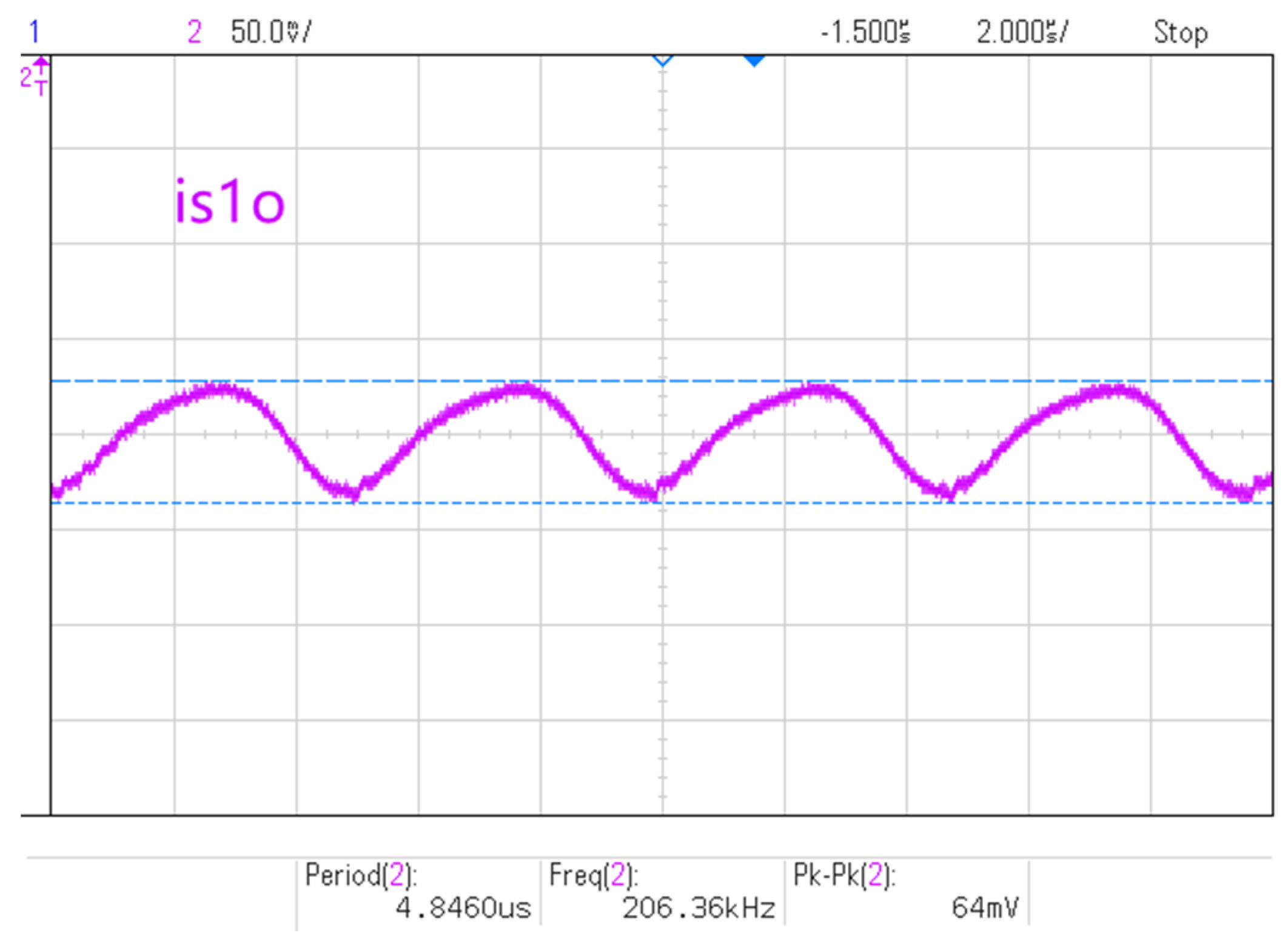
5. Experimental Verification
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yang, Y.; Wan, C.; Shen, X. Design of bidirectional DC-DC power supply software. J. Southwest Univ. (Nat. Sci. Ed.) 2017, 39, 175–180. [Google Scholar]
- Li, H.; Wang, C.; Yue, R. Research on single tube radio energy transmission circuit based on SiC device. Proc. CSEE 2020, 40, 1808–1817. [Google Scholar]
- Huang, X.; Zhao, J.; You, X. An improved interleeway control method based on input-series-output shunt phase-shifting full-bridge converters. Trans. China Electrotech. Soc. 2020, 35, 81–90. [Google Scholar]
- Sun, Y.; Liao, Z.; Ye, Z. Study on frequency splitting characteristics of MCR-WPT system based on vibration theory. Trans. China Electrotech. Soc. 2018, 33, 240–248. [Google Scholar]
- Cheng, L.; Cui, Y.; Yan, G. Research on magnetic coupled resonant radio energy transmission frequency tracking control. Power Electron. 2014, 48, 3–6. [Google Scholar]
- Li, Y.; Zhang, Y.; Yang, Q. Analysis and experimental verification of maximum power efficiency of magnetic coupled resonant radio energy transmission system. Trans. China Electrotech. Soc. 2016, 31, 18–24. [Google Scholar]
- Pan, C.; Liu, K.; Zheng, Y. Transmission characteristics of series-parallel radio energy system with mutual inductance parameters. Trans. China Electrotech. Soc. 2016, 31, 39–44. [Google Scholar]
- Li, J.; Cheng, B. Research on magnetic coupled resonance type serial radio energy transmission system. J. Shaoyang Univ. Nat. Sci. Ed. 2018, 15, 46–54. [Google Scholar]
- Pan, C.; Liu, K.; Zheng, Y. Research on the performance of electromagnetic coupled resonant radio energy transmission system. Power Electron. 2017, 51, 113–115. [Google Scholar]
- Zhou, H.; Sun, L.; Wang, S. Analysis of resonant mode of magnetically coupled resonant radio energy transmission system. Electr. Mach. Control 2016, 20, 65–73. [Google Scholar]
- Li, Y. High-efficiency class E inverter power for magnetic coupled resonant radio energy transmission system. Trans. China Electrotech. Soc. 2019, 34, 21–27. [Google Scholar]
- Wang, H.; Wang, A. Research on Relay Structure of Magnetic Coupling Resonance Wireless Power Transmission System. J. Northeast. Univ. Nat. Sci. Ed. 2016, 37, 913–917. [Google Scholar]
- Ahn, D.; Hong, S. Wireless Power Transfer Resonance Coupling Amplification by Load-Modulation Switching Controller. IEEE Trans. Ind. Electron. 2015, 62, 898–909. [Google Scholar] [CrossRef]
- Li, Z.; Wei, Z.; Xia, J. Modeling and analysis of magnetic coupled resonant radio energy transmission system. Electr. Appl. Energy Effic. Manag. Technol. 2017, 22, 12–16. [Google Scholar]
- Zhao, J.; Zhou, S.; Cui, Y. Research and implementation of design method of LCL magnet-coupled resonant radio energy transmission system. High Volt. Eng. 2019, 45, 234–241. [Google Scholar]
- Zhao, J.; Zhou, S.; Cui, Y. Study on stability of magnetic coupled resonant serial radio energy transmission power. Adv. Technol. Electr. Eng. Energy 2018, 37, 20–29. [Google Scholar]
- Cheng, Z.; Lei, Y.; Song, K. Design and loss analysis of loosely coupled transformer for an underwater high-power inductive power transfer system. IEEE Trans. Magn. 2015, 51, 8401110. [Google Scholar]
- McDonough, M. Integration of inductively coupled power transfer and hybrid energy storage system: A multiport power electronics interface for battery-powered electric vehicles. IEEE Trans. Power Electron. 2015, 30, 6423–6433. [Google Scholar] [CrossRef]
- Lee, S.Y.; Hsieh, C.H.; Yang, C.M. Wireless front-end with power management for an implantable cardiac microstimulator. IEEE Trans. Biomed. Circuits Syst. 2012, 6, 28–38. [Google Scholar]
- Cai, H.; Shi, L.; Li, Y. Harmonic-based phase shifted control of inductively coupled power transfer. IEEE Trans. Power Electron. 2014, 29, 594–602. [Google Scholar] [CrossRef]
- Gonzalez, J.; Alatise, O.; Hu, J. An investigation of temperature-sensitive electrical parameters for SiC power MOSFETs. IEEE Trans. Power Electron. 2017, 32, 7954–7966. [Google Scholar] [CrossRef] [Green Version]
- Chen, K.; Zhao, Z.; Yuan, L. The impact of nonlinear junction capacitance on switching transient and its modeling for SiC MOSFET. IEEE Trans. Electron Devices 2015, 62, 333–338. [Google Scholar] [CrossRef]











| Mode | Separate Topological Transmitter | Traditional Topological Transmitter |
|---|---|---|
| Stage 1 | iL1 increases linearly when the switch is on. | Switch tube continuation diode conduction. |
| Stage 2 | When the switch is off, iL1 decreases and C1 accumulates charge. | When the switch is on, iL2 increases linearly. |
| Stage 3 | The switch is closed and the capacitor charges the inductance. | The switch tube closes and the inductance and capacitor enter the resonant state. |
| Stage 4 | The switch tube is turned on with zero voltage, and the inductance current is continued through the continuing diode, which is reduced to zero, and stage 1 is repeated. | The inductance charges the capacitor in reverse, and the voltage withstand of the switch reaches its maximum. |
| Stage 5 | Capacitor discharges, voltage resistance of switch tube is reduced. | |
| Stage 6 | The inductance charges the capacitor, the voltage drop of the switch is zero, and the continuation secondary leads on. | |
| Stage 7 | The switch tube realizes zero voltage conduction. |
| Parameter Name | Parameter Value |
|---|---|
| Switching frequency | 206 kHz |
| Receiving/Transmitting resonant inductance | 7 µH |
| The receiver compensates the capacitance | 0.094 µF |
| load | 15 Ω |
| The coupling coefficient | 0.3 |
| Input Current/A | Output Voltage/V | Output Current/A | Transmission Efficiency/% | |
|---|---|---|---|---|
| Traditional PP system | 1.05 | 5.25 | 2.01 | 83.75 |
| IDC PP-type system | 1.03 | 5.21 | 2.02 | 85.15 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; Zhang, X.; Luo, L.; Xie, S.; Zhou, Q. Research on High Power Factor Single Tube Variable Structure Wireless Power Transmission. World Electr. Veh. J. 2021, 12, 214. https://doi.org/10.3390/wevj12040214
Yang Y, Zhang X, Luo L, Xie S, Zhou Q. Research on High Power Factor Single Tube Variable Structure Wireless Power Transmission. World Electric Vehicle Journal. 2021; 12(4):214. https://doi.org/10.3390/wevj12040214
Chicago/Turabian StyleYang, Yi, Xuejian Zhang, Lei Luo, Shiyun Xie, and Qingshan Zhou. 2021. "Research on High Power Factor Single Tube Variable Structure Wireless Power Transmission" World Electric Vehicle Journal 12, no. 4: 214. https://doi.org/10.3390/wevj12040214
APA StyleYang, Y., Zhang, X., Luo, L., Xie, S., & Zhou, Q. (2021). Research on High Power Factor Single Tube Variable Structure Wireless Power Transmission. World Electric Vehicle Journal, 12(4), 214. https://doi.org/10.3390/wevj12040214







