Modeling and Fuzzy Feedforward Control of Fuel Cell Air Supply System
Abstract
:1. Introduction
2. Materials and Methods
2.1. PEMFC Air Supply System Model
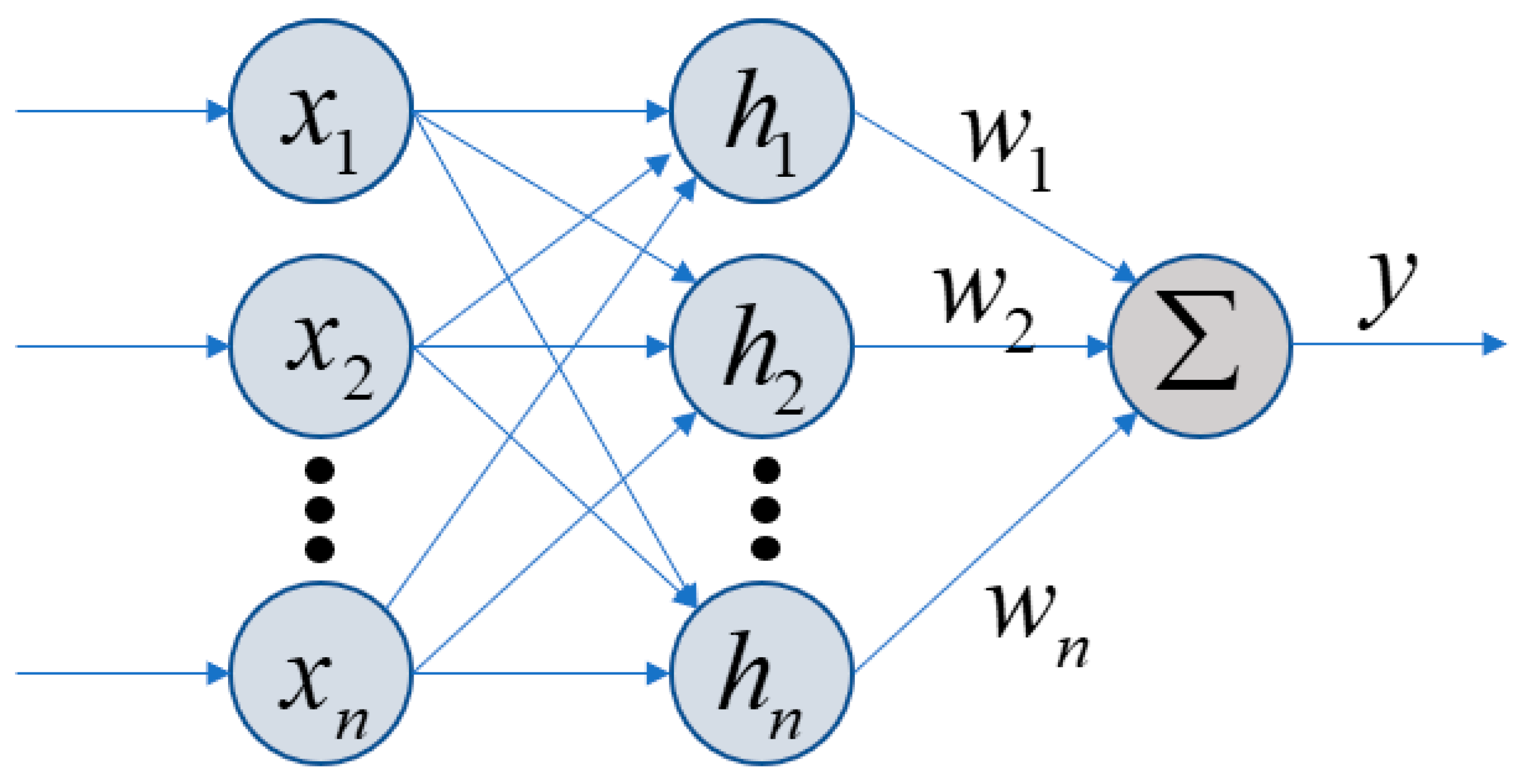
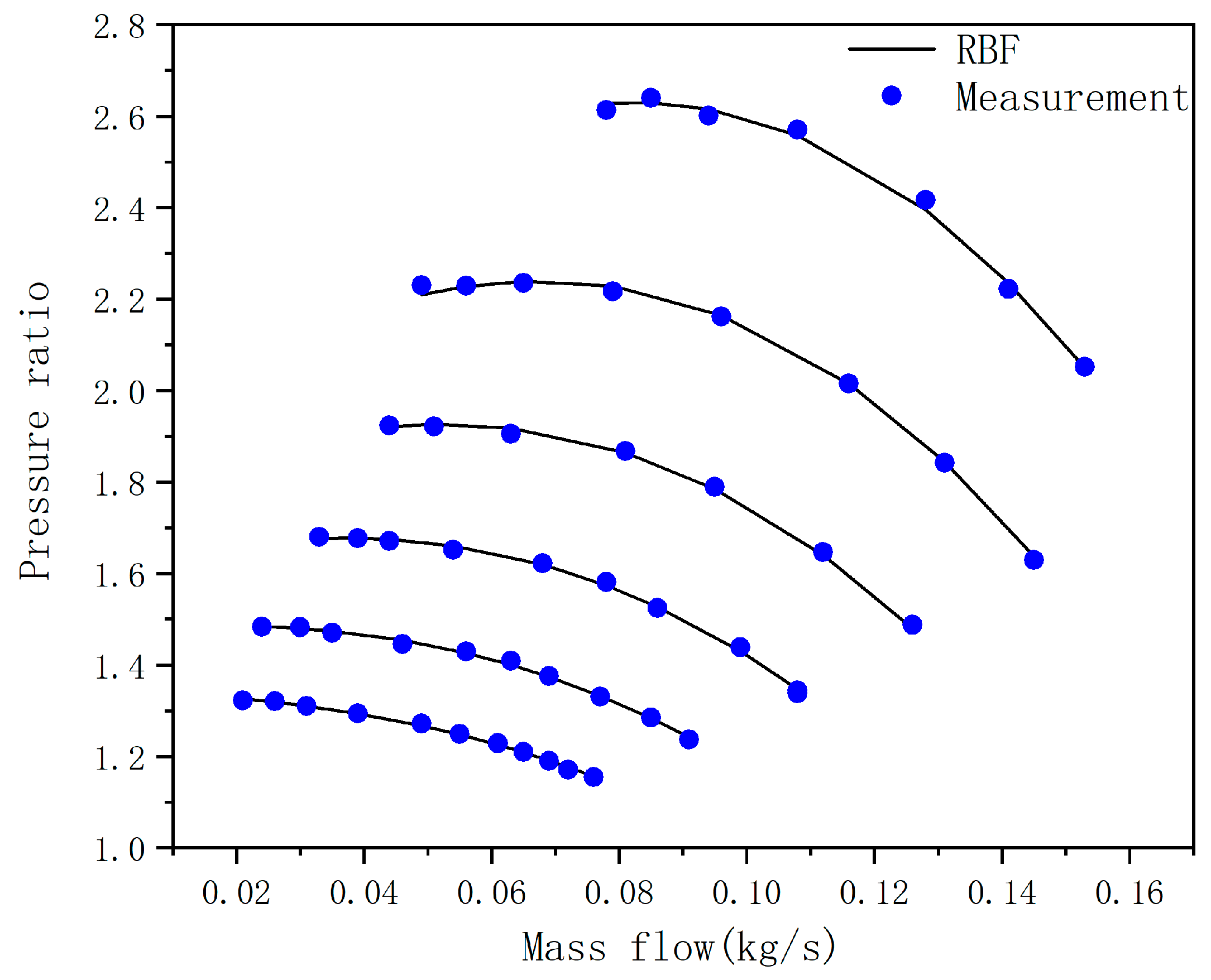
2.1.1. Compressor Model
2.1.2. Pipeline and Cathode Modeling
2.1.3. Intercooler and Humidifier Modeling
2.1.4. Out Flow Modeling
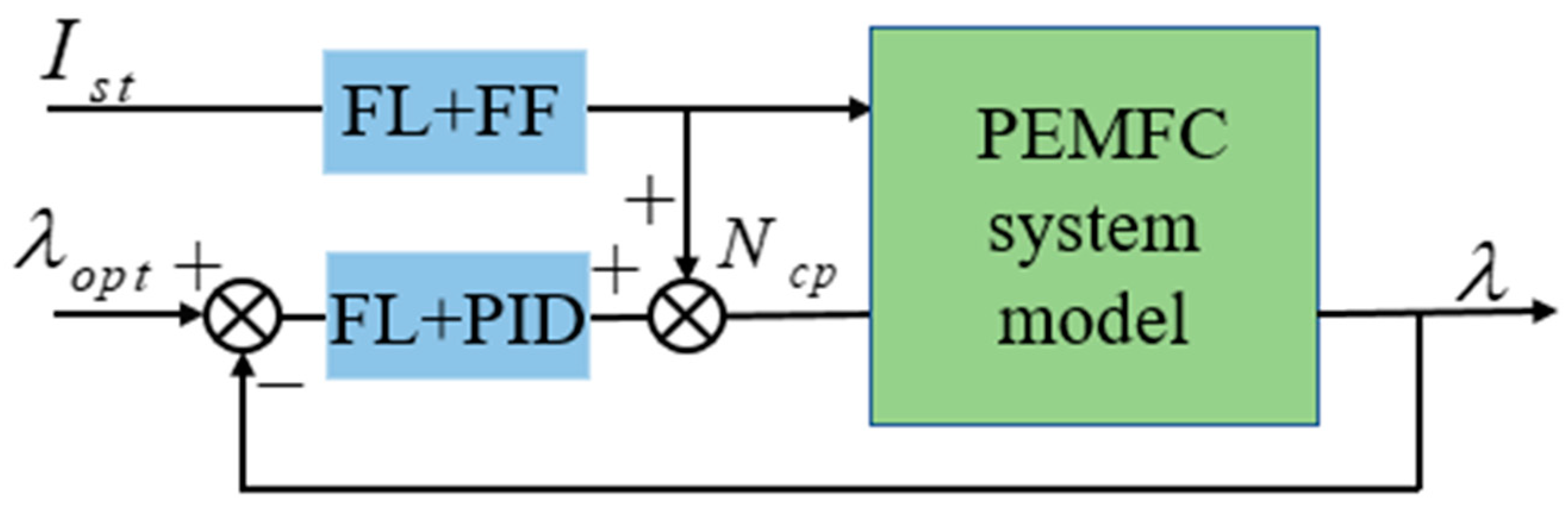
2.2. Four Different Control Strategies
2.2.1. PID Controller
2.2.2. Feedforward plus PID Controller (FF + PID)
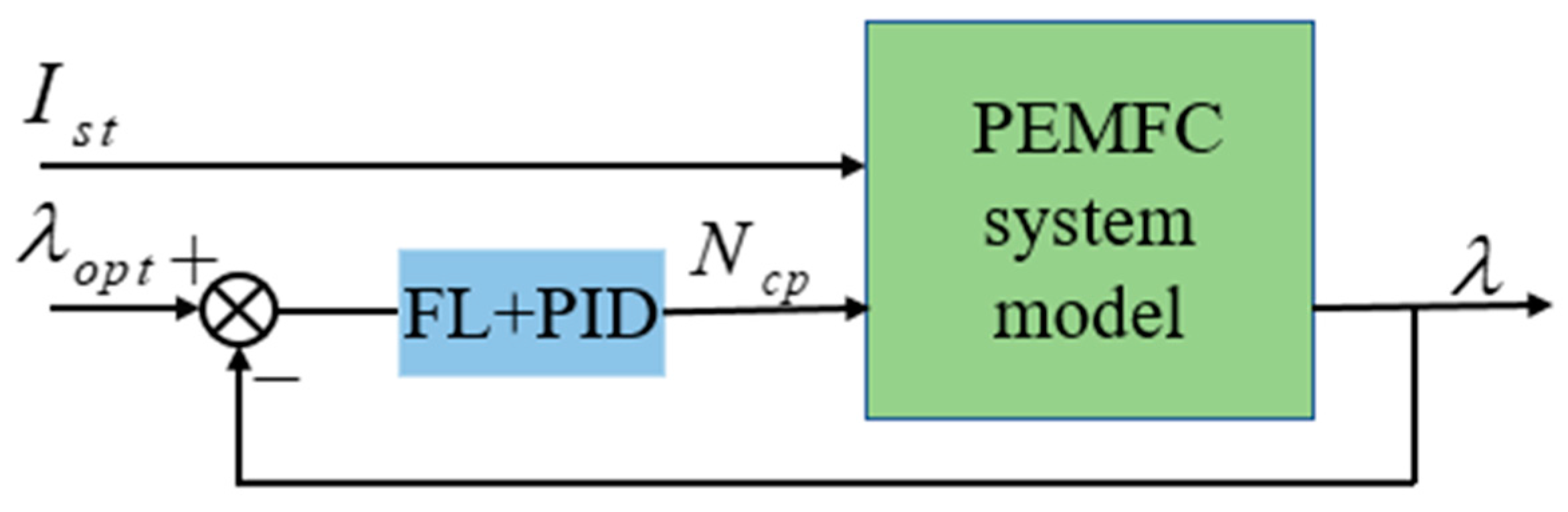
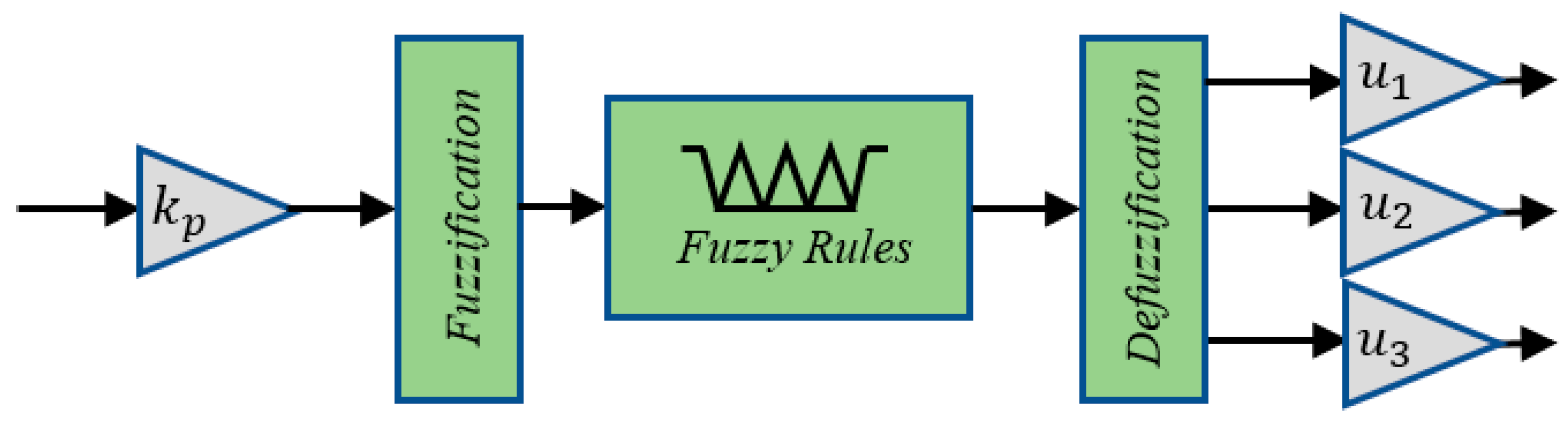
2.2.3. Fuzzy PID Control (FL + PID)
2.2.4. Fuzzy Feedforward plus Fuzzy PID (FF + FLPID)
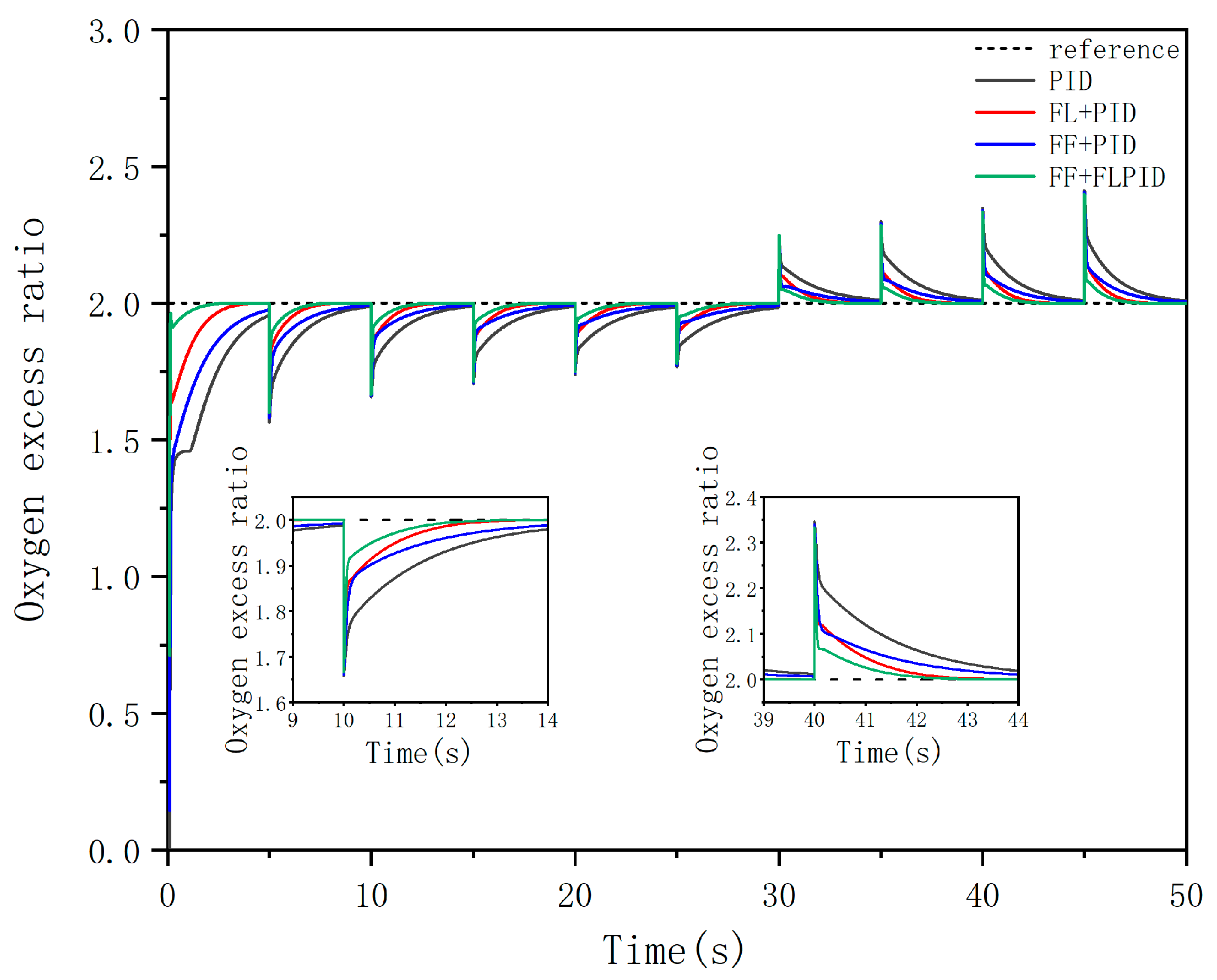
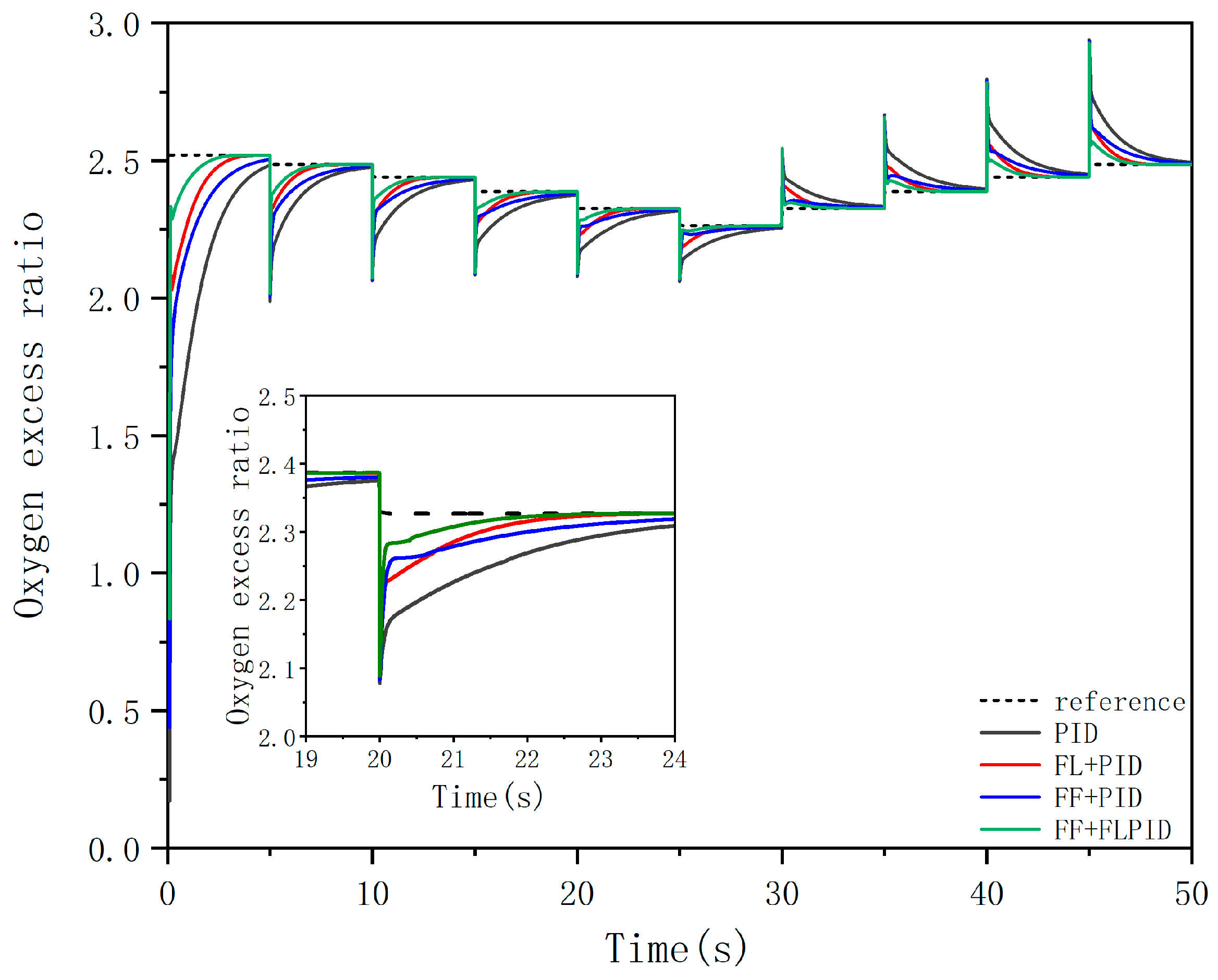
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pukrushpan, J.T.; Stefanopoulou, A.G.; Peng, H. Control of fuel cell breathing. Control Syst. IEEE 2004, 24, 30–46. [Google Scholar]
- Moraal, P.; Kolmanovsky, I. Turbocharger Modeling for Automotive Control Applications. SAE Techn. Pap. Ser. 1999, 108, 1324–1338. [Google Scholar] [CrossRef]
- Sankar, K.; Jana, A.K. Nonlinear multivariable sliding mode control of a reversible PEM fuel cell integrated system. Energy Convers. Manag. 2018, 171, 541–565. [Google Scholar] [CrossRef]
- Baroud, Z.; Benmiloud, M.; Benalia, A.; Ocampo-Martinez, C. Novel hybrid fuzzy-PID control scheme for air supply in PEM fuel-cell-based systems. Int. J. Hydrogen Energy 2017, 42, 10435–10447. [Google Scholar] [CrossRef] [Green Version]
- Danzer, M.A.; Wilhelm, J.; Aschemann, H.; Hofer, E.P. Model-based control of cathode pressure and oxygen excess ratio of a PEM fuel cell system. J. Power Sources 2008, 176, 515–522. [Google Scholar] [CrossRef]
- Qi, Y.; Espinoza-Andaluz, M.; Thern, M.; Li, T.; Andersson, M. Dynamic modelling and controlling strategy of polymer electrolyte fuel cells. Int. J. Hydrogen Energy 2020, 45, 29718–29729. [Google Scholar] [CrossRef]
- Gruber, J.; Doll, M.; Bordons, C. Design and experimental validation of a constrained MPC for the air feed of a fuel cell. Control. Eng. Pract. 2009, 17, 874–885. [Google Scholar] [CrossRef]
- Matraji, I.; Laghrouche, S.; Jemei, S.; Wack, M. Robust control of the PEM fuel cell air-feed system via sub-optimal second order sliding mode. Appl. Energy 2013, 104, 945–957. [Google Scholar] [CrossRef]
- Talj, R.; Ortega, R.; Astolfi, A. Passivity and robust PI control of the air supply system of a PEM fuel cell model. Automatica 2011, 47, 2554–2561. [Google Scholar] [CrossRef]
- Wang, F.; Ouyang, Q.; Chen, J.; Su, H. Feedback Linearization Control of the Air Supply System of PEM Fuel Cells. In Proceedings of the 2015 10th Asian Control Conference (ASCC), Kota Kinabalu, Malaysia, 31 May–3 June 2015; Institute of Electrical and Electronics Engineers (IEEE): Manhattan, NY, USA, 2015; pp. 1–6. [Google Scholar]
- Ou, K.; Wang, Y.-X.; Li, Z.-Z.; Shen, Y.-D.; Xuan, D.-J. Feedforward fuzzy-PID control for air flow regulation of PEM fuel cell system. Int. J. Hydrogen Energy 2015, 40, 11686–11695. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, Y.; Wang, D. Adaptive robust control of oxygen excess ratio for PEMFC system based on type-2 fuzzy logic Scheme. Inf. Sci. 2020, 511, 1–17. [Google Scholar] [CrossRef]







| e | |||
|---|---|---|---|
| NB | VL | L | S |
| NS | L | M | L |
| Z | S | S | M |
| PS | L | M | L |
| PB | VL | L | S |
| Controllers | Overshoot (%) | Settling Time (%5) (s) |
|---|---|---|
| PID | 17.5 | 2.51 |
| FL + PID | 17 | 1.08 |
| FF + PID | 17 | 1.63 |
| FF + FLPID | 16 | 0.65 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, J.; Zhang, B.; Mao, H.; Xu, S. Modeling and Fuzzy Feedforward Control of Fuel Cell Air Supply System. World Electr. Veh. J. 2021, 12, 181. https://doi.org/10.3390/wevj12040181
Cheng J, Zhang B, Mao H, Xu S. Modeling and Fuzzy Feedforward Control of Fuel Cell Air Supply System. World Electric Vehicle Journal. 2021; 12(4):181. https://doi.org/10.3390/wevj12040181
Chicago/Turabian StyleCheng, Jun, Baitao Zhang, Haoyu Mao, and Sichuan Xu. 2021. "Modeling and Fuzzy Feedforward Control of Fuel Cell Air Supply System" World Electric Vehicle Journal 12, no. 4: 181. https://doi.org/10.3390/wevj12040181
APA StyleCheng, J., Zhang, B., Mao, H., & Xu, S. (2021). Modeling and Fuzzy Feedforward Control of Fuel Cell Air Supply System. World Electric Vehicle Journal, 12(4), 181. https://doi.org/10.3390/wevj12040181






