A Simple Approach to Dynamic Optimisation of Flexible Optical Networks with Practical Application
Abstract
:1. Introduction and Background
2. Related Problems
- Instead, we require a dynamic, computationally-inexpensive solution to the problem, which can be implemented in real-time in response to changing traffic patterns.
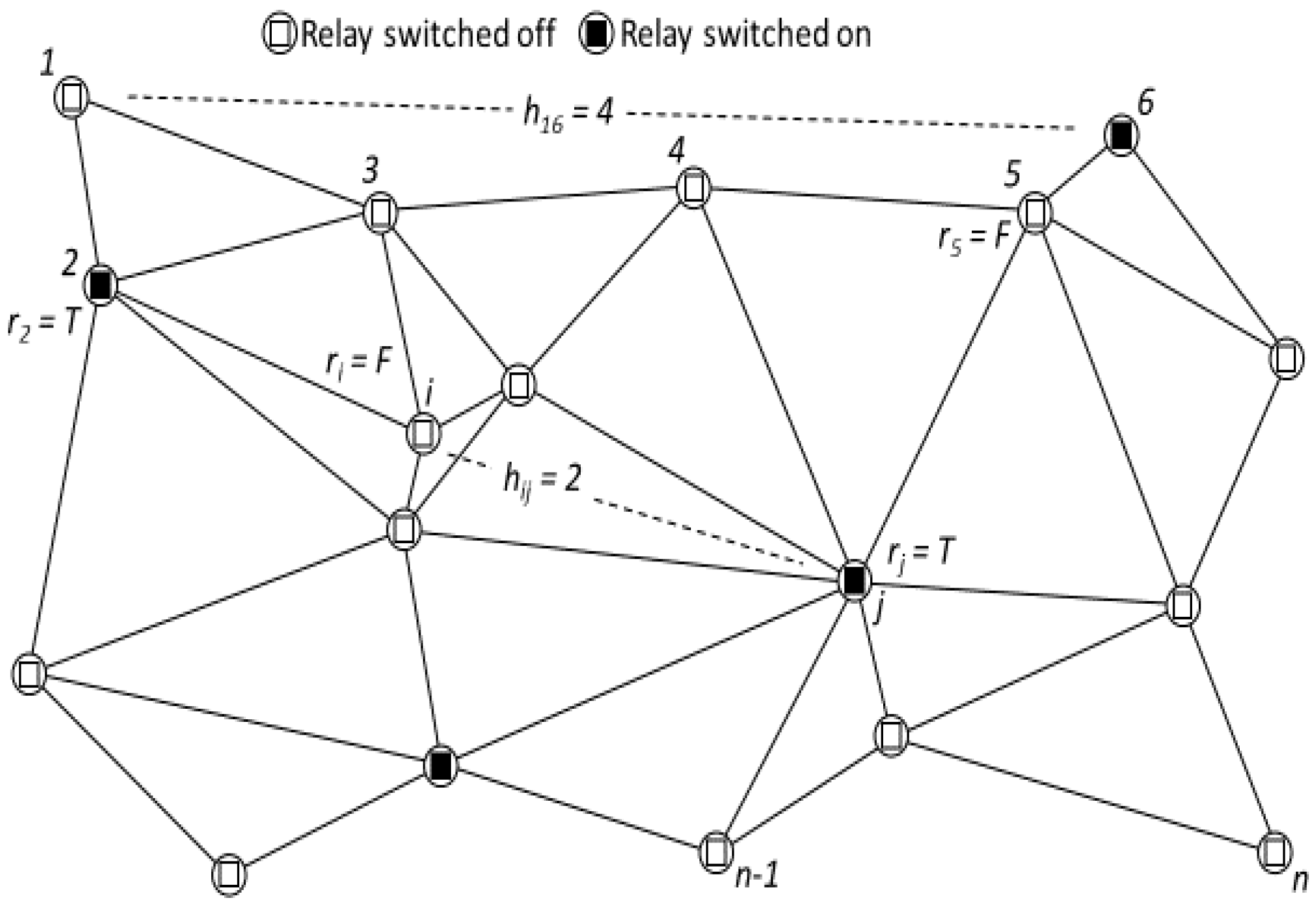
3. Formulation of the Problem
DRP-FON: Minimise C(r) [objective function] s.t. m [constraint]
4. Related Algorithms
5. A Fast Heuristic Solution
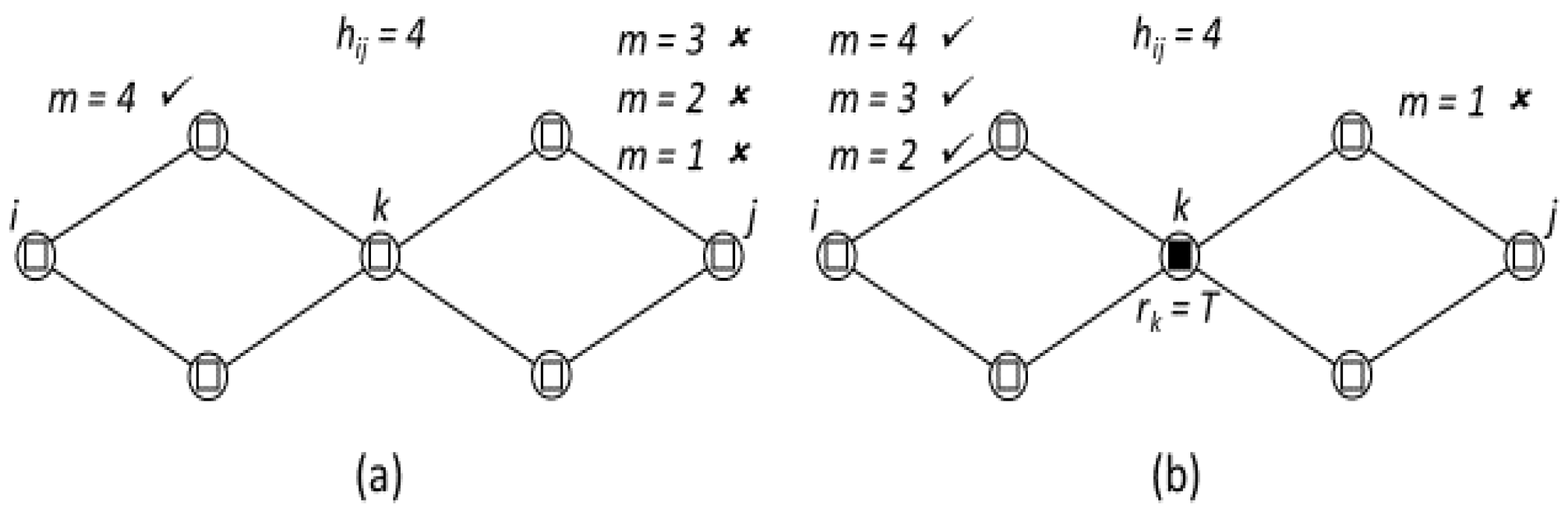
AlgH (Calculate the hop matrix): ∀ ij, run DSPA to calculate H = (hij)
AlgV (Calculate the viability matrix): ∀ ij, set vij = T if (hij ≤ m) ∨ (∃ k … l, … s.t. (rk ∧ … ∧ rl = T) ∧ (hik ≤ m ∧ … ∧ hlj ≤ m)); vij = F otherwise
A certificate for DRP-FON can be verified in polynomial time by the following algorithm:
run AlgH
run AlgV
if vij = T ∀ ij then
certificate valid
else
certificate invalid
AlgR (Optimise the relay array): // DRP-FON-heuristic setrk = F ∀ k // All relays switched off run AlgH // Calculate hop lengths run AlgV // Calculate viable paths while ∃ ij s.t. vij = F do // if more relays needed { find k s.t. |{i: (vik = T) ∧ (ri = F)}| // Find relay that ≥ |{ i: (vij = T) ∧ (ri = F)}| ∀ j // … reaches most nodes setrk = T // Power this new relay run AlgV } // Recalculate viable paths
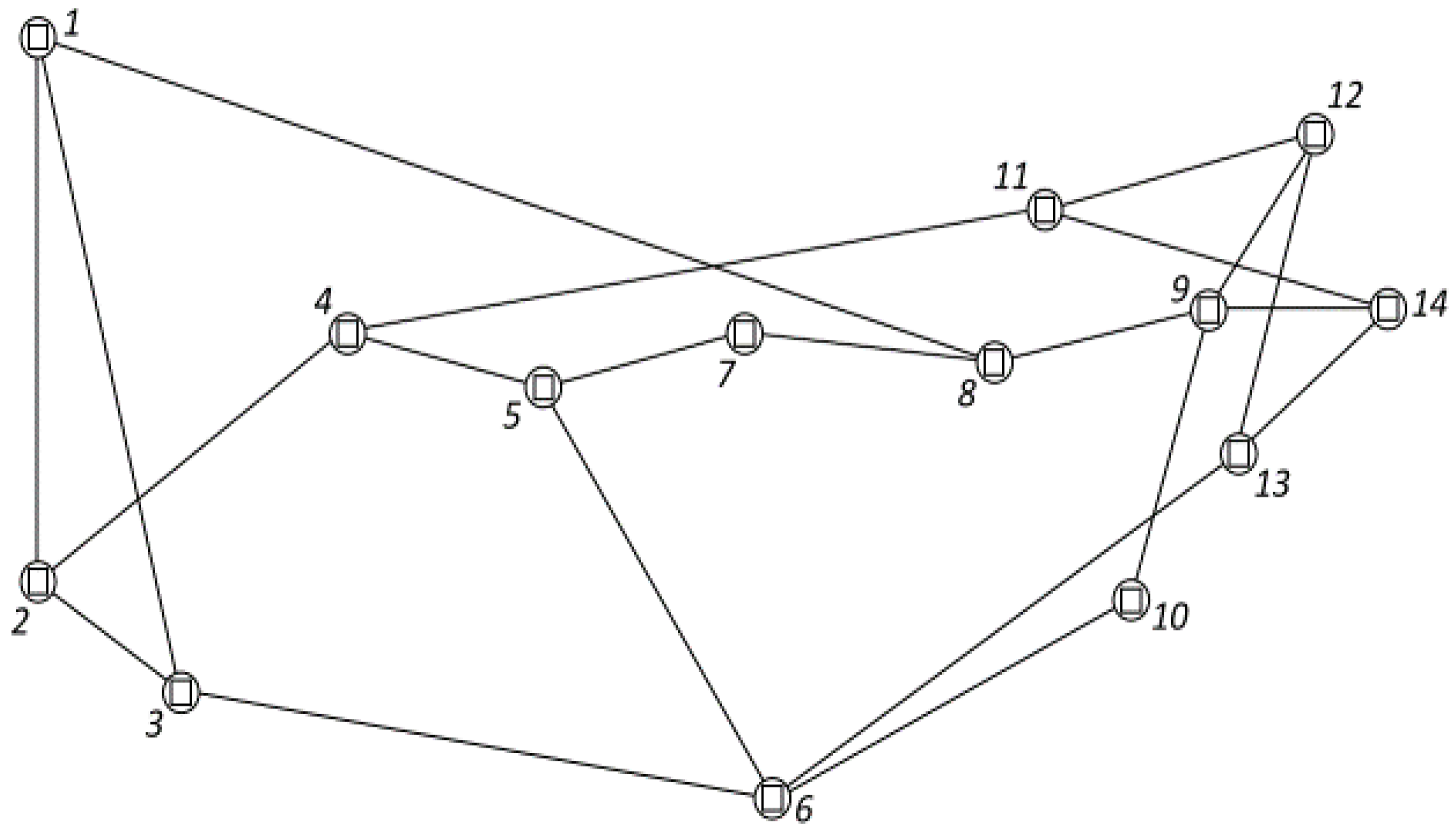
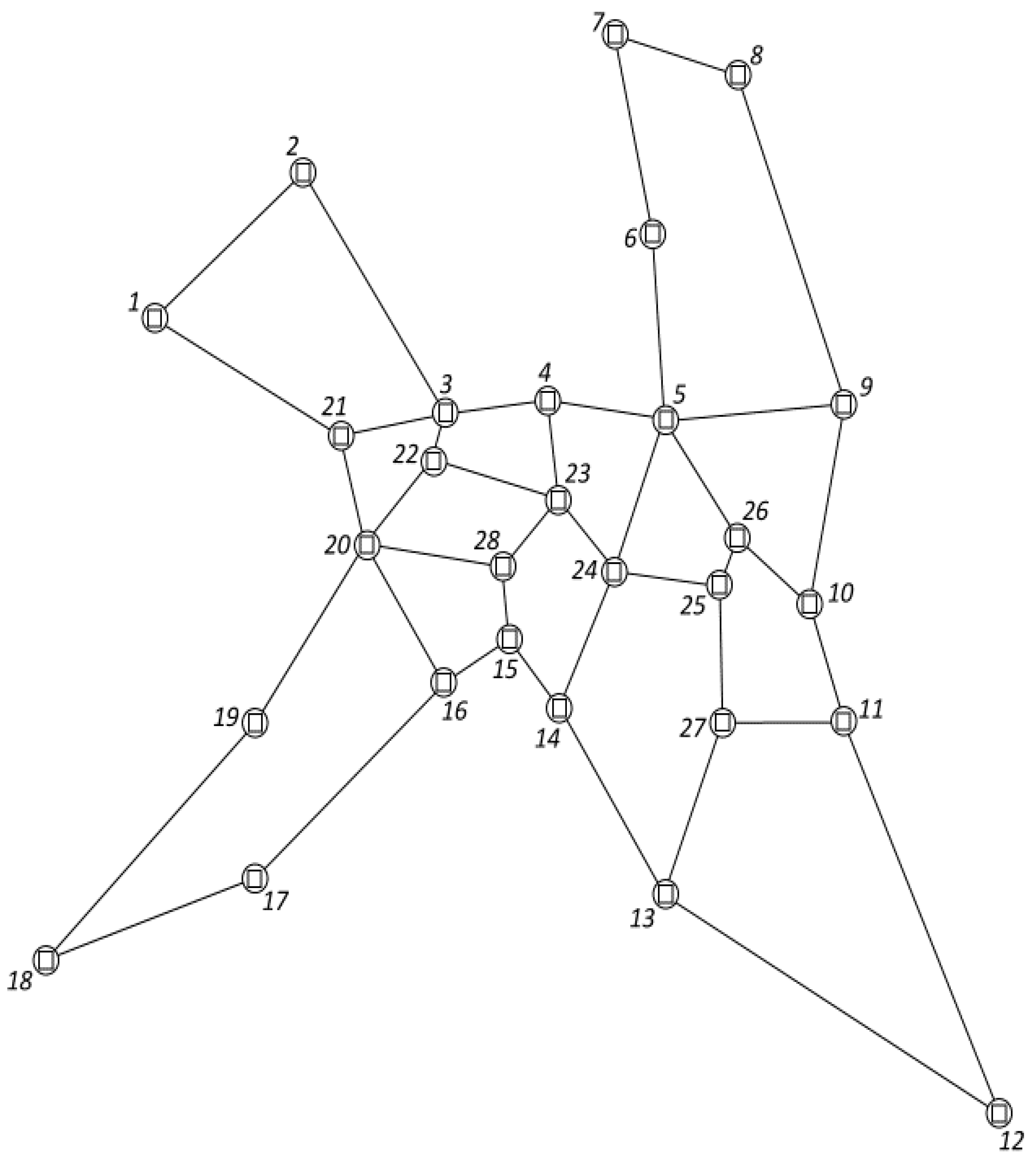
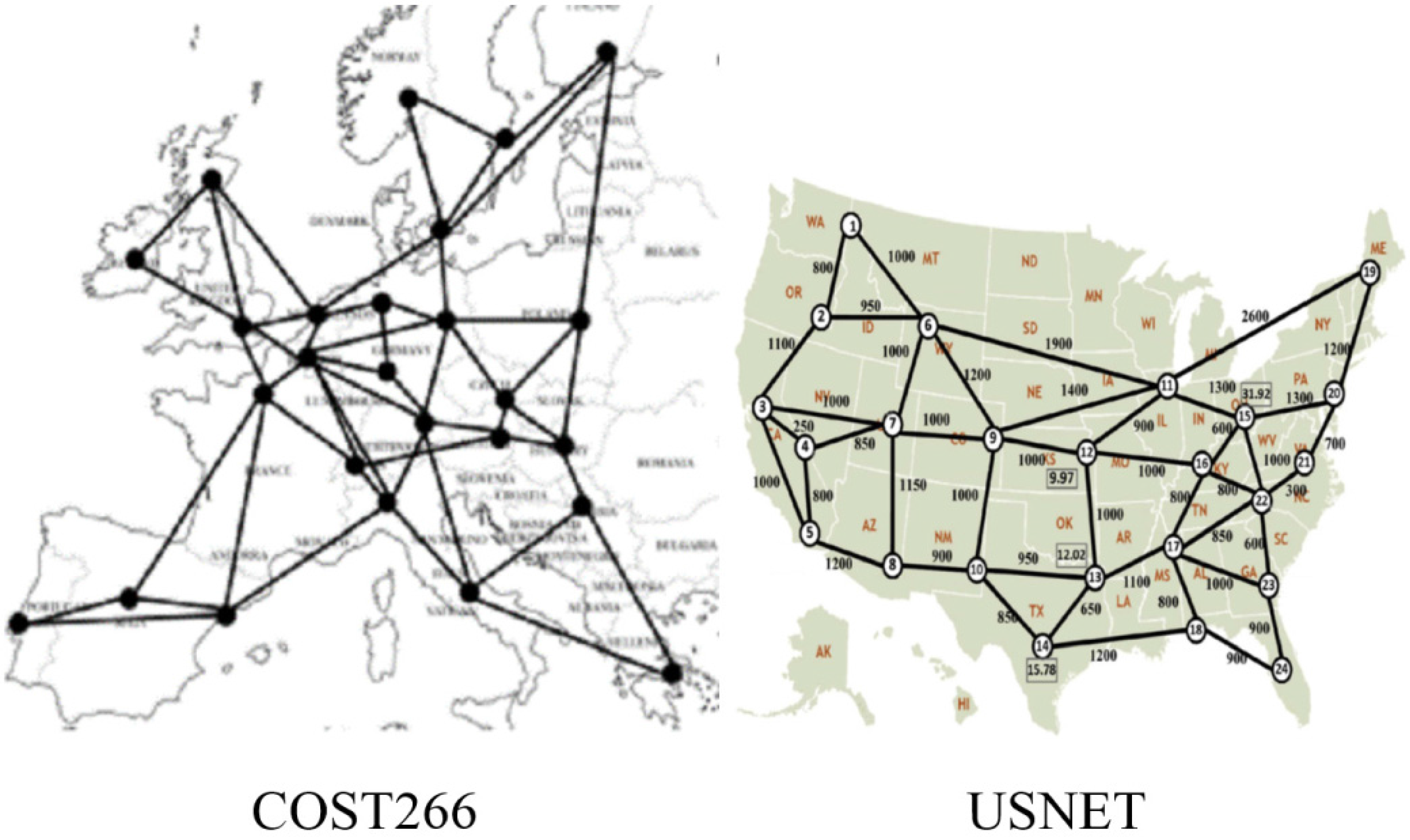
6. Testing and Evaluation
7. Extensions and Generalisations
GDRP-FON: Minimise C(r)[objective function] s.t. M, W [constraint]
AlgGV (calculate the viability matrix): ∀ij, setvij = Tif(hij ≤ mij) ∨ (∃k …l, … s.t. (pk ∧ … ∧ pl ∧ rk ∧ … ∧ rl = T) ∧ (hik ≤ mik ∧ … ∧ hlj ≤ mlj)); vij = Fotherwise
GDRP-FON is NP-hard since, for pk = T ∀k, dij = hij ∀ij and wij = mij = constant ∀ij, DRP-FON reduces to it. As before, a certificate for GDRP-FON can be verified in polynomial time by the following algorithm: run AlgGH run AlgGV if vij = T∀ij then certificate valid else certificate invalid Since GDRP-FON is NP-Hard and has polynomial time certificate verifiability, it is NP-complete.☐
AlgR (Optimise relay array): // GDRP-FON-heuristic setrk = F ∀k // All relays switched off run AlgGH // Calculate hop lengths run AlgGV // Calculate viable paths while ∃ij s.t. vij = F do // if more relays needed { find k s.t. |{i: (vik = T) ∧ (ri = F)}| // Find relay that ≥ |{ i: (vij = T) ∧ (ri = F)}| ∀j // … reaches the most nodes setrk = T // Power this new relay run AlgGV } // Recalculate viable paths
8. Conclusions and Future Work
- The algorithm may have to run, and frequently re-run, within the limited operating environment of production network equipment, implying that:
- The algorithm should be of polynomial complexity in both space and time (probably no worse than O(n3) steps and O(n2) memory).
Conflicts of Interest
References
- Yetginer, E.; Karasan, E. Regenerator Placement and Traffic Engineering with Restoration in GMPLS Networks. Photonic Netw. Commun. 2003, 6, 139–149. [Google Scholar] [CrossRef]
- Jinno, M.; Takara, H.; Kozicki, B.; Tsukishima, Y.; Sone, Y.; Matsuoka, S. Spectrum-Efficient and Scalable Elastic Optical Path Network: Architecture, benefits, and enabling technologies. IEEE Commun. Mag. 2009, 47, 66–73. [Google Scholar] [CrossRef]
- Yildiz, B.; Karasan, O.E. Regenerator Location Problem in Flexible Optical Networks. Available online: http://www.optimization-online.org/DB_HTML/2014/11/4659.html (accessed on 31 December 2015).
- Yildiz, B.; Karasan, O.E. Regenerators as Hubs. Trans. Res. Part B 2014, 94, 1823–1830. [Google Scholar]
- Essiambre, R.-J.; Kramer, G.; Winzer, P.J.; Foschini, G.J.; Goebel, B. Capacity Limits of Optical Fiber Networks. J. Light. Techbol. 2010, 28, 662–701. [Google Scholar] [CrossRef]
- Sen, A.; Murthy, S.; Bandyopadhyay, S. On Sparse Placement of Regenerator Nodes in Translucent Optical Networks. In Proceedings of the 2008 IEEE Global Telecommunications Conference, New Orleans, LA, USA, 30 November–4 December 2008; pp. 1–6. [Google Scholar]
- Le, H.-C.; Hasegawa, H.; Sato, K.-I. Performance Evaluation of Large-scale Multi-stage Hetero-granular Optical Cross-connects. Opt. Express 2014, 22, 3157–3168. [Google Scholar] [CrossRef] [PubMed]
- Jinno, M.; Kozicki, B.; Takara, H.; Watanabe, A.; Sone, Y.; Tanaka, T.; Hirano, A. Distance-Adaptive Spectrum Resource Allocation in Spectrum-Sliced Elastic Optical Path Network: Topics in optical communications. IEEE Commun. Mag. 2010, 48, 138–145. [Google Scholar] [CrossRef]
- Tomkos, I.; Palkopoulou, E.; Angelou, M. A Survey of Recent Developments in Flexible/Elastic Optical Networking. In Proceedings of the 2012 14th International Conference on Transparent Optical Networks, Coventry, UK, 2–5 July 2012; pp. 1–6. [Google Scholar]
- Chen, S.; Ljubic, I.; Raghavan, S. The Regenerator Location Problem. Networks 2009, 55, 205–220. [Google Scholar] [CrossRef]
- Yang, X.; Ramamurthy, B. Sparse Regeneration in Translucent Wavelength-Routed Optical Networks: Architecture, network design and wavelength routing. Photonic Netw. Commun. 2005, 10, 39–53. [Google Scholar] [CrossRef]
- Houlden, N.; Grout, V.; McGinn, J.; Davies, J. Extended End-to-End Cost Metrics for Improved Dynamic Route Calculation. In Proceedings of the 6th International Network Conference, Plymouth, UK, 11–14 July 2006. [Google Scholar]
- Grout, V.; Davies, J.N.; McGinn, J. An Argument for Simple Embedded ACL Optimisation. Comput. Commun. 2007, 30, 280–287. [Google Scholar] [CrossRef]
- Morgan, M. Optimisation Techniques for Wireless Networks. Ph.D. Thesis, Glyndŵr University, Wrexham, UK, 2010. [Google Scholar]
- Morgan, M.; Grout, V. Spanning Tree Objective Functions and Algorithms for Wireless Networks. In Proceedings of the 2006 IEEE Sarnoff Symposium, Princeton, NJ, USA, 27–28 March 2006; pp. 1–4. [Google Scholar]
- Grout, V. Principles of Cost Minimisation in Wireless Networks. J. Heuristics 2005, 11, 115–133. [Google Scholar] [CrossRef]
- Lucena, A.; Maculan, N.; Simonetti, L. Reformulations and Solution Algorithms for the Maximum Leaf Spanning Tree Problem. Comput. Manag. Sci. 2010, 7, 289–311. [Google Scholar] [CrossRef]
- Dijkstra, E.W. A Note on Two Problems in Connexion with Graphs. Numer. Math. 1959, 1, 269–272. [Google Scholar] [CrossRef]
- Garey, M.R.; Johnson, D.S. Computers and Intractability: A Guide to the Theory of NP-Completeness; Freeman: San Francisco, CA, USA, 1979. [Google Scholar]
- Gendron, B.; Lucena, A.; da Cunha, A.S.; Simonetti, L. Benders Decomposition, Branch-and-Cut and Hybrid Algorithms for the Minimum Connected Dominating Set Problem; Technical Report; Interuniversity Research Centre on Enterprise Networks, Logistics & Transportation: Montreal, QC, Canada, 2012. [Google Scholar]
- Morgan, M.; Grout, V. Metaheuristics for Wireless Network Optimisation. In Proceedings of the 2007 Third Advanced International Conference on Telecommunications, Morne, Mauritius, 13–19 May 2007; pp. 1–4. [Google Scholar]
- Barnhart, C.; Hane, C.A.; Vance, P.H. Using Branch-and-Price-and-Cut to Solve Origin-Destination Integer Multicommodity Flow Problems. Oper. Res. 2000, 48, 318–326. [Google Scholar] [CrossRef]
- Grout, V. Initial Results from a Study of Probability Curves for Shortest Arcs in Optimal ATSP Tours with Application to Heuristic Performance. In Proceedings of the 20th British Combinatorial Conference, Durham, UK, 10–15 July 2005; p. 93. [Google Scholar]
- Wagner, D.; Willhalm, T. Speed-up Techniques for Shortest-Path Computations. In Annual Symposium on Theoretical Aspects of Computer Science; Springer: Berlin/Heidelberg, Germany, 2007; pp. 23–36. [Google Scholar]
- Hulsermann, R.; Betker, A.; Jager, M.; Bodamer, S.; Barry, M.; Spath, J.; Gauger, C.; Kohn, M. A Set of Typical Transport Network Scenarios for Network Modelling. ITG FACHBERICHT 2004, 182, 65–72. [Google Scholar]
- Morgan, M. An Ant Colony Approach to Regenerator Placement with Fault Tolerance in Optical Networks. In Proceedings of the 2015 7th International Workshop on Reliable Networks Design and Modeling, Munich, Germany, 5–7 October 2015; pp. 85–91. [Google Scholar]
- Grout, V.; Houlden, N.; Davies, J.; McGinn, J.; Cunningham, S. A Unified Framework for Optimal Routing. Proceedings of CSSI International Conference System Integration in Integrated Europe (ISIE), Liberec, Czech Republic, 8–9 November 2004. [Google Scholar]
| m | US NSF a | COST-266 a |
|---|---|---|
| 1 | 1 | 2 |
| 2 | 1 | 1 |
| 3 | 1 | 2 |
| 4 | 0 | 1 |
| 5 | 1 | 0 |
| 6 | - | 1 |
| 7 | - | 0 |
| 8 | - | - |
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grout, V. A Simple Approach to Dynamic Optimisation of Flexible Optical Networks with Practical Application. Future Internet 2017, 9, 18. https://doi.org/10.3390/fi9020018
Grout V. A Simple Approach to Dynamic Optimisation of Flexible Optical Networks with Practical Application. Future Internet. 2017; 9(2):18. https://doi.org/10.3390/fi9020018
Chicago/Turabian StyleGrout, Vic. 2017. "A Simple Approach to Dynamic Optimisation of Flexible Optical Networks with Practical Application" Future Internet 9, no. 2: 18. https://doi.org/10.3390/fi9020018
APA StyleGrout, V. (2017). A Simple Approach to Dynamic Optimisation of Flexible Optical Networks with Practical Application. Future Internet, 9(2), 18. https://doi.org/10.3390/fi9020018





