Optimal Referral Reward Considering Customer’s Budget Constraint
Abstract
:1. Introduction
2. Literature Review
2.1. Referral Reward Programs
2.2. Budget Constraints
3. The Model and Result
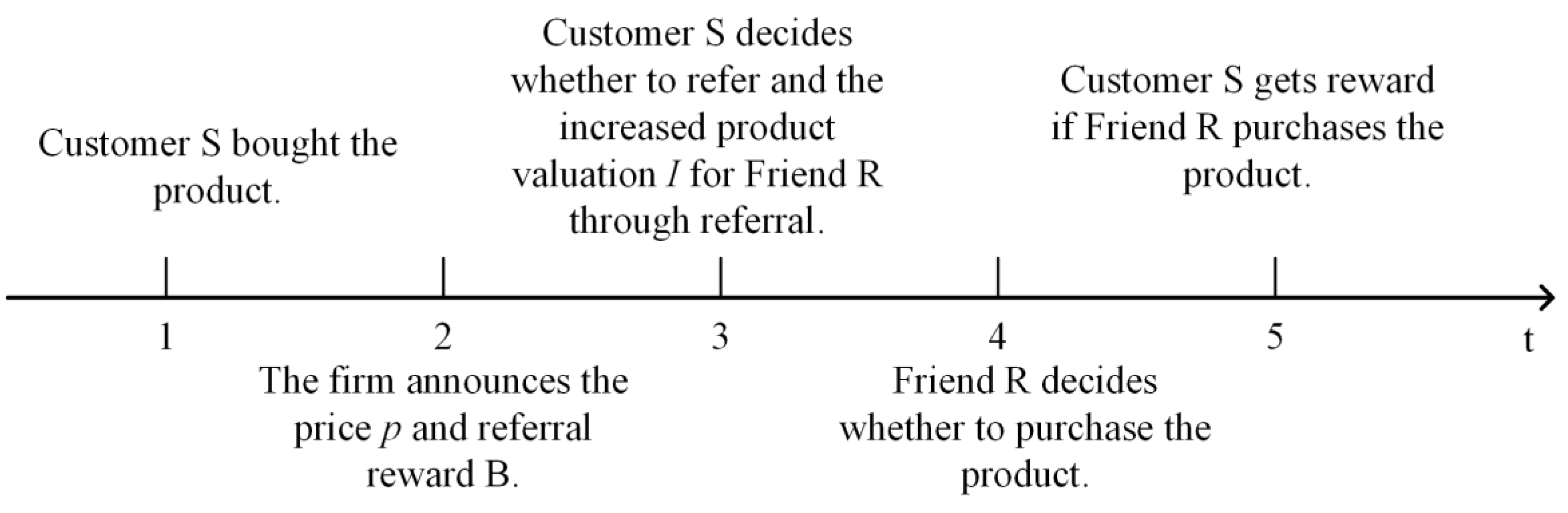
3.1. Friend R’s Problem
3.2. Customer S’s Problem
3.3. The Firm’s Problem
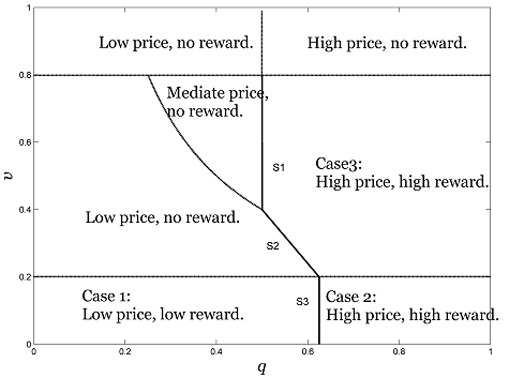
3.4. Analysis and Results
| Candidates | Price | Reward | Expected Profit |
|---|---|---|---|
| Candidate1 | |||
| Candidate2 | |||
| Candidate3 |
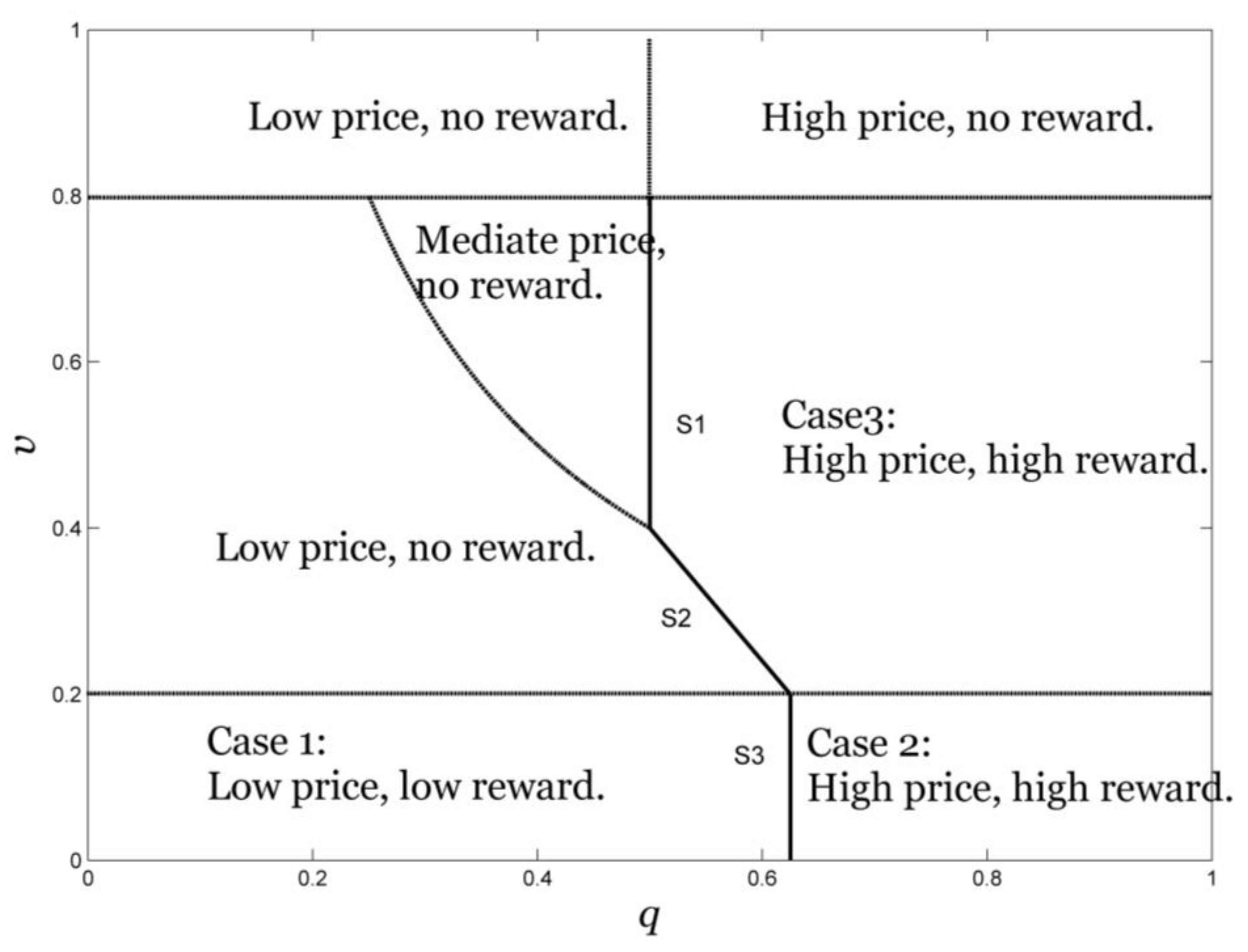
| Conditions | Optimal Price and Reward | |
|---|---|---|
| , ; | ||
| ,; | ||
| ,; | ||
| , . | ||
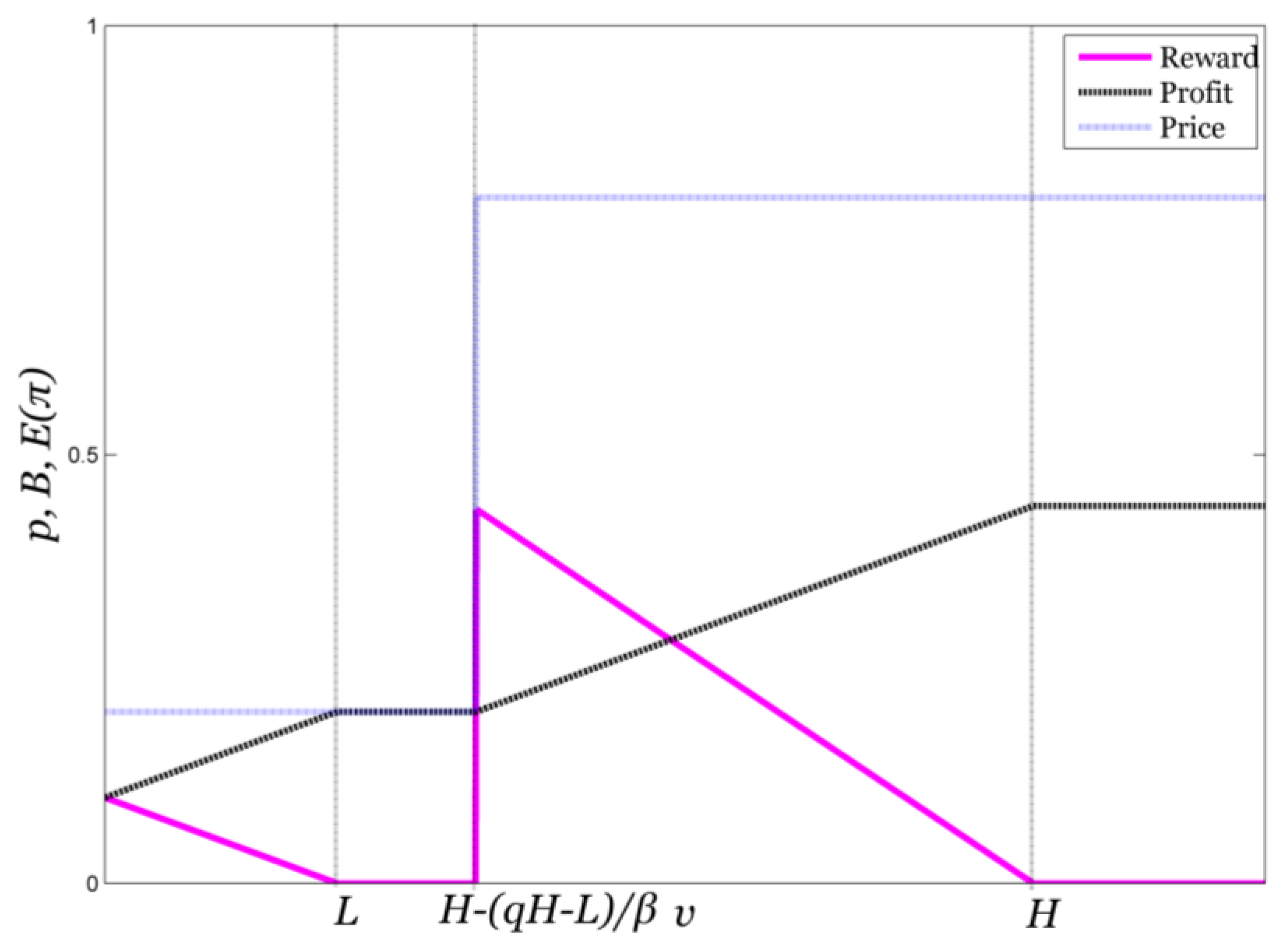
4. Firm Financing
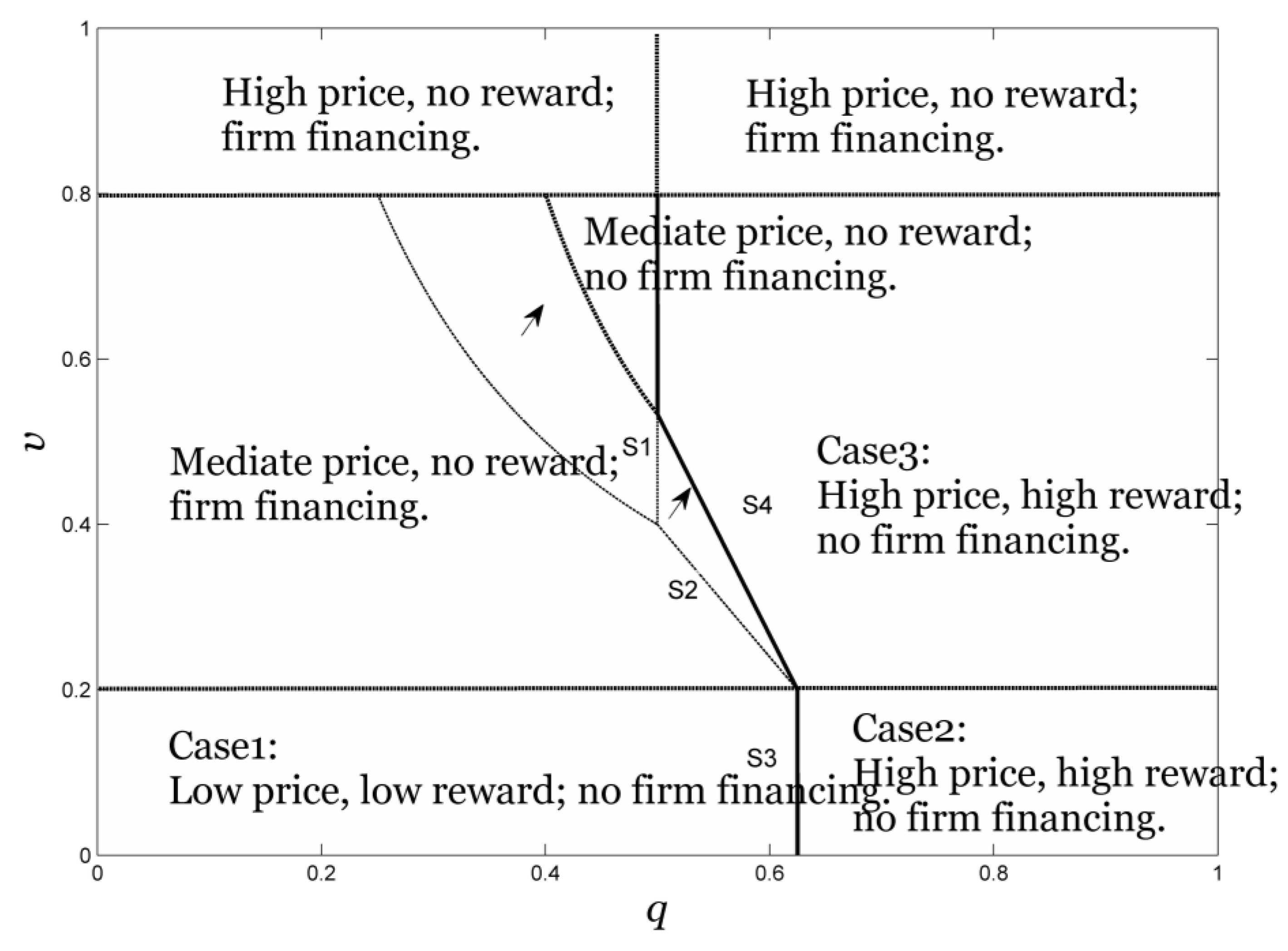
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix
| Case | Conditions | Optimal Priceand Reward |
|---|---|---|
| Case 1 | , | , , |
| Case 2 | , | , , |
| Case 3 | , , | ,, |
References
- Sen, A. Seller financing of consumer durables. Gen. Inf. 1998, 7, 435–460. [Google Scholar]
- Biyalogorsky, E.; Gerstner, E.; Libai, B. Customer referral management: Optimal reward programs. Mark. Sci. 2001, 20, 82–95. [Google Scholar] [CrossRef]
- Chen, Y.; Shi, M. The Design and Implications of Customer Recommendation Programs; Working paper; Stem School of Business, New York University: New York, NY, USA, 2001. [Google Scholar]
- Wirtz, J.; Chew, P. The effects of incentives, deal proneness, satisfaction and tie strength on word-of-mouth behaviour. Int. J. Serv. Ind. Manag. 2002, 13, 141–162. [Google Scholar] [CrossRef]
- Xiao, P.; Tang, C.S.; Wirtz, J. Optimizing referral reward programs under impression management considerations. Roan J. OraonalRarh 2011, 215, 730–739. [Google Scholar] [CrossRef]
- Jin, L.; Huang, Y. When giving money does not work: The differential effects of monetary versus in-kind rewards in referral reward programs. Int. J. Res. Mark. 2014, 31, 107–116. [Google Scholar] [CrossRef]
- Ryu, G.; Feick, L. A penny for your thoughts: Referral reward programs and referral likelihood. J. Mark. Q. Publ. Am. Mark. Assoc. 2007, 71, 84–94. [Google Scholar] [CrossRef]
- Lobel, I.; Sadler, E.D.; Varshney, L.R. Customer Referral Incentives and Social Media. Available online: http://ssrn.com/abstract=2520615 or http://dx.doi.org/10.2139/ssrn.2520615 (accessed on 18 November 2015).
- Garnefeld, I.; Eggert, A.; Helm, S.V.; Tax, S.S. Growing existing customers’ revenue streams through customer referral programs. J. Mark. 2013, 77, 17–32. [Google Scholar] [CrossRef]
- Kuester, M.; Benkenstein, M. Turning dissatisfied into satisfied customers: How referral reward programs affect the referrer’s attitude and loyalty toward the recommended service provider. J. Retail. Consum. Serv. 2014, 21, 897–904. [Google Scholar] [CrossRef]
- Kumar, V.; Andrew, P.J.; Leone, R.P. How valuable is word of mouth? Harv. Bus. Rev. 2007, 85, 185–196. [Google Scholar]
- Tuk, M.A.; Verlegh, P.W.J.; Smidts, A.; Wigboldus, D.H.J. Sales and sincerity: The role of relational framing in word-of-mouth marketing. Gen. Inf. 2008, 19, 38–47. [Google Scholar] [CrossRef]
- Kornish, L.J.; Li, Q. Optimal referral bonuses with asymmetric information: Firm-offered and interpersonal incentives. Mark. Sci. 2010, 29, 108–121. [Google Scholar] [CrossRef]
- Jing, X.; Xie, J. Group buying: A new mechanism for selling through social interactions. Manag. Sci. 2011, 57, 1354–1372. [Google Scholar] [CrossRef]
- Hauser, J.R.; Urban, G.L. The value priority hypotheses for consumer budget plans. J. Consum. Res. 1986, 12, 446–462. [Google Scholar] [CrossRef]
- Che, Y.-K.; Gale, I. The optimal mechanism for selling to a budget-constrained buyer. J. Econ. Theory 2000, 92, 198–233. [Google Scholar] [CrossRef]
- Salant, D.J. Up in the air: Gte’s experience in the mta auction for personal communication services licenses. J. Econ. Manag. Strateg. 1997, 6, 549–572. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, D.; Yao, Z. Optimal Referral Reward Considering Customer’s Budget Constraint. Future Internet 2015, 7, 516-529. https://doi.org/10.3390/fi7040516
Zhou D, Yao Z. Optimal Referral Reward Considering Customer’s Budget Constraint. Future Internet. 2015; 7(4):516-529. https://doi.org/10.3390/fi7040516
Chicago/Turabian StyleZhou, Dan, and Zhong Yao. 2015. "Optimal Referral Reward Considering Customer’s Budget Constraint" Future Internet 7, no. 4: 516-529. https://doi.org/10.3390/fi7040516
APA StyleZhou, D., & Yao, Z. (2015). Optimal Referral Reward Considering Customer’s Budget Constraint. Future Internet, 7(4), 516-529. https://doi.org/10.3390/fi7040516